0 引言
地基逆合成孔径雷达(Inverse Synthetic Aperture Radar，ISAR)可全天时、全天候对目标进行远距离观测，获得目标的高分辨率雷达图像，进而反演目标的结构和外形等特征，有着非常广泛的应用[1-4]。月球作为距离地球最近的自然天体和地球唯一的天然卫星，具有极高的科学研究价值，一直是天文探测和天体研究中的首选目标[5]。由于发射月球探测卫星对月球进行观测成本昂贵、技术复杂，而利用地基雷达对月球进行观测和成像处理，不受地球气象、光照等条件限制，雷达成像分辨率也和地月之间距离无关。因此，从1946年至今，国内外已开展了一系列地基雷达月球观测试验[6-13]。
1946年，美国海军某地基雷达站首次获得了月球的雷达回波，由此拉开了地基雷达月球探测的序幕[6]。文献[7]利用美国Haystack雷达发射X波段雷达信号(波长3.8 cm)对月球进行探测，反演了月球表面火山口分布以及大型岩浆流等月球表面地形地貌。基于Arecibo和Green Bank望远镜双基体制[7-8]或Arecibo望远镜单发单收体制[9]，国外学者利用合成孔径雷达分块聚焦技术，实现了长相干时间的快速距离徙动校正和方位聚焦，获得了月球正面的雷达图像，月面及次表层月壤的介电特征和月岩分布等地质特征。文献[10]和[11]利用金石太阳系雷达开展了月球探测试验，获得了月球正面20 m分辨率图像，并分析了不同调制信号形式下的成像性能。文献[12]利用中国深空探测网干涉测量系统和地基雷达协同探测的方式进行了月球探测试验，获得了嫦娥三号着陆点区域月面回波频谱及多普勒频移，反演了雷达反照率与回波圆极化率，进而获得了月球表层波长量级的月面粗糙度反演结果。与国外相比，我国的地基雷达月球探测理论研究与试验起步较晚，相比双基探测时对高精度时频同步和波束指向一致性等的要求，单基体制均无需考虑，因此，本文从单基逆合成孔径雷达成像角度构建了月球观测的等效转台几何模型，分析了月面上等效散射中心与雷达站径向距离的变化特性，给出了雷达信号参数的设计准则和ISAR成像算法流程，并通过仿真实验验证了本文分析的有效性。
1 月球单基ISAR观测模型
地基雷达对月球观测模型如图1所示，地球存在自转，自转角速度为ωe，月球在绕地球公转的同时，其自身也在作自转运动，并且其自转周期和公转周期一致，也就是说月球自转平均角速度和公转平均角速度相等。因此，若将月球公转轨道看作一个标准圆的话，月球将严格仅有一面朝向地球。
图 1 地基ISAR系统对月球观测示意图
为了简化观测模型和运动分析，本文将地球和月球均看作标准球，地球半径为re，月球半径为rl，假设地球自转轴和月球自转轴平行，月球公转轨道面和赤道面平行[13]。同时，由于ISAR成像所需的相干积累时间相对于地球公转周期来说通常小得多，在地基ISAR对月球观测过程中不考虑地球公转运动。并且，可将月球公转轨道面看作标准的圆轨道。因此，可构建如图 2(a)所示的地球单基ISAR系统对月球观测示意图。构建地心惯性坐标系Oe-XYZ和月球固定坐标系Ol-UVW，其中，Oe和Ol分别为地球中心和月球中心，在观测的初始时刻，OeY、OlV和OeOl轴方向平行，OeZ轴和OlW轴分别为地球和月球自转轴方向，OeX轴和OlU轴分别由右手定则确定。在观测过程中，Oe-XYZ并不随地球的自转而转动，Ol-UVW则与月球保持姿态不变。假设观测初始时刻地基ISAR在Oe-XYZ坐标系中的方位角、俯仰角和距地面高度分别为θrd、φrd和0，那么初始时刻地基ISAR系统在地球惯性坐标系中的坐标为
(1)
式中，T表示向量或矩阵转置，上标(e)表示该坐标值是地球惯性坐标系下的。在月球固定坐标系下，不考虑月球表面起伏，假设月球表面某散射中心的方位角和俯仰角分别为θl和φl，则该点在月球固定坐标系下的坐标为
(2)
式中，上标(l)表示该坐标值是月球固定坐标系下的。根据图2(a)所示观测模型，可知初始时刻该散射中心在地心惯性坐标系中的坐标为
(3)
式中，b=[0,h,0]T为初始观测时刻月心在地心惯性坐标系中的坐标。
在观测时刻t，地基ISAR系统在地心惯性坐标系中的坐标变为
(4)
式中，Re(t)为地球自转对应的基本旋转矩阵，旋转角度为ωet。由于月球公转角速度和自转角速度严格相等，月球可看作绕地心以月球公转角速度ωl作旋转运动，因此，在观测时刻t月面上散射中心在地心惯性坐标系中的坐标值为
(5)
式中，Rl(t)为月球自转对应的基本旋转矩阵，旋转角度为ωlt。在式(4)和式(5)的两端分别乘以
即可将月球的公转和自转引起的散射中心坐标变化转化到地基ISAR系统绕地球自转轴的转动中，此时地基ISAR系统对月球成像模型可转化为如图2(b)所示的等效地基ISAR转动观测模型。与ISAR成像中经典的绕目标中心的转动模型略有不同，在图2(b)所示的观测模型中，雷达绕地球自转轴转动而观测目标保持姿态不变。此时，地基ISAR系统绕地球以ωe-ωl的角速度由西向东进行旋转，图 2(b)所示的模型可进一步转化为图2(c)所示的等效转台模型，平行雷达-月心连线的速度分量在ISAR成像处理时可统一补偿掉，垂直雷达-月心连线的速度分量等效为图2(c)中月球以ωf的旋转角速度绕月心作旋转运动，其中，OlV′由雷达指向月心，OlW′与OeZ、OlV′共面且垂直于OlV′，OlU′根据右手定则确定。根据上述分析，可获得ωf的表达式为
(a) 地基ISAR对月球平面观测模型
(b) 等效地基ISAR转动观测模型 (c) 等效转台模型
图2 简化的地基ISAR系统对月球观测模型
(6)
在式(6)中，由于地月之间距离远大于地球半径，因此近似认为雷达与月心连线方向和OeOl方向平行，rrd为雷达与月心在初始观测时刻的距离。对于月球观测来说，在雷达初始观测时刻方位角为90°、俯仰角为0°时其月面散射中心的等效转动角速度最大，此时在相同的相干积累时间内月球等效转动角度最大，方位成像分辨率最高。在图 2(c)所示转台模型下，对于月面上一点，其初始观测在Ol-U′V′W′坐标系下的方位角和俯仰角分别为
和
则在Ol-U′V′W′坐标系下，雷达与月面上散射中心在观测时刻t的瞬时斜距可近似表示为
(7)
式中，r0(t)为月心与雷达的瞬时距离，u′和v′分别为该散射中心在OlU′轴和OlV′轴上的坐标值。α和β分别为月球等效旋转运动引起的散射中心径向距离变化速度和加速度，其表达式可由二阶泰勒展开推导得到：
(8)
(9)
由式(7)可知，月面散射中心的瞬时多普勒为
(10)
式(10)最右边第一项表明，月面散射中心多普勒的大小和该散射中心在OlU′轴的坐标成正比，也就是说，ISAR成像结果中的等多普勒面是垂直于OlU′轴的，该分析结果与国内外学者利用合成孔径雷达成像原理进行月面成像模型的分析结果是一致的[8]。式(10)最右边第二项表明月面散射中心多普勒变化率与该散射中心在OlV′轴的坐标成正比，也就是说，月面散射中心多普勒变化率仅和当前散射中心所处的距离单元有关系，使得相同距离单元内的回波在方位成像时可使用相同的高阶相位补偿系数进行聚焦成像。
2 信号模型与ISAR成像算法
国内外已开展了一系列针对月球的地基雷达探测试验，成功获得了月球的探测回波[6-13]，表明了基于现有地基雷达开展月球探测的可行性，因此本文对于雷达天线和功耗等系统参数的设计不作讨论。由于现有研究多基于双基体制，因而本文重点针对月球尺度下地面单基体制雷达的信号参数设计准则进行分析，并给出地面单基雷达对月球的成像处理流程，为基于我国现有地基雷达系统开展月球探测试验时的信号参数设计提供参考。
2.1 雷达信号参数设计
1) 重复频率
雷达重复频率不仅需要满足月球径向距离深度的要求，还要满足月面照射区域多普勒不混叠的限制。雷达发射的电磁波最大仅能照射月球半个球面，因此月面回波在径向距离向的深度不会超过月球平均半径rl，因而，雷达重复频率需要满足下式：
(11)
同时，雷达发射信号的重复频率需要满足月球成像方位多普勒不混叠的条件，即
(12)
式中，θbeam表示雷达波束宽度。对于单基ISAR系统来说，由于地月之间距离较远，月球回波会相比当前脉冲周期延迟一定数量的脉冲重复周期。因此，需要确保月面回波不会与后续天线的发射时间区间重叠，使得天线具备接收月球回波的时间窗口。因此，重复频率还需满足如下条件：
式中，
表示对元素向下取整，hsub-rd表示雷达到月面最近点的距离。综上所述，重复频率需要同时满足式(11)～(14)所示的约束条件，才能成功实现月球回波的接收和后续处理。
2) 载频
雷达的工作频率越高，波长越短，而波长的长度决定了电磁波对月球表面的探测深度，通常波长越短，对月面的穿透性越差，波长越长，对月球表面的穿透性越强[6]。同时，根据式(10)，月面回波的多普勒谱宽与雷达载频有关，载频越高，多普勒谱宽越宽，因此，雷达载频具体频点的选择需要结合探测需求、探测场景等与重复频率综合考虑。
3) 脉冲宽度
雷达发射信号的脉冲宽度太短，会使得雷达发射电磁波信号能量不足，雷达回波的信噪比较低，不利于后续成像。同时，根据式(13)和式(14)，脉冲宽度的设置又会影响到重复频率选择，在实际的观测方案设计中，可根据回波信噪比需求首先设置脉冲宽度的值，然后再计算重复频率的选择范围，设计重复频率的值。
4) 带宽
ISAR成像的距离分辨率与发射信号带宽直接相关，带宽越大，ISAR成像距离维分辨率越高，然而，较高的距离分辨率也会使得月面上散射中心的越距离单元徙动现象更加明显，给后续的ISAR成像算法带来挑战。因此，成像带宽的选择应根据月球成像分辨率的需求合理选择。
5) 采样频率
在ISAR成像处理中，通常可利用匹配滤波和去斜处理两种方式实现脉冲压缩处理，由于月球尺寸相比空间目标大得多，去斜处理在降低采样频率方面的优势将不再具备。而且，去斜处理中月面不同区域回波在时间上并不对齐，不利于方位成像处理。因此，本文采用匹配滤波方式实现脉冲压缩处理，根据奈奎斯特采样定理，采样频率一般取1.2倍的发射信号带宽。
2.2 回波信号模型
在ISAR成像中，雷达一般发射线性调频信号，假设雷达天线波束照射范围内月面上共有K个等效散射中心，每个散射中心在Ol-U′V′W′坐标系中的方位角和俯仰角分别为θk和φk，根据式(7)可计算获得每个散射中心与雷达的瞬时距离rk(t)，则ISAR接收到的月球回波可表示为
s(τ,t)=
exp{jπγ(τ-2rk(t)/c)2}·
(15)
式中，σk表示散射中心k的后向散射系数，ar[·]为距离窗函数，一般为矩形窗函数,τ表示距离维快时间，TP为发射信号的脉冲宽度，γ为调频斜率，fc为雷达发射信号载频，c为电磁波的传播速度。接着，利用匹配滤波对上述回波进行脉冲压缩处理，其中参考距离选取月球上雷达下点到雷达测站的瞬时距离序列，可得到距离压缩后的回波表达式为
s(τ,t)=
(16)
式中，
为脉冲压缩后每个散射中心幅度，B为信号带宽，Δrk(t)为散射中心到雷达瞬时距离与参考距离的差值。根据式(7)～(9)，Δrk(t)可近似表示为
(17)
式中，
和
为月面上第k个散射中心的坐标值。上式右边第二项和第三项在包络中会引起距离走动和弯曲，一般在设计地基ISAR系统对月球的观测方案时，可以通过相干积累时间和雷达参数的合理选择，使得距离弯曲不超过1/2个距离分辨单元，从而在包络中忽略距离弯曲的影响，线性走动项可通过Keystone变换对越距离单元徙动(Migration Through Range Cells，MTRC)项进行校正。同时，第三项对相位的影响不可忽略，在方位成像时会引起多普勒模糊，可利用基于调频率搜索的方位高阶相位校正方法实现高阶相位的估计和补偿。
2.3 成像算法
根据上文分析，利用地基ISAR系统对月球进行观测，基本原理和ISAR系统对卫星等空间目标的观测原理一致。但是由于月球远距离、大尺度特性，使得地基ISAR系统雷达参数设置需要综合考虑月球延迟深度、雷达波束宽度和多普勒谱宽等因素的影响。本文提出的地基ISAR系统参数设置与月球成像流程如图3所示。
图3 地球单基ISAR对月球观测回波成像流程图
3 仿真实验与分析
3.1 仿真场景设置
仿真雷达工作频率为3 GHz，波长为0.1 m，发射的线性调频信号带宽为1.5 MHz，脉冲宽度为0.1 ms，天线的波束宽度为0.2°。为了利用最少的相干积累时间获得最大的等效转动角度，令ISAR系统初始观测时刻的方位角为90°，俯仰角为30°，也就是说，在月球处于雷达的“过顶”弧段时进行观测。成像仿真所用的地月轨道和运动参数如下：月球公转轨道半径取为388 440 km，平均公转和自转周期为2.66×10-6 rad/s，地球半径为6 378.137 km，地球自转周期为7.27×10-5 rad/s。根据式(11)～(12)，可得到雷达重复频率的上界和下界分别为86.3 Hz和27.01 Hz，为了方便计算，选取整数点的重复频率值，代入式(13)和(14)中，即可得到合理的重复频率值，本文设定雷达发射信号的重复频率为28 Hz。为了避免月球成像中的南北模糊现象，令天线波束中心的下沿与雷达下点持平，也就是说雷达天线波束在月面上照射的区域均分布在雷达下点以上，不会出现南北模糊现象。根据雷达测站位置，若想获得和距离分辨率相当的方位分辨率，所需要的相干积累时间约为490 s，对应的积累回波数为13 712次。仿真所用的点目标模型所处坐标系为Ol-U′V′W′，沿OlU′轴和OlV′轴均匀分布，每个点散射中心OlW′的坐标根据月球半径计算得到。假设ISAR系统在月球观测过程中可根据月球轨道信息自适应调整波束指向，确保天线波束始终指向月球相同区域。仿真所用的点目标模型如图 4所示。
图4(a)所示为点目标在Ol-U′V′W′坐标系中的三维位置，图4(b)为点目标在Ol-U′V′平面的投影位置，根据式(7)～(9)的分析，点目标在OlU′轴和OlV′轴的坐标分别决定了点散射中心的多普勒大小和与雷达的径向距离，因此，可将图4(b)作为点目标的理论成像结果，用来对本文所提成像算法的有效性进行分析。
3.2 ISAR成像仿真与分析
根据ISAR系统参数，ISAR成像距离向分辨单元为83 m，方位向多普勒分辨率约为0.002 Hz，根据仿真场景设置，可计算得到点散射中心在相干积累时间内最大线性走动约为319 m，横跨约4个距离单元，最大距离弯曲约为0.018 m，远小于距离分辨单元的大小，因此，在图3所示成像流程中，仅需利用一阶Keystone变换校正线性的MTRC即可。但是，距离弯曲引起的多普勒展宽不能忽略，相干积累时间内距离弯曲引起的多普勒展宽约为0.003 Hz，约占1.5个多普勒分辨单元，需要在ISAR方位成像时进行消除，提高成像结果聚焦度。利用图3所示成像处理流程对仿真数据进行处理的结果如图 5所示。
图5 仿真数据处理结果及对比
图5(a)所示为原始雷达回波数据匹配滤波之后的结果，图5(b)为相对径向距离-9 500 m左右处的距离压缩结果局部图，可看出存在明显的MTRC现象。通过一阶Keystone变换可消除线性MTRC现象，图5(c)为校正之后的距离压缩局部结果，与图5(b)对比可以看出，MTRC现象得到了校正。图5(d)为原始雷达回波数据直接应用两维傅里叶变换获得的成像结果，图5(g)为应用图3所示流程获得的成像结果，为了清晰对比本文所提算法对MTRC和距离弯曲引起的多普勒展宽的校正效果，选取图5(d)中的A、B点和图 5(g)中的C、D点，其中A点和C点是同一个散射中心，其成像结果分别如图5(e)和(h)所示，通过对比可以看出由于线性MTRC的存在，图5(e)中散射中心的成像结果横跨多个距离分辨单元，无法聚焦，经过校正后，图5(h)所示的成像结果则聚焦良好。B点和D点是同一个散射中心，其成像结果分别如图5(f)和(i)所示，通过对比可以看出图5(i)所示成像结果方位向的聚焦度更好。上述成像结果对比表明了本文所提成像算法的有效性。
根据ISAR系统参数及仿真场景设置，利用式(6)可计算得到月球相对雷达视线的等效转动角速度约为1.02×10-6 rad/s，据此，可计算得到方位向的分辨率为100 m，与3.1节设置相干积累回波次数使方位向分辨率与距离向分辨率一致的考虑相吻合，定标后的成像结果如图6(a)所示，与图4(b)所示的点目标分布一致。选取图4(b)中点目标沿OlV′轴从上到下第8行散射中心和沿OlU′轴从左到右第13列散射中心为基准，对比图6(a)中相同位置散射中心的分布情况，对比结果分别如图6(b)和(c)所示，可以看出，ISAR成像结果中点目标的相对位置分布与仿真场景一致，进一步验证了本文理论分析及成像算法的有效性。
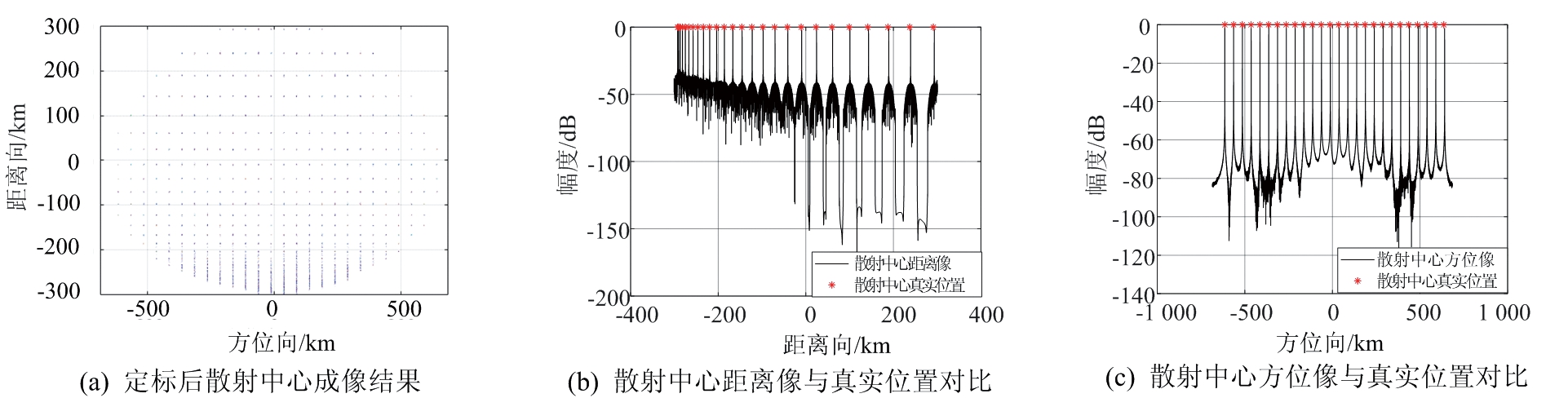
图6 定标后ISAR成像结果及与仿真场景的对比
4 结束语
基于地基雷达的月球探测不受光照限制，具有一定的穿透性，可全天时全天候地对月球表面及浅表层进行高分辨成像，具有周期短、可重复性高、经济、灵活等优点。国内外基于地基雷达的月球成像多是利用雷达和射电望远镜组合方式进行，对地面单基雷达月球成像的信号参数设计和成像方法的研究较少。本文在国内外地基雷达月球探测技术的基础上，从ISAR成像的角度详细推导了地球单基雷达对月球观测的成像和信号模型，对地球单基雷达月球成像的系统参数设计进行了理论分析并提出合理建议，可为我国对月地面单基雷达探测提供技术基础，推进我国深空探测技术的发展。
[1] NING Y, ZHOU F, BAI X, et al. A Method for 3-D ISAR Imaging of Space Debirs[J]. IEEE Trans on Aerospace and Electronic Systems, 2019, 55(2):864-876.
[2] ZHOU F, TIAN X D, WANG Y, et al. High Resolution ISAR Imaging Under Low SNR with Sparse Stepped-Frequency Chirp Signals[J]. IEEE Trans on Geoscience and Remote Sensing, 2021, 59(10):8338-8348.
[3] CHEN V C, MARTORELLA M. Inverse Synthetic Aperture Radar Imaging[M]. 胡明春, 孙俊, 译. 北京:国防工业出版社, 2020.
[4] 朱晓秀,胡文华,郭宝锋,等.基于快速SBL的双基地ISAR成像[J]. 雷达科学与技术, 2019,17(3):289-298.ZHU Xiaoxiu，HU Wenhua，GUO Baofeng，et al. Bistatic ISAR Imaging Based on Fast SBL Algorithm with Sparse Apertures[J]. Radar Science and Technology, 2019,17(3):289-298. (in Chinese)
[5] 金亚秋, 法文哲. 行星微波遥感理论方法与应用[M]. 北京:科学出版社, 2019.
[6] 丁春雨, 封剑青, 郑磊, 等. 雷达探测技术在探月中的应用[J]. 天文研究与技术, 2015, 12(2):228-242.
[7] ZISK S H, PETTENGILL G H, CATUNA G W. High-Resolution Radar Maps of the Lunar Surface at 3.8-cm Wavelength[J]. Moon, 1974, 10(1):17-50.
[8] CAMPBELL B A, CAMPBELL D B, MARGOT J L, et al. Focused 70-cm Wavelength Radar Mapping of the Moon[J]. IEEE Trans on Geoscience and Remote Sensing, 2007, 45(12):4032-4042.
[9] STACY N J S, CAMPBELL D B, FORD P G. Arecibo Radar Mapping of the Lunar Poles: A Search for Ice Deposits[J]. Science,1997,276(5318):1527-1530.
[10] HESLEY S, GURROLA E, ROSEN P, et al. An Improved Map of the Lunar South Pole with Earth-Based Radar Interferometry[C]∥2008 IEEE Radar Conference, Rome, Italy:IEEE, 2008:1-6.
[11] QUIRK K J, SRINIVASAN M. GSSR Waveforms for Lunar Observations[J]. Interplanetary Network Progress Report, 2013, 192(42):1-46.
[12] SUN J, PING J, BONDARENKO Y, et al. Promoting Earth-Based Radar Astronomical Observations of the Moon[J]. Sensors, 2020, 20(7):1874-1880.
[13] 郑磊. 地基雷达对月成像数据处理方法研究[D]. 北京:中国科学院国家天文台, 2011.
