0 引言
当脉冲雷达使用简单长脉冲对目标进行检测时，距离分辨率取决于发射的脉冲长度，如果想要更高的距离分辨率就要减小脉冲长度，但是这同时会降低回波信号强度。这就导致了一个矛盾，高距离分辨率意味着牺牲信号强度，而想要强的信号就要牺牲距离分辨率。为了解决这一问题，各种调制波形以及相应的匹配滤波器被设计出来，即通过发射脉冲长度较长的调制波形来获取较高的信号强度，在接收到信号后通过匹配滤波对其进行脉冲压缩处理，将信号的能量压缩到较小的距离分辨率单元中，从而达到提升距离分辨率的同时又保留信号强度的目的。
根据探测目标特性的不同，发射信号的调制方式也有很多种，通常情况下的空间硬目标探测都是使用线性调频信号。通过发射频率调制后的信号，并对接收信号进行脉冲压缩处理得到高分辨率的目标信息，获得的距离分辨率取决于信号带宽。而对于电离层这种软目标的非相干散射探测，则会用到更复杂的编码方式，比如多脉冲编码[1-2]、相位编码[3]、交替码[4-6]等，来达到探测要求。
众多波形调制方式中相位编码使用得较为广泛，巴克码是相位调制编码中常用的一种[7]。巴克码将一个脉冲长度分成了若干个码元长度(目前最多能达到13位)，每个码元都被0°(+1)或180°(-1)的相位以特定的方式调制。在收到回波后需要进行解码，通常情况下都是使用匹配滤波器(Matched Filter，MF)进行解码，即使用发射脉冲包络的镜像码作为滤波器函数对回波进行卷积处理。以这种方式解码后的信号可以达到最佳信噪比，距离分辨率取决于巴克码的码元宽度，且信号强度是对应整个巴克码脉冲长度所积累的能量。虽然巴克码的匹配滤波性能已经很好，但它仍存在旁瓣问题，在一些特定情况下会对目标检测带来许多干扰。比如在检测一个较强的点目标回波时，巴克码的旁瓣会将点目标回波扩散到周围的距离门，使得距离分辨率达不到预期，而且目标距离估计不准确。
关于巴克码匹配滤波的旁瓣问题已经有很多研究提出了解决办法，比如可以在标准的MF之后放置一个设计好的加权网络来有效抑制旁瓣效应，甚至可以找到一种实现无旁瓣脉冲压缩的解码滤波器(Sidelobe-free Decoding Filters，也可称为Inversed Filter，IF)，Lehtinen等人[8]在实验数据分析中就应用了Sulzer提出的无旁瓣解码方法[5]。不过Sulzer也提到IF解码不能达到像MF那样的最佳信噪比，信噪比恶化程度取决于编码方式[5]。在7位巴克码情况下，IF解码的信噪比比MF解码差近30%，而对于13位巴克码，只有5%左右[3]。但IF可以完美地解决巴克码MF带来的旁瓣问题，所以对于13位巴克码来说，通常情况下IF的优势完全可以弥补其信噪比恶化带来的劣势。
本文提出在地基雷达月球成像实验中可以应用13位巴克码IF来避免MF的旁瓣问题，从而带来成像质量的提升，并用实测数据进行了验证。成像算法是借鉴合成孔径成像中的距离-多普勒算法[9-10]，该算法通过在距离维作解码滤波，方位维作傅里叶变换来实现二维脉冲压缩，对目标进行距离-多普勒二维分辨进而成像。月球可以看作是一个由无穷多个点目标组合而成的球面散射体。若使用13位巴克码对月球进行成像并使用MF作解码处理，那么旁瓣效应会很大程度上影响成像的距离维分辨率，导致成像质量不能达到预期，不过若使用IF作解码，那么旁瓣效应会得到很好的改善，从而提高成像质量。
我国在地基雷达月球探测方面已初步开展相关工作，例如基于喀什深空站和昆明40 m射电望远镜的连续波信号双基地探月试验，基于曲靖雷达的脉冲信号自发自收探月试验[11]，以及三亚非相干散射雷达自发自收的线性调频月球南北半球拼接成像实验[12]。
1 巴克码匹配滤波与无旁瓣滤波
由于巴克码的位数最长是13位，可以获取最高的回波能量，所以本文重点分析13位巴克码的MF与IF在地基雷达月球成像中的应用。本节主要通过公式推导介绍MF和 IF的工作原理。
1.1 雷达探测方程
首先我们根据Vierinen和Lehtinen在2009年文章中的定义给出雷达探测方程[13]：
m=ε*ρ+δ
(1)
式中，m为雷达探测到的回波信号，ε为发射脉冲包络，ρ为目标散射信号，δ为高斯复噪声，*运算符表示卷积运算。所以可以认为雷达探测到的信号是发射脉冲包络与目标散射信号卷积后叠加上噪声得到的，那么在接收端用滤波器脉冲响应函数λ对回波信号m进行卷积后可以得到：
m′=m*λ=ε*λ*ρ+δ*λ=w*ρ+δ′
(2)
式中，m′为滤波后的信号，w=ε*λ为权重函数，它由发射脉冲包络与滤波器函数共同决定，δ′为通过滤波器后的噪声，也可称为后验噪声。根据式(2)我们可以认为通过滤波器后的信号是权重函数与目标散射信号的卷积加上后验噪声得到的，这样一来权重函数的目标检测性能就尤为重要，它决定了目标检测的模糊程度，称为模糊函数。
1.2 巴克码脉冲包络
接下来构建一个13位巴克码脉冲包络，如图1所示。巴克码的脉冲包络ε可以看作是由一个码元宽度的矩形脉冲p与一个编码狄拉克函数hc相互卷积而成的。数学上的定义如下：
ε(n)=p(n)*hc(n)
(3)
FD{ε}=FD{p}FD{hc}
(4)
由于我们讨论的是离散信号，所以用n表示离散采样。根据卷积定理(时域的卷积等于频域的乘积)式(3)在频域中的表示形式就是式(4)，其中FD运算符表示离散傅里叶变换。可以看到图1中巴克码的脉冲包络由1或-1组成，它们代表相位相差180°，所以也称为二相位编码。
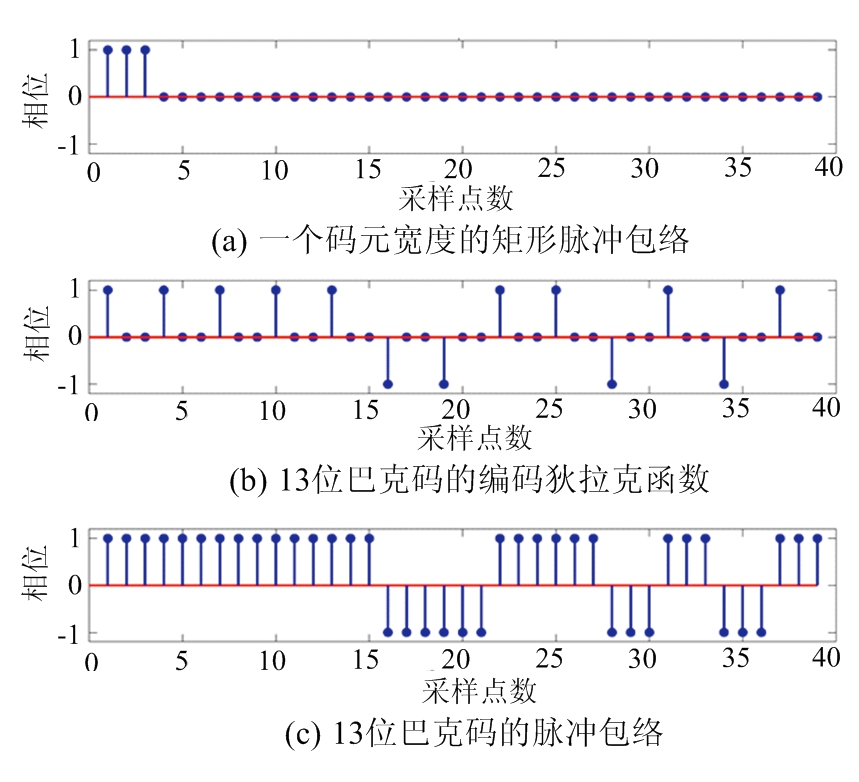
图1 13位巴克码脉冲包络的组成分析图
1.3 匹配滤波
如图2所示，MF的脉冲响应函数λM设置为发射脉冲包络的镜像，即
λM(n)=ε(-n)=p(n)*hc(-n)
(5)
那么MF的权重函数wM可以定义为
wM(n)=ε(n)*λM(n)=ε(n)*ε(-n)=
p(n)*hc(n)*p(n)*hc(-n)
(6)
从图2可以看到MF的权重函数在主瓣的两边分布有若干旁瓣，这些旁瓣会在与目标散射信号卷积的过程中将强的信号扩散到弱信号区域，导致模糊效应影响距离分辨率。
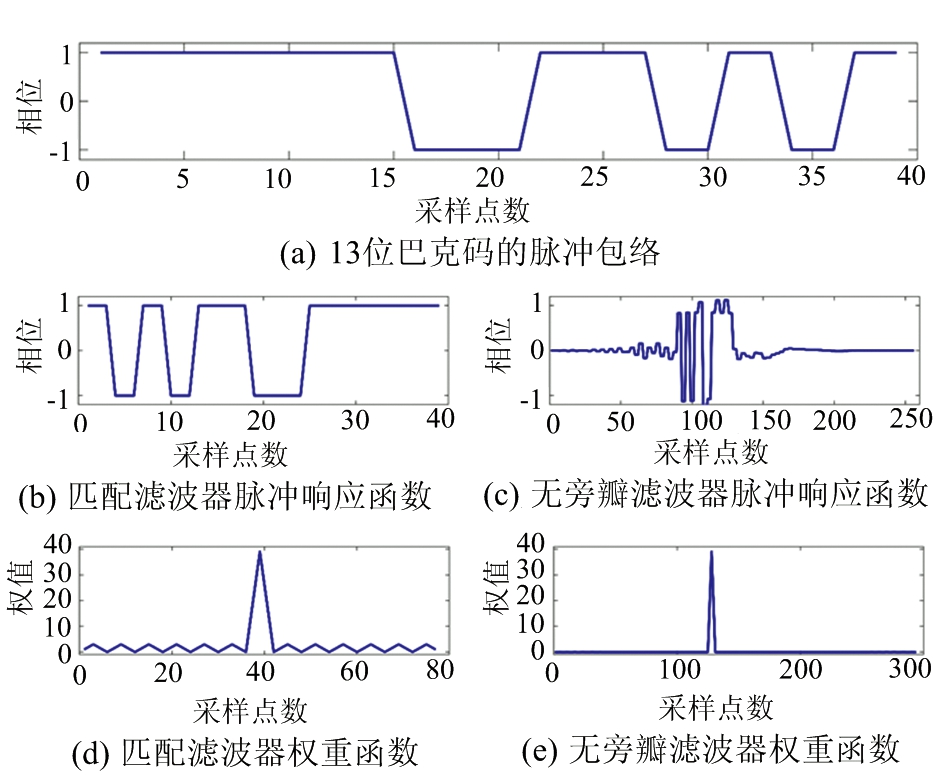
图2 13位巴克码的匹配滤波器与无旁瓣滤波器脉冲相应函数以及权重函数曲线图
1.4 无旁瓣滤波
如果使用IF就不会出现旁瓣干扰的情况，下面介绍IF的工作原理，首先我们定义IF脉冲响应函数λI为
λI(n)=q(n)*hd(n)
(7)
FD{λI}=FD{q}FD{hd}
(8)
式(7)中q(n)=p(-n)，即p(n)的匹配滤波器，hd(n)为解码狄拉克函数，式(8)是式(7)在频域中的表示形式。则IF的权重函数wI为
wI(n)=ε(n)*λI(n)=
[p(n)*q(n)]*[hc(n)*hd(n)]
(9)
FD{wI}=FD{ε}FD{λI}=
FD{p}FD{q}×FD{hc}FD{hd}
(10)
从式(9)和式(10)可以看到，IF的权重函数是由两组信号卷积得到的，一组是矩形脉冲p的匹配滤波结果，一组是编码狄拉克函数hc与解码狄拉克函数hd的卷积结果。所以若想实现无旁瓣滤波就要找到特定的hd使得FD{hc}FD{hd}=1，即
(11)
式中
为离散逆傅里叶变换运算符。式(11)中要注意到的一点就是：能够实现无旁瓣滤波的解码狄拉克函数hd存在条件是编码狄拉克函数hc在频域不能有零。实际上这个条件在大多数二相位编码情况下都可以满足[3]。
找到满足条件的hd后式(9)和式(10)就可以改写为
wI(n)=p(n)*q(n)
(12)
FD{w}=FD{p}FD{q}
(13)
也就是说这样找到的hd可以令IF权重函数变成跟p(n)的匹配滤波权重函数一样，是一个主瓣为三角形峰且没有旁瓣的函数，这样就可以实现了无旁瓣滤波。所以根据这样的定义可以将IF脉冲响应函数写为如下形式：
(14)
不过为了得到与MF同样的主瓣权重，可以令
q(n)= nBp(-n)
(15)
式中nB为巴克码的位数。这样IF权重函数的主瓣就拥有跟MF权重函数主瓣同样的权值和宽度，而且IF权重函数没有旁瓣，如图2所示。
2 在月球成像中的应用对比
在地基雷达月球成像实验中，如果使用13位巴克码进行探测，那么使用MF解码会因为旁瓣原因使图像产生模糊，然而应用上述IF解码就可以有效避免这一问题。
我们使用三亚非相干散射雷达进行了一次月球成像实验。前人研究中通常都会发射圆极化电磁波，并同时接收左旋与右旋两种极化方式的回波。因为它们对应的是极化回波(与发射极化方向相反)与去极化(与发射极化方向相同)回波，反映了不同的散射机制，进而研究者们可以利用这一点挖掘月球表面和次表面信息[14]。但受雷达系统设计的限制，实验时发射右旋圆极化电磁波，只接收左旋圆极化回波，意味着只接收了极化回波，没有获取去极化回波信息。另外发射波形为390 μs脉冲长度的13位巴克码，码元长度为30 μs，实验的具体参数如表1所示。在成像前我们分别使用了巴克码MF以及IF对回波进行了解码滤波处理，之后对解码后的信号进行成像处理，处理算法参考前人使用的距离-多普勒算法[10,14-15]。整个过程可以概括为以下几步：
表1 SYISR月球成像实验参数
参数名称参数值或说明极化方式发射右旋圆极化电磁波接收左旋圆极化回波发射波形13位巴克码脉冲长度390μs码元长度30μs脉冲重复频率～76.9Hz脉冲重复周期13ms相干积累时间60s采样周期10μs距离分辨率4.5km多普勒分辨率～9.4mHz方位向分辨率～4.8kmFFT点数8192
1) 对每个重复周期内的回波分别进行解码滤波处理，获得距离向分辨能力；
2) 进行月球的距离徙动校正以及运动速度多普勒校正，具体包括距离变化带来的时延校正和相位校正，以及运动速度带来的多普勒频移校正；
3) 对同一距离门的连续脉冲采样进行快速傅里叶变换(FFT)，获得方位向分辨能力，并得到距离-多普勒二维成像图；
4) 将距离-多普勒图中的像素点根据几何关系投影到月球坐标系下(笛卡尔坐标系或经纬度坐标系)。
图3(a)和(b)分别展示的是应用巴克码MF以及IF获得的月球距离-多普勒二维成像图，图中圆弧状内的回波即为月球回波图像，圆弧的弧顶代表月球表面的雷达下点位置，由于雷达下点附近的电磁波入射角接近法线入射，所以回波强度较其他区域要强很多。
然而只从两幅图对照来看并不能看出IF对成像质量有明显提升，于是我们将两幅图中的对应像素值做差，得到了MF图像相较于IF图像的像素值增量，即MF-IF，如图3(c)所示。可以看到增量基本都为正值且有沿距离方向的竖条纹状分布，这证明了MF的旁瓣效应将目标回波在距离方向扩散并叠加到了其他距离门，对其他距离门造成了污染，并且还证明了IF可以有效避免这种污染。为了进一步分析增量增加的程度，我们将增量除以IF图像中的像素值得到增量占原图的百分比，即(MF-IF)/IF，如图3(d)所示。可以看到增量占IF原图的比重约为10%～30%之间，但在回波边界外侧附近区域增量可达原图的60%～100%甚至更高，这是因为边界是月球回波强信号与背景噪声弱信号的分界，MF的旁瓣会将强信号扩散到弱信号区域，使得在弱信号区域的回波污染程度要明显很多。不过在成像处理步骤的坐标转换这一步中，月球回波信号边界外的区域会被“切割”掉，所以不用考虑边界外的污染程度问题。另外图3(d)也存在沿距离方向的竖条纹状分布，这再次证明了MF旁瓣效应会导致在距离向的污染现象，同时也证明了IF可以避免污染并恢复距离分辨率，达到了一定的图像质量改善效果。
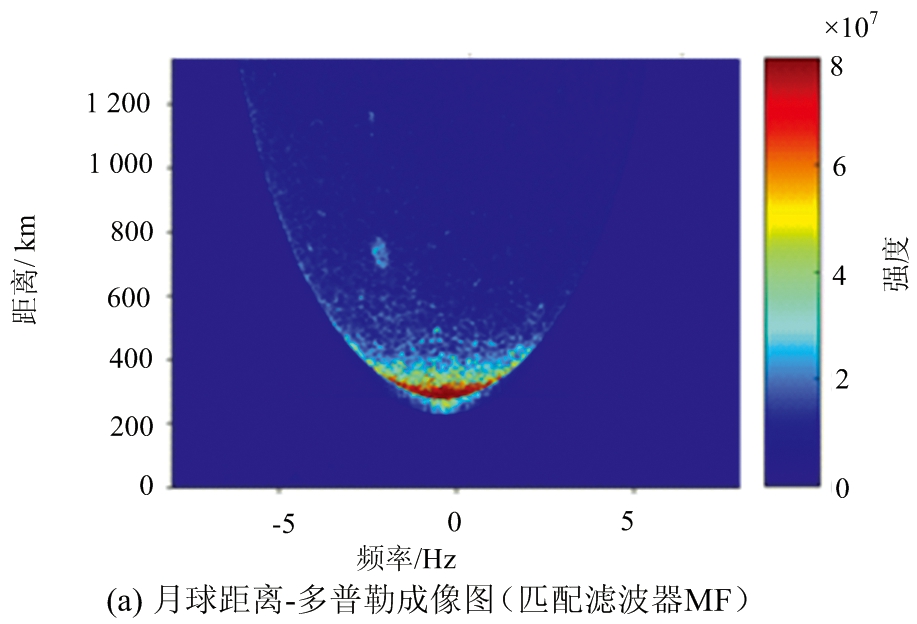
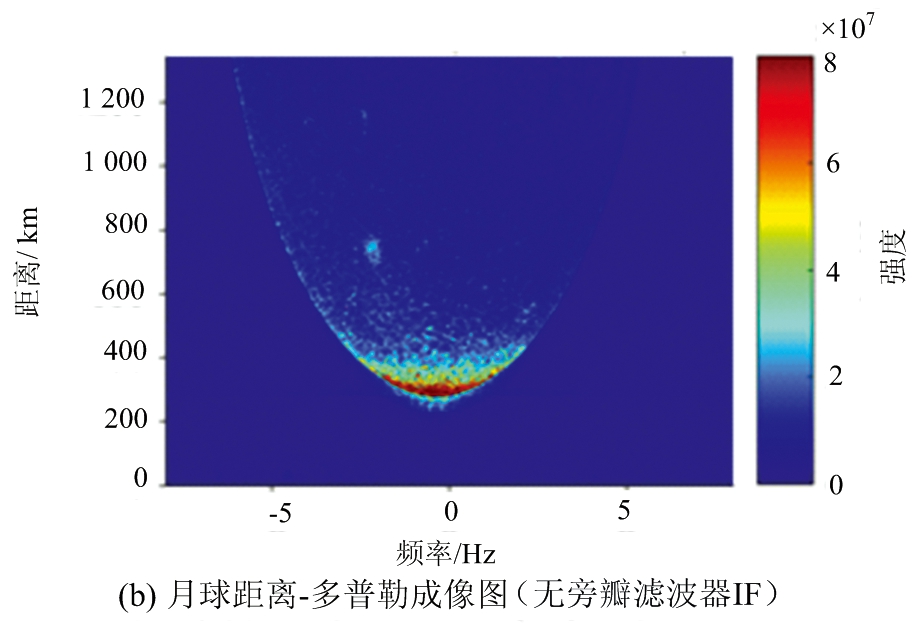
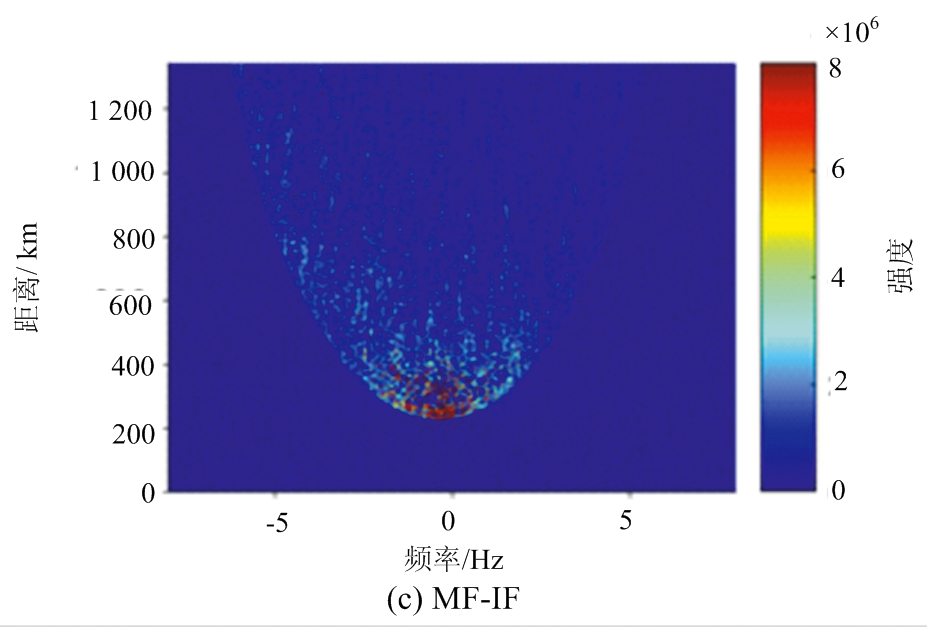
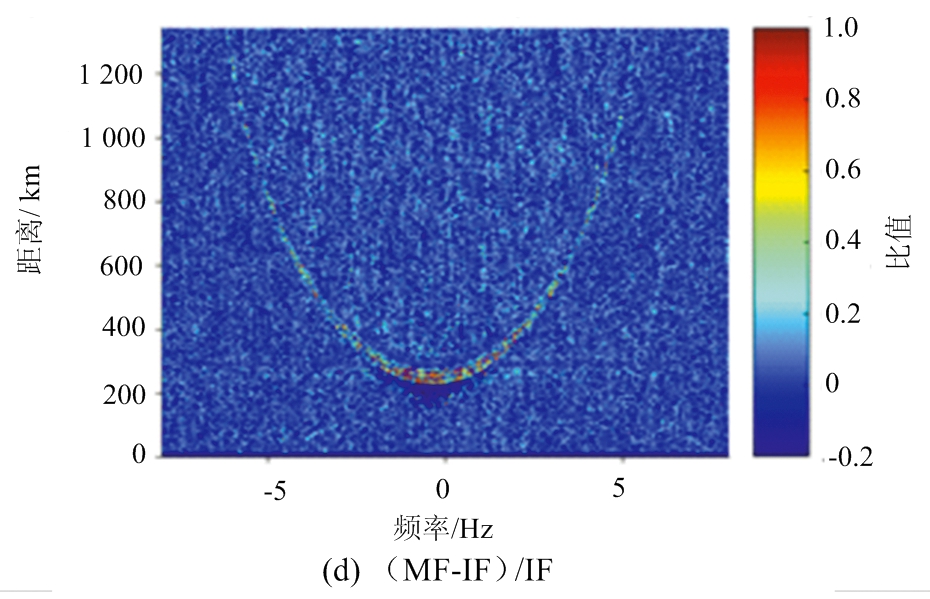
图3 13位巴克码的匹配滤波器与无旁瓣滤波器对月球距离-多普勒成像图的影响对比分析图
3 结束语
本文提出了在地基雷达月球成像实验中使用13位巴克码IF解码方法可以有效避免MF解码带来的旁瓣问题，通过数学公式推导和画图的形式论述了13位巴克码IF的工作原理，最后用三亚非相干散射雷达进行了13位巴克码月球成像实验，将IF处理结果与MF处理结果进行了对比分析，得出如下结论：
1) IF解码可以使用的条件是编码狄拉克函数hc在频域内没有零值；
2) 13位巴克码MF解码结果会导致月球距离-多普勒图像在距离方向上产生10%～30%的回波强度扩散，从而污染周围距离门，导致图像距离分辨率恶化，成像质量下降；
3) 13位巴克码IF解码结果可以有效避免MF的旁瓣污染问题，从而使距离分辨率得到优化，成像质量得到改善。
综上所述，在地基雷达月球成像实验中使用13位巴克码IF解码方法确实可以有效避免MF解码带来的旁瓣污染问题，使月球成像距离分辨率得到改善。并且IF解码在其他形式的二相位编码情况下仍然大有可为。后续的月球成像实验可以设计脉冲长度更长、距离分辨率更高的二相位编码，结合IF解码方法能够大幅提升月球成像质量。
[1] FARLEY D T. Multiple-Pulse Incoherent-Scatter Correlation Function Measurements[J]. Radio Science, 1972, 7(6):661-666.
[2] ZAMLUTTI C J, FARLEY D T. Incoherent Scatter Multiple-Pulse Measurements at Arecibo[J]. Radio Science, 1975, 10(5):573-580.
[3] LEHTINEN M S, DAMTIE B, NYGREN T. Optimal Binary Phase Codes and Sidelobe-Free Decoding Filters with Application to Incoherent Scatter Radar[J]. Annales Geophysics, 2004, 22(1):1623-1632.
[4] LEHTINEN M S, H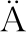
GGSTRÖM I. A New Modulation Principle for Incoherent Scatter Measurements[J]. Radio Science, 1987, 22(4):625-634.
[5] SULZER M P. Recent Incoherent Scatter Techniques[J]. Advances in Space Research, 1989, 9(5):153-162.
[6] SULZER M P. A New Type of Alternating Code for Incoherent Scatter Measurements[J]. Radio Science, 1993, 28(6):995-1001.
[7] BARKER R H. Group Synchronizing of Binary Digital Systems, in: Communications Theory[M]. New York: Academic Press,1953:273-287.
[8] LEHTINEN M S, MARKKANEN J, V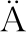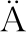N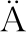NEN A, et al. A New Incoherent Scatter Technique in the EISCAT Svalbard Radar[J]. Radio Science, 2002, 37(4)：1-15.
[9] PETTENGILL G H, HENRY J C. Enhancement of Radar Reflectivity Associated with the Lunar Crater Tycho[J]. Journal of Geophysical Research, 1962, 67(12):4881-4885.
[10] PETTENGILL G H, ZISK S H, THOMPSON T W. The Mapping of Lunar Radar Scattering Characteristics[J]. The moon, 1974, 10(1):3-16.
[11] 孙靖，杨嵩，周峰，等. 我国地基雷达观测月球的现状和研究进展[J]. 天文研究与技术, 2022,19(1):29-40.
[12] 李鸣远, 王永辉, 尹翰林,等. 基于三亚非相干散射雷达的月球正面南北半球拼接成像研究[J]. 地球与行星物理论评, 2021, 52(4):450-458.
[13] VIERINEN J, LEHTINEN M S. 32-cm Wavelength Radar Mapping of the Moon[C]∥ 2009 European Radar Conference (EuRAD), Rome, Italy:IEEE, 2009:1-4.
[14] CAMPBELL B A, CAMPBELL D B, MARGOT J L, et al. Focused 70-cm Wavelength Radar Mapping of the Moon[J]. IEEE Trans on Geoscience & Remote Sensing, 2007, 45(12):4032-4042.
[15] VIERINEN J, TVEITO T, GUSTAVSSON B, et al. Radar Images of the Moon at 6-meter Wavelength[J]. Icarus, 2017, 297(2):179-188.
