0 引言
机载雷达主要承担空中警戒巡逻任务，其一方面可以弥补地面雷达盲区，另一方面可以监视、探测、跟踪和识别来袭的空中目标，实现对战场态势的监控。非正侧视阵机载雷达下视工作时，存在距离模糊的情况下，杂波多普勒频谱严重展宽且近远程杂波相互交叠，其中近程强杂波分布具有严重的非平稳性，而远程杂波相对平稳，同时还存在清晰区。传统STAP方法大多是对全部的多普勒通道数据进行自适应处理，虽然可以获得较好的杂波抑制效果，但同时也会引起清晰区目标的信杂噪比损失，不利于弱目标的检测。此外，近程杂波引起的杂波非平稳分布，均匀训练样本数严重不足，导致传统STAP方法在近程杂波区性能下降。
针对上述问题，目前在实际工程中通常首先基于先验知识，对机载雷达回波在距离-多普勒域进行划分，然后对不同区域采用相应的信号处理方法进行处理。但是实际机载雷达受空时误差的影响，导致回波在距离-多普勒域的分布与理论相比存在一定程度偏差。为了解决先验知识的不足，文献[1]采用自适应的方式将整个距离-多普勒谱进行划分区段处理，其中非平稳杂波区采用3D STAP方法[2-4]，但同时3D STAP也存在着样本需求量大以及计算量大的问题。为此，文献[5]通过子阵合成的方式抑制近程杂波，该方法性能受俯仰维阵元数的影响，当俯仰阵元数较少时，产生的凹口深度不够。文献[6]提出了一种俯仰维鲁棒的Capon波束形成(ERCB)方法，该方法利用待处理单元上的所有脉冲数据估计俯仰维协方差矩阵，由于样本中混有远程杂波，形成的俯仰方向图会发生主瓣畸变，这降低了近程杂波抑制效果。文献[7]提出了一种基于正交波形的近程杂波获取方法，但该方法需要改变雷达的系统结构。文献[8]和文献[9]利用机载雷达发射的第一个填零脉冲获取只含近程杂波的样本来抑制近程杂波，然而机载雷达通常工作在多重频模式下，因此第一个脉冲容易被前PRF的最后一个接收脉冲污染。
本文提出了一种基于自适应分区和正交投影的机载雷达非平稳杂波抑制方法。该方法首先自适应划分出非平稳杂波区、平稳杂波区和清晰区，对非平稳杂波区采用俯仰正交投影方法进行抑制；对于平稳杂波区通过传统的方位-多普勒STAP进行处理；对清晰区采用副瓣加权PD处理。
1 传统方法
1.1 STAP处理器
空时最优处理器由Brennan等人于1973年提出。假设机载雷达回波信号为
X=aS+Xc+n=aS+q
(1)
式中，干扰矢量q是一个多变量复高斯分布的零均值随机矢量，杂波信号Xc空时相关，噪声信号n空时不相关，目标信号aS为确定信号。
则从背景干扰q中检测目标信号aS的最优线性权值为
Wopt=μR-1S
(2)
式中，R表示杂波噪声协方差矩阵，S表示预设的目标空时导向矢量。
STAP滤波器在对目标信号进行相干累积的同时在空域和时域形成二维响应凹口抑制杂波。然而，在实际场景中，R是未知的，需要通过与待处理单元中杂波独立同分布的训练样本
估计得到，而杂波的非平稳性会导致满足独立同分布样本数严重不足，从而导致传统STAP技术的杂波抑制性能恶化，目标检测性能下降。
1.2 杂波分区处理方案
当机载雷达工作于HPRF模式下时，杂波在距离多普勒域可划分成杂波区和清晰区2个部分，其中杂波区包含杂波、噪声和目标信号。不同角度的旁瓣杂波具有不同的多普勒频率。对于俯视角为φ的距离环的旁瓣杂波信号，其频谱的分布范围为
为载机速度，λ为雷达工作波长。根据文献[10]，杂波主要的距离依从性位于R≤5H区域内，因此非平稳杂波区距离分布范围为R⊆[H，5H]，平稳杂波区距离分布范围为R⊆[5H，Ru]。
清晰区仅包含噪声和目标信号，结合前面的分析，具体分区结果如图1所示。图1中清晰区采用常规PD处理，而杂波区则采用2D STAP方法处理。基于杂波分布的机载雷达分区处理方案流程如图2所示。
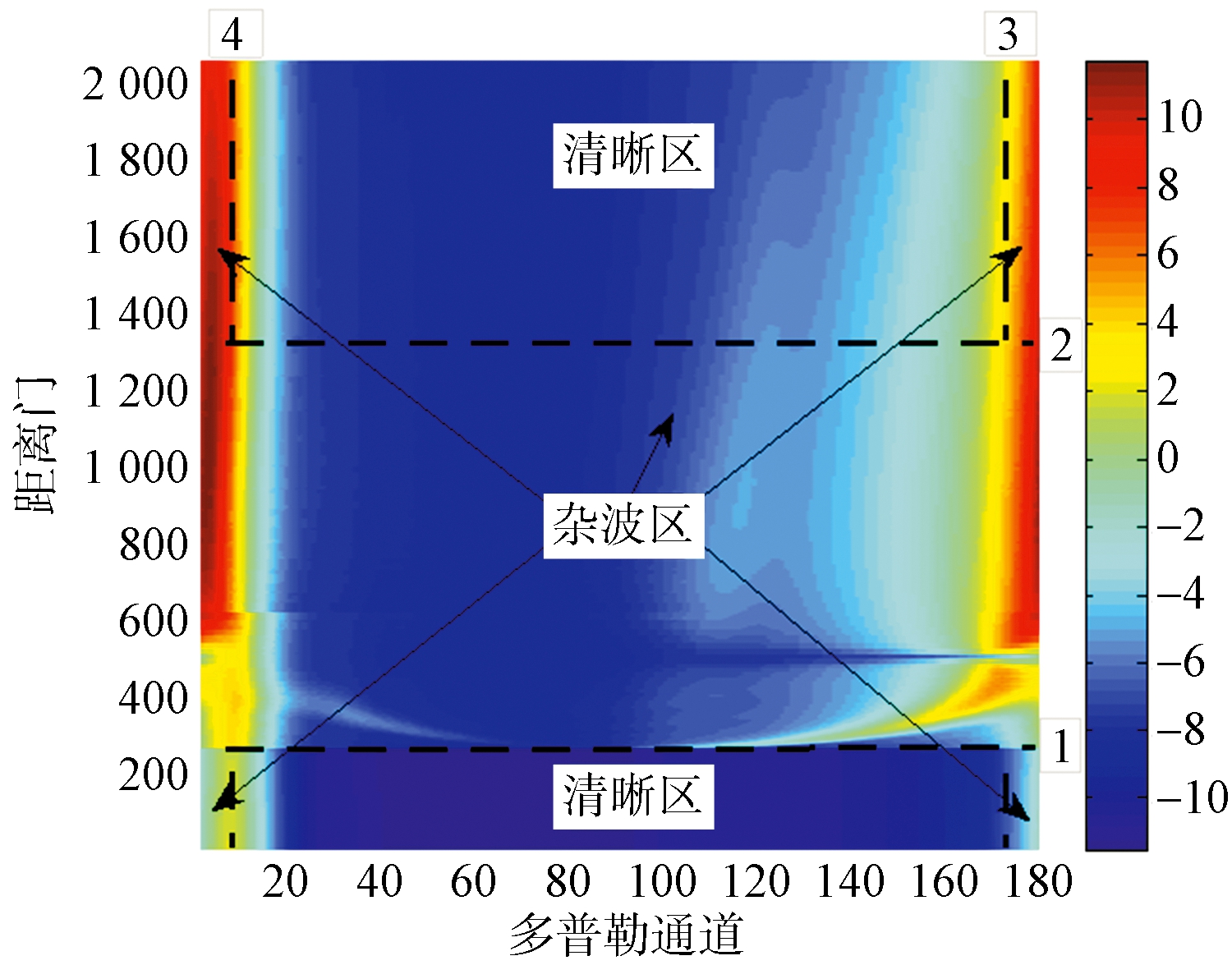
图1 前视阵机载雷达传统分区示意图
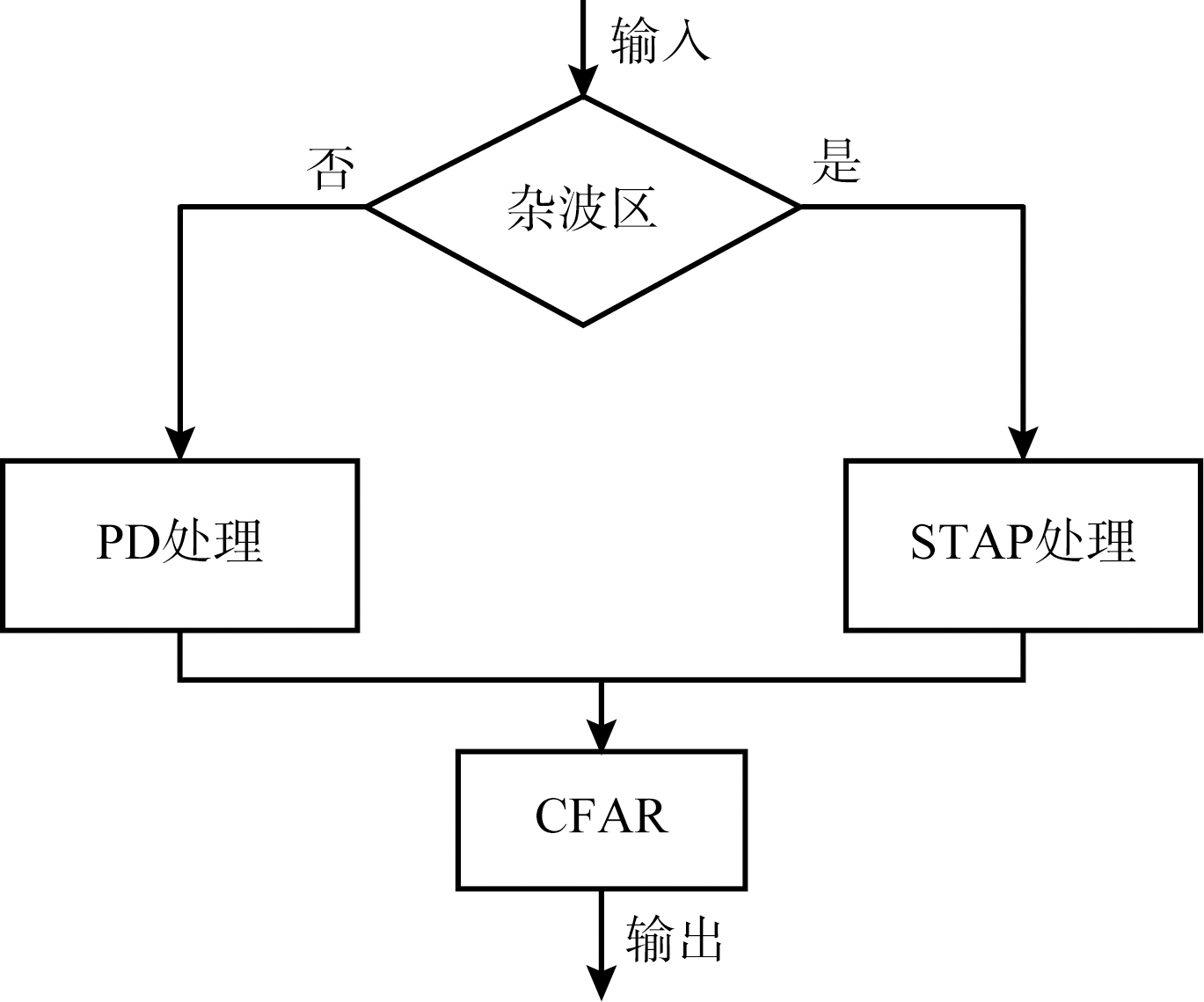
图2 机载雷达传统杂波分区处理流程
从图1可以看出,基于先验知识进行划分，其划分结果不一定准确，工程可操作性较差，而传统2D STAP方法对于非平稳杂波区杂波抑制性能不佳。因此本文采用自适应分区处理方案。
2 基于自适应分区段和正交投影的杂波抑制方法
非正侧视阵机载雷达杂波在近程具有严重的非平稳性，但是随着距离的增加，杂波趋于平稳；同时，对于杂波信号而言，机载雷达通常采用高脉冲重复频率，因此在多普勒频率维存在清晰区。图3给出了前视阵某一阵元回波信号的距离-多普勒谱图，根据杂波分布特性将距离-多普勒谱在(距离，多普勒)二维域上分为非平稳杂波区，平稳杂波区以及清晰区3个区段，如图3所示，其中线条1,2,3,4为各区域的分界线。在不同的区段分别采用正交投影方法、2D STAP方法以及脉冲多普勒(PD)处理，其处理流程如图4所示。
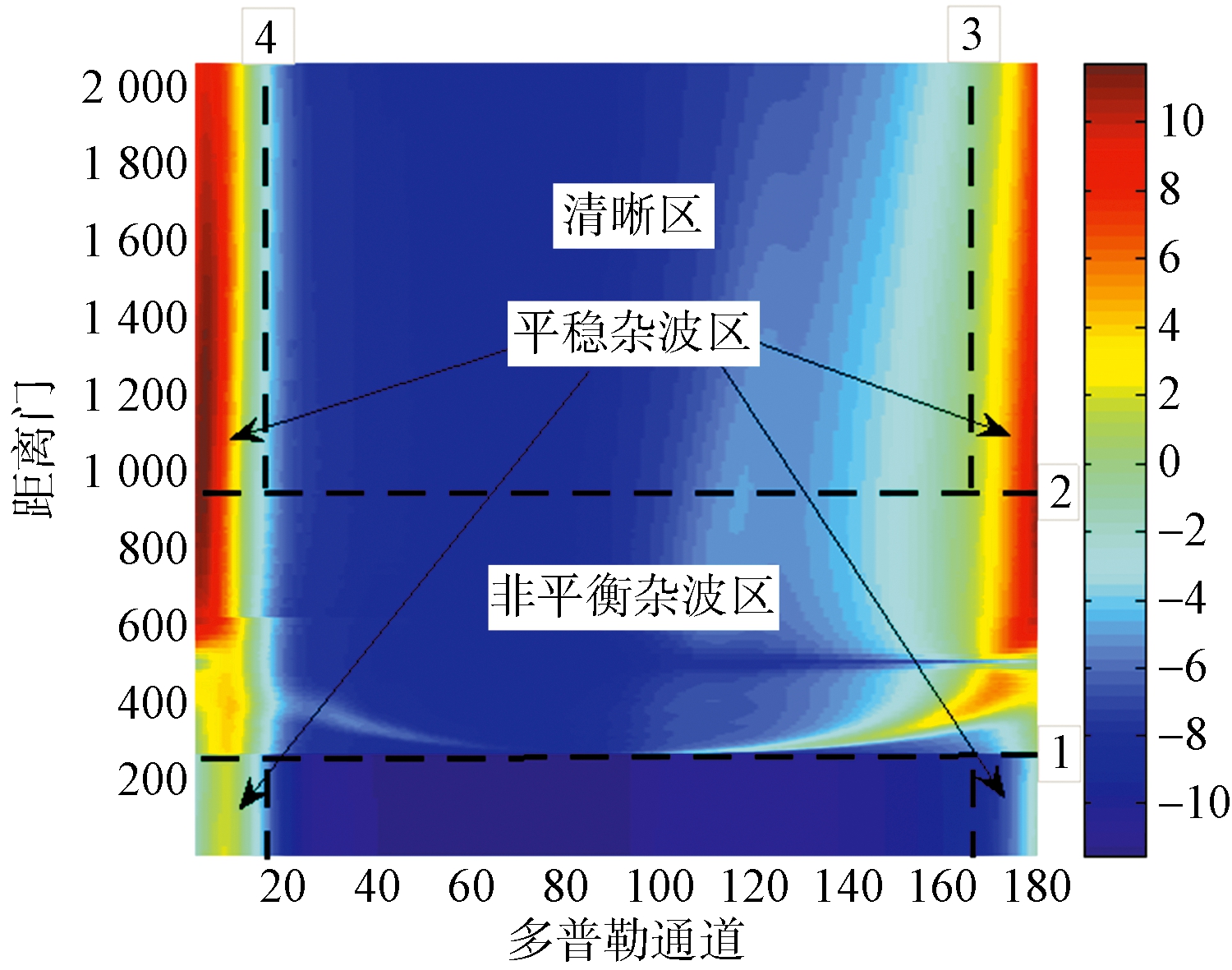
图3 前视阵机载雷达自适应分区示意图
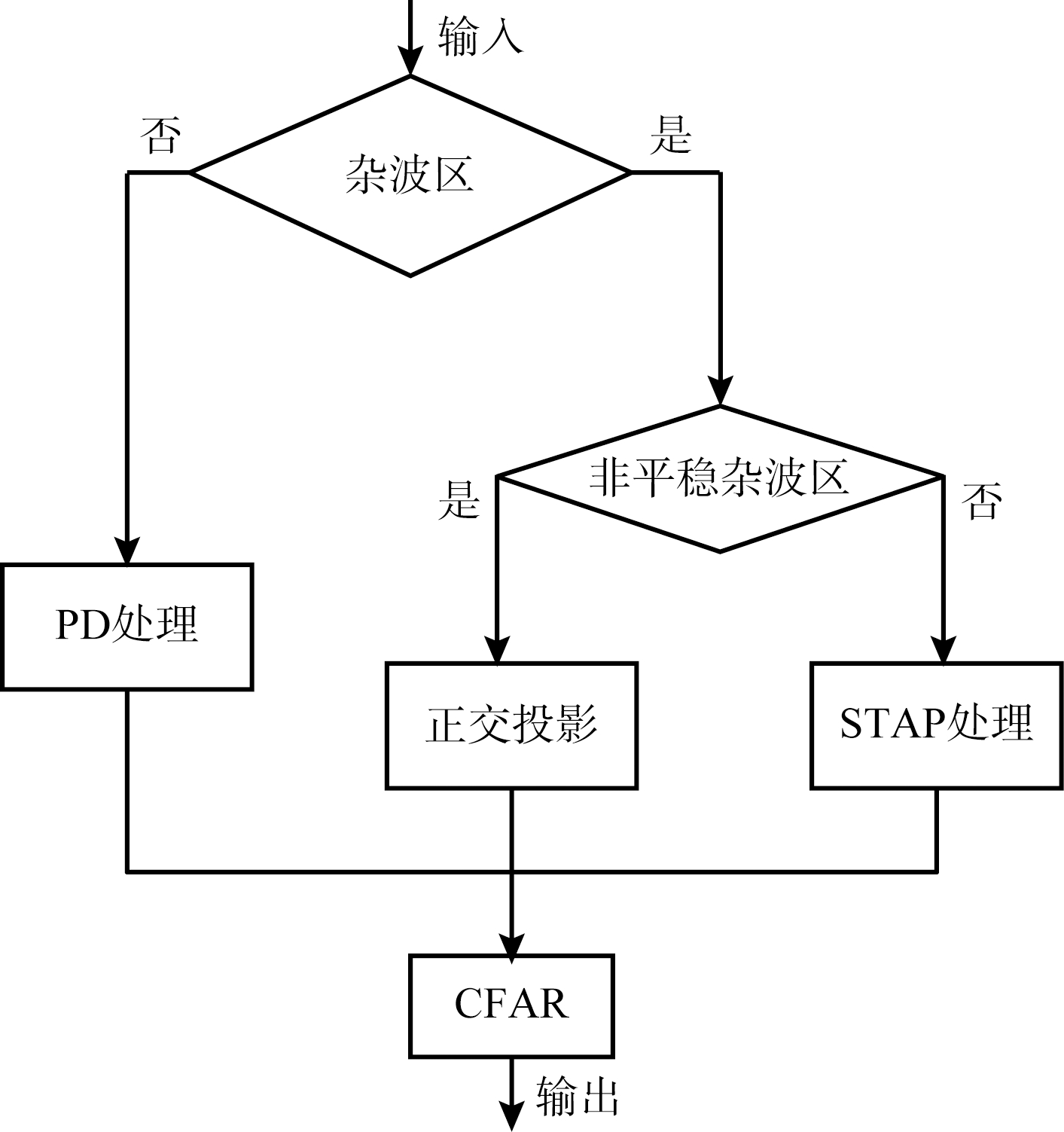
图4 机载雷达自适应杂波分区处理流程
2.1 非平稳杂波区的自适应划分
由于离雷达天线最近的地杂波是处于载机正下方的高度线杂波，即处于R=H处的近程杂波。所以高度线杂波所处距离对应的距离门就是近程非平稳杂波区的起始距离门，即
Ll=int(H/ΔR)
(3)
式中，ΔR为距离门宽度，int(·)表示向下取整函数。因此根据机载雷达系统参数易求得第266个距离门为图3中的分界线1。
由于杂波距离非平稳性的本质表现为杂波功率在多普勒域的分布随着距离的变化而变化，而杂波的时域协方差矩阵恰好包含了杂波功率在多普勒频率维的分布信息。因此可以考虑利用不同距离门的时域杂波协方差矩阵的差别来衡量杂波的非平稳性。
假设对于第n个阵元，K个脉冲接收到的第l个距离单元的杂波数据为Xl((n-1)K+1:nK)，则第n个接收通道的时域协方差矩阵为
Rt;l;n=E[Xl((n-1)K+1:nK)·
(4)
值得注意的是，根据RMB准则，杂波协方差矩阵估计需要样本数大于两倍的系统自由度才能保证SCNR损失小于3 dB。在利用各阵元的数据估计时域协方差矩阵时也需要阵元数大于脉冲数的两倍。在实际场景中，上述条件不一定满足，所以需要通过选取部分脉冲或多普勒滤波来达到这一要求，上述处理则可通过降维矩阵Tt来实现。同时，为了保证时域杂波协方差矩阵的可逆性，可使用对角加载技术。则第l个距离门的时域杂波协方差矩阵可被估计为
Rt;l=
Xl((n-1)K+1:nK)HTt+δ2I
(5)
式中，δ2为对角加载系数，I为单位矩阵。
为了精确反映两个时域杂波协方差矩阵的差别，我们引入黎曼距离。可逆矩阵A和B的黎曼距离定义式为
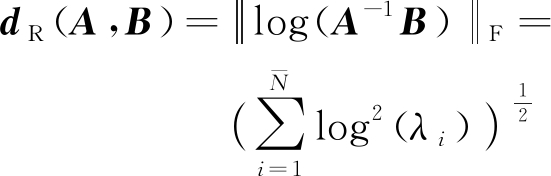
(6)
式中，λi为A-1B的特征值，
为矩阵A或B的维度。黎曼距离反映的是A对B的白化程度，如果A和B由独立同分布的杂波数据构建而成，则A-1B≈I，此时dR(A,B)≈0。
但式(6)定义的黎曼距离不满足数学距离的对称性，即
dR(A,B)≠dR(B,A)
(7)
如果A和B的杂波具有相同的协方差矩阵结构，但构成矩阵A的杂波功率大于B，那么“距离”不会增加，因为B中的杂波被A过度白化。而反过来，“距离”会增加。这在度量两个杂波协方差矩阵的差别时将面临问题。因此，我们可以通过定义一个对称的黎曼距离来解决这个问题，即
(8)
由于杂波的距离非平稳现象是一个连续的渐变过程，需要通过多个距离门来表现，因此仅仅通过两个距离门的时域杂波协方差矩阵的黎曼距离来衡量并不准确。为了解决这一问题，我们引入Lp个时域杂波协方差矩阵的黎曼均值距离，具体定义为
(9)
式中
因此，各距离门杂波的非平稳性便可通过式(8)所求值的大小来衡量，这实现了对杂波距离非平稳性的量化度量，同时也为实现图3中非平稳杂波区的自适应划分提供了途径。
假设一个不模糊距离内共包含L个距离门，我们从最远处开始选取Lp个距离门，即估计第L-Lp+1到第L个距离门的时域协方差矩阵，并计算它们的黎曼均值距离 DRL-Lp+1 且与门限值 DRm 进行比较。若小于门限值，则继续选取第L-Lp到第L-1个距离门的时域协方差矩阵并重复上述步骤直到出现某一黎曼均值距离DRLf≥DRm，此时认为第Lf距离门即为图3中的非平稳区分界线2。
图5给出了Lp=100时的黎曼均值距离随距离门变化的曲线图，若设定门限值 DRm=0.25，则据此可确定第935个距离门为图3中的非平稳杂波区分界线2。
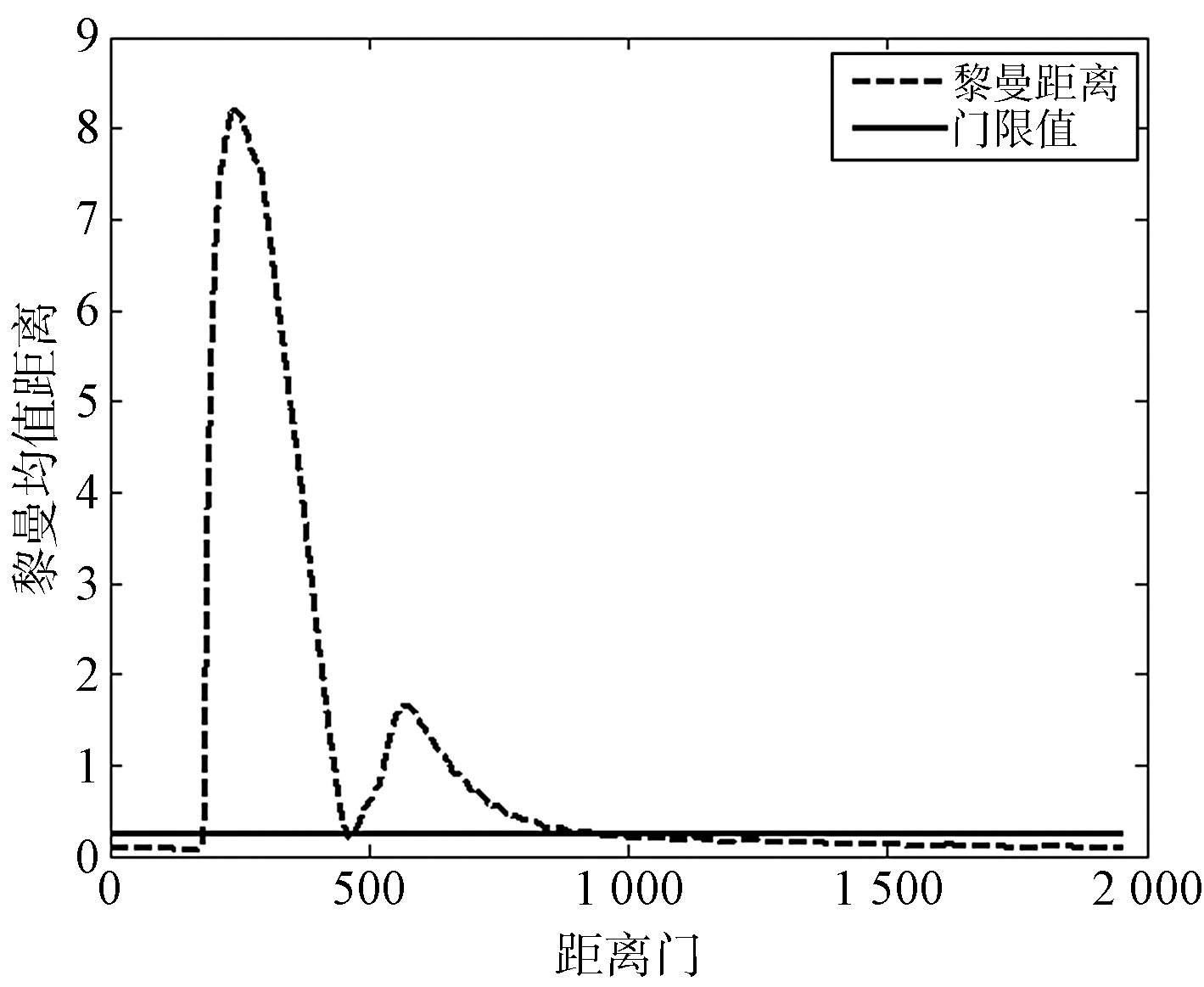
图5 黎曼均值距离变化曲线图
2.2 清晰区的自适应划分
从图3可以看出，前视阵机载雷达杂波主要分布于多普勒频率的两端，故其杂波最弱的点应该处于中间多普勒单元处。假设共有Kd个多普勒单元，我们在分界线2所处距离门的中间多普勒单元处连续取h个多普勒单元，即第Kd/2-h/2+1到Kd/2+h/2个多普勒单元并求其平均功率作为噪声基底值σ0；并设相对门限值为σm，而后再向右滑动一个多普勒单元，即取第Kd/2-h/2+2到Kd/2+h/2+1个多普勒单元再求其平均功率值σKd/2+1，并与门限值σ0+σm进行比较；若小于此值，则继续重复上述步骤直至出现σKr≥σ0+σm，此时认为第Kr个多普勒单元即为图3中的清晰区分界线3。
图6给出的是h=20，门限值σm=6 dB时分界线2所处距离门的杂波平均功率随多普勒单元变化的曲线图，则据此可确定第14个多普勒单元与第165个多普勒单元为图3中的清晰区分界线3和4。
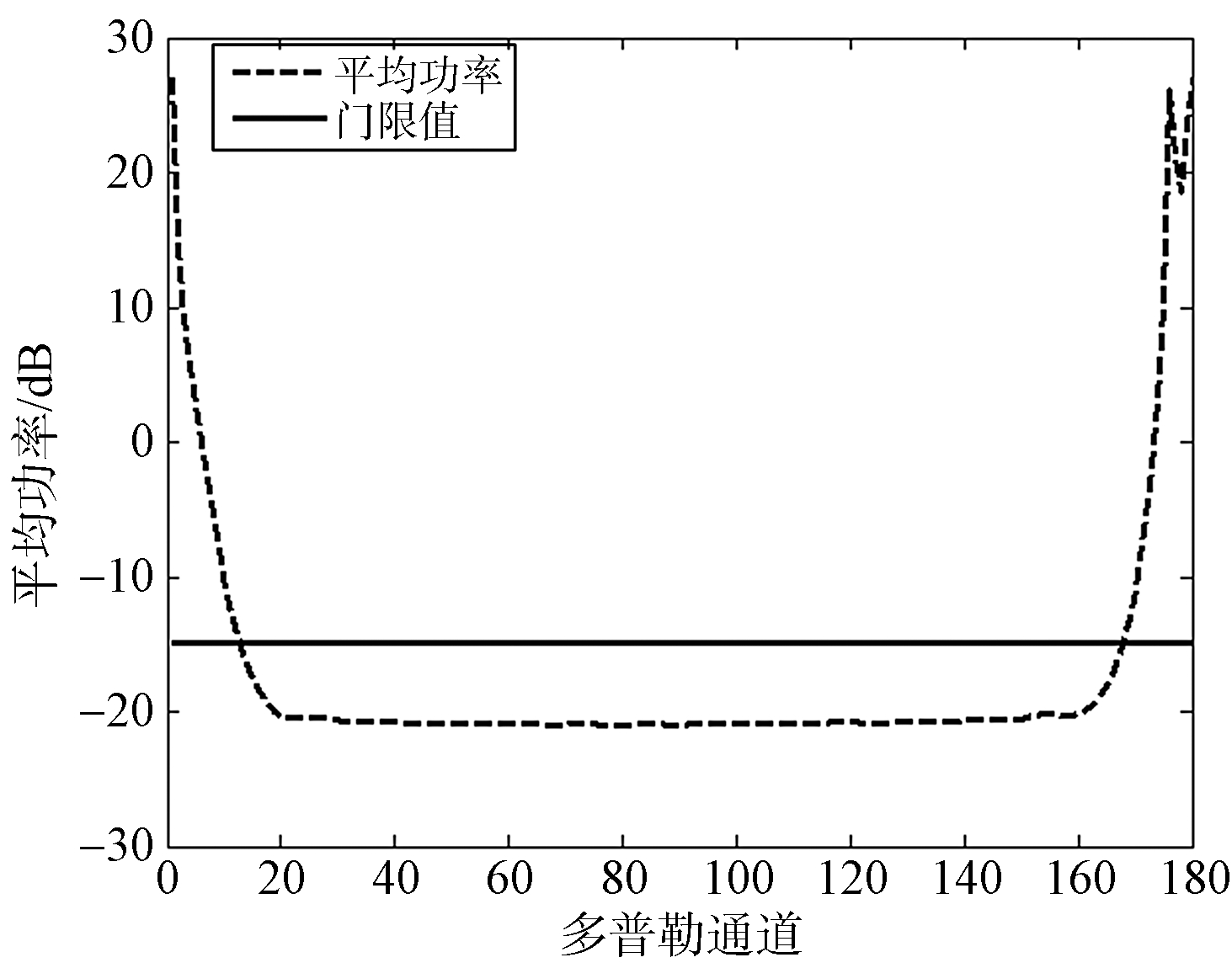
图6 回波平均功率变化曲线图
2.3 基于正交投影和2D STAP的非平稳杂波抑制
自适应划分区段后，对图3中非平稳近程杂波可以通过俯仰维正交投影进行抑制，即
(10)
式中，
为近程杂波对应的俯仰导向矢量。需要注意的是，本文采用机载雷达参数和近程杂波位置估算得到的近程俯仰角，会由于载机高度变化存在很小的误差，所以本文取
以载机高度变化带来的角度误差，其中σφ′0表示俯仰角估计值的方差。
最后，图3中平稳杂波区采用传统的方位-多普勒STAP进行抑制，清晰区则采用加切比雪夫权PD处理。
3 仿真及分析
本文仿真采用前视6行8列阵列，在二维STAP中空域合成一行线阵，即空域自由度为8；在三维STAP中空域为六行面阵，即空域自由度为6×8。本文仿真中非平稳杂波区黎曼均值距离门限DRm=0.25，清晰区杂波功率值的相对门限值σm=6 dB。PD处理采用90 dB切比雪夫空时锥销。
3.1 SCNR损失
图7给出了分别经过传统分区方法以及本文方法处理后的距离-多普勒信杂噪比损失图。由图7可以看出：1) 2D STAP处理能够抑制掉远程的副瓣杂波，但在近程的非平稳杂波区SCNR损失较大；2) 本文方法通过自适应划分区段，近程非平稳杂波区SCNR损失很小，主瓣杂波也能得到有效抑制，平稳杂波区仅剩部分主瓣杂波，整体性能优于传统方法。
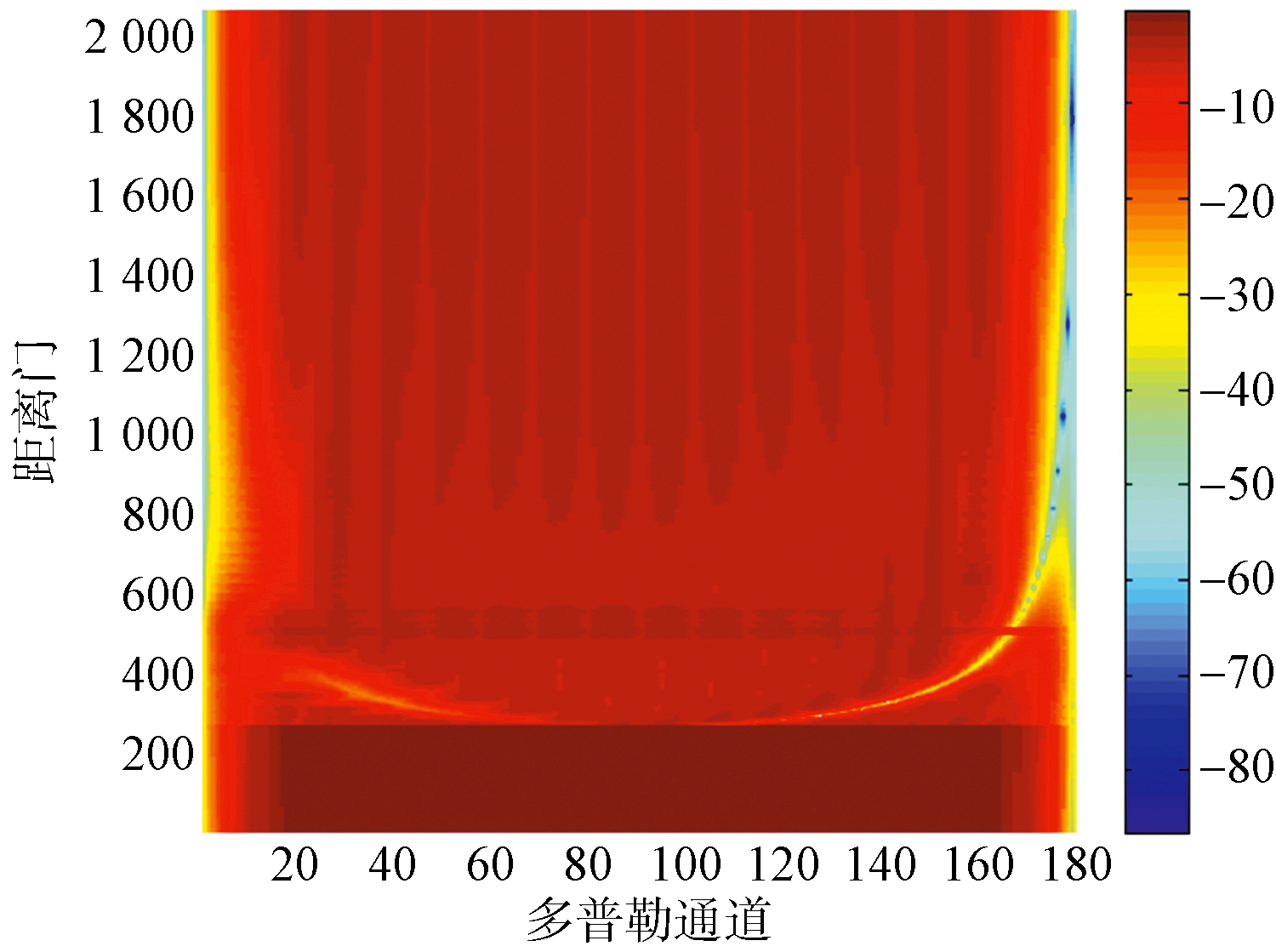
(a) 传统分区方法
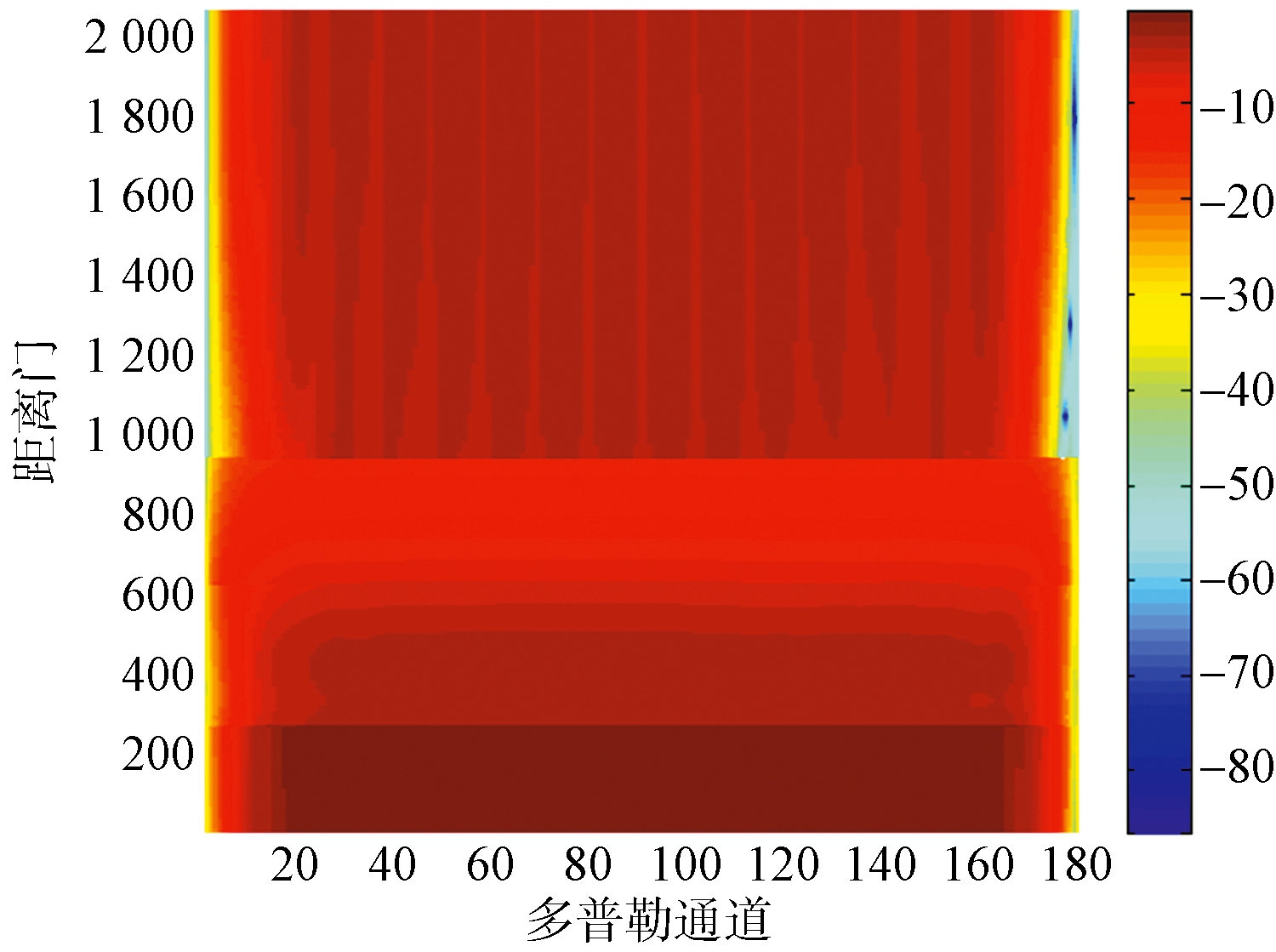
(b) 本文方法
图7 信杂噪比损失比较
3.2 输出杂波剩余比较
为了更清晰地比较各方法的杂波抑制效果，我们在原始回波数据中插入了3个目标，各目标所处的位置分别为：目标1(100，1 500)，目标2(170，1 500)，目标3(157，400)，其中横坐标为多普勒通道数，纵坐标为距离门数。目标1，2，3分别位于清晰区、平稳杂波区和非平稳杂波区，目标输入SNR为0 dB。
图8分别给出了经过传统分区处理以及本文方法处理后的剩余杂波距离-多普勒谱图。由图8可以看出：1) 传统分区方法处理后只有处于清晰区的目标1和位于副瓣杂波区的目标2可以被有效检测到，但处于非平稳杂波区的目标被杂波淹没；2) 本文方法能对所有3个目标均能实现有效检测。
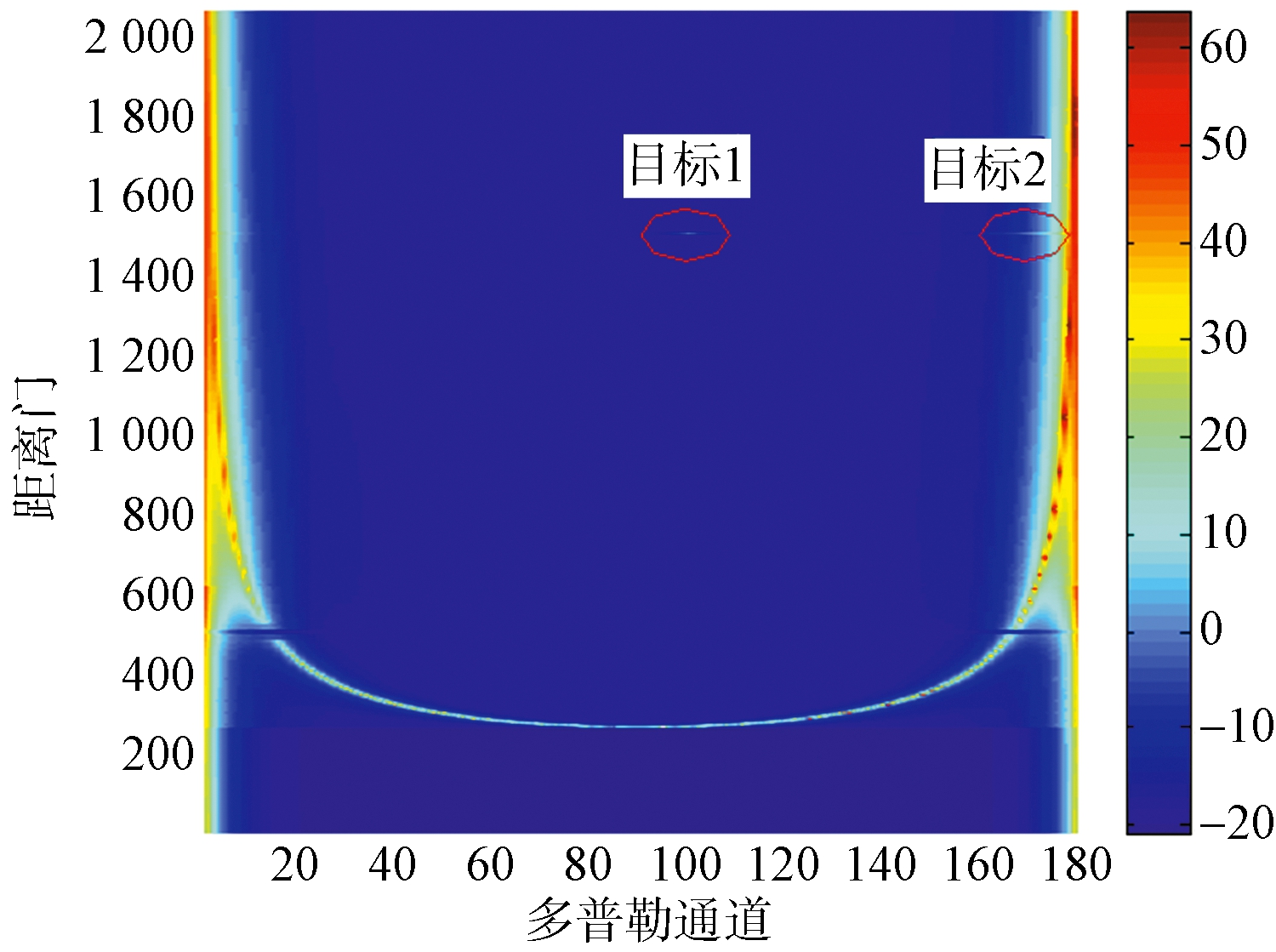
(a) 传统分区方法
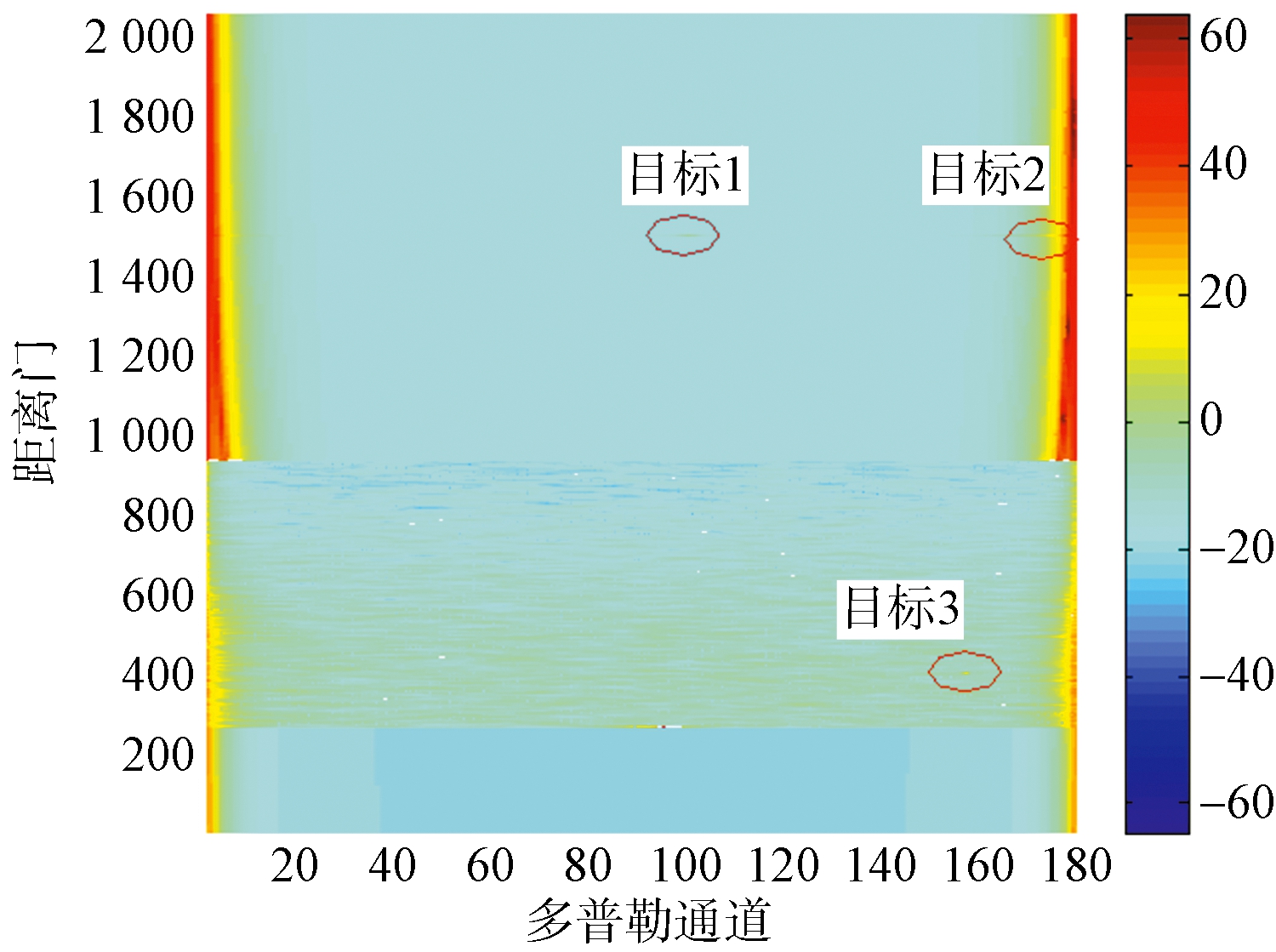
(b) 本文方法
图8 杂波剩余比较图
3.3 距离-速度二维盲区比较
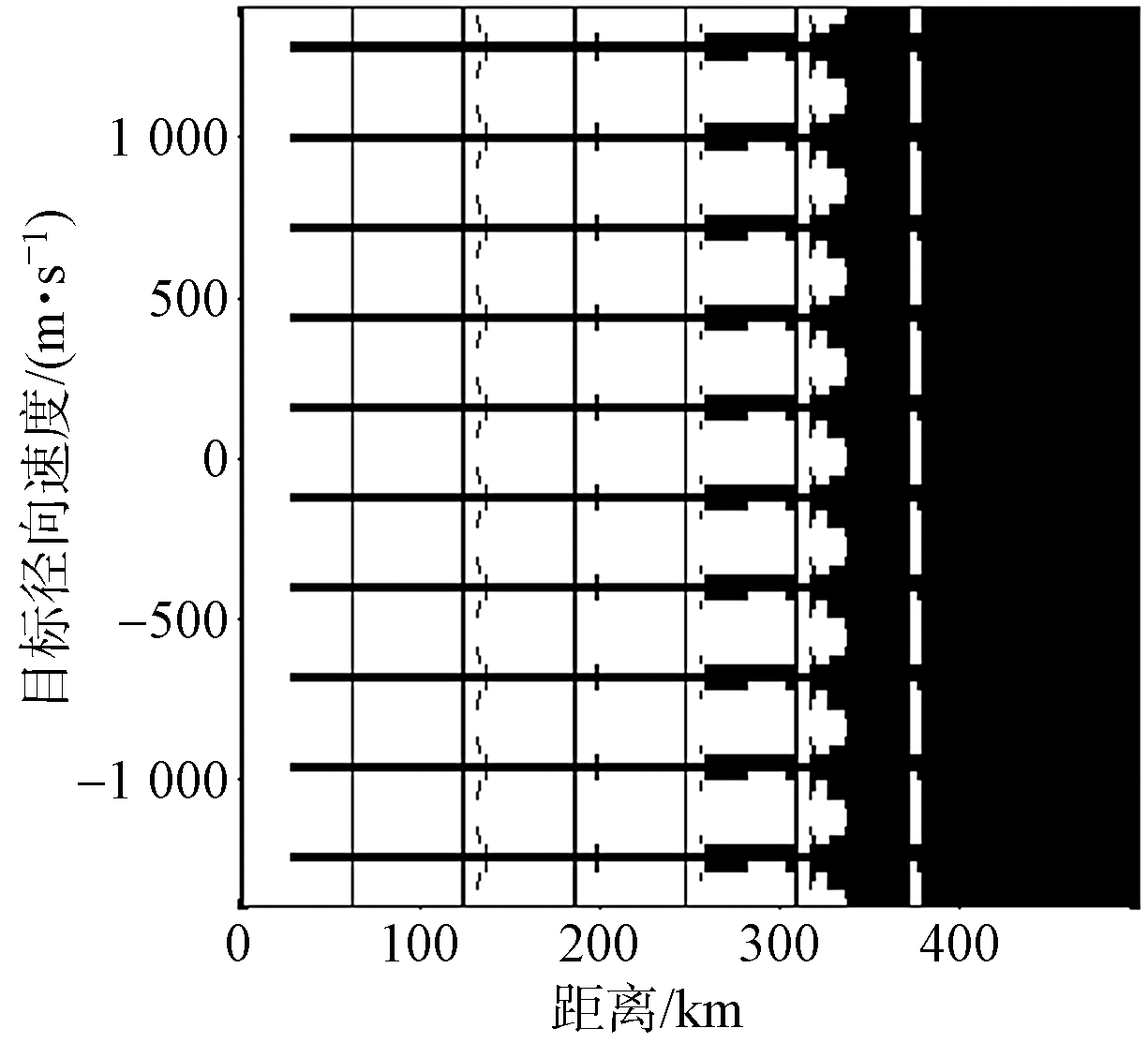
机载雷达技术指标中距离-速度二维盲区图是一项重要的指标。为体现本文方法的优势，图9给出了单重频情况下传统分区方法与本文分区方法的距离-速度二维盲区比较，其中设定目标RCS为3 m2。从雷达原理可知，当检测性能Pf=10-6，Pd=80%时，识别系数为12.8 dB。由图9可以看出：在距离400 km以内，传统分区方法和本文方法的清晰区占比分别为64.39%和70.23%。因此经过本文方法处理后的距离-速度二维盲区面积显著减小，全距离-全速度域运动目标检测性能提高近6%。
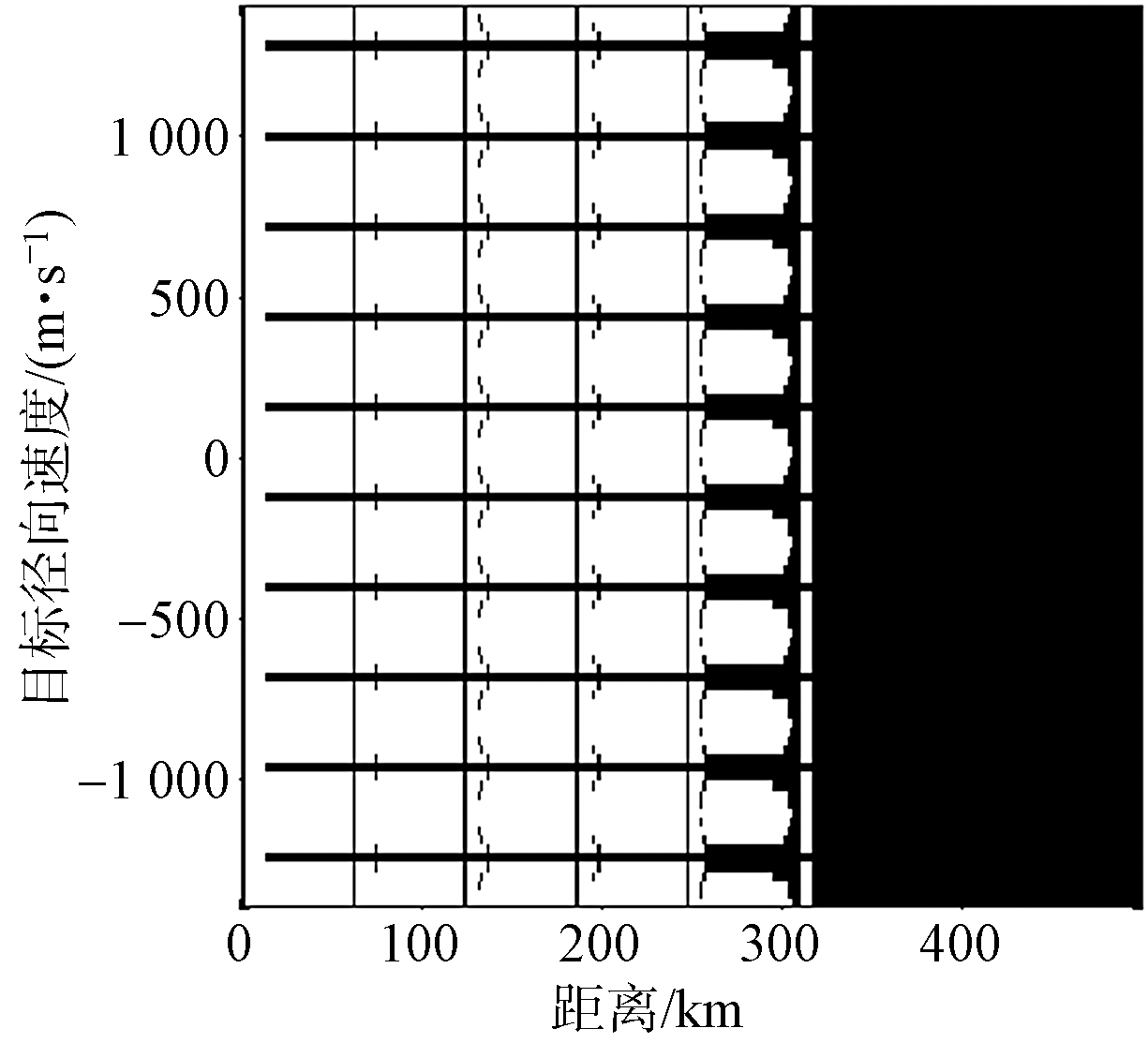
(a) 传统分区方法
(b) 本文方法
图9 距离-速度二维盲区比较(单重频)
4 结束语
针对实际工程中先基于先验知识对杂波距离-多普勒谱进行划分，后进行2D STAP处理方案中存在的问题，本文提出了一种基于自适应分区和正交投影的非平稳杂波抑制方法。该方法在对非平稳杂波进行自适应分区段之后，充分利用近程杂波的俯仰维信息，采用正交投影的杂波抑制方法，然后通过级联的方位-多普勒维STAP来抑制剩余的远程杂波。本文方法能解决先验知识的不足，同时在近程杂波区获得良好的杂波抑制效果，主瓣杂波也得到一定程度抑制，且显著提升了全距离-全速度域的目标检测性能。
[1] LI Yongwei, XIE Wenchong, MAO Huihuang, et al. Clutter Suppression Approach for End-Fire Array Airborne Radar Based on Adaptive Segmentation[J]. IEEE Access, 2019, 7:147094-147105.
[2] DUAN K, XU H, YUAN H, et al. Reduced-DOF Three-Dimensional STAP via Subarray Synthesis for Nonsidelooking Planar Array Airborne Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2020, 56(4):3311-3325.
[3] REN Zhengjiang, WU Di,GAO Mingwei, et al. Clutter Suppression for Airborne Weather Radar Using 3D-STAP[C]∥2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing: IEEE, 2020:468-473.
[4] 岳琦,吕晓德,杨璟茂,等.机载双基雷达3D-STAP杂波抑制方法[J].雷达科学与技术,2018,16(4):416-422.
YUE Qi, LYU Xiaode, YANG Jingmao, et al. Research on 3D-STAP for Airborne Bistatic Radar Clutter Suppression [J]. Radar Science and Technology, 2018, 16(4):416-422.(in Chinese)
[5] MENG Xiangdong, WANG Tong, WU Jianxin, et al. Short-Range Clutter Suppression for Airborne Radar by Utilizing Prefiltering in Elevation[J]. IEEE Geoscience and Remote Sensing Letters , 2009, 6(2):268-272.
[6] WU J, WANG T, MENG X, et al. Clutter Suppression for Airborne Non-Sidelooking Radar Using ERCB-STAP Algorithm[J].IET Radar Sonar and Navigation, 2010 ,4(4):497-506.
[7] WEN C, WANG T, WU J. Range-Dependent Clutter Suppression Approach for Non-Side-Looking Airborne Radar Based on Orthogonal Waveforms[J]. IET Radar Sonar and Navigation, 2015, 9(2):210-220.
[8] SHEN M, MENG X, ZHANG L. Efficient Adaptive Approach for Airborne Radar Short-Range Clutter Suppression[J]. IET Radar Sonar and Navigation,2012, 6(9):900-904.
[9] LI X, XIE W, WANG Y. Clutter Suppression Algorithm for Non-Side Looking Airborne Radar with High Pulse Repetition Frequency Based on Elevation-Compensation-Prefiltering[J]. IET Radar Sonar and Navigation, 2020, 14(1):19-26.
[10] KLEMM R. 空时自适应处理原理[M]. 北京: 高等教育出版社, 2009.
