0 引言
随着高级辅助驾驶系统的发展,传感器作为车辆感知的重要组成部分被广泛使用,主要有激光雷达、毫米波雷达、摄像头、超声波雷达等。毫米波雷达因其全天时、全天候的工作特点成为车辆感知系统中一个关键的传感器。77 GHz的线性调频连续波雷达由于其测量精度高、尺寸小、成本低以及信号处理简单等优点被广泛应用于汽车领域[1]。但随着道路上雷达数量越来越多以及有限的频谱资源,工作在同一频带内的雷达有可能会发生相互干扰的现象。当来自其他雷达的发射信号直接或间接地被本车雷达接收到,将会增大频域噪声基底,降低雷达的检测性能,甚至会产生虚假目标造成误检。因此车载毫米波雷达之间的相互干扰问题逐渐引起研究者们的关注[2-3]。
针对该问题,已有学者开展研究并提出了多种干扰抑制的方法。德国乌尔姆大学Goppelt等人研究了调频连续波雷达之间干扰的产生机理及其影响,并将调频连续波雷达之间的干扰分为交叉干扰和平行干扰两类[4]。交叉干扰会导致频域噪声基底升高从而降低雷达的检测性能,平行干扰会产生虚假目标造成雷达误检。文献[5]采用形态学成分分析(Morphological Component Analysis, MCA)方法将干扰信号从回波信号中分离出来,但该方法在干扰点数较少的情况下抑制效果会受到影响。在多输入多输出(MIMO)雷达系统中,通过数字波束形成技术在干扰到达方向形成零陷进行干扰抑制[6]。但该方法需事先对干扰到达方向进行估计且当干扰来自多个方向时,抗干扰性能将受到限制。深度学习可以在时域中恢复被干扰的信号[7],但是这种方法需要大量的带有标签的信号作为训练样本。文献[8]提出了一种使用迭代阈值进行干扰检测的方法。然而两个接收信号在无干扰段的信息是不同的,因此性能也将受到限制。文献[9]采用经验模态分解(Empirical Mode Decomposition, EMD)对回波信号进行分解,去掉干扰对应的分量。但该方法忽略了干扰对应的分量中可能包含有用信号的事实。
由于干扰雷达发射信号的能量远大于目标回波信号的能量[10],因此干扰信号会降低雷达的检测性能。干扰信号在时域可看作脉冲信号,在频域可作为白噪声处理。针对白噪声干扰,已有学者提出了不同的去噪方法。Seongwook Lee等人提出了基于小波去噪的雷达干扰抑制方法[11],但该方法会受到小波基选择的影响,进而影响干扰抑制的性能。文献[12]在频域采用自适应干扰消除算法对干扰进行抑制,该方法在不增加硬件开销的基础上可以起到一定的抑制效果,但是干扰抑制效果会受到算法中滤波器步长的影响。
针对现有方法的缺点,本文提出一种基于EMD和自回归(Autoregressive, AR)模型相结合的干扰抑制方法。该方法在进行干扰抑制的同时也尽可能地保留了有用信号。本文的实验步骤总结如下:首先将含有干扰的回波信号进行分解,通过本征模态函数的自相关函数能量找出有用信号主导的模态和干扰信号主导的模态。接着对干扰信号主导的模态采用阈值法进行干扰点检测,并采用自回归模型的方法对干扰点的值进行恢复。最后将所有的模态加起来得到干扰抑制后的信号。
1 信号模型
在这一小节,对FMCW雷达基本测量原理和含有干扰的回波信号模型进行了详细的描述。在1.1节中,对锯齿波FMCW测距测速原理进行了简要的描述。在1.2节中,给出了含有干扰的回波信号模型并对回波信号表达式进行了详细推导。
1.1 无干扰的回波信号模型
线性调频连续波又称为chirp信号,单个周期的FMCW雷达发射信号的表达式为
ST(t)=Acos{2π(f0t+0.5μt2)}
(1)
式中,A为发射信号的幅度,f0为载波信号的频率,μ=B/tm为调制斜率,B为信号的扫频带宽,tm为调制周期,如图1所示。
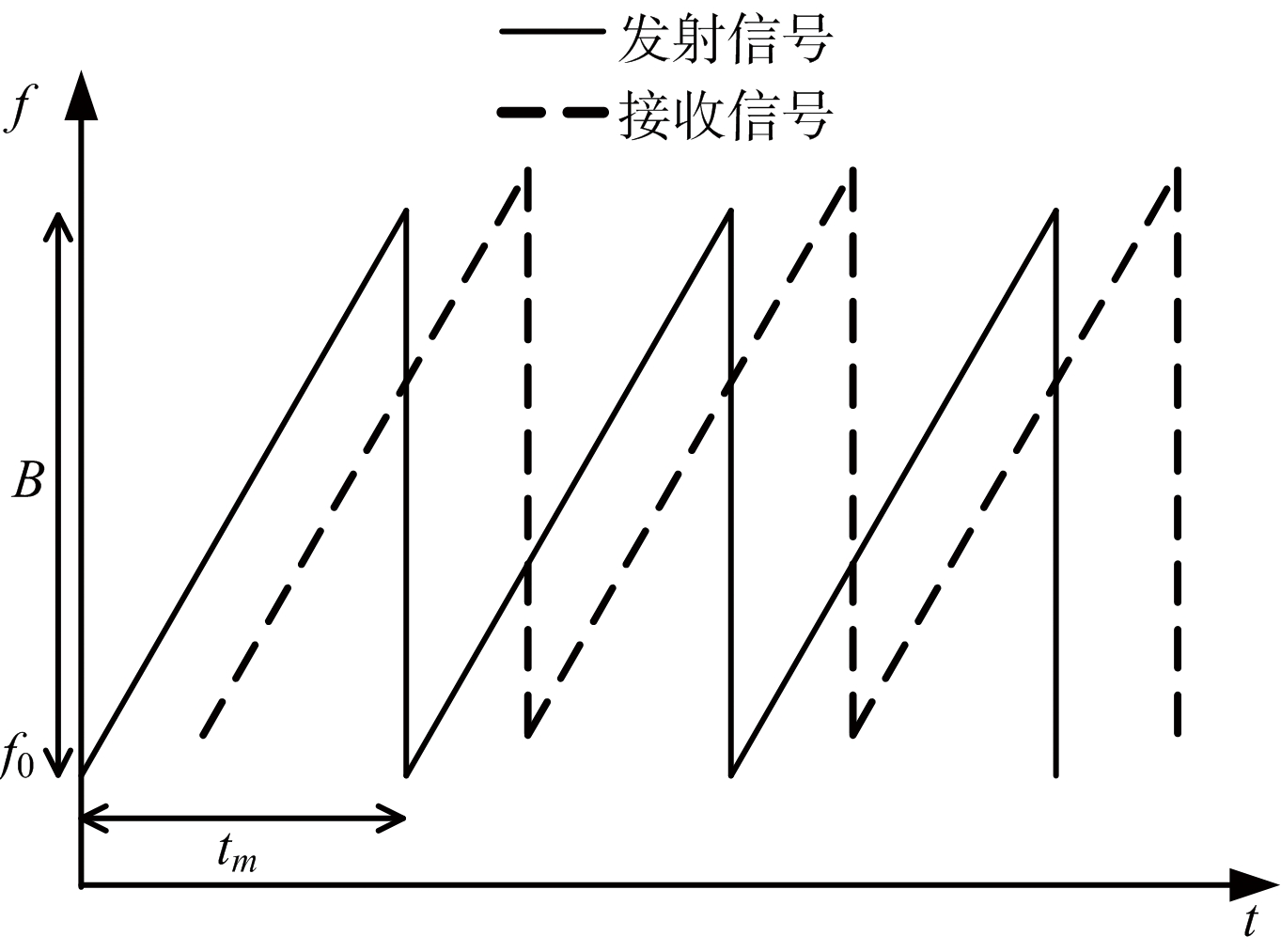
图1 FMCW信号示意图
多目标回波表达式为
SR(t)=![]()
0.5μ(t-td,i)2]}
(2)
式中,M为目标的个数,Bi为第i个目标回波信号的幅值,td,i和fd,i分别为第i个目标的延迟和多普勒频率。
发射信号和接收信号经过混频器后得到差拍信号,差拍信号经过低通滤波器后的输出表达式为
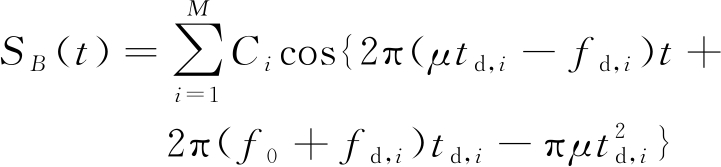
(3)
Ci为第i个目标差拍信号的幅值,由式(3)可知差拍信号的瞬时频率为
fb,i=μtd,i-fd,i
(4)
将td,i=2di/c带入式(4),得到第i个目标的距离为
(5)
通过二维FFT和目标检测算法得到第i个目标所在的距离单元和速度单元,将其转换成对应目标的fb,i和fd,i带入式(5)即可求出目标所在的距离。
1.2 有干扰的回波信号模型
雷达之间干扰的类型分为两类:交叉干扰和平行干扰。交叉干扰是指干扰信号的调制斜率和本车雷达相交,带来的影响在频域上表现为本底噪声的升高。平行干扰是指干扰信号的调制斜率和本车雷达相同,这会导致虚假目标的出现。由于平行干扰出现的概率很低[4],本文主要对交叉干扰进行分析。
当干扰存在时,接收信号的模型如图2所示,来自其他雷达系统的干扰信号的模型如式(6)所示,N是干扰源的个数,![]() 是第i个干扰源的幅值,
是第i个干扰源的幅值,![]() 是载波频率,
是载波频率,![]() 是多普勒频率,
是多普勒频率,![]() 是干扰源的调制斜率。
是干扰源的调制斜率。
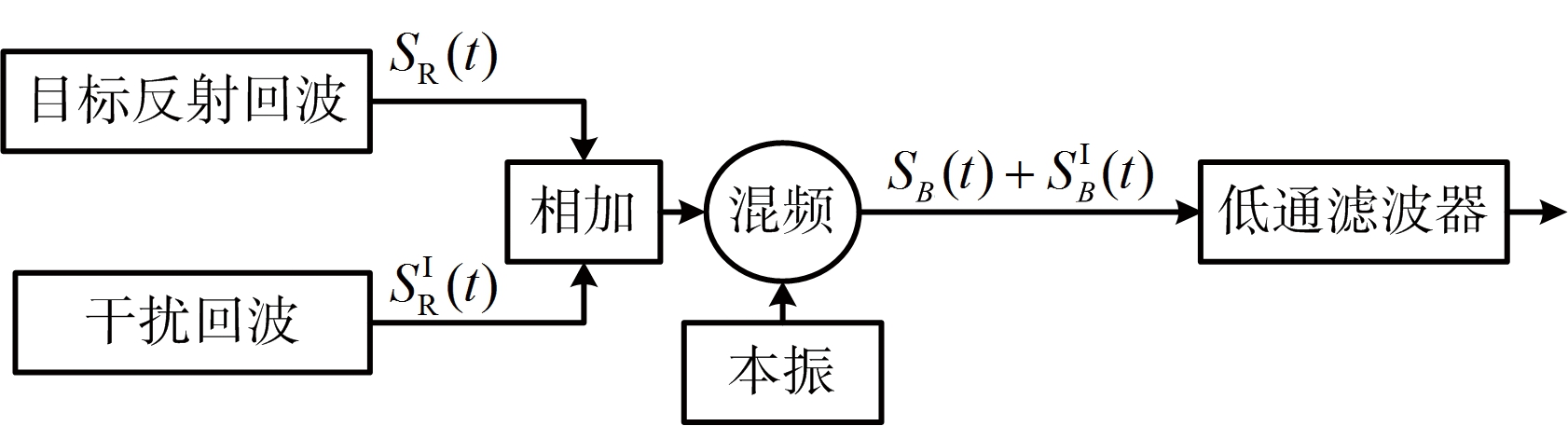
图2 接收信号模型
![]()
![]()
(6)
干扰信号与发射信号经过混频器之后的信号表达式为
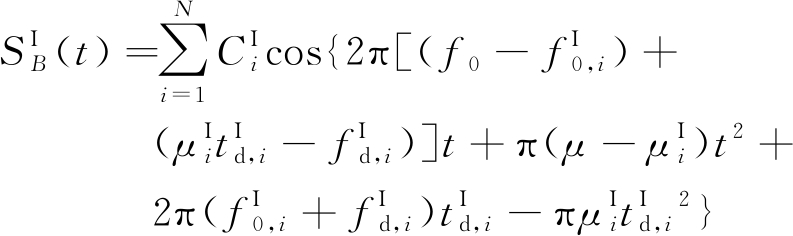
(7)
含有干扰信号的FMCW雷达信号模型的表达式为
(8)
混频后的信号需要通过低通滤波器,假设滤波器为理想低通滤波器,其频率响应函数为
(9)
fL为低通滤波器的截止频率。只有当干扰信号的频率落在低通滤波器的带宽内,才会对本车雷达产生干扰。假定本车雷达和干扰雷达采用的是同一型号的雷达,由式(7)可知,干扰信号的瞬时频率表达式为
(10)
由![]() 可以推导出干扰信号的持续时间为
可以推导出干扰信号的持续时间为
(11)
![]() 和μ分别为干扰信号和回波信号的调制斜率。那么干扰的点数为
和μ分别为干扰信号和回波信号的调制斜率。那么干扰的点数为
Nint=Tint·fs
(12)
fs为ADC采样率。信号最终的表达式如式(13)所示:
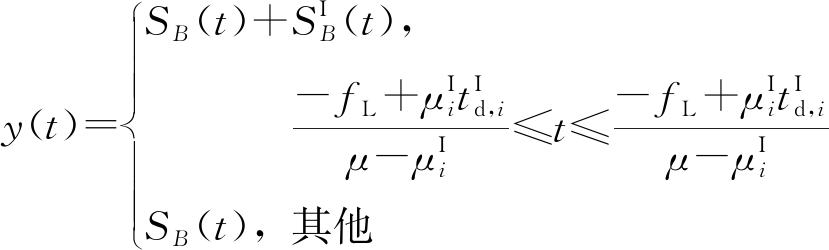
(13)
2 实验方法
在这一小节,对干扰检测和抑制所使用的具体步骤进行了详细的描述。在2.1节中,对EMD分解的基本原理作了阐述。在2.2节中,对如何确定分界IMF进行了概述。在2.3节中,对干扰检测和抑制所采用的方法进行了详细描述。
2.1 EMD算法的基本原理
经验模态分解是将信号自适应分解成有限个频率从大到小的本征模态函数(IMF)和一个残余信号[13],其中任意一个IMF都满足以下条件:(a) 整个信号中,过零点的个数和极值点的个数相等或至多相差1;(b) 信号上任意一点,由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值为零,即信号关于时间轴局部对称。
经验模态分解的步骤如下所示:
1) 找到信号x(t)的所有极大值点和极小值点,通过三次样条函数拟合出极大值和极小值包络曲线。上下包络曲线的均值作为原信号的均值包罗m1(t)。
2) 用原信号减去m1(t)得到一个新信号h1(t):
h1(t)=x(t)-m1(t)
(14)
3) 判断h1(t)是否满足IMF的条件。若满足,则h1(t)为首个IMF,记为c1(t);否则将h1(t)作为新的待处理信号,重复步骤1)~3),知道得到第一个IMF,记为c1(t)。
4) 将原信号x(t)减去c1(t)得到新的待处理信号r1(t):
r1(t)=x(t)-c1(t)
(15)
5) 对r1(t)重复上述得到c1(t)的过程,得到第二个IMF分量c2(t),如此反复进行,直到趋势项rn(t)是一个单调信号或rn(t)小于预设阈值,EMD分解结束。最后,x(t)经EMD分解之后得到:
(16)
含有干扰的回波信号经EMD分解为6个IMF和1个红色曲线表示的趋势项,如图3所示。
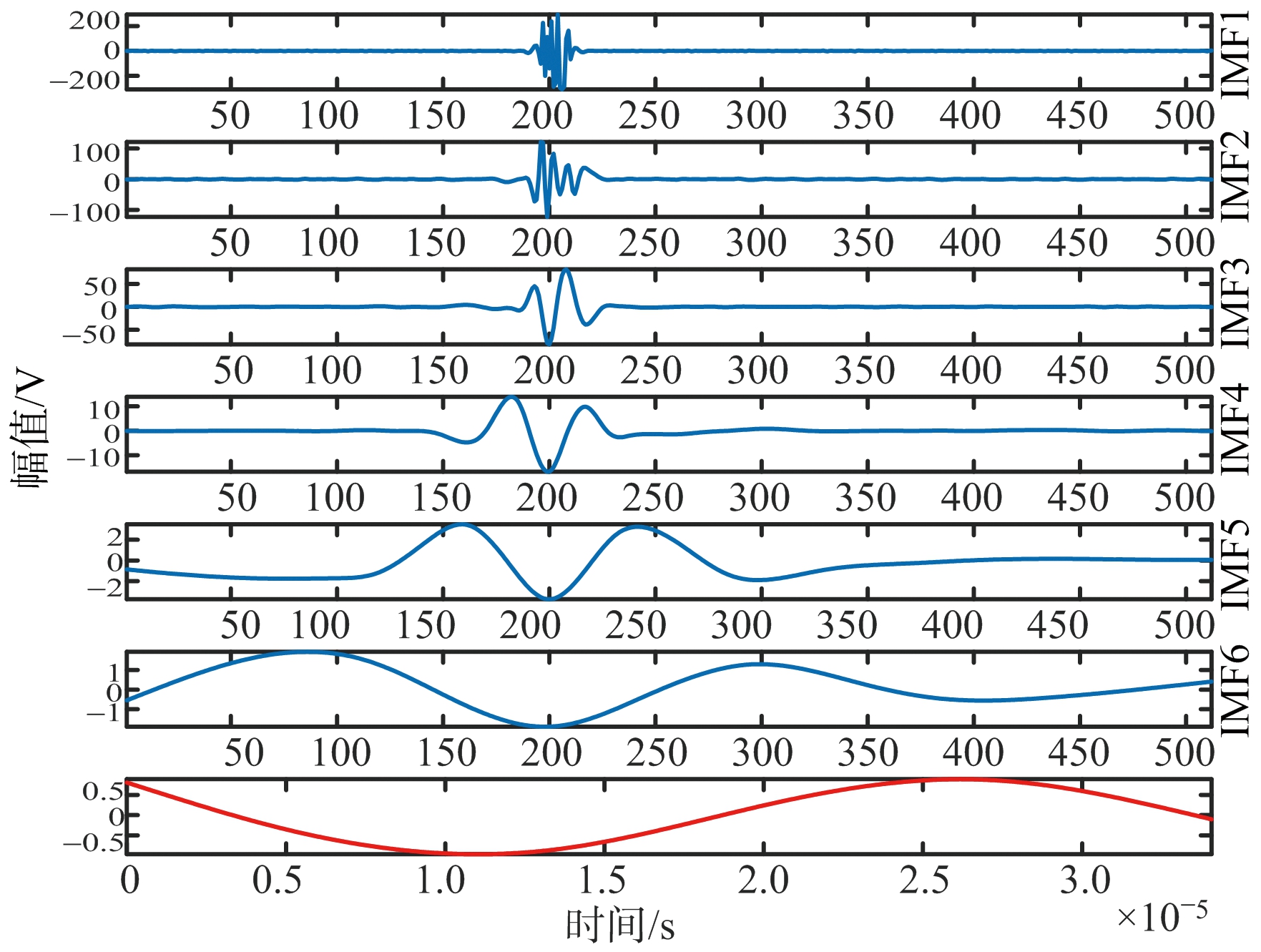
图3 EMD分解结果
2.2 IMF筛分准则
雷达回波信号包含目标回波以及干扰信号,经EMD分解后得到一系列的IMF,判断各个IMF中有用信号和干扰信号的权重尤为重要。随机信号的自相关函数反映了同一序列在不同时刻的取值之间的相关程度。由于干扰信号在频域上表现为白噪声,根据白噪声的统计特性,噪声含量高的信号在零点处相关函数最大,在其他位置衰减速度快,接近于零。因此,可通过求解各个IMF分量的自相关函数和其能量判断各个IMF分量噪声含量的高低,以此判断出分界IMF。
使用EMD算法对信号x(t)进行分解之后,对分解后的IMF求自相关函数的能量,结果如图4所示。由图4可知,低阶IMF通常包含干扰成分,称为干扰主导的IMF,高阶的IMF包含有用信号成分,称为信号主导的IMF[14]。分界的IMF为第二IMF分量,干扰信号主要集中在第一和第二分量。
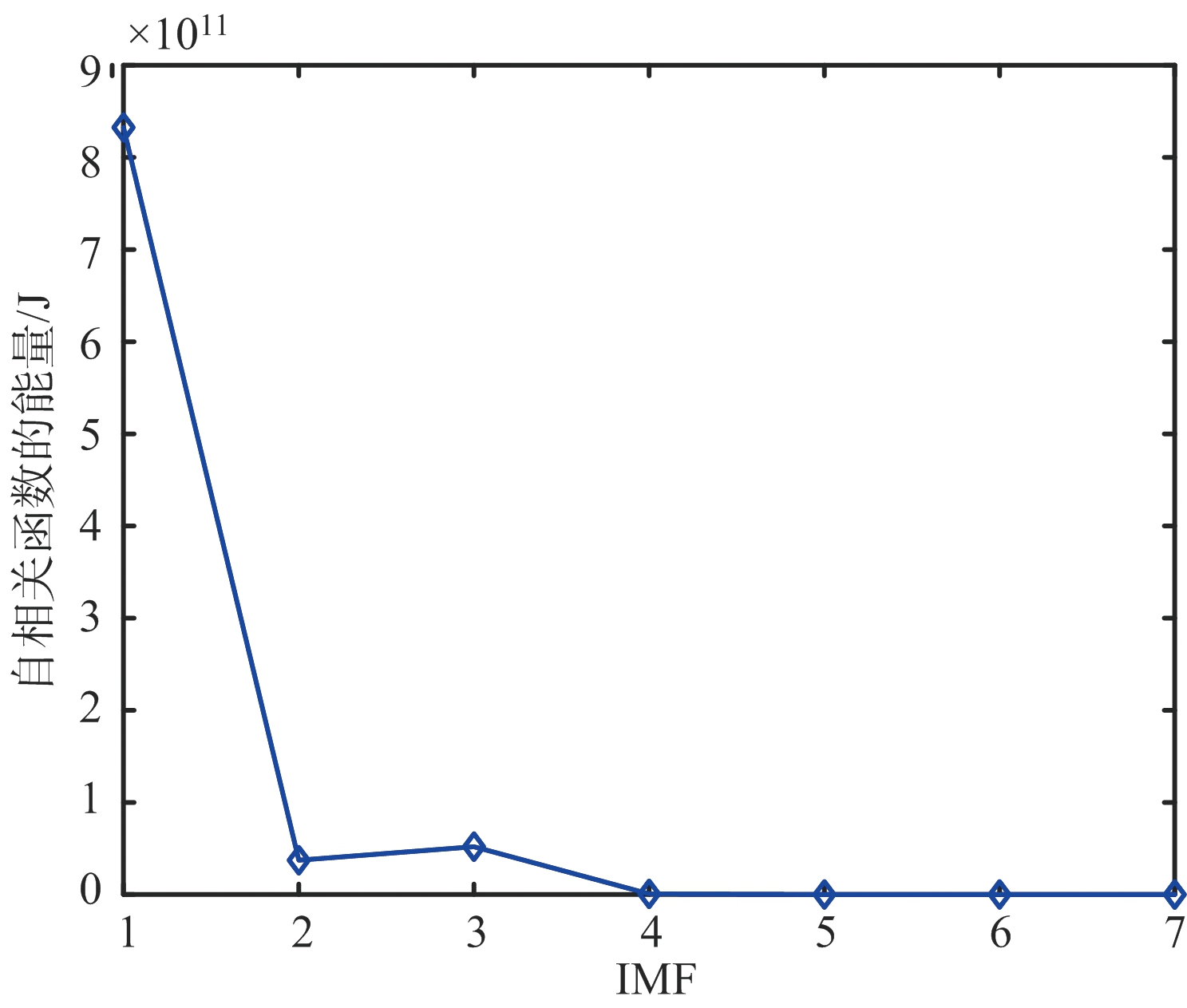
图4 IMF自相关函数能量
2.3 干扰检测和抑制
通常干扰信号的功率水平远高于回波信号的功率水平,在时域上表现为一个脉冲信号,所以通过设置阈值即可达到干扰检测的目的。以IMF1为例,图5为干扰点检测的示意图。红色虚线代表设定的阈值,大于该阈值的采样点值设为零。
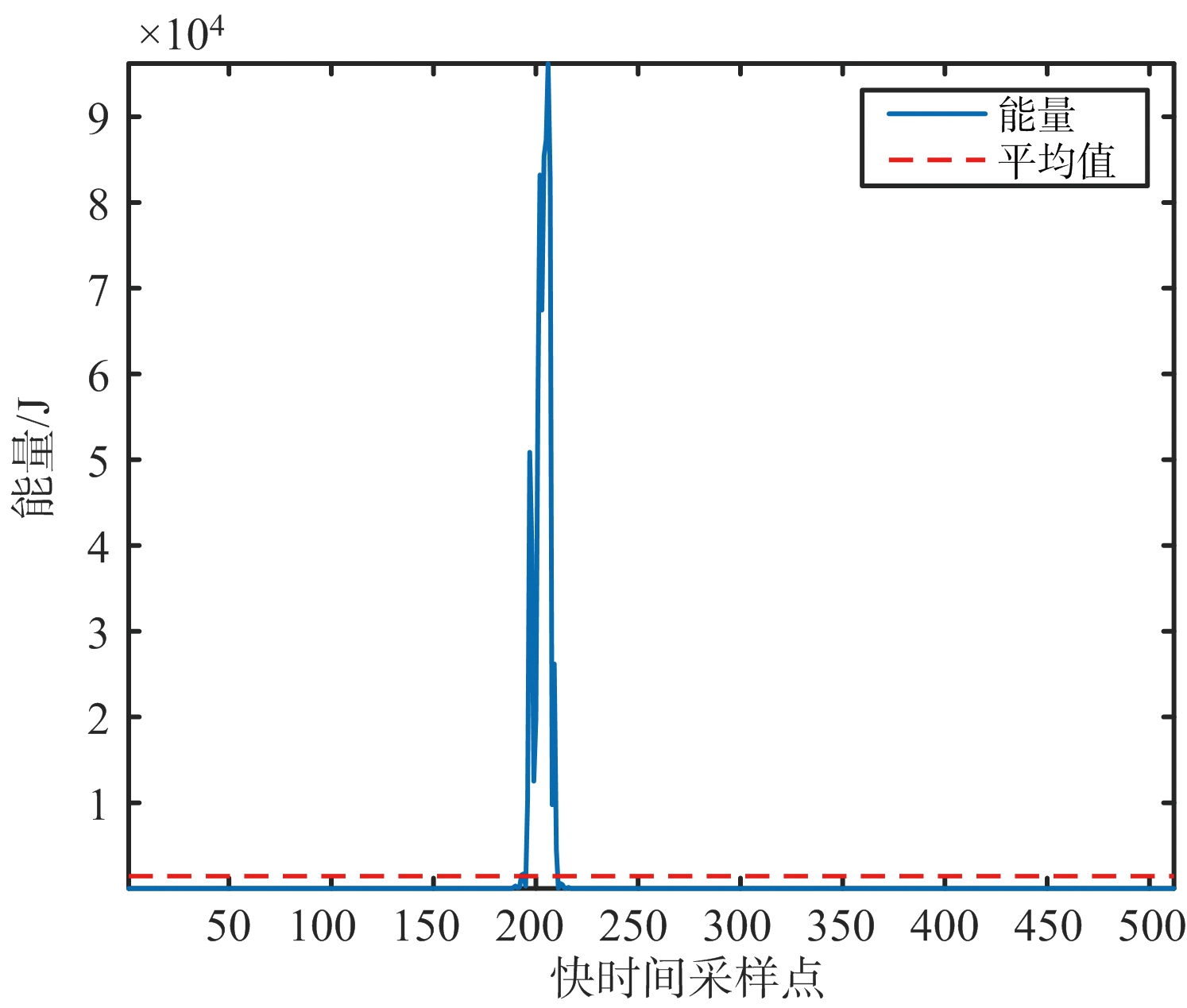
图5 IMF1干扰检测
自回归模型是统计学中一种处理时间序列的方法,用同一变量的之前各期的值来预测本期的值。实际上,一般应用中只采集到一个时间序列的有限个样本,可以通过模型预测出前面或者后面的数据。AR模型可以用差分方程来表示,如式(17)。
(17)
式中u(n)是均值为零、方差为σ2的高斯白噪声序列,p是AR模型的阶数,ap(i)是p阶AR模型的参数。使用AR模型之前,必须先计算出AR模型的参数。对于样本预测,本文选择Akaike信息准则(AIC)。AIC定义如式(18)。
(18)
i代表AR模型的阶,![]() 代表模型误差。当模型的阶确定之后,根据AR模型的阶次来计算模型参数。当模型的阶和模型参数确定后,就可以根据模型对干扰部分的采样点进行估计。目前计算模型参数的方法有Yule-Walker法,协方差法和Burg法。Burg法并不直接计算AR参数,而是先估计反射系数,避免了对采集信号两端未知数据的估计,具有较高的精确度。
代表模型误差。当模型的阶确定之后,根据AR模型的阶次来计算模型参数。当模型的阶和模型参数确定后,就可以根据模型对干扰部分的采样点进行估计。目前计算模型参数的方法有Yule-Walker法,协方差法和Burg法。Burg法并不直接计算AR参数,而是先估计反射系数,避免了对采集信号两端未知数据的估计,具有较高的精确度。
使用自回归模型进行信号估计的步骤可总结如下:
1) 将干扰信号分为三部分:干扰前的信号、干扰信号和干扰后的信号,记为yF,yI,yB,信号的长度分别记为Nf,Ni,Nb;
2) 计算F(i)=B/(i+A)+C(i>0,B<0),其中A=DNi/(1-2D),B=-ANi-A2,C=-B/A,D=Nf/(Nf+Nb);
3) 根据v(i)=0.5(1+cos(π(1+i/Ni))),计算窗函数ω(q)=v(F(q));
4) 重构干扰的信号,yI(q)=(1-ω(q))·yF(q)+ω(q)yB(q),q=1,2,…,Ni。
3 仿真实验
本文采用仿真实验对所提方法进行验证。本车雷达的载波频率为77 GHz,扫频带宽为600 MHz,雷达的距离分辨率可达0.25 m。(距离分辨率Rres=c/(2B),c为光速)。低通滤波器的带宽设置为7.5 MHz,可知雷达的最大无模糊测量距离为128 m(μ·(2R/c)≤BLPF,μ为信号的调制斜率,BLPF为低通滤波器的带宽),具体参数见表1。
表1 本车雷达的参数
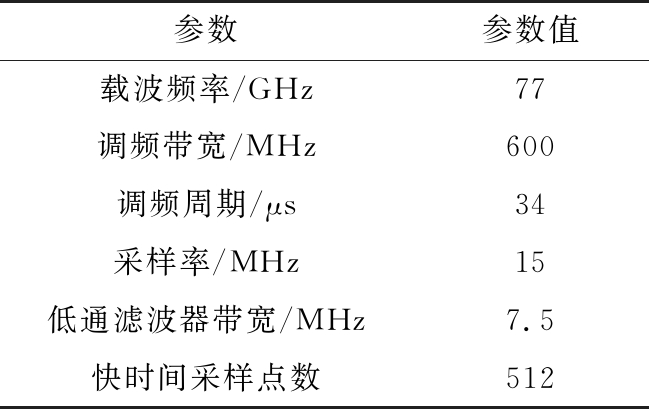
参数参数值载波频率/GHz77调频带宽/MHz600调频周期/μs34采样率/MHz15低通滤波器带宽/MHz7.5快时间采样点数512
4个目标和雷达的距离分别为10,20,30和40 m,目标的信噪比设为10 dB,信干比设为20 dB。干扰雷达的参数设置如表2所示。
表2 干扰雷达的参数

参数参数值载波频率/GHz77调制斜率/(Hz·s-1)1.75×1011调制周期/ms4快时间采样点数512
仿真信号如图6所示,其中图6(a)为信号的时域图,红色曲线表示没有干扰的信号,蓝色曲线为含有干扰的回波信号,干扰信号在时域上表现为一个脉冲信号且干扰信号的功率远远高于回波信号。图6(b)为信号的频域图,没有干扰的情况下,目标的信噪比很高利于目标检测。当干扰存在时,导致频域噪声基底升高,不利于目标的检测。
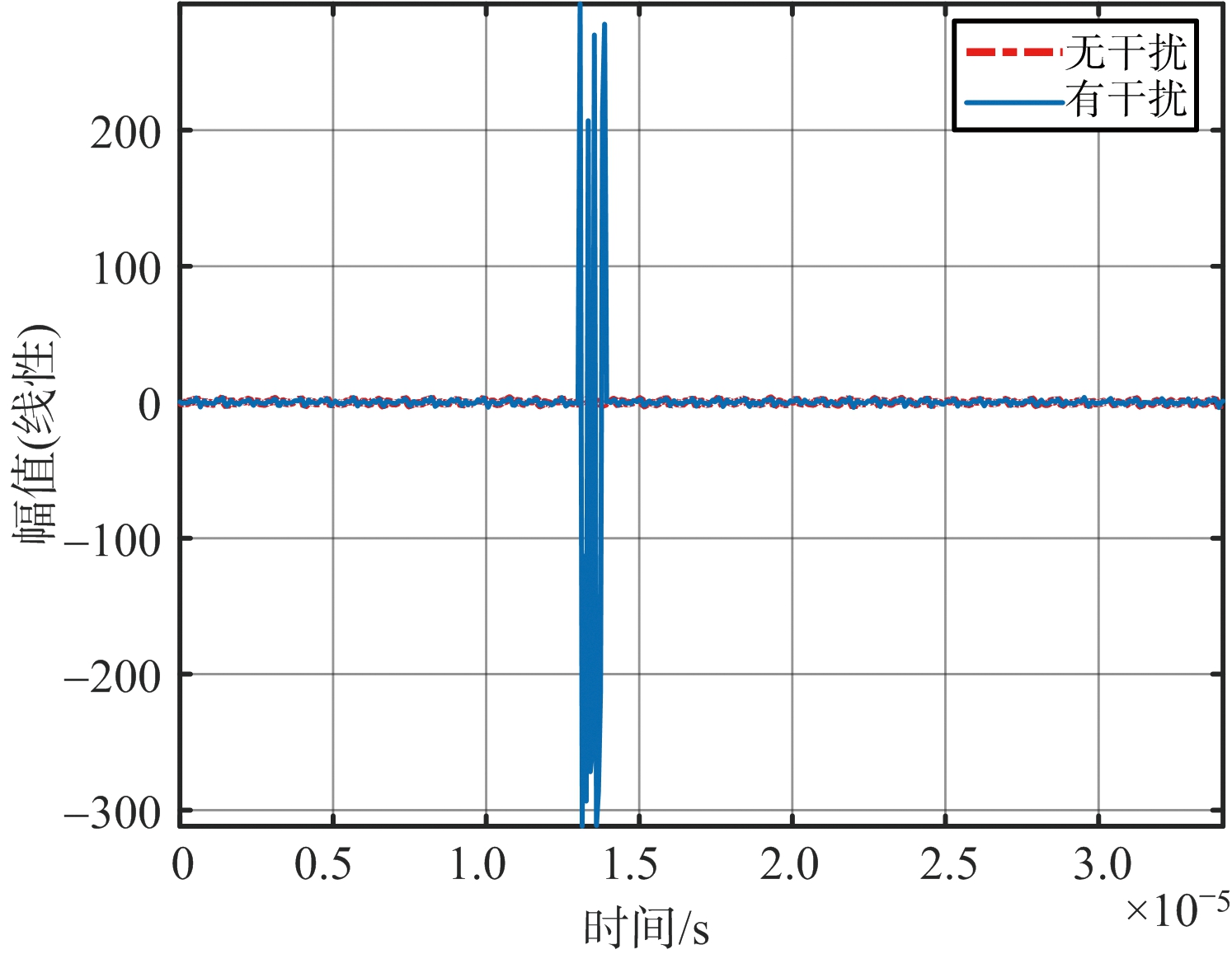
(a) 时域图
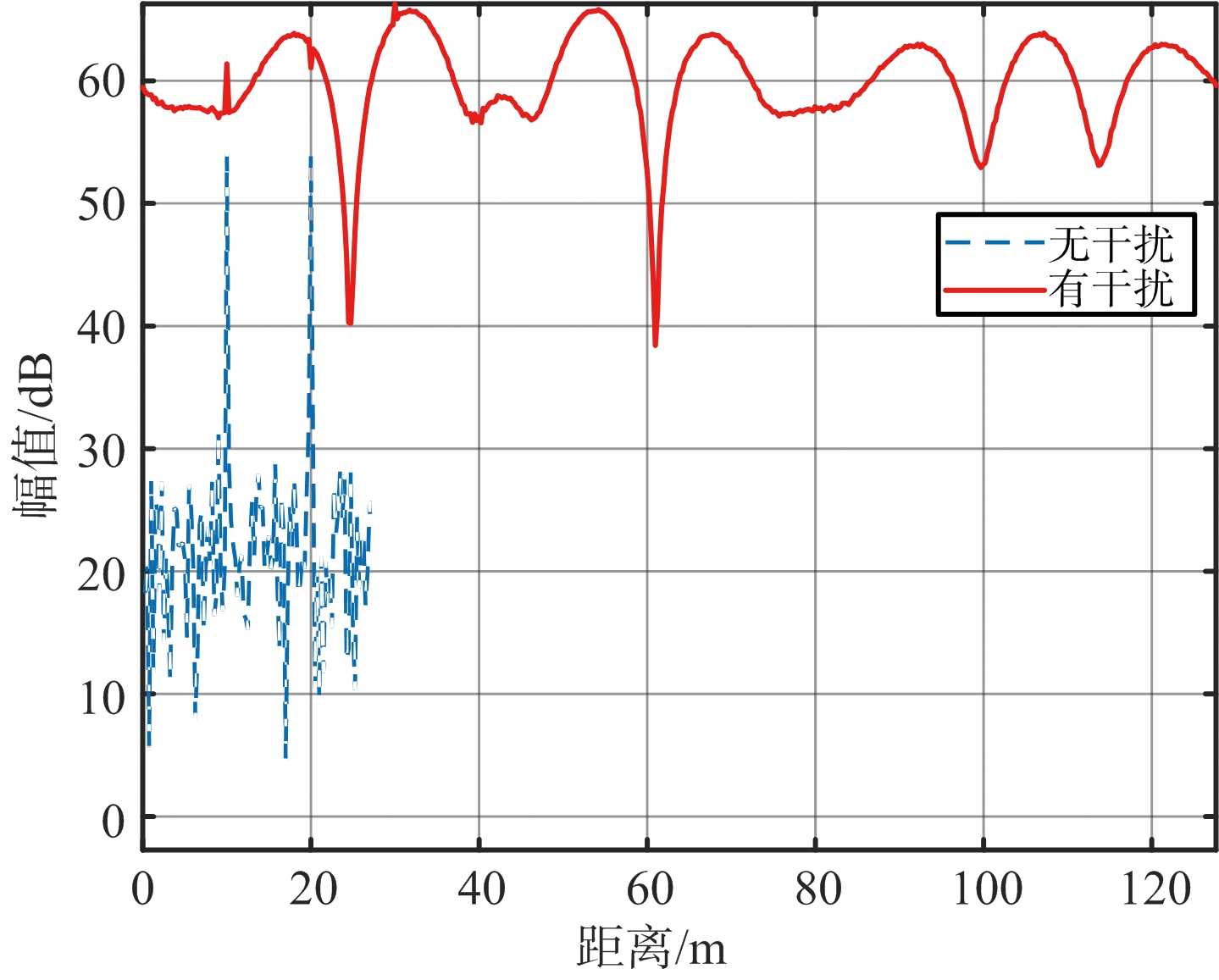
(b) 频域图
图6 仿真信号示意图
采用本文所提方法对干扰进行抑制。首先对信号进行EMD分解,含有干扰的回波信号经EMD分解为6个IMF和1个趋势项,结果如图3所示。其次,为了对干扰主导的模态进行处理,先要确定分界IMF,结果如图4所示。最后,采用AR模型对干扰主导的IMF进一步处理,最终的结果如图7所示。和图6(b)中红色曲线相比,该方法降低了频域噪声基底水平,使得目标更利于检测。
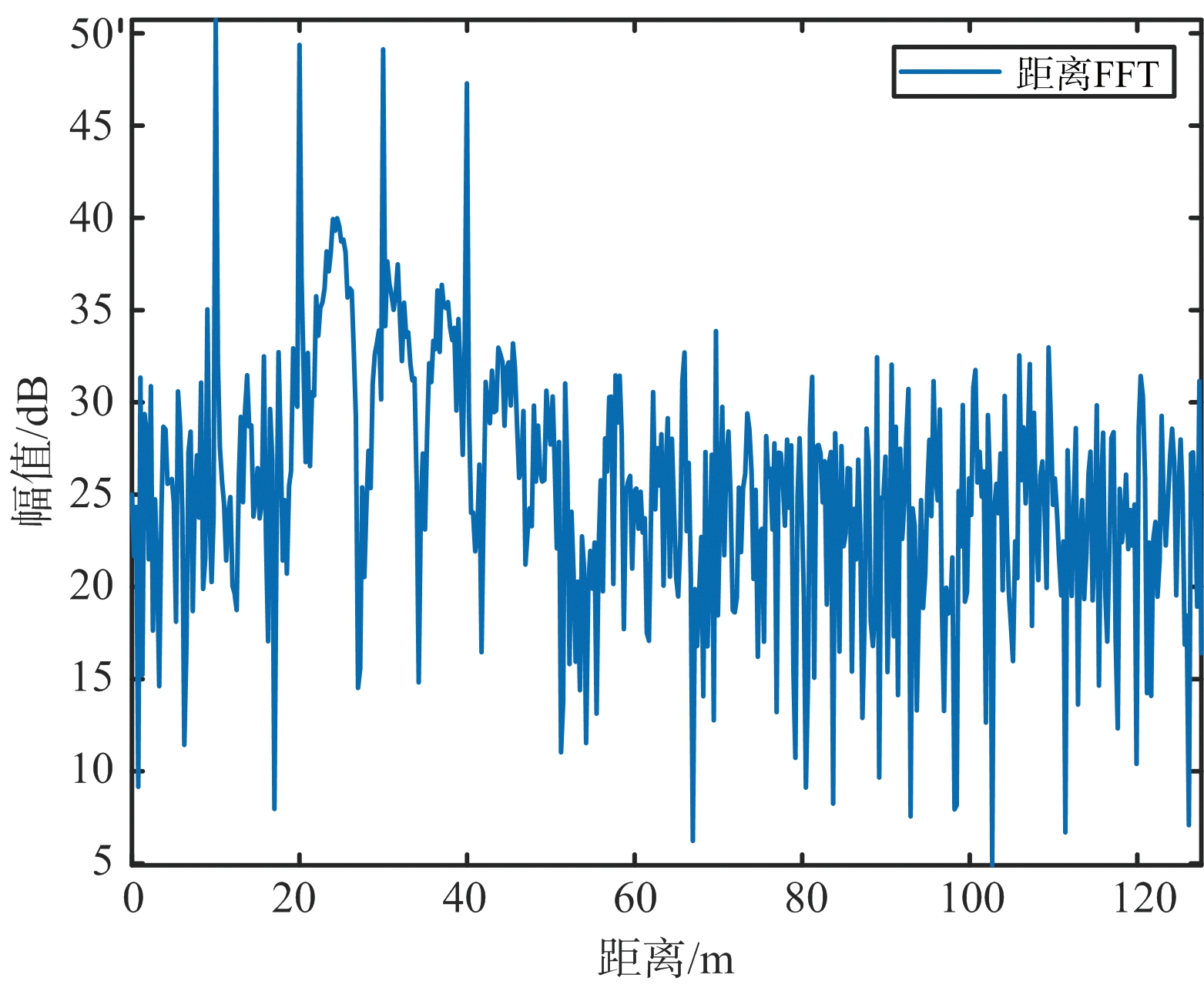
图7 干扰抑制结果
通过将本文的方法与其他方法进行比较,进一步验证所提方法的有效性。所选方法为加窗法和自适应噪声消除法(Adaptive Noise Cancellation, ANC),简要描述如下:
1) 余弦窗函数: 该方法首先需要进行干扰的检测,然后将回波信号中被影响的采样点通过加窗的方式填补。
2) ANC: 通过FFT频谱的负半部分来估计干扰的功率水平,然后将FFT频谱的正半部分和负半部分分别输入到自适应噪声消除器的主通道和参考通道,以此来达到抑制干扰的目的。
对比实验结果如图8所示。曲线1为干扰信号的频谱图,曲线3为采用ANC方法之后的频谱图。比较曲线1和曲线3可知,该方法对干扰抑制的效果不是特别明显。曲线2为使用加窗法之后的频谱图,将其与曲线3比较可知,该方法相较于ANC对干扰抑制的效果更好,但副瓣水平同样也很高。这种影响很可能会带来目标遮蔽现象,造成对弱小目标的漏检。曲线4为本文所提出的方法,和曲线2相比,该方法在进一步降低本底噪声的同时,也很好地改善了旁瓣的影响。以上方法对信噪比提升的结果见表3。
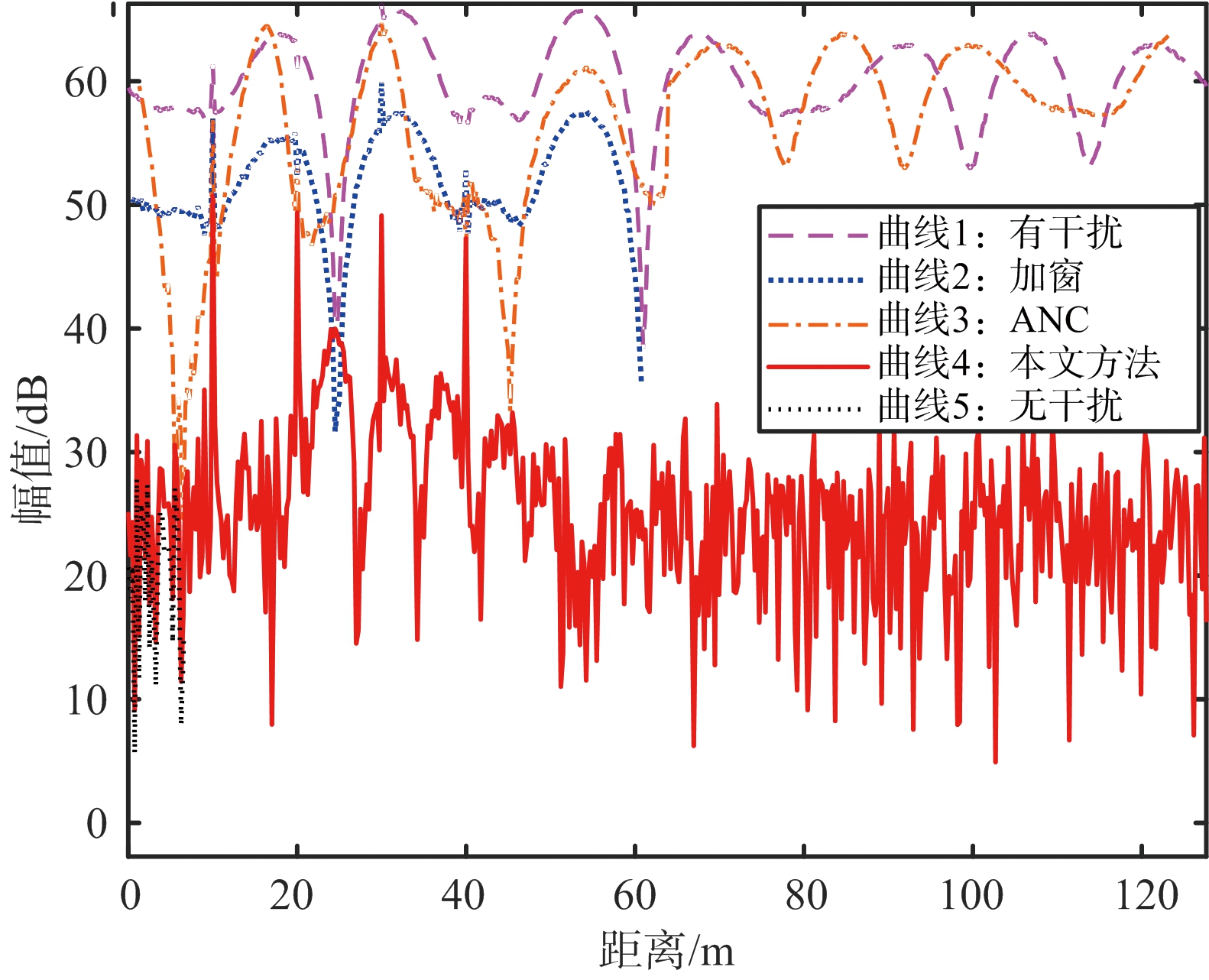
图8 实验结果对比
表3 不同方法的SNR dB
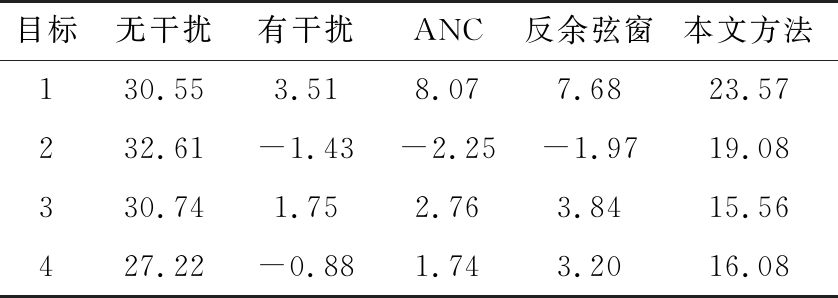
目标无干扰有干扰ANC反余弦窗本文方法130.553.518.077.6823.57232.61-1.43-2.25-1.97 19.08330.741.752.763.8415.56 427.22-0.88 1.743.20 16.08
4 结束语
针对FMCW雷达之间的交叉干扰导致目标信噪比下降的问题,本文采用经验模态分解和自回归模型相结合的方法进行干扰抑制。首先通过经验模态分解,对干扰主导的模态进行处理,在处理干扰的同时尽可能地保留了有用信号。其次,针对干扰主导的模态使用自回归模型对干扰点进行重构,得到干扰抑制后的信号。相较于其他方法,本文提出的方法降低了频域噪声基底,极大地提高了目标的信噪比,利于目标的检测。对比实验结果显示该方法对交叉干扰能够起到很好的抑制效果。
[1] BILIK I, LONGMAN O, VILLEVAL S, et al. The Rise of Radar for Autonomous Vehicles: Signal Processing Solutions and Future Research Directions[J].IEEE Signal Processing Magazine, 2019, 36(5):20-31.
[2] ALLAND S, STARK W, ALI M, et al. Interference in Automotive Radar Systems: Characteristics, Mitigation Techniques, and Current and Future Research[J]. IEEE Signal Processing Magazine, 2019, 36(5): 45-59.
[3] TERBAS D, LAGHEZZA F, JANSEN F, et al. Radar to Radar Interference in Common Traffic Scenarios[C]∥2019 16th European Radar Conference, Paris, France:IEEE, 2019:177-180.
[4] TOTH M, MEISSNER P, MELZEA A, et al. Analytical Investigation of Non-Coherent Mutual FMCW Radar Interference[C]∥ 2018 15th European Radar Conference, Madrid, Spain:IEEE,2018:71-74.
[5] UYSAL F, SANKA S. Mitigation of Automotive Radar Interference[C]∥2018 IEEE Radar Conference, Oklahoma City, OK:IEEE, 2018:405-410.
[6] BECHTER J, EID K, ROOS F, et al. Digital Beamforming to Mitigate Automotive Radar Interference[C]∥2016 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility, San Diego, CA:IEEE, 2016:1-4.
[7] MUN J, KIM H,LEE J. A Deep Learning Approach for Automotive Radar Interference Mitigation[C]∥2018 IEEE 88th Vehicular Technology Conference, Chicago, IL, USA:IEEE,2018:1-5.
[8] UMEHIRA M, NOZAWA T, MAKINO Y, et al. A Novel Iterative Inter-Radar Interference Reduction Scheme for Densely Deployed Automotive FMCW Radars[C]∥2018 19th International Radar Symposium (IRS), Bonn, Germany:[s.n.],2018:1-10.
[9] MOSTAFANEZHAD I , YAVARI E , BORIC-LUBECKE O, et al. Cancellation of Unwanted Doppler Radar Sensor Motion Using Empirical Mode Decomposition[J]. IEEE Sensors Journal, 2013, 13(5):1897-1904.
[10] AYDOGDU C, KESKIN M F, CARVAJAL G K, et al. Radar Interference Mitigation for Automated Driving: Exploring Proactive Strategies[J]. IEEE Signal Processing Magazine, 2020, 37(4):72-84.
[11] LEE S, LEE J Y, KIM S C. Mutual Interference Suppression Using Wavelet Denoising in Automotive FMCW Radar Systems[J].IEEE Trans on Intelligent Transportation Systems, 2019,22(2):887-897.
[12] JIN F, CAO S. Automotive Radar Interference Mitigation Using Adaptive Noise Canceller[J]. IEEE Trans on Vehicular Technology,2019,68(4):3747-3754.
[13] LI M , WU X , LIU X . An Improved EMD Method for Time-Frequency Feature Extraction of Telemetry Vibration Signal Based on Multi-Scale Median Filtering[J]. Circuits Systems & Signal Processing,2015,34(3):815-830.
[14] ELGAMEL S A , SORAGHAN J. Empirical Mode Decomposition-Based Monopulse Processor for Enhanced Radar Tracking in the Presence of High-Power Interference[J]. IET Radar Sonar & Navigation, 2011, 5(7):769-779.

