0 引言
近些年来,星载编队干涉合成孔径雷达(Interferometric Synthetic Aperture Radar, InSAR)已经广泛应用于生成高精度的全球数字高程模型(Digital Elevation Model, DEM),地表形变测量,自然灾害监测等领域[1-3]。精确的基线是保证上述应用准确性的前提[4],因此基线误差的标定是星载编队InSAR系统定标的关键环节。
TwinSAR-L (Terrain Wide-swath Interferometric L-band SAR),也叫LuTan-1 (LT-1), 是由两颗L波段SAR卫星编队组成的,是我国第一个民用双星编队SAR,其主要任务是干涉测高和形变测量。相较于TanDEM-X (TerraSAR-X add-on for digital elevation measurements),TwinSAR-L具有波长更长,基线更长,高程精度及定标精度要求更高,编队构型更为复杂等特点,这些特点给干涉定标特别是基线定标带来了更多困难,也提出了更高的要求。
目前,针对星载编队InSAR系统的基线定标方法主要分为以下两类:1)基于分布目标(外源DEM,如激光高度计获取的DEM数据)的基线定标方法;2)基于点目标(如无源角反射器和有源定标器)的基线定标方法。第一种方法具有分布范围广,不需要人工布设的优点,表面上其定标精度仅受限于参考DEM的精度,实际上还受分布目标后向散射系数即信噪比去相干和外源DEM与InSAR观测波段不一致时,二者得到的高程上原理性差异影响。例如,相同地表激光高度计几乎没有穿透,其测量高程为地表高程,InSAR测量的高程受波段影响,波长越长,穿透深度越深,L波段InSAR实际上测得的是地表以下高程。第二种方法可以通过增大点目标的RCS (Radar Cross Section)来提高信噪比,并且避免了载荷波段的穿透性来提高定标精度,但是L波段角反射器一般尺寸超过2 m,重量体积大,布设非常困难,其数量分布也十分有限。2013年,德国的Antony等人提出了适用于TanDEM-X系统的分布目标基线定标方法[4],并利用实测数据验证了定标方法的有效性,但是该方法在TanDEM-X任务中隐含了两个前提条件,即:1) 不考虑雷达信号的穿透误差,分布目标(激光高度计)参考高程可以直接使用;2) 分布目标(通常沙漠区)的信噪比足够高,可以忽略由于信噪比去相关引起的参考高程误差。
但是根据近些年关于L波段穿透深度的研究表明,L波段的SAR信号具有较强穿透地表的能力[5-7],L波段雷达信号的穿透误差是不可忽略的。此外,文献[8]介绍了TwinSAR-L的载荷设计,编队结构,成像模式;文献[9-10]详细分析了TwinSAR-L的相位同步问题,但是TwinSAR-L的基线定标很少被提及和讨论。
本文在TanDEM-X分布目标基线定标方法的基础之上,对L波段由于穿透深度和信噪比去相干产生的参考高程误差进行研究,并结合日本L波段ALOS-2 SAR卫星的实际数据得到了后向散射系数图像并利用Oh等人提出的经验模型[11]反演了介电常数图,对由Christian 1994年建立的沙地介电常数模型计算的沙地介电常数进行验证,最后将介电常数值带入Ulaby[12]的穿透深度模型中计算出L波段在研究区域的穿透深度;同时,利用后向散射系数结合研究区域的噪声等效后向散射系数推导出了研究区域L波段的相干系数及由信噪比去相干引入的相位误差及参考高程误差。
本文余下章节安排如下,第1节回顾了基于分布目标的基线定标方法,介绍了TwinSAR-L在使用该基线定标方法时不同于TanDEM-X的分别由穿透深度和信噪比去相干引入的参考高程误差ΔherrPen,ΔherrSNR;第2节详细分析了ΔherrPen和ΔherrSNR的仿真机理;第3节结合TwinSAR-L系统参数及日本ALOS-2 SAR卫星获取的新疆哈密沙漠地区的真实数据和仿真模型分别对由ΔherrPen和ΔherrSNR引起的基线误差进行了定量分析;第4节给出结论。
1 星载编队InSAR分布目标基线定标模型
在星载编队InSAR系统中,基线指的是两颗卫星之间的径向和横向轨道之间的距离[4], 而基线误差可分解为顺轨基线误差、垂直视线基线误差和平行视线基线误差三个分量。下面分别给出这三个误差分量对干涉测高的影响。
1) 顺轨基线误差ΔBalong
顺轨基线误差一般可以通过图像配准的方法解决,不会产生地形相位误差,因此对高程测量影响不严重。
2) 垂直视线的基线误差ΔB⊥
垂直视线的基线误差会导致相位与高度比例的偏差, 由此所产生的高程误差[13]为
(1)
式中,h为地形高度,ΔB⊥为垂直于视线的基线估计误差,B⊥为垂直基线的长度。由于ΔB⊥/B⊥大约在10-5量级,而地球的最大高程h<9 000 m。故B⊥只会引起厘米级的高程误差,相较于平行视线的基线误差引起的高程误差而言可以忽略不计。
3) 平行于视线的基线误差ΔB‖err
根据文献[4]可知,平行于视线的基线误差ΔB‖err是对DEM误差影响最大的基线误差分量,其产生的高程误差为
(2)
式中,λ为波长,Hamb是代表系统高度灵敏度的模糊高度,模糊高度等于一个条纹(2π)的相位变化,可以表示为
(3)
式中,r是到目标的斜距,θi是相对于目标位置处的最低点矢量的入射角,B⊥是垂直于视线的基线矢量的分量[13〗,将式(3)带入式(2)中得
(4)
对于给定的具有精确高程参考区域上的原始DEM,可以通过干涉测量来估计每次采集时的平行于视线的基线误差ΔB‖err[4]。将测得参考DEM和原始DEM的高度差带入式(4),从而计算未知值ΔB‖err,但是由于所使用的分布目标参考DEM高程与实际地物高程不完全对应,所以高程误差中会包含参考高程误差。为了描述这种复杂的关系,引入下面的高程误差估计方法,高程误差的组成如图1所示。
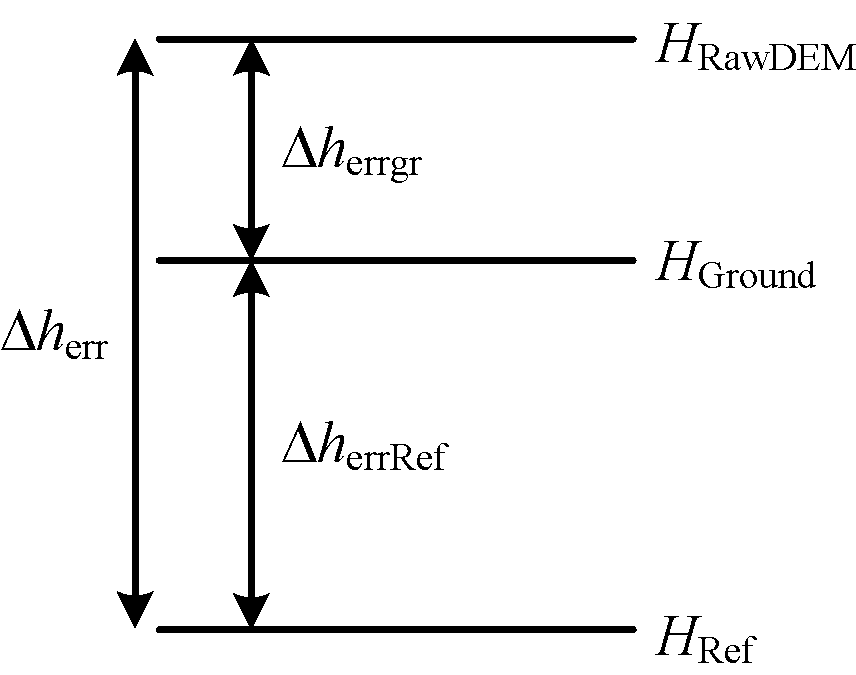
图1 高程误差组成示意图[4](HRawDEM为干涉测量DEM;HGround为地面真实高度;HRef为分布目标参考高程)
其中Δherr是上述定标原理中分布目标参考DEM和InSAR测量的原始DEM的高度差:
Δherr=HRawDEM-HRef
(5)
另外,由于所使用的分布目标参考DEM与实际地物高程不完全对应,因此参考高程误差由下式给出:
ΔherrRef=HRef-HGround
(6)
有效高度误差Δherrgf可以表示为
(7)
式中,Δφ是与视线方向的基线误差相对应的相位偏移。由文献[4]可知,Δφ可以假定为常数,将式(5)、(6)、(7)带入式(4)中得
(8)
将高程误差Δherr带入式(4)中可得
(9)
在L波段由于存在波段的穿透性和信噪比去相干的影响,我们认为ΔherrRef由3个误差量组成:ΔherrMea,ΔherrPen,ΔherrSNR,其中ΔherrMea为分布目标参考DEM自身测量上的误差,ΔherrPen为穿透深度引起的参考高程误差,ΔherrSNR为信噪比去相干引入的参考高程误差。故式(9)可以表示为
ΔB‖err=![]() Δφ-
Δφ-
(10)
在TanDEM-X项目中,没有考虑ΔherrPen和ΔherrSNR两项误差,通过递增地迭代参考高程HRef直到基线误差的方差最小来估计基准误差,但是TwinSAR-L系统中,必须先对ΔherrPen,ΔherrSNR这两项参考高程误差进行定量分析,深入地探讨这两项参考高程所产生的基线误差对基线定标精度带来的影响。
2 参考高程误差组成
由第1节内容可知,TwinSAR-L中参考高程误差由ΔherrMea,ΔherrPen,ΔherrSNR组成。本节将分析其中穿透深度引起的参考高程误差ΔherrPen和信噪比去相干引起的参考高程误差ΔherrSNR的仿真机理,为下一节内容提供理论支持。
2.1 穿透深度引起的参考高程误差ΔherrPen
近些年,对地表穿透深度的研究很多,主要分为以下两类:1) 基于实测的土壤湿度、粗糙度、土壤成分等数据利用经验模型计算介电常数,再通过乌拉比的穿透深度模型计算L波段在该地物下的穿透深度;2) 基于SAR信号穿过沙漠层时的散射和折射过程,构建反演模型。例如刘官鑫等人[14]提出了基于体相干性和成像几何的相干散射模型,用于沙漠地区穿透深度的研究,但是该模型对相干性和基线的要求较高。本文将利用SAR数据和经验模型相结合的方法对研究地区的穿透深度进行反演。
美国著名微波遥感学家Ulaby在其微波遥感著作中推导了有损介质遥感穿透深度计算模型,通过有损传输损耗的形式,给出穿透深度与波长和复介电常数的关系,为穿透深度的理论分析提供了依据。Ulaby将电磁波在有损介质中的穿透深度Lp定义为电磁波功率从介质表面到其功率衰减到1/e时的深度。当介质的介电常数满足![]() <0.1,则穿透深度Lp的公式[12]如下:
<0.1,则穿透深度Lp的公式[12]如下:
(11)
式中:λ为微波波长(cm),ε′,ε″分别为土壤复介电常数的实部和虚部。由式(11)可知,要想测量L波段在定标场的穿透深度,必先测量定标场土壤的介电常数。
1994年,Christian测量了0.245~6 GHz撒哈拉沙漠中沙地的复介电常数,他们根据导体或半导体背景成分中包含非导电沙砾混合物模型的Maxwell-Wagner损耗建立了沙地的介电常数模型(假设沙地的主要损耗来自沙砾部分),则沙地的介电常数ε表示为
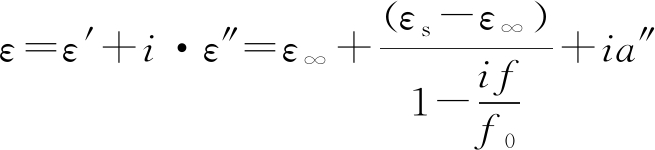
(12)
其中,当选择ε∞=2.53, εs=2.79, f0=0.27 GHz,a″ =0.002时,实际测量值与模型吻合良好。
如图2所示,本文首先利用Christian的介电常数模型(图2中经验模型(a))对哈密沙地的介电常数进行仿真,然后再利用ALOS-2的实测数据(图2中SAR幅度图)并结合Oh等人提出的经验模型[11](图2中经验模型(b))反演了介电常数图,对仿真的介电常数进行验证。最后将实验地区的介电常数带入Ulaby的穿透深度模型(图2中经验模型(c))中,即可完成研究地区的穿透深度反演。
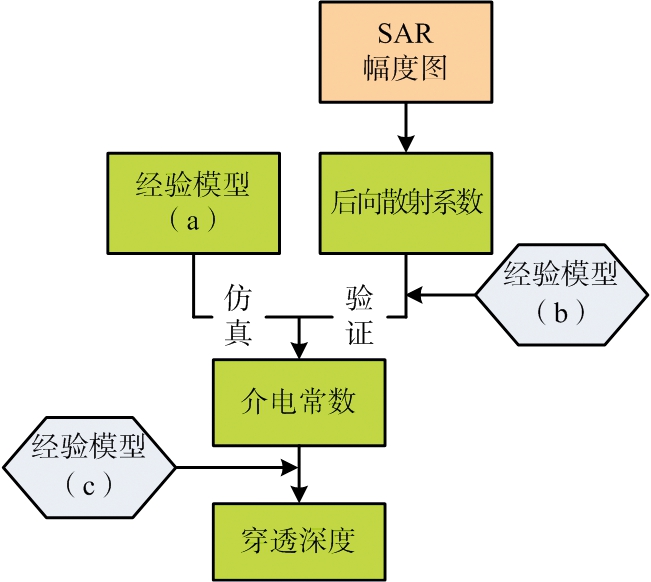
图2 穿透深度反演流程图
2.2 信噪比去相干引起的参考高程误差ΔherrSNR分析
相干性γ是估算干涉测量性能的关键参数之一,而信噪比是可能导致相干损失的重要误差源之一,L波段在沙漠的信噪比去相干会导致测量相位的误差,从而产生参考高程误差。后向散射系数与信噪比之间的关系可由下式表示:
SNR(dB)=σ0(dB)-NEσ0(dB)
(13)
其中 NEσ0 表示噪声等效后向散射系数,这是一个十分有用的参数代表了接收能量等于热噪声能量时的后向散射系数σ0,在TwinSAR-L项目中NEσ0的值为-28 dB。
信噪比是影响干涉图像的相干性重要因素,信噪比差会带来信噪比去相干,去相干越严重,则干涉相位误差越大,相应的干涉高程测量误差也会变大,信噪比去相干γSNR可以由以下方程表示:
(14)
而信噪比去相干γSNR与干涉相位误差之间的关系如下:
(15)
最后,由干涉相位误差引起的参考DEM变化为
(16)
如图3所示,本文首先利用ALOS-2的幅度数据提取研究地区后向散射信息,然后根据式(13)结合TwinSAR-L系统的噪声等效后向散射系数(Noise Equivalent Sigma Zero, NESZ) 计算出信噪比,然后根据方程生成研究地区的干涉系数图,然后根据式(15)和式(16)反演出研究地区的信噪比去相干参考高程误差反演图。
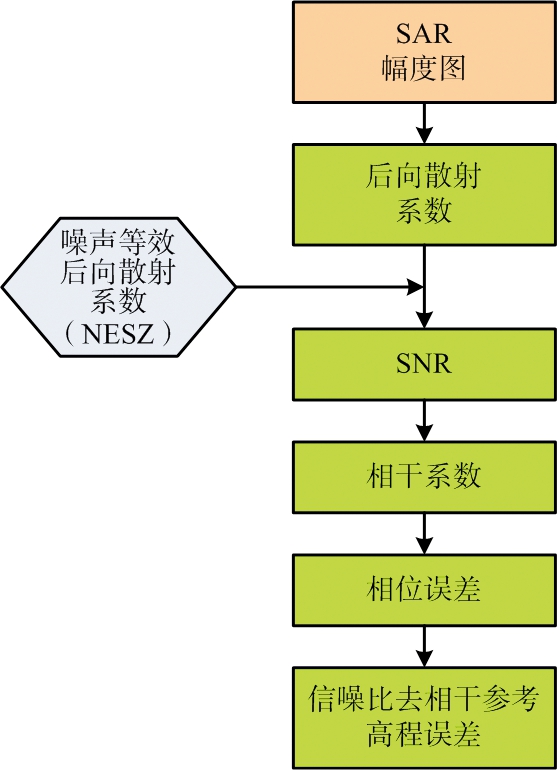
图3 信噪比去相干参考高程误差反演流程图
3 仿真试验与结果分析
3.1 实验场地和数据集
哈密位于中国新疆东部,面积超过13万平方公里,为温带大陆性干旱气候,干燥少雨,土壤极其干燥。沉积的风成沙形成沙丘和沙层覆盖沙漠表面。实验场地选在哈密地形相对平坦的沙漠地区。图4为谷歌地图中试验场地图像,如图所示该地区地形较为复杂,由沙土、裸露的岩石和沟壑。普通沙层如图4(c)、(e)所示;图4(b)为露岩区和浅沙覆盖区;图4(d)显示了以岩石和复杂沟壑为特征的区域。所选数据由ALOS-2型相控阵L波段合成孔径雷达(PALSAR)系统HH极化下获得。SAR图像的初始分辨率为10 m,入射角为36.6°。

图4 谷歌地图实验地区光学图像
3.2 结果及分析
结合TwinSAR-L的系统参数和第2节中介绍的ΔherrPen,ΔherrSNR的仿真机理,本节对TwinSAR-L任务中这两部分误差的仿真结果及产生的基线误差对基线定标的精度带来的影响进行分析,TwinSAR-L系统参数如表1所示。
表1 TwinSAR-L 系统参数
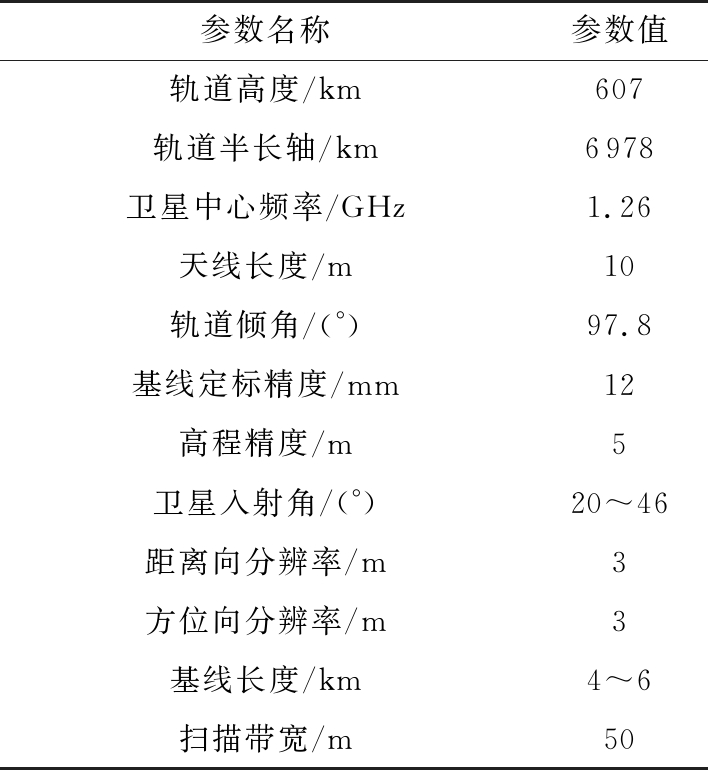
参数名称参数值轨道高度/km607轨道半长轴/km6978卫星中心频率/GHz1.26天线长度/m10轨道倾角/(°)97.8基线定标精度/mm12高程精度/m5卫星入射角/(°)20~46距离向分辨率/m3方位向分辨率/m3基线长度/km4~6扫描带宽/m50
3.2.1 穿透深度引起的参考高程误差分析
根据Christian的介电常数模型,我们对利用TwinSAR-L对L波段沙地介电常数进行了仿真,仿真结果如图5所示,介电常数的实部随着频率的升高而降低,当频率为1.26 GHz时,介电常数为(2.541 4,0.055 3)。
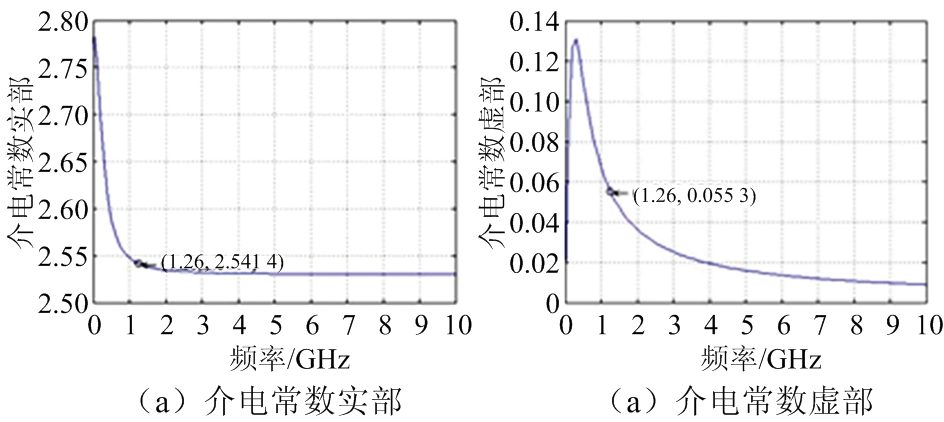
图5 介电常数仿真图
图6 (a)为HH极化下实验地区的幅度图像。较亮的部分与裸露的岩石覆盖的区域有关,这些岩石的表面是粗糙的,这有助于SAR传感器接收回波信号。较暗的部分对应均匀沙土覆盖的地区。按照第2节中穿透深度反演流程利用ALOS-2数据反演的介电常数值如图6(b)所示,其中红色矩形所包含区域的介电常数实部平均值为2.6,这与利用经验模型计算的大体一致。
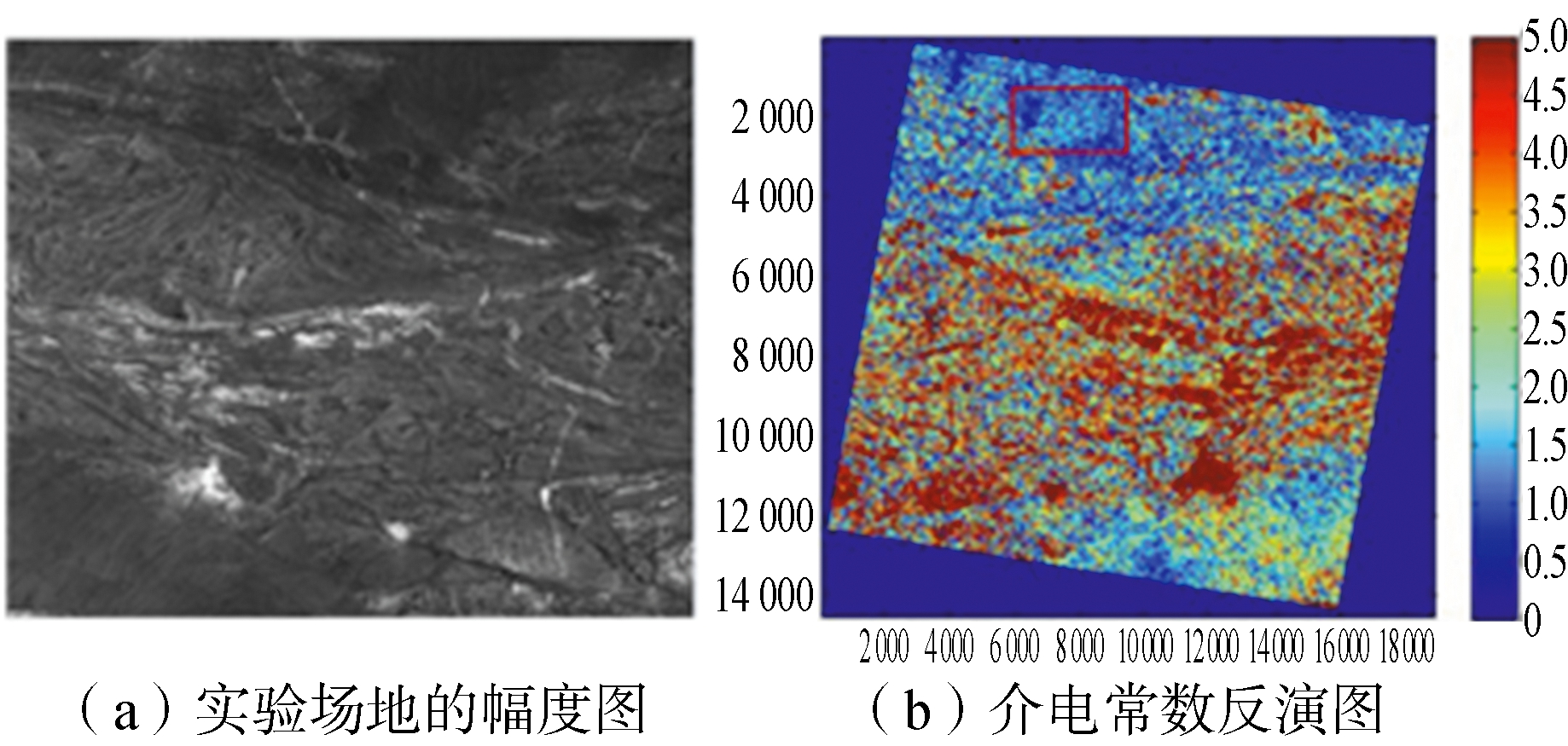
图6 实验场地幅度图与介电常数反演图
将上述过程获取的研究地区均匀沙地的平均介电常数值带入Ulaby穿透深度模型中得到L波段沙地穿透深度为Lp=1.0924 m。
在利用分布目标基线定标方法进行基线定标时,1.092 4 m 的穿透深度所导致的参考高程误差所导致的基线误差会达到7.9 mm (假设基线长度为4 km,入射角为33.6°)。
3.2.2 信噪比去相干引起的参考高程误差分析
根据2.2节中介绍的信噪比去相干参考高程误差反演流程,我们首先利用ALOS-2的幅度数据(HH极化)提取研究地区后向散射信息,然后根据式(13)结合TwinSAR-L系统的NESZ计算出信噪比,然后根据方程生成了研究地区的相干系数图,如图7(a)所示。高相干性表明在SAR数据采集期间荒漠表面没有明显变化。可以观察到,被岩石覆盖区域的相干系数值大于0.7,部分区域的相干性值甚至大于0.9。在均匀沙层覆盖区域,相干系数值在0.4~0.7之间,大部分都大于0.5。然后结合式(15)和式(16)反演出研究地区的信噪比去相干参考高程误差图。由图像可知,L波段SAR信号在沙层由于信噪比去相干引起的参考高程误差集中在1~2 m之间;对于被岩石覆盖的区域,对应的ΔherrSNR较小,范围在0~1 m之间。为了定量分析沙地的ΔherrSNR,选取均匀沙区,如图7(b)中的黑色矩形所示。该地区平均ΔherrSNR为1.39 m。

图7 相干系数图及信噪比去相干参考高程误差反演图
在利用分布目标基线定标方法进行基线定标时,1.39 m的信噪比去相干参考高程误差所导致的基线误差会达到10 mm(假设基线长度为4 km,入射角为33.6°)。
3.2.3 分布目标基线定标方法对TwinSAR-L系统的适用性分析
根据3.2.1节及3.2.2节中穿透深度及参考高程引入的参考高程误差分析结果可知,在利用分布目标基线定标方法进行基线定标时,1.092 4 m的穿透深度会引入7.9 mm的基线误差;1.39 m的信噪比去相干会引入高达10 mm的基线误差。从表1中TwinSAR-L的系统参数可知,其基线定标的精度要求为12 mm。这两项误差的存在将使得传统的分布目标基线定标方法不能满足TwinSAR-L系统的定标精度要求,并不直接适用于TwinSAR-L系统,因此在后续的工作中该系统若要使用分布目标基线定标,需要中对这两项误差进行补偿。
4 结束语
本文根据TanDEM-X分布目标基线定标模型修正了TwinSAR-L在使用该基线定标方法时不同于TanDEM-X的参考高程误差ΔherrPen,ΔherrSNR,并分别对这两项参考高程误差的原理进行研究,其中利用ALOS-2的数据及经验模型反演了研究地区的介电常数图,相干系数图以及信噪比去相干参考高程误差图,根据生成的结果分析了这两部分误差对基线定标精度的影响,为未来L波段星载编队InSAR分布目标基线定标方法提供了参考,对SAR系统设计、定标设计、InSAR处理有创新和借鉴意义。
[1] KUBANEK J, POLAND M P, BIGGS J. Applications of Bistatic Radar to Volcano Topography-A Review of 10 Years of TanDEM-X[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14(1):3282-3302.
[2] MARTINEZ M B, LOPEZ-SANCHEZ J M, MESTRE-QUEREDA A, et al. Exploring TanDEM-X Interferometric Products for Crop-Type Mapping[J]. Remote Sensing, 2020, 12(11):1774-1801.
[3] SEKERTEKIN A, MARANGOZ A M, ABDIKAN S. ALOS-2 and Sentinel-1 SAR Data Sensitivity Analysis to Surface Soil Moisture Over Bare and Vegetated Agricultural Fields[J]. Computers and Electronics in Agriculture, 2020, 171:1-11.
[4] ANTONY J W, GONZALEZ J H, SCHWERDT M, et al. Results of the Tandem-X Baseline Calibration[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3):1495-1501.
[5] Mccauley J. Paleodrainages of the Eastern Sahara—The Radar Rivers Revisited (SIR-A/B Implications for a Mid-Tertiary Trans-Afnrcan Drainage System)[J]. IEEE Trans on Geoscience and Remote Sensing, 1986, GE-24(4):624-648.
[6] FISCHER G, PAPATHANASSIOU K P, HAJNSEK I. Modeling and Compensation of the Penetration Bias in InSAR DEMs of Ice Sheets at Different Frequencies[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13(5):2698-2707.
[7] GUO H, LIU H, WANG X, et al. Subsurface Old Drainage Detection and Paleoenvironment Analysis Using Spaceborne Radar Images in Alxa Plateau[J]. Science in China Series D Earth Sciences, 2012, 43(4):439-448.
[8] LI C, ZHANG H, DENG Y K, et al. Focusing the L-Band Spaceborne Bistatic SAR Mission Data Using a Modified RD Algorithm[J]. IEEE Trans on Geoscience and Remote Sensing, 2020, 58(1):294-306.
[9] ZHANG Y Y, ZHANG H, OU N,et al. First Demonstration of Multipath Effects on Phase Synchronization Scheme for LT-1[J]. IEEE Trans on Geoscience and Remote Sensing, 2020, 58(4):2590-2604.
[10] JIN G D, LIU K Y, LIU D C,et al. An Advanced Phase Synchronization Scheme for LT-1[J]. IEEE Trans on Geoscience and Remote Sensing,2020, 58(3):1735-1746.
[11] OH Y, SARABANDI K, ULABY F T. An Empiri-cal Model and an Inversion Technique for Radar Scattering from Bare Soil Surfaces[J]. IEEE Trans on Geoscience and Remote Sensing, 1992, 30(2):370-381.
[12] ULABY F T, ELACHI C. Radar Polarimetry for Geoscience Applications[J]. Geocarto International, 1990, 5(3):38.
[13] GONZALEZ J H, BACHMANN M, KRIEGER G, et al. Development of the TanDEM-X Calibration Concept: Analysis of Systematic Errors[J]. IEEE Trans on Geoscience and Remote Sensing, 2010, 48(2):716-726.
[14] LIU G X, FU H Q, ZHU J J, et al. Penetration Depth Inversion in Hyperarid Desert from L-Band InSAR Data Based on a Coherence Scattering Model[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(11):1981-1985.
