0 引言
随着城市的快速发展，城市地下管线的分布也日趋复杂。当下很多老旧管线由于年代久远、缺乏管理和维护及设计图纸丢失等原因，已缺失管线位置、埋深等详细信息，给城市建设和施工等带来隐患。因此，精确确定地下管线位置、埋深等信息对城市建设和发展尤为重要。探地雷达(Ground Penetrating Radar, GPR)由于其高分辨率、高效性、无损性等优势，现已广泛应用于城市地下管线，尤其是非金属管线的探测中[1-3]。
探地雷达作为一种重要的地球物理手段，其原理是通过发射天线向地下发射电磁波，由接收天线接收电磁波在地下传播过程中产生的反射和散射信号。根据电磁波的传播规律，通过对接收信号的数据处理和解译便可得到地下介质的结构和物性信息[4-6]。
对于地下管线的探测，国内外学者已开展了大量基于探地雷达的管线探测研究。许崇华等利用天线阵技术对PVC管道进行探测，实现了对管道不同频率、不同角度的探测，并提高了探测的精度和速度[7]。杨剑等利用探地雷达对城市地下管线进行探测，为后续工程钻孔定位提供了指导依据[8]。Shihab 等通过对埋藏的圆柱体进行数学建模，提出了与波速、半径和移动位置等因素相关的双曲线时程方程，推导了半径和波速与双曲线实半轴和虚半轴的关系，之后使用最小二乘法拟合计算了波速、圆柱体半径以及埋深[9]。Ristic 等在没有介电常数等先验信息的前提下，使用Levenberg-Marquardt最优化算法和迭代方法更准确地估计了电磁波在地下介质中的波速，然后利用一阶最优准则估计了地下管线的半径[10]。Zhao 等通过迁移重建和稀疏重建方法重建探地雷达图像中的排水管目标，同时可以确定排水管的位置和管
等通过每列最大值拟合出双曲线，再确定双曲线对称的端点的列序号，则通过双曲线顶点位于中间列的思路确定顶点，来实现对散射体反射双曲线的定位[12]。尽管已有研究可以利用探地雷达结果来估计地下管线的埋深，但是这些方法存在计算成本高，计算精度不足、鲁棒性不足等问题，尚未在实际工程应用中得以推广应用。使用探地雷达数据实现对地下管线目标的准确定位和埋深估计仍然是一项技术难题。
本文提出了一种基于三维速度谱分析的探地雷达地下管线埋深估计方法。首先，对探地雷达获取到的共偏移距探地雷达数据应用三维速度谱算法精确计算电磁波在地下介质中的传播速度，然后使用该速度对所获得的雷达数据进行背向传播偏移处理来实现地下管线目标的准确定位。本文通过对数值仿真及现场实验验证了三维速度谱算法的精度和鲁棒性。
1 原理
1.1 三维速度谱
速度谱分析方法是地震资料处理中常用的估计地震波速度的方法，速度谱分析方法通常用于地震勘探和探地雷达共中心点(Common Midpoint，CMP)数据的处理分析，但也可以应用于共偏移距(Common Offset，CO)数据的处理[13]。它的原理是假定一系列可能的试验速度，由这些试验速度确定的双曲线计算在不同偏移距处或不同通道信号的相干性，然后叠加相干度绘制在速度与垂直行程时间图中，即得到速度谱。当试验速度接近真实速度时，叠加能量在速度谱中出现峰值，由此可以从速度谱中提取双曲线反射的速度和双向垂直传播时间[14-16]。信号相干通过叠加振幅计算，公式如下：
(1)
i=1,…，nt; j=1,…，nx; k=1,…，nv
式中，f为t-x域中的共偏移距数据，Ni为第i次选择的水平计算区域尺寸，nt、nx和nv为每条记录道的采样点数量、道数和迭代计算中使用的速度数，xj为第j个点与双曲线的极值点之间的水平距离，ti,j,k为双曲线第j个点的双向时间。
ti,j,k可通过以下公式获得：
(2)
式中，ti为双曲线顶点的双程走时，vk为计算中使用的速度。
然而，由于受到噪声或杂波干扰，以及背景介质速度不均的影响，实测雷达剖面中地下目标对应的双曲线形态经常会出现例如不完整、歪曲、交错或振幅不均匀等异常，导致计算得到的叠加振幅效果较差。为了解决这些情况带来的干扰，对叠加振幅进行归一化处理：
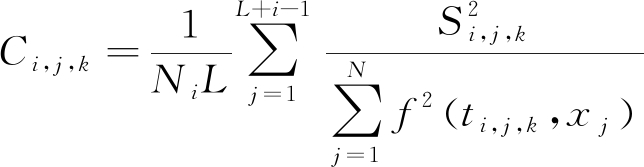
(3)
式中，L为反射双曲线在时间方向上的宽度。由于雷达剖面中的双曲线反射具有一定宽度，所以使用该双曲线宽度的平均值对叠加振幅进行归一化来保证计算结果Ci,j,k不受振幅变化的影响。重要的是，在式(3)中加入了1/Ni，以补偿沿纵向使用不同窗口Ni所引起的能量差异。Ci,j,k是三维数据，由其能力最大值所对应的三维坐标可以分别确定双曲线顶点的时间、水平位置以及电磁波在地下介质中的传播速度。
在计算得到的三维速度谱中，我们对Ci,j,k进行了归一化处理。随后，为了抑制干扰，本文应用了一个软阈值函数，如下式：
(4)
式中a的值设置为0.8。
通过沿距离轴的最大值找到双曲线顶点的位置，从三维速度谱中提取出该位置的速度切片。速度切片中能量最强点的速度坐标即为电磁波在地下介质中的传播速度。
1.2 背向传播偏移算法
电磁波在地下传播时，遇到点状或者圆柱状目标会发生散射现象，表现在雷达剖面中是双曲线形态的地下反射信号。但由于受到噪声或杂波干扰，以及背景介质速度不均的影响，所形成的双曲线会出现不完整、歪曲和交错等异常，其顶点并不能准确地反映目标的真实位置，因此将雷达剖面中的地下反射归位到其真实位置至关重要。背向传播偏移是基于射线理论的一种偏移方法，该方法的原理是各记录道的振幅值接近同相堆叠，叠加后的振幅值增大；反之，当没有反射界面或在绕射点时，由于背景介质的不均匀性，各记录道的随机振幅值没有同相叠加，它们会部分相互抵消，并且叠加后的总振幅值相对减小，从而完成反射波和绕射波的自动归位[17]。
图1(a)为探地雷达在地表沿着测线方向采集B-Scan数据的示意图。由于不同位置地下目标散射的电磁波传播时间不同，接收天线接收到的电磁波信号在雷达剖面图中显示为双曲线，如图1(b)所示。
图 1 探地雷达地下探测原理示意
在图1(a)中，对于位于点(x, h)的散射体，其中x为天线扫描方向(即测线方向)的距离，h为目标的地下埋置深度，发射天线和接收天线的位置分别为Tx，Rx。
在均匀地下介质中，发射天线发射电磁波遇到散射体目标后发生反射，最终被接收天线接收，整个过程的传播距离为
(5)
对应电磁波的行程时间为
t=
=
(6)
式中 v 为电磁波在介质中的传播速度。
对探地雷达数据进行背向传播偏移时，首先确定成像区域的范围和像素点的数量，对于成像空间的每个像素点，都将其视为散射体目标，计算该像素点对应的散射场。将各记录道t时刻的接收振幅叠加起来得到背向传播偏移结果[18]，即
(7)
在式(7)中，电磁波在介质中的传播速度 v 会严重影响背向传播偏移最终结果，故获取精确的速度尤为重要。本文采用前面介绍的三维速度谱法确定的散射目标速度，用于背向传播偏移，如果雷达剖面中存在多个散射目标，可以确定各散射目标的速度后，利用插值方法获取速度剖面用于偏移成像。
2 数值仿真试验
本文采用时域有限差分法(Finite-Difference Time-Domain，FDTD)进行地下管道模型数值仿真[19]。图2为采用的仿真模型，模型尺寸均为2 m×1 m。模型1、模型2、模型3和模型4的上层为均空气层，下层分别为0.9 m厚的干砂 、砂土、混凝土以及湿砂。该算例中干砂、砂土、混凝土和湿砂的相对介电常数分别为3.0，4.5，6.0和8.0。在各个模型的正中间放置了直径为0.15 m金属管。FDTD的网格大小设置为Δx=Δy=0.002 5 m，模型边界采用理想匹配层吸收边界条件(Perfectly Matched Layer，PML)。激励源采用中心频率为400 MHz的Ricker子波，时窗设为20 ns。收发天线间距为0.05 m，天线步长为0.02 m，通过仿真获得的探地雷达剖面包含90道数据。
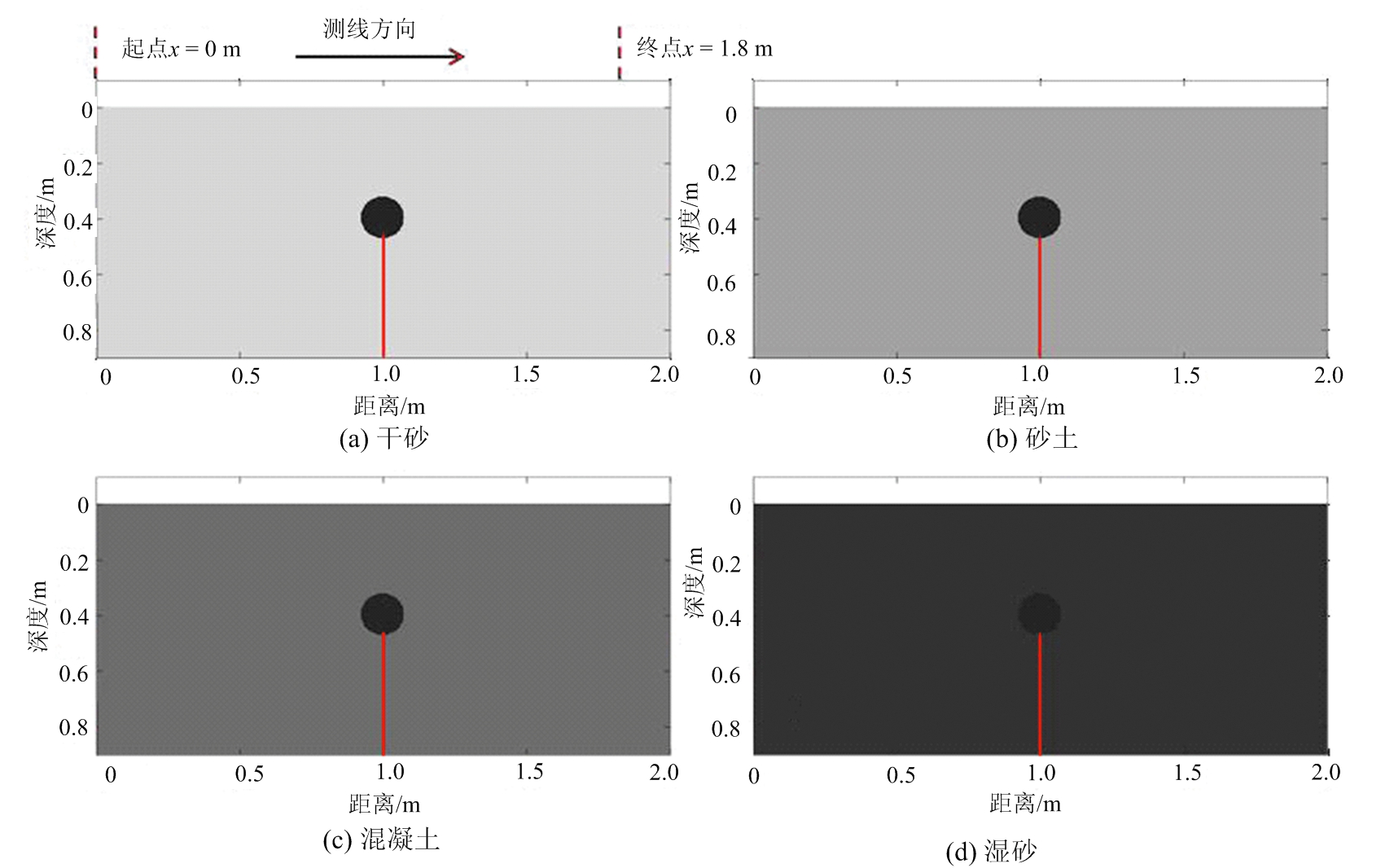
图2 仿真模型
图3为仿真得到的探地雷达剖面，从图中可以清楚地看到地下目标形成的双曲线散射。首先应用三维速度谱算法对探地雷达数据进行处理，得到如图4所示的三维速度谱。通过沿距离轴的最大值找到双曲线的位置，从三维速度谱中提取出该位置的速度切片，如图5所示。图5中包含了地下目标散射双曲线叠加的能量块，注意其中11 ns处的能量块为多次反射波双曲线叠加形成的。我们用黑色“十字”标出了所求的电磁波在介质中的传播速度。表1展示了使用三维速度谱方法计算得到的速度与真实值之间的对比，可以看出所估计的电磁波速度均具有较高的精度，相比真实速度的误差均小于3.8%。将计算得到的传播速度分别应用于背向传播偏移算法中，得到如图6所示的雷达剖面。从图中可以看出，尽管电磁波在各个模型介质中的传播速度不同，金属管产生的绕射能量都得到了很好的聚焦。能量聚焦的位置即对应管道的埋藏深度，从图6得到的管道埋置深度分别为0.340，0.330，0.330和0.335，与真实埋深之间的误差分别为4.6%,1.5%,1.5%和3.1%。仿真数据结果表明三维速度谱算法可以准确地计算出电磁波在地下介质中的波速，实现地下管道的准确定位。
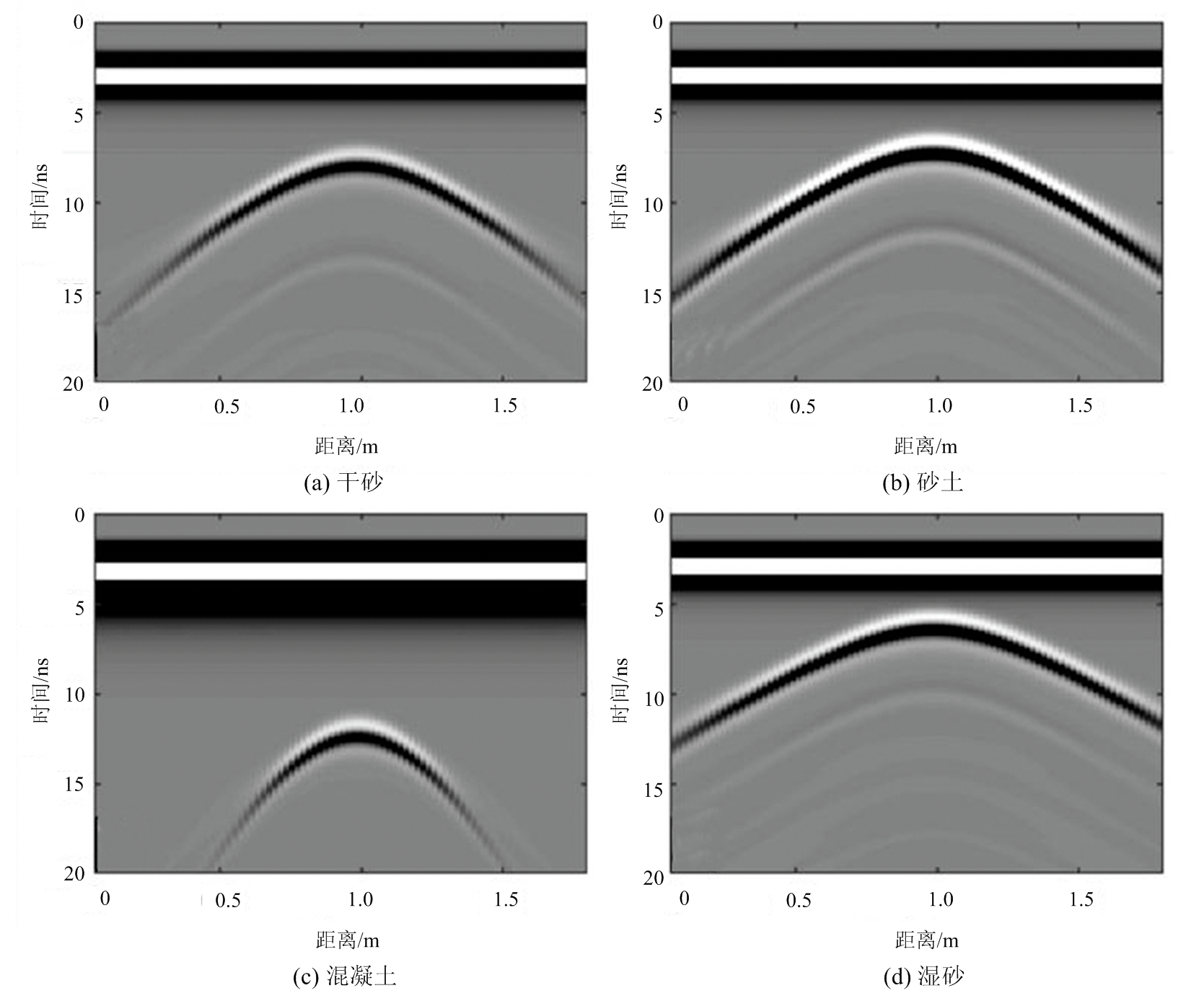
图3 仿真雷达剖面
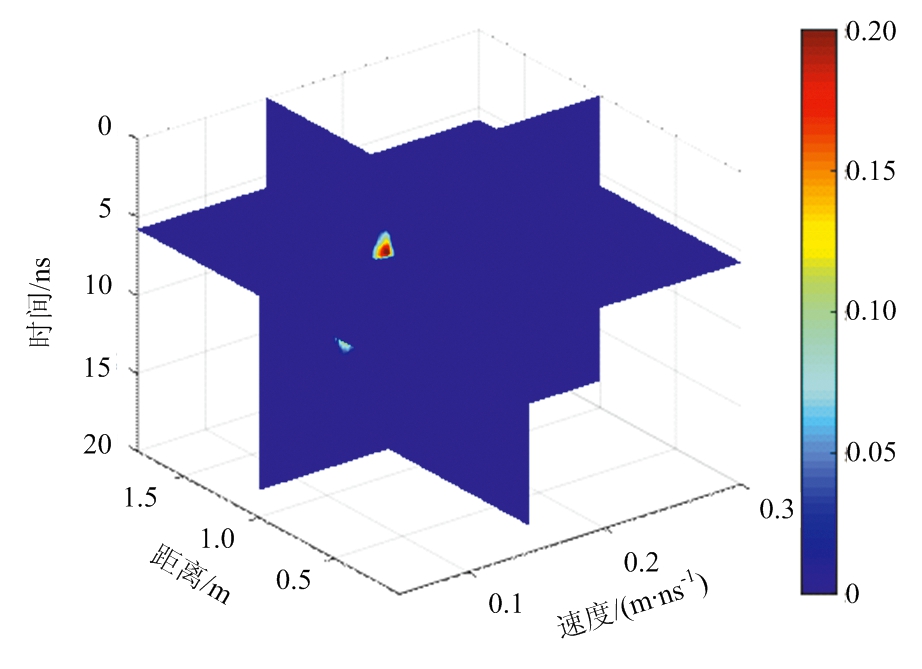
图4 砂土模型(图3(b))对应的三维速度谱结果
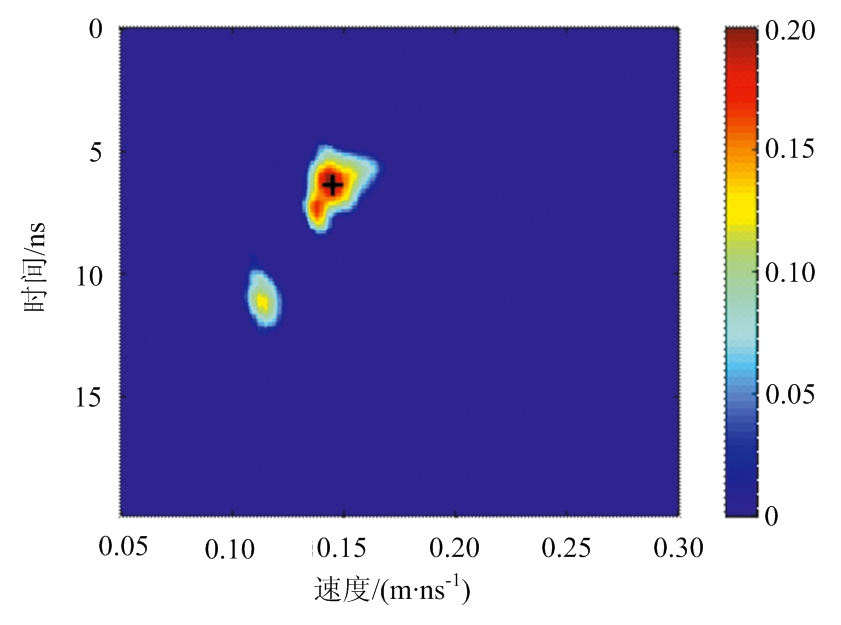
图5 砂土模型(图3(b))的三维速度谱切片(距离=1 m)
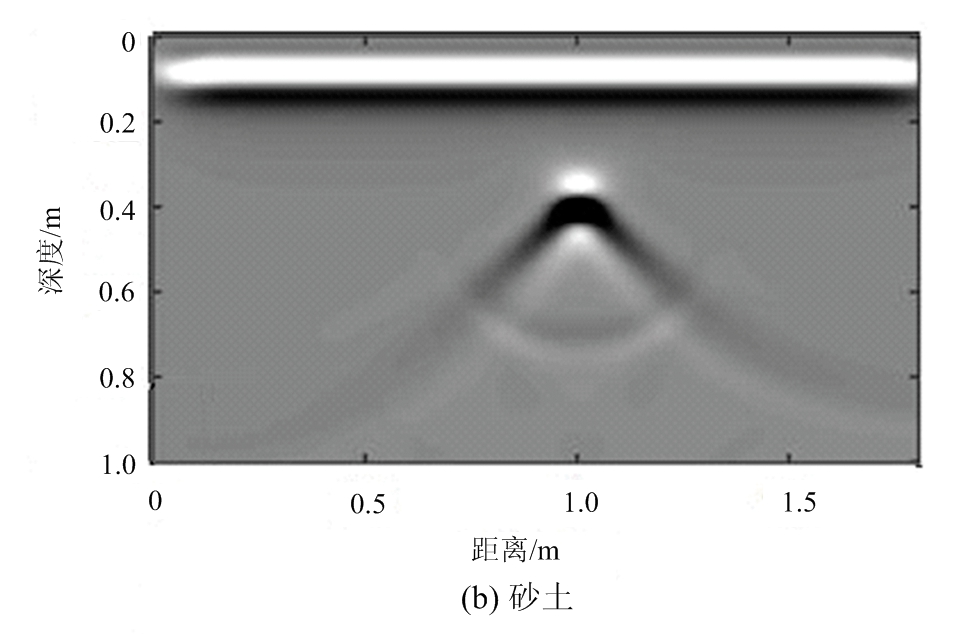
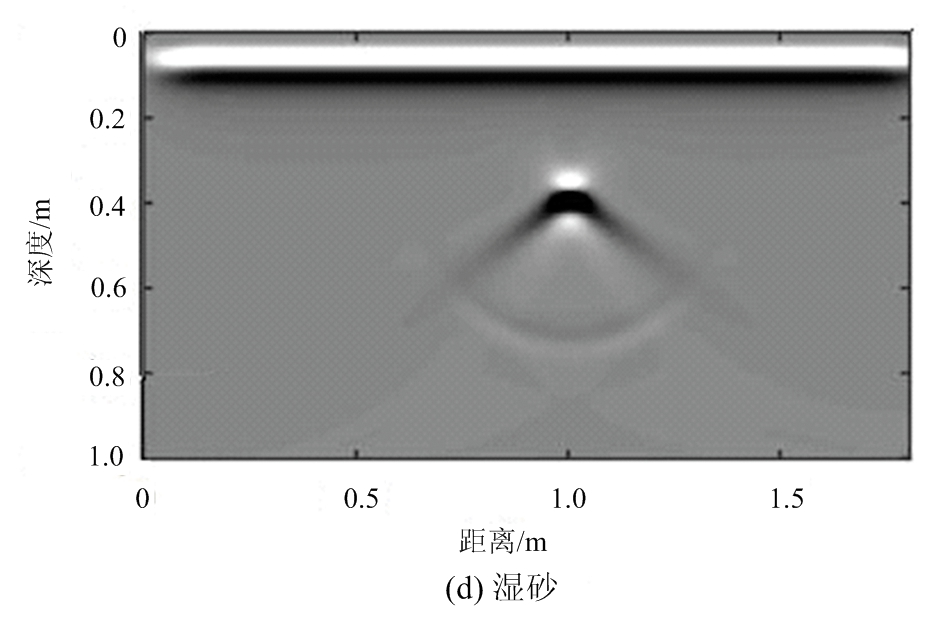
图6 仿真数据背向传播偏移结果
3 现场试验
为了进一步验证三维速度谱算法在探地雷达实测数据中的应用效果，本文将三维速度谱算法应用到某地下管线的实测数据处理，以验证本文所提算法的抗噪性和鲁棒性。实测数据的探测目标为广州大学校园内一根已知PVC管线，管线直径为35 cm，埋深为1.05 m。
实际数据采集过程中使用IDS公司的TR400探地雷达(如图7所示)和中心频率为400 MHz的屏蔽式天线，数据采集时窗为40 ns，采样点数为512。
图7 实际数据采集过程
图8为实测数据处理之后的雷达剖面图，数据处理过程包括去背景、道间均衡、去直流和带通滤波等。从图8中可以明显看出地下管线产生的双曲线散射特征，其顶点在12 ns左右，但管道上方的背景杂波非常严重，这是由于背景土壤介质不均造成的。同时，在管道双曲线反射的下方，还可以看到两条分别由管道爬行波和地面多次反射造成的双曲线反射。将三维速度谱算法应用到该实测数据中，得到三维速度谱，如图9所示。通过沿距离轴的最大值找到双曲线的位置，并从三维速度谱中提取出对应位置的速度切片，如图10所示。图中黑色“十字”为计算的电磁波在管道上方土壤介质中的传播速度(v=0.182 m/ns)。需要注意的是，另外两个能量块为爬行波和多次反射波叠加形成的。使用计算得到的土壤介质电磁波速对实测雷达数据进行背向传播偏移处理，结果如图11所示，可以看出管道形成的散射能够被很好地聚焦。根据图11可以清楚地定位到管道埋深为1.07 m，与实际埋深1.05 m相比，误差仅为1.4%。实际数据结果表明三维速度谱方法在实际应用中同样有很高的精度，能实现对地下管道的精确定位。
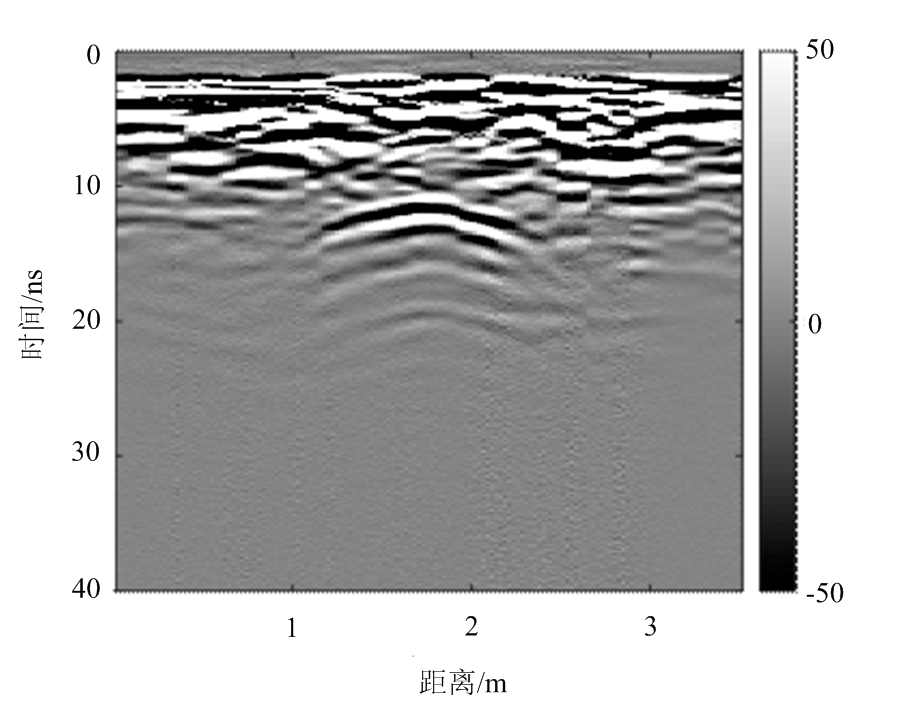
图8 某地下管道的现场试验探地雷达剖面图
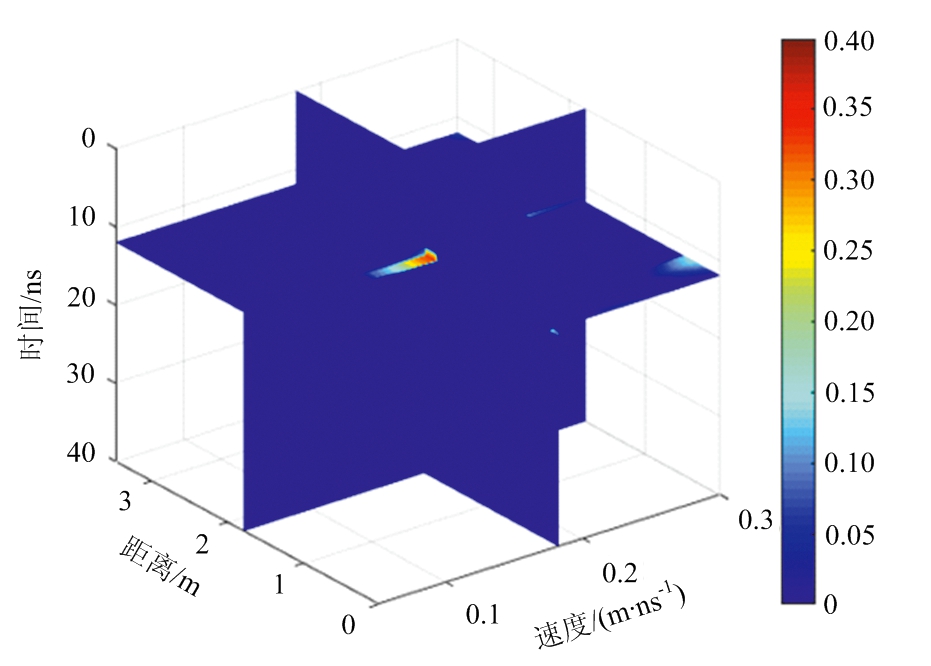
图9 实测数据的三维速度谱
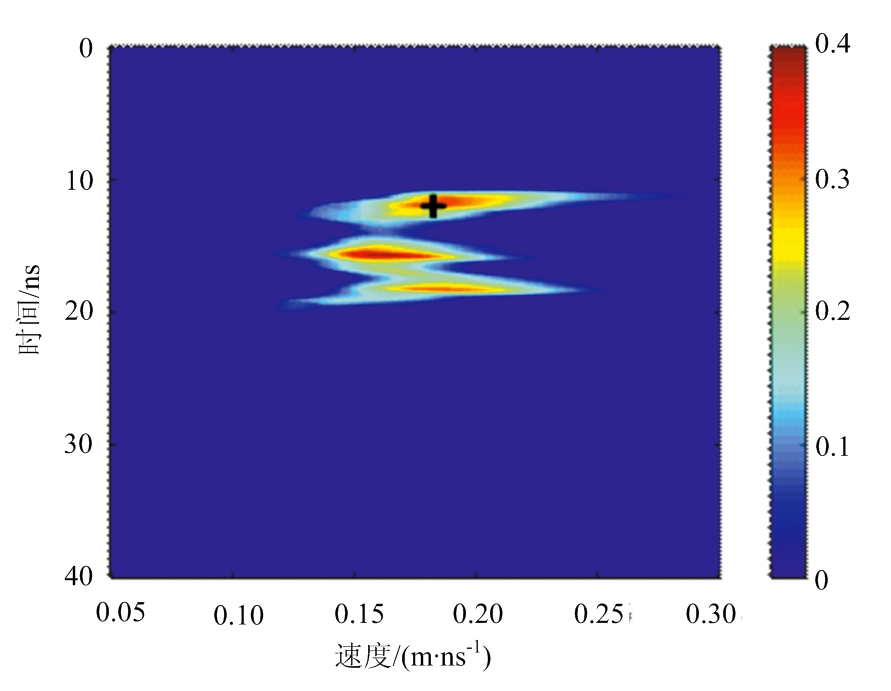
图10 实测数据的三维速度谱速度切片(距离=1.728 m)
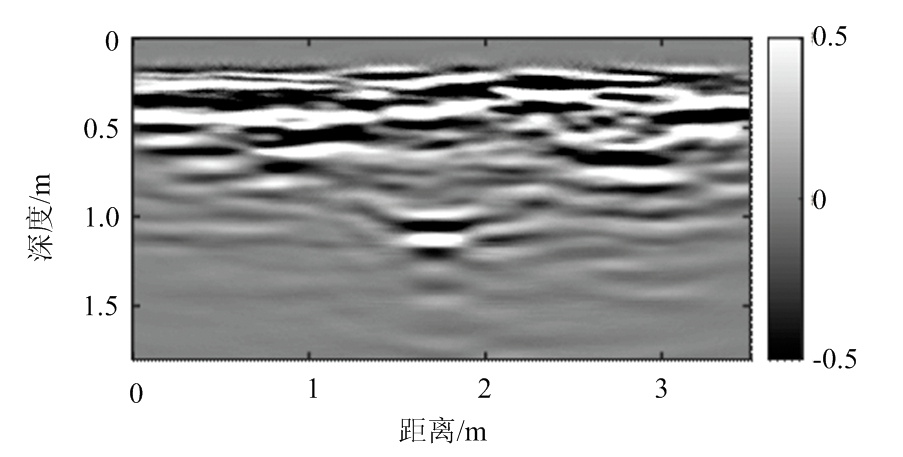
图11 现场试验探地雷达数据背向传播偏移成像结果
4 结束语
本文提出了一种基于三维速度谱和背向传播偏移算法的地下管线埋深估计和定位方法，其中三维速度谱方法避免了双曲线走时的提取，实现了速度的自动估计，提高了算法的鲁棒性。通过数值仿真试验以及现场试验证明了三维速度谱方法能通过自动搜索，来定位地下管线散射双曲线的水平位置、双向传播时间以及电磁波在地下介质中的波速，再通过背向传播偏移即可实现对管道位置的精确定位。本文得到以下结论：(1)在数值仿真模型中，应用三维速度谱算法计算得到的不同地下介质中的电磁波传播速度与实际速度的误差均小于3.8%；(2)将三维速度谱计算得到的地下介质中的电磁波传播速度应用到背向传播偏移算法当中，能够实现地下管线双曲线散射能量的聚焦，得到地下管线的埋藏深度。实际数据结果中管线目标的埋置深度误差为1.4%，表明三维速度谱算法具有实际应用价值，能够实现地下管线的精确定位。
[1] 韩佳明, 仲鑫, 景帅, 等. 探地雷达在黄土地区城市地质管线探测中的应用[J]. 物探与化探,2020, 44(6):1476-1481.
[2] 胡群芳, 郑泽昊, 刘海, 等. 三维探地雷达在城市市政管线渗漏探测中的应用[J]. 同济大学学报(自然科学版), 2020, 48(7):972-981.
[3] 张劲松, 丛鑫, 杨伯钢, 等. 地下管线探测雷达图特征分析[J]. 地球物理学进展,2019, 34(3):1244-1248.
ZHANG Jinsong, CONG Xin, YANG Bogang, et al. Characteristics Analysis of Radar Map on Underground Pipeline Detection[J]. Progress in Geophysics, 2019,34(3):1244-1248.(in Chinese)
[4] 罗传熙,张肖宁,虞将苗,等. 基于三维探地雷达对沥青路面厚度检测影响因素分析[J]. 公路, 2021, 66(1):95-99.
[5] 程江洲, 陈秋航, 卞九洲, 等. 探地雷达技术在变电站地层隐蔽管线探测中的应用[J]. 现代雷达, 2021, 43(2):82-88.
[6] 姚显春,闫茂,吕高,等. 地质雷达探测地下管线分类判别方法研究[J]. 地球物理学进展, 2018, 33(4):1740-1747.
YAO Xianchun, YAN Mao, LÜ Gao, et al. Research on Underground Pipeline Classification and Discrimination Method Based on Geological Radar Detection [J]. Progress in Geophysics, 2018,33(4):1740-1747.(in Chinese)
[7] 许崇华, 樊敬亮, 梁光胜, 等. 天线阵技术探测地下PVC管[J]. 物探与化探, 2009, 33(3):358-359.
[8] 杨剑, 李华焦, 彦杰. 探地雷达在城市地下管线探测中的应用[J]. 物探化探计算技术, 2010, 32(6):669-675.
[9] SHIHAB S,AL-NUAIMY. Radius Estimation for Cylindrical Objects Detected by Ground Penetrating Radar[J]. Subsurface Sensing Technologies and Applications, 2005, 6(2):151-166.
[10] RISTIC A V, PETROVACKI D, GOVEDARICA M. A New Method to Simultaneously Estimate the Radius of a Cylindrical Object and the Wave Propagation Velocity from GPR Data[J]. Computers and Geosciences, 2009, 35(8):1620-1630.
[11] ZHAO S, AL-QADI I. Pavement Drainage Pipe Condition Assessment by GPR Image Reconstruction Using FDTD Modeling[J]. Construction and Building Materials, 2017(15):1823-1893.
[12] 
Ž, VRTUNSKI M,et al. Point Coordinates Extraction from Localized Hyperbolic Reflections in GPR Data[J]. Journal of Applied Geophysics, 2017(144):1-17.
[13] DONG Zejun, FENG Xuan, ZHOU Haoqiu, et al. Properties Analysis of Lunar Regolith at Chang’E-4 Landing Site Based on 3D Velocity Spectrum of Lunar Penetrating Radar[J]. Remote Sensing,2020, 12(4):1-15.
[14] LIU Hai, SATO M. In Situ Measurement of Pavement Thickness and Dielectric Permittivity by GPR Using an Antenna Array[J]. NDT&E International, 2014,64:65-71.
[15] LIU Hai, XIE Xiongyao, TAKAHASHI K, et al. Groundwater Level Monitoring for Hydraulic Characterization of an Unconfined Aquifer by Common Mid-Point Measurements Using GPR[J]. Journal of Environmental and Engineering Geophysics, 2014, 19(4):259-268.
[16] LIU Hai, TAKAHASHI K, SATO M. Measurement of Dielectric Permittivity and Thickness of Snow and Ice on a Brackish Lagoon Using GPR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(3):820-827.
[17] ÖZDEMIR C, DEMIRCI S, YIGIT E, et al. A Review on Migration Methods in B-Scan Ground Penetrating Radar Imaging[J]. Mathematical Problems in Engineering, 2014(1):1-16.
[18] ZHOU L, HUANG C, SU Y. A Fast Back-Projection Algorithm Based on Cross Correlation for GPR Imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(2):228-232.
[19] 梁小强, 杨道学, 张可能, 等. FDTD数值模拟在GPR管线探测中的应用[J]. 地球物理学进展, 2017, 32(4):1803-1807.
LIANG Xiaoqiang, YANG Daoxue, ZHANG Keneng, et al. Application of FDTD Numerical Simulation of Ground Penetrating Radar Inpipeline Detection[J]. Progress in Geophysics, 2017,32(4):1803-1807.(in Chinese)
