0 引言
星载无源定位系统以其侦察范围广、不受天气气候影响、观测站是运动的等优点而受到国内外学者的广泛关注，目前已被普遍应用于军事和民用领域。星载无源定位技术中常用的观测量有到达时间差(Time Difference of Arrival，TDOA)[1]、到达频率差(Frequency Difference of Arrival，FDOA)[2]和到达角(Angle of Arrival，AOA)[3]等，其中多星时差频差定位凭借其可瞬时定位及高定位精度的优势，在对雷达等脉冲辐射源的定位中应用更加广泛。
国内外的学者对多星时差频差定位算法进行了大量的研究[4-6],但以上研究仅针对单次定位进行改进且卫星使用数量多为三颗以上。文献[7]指出卫星定位系统在过顶期间会多次截获到地球上静止辐射源发出的信号，而有效利用多次截获的数据进行融合并定位可以提高定位精度并减少成本。
针对多次观测融合算法的研究，贾兴江等人针对双/多无人机测角频差系统提出了一种融合多次观测数据的定位算法，该算法在单次定位的基础上，引入了批处理加权最小二乘融合算法以及序贯加权最小二乘融合算法，实现了多次观测信息的有效融合[8]。张莉等人提出了一种在观测站存在误差的情况下，运动双站对巡航目标的时差频差定位算法，该算法有效融合多次观测的数据并达到了克拉美罗下界(Cramer-Rao Lower Bound，CRLB)[9]。文献[7]针对三星编队过顶期间对辐射源多次观测，提出了一种基于高斯-牛顿(Gauss-Newton，G-N)迭代的三星时差定位融合算法，该算法仅使用多次观测的时差信息和辐射源高程信息进行定位。实验证明该算法定位性能达到了CRLB且优于现有的位置合批处理方法。
本文将在时差定位的基础上融入频差信息，提出一种将多次观测的时差频差数据与高程信息融合的双星时差频差定位算法。具体思路为将不同时刻下观测到的时差信息和频差信息融合并结合辐射源高程信息构建代价方程，利用G-N迭代求解非线性最小二乘问题，迭代初值可以通过单次定位粗略得出，在使用相同数据的条件下，获得比现有位置合批处理方法更高的定位精度。
1 定位数学模型
定位场景设置如下：假设两颗卫星组成的编队在过顶期间可以截获到N次地球上辐射源uo=[x,y,z]T的信号，则可利用这N次观测到的时差频差结合辐射源高程进行定位。本文考虑卫星位置和速度是有误差的，设n时刻下的双星位置为
其中
是卫星i真实但未知的位置，Δsi,n是卫星位置误差。n时刻下的双星速度为
其中
是卫星i真实但未知的速度，
是卫星速度误差。为方便表示，令
其中
因此n时刻下的卫星随机误差
其中
定义Δβn是均值为零、协方差矩阵为Qβ,n的高斯随机向量。由于双星共截获了N次辐射源信号，即共观测了N次，因此所有观测时刻下的卫星表示为
卫星随机误差Δβ=β-βo，其中
由上可得Δβ是均值为零，协方差矩阵为Qβ=diag{Qβ,1,…,Qβ,n,…,Qβ,N}的高斯随机向量。
将卫星1作为参考卫星，则双星在n时刻下观测到的卫星2与1之间的TDOA定义为d21,n，即
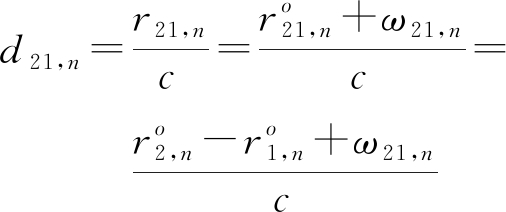
(1)
式中，c为已知的信号传播速度，r21,n=cd21,n为n时刻下双星间的到达距离差
为n时刻下真实的
为n时刻下的TDOA测量噪声，
为n时刻辐射源与卫星i之间的真实距离，其等于
(2)
令f为已知的辐射源载波频率，则双星在n时刻下观测的卫星2与1之间的FDOA定义为
即
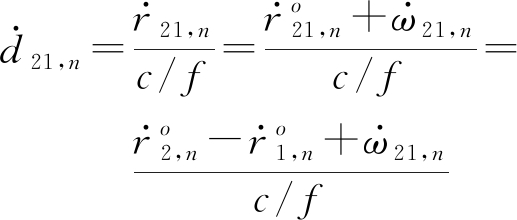
(3)
式中，
为n时刻下双星间的距离率差，
为n时刻下真实的距离率差,
为n时刻下的FDOA测量噪声，
为n时刻辐射源与卫星i之间的真实距离率，其等于公式(2)的时间导数，即
(4)
为便于计算，我们将获得的TDOA与c相乘得到距离差测量，将FDOA与c/f相乘得到距离率差测量，即n时刻下观测的量测为
其测量误差为
其中
定义Δmtf,n是均值为零、协方差矩阵为Qtf,n的高斯随机向量。令N次观测下的量测表达为
是观测的真值，规定不同时刻间的观测相互独立，则Δmtf是均值为零、协方差为Qtf=diag{Qtf,1,…,Qtf,n,…,Qtf,N}的高斯随机向量。本文算法同样将辐射源高程信息加进观测方程中，令高程观测
其中mh=(R+Δh)2，R是地球半径和辐射源真实高程之和，高程误差Δh是均值为零、方差为Qh的高斯随机变量。已知正球面模型下的地球方程为
(5)
忽略二阶误差项，令Δmh=2RΔh是均值为零、方差为4R2Qh的高斯随机变量。因此融合高程信息的量测表达为
为观测的真值，假设时差频差观测和高程观测相互独立，则Δm是均值为零、协方差为
的高斯随机向量。本文规定卫星误差Δβ和观测误差Δm相互独立。
2 位置合批的融合算法
2.1 CRLB
由于考虑卫星存在误差的情况，因此未知参数θ=[uoT,βoT]T，令v=[mT,βT]T，则
lnp(v;θ)=lnp(m;θ)+lnp(β;θ)=
(6)
式中K为常数。则未知参数θ的CRLB为
(7)
式中，
经计算可得辐射源uo的CRLB为
CRLB(uo)=X-1+
X-1Y(Z-YTX-1Y)-1YTX-1
(8)
2.2 位置合批处理
工程上现有的位置合批处理方法主要有三种：一是取理论上的最优单次定位结果。假设在卫星过顶期间可以在N个时刻截获到辐射源信号，则将n时刻的单次双星时差频差定位理论误差设为Bn(n=1,2,…,N)，理论上的最优单次定位结果表示为
(9)
由于单次定位时辐射源真实位置以及卫星真实位置和速度未知，无法计算每次的CRLB，因此我们可以将单次定位估计的结果设为
以此来代替辐射源真实位置uo，用带误差的卫星位置和速度信息βn代替真实的卫星位置和速度
进而求得Bn，其CRLB计算原理同2.1节。
二是取N个时刻的单次定位结果
直接平均,其表达式为
(10)
三是取N个时刻的单次定位结果进行加权平均，其原理为将
看作观测量构造代价函数：
(11)
式中，Wn为n时刻的定位误差协方差矩阵，n=1,2,…,N。由于单次定位时辐射源真实位置未知，无法计算每次的定位误差协方差矩阵，因此我们可以根据单次定位估计的结果
来求得CRLB近似作为辐射源定位误差协方差矩阵Wn来代入计算，同样用代替辐射源真实位置uo，用带误差的卫星信息βn代替真实卫星信息
经计算可得
(12)
以上三种位置合批处理方法从理论上讲并不是最优的数据融合方法：理论上的最优单次定位结果仅使用了一次观测的数据；所有定位点的直接平均结果没有考虑卫星编队在不同位置下的定位精度是不同的；所有定位点的加权平均结果所使用的加权矩阵Wn是单次定位所得。为此下文介绍了一种融合多次观测数据的理论最优定位算法。
2.3 基于G-N迭代的时差频差定位融合算法
本文算法参考文献[10]给出了一种仅需估计uo的加权最小二乘算法，其表达式如下：
(13)
式中，
其中
和
可表示如下：
uo-s1,n, n=1,…,n,…,N
(14)
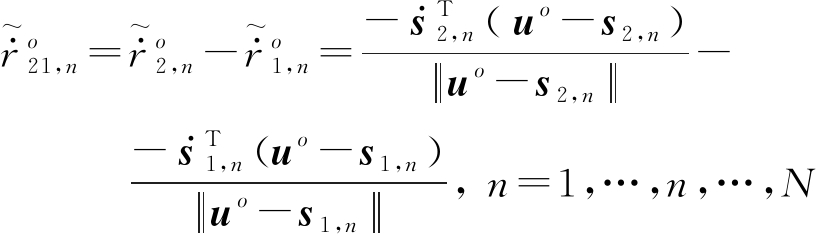
(15)
加权矩阵W=Qm+DQsDT，其中D的形式与
相同，需注意要用带误差的卫星信息β代替真实卫星信息βo。求解非线性最小二乘问题可采用G-N迭代，假设第k次迭代辐射源的位置估计为
则第k+1次迭代的结果为
(16)
式中，Jk为雅克比矩阵，
(17)
迭代初值可选取N个观测时刻中的任一时刻得到的单次定位结果，其单次定位求解可参考文献[11]。通过球面迭代可将算法从正球面模型转换到WGS-84椭球模型来提高定位准确性[7]。
3 仿真分析
本节通过实验验证上述算法。令辐射源位置的经纬度分别为117.8° W和19.6° N，其高程为零。用于实验的卫星星历点数据基于STK软件生成，将同轨双星的轨道高度设为1 100 km，轨道倾角设为63.4°，星间距设为104 km，轨道历元时刻规定从2020年8月29日4时开始，卫星采样间隔设为1 s，整轨取960个星历点数据作为样本。
将n时刻下观测的时差频差误差协方差阵Qtf,n设为
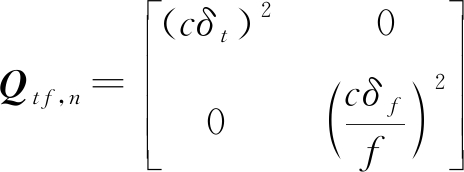
(18)
式中，δt表示TDOA噪声的标准差，δf表示FDOA噪声的标准差，c=3×108 m/s。令
为2N+1维方阵，其中δh表示高程噪声标准差。卫星误差协方差阵Qβ为Qβ=diag{Qβ,1,…,Qβ,n,…,Qβ,N}，其中Qβ,n为
(19)
式中，δs为卫星位置噪声的标准差，
为卫星速度噪声的标准差，I为6×6的单位矩阵。
令
载波频率f=5 GHz，使用STK生成的卫星星历点数据进行定位。在进行G-N迭代时，我们选择采样数据中的第一个星历点数据进行单次定位来作为迭代初值，其余三种位置合批处理方法均使用相同的星历点数据进行融合定位。为简单表示，我们称理论上的最优单次双星时差频差定位结果为最优单次定位；所有单次定位的直接平均结果为位置直接平均；将当作观测量的线性最小二乘结果为位置加权平均，蒙特卡洛仿真次数M为2 000次，定位结果分布如图1所示。
图1 卫星星下点轨迹和各种方法的定位点分布
通过计算位置估计的均方根误差(Root Mean Square Error，RMSE)来比较本文提出的算法和工程上常用的位置合批处理方法之间的性能，RMSE表达如下：
(20)
首先考虑理想情况下的电磁环境，这里的理想环境指卫星每秒都能截获到辐射源信号，测量误差和卫星误差依然存在。我们取融合次数N分别取30，60，120，240，320，480和960次，即对得到的960个星历样本每间隔960/N s进行一次均匀采样，用采样所得星历点数据进行融合定位，比较不同融合次数下各种位置合批处理方法的定位精度，实验结果如图2所示。
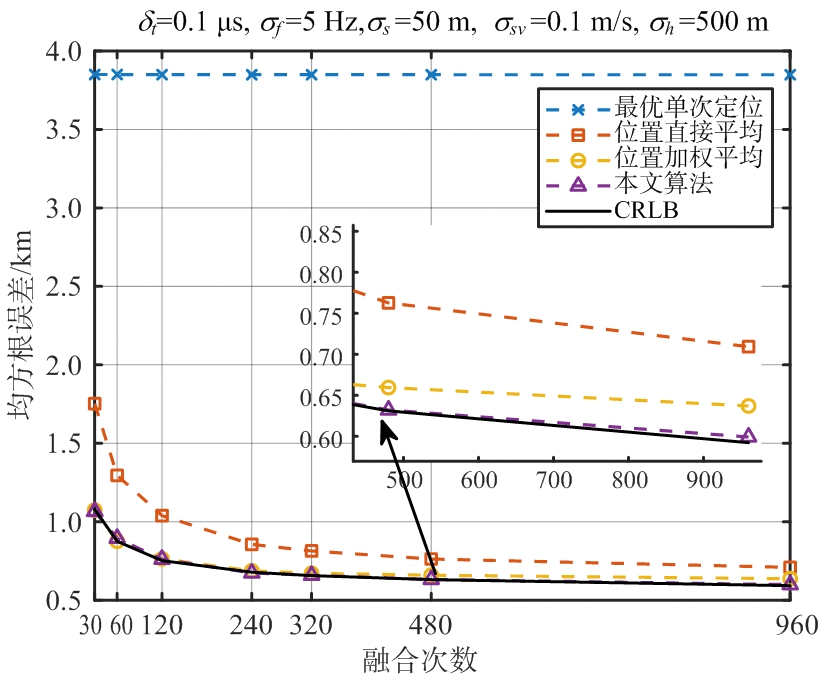
图2 理想电磁环境各种方法的定位精度对比
通过实验结果可以得出，在相同条件下，本文算法和位置加权平均都能达到CRLB，随着融合次数逐渐增多，本文算法的性能开始优于位置加权平均，而位置加权平均性能开始偏离CRLB；位置直接平均的性能要次于前两种方法，但是在融合次数较多的情况下要优于最优单次定位。
但是在实际工程应用中，空间电磁环境是复杂多变的，卫星过顶期间可能仅仅截获几次辐射源信号，因此这里取融合次数N分别为2，3，4，5，6，8和10次，同样对得到的960个星历样本每间隔960/N s进行一次均匀采样，用采样所得星历点数据进行融合定位，同样比较不同融合次数下各种位置合批方法的定位精度，实验结果如图3所示。
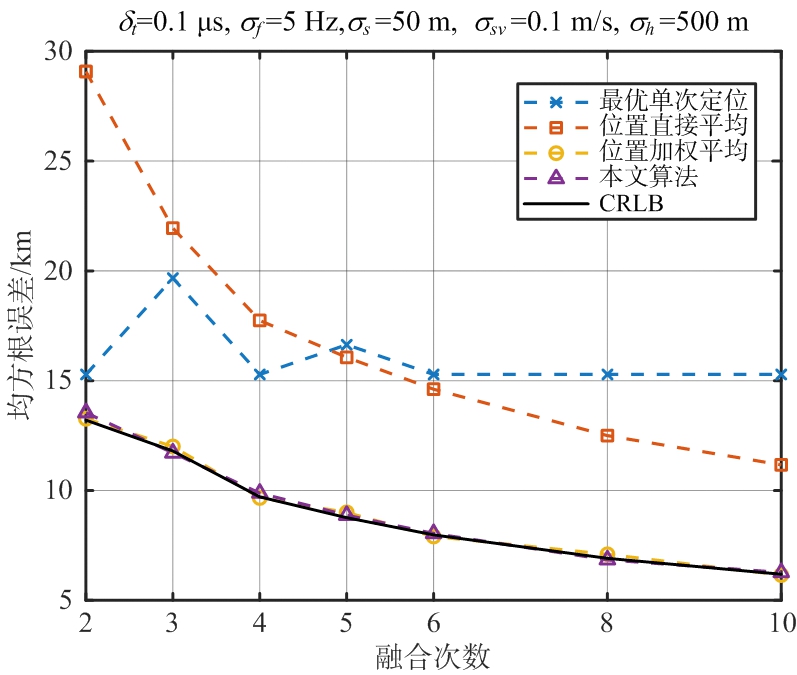
图3 复杂电磁环境各种方法的定位精度对比
通过实验结果可以得出，在相同条件下，本文算法和位置加权平均的性能都能达到CRLB且优于位置直接平均和最优单次定位；最优单次定位的性能一开始优于位置直接平均，当融合次数大于5次之后，位置直接平均的性能开始优于最优单次定位。
4 结束语
本文提出了一种基于G-N迭代的双星时差频差定位融合算法，有效地利用多次观测的时差频差和高程信息进行定位。通过实验验证，本文算法在理想电磁环境和复杂电磁环境下的定位精度要优于工程上现有的最优单次定位、位置直接平均和位置加权平均等位置合批处理方法。
[1] SUN Y, HO K C, WAN Q. Solution and Analysis of TDOA Localization of a Near or Distant Source in Closed Form[J]. IEEE Trans on Signal Processing, 2019, 67(2):320-335.
[2] MA F H, GUO F C, YANG L. Low-Complexity TDOA and FDOA Localization: A Compromise Between Two-Step and DPD Methods[J]. Digital Signal Processing, 2019, 96(1):102600.
[3] XU C, WANG Z, WANG Y, et al. Three Passive TDOA-AOA Receivers Based Flying-UAV Positioning in Extreme Environments[J]. IEEE Sensors Journal, 2020, 16(15):9589-9595.
[4] 孙霆, 董春曦, 毛昱. 一种基于半定松弛技术的TDOA-FDOA无源定位算法[J]. 电子与信息学报, 2020, 42(7):1599-1605.
[5] LIU Z X, HU D X, ZHAO Y S, et al. An Improved Closed-Form Method for Moving Source Localization Using TDOA, FDOA, Differential Doppler Rate Measurements[J]. IEICE Trans on Communications, 2018, 102(6):1-15.
[6] NOROOZI A, OVEIS A H, HOSSEINI M R, et al. Improved Algebraic Solution for Source Localization from TDOA and FDOA Measurements[J]. IEEE Wireless Communications Letters, 2018, 7(3):352-355.
[7] 徐英杰,郭福成.基于高斯-牛顿迭代的三星时差定位融合算法[J].航天电子对抗,2020,36(5):14-17.
[8] 贾兴江, 周一宇, 郭福成. 双/多机测角频差定位算法研究[J]. 信号处理, 2011, 27(1):37-42.
JIA Xingjiang, ZHOU Yiyu, GUO Fucheng. Research on Hybrid DOA and FDOA Passive Localization Using Dual/Multiple Aircrafts[J]. Signal Processing, 2011,27(1):37-42.(in Chinese)
[9] 张莉, 王鼎, 于宏毅. 基于多次观测的运动双站对运动目标时差/频差定位算法[J]. 信息工程大学学报, 2013, 14(6):719-726.
ZHANG Li, WANG Ding, YU Hongyi. Moving Source Localization Algorithm with Two Moving Receivers Using TDOA and FDOA Measurements Based on Multiple Observations[J]. Journal of Information Engineering University,2013,14(6):719-726.(in Chinese)
[10] CAO Y L, LI P, LI J Z, et al. A New Iterative Algorithm for Geolocating a Known Altitude Target Using TDOA and FDOA Measurements in the Presence of Satellite Location Uncertainty[J]. Chinese Journal of Aeronautics, 2015, 28(5):1510-1518.
[11] HO K C, CHAN Y T. Geolocation of a Know Altitude Object from TDOA and FDOA Measurements[J]. IEEE Trans on Aerospace and Electronic Systems, 1997, 33(3):770-783.
