0 引言
极化可调控天线阵列在现代无线通信中用途广泛,在收发系统中它可以切换到合适的极化方式来提高与发射或者接收天线之间的传输效率,同时减少甚至隔绝与其他极化方式的天线系统之间的信号传输,从而降低了传输过程中的能量损失,增强了抗干扰性。极化可调控天线阵列可通过二极管、开关、多端口馈电网络等方式来实现极化的调控,主要可以分为两大类:第一类是通过电路结构调节阵列单元本身的工作模式,进而调节阵列的极化方式,这占据了极化可调控天线阵列中的绝大部分[1-5];第二类是通过切换馈电网络控制阵列单元的位置和相位,通过空间波束的叠加来实现整个阵列的极化可调[6-8]。第一类调控方式通过单元上多个端口的切换实现调控,其单元都是有针对性地设计好的,因而第一类调控方式对于普通的单元(如单馈点的天线结构)不具有普适性;而且附加在天线单元上的电路结构也在一定程度上增加了结构的复杂性和损耗。第二类方式通过切换馈电网络来控制阵列中单元的激励幅值和相位,每一个馈电网络对应一种极化方式,因而极化的多样性受到制约。
上述两类极化调控方式在进行水平线极化与垂直线极化切换或进行线极化和圆极化切换的时候,要求阵列结构本身具有垂直极化和水平极化工作的线极化单元。对更加一般的随机单元排布方式(如阵列中任意两个单元的极化方向在空间上都不正交),传统的极化调控设计方式使用起来局限性非常大。
任何无线系统都以传输效率最大为设计目标。最大功率传输效率法(MMPTE)[9-10]以传输效率作为优化目标函数来设计一般阵列天线,抓住了天线设计的核心,故其设计性能优于现今所有其他阵列天线设计方法。本文将MMPTE进一步推广到极化可调控阵列天线的设计。通过引入极化控制接收天线,将天线阵列的极化调控问题转化为功率传输问题。该方法适用于任意具有极化可调控性的阵列,而且不受阵列所使用的单元以及阵列本身布局的限制。相比于传统的设计方法,优势十分明显。
1 设计方法简介
1.1 MMPTE原理
以如图1所示的传输系统为例,它包含一个具有4个天线单元的发射阵列(待设计阵列)和一个极化控制接收天线。根据极化调控目标,接收天线可以有多种不同的极化形式,如圆极化天线、线极化天线和双极化天线。以图1中的圆极化接收天线为例,将整个收发系统视为一个5端口网络。用下标“t”表示发射阵列,下标“r”表示接收天线,该系统可用S参数表示为
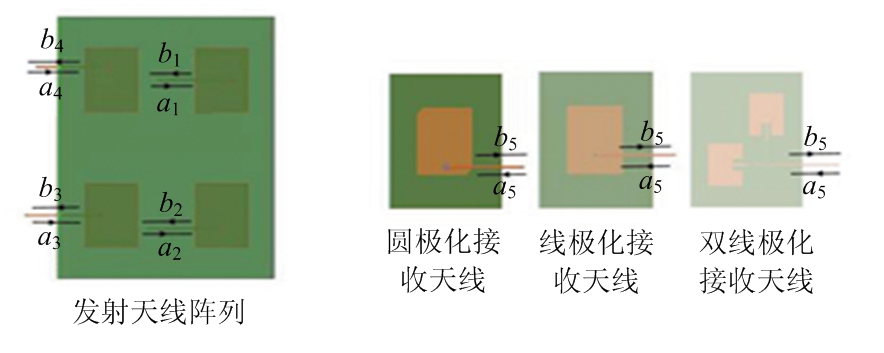
图1 功率传输系统
(1)
其中天线阵列和接收天线的归一化入射波和反射波分别为
[at]=[a1,a2,a3,a4]T[ar]=[a5][bt]=[b1,b2,b3,b4]T[br]=[b5]
(2)
接收功率与发射天线阵列的输入功率之比即为传输效率,可以表示为
Tarray=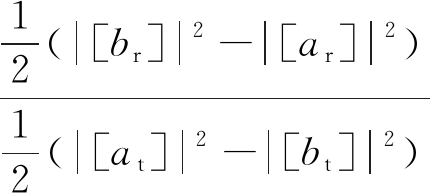
(3)
在接收天线完全匹配的情况下有[ar] = 0, 式(3)可以由式(1)写为
Tarray=![]()
(4)
在系统完全匹配下,若上式达到最大可以得到如下特征值方程[9-10]:
[A][at]=Tarray[at]
(5)
发射阵列与接收天线之间的最大功率传输效率对应式(5)的唯一非零特征值,相应的特征向量为最优激励。根据MMPTE所计算出的最优激励分布保证发射端与接收端之间的功率传输效率最大。
1.2 用MMPTE实现极化可调控的原理
两个线极化的天线之间的功率传输效率只有两者极化匹配时才能达到最大化,因此,在发射阵列具有可极化重构可能性的物理前提下,由MMPTE计算出的最优激励分布,一定会保证发射阵列具有与接收天线相同的极化方式,从而将极化调控问题转化为了传输效率优化问题。通过HFSS等仿真软件计算出接收天线和发射阵列各个单元之间的散射参数,即可将散射参数矩阵代入到MMPTE中进行计算得出每个端口的幅值和相位,实际测试过程中直接将天线阵列外接移相器即可对每个端口施加对应的激励。值得指出的是发射阵列必须具有实现极化可调的物理基础。MMPTE方法可以获得阵列在各种极化方式下的增益大小或极化效果。如果发射阵列的极化效果差,表示该阵列在物理上不能产生与接收天线相一致的极化。
1.3 接收天线阵列的设计
为了说明MMPTE用于极化可重构天线设计的步骤与可行性,特将文献[11]提出设计结果与MMPTE的结果进行比较。图2为工作在2.45 GHz的阵列。阵列由4个线极化单元组成,基板选用了FR4_Epoxy,单元间距约为半波长,采用同轴馈电。众所周知[11],对4个完全相同且以90°角度差依次旋转排列的线极化天线阵列(如图2所示),若其激励为等幅并且相位依次差90°,则该四单元阵列辐射圆极化波。用MMPTE可得到同样的结论。将置于远场区的接收天线选为最常见的切角右旋圆极化微带贴片天线(如果要产生左旋圆极化波,只需用左旋圆极化天线替换接收天线即可)。 通过MMPTE计算得到的最优激励列于表1。显然,由MMPTE计算出的4个端口的电压幅值比例近似为1∶1∶1∶1,相位也几乎按0°,90°,180°,270°的形式分布。

图2 2×2阵列的布局
表1 2×2右旋圆极化阵列的幅值和相位

端口优化后的激励分布10.5593∠95.4614°20.4267∠-178.3127°30.5634∠-81.9219°40.4332∠0°
对上面简单的2×2阵列而言,实现特定极化的激励分布可以通过理论分析得到。当单元数目增加且单元排列不规则时,从理论上获得实现特定极化的激励分布变得十分困难,而MMPTE可以解决这一难题。文献[12]和[13]提出了一种由不规则排布的线极化阵列产生圆极化波束的方法,该方法以阵因子和单元因子叠加计算总场的方式确定激励分布,其中单元采取等幅馈电的方式,相位分布则是通过给每个单元施加一个等同于其旋转角的相移给出。MMPTE相比于该方法存在如下优势:首先MMPTE的激励分布并非等幅而是优化之后的结果,提高了阵列的增益;其次在该方法采用的阵列中,对于任意一个随机摆放的单元,必定存在另一个与其在空间中形成90°旋转角的单元,因此施加完相移后就形成了等幅正交的两个线极化分量,因而MMPTE相比于该方法可以适用于更为一般的不规则阵列;最后该方法仅针对圆极化,对各个方向的线极化以及双线极化并未作探讨。图3是一个由12个线极化天线单元组成的阵列,采用的单元和基板材料与图2中的相同,它不同于普通的阵列排列方式。从实现圆极化的角度来看,该阵列不存在两个单元极化方向正交的且相差90°的排列方式;从实现线极化的角度来说,该阵列没有严格的行与列之分;从实现双线极化的角度来说,该阵列从x和y方向看过去是两种截然不同的布局。与图2中的阵列一样,该阵列本身并不具备特定的极化方式,其辐射的波束的极化方式完全由阵列单元的激励分布决定。对于这种复杂的排列方式,利用MMPTE同样可以得到实现不同极化的最优激励分布。当远场区所设置的接收天线分别为左旋圆极化天线和右旋圆极化天线时,用MMPTE得到激励分布如表2所示。
表2 圆极化天线的激励分布
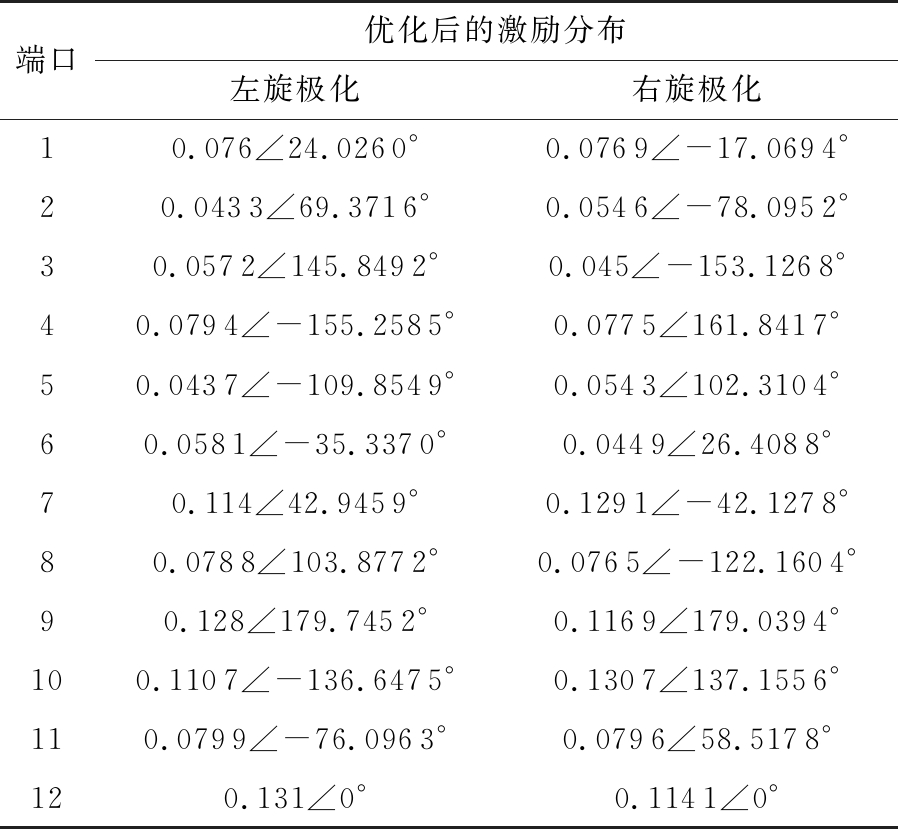
端口优化后的激励分布左旋极化右旋极化10.076∠24.0260°0.0769∠-17.0694°20.0433∠69.3716°0.0546∠-78.0952°30.0572∠145.8492°0.045∠-153.1268°40.0794∠-155.2585°0.0775∠161.8417°50.0437∠-109.8549°0.0543∠102.3104°60.0581∠-35.3370°0.0449∠26.4088°70.114∠42.9459°0.1291∠-42.1278°80.0788∠103.8772°0.0765∠-122.1604°90.128∠179.7452°0.1169∠179.0394°100.1107∠-136.6475°0.1307∠137.1556°110.0799∠-76.0963°0.0796∠58.5178°120.131∠0°0.1141∠0°

图3 12单元阵列的布局
图3所示阵列也可实现线极化或双线极化,其最优激励可以通过MMPTE利用线极化接收天线或双线极化接收天线获得。双线极化接收天线效果类似文献[14]中的天线,本文中采用的天线结构如图1所示。该天线的两个相同单元分别沿x轴和y轴放置(两单元增益相等,方位上相差90°),并通过微带线相连。用MMPTE获得的线极化情况下的阵列激励如表3所示。从表3可以发现,当阵列极化沿x方向时,自身极化方向是x方向的单元获得较大的激励,而自身极化方向是y方向的单元所获得的激励几乎可以忽略不计,这也从理论上验证了MMPTE方法的正确性。
表3 线极化天线的激励分布

端口优化后的激励分布x-线极化y-线极化双线极化10.076∠24°0.0002∠90°0.0552∠10°20.0433∠69°0.0906∠174°0.1175∠-3.3°30.0572∠146°0.0894∠174°0.0075∠28°40.0794∠-155°0∠121.6799°0.064∠177°50.0437∠-110°0.0901∠-5°0.1064∠176°60.0581∠-35°0.0903∠-4.8°0.0108∠171°70.114∠43°0.0476∠-179°0.2084∠1.8°80.0788∠104°0.2268∠167°0.1348∠-3.4°90.128∠179.7°0.047∠-178°0.021∠156.4°100.1107∠137°0.0467∠-0.2°0.166∠-178°110.0799∠-76°0.2257∠-13°0.0925∠170°120.131∠0°0.00456∠0°0.0159∠0°
2 实验与结果分析
工作在2.45 GHz的2×2圆极化阵列的反射系数|S11|和轴比如图4所示。可以看出该阵列的轴比在很宽的频带内都小于3 dB。值得指出,发射阵列的极化效果与接收天线选择有关。本设计选用的接收天线是一个普通的切角圆极化接收天线,基本满足设计要求。
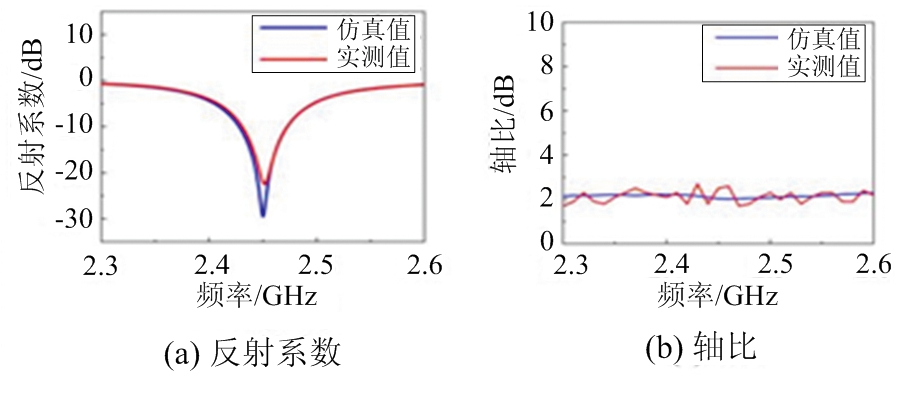
图4 2×2圆极化阵列的实测和仿真结果
图5是12单元阵列的反射系数和轴比。在图6中给出了接收天线为x方向极化的条件下阵列的Gφ(增益φ分量)和Gθ(增益θ分量)的对比图,可以看出x轴方向的Gθ远大于Gφ;而在y轴方向的结果刚好相反。这表明阵列的极化方向是x轴方向,而在y轴方向极化分量特别小。图7是接收天线为y方向极化条件下的结果。与图6中的结果截然相反,阵列在xoz平面上Gθ远远小于Gφ, 而在yoz平面上的Gθ比Gφ大得多。这说明阵列的主极化方向是y轴方向。最后由极化分量分别沿着x轴和y轴的双线极化天线作为接收天线的结果如图8所示。图8(a)和(b)分别是xoz平面和yoz平面的Gφ和Gθ的对比。仿真与实测结果均说明x轴方向上和y轴方向上的极化分量相差不大,具有良好的双线极化效果。

图5 12单元圆极化阵列的实测和仿真结果
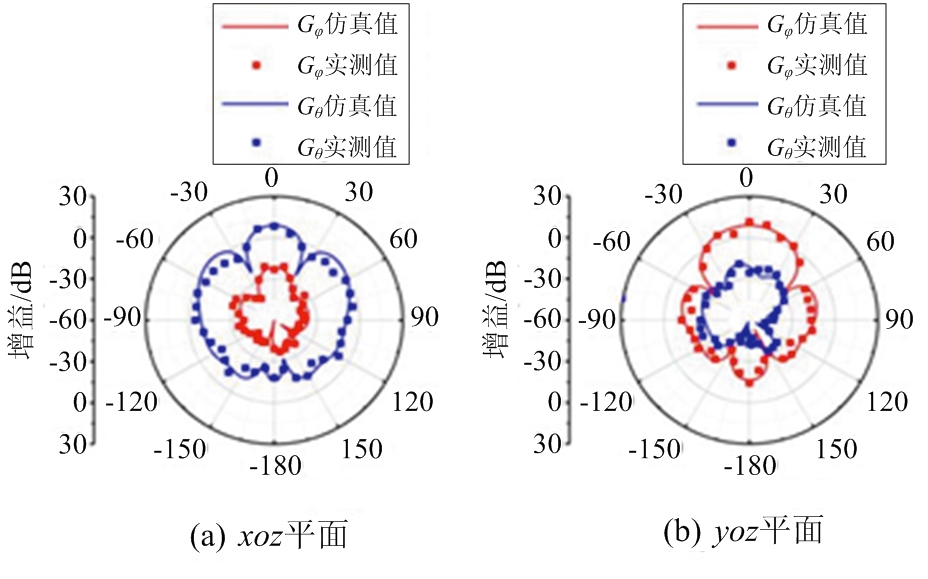
图6 12单元x方向线极化阵列的实测和仿真结果
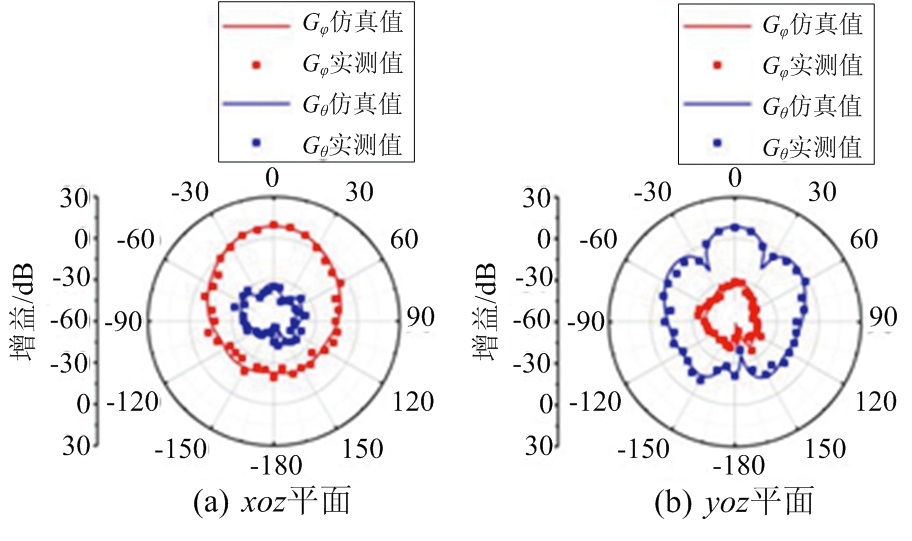
图7 12单元y方向线极化阵列的实测和仿真结果
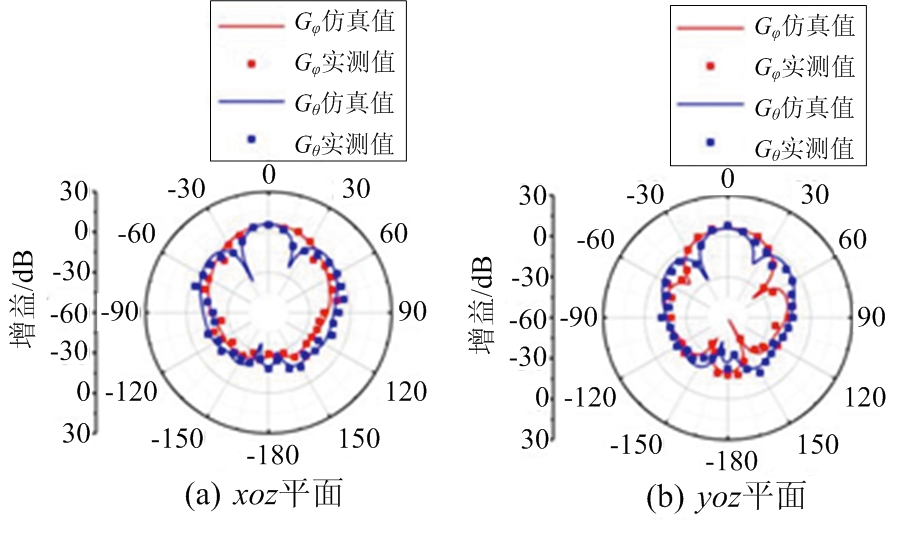
图8 12单元双线极化阵列的实测和仿真结果
3 结束语
本文将MMPTE用于极化可调控天线阵列设计,并给出了2×2阵列和12单元阵列的设计实例,两个阵列采用常见的线极化微带贴片单元。通过在远场区选用不同的极化方式的接收天线,在12单元的阵列上实现了多种极化切换功能。实验结果与仿真结果表明,MMPTE不仅可用于极化可调控天线阵列的设计,而且还能保证最佳的极化效果与增益特性。尤其在单元不规则排列情况下,该方法总能给出问题的最优解,故与传统设计方法相比,MMPTE的优越性十分明显。
[1] ESHAGHI A, SUPINSKI M, TAZLAUANU M. 60-GHz Polarization-Diversity Compact Phased Array Antenna [C]∥Proceedings of 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston: IEEE, 2018:1705-1706.
[2] ZHU N D, YANG X X, LOU T, et al. Broadband Polarization-Reconfigurable Slot Antenna and Array with Compact Feed Network [J]. IEEE Antennas and Wireless Propagation Letters, 2019,18(6):1293-1297.
[3] DEWAN R, HIMDI M, RAHIM M K A. Vertical,Horizontal to Circular Polarization Reconfigurable Array Antenna with EBG Unit Cells [C]∥Proceedings of 2019 Photonics & Electromagnetics Research Sym-posium-Fall(PIERS-Fall), Xiamen:IEEE, 2019:2478-2483.
[4] YIN L, YANG P . In-Band RCS Reduction of Microstrip Patch Array Antenna Using Polarization Reconfigurable Technique[C]∥ International Applied Computational Electromagnetics Society Symposium-China, Beijing:IEEE,2018:1-2.
[5] PHAM K, SAULEAU R, CLEMENTE A, et al. Electronically Reconfigurable Unit-Cell and Transmitarray in Dual-Linear Polarization at Ka-Band [C]∥Proceedings of 2019 13th European Conference on Antennas and Propagation, Krakow, Poland:IEEE, 2019:1-4.
[6] AL ABBAS E, NGUYEN-TRONG N, MOBASHSHER A T, et al. Polarization-Reconfigurable Antenna Array for Millimeter-Wave 5G [J]. IEEE Access, 2019, 7:131214-131220.
[7] OLIVERI G, LIZZI L, MASSA A. ADS Interleaved Arrays with Reconfigurable Polarization [C]∥2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada:IEEE,2010:1-4.
[8] KUMARI R, BEHERA S K, SHARMA S K. Aperture Coupled Wideband Dielectric Resonator Antenna Array with Polarization Reconfiguration [C]∥Proceedings of 2013 IEEE Applied Electromagnetics Conference, Bhubaneswar, India:IEEE, 2013:1-2.
[9] WEN G Y. Foundations of Applied Electrodynamics [M].Chichester, UK: John Wiley & Sons, Ltd, 2010:153-201.
[10] WEN G Y. Foundations for Radio Frequency Engineering [M]. Singapore: World Scientific, 2013:617-646.
[11] HUANG J. A Technique for an Array to Generate Circular Polarization with Linearly Polarized Elements [J]. IEEE Trans on Antennas and Propagation, 1986, 34(9):1113-1124.
[12] SMOLDERS A B, VISSER H J. Low Side-Lobe Circularly-Polarized Phased Arrays Using a Random Sequential Rotation Technique [J]. IEEE Trans on Antennas and Propagation, 2014, 62(12):6476-6481.
[13] SMOLDERS A B, GELUK S J, RENIERS A C F. Circularly Polarized Sparse Arrays Realized by Randomly Rotated Linearly Polarized Antennas [J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16:736-739.
[14] LI X H, YE Z H. Design of Broadband Dual Linearly-Polarized Microstrip Patch Antenna [C]∥Proceedings of 2019 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference(CSQRWC),[S.l.]:IEEE, 2019:1-3.

