0 引言
天气雷达是监测和预警突发灾害性天气最有效的手段,常规的天气雷达通过反射率与降雨率的经验关系实现对降雨的探测和预报[1],然而此类雷达无法满足对大范围降水测量准确度的要求,双偏振雷达能提高天气雷达的探测能力,包括降水估算能力和粒子相态识别能力。与C波段和S波段相比,X波段双偏振雷达对目标的定位更准确,并且具有天线尺寸小、易于移动等优点[2]。当双偏振雷达探测气象环境时,回波信号会被路径中降雨区域吸收,使接收端的反射率产生衰减,特别是X波段(中心波长3 cm),由于其波长较短,反射率衰减问题更为严重,使实测的反射率与真实的反射率之间存在差异,导致双偏振雷达对降雨估计不准确,因此必须进行衰减订正[3]。
Zhang等[4]根据雷达气象方程和ZH-AH关系,提出了雷达径向逐库算法进行衰减订正,该算法减小了过度订正问题,但没有解决衰减订正中不稳定的ZH-AH关系。随着双偏振雷达的发展,Rahimi[5]提出差分传播相移与衰减率之间可以近似为线性关系,在使用差分传播相移进行衰减订正时需消除后向散射以及环境噪声的影响,得到准确的差分传播相移。常见的平滑滤波,中值滤波等方法虽然能够改善差分传播相移数据的平滑性,但失去了对原有数据变化趋势的反映[6]。Hubbert等[7]提出采用FIR和IIR低通滤波器估计差分传播相移,该方法可得到差分传播相移的平均走势,但随着距离库的增加,不能有效抑制差分传播相移波动。何宇翔等[8]提出的卡尔曼滤波方法能够对差分传播相移进行较精确的估计,但这类方法对于距离门之间数据的关联性较强,导致运算速度较慢。杜牧云等[9]提出了小波分析法,通过小波分析估计得到的差分传播相移具有良好的平滑度,并减少了差分传播相移率的负值,但是此方法需要选择合适的小波基,影响运行速度。Bringi等[10]提出了迭代滤波方法,该方法能够达到剔除干扰的目的,但是迭代次数难以确定,数据处理时间较长。文献[11]利用MCMC方法对差分传播相移进行处理,该方法能对差分传播相移进行滤波处理,但MCMC方法存在一个显著问题就是需要计算接受率,导致计算量大,并且由于接受率的原因导致算法收敛时间变长。目前,上述方法均是将降水区域视为连续的区域进行衰减订正处理,且将天气雷达不同偏振参量的关系理想化为线性关系,当雷达测量值出现不连续或缺测点时将影响整个降雨区域的衰减订正效果,因而这些方法具有一定的局限性。
本文提出了一种基于EMD方法的X波段双偏振雷达衰减订正,该方法首先利用EMD方法对总差分传播相移进行自适应分解,获得由高频到低频分布的多个IMF,其次通过皮尔逊相关系数准则对IMF进行筛选,将有用的IMF进行重构获得差分传播相移,且将差分传播相移采用最小二乘法拟合差分传播相移率,然后将求得的差分传播相移与差分传播相移率采用自适应约束方法进行反射率衰减订正,最后对所提方法进行了仿真实验。实验结果表明所提方法可以降低观测数据带来的误差,并极大程度上保证差分传播相移的递增性,从而实现更加准确的衰减订正。
1 基于EMD的衰减订正方法
本文使用EMD方法进行衰减订正,首先采用EMD方法估计差分传播相移,之后再对差分传播相移采用最小二乘法估计差分传播相移率,最后对求得的差分传播相移与差分传播相移率采用自适应约束方法进行反射率衰减订正。下面将分别进行详细描述。
1.1 基于EMD的差分传播相移估计
假设降水区域包含K个距离库,将第k个距离库的水平和垂直偏振波相位分别记为ΦH(k)、ΦV(k),则该距离库的差分传播相移Φdp(k)为
Φdp(k)=ΦH(k)-ΦV(k)
(1)
它表示水平、垂直偏振波传播到第k个距离库之后散射回来的信号相位差。实际雷达观测到的总差分传播相移Ψdp(k)由差分传播相移与后向散射差分相移构成,表示为
Ψdp(k)=Φdp(k)+δhv(k)
(2)
式中,δhv(k)表示该距离库后向散射差分相移,是散射过程中降雨粒子本身引起的相位差[12]。从频率上看,δhv(k)属于高频噪声[6]。对于不同强度的降雨区,δhv(k)会随着雨滴直径的增大而增大,导致Ψdp(k)在距离廓线上表现出短距离内的波动。由式(2)可以看出,当δhv(k)近似为常数或能被忽略时,可以将Ψdp(k)作为Φdp(k)的估计值,否则就需要滤除δhv(k),估计准确的Φdp(k)。
1.1.1 EMD分解
EMD算法是一种自适应的信号去噪方法,该算法可将总差分传播相移自适应分解为多个IMF和残余项之和,且每个IMF都应满足以下2个条件[13]:1)在整个曲线中,极值点和过零点的数目相等或至多相差1个;2)在任意局部区间,曲线的局部极大值包络线和局部极小值包络线的平均值为0。EMD分解包括提取分量、筛选IMF、计算余项三个部分:
(a) 提取分量
确定原始序列X={Ψdp(1),Ψdp(2),…,Ψdp(k),…, Ψdp(K)}的局部极值序列,记为X′={Ψdp(i)|i⊂I},其中,I表示所有极值点的集合。局部极值序列分为局部极大值序列与局部极小值序列(例如,局部极大值定义为序列中的某个距离门所对的总差分传播相移值,其前一距离门的值比它小,后一距离门的值也比它小)。
从序列X中提取相邻极值点Ψdp(i)、Ψdp(j)之间的局部序列设为Xpart={Ψdp(i),…,Ψdp(s),…,Ψdp(j)},其中,i≤s≤j。根据文献[14],求Xpart的局部均值m(ss)为
(3)
式中,![]() 利用上述方法对所有相邻极值点依次求取局部均值点,采用三次样条插值方法[15]拟合所有局部均值点构建出均值曲线,并对均值曲线进行采样得到均值序列M={m(1),m(2),…,m(k),…,m(K)},其中,m(k)即为均值曲线上第k个距离库的数据,则第一个分量h1={h1(1),h1(2),…,h1(k),…,h1(K)}表示为
利用上述方法对所有相邻极值点依次求取局部均值点,采用三次样条插值方法[15]拟合所有局部均值点构建出均值曲线,并对均值曲线进行采样得到均值序列M={m(1),m(2),…,m(k),…,m(K)},其中,m(k)即为均值曲线上第k个距离库的数据,则第一个分量h1={h1(1),h1(2),…,h1(k),…,h1(K)}表示为
h1=X-M
(4)
(b) 筛选IMF
若h1符合IMF条件,h1就是X的第一个IMF;若h1不满足IMF的条件,继续将h1作为新的信号,重复步骤(a)进行分解。在实际中,h1通常无法满足IMF条件,假设经过t(t一般小于10)[16]次分解后,有以下式(5)成立,则认为其满足IMF条件:
(5)
式中,ε为门限,一般取值为0.2~0.3 [16]。
那么原始信号X的第一个IMF可记为
(6)
(c) 计算余项
将得到的a1从X中分离出来,得到余项r1=X-a1,将r1作为新的信号,重复步骤(a)~(b)继续进行分解,依次可得到第2,第3,…,第n个,…,第N个IMF,记为
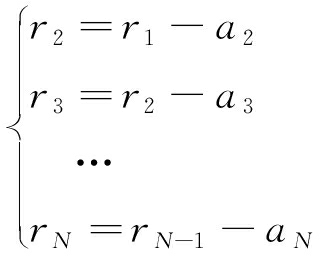
(7)
当余项rN变成一个单调信号时,EMD分解过程停止。
通过上述分解过程,可将X分解为N个IMF与余项的和,记为
(8)
基于EMD的总差分传播相移分解流程如图1所示。

图1 总差分传播相移分解流程图
1.1.2 EMD重构
传统的EMD凭借经验选取前几个IMF重构差分传播相移,这会导致重构的差分传播相移中混入多余的后向散射或漏掉某些有用信息,为了克服这一问题,本文提出利用皮尔逊相关系数准则(|PCC|)分析原始信号与EMD分解得到的N个IMF相关性,确定最佳IMF数目。
首先计算X=(Ψdp(1),Ψdp(2),…,Ψdp(k),…,Ψdp(K))与an=(an(1),an(2),…,an(k),…,an(K))的PCC值,定义式为
PCC=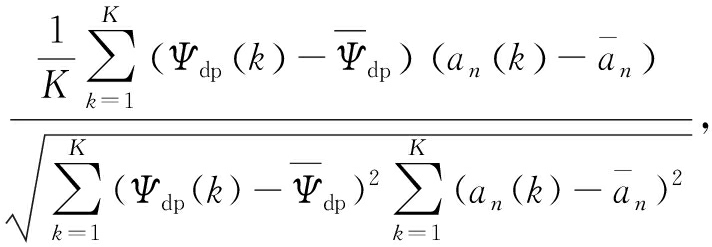
k=1,2,…,K
(9)
式中:K表示距离库;![]() 是X的平均值,表示为
是X的平均值,表示为![]() 是an的平均值,表示为
是an的平均值,表示为![]() 的取值范围为[-1,1],若PCC>0,表明2个信号是正相关,若PCC<0,表明 2个信号是负相关。PCC的绝对值越大表明相关性越强,即该IMF中包含的原始信号的信息越多。根据文献[17],皮尔逊相关系数的评估标准如表1所示。
的取值范围为[-1,1],若PCC>0,表明2个信号是正相关,若PCC<0,表明 2个信号是负相关。PCC的绝对值越大表明相关性越强,即该IMF中包含的原始信号的信息越多。根据文献[17],皮尔逊相关系数的评估标准如表1所示。
表1 皮尔逊相关系数评估标准
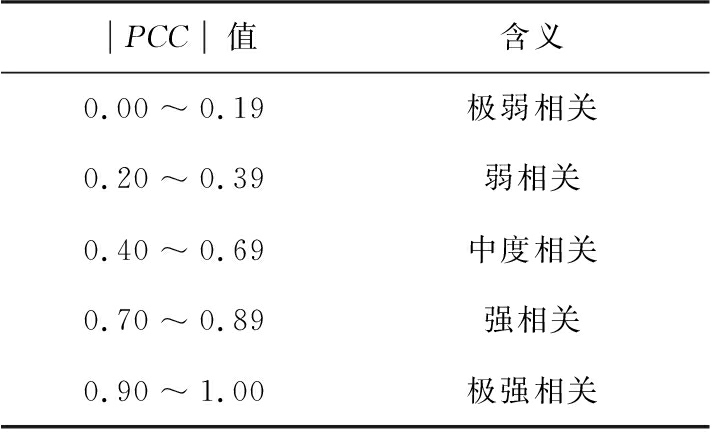
PCC值含义0.00~0.19极弱相关0.20~0.39弱相关0.40~0.69中度相关0.70~0.89强相关0.90~1.00极强相关
通过计算EMD分解得到的N个IMF与原始信号的|PCC|值,找到合适的分界点l∈(0,1),确保除去噪声较大的前j(j∈(1,2,…,N))个,其他IMF的|PCC|值稳定在评估标准范围内。
经过EMD分解后,总差分传播相移X可以表示为
(10)
式中,a1~aj表示噪声分量,aj+1~aN表示信号分量,rN表示余项。差分传播相移Φdp由信号IMF与余项rN共同构成,即
(11)
基于EMD的差分传播相移重构流程如图2所示。
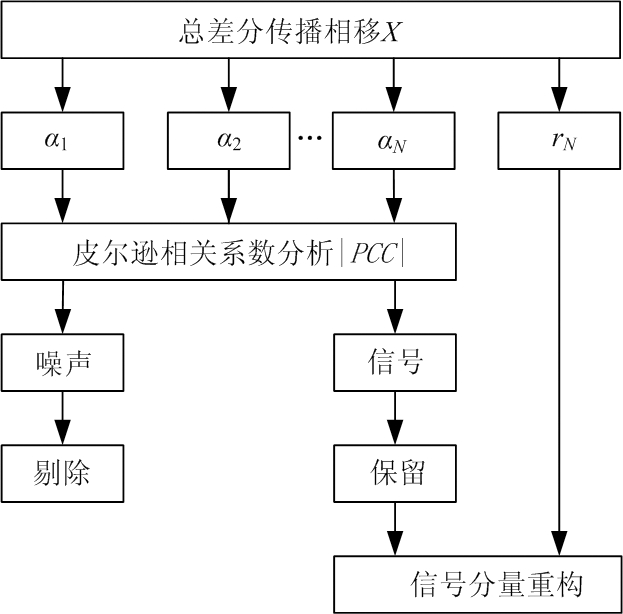
图2 差分传播相移重构示意图
1.2 基于最小二乘法的差分传播相移率估计
在降水区距离r内含有K个距离库,第k个距离库对应值为Φdp(k),用最小二乘法拟合这K个库对应的Φdp,根据拟合曲线的斜率即可得到雨区距离r的Kdp值,表示为
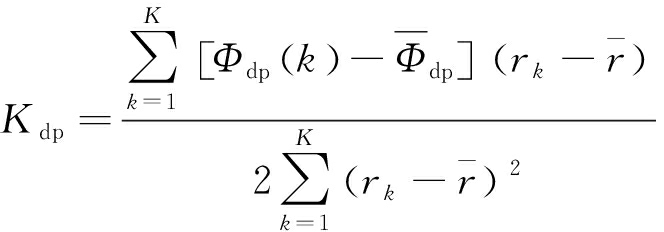
(12)
式中,![]() 为第k个距离库与雷达之间的径向距离,
为第k个距离库与雷达之间的径向距离,![]() 为K个距离库的Φdp的平均值。
为K个距离库的Φdp的平均值。
1.3 基于自适应约束方法的反射率衰减订正
衰减率AH对接收的反射率影响较大,且AH随着探测距离的增加而增加,造成反射率估计误差,因此本文在自适应约束算法[18]的基础上,根据EMD方法处理得到的Φdp与最小二乘法拟合的Kdp,提出了适用于双偏振雷达的自适应约束方法进行反射率衰减订正。该方法首先对雨区径向数据划分区间,根据AH-Kdp的关系,计算所有区间的衰减系数α,完成整个径向数据的衰减订正。
由文献[18]可知,雷达反射率衰减订正原理如式(13)所示:
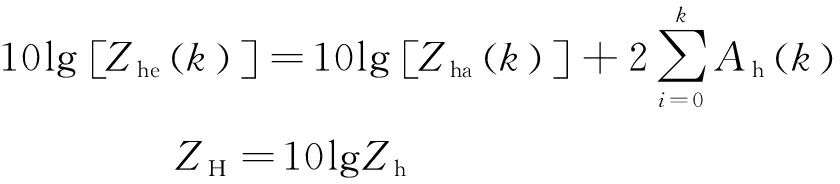
(13)
式中,Zha(k)与Zhe(k)分别为订正前后的第k个距离库反射率,Ah(k)为第k距离库的衰减率。
根据径向距离(r0,rk)内衰减积分![]() 与差分传播相移变化ΔΦdp(r0:rk)相等的特点[18],可得到第k个距离门的衰减率(Ah(k))的计算公式为
与差分传播相移变化ΔΦdp(r0:rk)相等的特点[18],可得到第k个距离门的衰减率(Ah(k))的计算公式为
(14)
式中:![]() 表示从距离门r0至rk差分传播相移Φdp(k)的变化;衰减系数α与衰减指数β可通过衰减率(Ah(k))与差分传播相移率(Kdp(k))的经验公式获得,即
表示从距离门r0至rk差分传播相移Φdp(k)的变化;衰减系数α与衰减指数β可通过衰减率(Ah(k))与差分传播相移率(Kdp(k))的经验公式获得,即
(15)
假设雨滴谱服从Gamma分布[10],利用雨滴谱拟合得到衰减指数β=0.8,由于衰减系数α受环境温度影响较大,若运用固定系数α来计算Ah(k),Ah(k)会产生较大的偏差,因此本文设定衰减系数α的取值范围为amin<a<amax,步长取μ。首先根据公式(15)计算α取值范围(amin,amax)内的每一个α值对应衰减率AH(k|α)。接着利用AH(k|α)计算重构的差分传播相移![]() 重构方程如式(16)所示:
重构方程如式(16)所示:
(16)
然后以![]() 与经过EMD方法估计得到的Φdp(k)残差最小作为约束条件获得最优α值,并将最优α代入式(14)计算得到最优的Ah(k)值。
与经过EMD方法估计得到的Φdp(k)残差最小作为约束条件获得最优α值,并将最优α代入式(14)计算得到最优的Ah(k)值。
最后将最优Ah(k)代入式(13)中得到订正后的Zhe(k)。
对反射率处理的具体流程如图3所示。
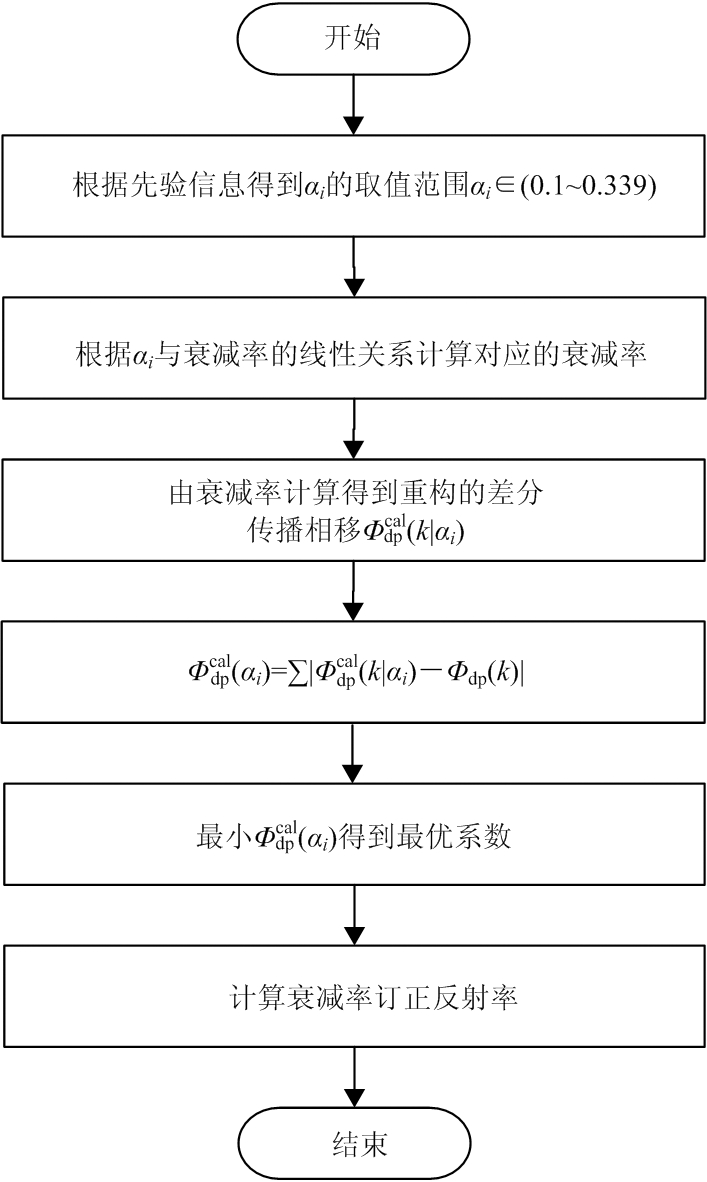
图3 衰减订正处理流程图
2 实验结果及分析2.1 差分传播相移估计效果分析
本文使用的是ARM(Atmospheric Radiation Measurement Climate Research Facility)探测到的X波段天气雷达数据。该雷达采用双偏振体制,同时在水平和垂直偏振中传输,其主要包括偏振参数Ψdp,Kdp,ZH等。下面通过仿真试验分析了不同滤波方法的估计效果。
图4为X-SAPR雷达于0.5°俯仰角、30°方位角的雷达Ψdp观测数据,以及经过不同滤波方法的径向距离廓线图。从图中可以看出,原始信号(图4(a))由于外界噪声存在较大的波动,但基本保持递增趋势。由均值滤波(图4(b))与FIR滤波(图4(c))后的处理效果可以看出,这两种方法对Ψdp的波动起伏有较好的平滑效果,但随着平滑库数k增大,不能有效抑制Ψdp波动。卡尔曼滤波(图4(d))由于缺乏先验数据,造成初始数据失真。采用EMD方法对原始信号进行分解得到7个IMF,从低到高依次计算各IMF与原信号的|PCC|值分别为0.07,0.13,0.15,0.20,0.23,0.36,0.58,可知前3个IMF的|PCC|值均在0.00~0.19极弱相关这一范围内,为噪声分量,后4个IMF的|PCC|值均大于0.19,为信号分量,对后4个IMF进行有效重构,其结果如图4(e)所示,可以看出,Ψdp数据的毛刺和波动均得到很好抑制,数据的连续性和平滑度有了显著提升,即去除了后向散射的影响,这也有利于对数据进行后续处理及应用。综上可见,EMD方法较之常规方法具有更明显的处理效果。
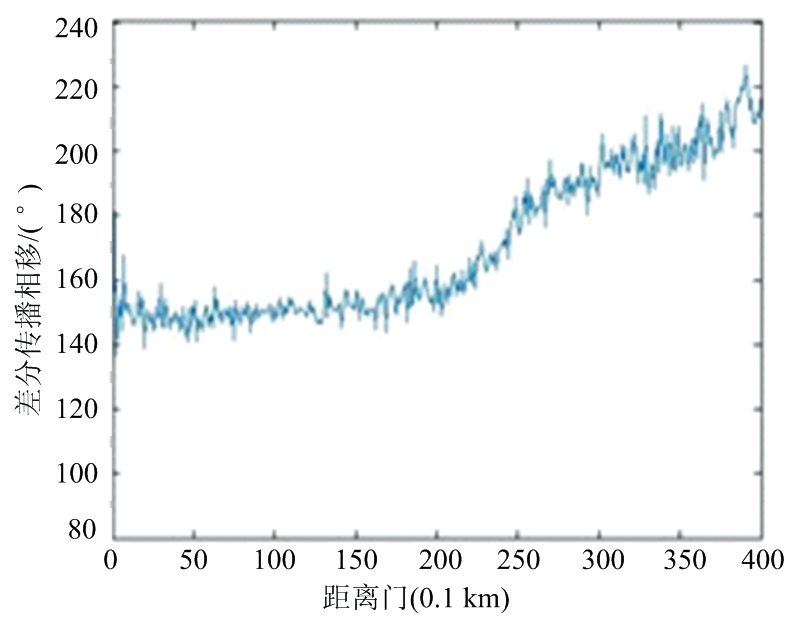
(a) 原始数据
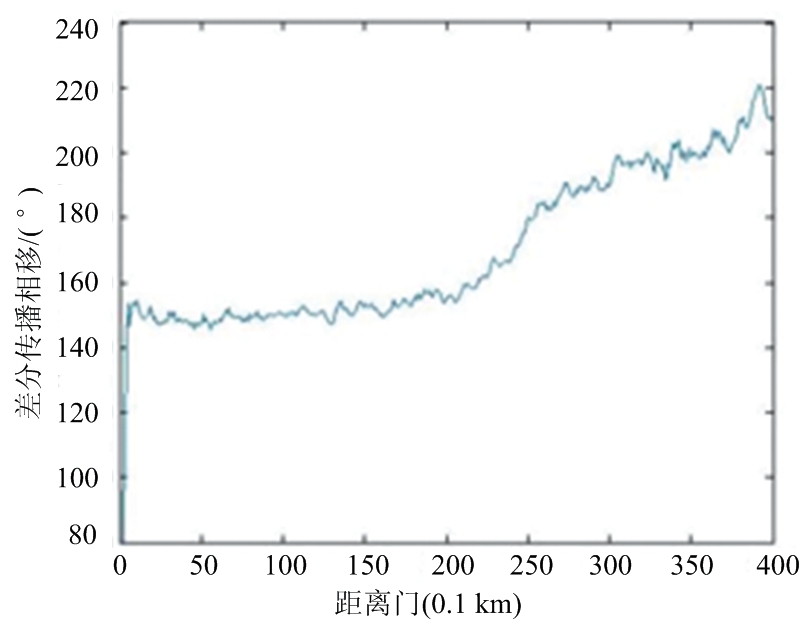
(b) 均值滤波
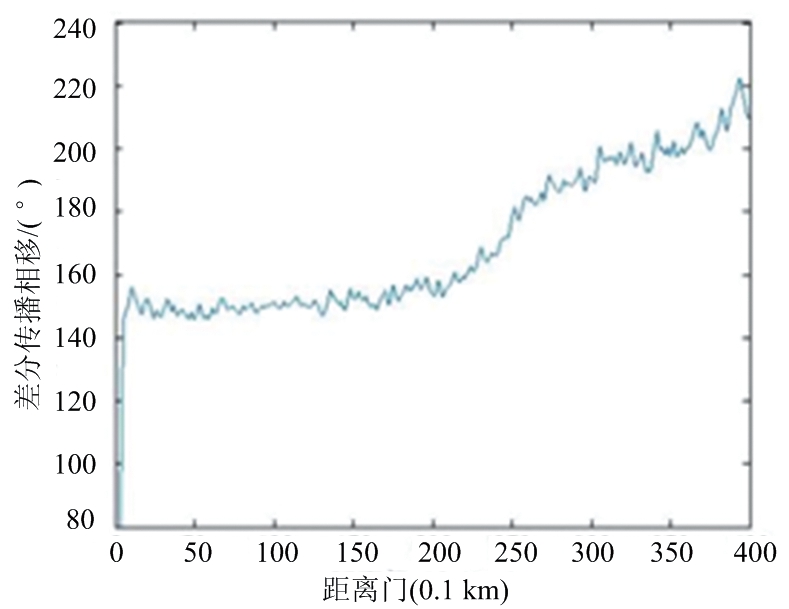
(c) FIR滤波
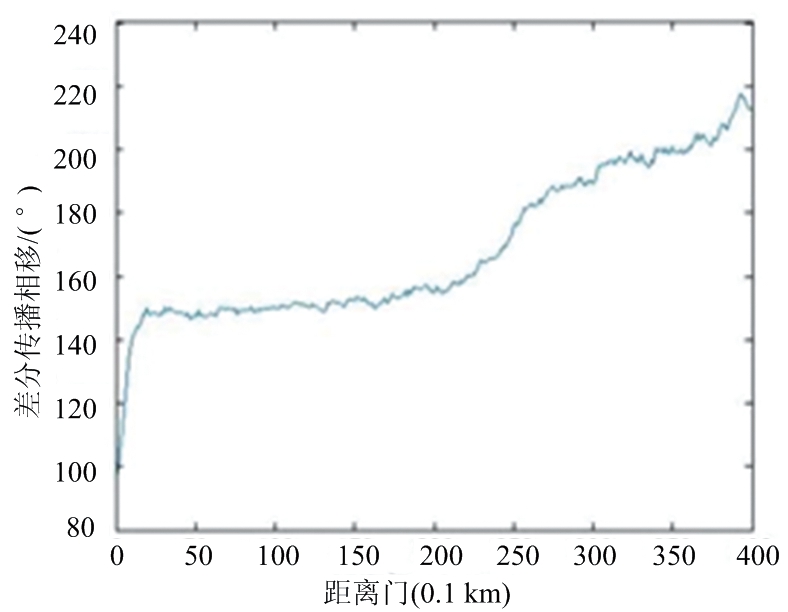
(d) 卡尔曼滤波
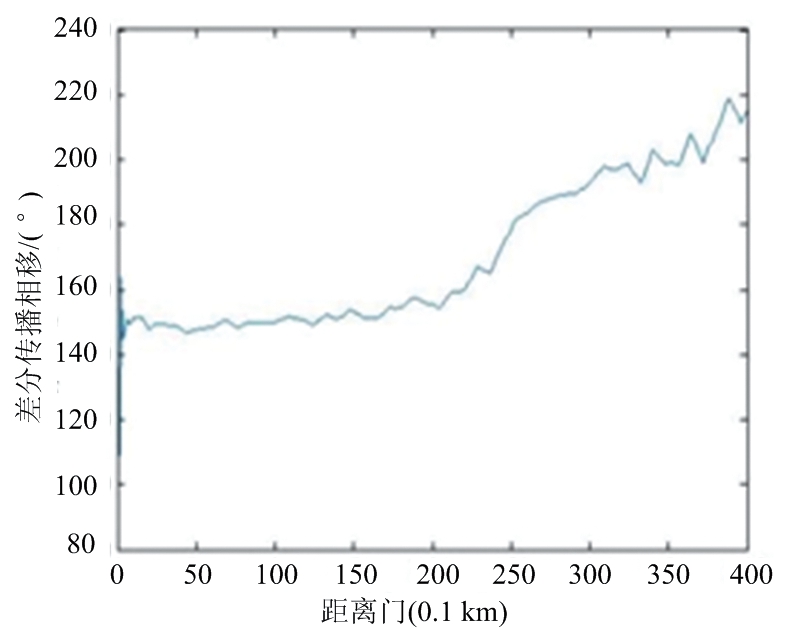
(e) EMD方法
图4 不同方法Ψdp径向对比图
图5为X-SAPR雷达于0.5°俯仰角观测数据Ψdp的PPI图及经过EMD方法后的PPI图。从图中可见,在Ψdp原始数据PPI图(图5(a))中,大部分径向都具有较为明显的层次性,颜色上表现为分层渐进递增形式,但也存在许多“麻点”(黑框所选区域为麻点),即为波动数据点;经过EMD方法后(图5(b)),Ψdp数据整体层次性得到明显加强,颜色分布均匀,且原始数据的有效的气象回波也得到了很好的保留。
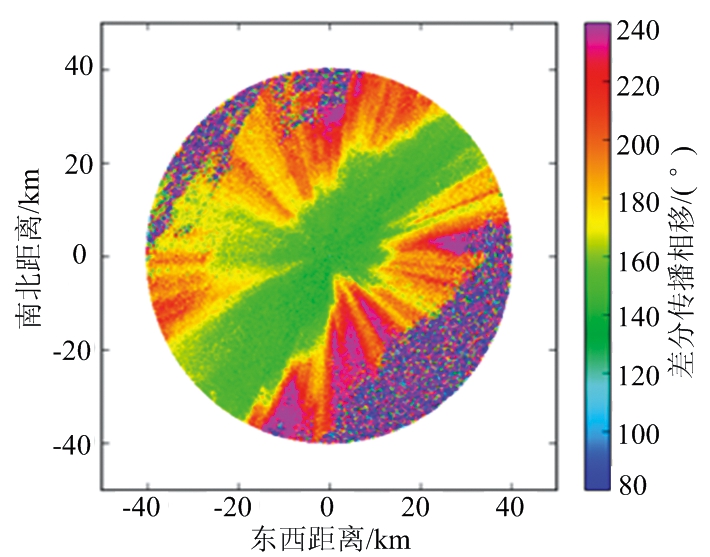
(a) Ψdp原始数据
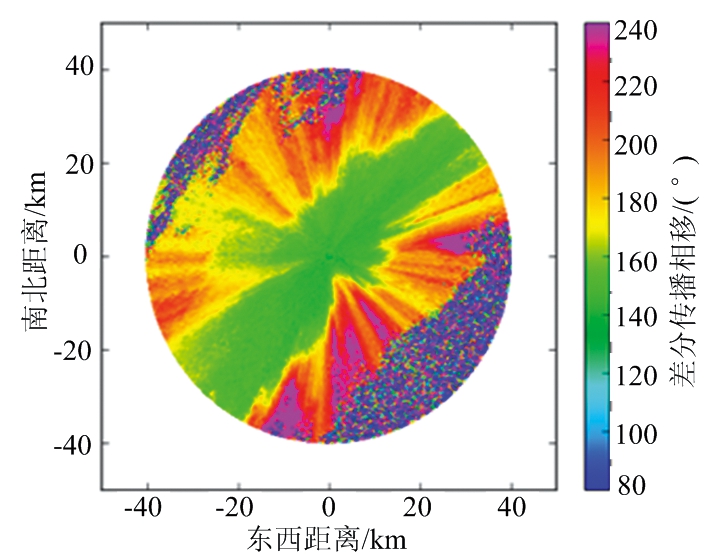
(b) EMD方法
图5 EMD方法处理前后ΨdpPPI图
为了进一步分析不同滤波方法对差分传播相移估计的影响,分别通过平均波动指数FIX、相对误差RE、互相关系数ρ进行降雨估计性能分析,计算公式为
(17)
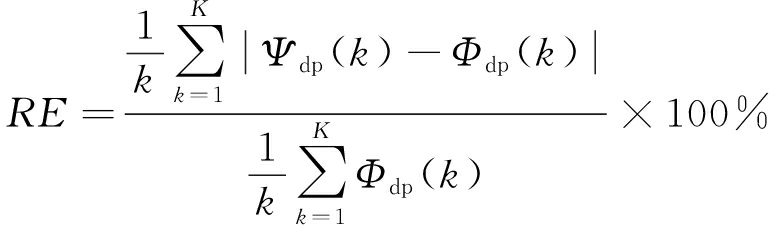
(18)
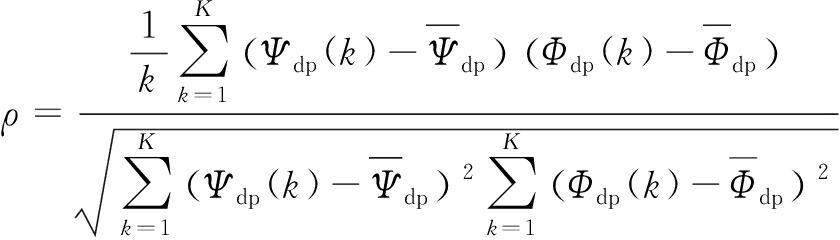
(19)
式中,Ψdp(k)表示实测值,Φdp(k)表示经过处理后的值,通过FIX来比较距离廓线的波动情况,FIX的值越大,说明径向距离廓线的波动性越大;通过RE来比较数据可靠性,RE值越小数据的可信度越高;通过ρ来比较数据变化趋势的一致程度,ρ值越大表明线性一致程度越高。
表2统计了Ψdp(k)经本文提出的方法与常规方法处理并应用于降水估计Φdp(k)的FIX、RE和ρ。根据统计结果可以看出,Ψdp(k)经常规方法处理后的FIX和RE较大,而EMD方法处理的Ψdp(k)的FIX与RE较小,且ρ值相对较大,说明EMD方法对Ψdp(k)数据的处理波动较小,可靠性高,应用于降水估测的精度最高。
表2 不同滤波方法对QPE影响的对比图
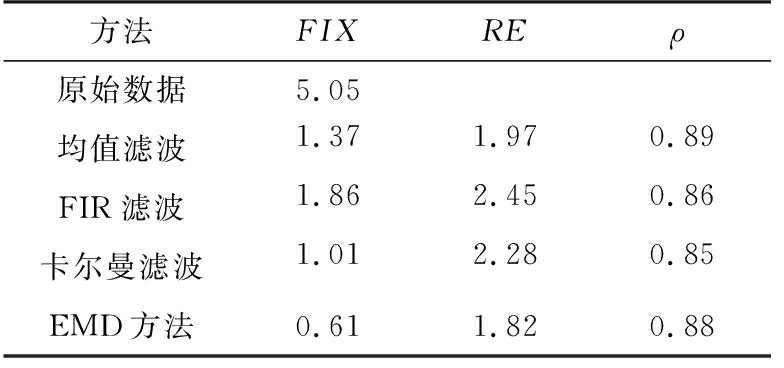
方法FIXREρ原始数据5.05均值滤波1.371.970.89FIR滤波1.862.450.86卡尔曼滤波1.012.280.85EMD方法0.611.820.88
2.2 差分传播相移率估计效果分析
图6为X-SAPR雷达于0.5°俯仰角、30°方位角的雷达kdp观测数据,以及经过不同滤波方法的径向距离廓线图。结果表明,经过均值滤波、FIR滤波、卡尔曼滤波和EMD方法处理后估计的kdp的负值数量分别为182,185,167和148。说明EMD方法能够有效地减少kdp的负值,保证数据的基本趋势。
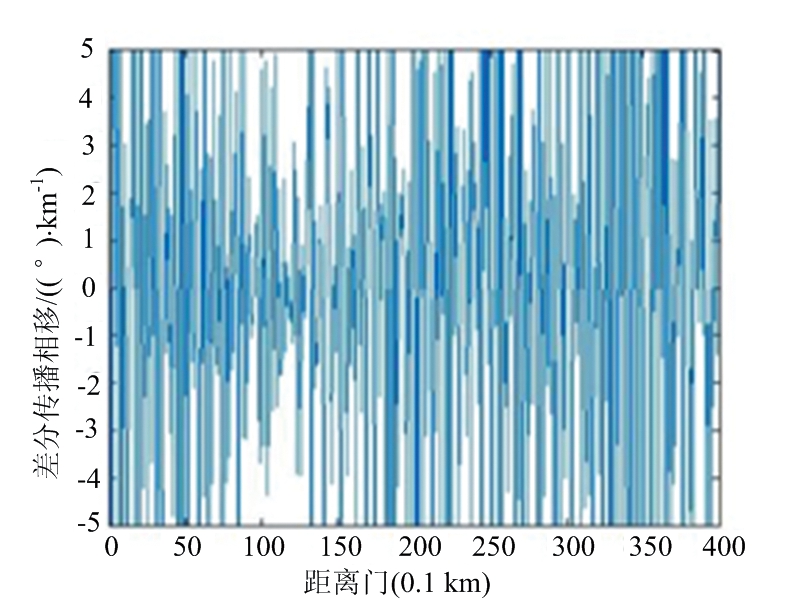
(a) 原始数据
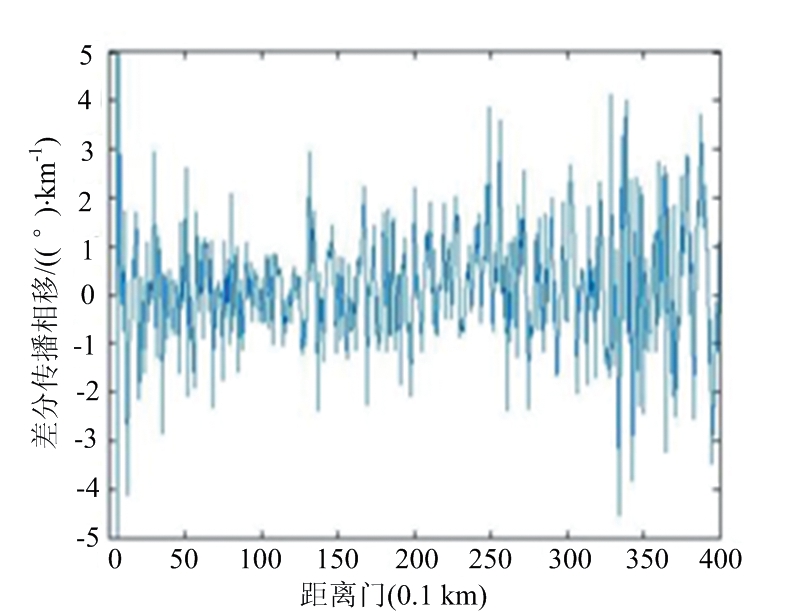
(b) 均值滤波
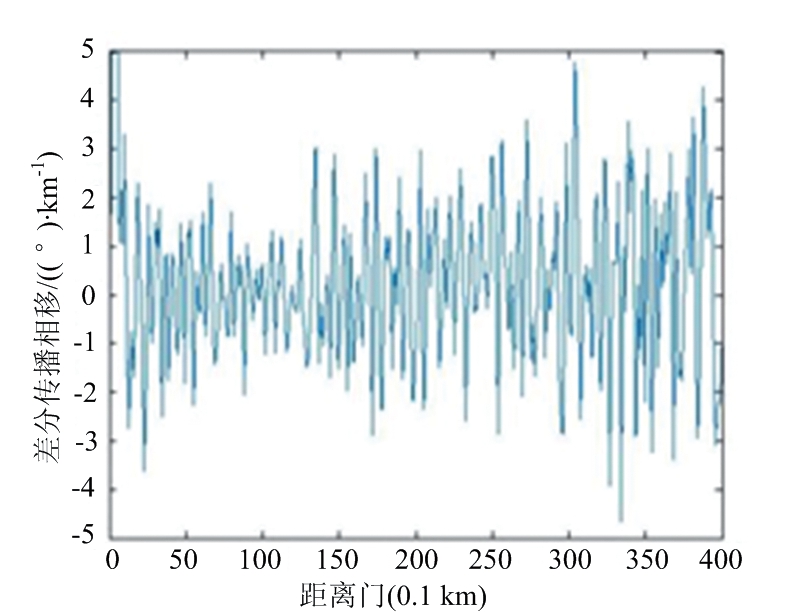
(c) FIR滤波
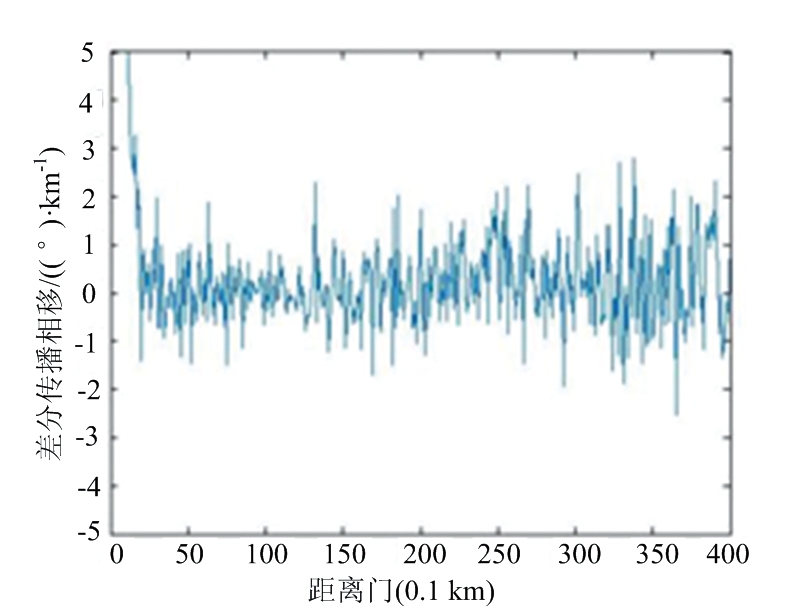
(d) 卡尔曼滤波
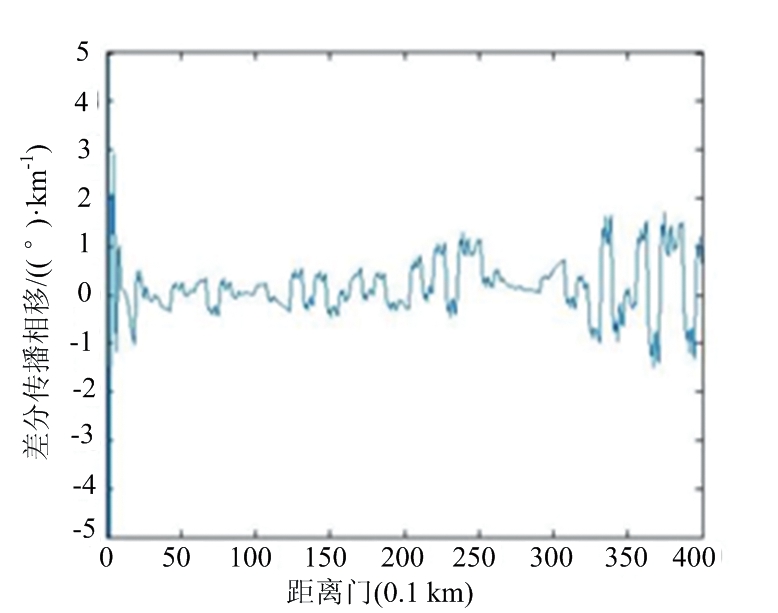
(e) EMD方法
图6 不同方法kdp径向对比图
2.3 反射率衰减订正效果分析
X波段双偏振雷达探测的径向距离为40 km,一个距离库表示100 m。图7为同一径向的反射率衰减订正结果对比图,从图中可以看到,ZH变化与Φdp的变化趋势是相对应的。在初始距离库,雨区的衰减较少,反射率基本在20dBz左右,而在第200个距离库处有一强回波区域,雨区的衰减较多,使用EMD方法进行订正后的反射率因子能够在保持原始数据变化趋势的同时,对其进行有效的衰减订正。

图7 反射率衰减订正对比图
图8为反射率因子订正前后PPI对比图。由图8(a)可知,强回波的区域分布离散,主要集中在图中心位置,雷达强回波反射率因子一般在30~40 dBz,由图8(b)可知,经过衰减订正后,雷达回波反射率因子的订正值一般在1~5 dBz。强回波区域扩大,回波中心更为明显,订正值达到了5~10 dBz。
由于S波段雷达基本上不存在雨区衰减,除非在一些湿雹区。因此将同时间同一区域内的反射率因子订正后的效果与S波段数据进行对比,其效果与S波段探测结果越相似,则认为订正效果越好。S波段双偏振雷达的探测距离范围为230 km,而X波段的探测距离范围为40 km,所以X波段气象雷达包含在S波段双偏振雷达的探测范围内,图8(c)为S波段双偏振雷达回波反射率因子,黑色方框中的区域作为X波段双偏振雷达衰减订正后的效果参照图。对比图8(a)、图8(c)可以看到,X波段双偏振雷达衰减更为严重。对比图8(b)、图8(c)可以看到,经过EMD方法处理后,X波段双偏振雷达的反射率因子中心处强回波有所加强,与S波段雷达回波反射率因子差异显著减小,表明EMD方法对X波段双偏振雷达衰减订正具有一定的效果。
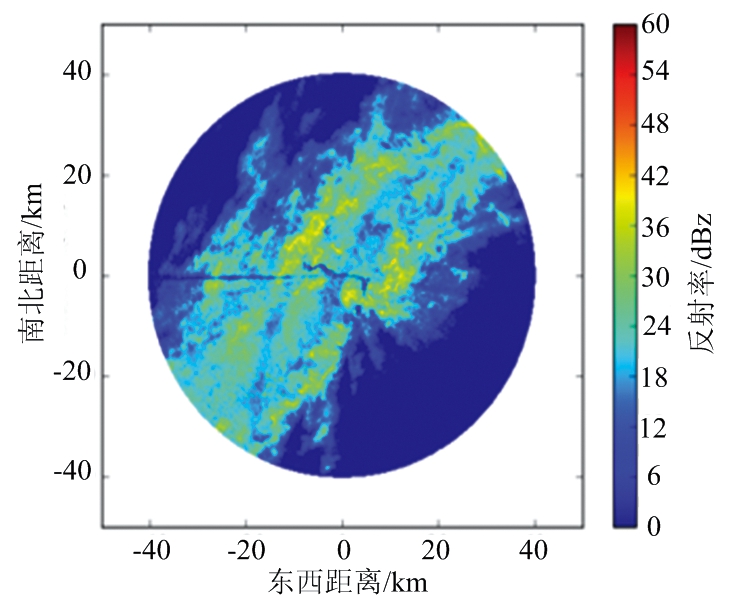
(a) X波段ZH原始数据
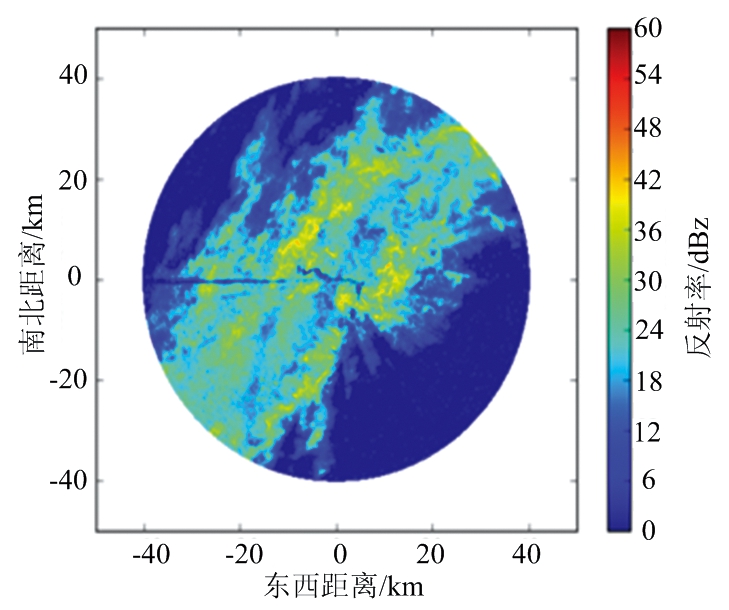
(b) EMD方法
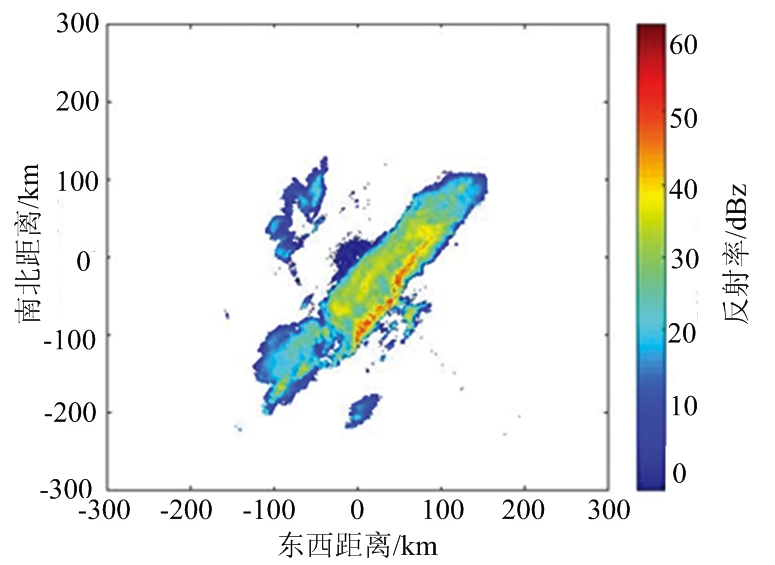
(c) S波段ZHPPI图
图8 不同方法反射率PPI对比图
3 结束语
本文提出了基于EMD方法的X波段双偏振雷达衰减订正,首先使用经验模式分解方法将总差分传播相移按照频率分布自适应地分解为多个IMF,使得原始序列平稳化,从而提高差分传播相移的预测精度,接着利用最小二乘法估计差分传播相移率,最后根据得到的差分传播相移与差分传播相移率采用自适应约束算法对反射率因子进行衰减订正。实验结果表明,利用EMD方法能够实现对差分传播相移滤波处理,并且保留原始信号的基本趋势;利用自适应约束的方法能够对反射率进行有效的衰减订正,这对雷达降水量估计以及降水分类等有重要的现实意义,所以本方法具有一定的实际应用价值。
[1] DAS S K, KRISHNA M, KOLTE Y, et al. Assessment of Ground-Based X-Band Radar Reflectivity: Attenuation Correction and Its Comparison with Space-Borne Radars over the Western Ghats, India[J]. Earth and Space Science,2020, 7(11):1-15.
[2] 吕博,杨士恩,王俊,等.X波段双线偏振雷达电磁波衰减订正效果评估[J].气象水文海洋仪器,2018,35(4):115-120.
[3] 郭春辉,袁微,王旭,等.基于保序回归的X波段天气雷达衰减订正算法[J].广东气象,2020,42(5):70-75.
[4] ZHANG P C,WANG Z H. A Study on Algorithm to Make Attenuation Correction to Radar Observations of Radar Reflectivity Factor(I):Theoretical Analysis[J]. Plateau Meteorol,2001,20:1-5.
[5] RAHIMI A R. Statistical Validation of Rainfall Estimates Obtained from Microwave Attenuation[D]. UK: University of Essex, 2004.
[6] 魏庆,胡志群,刘黎平.双偏振雷达差分传播相移的五种滤波方法对比分析[J]. 成都信息工程学院学报, 2014, 29(6):596-602.
[7] HUBBERT J V,CHANDRASEKAR V,BRINGI V N,et al. Processing and in-Terpretation of Coherent Dual-Polarized Radar Measurements[C]∥ International Conference on Radar Meteorology,Paris:IEEE,1991, 10(4):155-164.
[8] 何宇翔,吕达仁,肖辉,等.X波段双线极化雷达反射率的衰减订正[J].大气科学,2009,33(5):1027-1037.
[9] 杜牧云,刘黎平,胡志群,等.双线偏振雷达差分传播相移的小波滤波初探[J].暴雨灾害,2012,31(3):248-254.
[10] HUBBERT J, BRINGI V N. An Iterative Filtering Technique for the Analysis of Copolar Differential Phase and Dual-Frequency Radar Measurements[J]. Journal of Atmospheric and Oceanic Technology, 1995, 12(3):643-648.
[11] 罗原. 基于MCMC方法的雨衰补偿算法研究[D].天津:中国民航大学,2020.
[12] 曹杨,苏德斌,周筠珺,等.C波段双线偏振多普勒雷达差分相位质量分析[J].高原气象,2016,35(2):548-559.
[13] ZHAO Juan, SHE Jinhua, FUKUSHIMA E F, et al. Muscle Fatigue Analysis with Optimized Complementary Ensemble Empirical Mode Decomposition and Multi-Scale Envelope Spectral Entropy[J]. Frontiers in Neurorobotics,2020,11:1-10.
[14] 牛晓东,卢莉蓉,王鉴,等.基于改进经验模态分解域内心动物理特征识别模式分量的心电信号重建[J].物理学报,2021,70(3):311-319.
[15] 莫跃爽,索惠英,焦树林,等.喀斯特地区降水量空间插值方法对比——以贵州省为例[J].水土保持研究,2021,28(1):164-170.
[16] 王婷. EMD算法研究及其在信号去噪中的应用[D]. 哈尔滨:哈尔滨工程大学,2010.
[17] 杨菊花,刘洋,陈光武,等.基于改进EMD的微机械陀螺随机误差建模方法[J].仪器仪表学报,2019,40(12):196-204.
[18] 李宗飞,肖辉,冯亮,等.X波段双偏振天气雷达衰减订正方法及效果检验[J].气象科技,2019,47(5):731-739.

