0 引言
车载毫米波雷达作为汽车主动安全领域的关键传感器部件，可有效穿透雾、烟、灰尘，实现全天时、全天候工作负荷要求[1]。这种雷达采用的体制现有合成孔径雷达(SAR)和多发多收(MIMO)雷达等。相比于SAR，MIMO雷达是利用发射和接收天线间的位置关系形成更大孔径的虚拟天线阵列[2]。考虑到车载雷达的实现复杂度及半导体器件成本限制，本文采用时分复用MIMO(TDM-MIMO)雷达工作机制[3]，该方式对硬件性能需求较低、实现简单，减少MIMO雷达的数量和复杂性，降低了成本。
传统的成像方法包括后向投影[4](Back Projection，BP)、延时求和[5](Delay-And-Sum，DAS)和数字波束形成 [6](DBF)等。文献[4]基于SAR成像几何模型，结合车载平台推导了BP算法，通过仿真实验验证了其在车载前视阵列雷达的适用性。文献[5]提出了在距离向进行距离压缩与方位向进行DAS，最后结合距离-方位信息得到二维成像结果。文献[6]提出的DBF通过加权求和使多路信号变为一路信号，使得目标方向的信号得到增强，同时对非目标方向的信号进行抑制。
尽管这些算法能够快速而简单地实现目标的成像，但是都存在分辨率低且旁瓣较高的问题。为此，采用高分辨成像方法是必要的。文献[7]和[8]分别介绍了在获得距离向信息后采用ESPRIT、MUSIC超分辨算法，虽然相比于传统算法有着更好的角度分辨率，但这些算法需要对接收信号的协方差矩阵作特征分解，需要的数据帧数较多，对均匀线阵中天线的数量也有着较高的要求。文献[9]提出了IAA在FMCW MIMO雷达系统中的应用，该方法在帧数较少的情况下可使角分辨率从DAS波束形成的10°提高到5°，但存在算法复杂度较高，无法实现工程实时性的问题。
针对上述问题，本文提出了一种车载毫米波FMCW MIMO雷达IAA高分辨成像的快速实现方法，该方法首先基于MIMO机制采用FFT来获取目标的距离信息，然后对存在目标的距离单元内利用傅里叶算子特性和GS因子分解进行数据协方差矩阵及其逆矩阵的快速计算，利用快速Toeplitz矩阵向量乘法有效计算目标反射系数，迭代次数少(10次左右)、计算量适中。
1 信号模型
雷达系统模型如图1所示，采用时分复用FMCW MIMO雷达(时分复用带来的相位误差补偿方法具体见文献[10])，根据MIMO雷达原理，以第一个接收阵元为参考点，有I个发射阵元，各阵元距离参考点的间距为dti,i=1,2,…,I；接收阵元有J个，各阵元距离参考点的间距为drj,j=2,3,…,J-1。假设第i个阵元发射信号为
si(t)=exp(j2πf0t+jπμt2)
(1)
式中，t为信号时间， f0为载波频率，μ=B/T为调频斜率，B为信号带宽，T为调频周期。
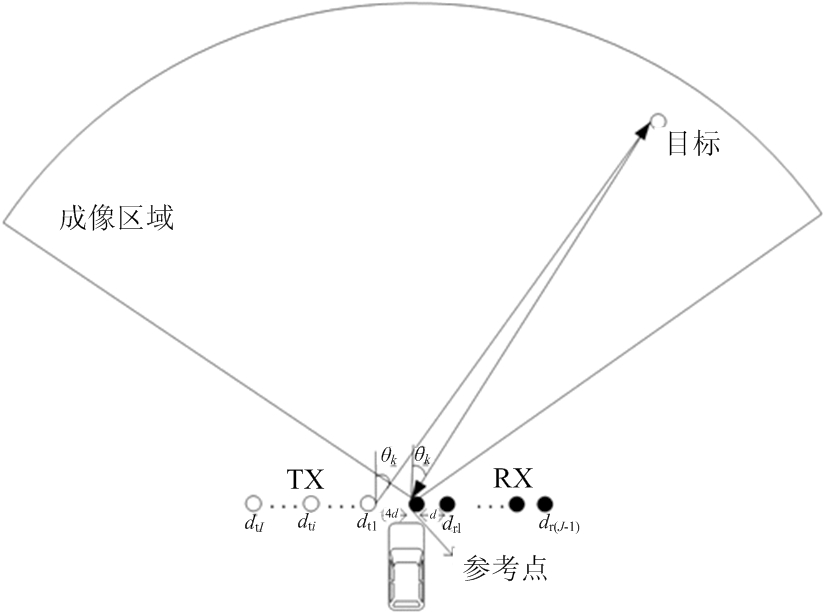
图1 系统模型
将成像区域划分为M个距离单元R1,R2,…,RM，K个角度单元θ1,θ2,…,θK，则对于第j个接收阵元来说接收到该区域内所有目标的回波信号可以表示为
rij(t)=
(2)
式中:σ(Rm,θk)表示加权指示函数，若在(Rm,θk)位置上有目标，则σ(Rm,θk)≠0，反之σ(Rm,θk)=0；τij(Rm,θk)表示目标与第i个发射阵元和第j个接收阵元之间的传播时延，其为
(3)
式中，c为电磁波在自由空间的传播速度，
为雷达与目标径向距离产生的双程传播时延，
和
分别为第i个发射阵元和第j个接收阵元相对于参考点附加的双程传播时延。将回波信号与发射信号进行混频后，经过低通滤波器进行滤波得到中频信号为
rij(t)=
θk)+j2πμτij(Rm,θk)t]
(4)
对中频信号进行采样得到离散采样序列：
rij(l)=
θk)+j2πμτij(Rm,θk)lTs]
(5)
式中，Ts为采样间隔，l=1,2,…,L为采样点数。对rij(l)计算M点FFT并取单边谱，得到该通道的一维距离像为
rij(p)=
exp[j2πf0τij(Rm,θk)],p=1,2,…,M
(6)
从式(6)可以看出，谱峰位于p处，即p=Bτij(Rm,θk)。将式(3)代入式(6)并化简，则
rij(p)=
(7)
从式(7)可以看出，在p最接近
处取得谱峰，若划分的距离单元以距离分辨率为准，则p对应的距离
此时sinc函数值为1，则式(7)变为
(8)
式中，σm(θk)为对应第m个距离单元角度目标的散射系数。
最后，将所有发射阵元和接收阵元组合的回波数据堆叠，并将距离Rm的产生的双程时延补偿，得到第m个距离单元的测量向量，即
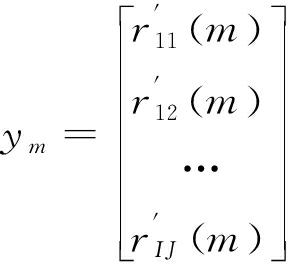
(9)
令σm=[σm(θ1) … σm(θK)]T，Am=[am(θ1) … am(θk)…am(θK)]，其中
则
ym=Amσm+em
(10)
2 算法描述
根据文献[11]所述，IAA通过最小化下面的加权最小二乘(WLS)代价函数来求解式(10)，即
(ym-σm(θk)am(θk))HQ-1(ym-σm(θk)am(θk))
(11)
式中，Q为干扰数据协方差矩阵，且
(12)
这里的R为数据协方差矩阵，即
(13)
将式(11)最小化并代入式(12)，再根据矩阵求逆引理，得到目标散射系数σm(θk)为
(14)
根据式(13)可知，R依赖于σm(θk)的值。首先，使用DAS估计值初始化IAA，即
(15)
如式(13)、式(14)所示， IAA的计算负担主要来自每一次迭代的矩阵R及其逆矩阵R-1的计算和σm(θk)中分子、分母的计算，因此需要的存储空间大，计算复杂度也高。接下来，根据am(θk)的傅里叶矩阵特性快速计算R，然后根据快速Toeplitz矩阵向量乘法分别计算σm(θk)中的分子、分母，以减少每次迭代的计算量。令
(16)
(17)
2.1 R的快速计算
根据公式(13)，令p(θk)=|σm(θk)|2，P=diag([p(θ1) p(θ2) … p(θK)]T)，则R可以表示为
(18)
将Am代入式(18)，可得
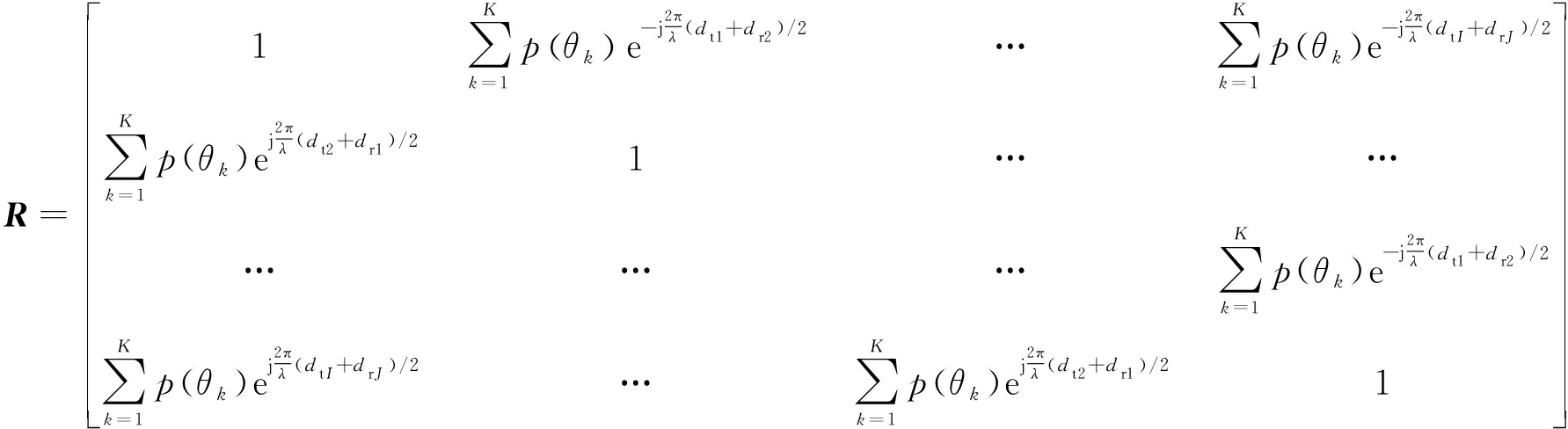
(19)
将图1所示的MIMO雷达的I个发射阵元和J个接收阵元经过合理布局，可以虚拟为1发Q收(Q=I×J)的均匀线阵。以第1个接收阵元为参考点，设第1个发射阵元与参考点距离为dt0=4d，相邻发射阵元间距4d，第2个接收阵元与参考点距离为dr1=d，相邻接收阵元间距d，其中d≤λ/2，λ=c/f0，则对应第q个虚拟阵元到参考点的间距
令
则R变为
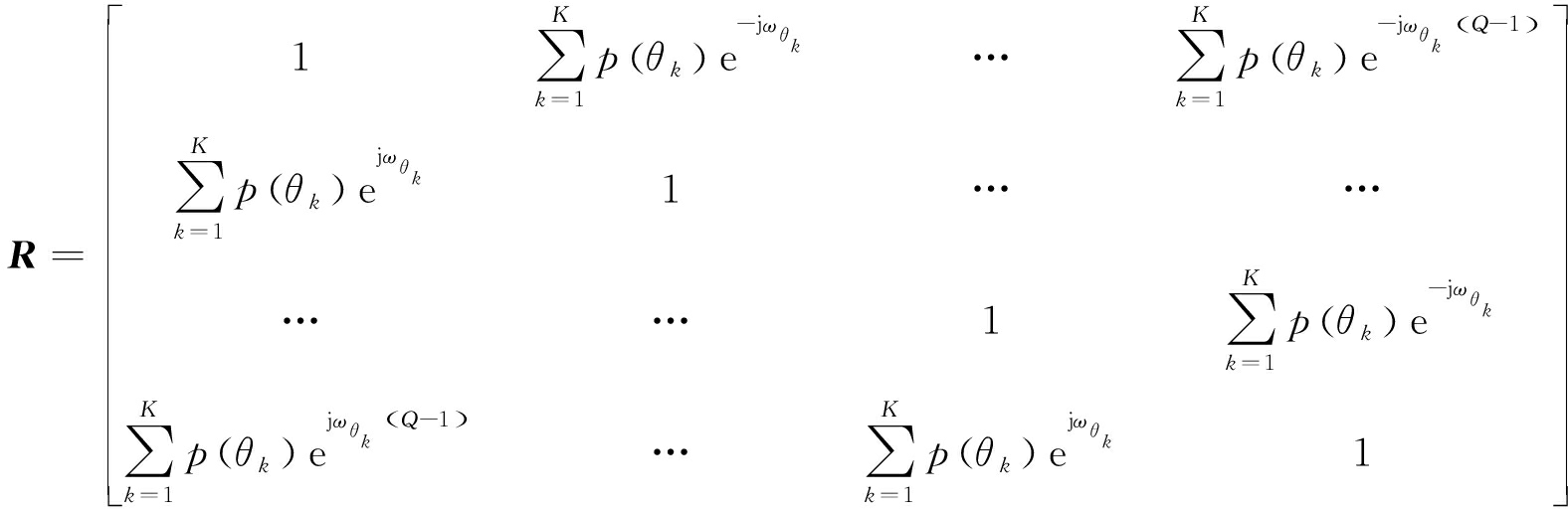
(20)
由式(20)可以看出，R是Toeplitz矩阵，令
rq=
1,…,Q-1
(21)
则式(19)的R可以简化为
(22)
式中，
根据式(21)，我们可以通过对p(θk)进行FFT运算求解rq，以此类推，就可以通过矩阵P的FFT运算来实现R的快速计算。
2.2 φD(θk)的快速计算
令
表示R中除了第一行第一列元素外的其他元素组成的子矩阵，则R可以改写为
(23)
定义线性预测和相关的预测误差如下：
(24)
(25)
由式(24)给出的线性方程组可以通过Levinson-Durbin算法[12]。根据文献[13]，R-1的GS因子分解表达式可表示为
R-1=Ψ(x,ZQ)ΨH(x,ZQ)-Ψ(w,ZQ)ΨH(w,ZQ)
(26)
式中，Ψ是下三角Toeplitz矩阵，其中的x，w和Q×Q维移位矩阵ZQ分别为
(27)
(28)
(29)
由式(26)可知，R-1也是Toeplitz矩阵，则式(16)中的x=R-1ym可以通过一系列Toeplitz矩阵向量乘积来计算，这些乘积可以转换为循环矩阵向量乘积，从而转换为FFT/IFFT[14](计算复杂度为O(Q)，对算法总计算复杂度影响不大，具体方法见文献[15-16])。在得到x之后，利用am(θk)的傅里叶算子特性对x进行FFT运算来快速计算
2.3 φN(θk)的快速计算
将式(26)的R-1代入式(17)，可得
φN(θk)=
Ψ(w,ZQ)ΨH(w,ZQ)]am(θk)=
(30)
令
所以φN(θk)可以表示为
(31)
定义c=(c-Q+1,c-Q+2,…,c0)T，则其可以表示为
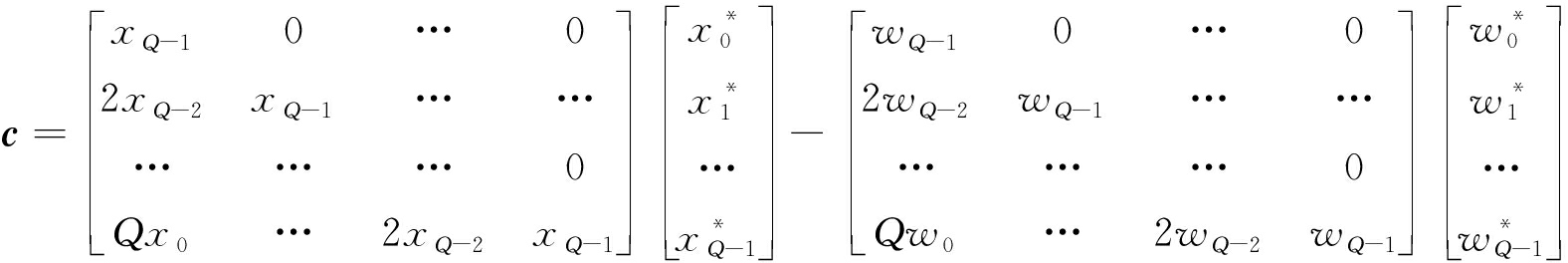
(32)
由式(32)可知,c是两个下三角Toeplitz矩阵与向量乘积的相减。因此,c也可以通过快速Toeplitz矩阵向量乘法来快速计算。令ΦN=[φN(θ1),…,φN(θk),…,φN(θK)]T,根据式(31),ΦN也可以类似于φDθk 那样,通过对c进行FFT运算来实现其快速计算。2.4 算法流程及复杂度分析 算法流程如表1所示。首先采用FFT计算估计初始值,迭代计算式(13)、式(14)的过程中通过FFT运算快速计算R,根据GS因子分解求解R-1,采用Toeplitz矩阵向量乘法的快速算法及am(θk)的傅里叶算子特性快速计算φD(θk)、φN(θk),直至算法收敛,结束迭代。
表1 FIAA算法流程
初始化 根据式(15),使用FFT计算估计初始值σmθk ,初始化迭代次数n=0,设置收敛条件δ=0.01,最大迭代次数为N=10。for n=0:N步骤1 根据式(15)初始值σm(θk),通过FFT计算R;步骤2 通过Levinson-Durbin算法求解式(24),根据GS因子分解求解R-1;步骤3 通过快速Toeplitz矩阵向量乘法求解x,根据am(θk)的傅里叶算子特性对x进行FFT运算计算φD(θk);步骤4 通过快速Toeplitz矩阵向量乘法求解系数c,根据am(θk)的傅里叶算子特性对c进行FFT运算计算φN(θk);步骤5 令n=n+1,若‖σnmθk -σn-1mθk ‖2≤δ或n=N,则迭代停止,否则返回步骤2继续迭代。end
从前面的分析可以知道，文献[9]提出的IAA每次迭代过程都需要对σm(θk)和R进行更新，总共需要的计算复杂度为O(2Q2K+QK+Q3)，其中对σm(θk)的求解过程需要进行R-1，其计算复杂度为O(Q2K)，而本文提出的FIAA在计算R-1的过程中的复杂度仅为O(Q2)。此外，通过Levinson-Durbin算法求解式(24)需要计算O(Q2)次，根据GS因子分解求解R-1需要5(2Q)次。求解φD(θk)、φN(θk)过程中两次使用的快速Toeplitz矩阵向量乘法需要7(2Q)次，加上FFT运算需要的3(Q)次，FIAA共需要计算复杂度为O(Q2+12(2Q)+3(K))。所以，整体看来本文给出的FIAA处理计算复杂度都有较大程度的降低。
3 仿真与实验结果分析
3.1 仿真结果分析
为保证距离和角度的解算范围以及对多目标的分辨能力，要对车载毫米波雷达系统的工作参数做出限定和选取。系统的距离及角度分辨率分别为
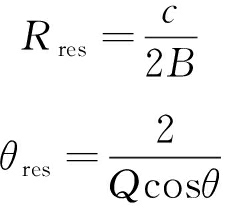
(33)
为了评估雷达性能并比较DAS波束形成、文献[9]提出的IAA和本文提出的FIAA算法，在MATLAB中对场景目标进行仿真，参数如表2所示。
表2 系统参数
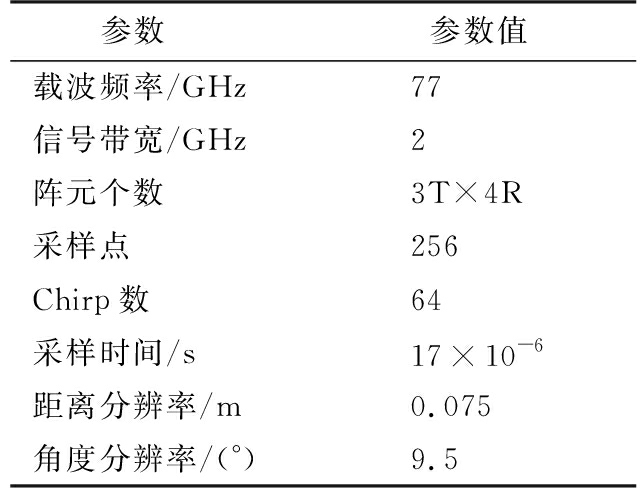
参数 参数值 载波频率/GHz77信号带宽/GHz2阵元个数3T×4R采样点 256Chirp数64采样时间/s17×10-6距离分辨率/m0.075角度分辨率/(°)9.5
假设目标场景的距离单元数为M=256，角度范围是-60°～60°，角度单元间隔为1°，即角度单元数K=121。设置3个点目标，参数如表3所示，图2给出了不同算法功率谱对比，其中图2(a)～(c)分别为DAS波束形成、IAA、FIAA算法的功率谱图。目标的成像结果如图3所示，其中图3(a)～(c)分别为DAS波束形成、IAA、FIAA算法的仿真数据的距离-角度二维成像图。从这些图中可以看出，DAS波束形成算法只能分辨出目标1和目标3，分辨不出相距5°的两个目标，由此可见分辨率大约为10°，而且旁瓣较高。而IAA与FIAA算法可以很清晰地分辨出3个目标，其分辨率可达到5°，旁瓣较低。因此，相比于DAS波束形成算法具有很高的旁瓣和很低的分辨率，很难分辨具体的方位角， IAA与FIAA算法都获得了较好的角度估计以及有效地降低了旁瓣。
表3 目标参数
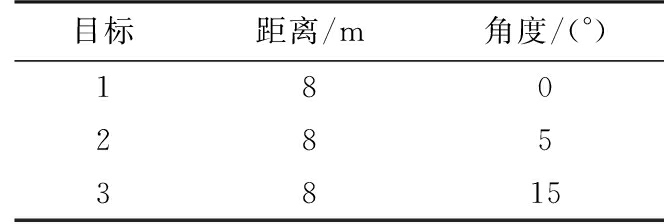
目标距离/m角度/(°)1802853815
(a) DAS波束形成
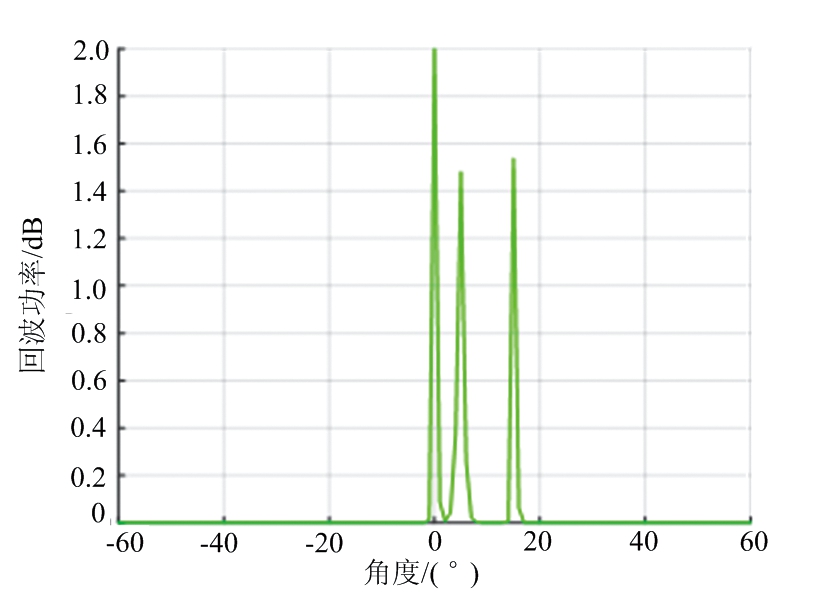
(b) IAA
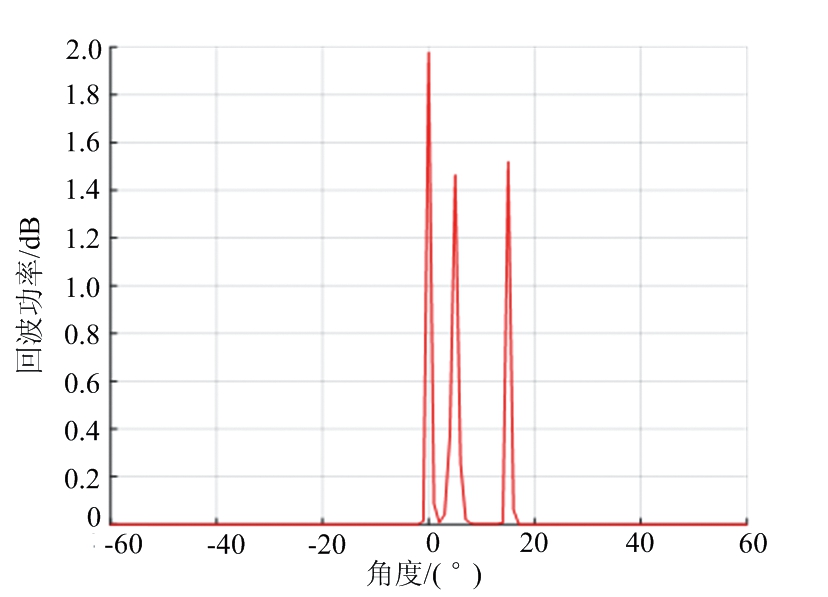
(c) FIAA
图2 功率谱图
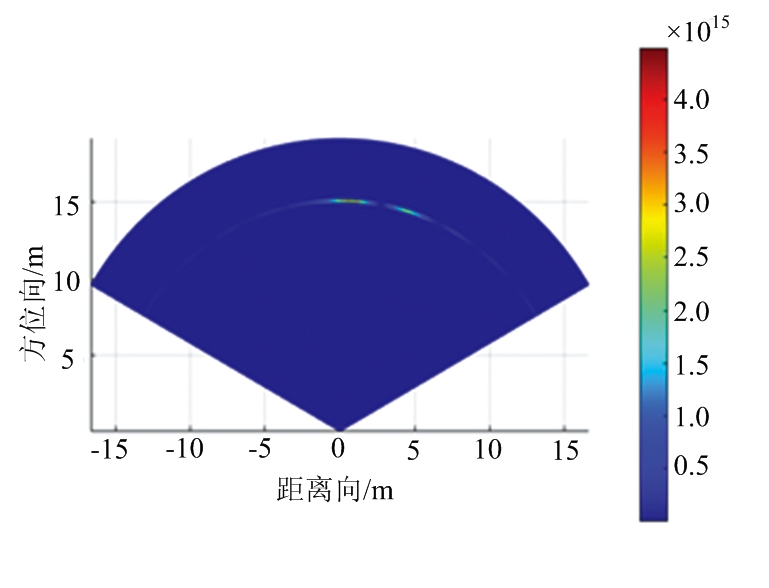
(a) DAS波束形成
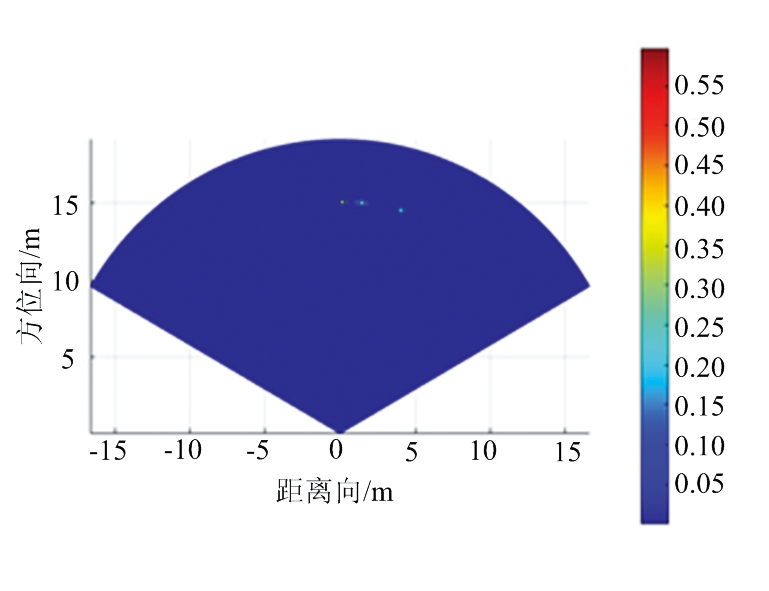
(b) IAA
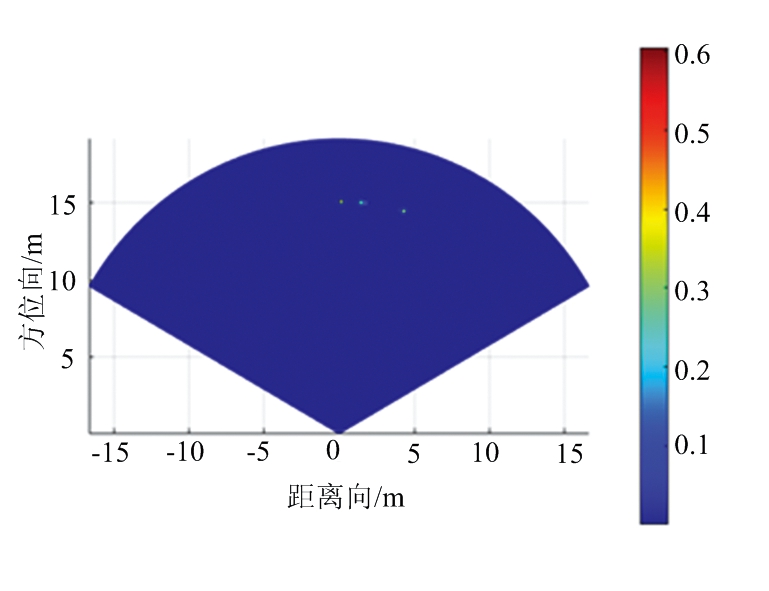
(c) FIAA
图3 仿真数据的距离-角度二维成像图
下面对算法的运行时间进行对比，以单个目标为例，设置单目标距离R=12 m，角度θ=10°；以多个目标为例则设置多目标参数如表3所示。表4给出了DAS波束形成、文献[9]提出的IAA与本文提出的FIAA分别在单目标场景及多目标场景中运行时间的对比结果。从表中可以看出，无论是在单目标还是多目标场景，DAS波束形成算法所需时间最短，实时性最高；IAA所需时间最长，不符合车载雷达实时性的需求；而FIAA的运行速度虽比不上DAS波束形成，但相比于IAA，在单目标场景中FIAA的运算时间减少7倍左右，在多目标场景中运算时间减少了4倍左右。由此可以说明所提算法性能较好，有效地减少了运行时间，更适合应用于要求实时性的车载场景中。
表4 DAS波束形成、IAA、FIAA的对比
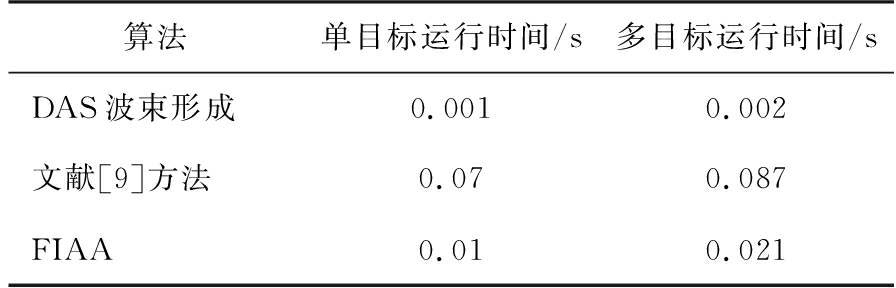
算法单目标运行时间/s多目标运行时间/sDAS波束形成0.0010.002文献[9]方法0.070.087FIAA0.010.021
综上所述，DAS波束形成运行时间短，但存在分辨率低和高旁瓣的问题，文献[9]提出的IAA虽然提高了分辨率但算法复杂度高且运算时间较长，本文提出的FIAA在保证有效提高分辨率、降低旁瓣的基础上，能够减少算法的运行时间，提高性能。
3.2 实测数据处理结果分析
实际探测场景如图4所示，雷达系统主要由 TI(德州仪器)公司的高性能毫米波雷达前端IWR6843 评估板卡和DCA1000数据采集卡组成。数据采集卡连续接收雷达前端输出的数字差频信号并通过 USB 接口将原始回波差频数据发送给计算机存储，为FMCW MIMO 雷达信号处理提供实测数据。
图4 实验场景
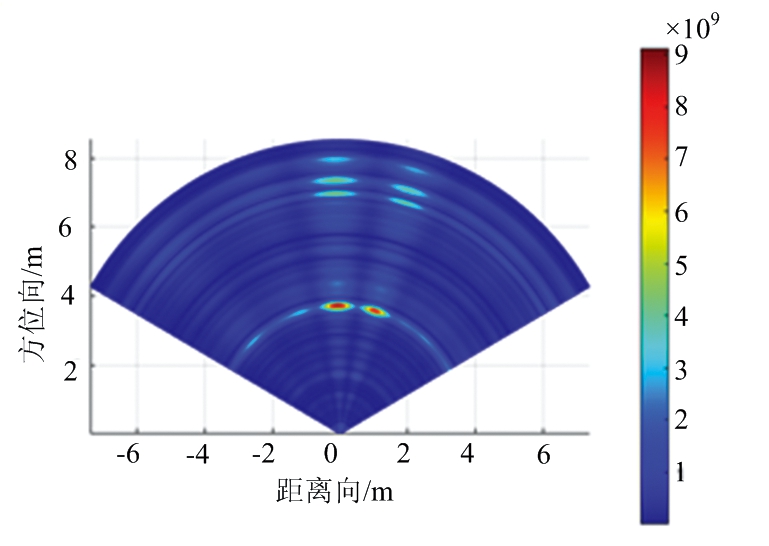
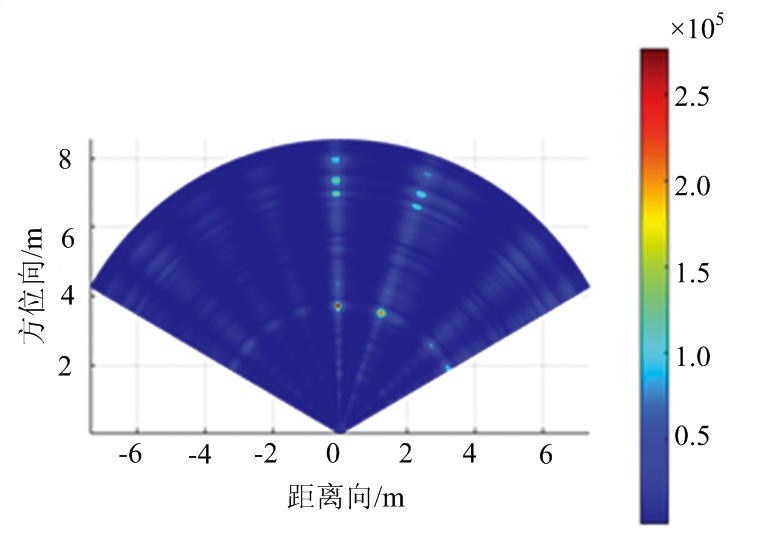
实验过程中，首先对暗室无目标场景进行测量，为后续数据预处理作准备。然后测量的是相同距离3 m处不同角度(θ1=0°，θ2=20°)的双目标，经过去除耦合波处理后结果如图5所示，其中图5(a)～(c)分别为DAS波束形成、IAA、FIAA算法的实测数据的距离-角度二维成像图。从图中可以看出，相比于DAS波束形成算法，FIAA得到的方位图像具有更清晰的亮点以及更好的角度分辨率。在运行时间上，采用DAS波束形成算法、文献[9]提出的IAA、本文提出的FIAA分别为0.002，0.106和0.022 s，FIAA比IAA的运行时间缩短了5倍左右，可以发现本文方法在提高分辨率的基础上有效地降低了运行时间，满足了车载场景对实时性的需求。
(a) DAS波束形成
(b) IAA
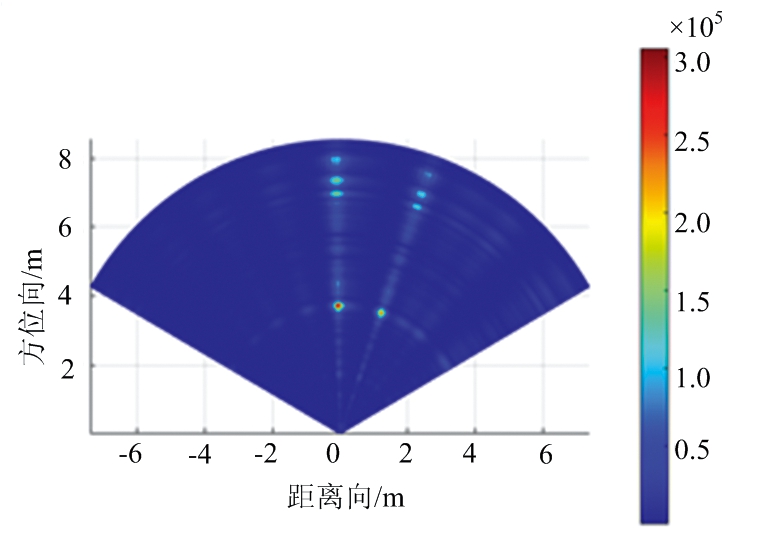
(c) FIAA
图5 实测数据的距离-角度二维成像图
4 结束语
本文提出的车载毫米波FMCW MIMO雷达快速成像方法，解决了DAS波束形成算法测角分辨率较低、旁瓣多和子空间类算法需要的数据帧数较多以及运算复杂度较高的问题。仿真数据和实验数据的处理结果表明：相比于波束形成与其他高分辨率算法，FIAA得到的方位图像具有更清晰的亮点以及更好的角度分辨率。在今后的工作中，继续探索车载毫米波雷达高分辨测角方法的快速算法，并将其扩展到 3D成像中，致力于将该方法更完善地应用于更复杂真实的环境中。
[1] 叶常青.车载毫米波雷达应用研究[J].电子测试,2019(13):79-80.
[2] KISHIGAMI T, YOMO H, MATSUOKA A, et al. Millimeter-Wave MIMO Radar System Using L-Shaped Tx and Rx Arrays[C]∥ European Radar Conference, London, UK:IEEE, 2016:29-32.
[3] JIANG Liubing, WEN Hexin, CHE Li, et al. A Phase Compensation Method for Moving Targets in TDM-MIMO Radar [J]. Journal of Terahertz Science and Electronic Information, 2020,18(4):575-580.
[4] 黄平平,李婷婷,徐伟,等. 车载前视阵列雷达BP成像算法研究[C]∥第五届高分辨率对地观测学术年会论文集,西安：高分辨率对地观测学术联盟,2018:255-265.
[5] 王伟,梁栋,刘琦,等.基于方位向门限的FMCW MIMO雷达波束形成成像算法[J].系统工程与电子技术,2015,37(12):2745-2750.
[6] 李红丽,赵崇辉,于丹茹. 车载防撞雷达的大角度快速搜索方法研究[J]. 雷达科学与技术, 2017, 15(5): 474-478.
[7] KIM S，OH D ，LEE J. Joint DFT-ESPRIT Estimation for TOA and DOA in Vehicle FMCW Radars[J]. IEEE Antennas and Wireless Propagation Letters, 2015,14:1710-1713.
[8] XU Shengzhi, WANG Jianping,YAROVOY A. Super Resolution DOA for FMCW Automotive Radar Imaging[C]∥2018 IEEE Conference on Antenna Measurements & Applications (CAMA), Vasteras, Sweden:IEEE, 2018:1-4.
[9] ECKHARDT J M,JORAM N, FIGUEROA A, et al. FMCW Multiple-Input Multiple-Output Radar with Iterative Adaptive Beamforming[J].IET Radar,Sonar & Navigation,2018,12(11):1187-1195.
[10] GUETLEIN J, KIRSCHNER A, DETLEFSEN J. Motion Compensation for a TDM FMCW MIMO Radar System[C]∥ 2013 European Radar Conference, Nuremberg, Germany:IEEE,2013:37-40.
[11] ROBERTS W, STOICA P, LI J, et al. Iterative Adaptive Approaches to MIMO Radar Imaging[J]. IEEE Journal of Selected Topics in Signal Processing, 2010,4(1):5-20.
[12] STOICA P,MOSES R. Spectral Analysis of Signals[M].Upper Saddle Rive,NJ,US:Prentice-Hall,2005.
[13] ZHANG Y C, ZHANG Y, LI W C, et al. Super-Resolution Surface Mapping for Scanning Radar: Inverse Filtering Based on the Fast Iterative Adaptive Approach[J]. IEEE Trans on Geoscience and Remote Sensing,2018,56(1):127-144.
[14] AMMER G,GADER P. A Variant of the Gohberg-Semencul Formula Involving Circulant Matrices[J]. SIAM Journal on Matrix Analysis and Applications, 1991, 12(3):534-540.
[15] GOHBERG I,OLSHEVKSY V. Complexity of Multiplication with Vectors for Structured Matrices[J]. Linear Algebra and Its Applications, 1994, 202:163-192.
[16] GLENTIS G O. A Fast Algorithm for APES and Capon Spectral Estimation[J].IEEE Trans on Signal Processing,2008, 56(9):4207-4220.
