0 引言
炮位侦校雷达是保障炮兵全天候、全天时获取战场情报信息不可或缺的重要侦察装备。弹道外推算法是炮位侦校雷达实现炮位侦察校射功能的关键[1],算法的适用性和优劣直接影响弹道外推的精度。在弹道外推过程中,任何数据都要受到设备或仪器、方法、环节和人员等因素的影响,因此所得到的外推结果存在误差。
现将主要误差因素描述如下:
1) 地球曲率:在建立炮位侦校雷达数据处理系统时,通常将地球表面看作水平面,而实际上由于地球表面是球面,外推炮位与真实炮位存在高程差;2) 时间不同步误差:测量数据因采样时间不同步间隔(不一致)引起的误差称为时间不同步误差。当前弹道测量系统的各设备和计算机均应工作在统一时间基准上,时间不同步会产生测量误差和数据处理误差;3) 弹道模型误差:建立弹道方程最初的目的主要是为了编制射表,因此弹道方程只是较好地拟合了火炮射程,但对整条弹道曲线的空间位置拟合效果并不理想。即弹道模型和真实弹道并不完全重合,存在模型误差;4) 信噪比变化:雷达的检测能力测量误差实质上受信噪比影响,雷达量测信噪比受雷达与目标距离的影响,并随着距离的增加而减小。
本文结合精密雷达测量数据和七态滤波外推算法[2-3]对以上误差因素进行详细建模和量化分析,为算法优化奠定了基础。
1 建模分析1.1 地球曲率对定位精度的影响
炮位侦察过程中,考虑地球曲率所引起的外推落点高程差可概略用下式计算。
(1)
式中,r为地球半径,L为雷达到炮位的距离。
如图1所示,雷达在利用P1…P19采样点进行外推时,将地球表面当做一个水平面。外推炮位在c,而实际上由于地球表面是球面,炮位并未在c点而是继续下落到G点,在原来假设落点处实际还存在一个弹道高度cc'。从平面几何可知:
Rc≈RG=L
(2)
(3)
解算弹道方程时,根据落点高程来确定落点。因此,高程差的存在对定位精度存在较大影响。考虑到地球曲率的影响,在外推到炮位高程时,再继续向下递推H。
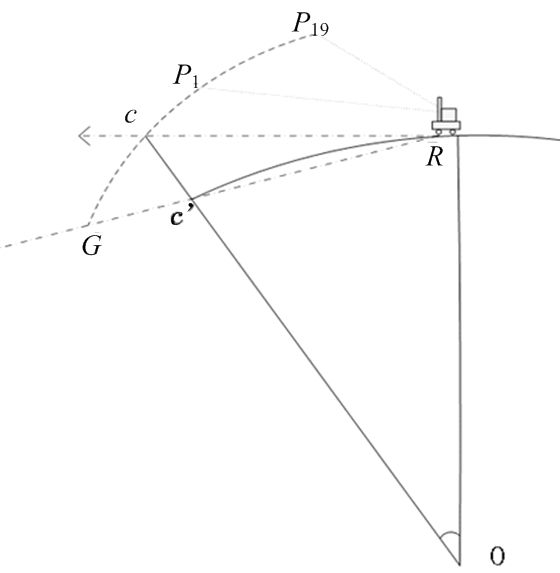
图1 地球表面曲率对坐标转换的影响
1.2 时间不同步误差
理想条件下,某炮位侦校雷达采样点间隔取固定值0.3 s,但由于发射机电路及波导系统对发射脉冲的延时作用,造成扫描起始时刻超前于天线口辐射的时刻,可能造成实际采样间隔大于0.3 s,以某炮位侦校雷达为例,其实际采样步长接近0.4 s。靶场试验证明:采样点间隔取0.4 s,外推结果更接近真实炮位,由于雷达系统不同,采样步长可能会有所不同。
1.3 真实弹道与模型匹配情况
射表用的弹道模型存在模型误差,并且外推距离越远,外推误差越大[4],如图2所示。

图2 模型误差影响外推精度示意图
外推距离受遮蔽角影响,遮蔽角越大,雷达起始波束俯仰角增大,开始采样时间距发射时间越长,外推距离增加,模型误差累积越多,雷达的侦察定位精度误差就会越明显。
图 3为遮蔽角影响外推精度示意图。正常情况下,起始波束到截止波束的角度为固定值。S1和S2分别为不同遮蔽角下起始波束俯仰角低和高时的外推起点,外推距离分别为点S1、S2到外推炮位的弹道曲线长度。从图中可以看出,在作用距离和火炮射角相同的情况下,遮蔽角越大,截止波束俯仰角就越大,外推距离也就越远,导致外推误差越大。其弹丸位置对应的俯仰角可用下式表示:
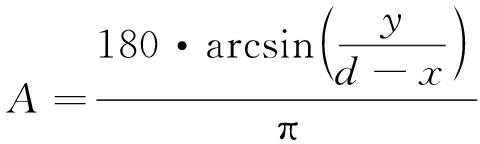
(4)
式中,x为弹丸北向坐标,y为弹丸高度,d为炮位距雷达距离,A为弹丸位置对应的俯仰角。
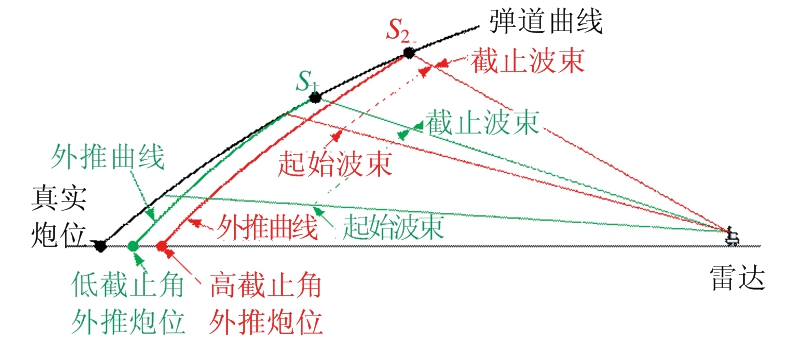
图3 遮蔽角影响外推精度示意图
图4为雷达作用距离影响外推精度示意图。S1和S2分别为近作用距离和远作用距离时的外推起点,外推距离分别为点S1、S2到外推炮位的弹道曲线长度。从图中可以看出,在火炮射角和雷达起始波束俯仰角相同的条件下,雷达的作用距离越远,外推距离就会越远,导致外推误差也就越大。
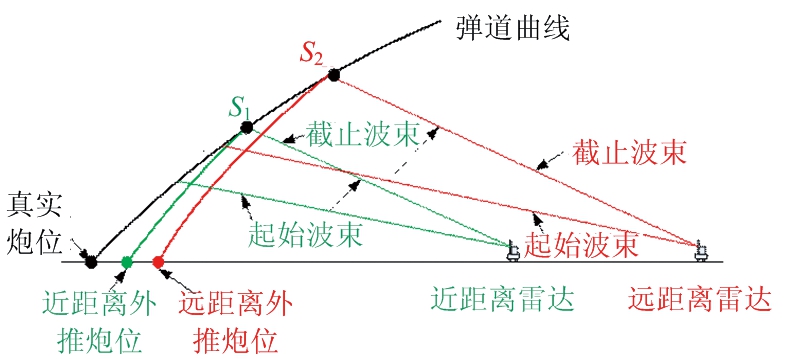
图4 雷达作用距离影响外推精度示意图
以上情况均以侦察作业为例,其分析结果同样适用于校射作业。
1.4 弹丸与雷达距离决定信噪比
设雷达的发射功率为Pt,天线增益为Gt,则在自由空间工作时,距离天线R处目标的功率密度S1为
(5)
假设目标可将接收到的功率无损耗、均匀地辐射出来,用目标的散射截面积σ来表征其散射特性,接收天线的有效接收面积为Ar,则在雷达接收处接收回波功率为
(6)
由式(6)可以看出,接收的回波功率反比于目标和雷达站间的距离R的四次方。
若误差的度量是测量值(估计值)和真实值之间差的均方根值(RMS),雷达测量M的理论均方根误差δM可表示为
(7)
式中,k是大约为1的常数,Er是接收信号能量,N0是单位带宽噪声功率。
从一个简单的信号脉冲波形来看,若其宽度为τ,则接收信号能量Er=Pr·τ,噪声功率N和噪声功率谱密度N0之间的关系为N=N0Bn。一般情况下可认为Bn=1/τ,这样可得到信号功率比的表达式如下:
(8)
故δM正比于R-2,可表示为
(9)
引入零均值高斯白噪声V,其方差为Q,则量测方程为
Z=h(x)+V
(10)
由式(9)可知
(11)
式中,a1、a2、a3分别为观测量中距离、方位角、俯仰角噪声方差与以弹丸距雷达距离四次方为分母函数的系数,表示两者之间的正比关系。
2 仿真实验
2.1 仿真条件
以122榴弹为例,利用靶场弹道精密测量雷达数据进行数值仿真计算。主要仿真条件如下:
1) 弹丸发射条件:初速v0=700 m/s,射角θ0=19.5°;2) 取雷达测量误差:σr=6.5 m,σβ=σε=1.5 mil;3) 雷达距离炮位15 km,雷达初始采样点的俯仰角为3.1°,采样间隔 300 ms,从初始采样点继续探测18个弹道点后采样中止。采用两点差分法对状态进行初始化。
建立考虑弹道系数的七维状态向量、三维量测模型,在此过程中使用经典的动力学模型[4]。分别利用扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)[5]进行滤波处理,得到外推起点,用龙格-库塔法[6]外推发射点。进行10 000次蒙特卡洛仿真实验,统计结果并分析。
2.2 地球曲率对定位精度的影响
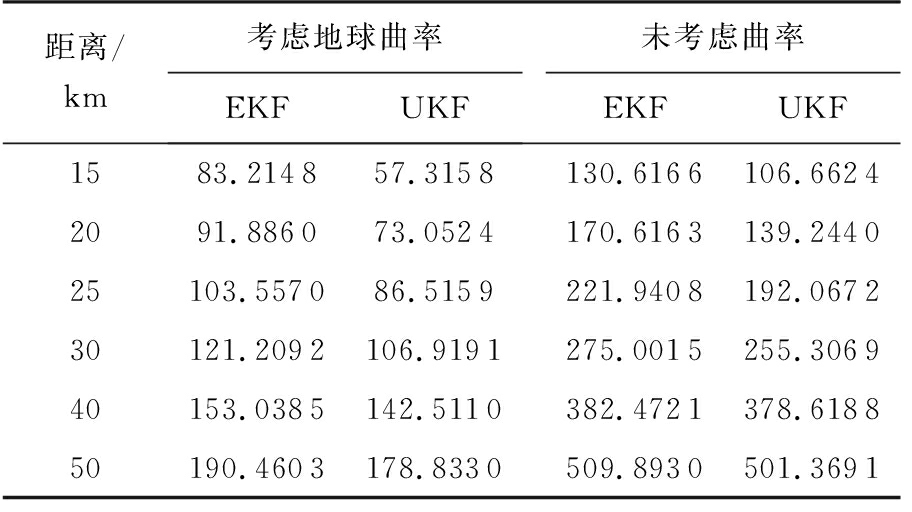
对地球曲率影响下的坐标变换进行建模,代入弹道外推算法中,通过比较考虑地球曲率的弹道外推算法在不同雷达和炮位距离条件下定位的圆中心概率误差(Ecp)[6],研究地球曲率对定位精度的影响,如表1所示。
由表1可以看出,雷达距离炮位越远,地球曲率对定位精度的影响越大,采用考虑地球曲率模型的算法估计精度优势越明显。以UKF算法为例,当雷达距离炮位15 km时,新算法定位精度提高83.2%;当雷达距离炮位40 km时,新算法定位精度提高168.3%。
表1 雷达与炮位在不同距离条件下受地球曲率的影响
距离/km考虑地球曲率EKFUKF未考虑曲率EKFUKF1583.214857.3158130.6166106.66242091.886073.0524170.6163139.244025103.557086.5159221.9408192.067230121.2092106.9191275.0015255.306940153.0385142.5110382.4721378.618850190.4603178.8330509.8930501.3691
2.3 时间不同步对定位精度的影响
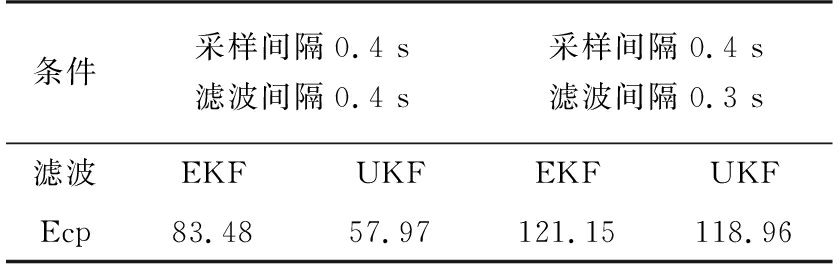
仿真中取采样步长0.3 s,而由于存在采样时间不同步,实际采样步长为0.4 s。对造成时间不同步的采样时间误差进行研究,通过仿真实现了采样间隔和滤波间隔不同步条件下的滤波,求其圆中心概率误差(Ecp),得到表2。
表2 时间不同步对定位精度的影响
条件采样间隔0.4 s滤波间隔0.4 s采样间隔0.4 s滤波间隔0.3 s滤波EKFUKFEKFUKFEcp83.4857.97121.15118.96
可以看出:考虑时间不同步的外推算法(以UKF算法为例)定位精度提高了127.2%。为进一步分析以上结论,对滤波终点的位置、速度、弹道系数误差进行比较,如图5、图6所示。
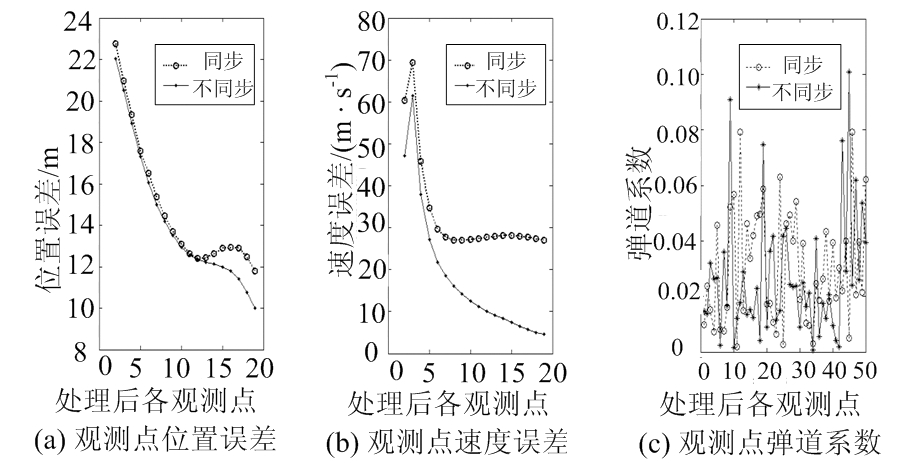
图5 EKF中考虑时间不同步误差与否的对比
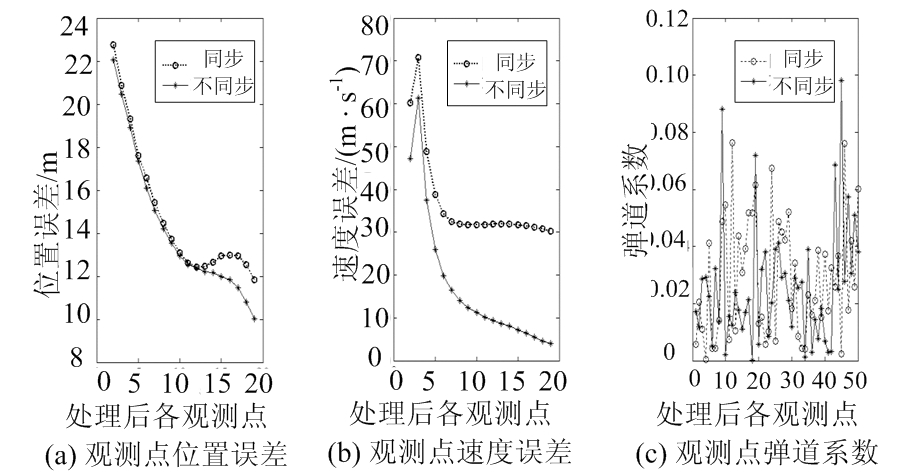
图6 UKF中考虑时间不同步误差与否的对比
图5、图6分别为用EKF、UKF算法对是否考虑采样点时间不同步进行数据处理的结果,将精密测量雷达数据作为采样点真实位置、速度,结合动力学方程得到真实弹道系数[6]。由图5、图6可以看出:时间不同步对弹道系数的估计精度没有明显影响,但随着处理采样点个数的增加,位置误差、速度误差逐渐增大,造成外推精度的降低。
2.4 弹道模型误差对定位精度的影响
为研究模型误差,利用经典动力学模型和精简动力学模型[4]结合四阶龙格-库塔方程仿真弹道。标准条件下一条弹道由弹道系数(Cb)或阻力系数(α)、初速(v0)和仰角(θ0)唯一确定。阻力系数(α)利用精简动力学方程求取:

(12)
初速(v0)、仰角(θ0)取精密弹道数据采样点初值的对应值。得到各弹道和仿真弹道对应点的位置误差如图7、图8所示。
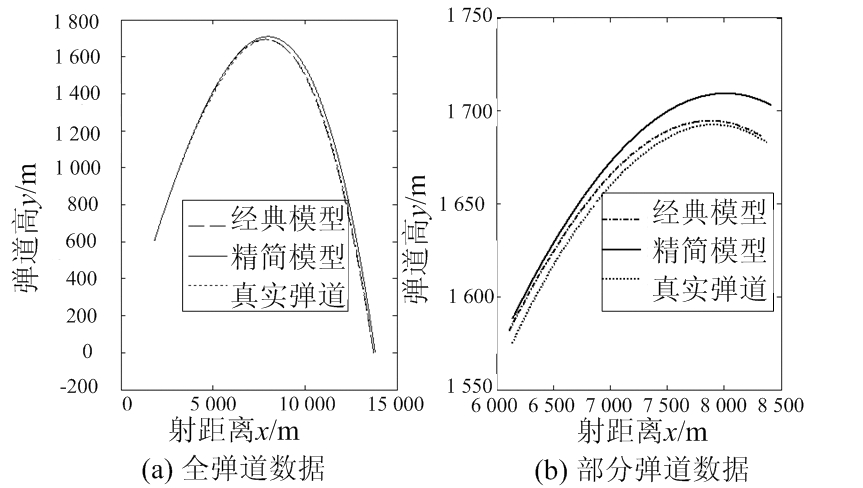
图7 仿真弹道与真实弹道对比

图8 不同模型仿真弹道的位置误差
通过计算得到图7、图8中数据弹道系数为0.571 4,阻力系数为0.07。为方便观察,图7(b)对图7(a)部分弹道进行放大。从以上仿真结果中可以看出:1)仿真弹道在上升沿时有较高的精度,与真实弹道的位置误差较小,在上升到弹道顶点附近时误差开始变大。2)在到达顶点之前,即上升沿经典和精简两种动力学模型都有较高的拟合程度。因此,相对炮位校射仿真,在进行炮位侦察仿真时,精度较高。而在全弹道的位置误差分析中,经典动力学模型位置误差较小,拟合程度较高。
为研究遮蔽角对定位精度的影响,利用精密弹道数据,变换俯仰角大小进行仿真。在炮位距雷达R =15 km时,因为雷达从第三秒开始采样,可仿真最小俯仰角为2.646 0°,俯仰角从3°开始每间隔0.5°采样,得到仿真结果如表3所示。
表3 雷达距炮位15 km时不同俯仰角对应的定位精度
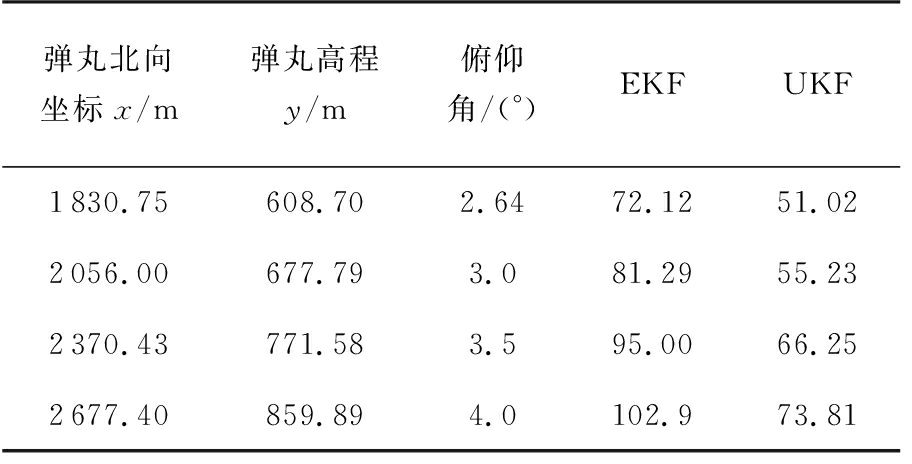
弹丸北向坐标x/m弹丸高程y/m俯仰角/(°)EKFUKF1830.75608.702.6472.1251.022056.00677.793.081.2955.232370.43771.583.595.0066.252677.40859.894.0102.973.81
当炮位距雷达R=40 km时,可仿真最小俯仰角为1°,俯仰角从1°开始每间隔0.5°采样,得到仿真结果如表4所示。
表4 雷达距炮位40 km时不同俯仰角对应的定位精度
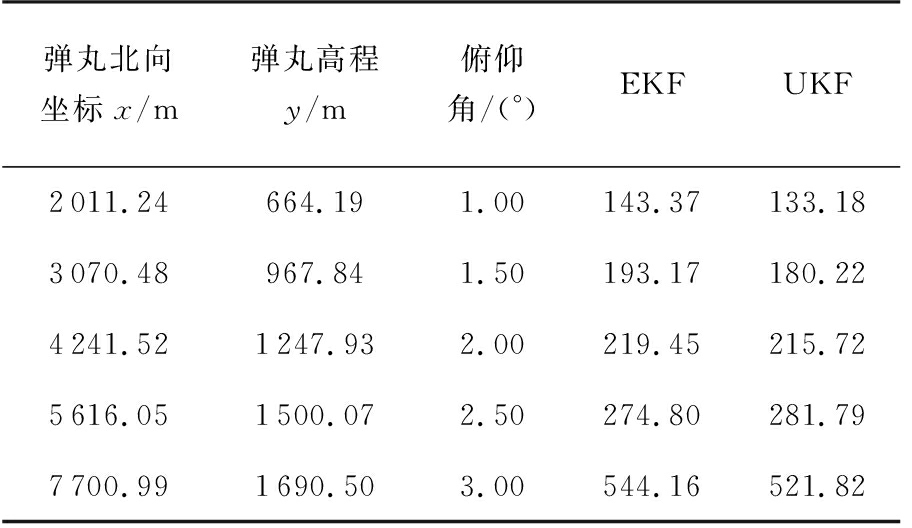
弹丸北向坐标x/m弹丸高程y/m俯仰角/(°)EKFUKF2011.24664.191.00143.37133.183070.48967.841.50193.17180.224241.521247.932.00219.45215.725616.051500.072.50274.80281.797700.991690.503.00544.16521.82
由表3、表4可以看出:1)其他条件不变,外推误差随着俯仰角增大而增大;2)相同俯仰角条件下,雷达与炮位距离越远,定位精度越差。
2.5 定位精度与信噪比的关系
当雷达与弹丸相距为X时,取雷达测量误差:σr=6.5 m,σβ=σε=1.5 mil。由式(9)可假设,雷达弹丸距离为R时,雷达测量噪声:
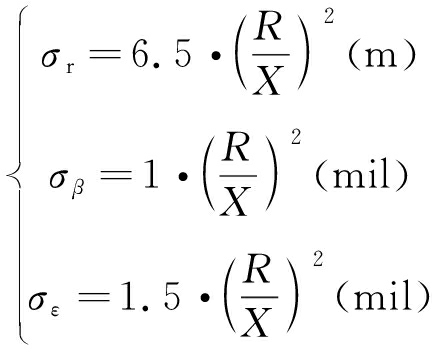
(13)
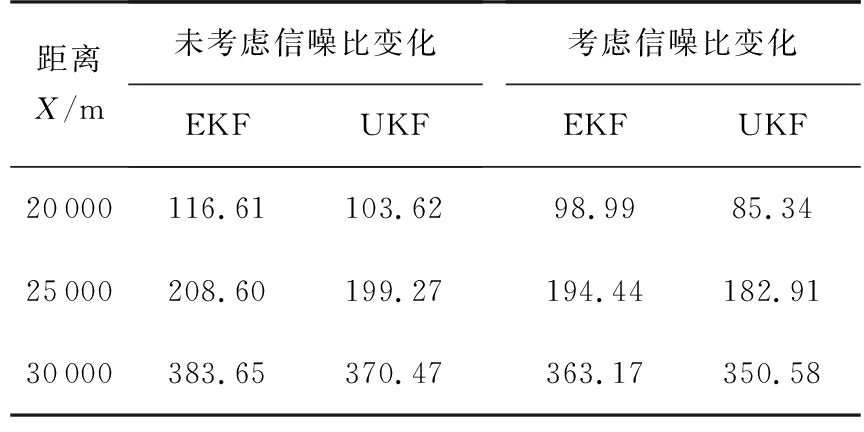
表5列出了初始弹丸与雷达距离,以及对应的是否考虑信噪比变化的雷达定位精度。由表5可知:考虑目标信噪比变化时,由于模型更符合实际情况,因而炮位侦校雷达定位精度比不考虑雷达定位精度要提高10%左右。
表5 定位精度与信噪比的关系
距离X/m未考虑信噪比变化EKFUKF考虑信噪比变化EKFUKF20000116.61103.6298.9985.3425000208.60199.27194.44182.9130000383.65370.47363.17350.58
3 因素比较与优化方案
前面从外推精度、估计精度、弹道模型误差等方面建模并量化分析了地球曲率、时间不同步、弹道模型误差、信噪比变化等因素对炮位侦校雷达外推过程的影响。为综合比较各因素对定位精度的影响程度,在2.1节仿真条件的前提下,每次调整其中一项进行UKF滤波处理。结合表1~表5,对比外推结果,如表6所示。
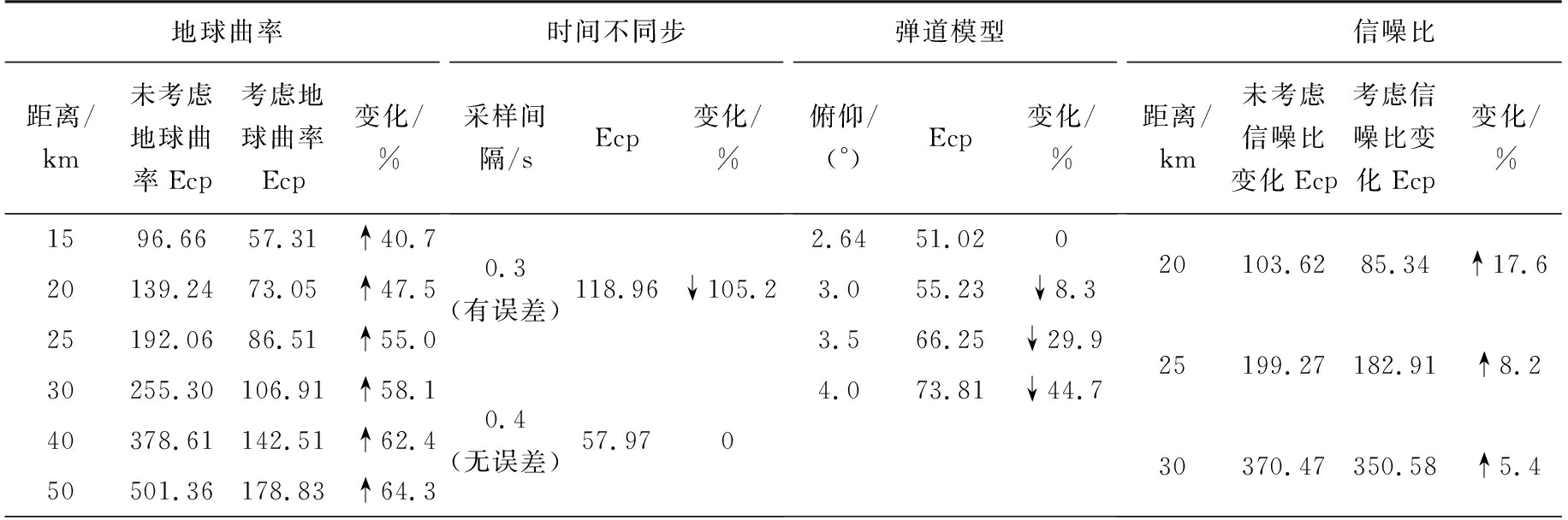
表6 各因素对定位精度影响比较
地球曲率时间不同步弹道模型信噪比距离/km未考虑地球曲率Ecp考虑地球曲率Ecp变化/%采样间隔/sEcp变化/%俯仰/(°)Ecp变化/%距离/km未考虑信噪比变化Ecp考虑信噪比变化Ecp变化/%15202530405096.66139.24192.06255.30378.61501.3657.3173.0586.51106.91142.51178.83↑40.7↑47.5↑55.0↑58.1↑62.4↑64.30.3(有误差)0.4(无误差)118.9657.97↓105.202.643.03.54.051.0255.2366.2573.810↓8.3↓29.9↓44.7202530103.62199.27370.4785.34182.91350.58↑17.6↑8.2↑5.4
由表6可以看出:各因素对定位精度的影响均较大,无法忽略。其中,通过比较是否考虑各误差因素的外推结果,可知各因素对定位精度影响幅度依次为:地球曲率>时间不同步>弹道模型误差>信噪比变化。在此基础上,提出优化方案如表7所示。
表7 炮位侦校雷达定位精度优化方案

影响因素优化方案地球曲率解算弹道方程时,外推到炮位高程后,计算雷达到炮位的距离L,再向下推H m(根据式(1))采样时间不同步数据处理中采用实际步长弹道模型误差通过反向滤波[3]进行降噪处理信噪比变化由式(11)建立噪声方差模型
4 结束语
本文通过研究炮位侦校雷达工作的原理,对地球曲率变换、时间不同步、外推距离影响弹道模型误差、弹丸与雷达距离和信噪比的关系等一系列问题进行建模与仿真。通过理论分析和仿真实验结果验证,得到了一些指导性的结论,可为炮位侦校雷达优化数据处理系统提供参考。
[1] FISHBEIN W. Firefinder, a Radar Forty Years in the Making[J]. IEEE Trans on Aerospace and Electronic Systems, 2008, 44(2):817-829.
[2] 谢恺, 秦鹏程. 基于多普勒信息的炮位侦校雷达外推算法研究[J].弹道学报,2018,30(4):53-58.
[3] 谢恺, 秦鹏程. 基于七维状态向量反向无迹卡尔曼滤波的弹道外推算法[J].兵工学报,2018,39(10):1945-1951.
[4] 谢恺, 秦鹏程. 炮位侦校雷达弹道外推模型研究[C]∥第十五届全国雷达学术年会论文集, 广州:中山大学,2020:642-649.
[5] NING Xiaolin, WANG Fan, FANG Jiancheng. An Implicit UKF for Satellite Stellar Refraction Navigation System[J]. IEEE Trans on Aerospace Electronic Systems, 2017, 53(3):1489-1503.
[6] 国防科工委第三十一试验训练基地. GJB2421-95地炮雷达实验方法[S].华阴:国防科学技术工业委员会,1995.
