0 引言
炮位侦校雷达具备全天候、全天时、火炮类目标侦察校射能力,为炮兵火力打击提供重要保障[1]。弹道外推算法是决定炮位侦校雷达性能的关键技术之一,炮位侦校雷达的定位精度[2]性能直接受其影响。
当前的弹道外推算法主要包括两大类:一是基于先验样本的机器学习算法;二是基于弹道模型的卡尔曼滤波估计算法。前者受实际弹道样本的限制,算法实用性不高,目前在炮位侦察校射雷达弹道外推领域,更多地采用卡尔曼滤波及其衍生算法[3]。然而,基于卡尔曼滤波的外推算法受弹道、气象条件以及量测点迹质量影响较大,故外推精度会受到影响。针对不同弹道,如何提升外推结果的一致性及外推精度是炮位侦校雷达领域亟待解决的一大难题。
为此,本文将聚类思想引入至弹道外推过程中,将聚类思想与七态UKF滤波算法相结合。对量测数据进行多次滤波外推,获取多个外推结果,然后采用K-均值聚类算法对外推结果进行聚类处理,最后采用综合多因子方法计算簇品质,选取最优簇对应的聚类中心作为最终的火炮位置进行输出。经实验仿真验证,本算法有效提升了外推结果的一致性及定位精度。
1 弹道运动模型
在炮位侦察模式下,因炮弹种类未知,相关弹道参数均未知,射表中的标准条件与实际条件也不能保证完全一致,并且在炮位侦察过程中炮口是未知的,这时,我们采用前序数个量测点粗略拟合出炮口位置,并以此作为坐标中心进行后续滤波预测及外推处理,故我们以炮口为坐标中心,基于弹丸质心运动微分方程组(非标准条件下)建立弹道运动模型:
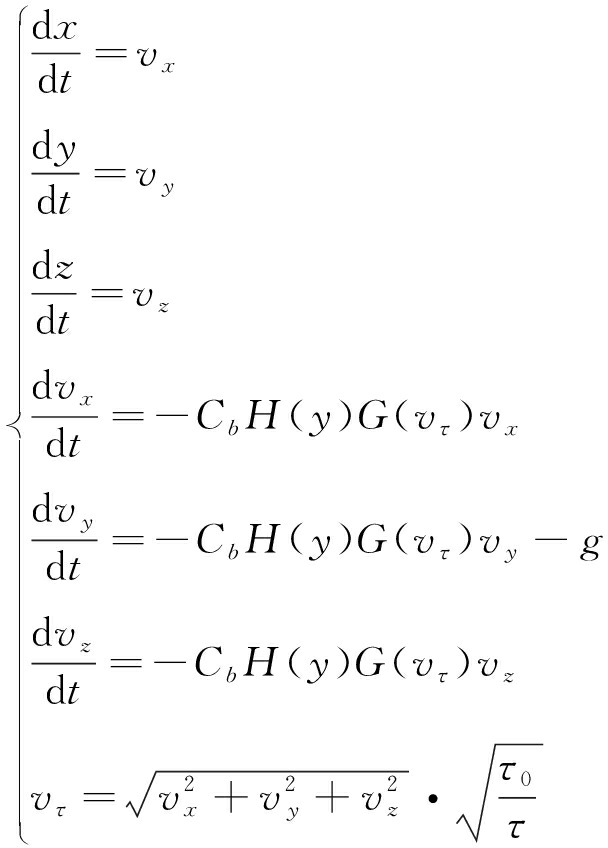
(1)
式中:x,y,z为炮弹离开炮口后在射向上的水平分量、垂直分量和侧偏分量;vx,vy,vz为对应的水平速度、垂直速度以及侧偏速度;vτ为弹道上对应t时刻的合成速度;Cb为弹道系数;H(y)为空气密度函数;G(vτ)为空气阻力函数;τ0为标准状态下的虚温,τ对应于不同高程上的虚温;g为重力加速度。
图1表示炮口坐标系。其中,o为炮口中心,ox对应射击方向,oy垂直水平面向上,基于右手螺旋法则,oz指向右方。弹道方程组的解算基于炮口坐标系完成。射击方向与坐标北的夹角φ为射向(顺时针为正)。
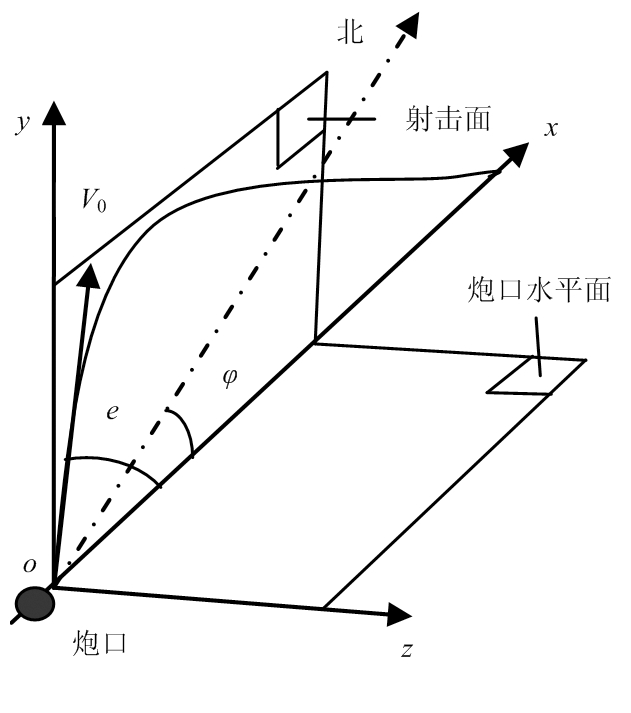
图1 炮口坐标系
2 弹道外推
弹道外推的主要任务是接收弹道量测数据,根据弹道目标飞行特征采用相应的滤波模型进行跟踪滤波处理,完成弹丸类目标轨道的正反向外推,获取炮弹发点(侦察)或落点(校射)。本文弹道处理算法专注于侦察模式发点推算,具体处理流程如图2所示。
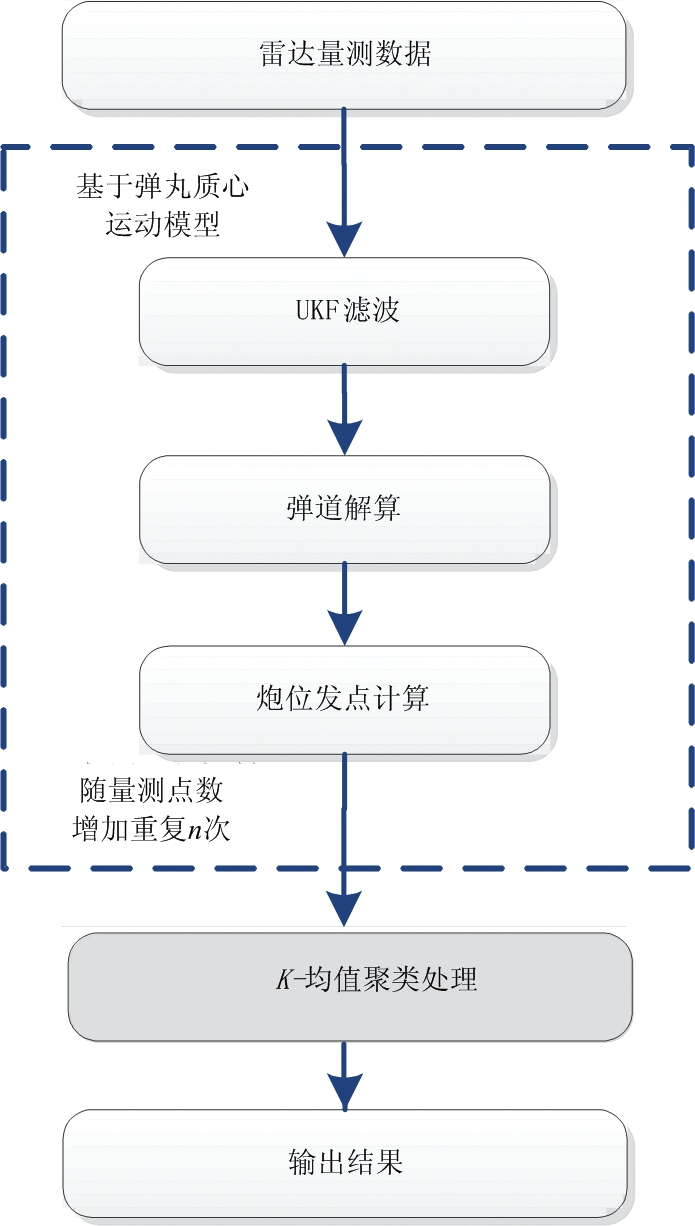
图2 弹道外推流程图
弹道外推软件实时接收来自弹丸飞行过程中的雷达量测数据,当量测点数积累至一定数量后,开始启用弹道处理算法。首先,基于弹丸质心运动模型创建UKF滤波器进行弹道滤波处理。然后,采用四阶龙格-库塔算法进行弹道解算并依据炮位高程计算炮位发点。随雷达观测点增加个数n,上述过程重复n次。最后,对前序过程求解出的炮位发点进行K-均值聚类处理,并采用综合多因子算法选取最优簇,以该簇对应的聚类中心作为最终外推结果输出。
2.1 七态UKF滤波
UKF滤波[4-5]算法对非线性问题的处理效果显著且该方法估计精度至少达到2阶,计算量与EKF 算法处于同一量级,不需要计算Jacobian 矩阵,可以处理不可导的非线性函数[6]。基于上述优点以及弹道运动方程非线性特性,本文采用七态UKF滤波方法,将弹道系数作为第七维状态进行滤波,实时估计并更新弹道系数。
基于第1节中弹道运动模型建立状态方程和量测方程。
状态方程:是描述动态系统各状态变量和输入之间关系的方程。公式(2)描述了关于七维向量X = [x, y, z, vx, vy, vz, Cb]T状态方程:
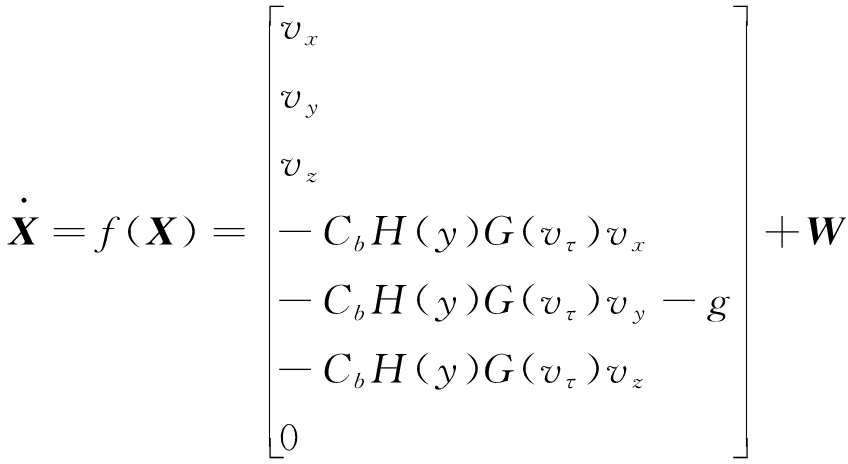
(2)
式中,W为高斯白噪声,协方差矩阵为Q。
量测方程:量测方程用来表示状态向量、测量向量以及输入之间关系。本文算法中量测向量Z = [r a e]T,量测方程描述如下:
XENU=LPK2ENUX
(3)

(4)
式(3)中LPK2ENU为坐标转移矩阵,将炮口坐标系下的状态向量X转移至以雷达站址为中心的东北天坐标系XENU。式(4)中V代表高斯白噪声,协方差矩阵为R。
考虑如下非线性模型:
(5)
式中,xk∈Rn为七维状态向量,wk为七维过程噪声,fk-1为七维状态向量函数,hk为状态与量测转换函数,vk为三维随机量测噪声。其中,过程噪声与量测噪声为相互独立,不相关的高斯白噪声,Qk和Rk分别为对应的协方差阵。具体滤波过程描述如下:
1) 状态初始化。
(6)
式中,![]() 表示系统初始状态,P0表示初始状态协方差矩阵。
表示系统初始状态,P0表示初始状态协方差矩阵。
2) 已知状态估计![]() 状态估计误差协方差阵Pk-1|k-1,预测下一步状态
状态估计误差协方差阵Pk-1|k-1,预测下一步状态![]() 并计算预测误差协方差矩阵Pk|k-1。
并计算预测误差协方差矩阵Pk|k-1。
①计算σ点![]() 即
即
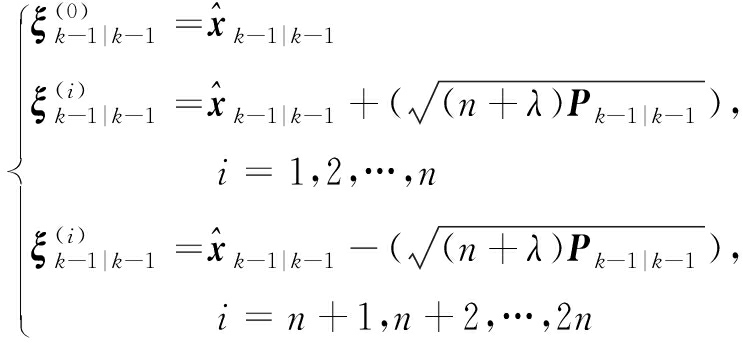
(7)
②计算![]() 即
即
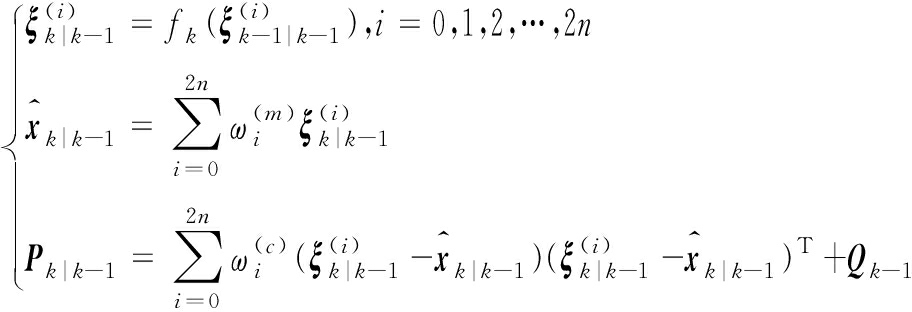
(8)
3) 基于UT变换计算σ点![]() 的传播。
的传播。
①求解σ点![]() 和Pk|k-1经量测方程的传播,如式(9)所示:
和Pk|k-1经量测方程的传播,如式(9)所示:
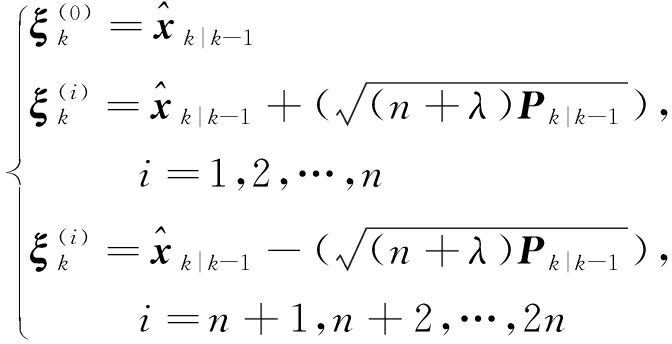
(9)
②公式(10)描述了一步提前预测计算过程。
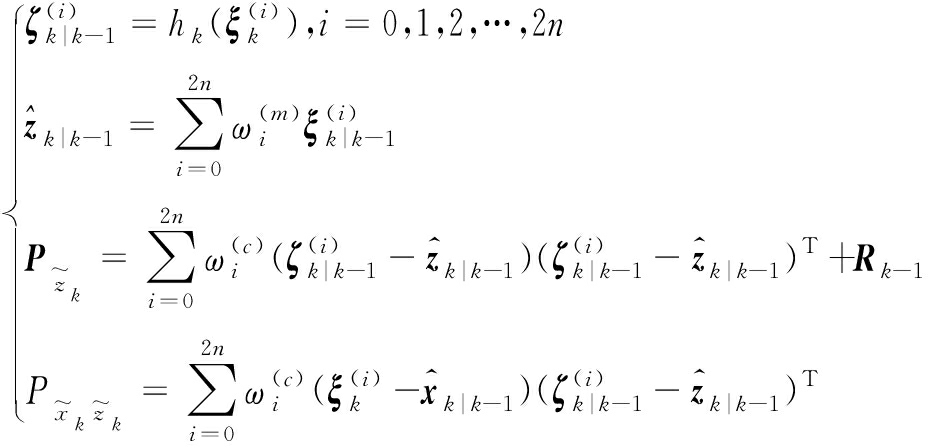
(10)
4) 滤波更新。
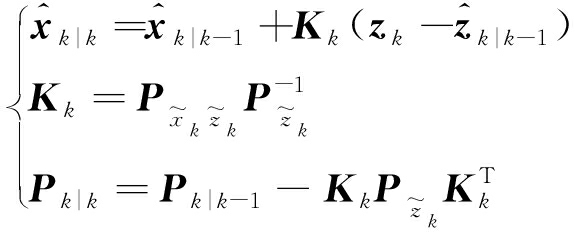
(11)
式中,Kk表示滤波器增益矩阵。
各采样点权值计算:
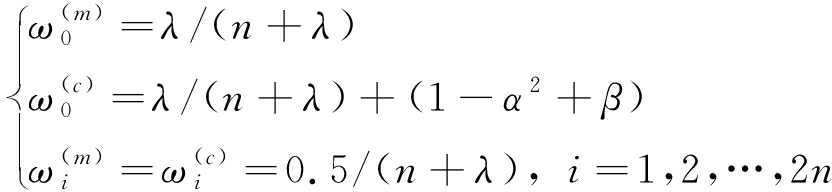
(12)
式(12)中具体参数取值过程为λ = α2(n + κ)-n, 其中α代表σ点的散布程度,一般取一小的正值(如0.02),κ一般取0;β表示x的分布信息;![]() 代表计算一阶统计特性时的权系数,
代表计算一阶统计特性时的权系数,![]() 代表计算二阶统计特性时的权系数。
代表计算二阶统计特性时的权系数。
2.2 弹道解算
目前弹道解算主要通过数值计算方法求解弹道方程组,进而完成发点或落点的推算。弹道方程组[7]通常由一阶变系数联立方程组表示,一般情况下采用数值方法求解其数值解是唯一手段,在某些特殊情况下对其简化处理后才能求得近似解析解。对微分方程求解的方法较多,如阿当姆斯预报-校正法和龙格-库塔法,而四阶龙格-库塔法在工程中得到广泛应用[8],故本文算法采用龙格-库塔法进行弹道解算。
龙格-库塔法是基于泰勒级数的一种改进算法,四阶龙格-库塔法的具体描述如公式(13)~(15)所示,其中公式(13)表示微分方程组及初值:
![]() fi(t,y1,…,ym)yi(t0)=
fi(t,y1,…,ym)yi(t0)=
yi0(i=1,2,…,m)
(13)
方程组在第n点处的所有变量的值为 (tn, y1n, y2n,…, ymn),那么n+1点处各变量的四阶龙格-库塔计算公式为
(14)
其中:
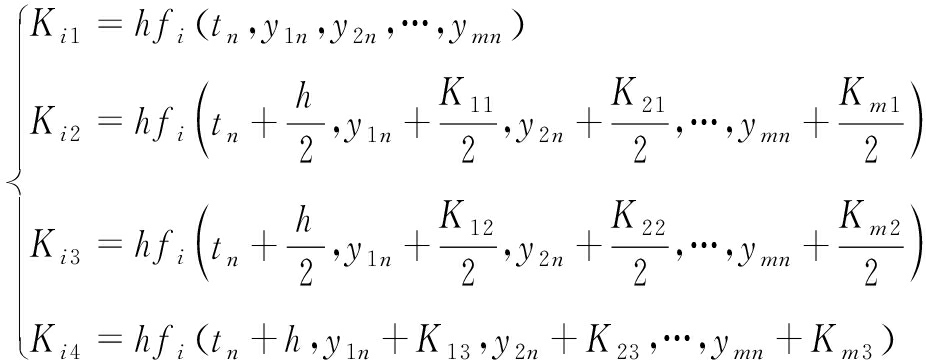
(15)
式中,h代表步长,步长的选取会影响四阶龙格-库塔法的计算精度。步长越小计算精度越高,然而过小的步长会导致迭代计算过程中的累计误差变大,同时会消耗更多的计算时间,影响时效性。本文h的选择分为两步,先进行粗粒度外推,再进行细粒度外推,这样既保证了外推精度,又不会影响时效性。
2.3 K-均值聚类处理
为了进一步提升弹道外推精度及外推结果的一致性,引入聚类思想,采用K-均值聚类算法对多次外推结果进行聚类处理,选取最优簇对应的聚类中心作为外推结果输出。K-均值聚类算法[9]属于划分型的动态聚类算法,其计算过程需要给定待聚类的数目k,通过聚类处理后数据集被划分成k个不同的类。该算法的核心思想是:给定聚类的个数k后,第一次迭代的k个中心点被随机选取。这时,依次计算k个中心点与数据集中其他数据之间的距离,通过比较筛选,数据被划分至距离其最近的类中。然后,计算新生成的数据类的聚类中心,同时调整数据集。倘若新旧类之间的聚类中心[10]没有变化或者在某个较小的范围内变化,那么聚类完成。
图3描述了在弹道外推过程中K-均值聚类的具体处理步骤,详细处理流程如下:
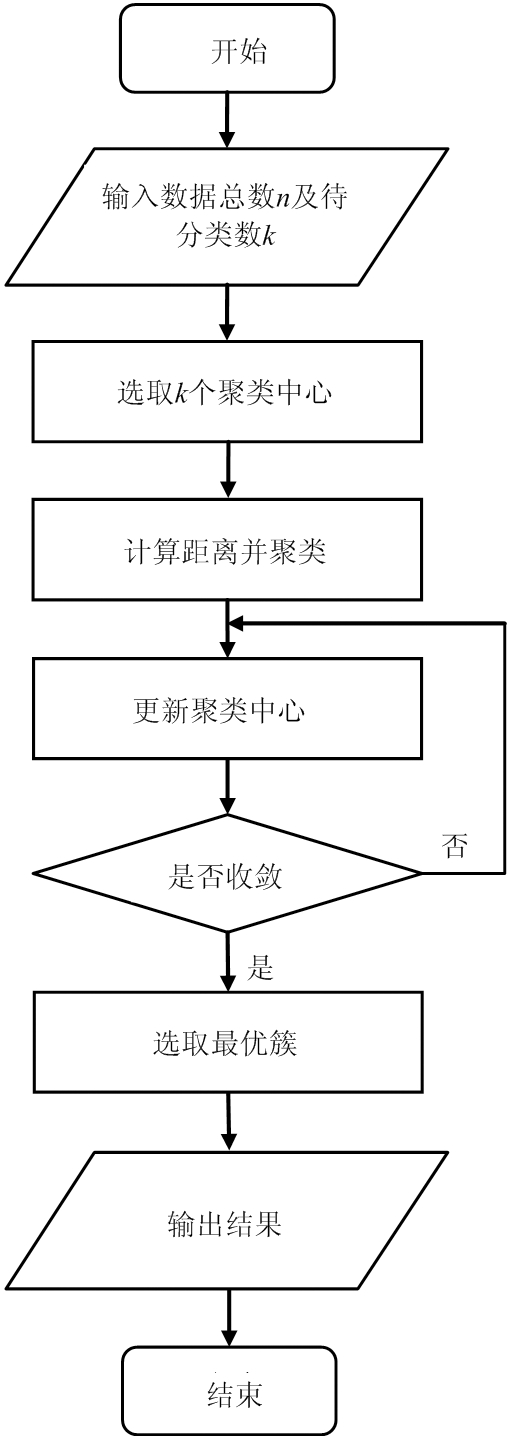
图3 K-均值聚类算法流程
输入: 弹道外推发点数据集Y={y1, y2,…, yn},待聚类的个数为k,本文算法k值可以取2~5;
输出: k个聚类{C1, C2,…, Ck};
1) 在给定的弹道外推发点数据集Y={y1, y2,…, yn}中,随机抽取k个不相同的发点样本用作初始聚类中心点{m1, m2,…,mk};
2) 计算m1, m2,…,mk这k个中心点与数据集中其他数据之间的距离,记作d(yi, mj),其中,i = 1,2,…,n,j = 1,2,…,k。当
d(yi,mj)=min{d(yi,mj)},
j=1,2,…,k
(16)
则表明yi属于mj类。
3) 当所有数据的归属类调整之后,利用公式(18)重新生成k个类的聚类中心:
(17)
并计算误差平方和准则函数E(l),E(l)代表第l次迭代计算得出的误差平方和值[11]。其中公式(18)描述了某一次误差平方和的计算过程。
(18)
4) 倘若第l和l +1次迭代,误差平方和没有发生较大的变化,则表明误差平方和已经收敛,可以跳出迭代过程。反之,进入步骤2)继续迭代。
5) 当聚类收敛后采用综合多因子方法选取最优簇。为此定义了簇品质以及三类因子:
簇品质c_q:用于表示簇优劣程度的量称为簇品质。
簇体积因子c_v:假设簇成员体积大小相同,均为1 m3,则此时,可用簇成员个数表示簇体积。
簇质量因子c_m:用簇成员质量平均值表示簇质量。簇成员质量定义为参与滤波的量测点迹的数目,簇成员中参与滤波的量测点迹个数越多,表示该成员质量越大。
簇一致性因子c_u:用该簇外推发点位置的方差表示簇一致性。方差越小,一致性越好。
对上述三类因子分别做归一化处理,得到归一化簇体积因子C_Vres=[c_vres1,c_vres2,…, c_vresk]T,归一化簇质量因子C_Mres=[ c_mres1,c_mres2,…, c_mresk]T和归一化簇一致性因子Ures=[c_ures1, c_ures2,…, c_uresk]T,然后利用公式(19)计算簇品质:
C_Q=[C_Vres C_Mres C_Ures][α β γ]T
(19)
式中,C_Q=[ c_q1, c_q2,…, c_qk]T为簇品质向量,α, β, γ分别表示归一化簇体积因子、归一化簇质量因子及归一化簇一致性因子对应的权值。最优簇的品质即为
c_qbest_cluster=max{c_q1, c_q1,…, c_qk},
best_cluster∈[1,k]
(20)
式中,best_cluster对应的簇即为最优簇。
3 算法仿真与分析
本文以155榴弹炮为例,利用弹道仿真软件生成雷达量测数据,进行数值仿真计算,仿真平台为Intel Core i7-5600U、主频2.6 GHz、四核CPU 计算机,仿真软件为MATLAB。具体仿真条件如下:
1) 155榴弹发射条件: 初速v0设置为900 m/s,射角θ0设置为35°;
2) 取雷达随机测量误差: σr = 7.6 m,σa = 1.7 mil,σe = 1.6 mil;
3) 雷达距离炮48 km。
基于上述数据对六态_EKF(原算法)、六态_UKF、七态_UKF算法、聚类_七态_UKF算法分别进行10 000次蒙特卡洛仿真实验,并采用炮位侦察定位精度计算方法圆中间误差[12](ECP)统计外推精度。
图4在ENU坐标系下分析了六态_EKF(原算法)与聚类_七态_UKF弹道滤波情况,可以看出相比六态_EKF算法,聚类_七态_UKF算法滤波结果更接近真实值,效果更优。
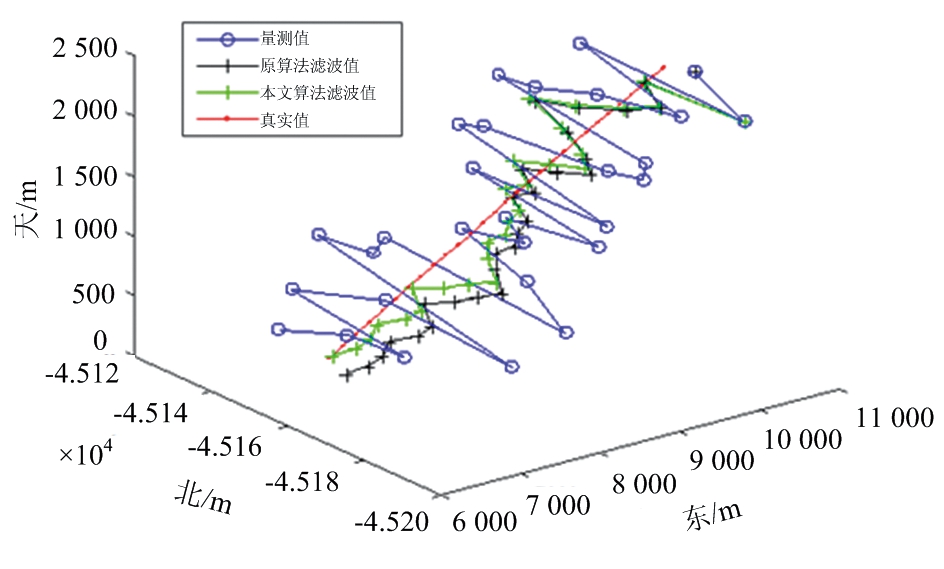
图4 原算法与本文算法东北天坐标系下滤波结果
图5从滤波后位置误差角度分析了二者滤波效果。结果表明本文算法在3个坐标轴上的滤波误差明显小于原算法,进一步验证本文算法滤波效果优于原算法。
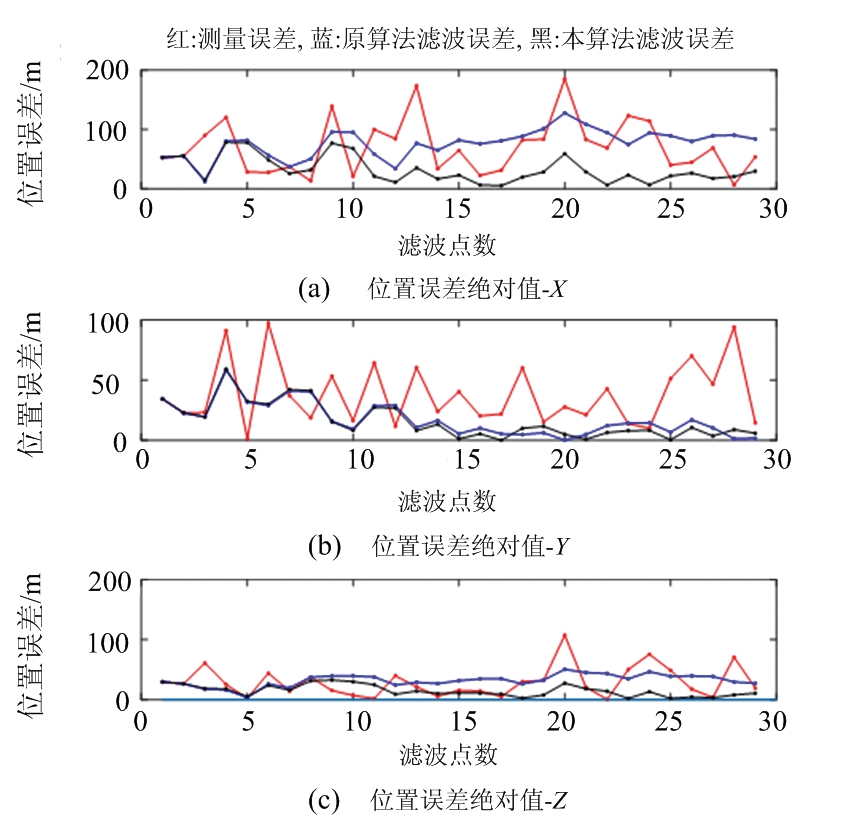
图5 原算法与本文算法滤波后位置误差比对
图6和图7给出了七态_UKF算法与聚类_七态_UKF算法目标外推发点位置散布情况,仿真结果可以看出,聚类_七态_UKF算法发点外推结果一致性明显优于原算法,验证了聚类处理的有效性。
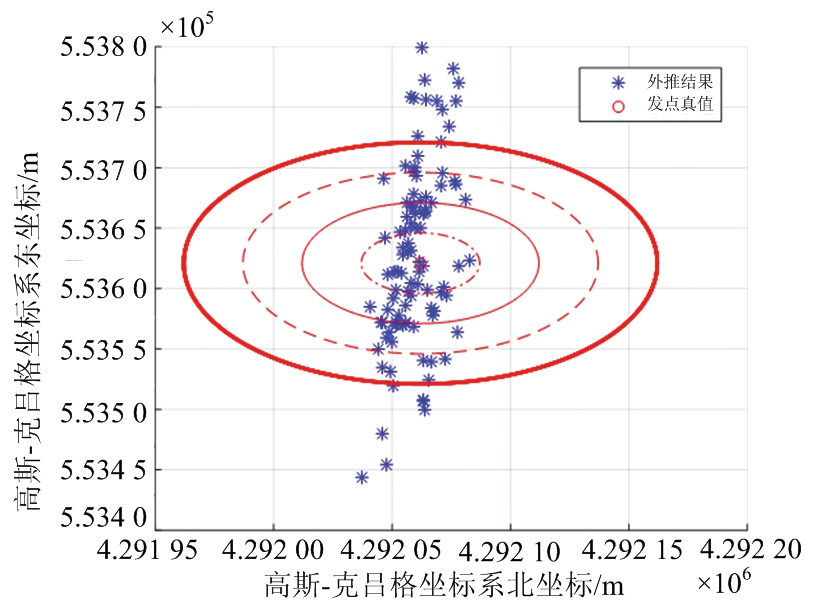
图6 七态_UKF算法外推发点散布情况
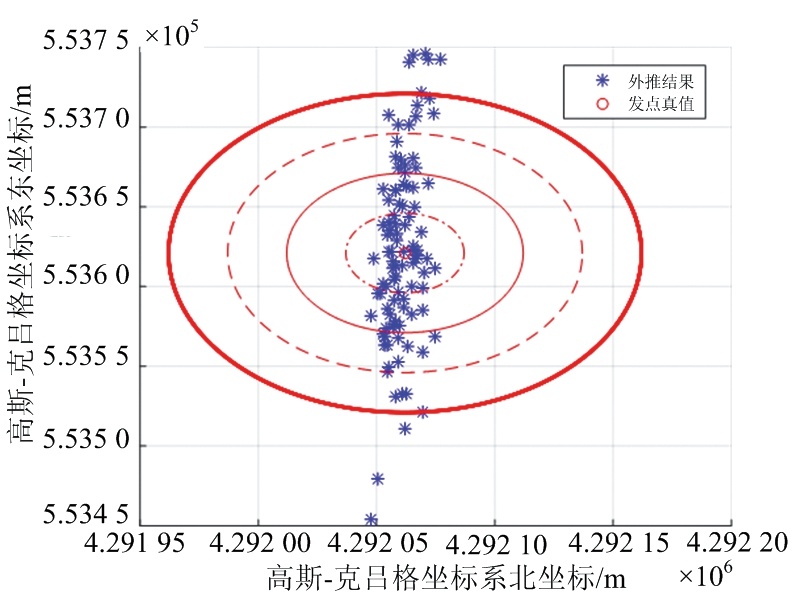
图7 聚类_七态_UKF外推发点散布情况
表1 给出了本文算法与其他算法的比较结果,几种算法相比,六态_EKF算法圆中间误差最大,聚类_七态_UKF圆中间误差最小,定位精度相比原算法提升42.62%,精度最佳,六态_UKF和七态_UKF算法较原算法定位精度也有明显提升。然而算法耗时角度分析,六态_EKF算法耗时最短,六态_UKF和七态_UKF次之,聚类_七态_UKF耗时最长。
表1 外推算法仿真结果对照表
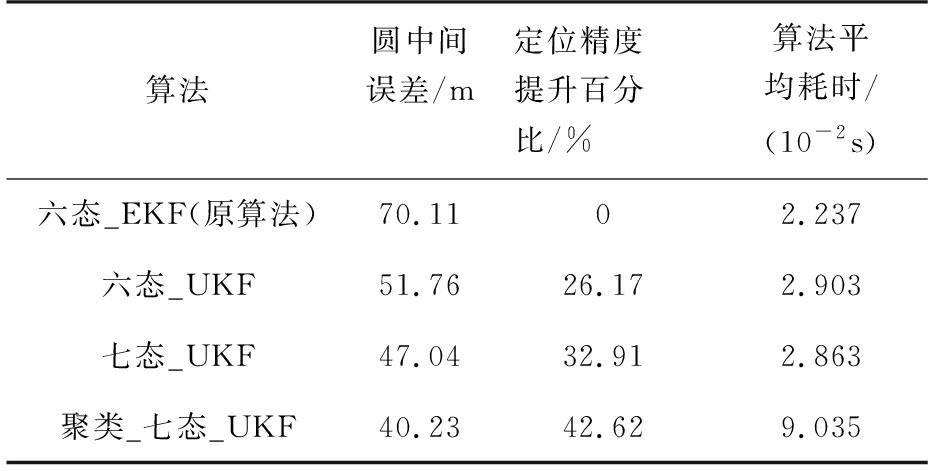
算法圆中间误差/m定位精度提升百分比/%算法平均耗时/(10-2s)六态_EKF(原算法)70.1102.237六态_UKF51.7626.172.903七态_UKF47.0432.912.863聚类_七态_UKF40.2342.629.035
4 结束语
本文针对一定条件下炮位侦校雷达定位结果一致性较差及定位精度偏低的问题,提出一种基于K-均值聚类的弹道外推算法。该算法对单发炮弹轨迹进行多次反向UKF滤波和外推处理,获取多个发点。然后将聚类思想引入其中,采用K-均值聚类及综合多因子算法获取最优结果,起到剔除奇异值以及较差发点位置的效果,同时可以进一步消除随机误差。仿真结果表明,本文算法显著提升了弹道外推的定位精度及一致性。本文所采用的外推算法虽然具有较高的精度和一致性,但是对于当前各种新型炮弹的弹道滤波及外推处理技术仍需作进一步研究。
[1] RAVINDRA V C, BAR-SHALOM Y, WILLETT P. Projectile Identification and Impact Point Prediction[J]. IEEE Trans on Aerospace & Electronic Systems, 2010, 46(4):2004-2021.
[2] FIREFINDER W F.A Radar Forty Years in the Ma-king[J]. IEEE Trans on Aerospace & Electronic Systems, 2008, 44(2):817-829.
[3] 武瀚文, 查启程, 梁燊, 等. 基于遗传算法的弹道外推方法[J]. 指挥控制与仿真, 2021, 43(5):102-106.
[4] 谢恺, 秦鹏程. 基于七维状态向量反向无迹卡尔曼滤波的弹道外推算法[J]. 兵工学报, 2018,39(10):1945-1950.
[5] 霍李, 魏五洲, 李军明, 等. 基于无迹卡尔曼滤波算法的弹道落点预测方法[J]. 兵工自动化, 2022, 41(2):70-74.
[6] 单奇, 钮俊清, 李川. 炮位侦校雷达的数据处理研究[J]. 雷达科学与技术, 2010, 8(2):171-176.
SHAN Qi,NIU Junqing, LI Chuan. Study on Data Processing of Firefinder Radar [J]. Radar Science and Technology, 2010, 8(2):171-176. (in Chinese)
[7] 王干, 熊风, 欧能杰, 等. 基于反向扩展卡尔曼滤波的弹道外推算法[J]. 光电与控制, 2020, 27(12):49-52.
[8] 赵新生, 舒敬荣. 弹道解算理论与应用[M].北京: 兵器工业出版社, 2006:32-39.
[9] 夏显召, 朱世贤, 周意遥, 等. 基于阈值的激光雷达K均值聚类算法[J]. 北京航空航天大学学报, 2020, 46(1):115-121.
[10] 李玥, 穆维松, 褚晓泉, 等. 基于改进量子粒子群的K-means聚类算法及其应用[J]. 控制与决策, 2021, 37(4):839-849.
[11] 行艳妮, 钱育蓉, 南方哲, 等. Spark环境下K-means初始化中心点优化研究综述[J]. 计算机应用研究,2020, 37(3):641-647.
[12] 第31 试验训练基地. GJB2421-95 地炮雷达定型实验方法[S].北京: 国防科学技术工业委员会,1995.
