0 引言
最早关于DOA估计的方法是由傅里叶变换的线性谱引出的，该方法受空域“瑞利极限”的限制[1]，很难实现对来波信号的高分辨估计，同时这些算法的抗噪声性能较差，并没有获得满意的估计效果。上世纪70年代以Schmidt为代表的学者相继提出的多信号分类(Multiple Signal Classification, MUSIC)算法[2]真正实现了角度的超分辨测量。MUSIC算法通过对接收数据进行特征值分解得到信号子空间和噪声子空间，然后利用信号子空间与噪声子空间的正交性构造谱函数进行峰值搜索来确定目标角度。然而MUSIC算法计算量大，要求较高的信噪比、较多的样本数据[3-4]。此外，MUSIC算法对于相干信源的估计性能较差，虽然可以通过空间平滑方案进行预处理解，但这是以损失性能为代价的[5-6]，从而限制了其在实际场景中的适用性。
快速迭代插值波束形成器(Fast Iterative Interpolated Beamforming, FIIB)[7]能够实现角度的无偏估计，同时具有与快速傅里叶变换(FFT)相当的计算速度。该算法结合了有效的插值策略和泄漏减法方案，成功地解决了频谱泄漏的问题。因此，它可以实现DOA的无偏估计。该算法的前提是信源个数已知，然而在实际环境中对于估计的目标个数是未知的，因此这一关键参数将无法使用，从而影响整体算法的性能。文献[8]中，在应用FIIB算法前，采用了基于奇异值分解(Singular Value Decomposition, SVD)的信息论准则进行信源个数估计，该方案可以解决信源个数未知的问题，但仍需要SVD步骤，从而抵消了FIIB算法带来的计算优势。
本文提出一种基于FFT和迭代插值的改进超分辨测角方案。本方案将简单的空域FFT测角与迭代插值及干扰对消策略相结合，迭代插值的角度不再从第1个信源开始，而是由空域FFT提供的粗略角度进行细化，并通过干扰对消估计空域FFT测角未能分辨的信源，最后通过判断对消残差功率和MDL(Minimum Description Length)准则[9-10]对信源个数进行估计。为降低算法的运算量，本文提出了一种基于残差变化率的细化估计收敛策略，能够在不降低性能的情况下有效地减少迭代次数。本方案不仅实现了超分辨算法的信源个数自估计，并且大大降低了原算法的复杂度。仿真结果表明，本文提出的方案在估计精度及分辨率方面性能接近FIIB算法。
1 数据模型及FIIB算法介绍
1.1 数据模型
如图1所示，考虑M元均匀线阵，阵元间距d=λ/2，L个波长为λ的远场窄带信号入射到该阵列，入射方向与阵列法线夹角定义为入射角度θl(l=1,2,…,L),则该阵列接收的单快拍数据矢量可表示为
(1)
式中，αl为第l个信源的复振幅，n为均值为0、方差为σ2的加性高斯噪声。令
第l个信源的导向矢量表示为α(θl)=[1,ej2πv(θl),…,ej2π(M-1)v(θl)]T。
图1 阵列信号模型
1.2 FIIB算法介绍
基于FIIB的单快拍DOA估计通过一种估算-减法策略在内循环中连续的提取目标源，再通过外循环细化估计值，以消除收敛时的偏差。该算法的核心是一个简单而高精度的插值策略，与泄露减法方案相结合，从而实现多源DOA的无偏估计。
相较于RELAX算法对于每次信源估计均需要一次FFT[11-13]，FIIB算法仅需一次FFT计算，即通过K点(K=z*M)FFT得到传统波束形成系数X[n]，后续处理均在频域进行，从而避免了FFT的重复使用。在第一次迭代中，从最强的信源开始依次获得L个目标的粗略估计。即对于第l个信源，从阵列信号中减去之前已估计出的信号源，然后通过傅里叶变换在频谱中确定最高的峰值。再通过傅里叶系数插值来细化目标的粗估计。通过插值策略与连续估计减法相结合，消除了频谱泄漏导致的偏差，从而得到准确的估计。
1.3 FIIB算法的超分辨性能分析
文献[7]重点对于FIIB算法的无偏估计进行了讨论，并进行了相关仿真验证，但是对于算法的超分辨性能并未过多讨论。当两个目标落在同一波束内时，传统的波束形成算法将无法进行分辨，在FIIB算法中通过去除其他目标的影响，可以显露出剩余的目标，并通过迭代插值不断地细化目标的估计值，从而能够实现对目标的超分辨并得到各自精确的估计值。
本节对FIIB算法的超分辨性能进行了仿真。仿真构建了一个32阵元的均匀等距的线性阵列，阵元间距d=λ/2，噪声为零均值、方差
的高斯噪声。重点探究FIIB算法对两个目标的分辨能力，设置两个目标源，目标幅值|α1|=|α2|，信源个数已知，目标1与目标2之间的电角度间隔由BW/5至3BW变化，其中BW=2π/M。在信噪比分别为0，10，20和30 dB的情况下进行了1 000次独立实验，仿真结果如下。
图2和图3分别给出了不同角度间隔下算法的检测概率、均方根误差(Root Mean Squared Error, RMSE)的曲线图。如图所示，当两个目标的角度间隔为BW/2，即角度间隔为实孔径理论分辨率的二分之一，也就是常说的两倍超分辨，在信噪比为0 dB时，算法分辨性能较差，两倍超分辨的检测概率为30.7%；随着信噪比的提升，算法的超分辨能力逐渐提升，在高信噪比30 dB下，FIIB算法的五倍超分辨检测概率可达85.6%。
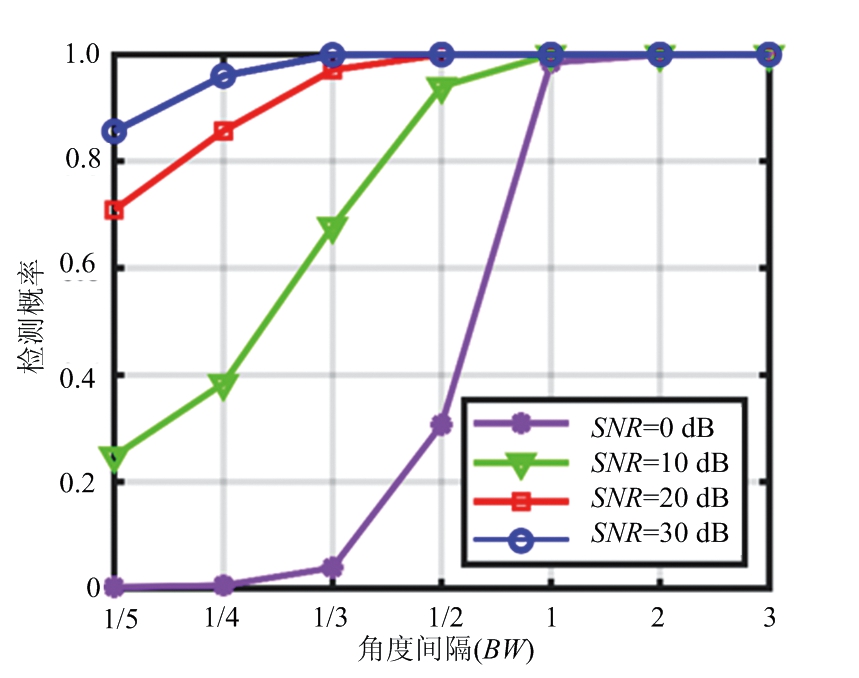
图2 不同信噪比下的检测概率
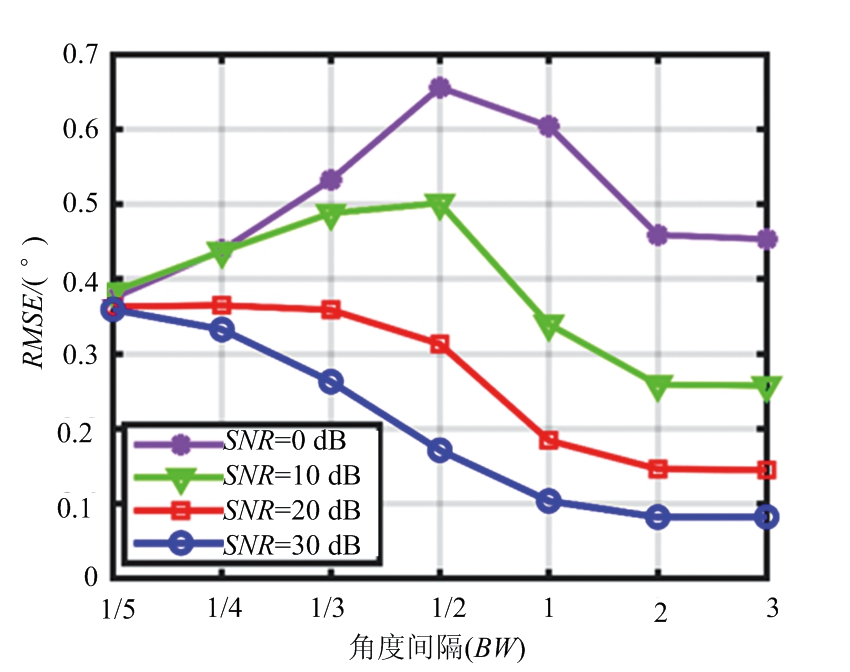
图3 不同信噪比下的均方根误差
2 基于FFT和迭代插值的改进型超分辨算法
本文提出的基于FFT和迭代插值的超分辨算法，有效地将传统的FFT算法测角方案与迭代插值-干扰对消相结合，并提出一种新的收敛策略，能够高精度、低复杂度地实现信源的角度估计及个数估计。传统的空域FFT测角方法简单，但分辨率低，不能分辨落在同一波束内的目标。因此，将FFT测角得到的目标粗略角度进行迭代插值，对粗略角度进行细化估计，并经过信号对消，显露出位于同一个分辨单元的其余目标，再次利用插值迭代，得到精确的目标角度值，从而实现所有目标的估计。其次，本文提出了一种基于残差变化率的插值迭代收敛策略，在不损失性能的情况下能够有效地减少算法迭代的次数，从而大大地降低算法的计算量。此外，采用对消残差功率与MDL准则相结合的方法进行信源个数估计。当残差功率小于噪声功率阈值时，我们认为剩余信号中不再存在信源而是仅剩噪声，并结合MDL信源估计准则对信源个数的最优性进行判断，进一步提升估计的正确率。
算法的流程图如图4所示，共包含三层循环，内层循环逐目标进行插值，对目标的空间频率和幅度进行更新，并通过第二层细化估计的循环不断细化估计值。外层循环则进行信号对消，估算新目标，并通过功率残差和MDL准则进行信源个数判定。算法首先对FFT测角估计出的I个目标进行插值，逐目标计算该目标的无泄漏系数。对第l个信源有
X[n]=
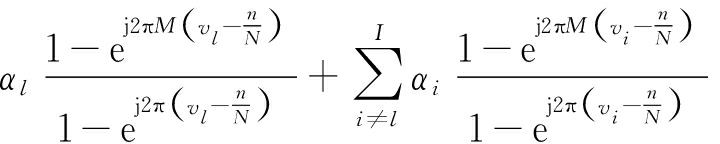
(2)
对第l个信源进行插值，计算插值系数，假设l信源对应的DFT(Discrete Fourier Transform)峰值位置为ml，则信源l的精确频率可表示为
(3)
式中，δl∈[-p,p]为当前估计的偏差。
则ml+p的DFT系数为
X(ml+p)=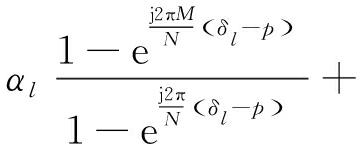
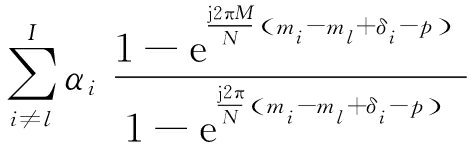
(4)
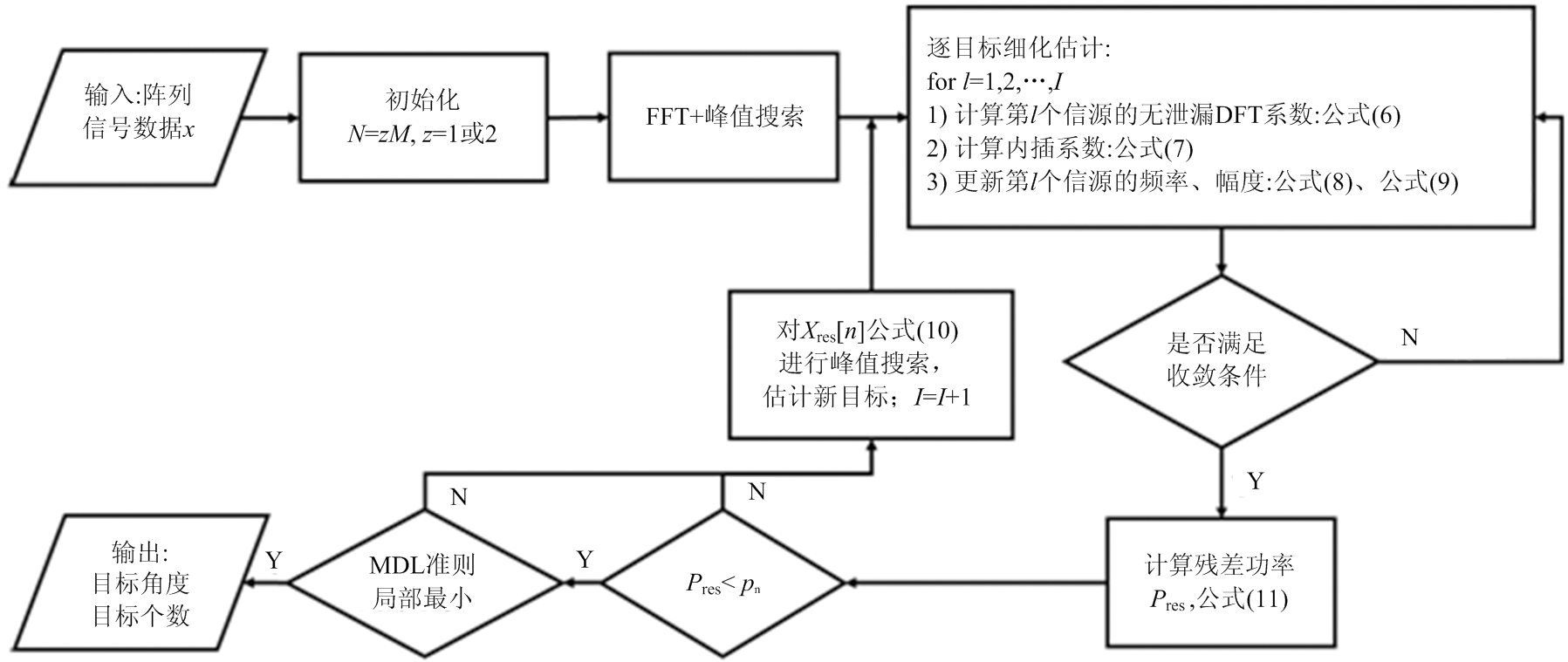
图4 基于FFT和迭代插值的超分辨算法流程图
式中，第二项为其余分量在ml+p处的系数，即其他目标能量的泄漏对第l个信源的干扰。将第一项剥离出来，通过插值估计偏差，对第l个信源的频率进行更新。记第二项干扰项为
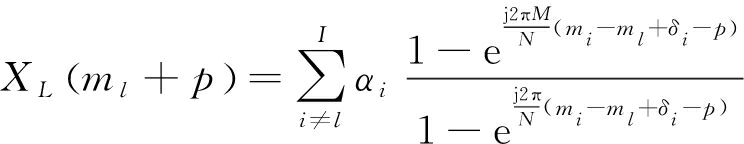
(5)
则第l个信源在ml±p处的无泄漏的DFT系数为
XR(ml±p)=
(6)
利用傅里叶系数插值得到
(7)
根据得到的估计偏差对信源的频率和幅值进行更新，
(8)
(9)
更新后的目标空间频率，再通过第二层的细化估计循环不断地细化估计值，从而得到目标的精确估计值。
在完成对现有目标的细化估计后，通过干扰对消从阵列信号中减去已估计的目标分量，根据剩余信号的功率(残差功率Pres)预判是否还存在其他目标，
Xres[n]=
n=0,1,2,…,N-1
(10)
Pres=mean(|Xres|2)
(11)
对阵列信号x进行噪声估计，并以此作为噪声门限Pn。当残差功率小于噪声门限时，则认为信号中仅剩噪声不再存在其他信源。结合MDL准则对当前估计出的信源个数的是否最优进行判断，从而实现对信源个数的估计。
3 精估计收敛策略
在FIIB中对单源、多源的收敛策略进行了分析讨论[14]，提出了一种克拉美罗界(Cramer Rao Bound, CRB)自适应方法，即精估计循环至两次连续频率估计之间的最大差值小于指定的容差为止，该容差根据CRB自适应设置。该策略保证了在高SNR下具有与其CRB一致的较小的容差值。然而在实际的工程应用中，算法的计算量往往是第一考虑要素，甚至可以牺牲算法的性能来换取计算量的降低。而FIIB算法主要的运算开销便是细化估计的迭代。CRB自适应收敛策略的算法确实能够获得较好的性能，但是在工程中也因其迭代次数过大而难以得到应用。
本文从信源残差功率的变化曲线出发，提出一种基于残差变化率的新收敛策略，能够在不损失算法性能的前提下大大降低迭代次数，从而降低算法的计算量。图5显示了细化估计迭代中残差功率以及目标估计值与真实值之间的误差随迭代次数的变化曲线图，根据曲线变化可以看到，随着迭代次数增多，信源估计值不断精确，残差功率在逐渐降低后趋于平稳，此时信源的估计角度偏差开始缓慢趋于0。因此，建议细化估计在两次迭代间的残差功率变化率ΔPres小于指定阈值时停止迭代。
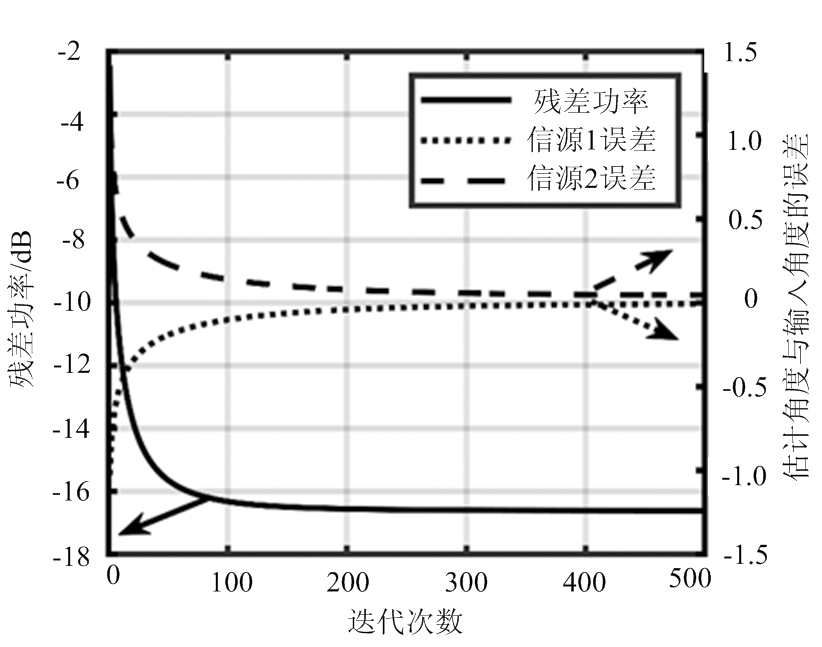
图5 细化估计残差功率、角度误差随迭代次数变化曲线图
对不同阈值下的残差功率收敛策略及CRB收敛策略的FIIB算法性能进行了仿真，并对不同策略的迭代次数进行了统计分析。仿真采用一个32阵元的等距均匀的线性阵列，阵元间距d=0.5λ，噪声建模为零均值、方差的高斯噪声。设置两个信源，角度间隔为两倍超分辨，蒙特卡洛次数1 000次。不同收敛策略的FIIB算法的均方根误差随着SNR变化的曲线如图6所示，当ΔPres的门限值设为1×10-3时，算法性能已比较接近CRB策略，当阈值为1×10-4时，残差功率收敛策略的性能与CRB策略的性能已相差无几。表1为不同策略下迭代次数的统计平均值。由仿真统计结果可知，本文提出的收敛策略在与CRB策略性能相差无几的情况下，迭代次数几乎降低了二分之一。值得注意的是，随着信噪比的升高，信源之间的频谱泄漏增大，从而导致精估计收敛慢，迭代次数随之增加。
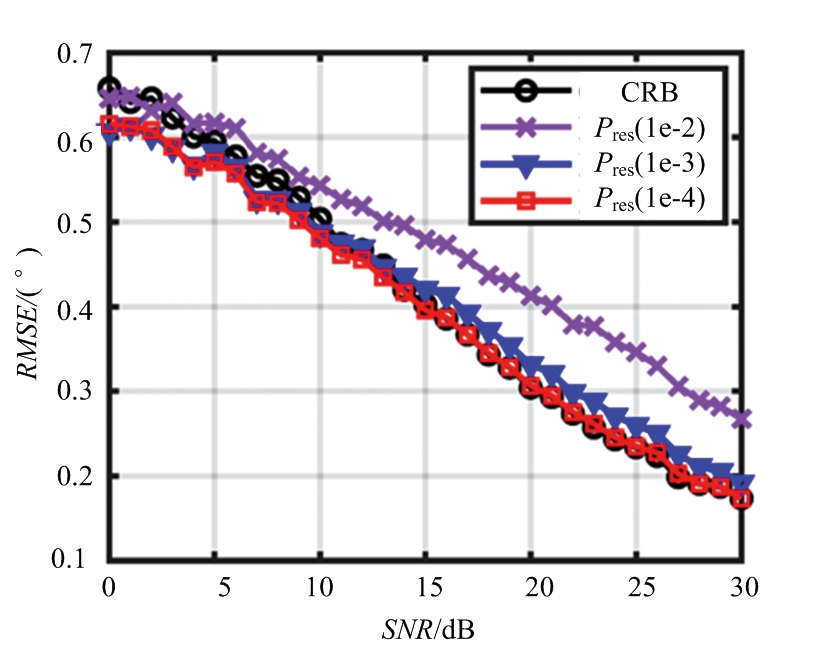
图6 不同收敛策略的RMSE随SNR变化的曲线图
表1 不同收敛策略下精估计迭代的平均次数
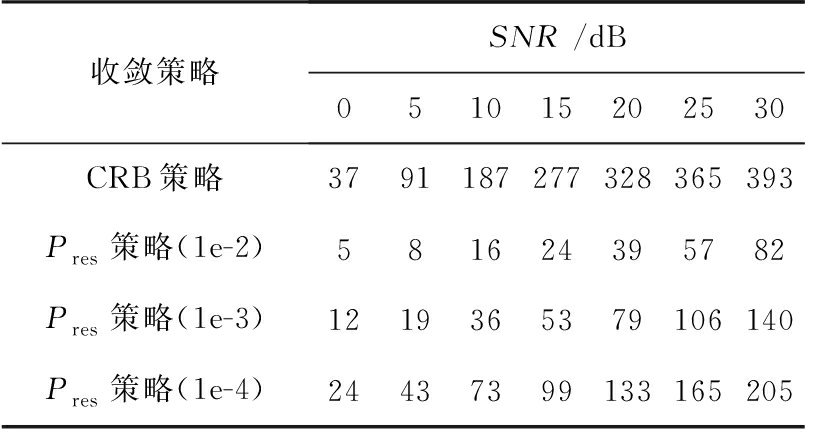
收敛策略SNR /dB051015202530CRB策略3791187277328365393Pres策略(1e-2)581624395782Pres策略(1e-3)1219365379106140Pres策略(1e-4)24437399133165205
4 仿真结果与分析
仿真条件如下，考虑一个均匀的线性阵列，阵元个数M=32，阵元间距d=0.5λ，来自远场的信号入射角度为θ，相应的空间频率v=0.5sinθ。信号源的幅度|α|根据所需的SNR进行设置，相位在(0,2π)内均匀变化。噪声建模为均值为0、方差的高斯噪声。对所有情况的仿真均进行了1 000次蒙特卡洛实验，并将改进后的算法与FIIB算法及其他子空间类的算法进行比较。其中本文改进算法及FIIB的零填充因子均设置为z=1。
由于在原FIIB算法中信源个数已知，为排除本文算法基于对消残差功率的MDL信源个数估计方案的性能影响，在4.1节的仿真中，我们将信源个数设为已知，比较各个算法的性能；在4.2节中设置为信源个数未知，探究本文算法与FIIB算法、采用信源个数自估计的FIIB算法[15]三种算法的性能。
4.1 信源个数已知情况下不同算法的估计性能与SNR、角度间隔的关系分析
在本小节中，假设信源个数已知，对FIIB算法、本文改进算法及Root-MUSIC算法进行仿真。
场景一：设置两个目标源，两个目标源的幅度|α1|=|α2|，电角度间隔设置分别设置为BW/2，探究两个信源下不同算法的性能与SNR的关系，仿真结果如图7、图8所示。
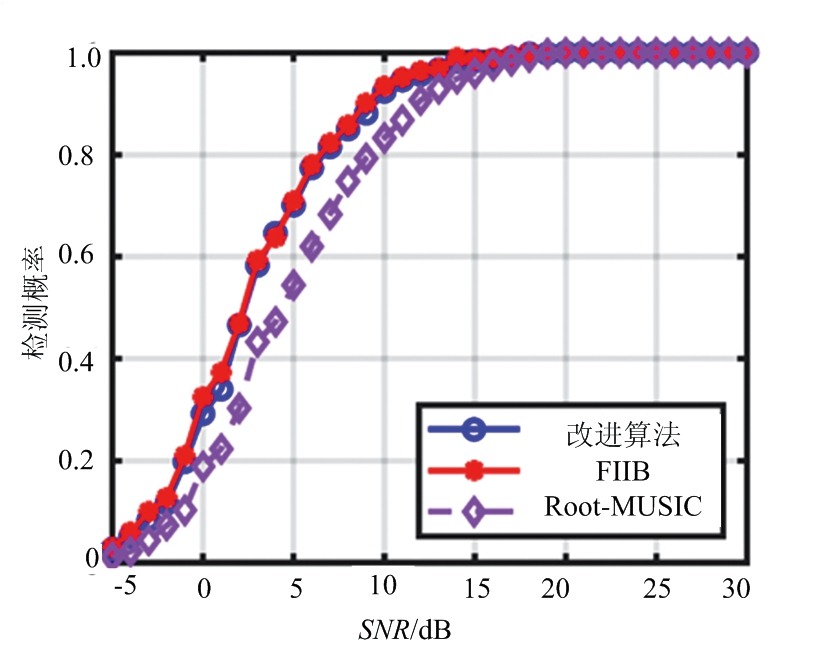
图7 不同算法的检测概率与SNR的关系
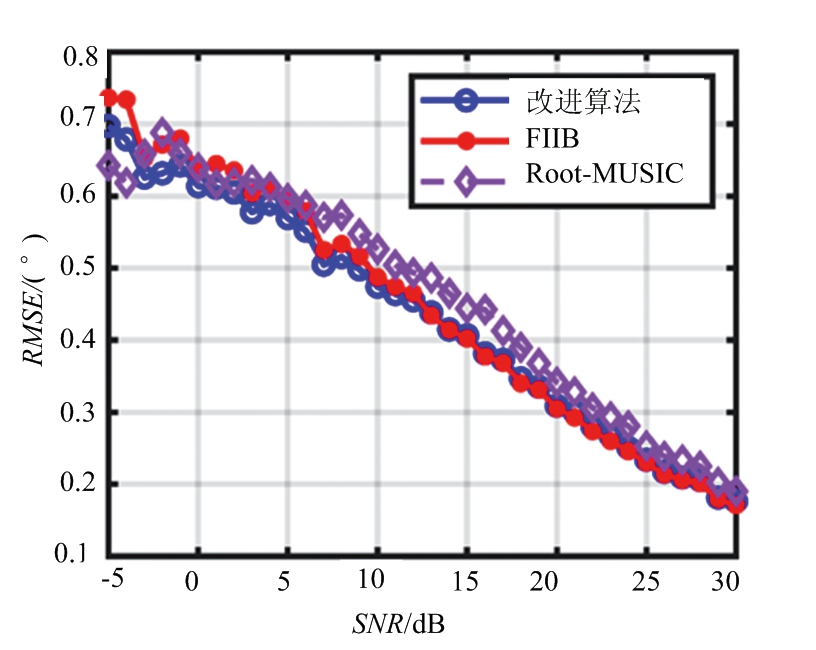
图8 不同算法的RMSE与SNR的关系
场景二：设置两个目标源的幅度|α1|=|α2|，电角度间隔设置由BW/5至2BW变化，信噪比设置为0 dB、30 dB，探究不同算法对两个信源的分辨能力，仿真结果如图9、图10所示。
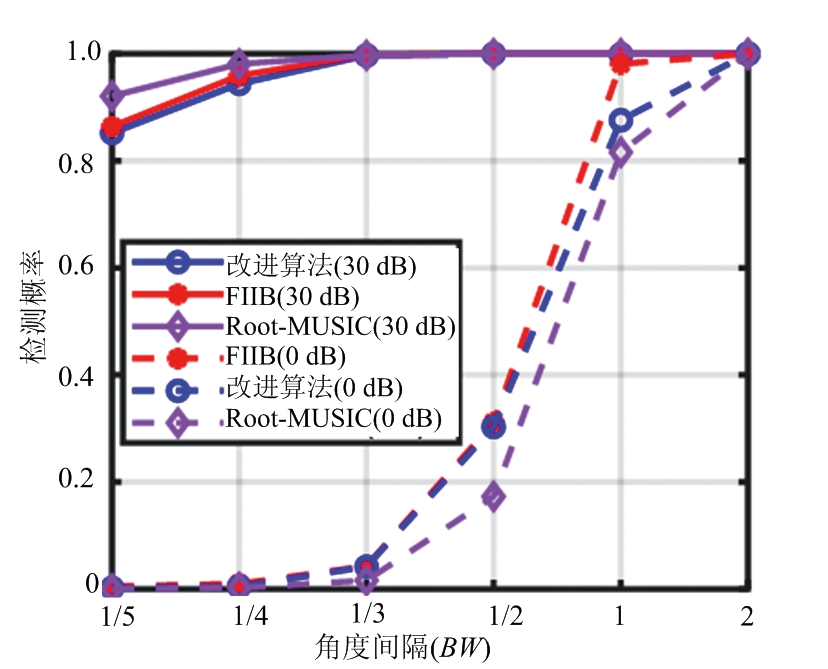
图9 不同算法的检测概率与角度间隔的关系
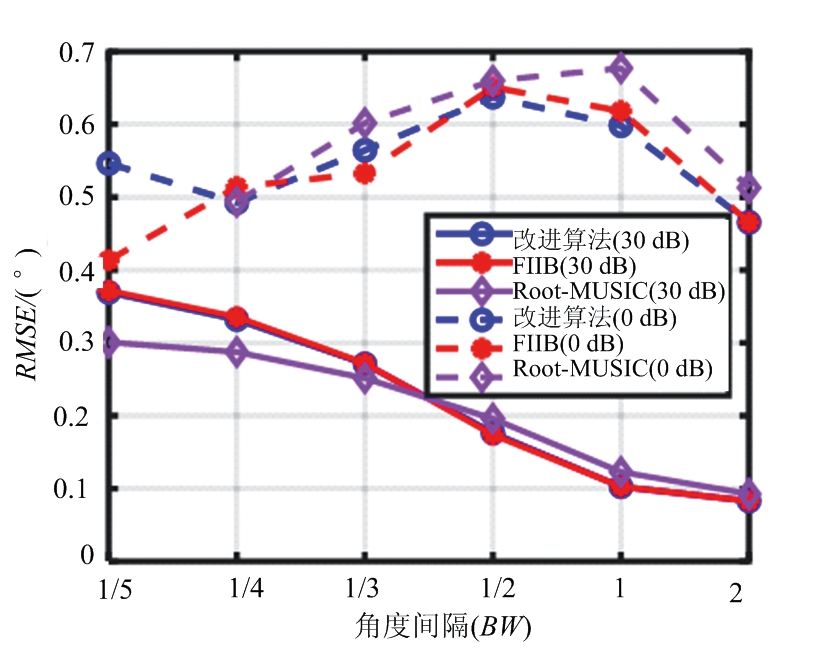
图10 不同算法的RMSE与角度间隔的关系
图7、图8分别给出了信源个数已知下，不同算法的检测概率、RMSE性能与SNR的关系。在两个目标间隔为两倍超分辨下，在高信噪比下本文提出的改进算法与FIIB算法性能接近，检测概率可达到100%。在低信噪比检测概率略低于FIIB算法，但比FIIB算法RMSE更低，估计值更加准确。显然本文算法在所有信噪比下性能优于Root-MUSIC算法。图9、图10则分别给出了不同算法的检测概率、RMSE性能与角度间隔的关系。在低信噪比下本文算法对于两个目标的分辨能力略弱于FIIB算法，但是随着SNR的提升，性能逐渐接近FIIB算法。
4.2 信源个数未知情况下不同算法的估计性能与SNR、角度间隔的关系分析
在本小节中，信源个数设置为未知，对本文改进算法、FIIB算法及采用信息论准则进行信源估计的FIIB算法三种算法进行仿真，其中本文算法采用基于对消残差功率和MDL准则的信源估计法对信源个数进行估计。其余仿真参数与4.1节中相同。
场景一：两倍超分辨下不同算法的性能与SNR的关系，仿真结果如图11、图12所示，图13显示了信源个数的估计正确率与SNR的曲线图。
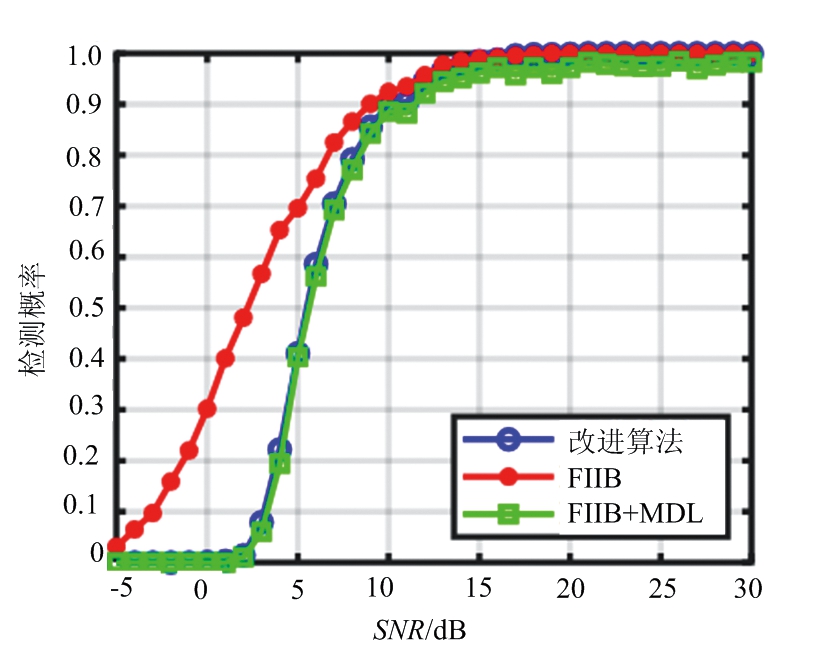
图11 不同算法的检测概率与SNR的关系
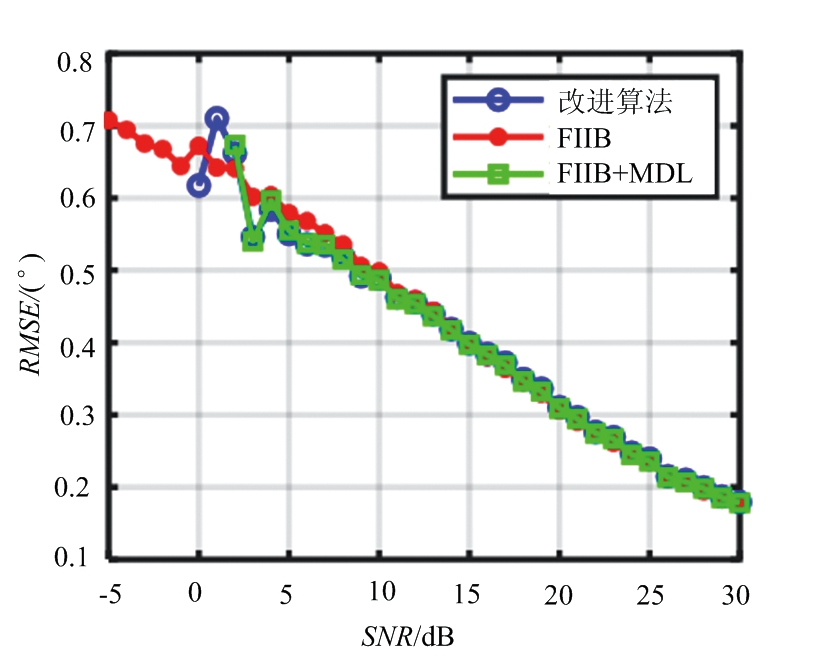
图12 不同算法的RMSE与SNR的关系
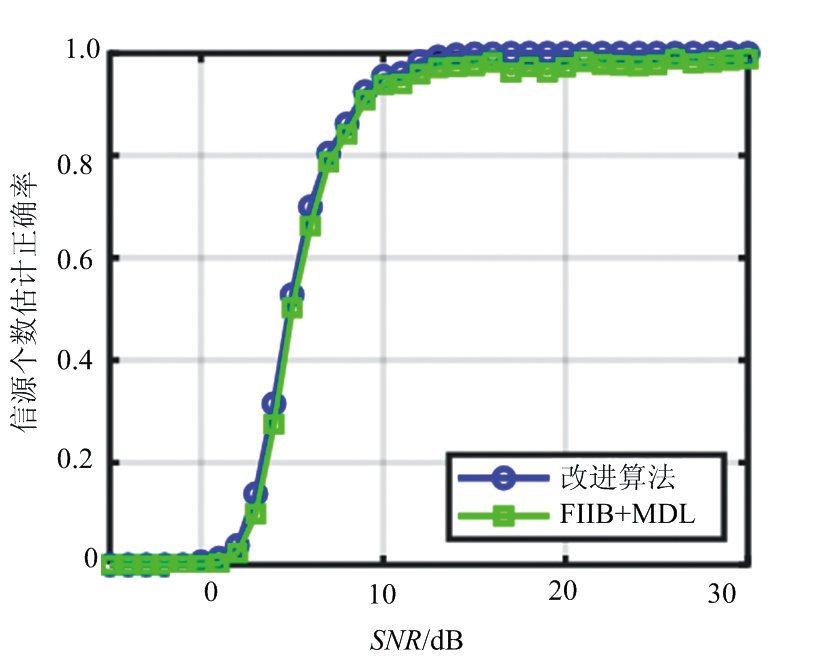
图13 信源个数估计正确率与SNR的关系
场景二：不同算法的性能与角度间隔的关系，仿真结果如图14、图15所示，图16显示了信源个数的估计正确率与角度间隔的关系图。
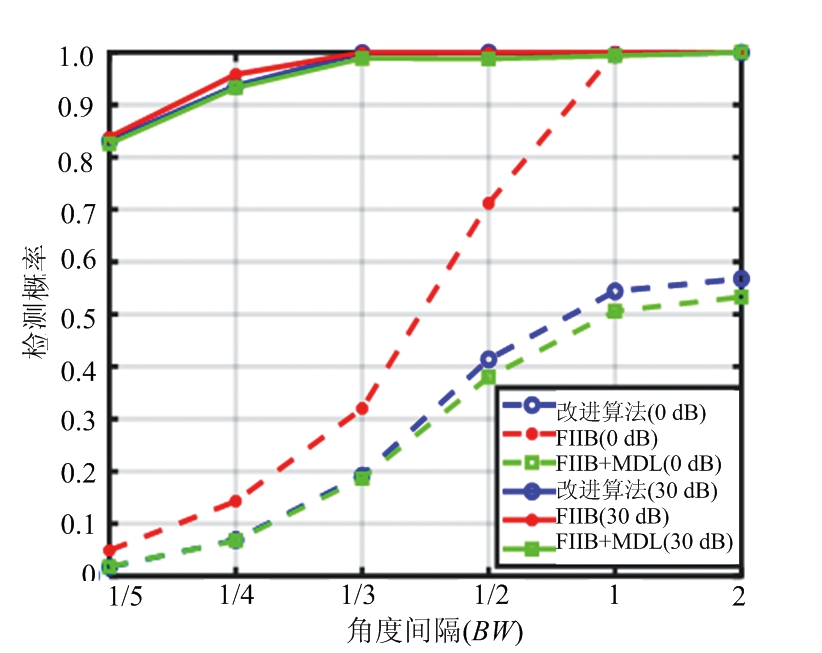
图14 不同算法的检测概率与角度间隔的关系
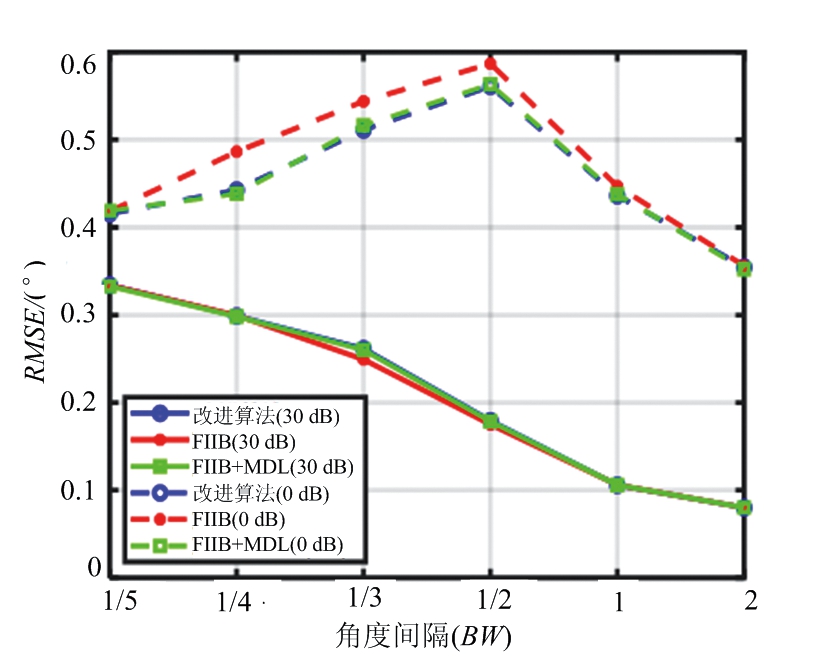
图15 不同算法的RMSE与角度间隔的关系
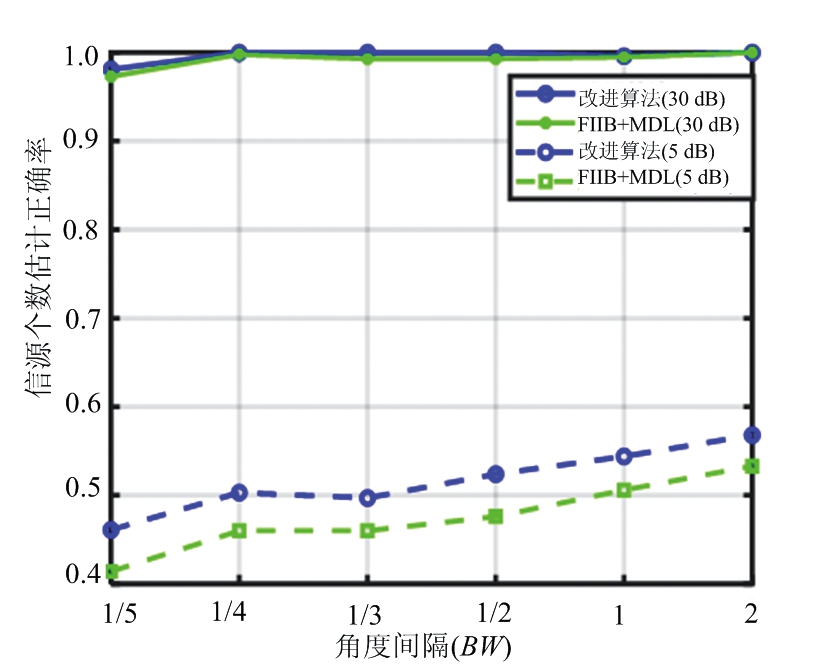
图16 信源个数估计正确率与角度间隔的关系
4.2节重点讨论本文改进方案中基于对消残差和MDL准则的信源个数估计法的性能，及信源个数估计的正确率对算法的影响。在场景一中，如图11和图12所示，本文算法与FIIB算法估计精度的性能接近，但是检测概率在信噪比为0 dB时明显低于FIIB算法。由图13展示的信源个数估计正确率的曲线图可以看出，信源个数估计错误直接导致了本文算法检测概率性能恶化，这是因为本文采用的MDL准则在低信噪比下存在欠估计[16-18]的问题，导致信源个数估计错误，从而影响检测概率。而在场景二中，同样存在该问题，如图14至图16所示，在SNR为30 dB时，本文算法的检测概率与RMSE都接近于信源个数已知的情况。但当SNR为0 dB时，本文算法的检测概率因信源个数估计错误而低于FIIB算法。由仿真结果可见，本文提出的信源个数自估计的超分辨算法在高信噪比下接近FIIB原始算法，然而随着信噪比降低，算法性能逐渐下降。
5 结束语
本文研究了低复杂度、高分辨率的DOA估计问题，提出了一种基于FFT和迭代插值的快速超分辨算法。该算法将简单的空域FFT与迭代插值的策略相结合，由空域FFT得到的粗略角度作为细化估计迭代的入口，而非低效率的逐个目标开始估计。然后进行插值迭代细化估计值，并通过干扰对消来消除频谱泄漏的影响，最终利用对消后的残差功率与信息论准则联合进行信源个数估计。该算法无需信源个数的先验信息，不但能在高信噪比下实现五倍超分辨，并且通过基于残差变化率的收敛策略能够大大降低算法的计算量。仿真结果表明，本文算法在估计精度、分辨率方面与FIIB算法性能相差无几，优于Root-MUSIC算法。
[1] 徐豪. 基于MIMO的汽车毫米波雷达信号体制及超分辨测角研究[D]. 成都：电子科技大学, 2020.
[2] SCHMIDT R O. Multiple Emitter Location and Signal Parameter Estimation[J]. IEEE Trans on Antennas and Propagation, 1986, 34(3):276-280.
[3] 田剑豪. 三种典型空间谱测向算法的分析比较[J]. 中国无线电, 2021(2):71-73.
[4] 朱国辉, 汪洋, 米胜男. 加权最小二乘法和MUSIC法联合测向技术研究[J]. 雷达科学与技术, 2019, 17(3):319-323.
[5] PILLAI S U, KWON B H. Forward/Backward Spatial Smoothing Techniques for Coherent Signal Identification[J]. IEEE Trans on Acoustics, Speech, and Signal Processing, 1989, 37(1):8-15.
[6] 吴孙勇,邹宝红,薛秋条,等.基于单快拍空间平滑的多伯努利DOA跟踪算法[J].系统工程与电子技术,2021,43(9):2430-2438.
[7] ABOUTANIOS E, HASSANIEN A, AMIN M, et al. Fast Iterative Interpolated Beamforming for Accurate Single-Snapshot DOA Estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(4): 574-578.
[8] KOCHERRY D L, YE S L, ABOUTANIOS E. Estimating Parameters of Multiple Damped Complex Sinusoids with Model Order Estimation [C]∥2016 IEEE International Workshop on Signal Processing Systems (SiPS), Dallas, TX, USA:IEEE, 2016:86-91.
[9] RISSANEN J. Modeling by Shortest Data Description[J]. Automatica, 1978, 14(5):465-471.
[10] 葛生国. 小快拍数下的远场窄带信源个数估计研究[D].广州：广东工业大学, 2020.
[11] LI J, STOICA P. Efficient Mixed-Spectrum Estimation with Applications to Target Feature Extraction[J]. IEEE Trans on Signal Processing, 1996, 44(2):281-295.
[12] 李海, 陈筱浅. 基于NLS-RELAX的空中多机动目标参数估计[J]. 雷达科学与技术, 2018, 16(2):214-220.
LI Hai, CHEN Xiaoqian. Parameter Estimation of Multiple Air Maneuvering Targets Based on NLS-RELAX[J]. Radar Science and Technology, 2018, 16(2):214-220. (in Chinese)
[13] 段永昌, 李欣, 黄耀辉, 等. 基于快速迭代插值的FMCW雷达距离估计算法[J]. 通信学报, 2019, 40(9):175-183.
[14] YE S, ABOUTANIOS E. Rapid Accurate Frequency Estimation of Multiple Resolved Exponentials in Noise[J]. Signal Process, 2017, 132:29-39.
[15] ABOUTANIOS E, HASSANIEN A. Low-Cost Beamforming-Based DOA Estimation with Model Order Determination[C]∥ 2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hangzhou, China:IEEE, 2020:1-5.
[16] ICHIGE K, HAMADA S, KASHIWAGI K, et al. Robust Source Number Estimation Based on Denoising Preprocessing[C]∥ 2020 Sensor Signal Processing for Defence Conference (SSPD), Edinburgh, UK:IEEE,2020:1-5.
[17] WONG K M, ZHANG Q T, REILLY J P, et al. On Information Theoretic Criteria for Determining the Number of Signals in High Resolution Array Processing[J]. IEEE Trans on Acoustics, Speech, and Signal Processing, 1990, 38(11):1959-1970.
[18] 许佳奇, 王川川, 曾勇虎, 等. 盖尔圆定理和最小描述长度准则相结合的信源数目估计方法研究[J]. 信号处理, 2017, 33(S1):53-57.
