0 引言
雷达散射截面积(Radar Cross Section,RCS)是表征目标散射强弱的物理量[1],它是一个假想面积,用来度量目标在雷达波照射下产生回波的强度。实际上,目标的雷达散射截面积不是一个单值[2],而是一种目标特性,它不仅与目标自身尺寸、形状、材质和结构等几何参数和物理参数相关,还与雷达发射的波长、极化和入射观测角度等参数有着紧密的联系。通过雷达基本方程可知,雷达对目标的探测能力取决于距离、角度等多种因素,其中目标RCS对雷达探测威力的影响尤为重要[3]。在实际应用中,为降低被雷达探测的概率会采取多种隐身措施降低目标雷达散射截面积,有效提高目标雷达波束隐身能力。因此,准确地估算目标RCS对雷达系统参数设计、目标雷达波隐身、目标探测与识别等方面均具有极其重要的作用。
目前,目标RCS计算可分为两类:实际测量与数值计算[4]。实际测量又可分为外场实测与微波暗室实测,这两种方法需要构建实际的模型,并在室内或者室外实际测量,虽然能够得到较为真实的结果,但是这种方法耗费大量资源且效率低下,因此很难在实际工作中得到广泛的应用。而随着计算机技术的快速发展,数值计算逐渐流行起来,利用计算机技术进行目标建模,利用其强大的计算能力,结合电磁波的相关理论,仿真得到目标的雷达散射截面[5]。这种方法计算周期短,成本较低,计算灵活,既可以计算现有目标,也可以对尚未成型目标进行预估,从而可以为目标的设计提供技术支撑。
本文首先介绍了属性散射中心模型及其简化模型,给出了根据目标几何模型确定参数集的方法,结合模型便能够快速预估目标在不同方位角度与不同频率下的目标RCS;再详细阐述物理光学方法及其算法实现,通过计算机仿真得到不同情况下的目标RCS。针对复杂目标RCS估计问题,文献[6]提出了一种联合不同计算方法对预估结果进行误差分析以确定最终RCS,但这种方法需要运用不同方法仿真计算,计算量大,难以应用于实际工作处理。为解决该问题,通过分析对比属性散射中心模型和物理光学两种RCS预估方法的优缺点,本文进一步提出了一种联合两种方法优势处理的估计方法,可以快速获得目标不同频率、任意观察角度的RCS估计值。最后通过FEKO软件仿真结果为基准,对比分析了所提预估方法的有效性。
1 基于属性散射中心模型预估方法
根据几何光学理论与物理光学原理,当目标为大尺寸目标时,其后向散射回波可通过若干离散点的回波响应相干叠加近似表示[7],进而可根据强散射点信息以及回波模型得到目标的RCS。基于模型预估目标回波及RCS的方法主要依赖回波模型的准确性,下面将从参数化模型出发,详述基于属性散射中心模型的目标RCS预估方法。
属性散射中心模型是一种参数化回波模型。相比于传统的理想点模型、衰减指数和模型、GTD(Geometrical Theory of Diffraction)模型,属性散射中心模型充分考虑了观察方位以及散射体类型对散射回波造成的变化,并通过辛克函数与指数函数分别描述了散射回波与散射中心类型与观察角度的依赖关系[8]。考虑到属性散射中心模型对频率和角度依赖特性描述更加准确,属性中心参数一定程度地反映了目标的几何与物理属性,选择属性散射中心模型作为理论回波模型对目标RCS进行预估。属性散射中心模型的形式如下:
![]()
exp(-kcγisinφ)·
exp[-j2k(xicosφ+yisinφ)]
(1)
因此,目标的散射回波可看作多个等效散射中心的回波响应和:
(2)
从式(1)可以看出,除了入射波长、观测方位角两个自变量,模型中还有7个未知参数Ai,αi,γi,Li,φ′i,xi,yi待确定,这几个参数就是散射模型的参数集Θi。其中γi参数表示局域式散射中心的回波幅值与观察角度的衰减关系,一般取10-12这种特别小的值来描述之间的变化关系,而对于分布式散射中心该参数为0。由于γi参数与它所在的指数函数对回波幅值的影响很小,所以在确定参数集时可以不考虑γi而认为对于所有物体该参数都为0,最终得到简化后的回波模型[8]:
![]()
exp[-j2k(xicosφ+yisinφ)]
(3)
在确定式(2)与式(3)所示的回波模型之后,接下来就可直接根据目标的几何模型估计简化后的参数集Θ={Ai,αi,Li,φ′i,xi,yi}以实现目标的回波及RCS估计,详见文献[7-8],这里不再赘述。
2 物理光学方法
不同于基于属性散射中心模型的RCS预估方法,物理光学方法能够准确计算目标在任意观察角度、不同雷达波长下的回波贡献,究其根本就是斯特兰顿-朱兰成散射积分方程的求解。但是这个散射积分方程在实际计算电大尺寸目标散射回波过程中非常复杂,因此物理光学方法通过几个合理的假设将散射积分方程简化,在保证远场回波计算准确的同时实现快速计算。斯特兰顿-朱兰成散射积分方程[9]如下:
![]()
![]() ∇G0+
∇G0+
![]() ∇G0]ds
∇G0]ds
(4)
![]()
![]() ∇G0-
∇G0-
![]() ∇G0]ds
∇G0]ds
(5)
式中,![]() 为目标表面外法向单位矢量,
为目标表面外法向单位矢量,![]() 为目标表面电磁波矢量,G0、∇G0分别为空间中格林函数与梯度:
为目标表面电磁波矢量,G0、∇G0分别为空间中格林函数与梯度:
(6)
∇![]()
(7)
在满足电磁场基本理论前提下,公式(4)和(5)的积分方程简化过程包括一个基本假设、两个合理近似:
假设一:在给定入射波照射下目标表面信息如图1所示,其中与入射电磁波直接作用的面元处会产生感应电流并产生散射场,而不在入射波照射下的面元对远场回波没有贡献。并且面元上的感应电流只由入射波照射产生,相邻面元产生的感应电流没有相互作用。
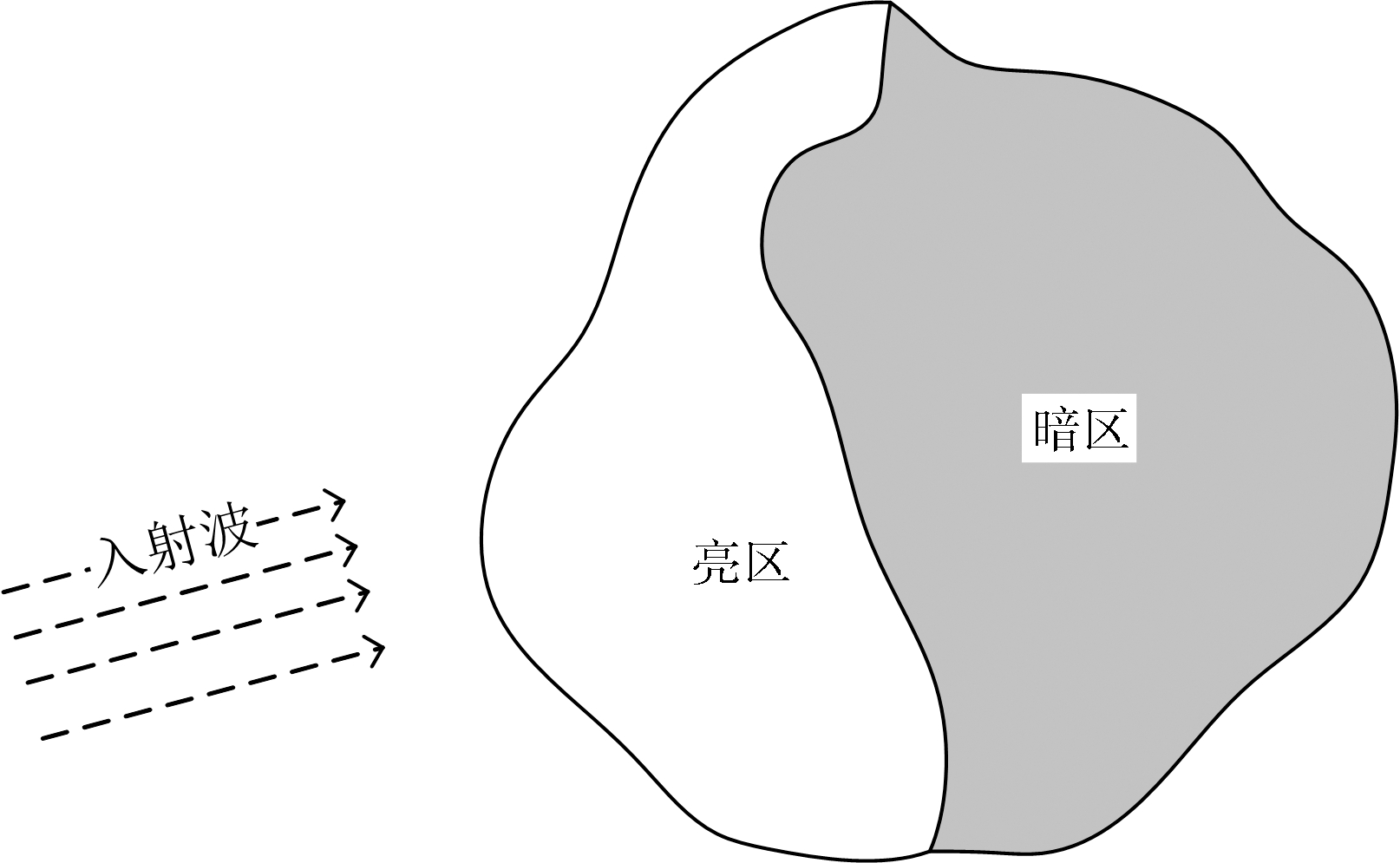
图1 目标表面信息图
近似一:在实际雷达系统探测过程中,雷达与目标之间的距离特别大。因此在计算人造目标散射回波时可认为目标与观察点处无限远,即可将式(7)的梯度表达式改为
∇![]()
(8)
式中,![]() 表示散射方向单位矢量。
表示散射方向单位矢量。
近似二:当入射波照射到目标表面时,入射波波长远远小于目标尺寸,入射点处的切向面元可近似看作无限大平面。因此目标表面的感应电流、感应磁流可根据入射电磁波简便、快速地得到。
在计算电大尺寸人造目标散射过程中,通常认为人造目标由理想导体构成且目标表面光滑。再结合上述简化条件,理想导体电大尺寸人造目标散射回波计算公式可表示为
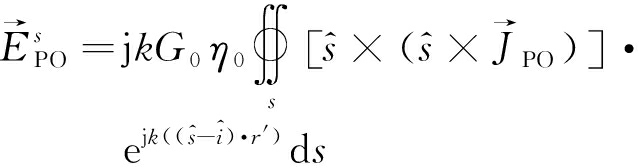
(9)
(10)
式中,η0等于自由空间阻抗值,积分项可通过gordon法[10]、高斯法[11]等方法计算。感应电流![]() 可通过入射波磁矢量计算:
可通过入射波磁矢量计算:
(11)
综上所述,物理光学方法整体实现流程如图2所示。

图2 物理光学实现流程图
3 基于联合模型处理的复杂目标RCS估计方法
通过属性散射中心参数化模型预估的方法只有在一定观察角度范围内才能准确预估目标的雷达散射截面积。而对于物理光学方法来说,虽然在任意角度下都能够得到较为准确的目标RCS结果,但在每个观察角度下,物理光学方法都需要对目标模型重新判断遮挡以更新目标的可照射面元,这一步骤使得计算量增加,所需要的时间也会增加。特别地,当目标结构更加复杂、尺寸更大时,物理光学方法的计算量变得非常大。
因此针对复杂结构目标,这里提出一种联合处理的目标RCS预估方法,通过将目标观察角度范围分段,利用物理光学方法分析每段角度内中心观察角度下目标强散射中心的属性参数集,带入属性散射中心模型拟合其他观察角度的散射场,再结合雷达散射截面积计算公式得到RCS结果,最后将不同角度范围的RCS预估结果合并得到目标整体的RCS预估结果。这种联合模型的处理方法不仅能修正单一基于属性散射中心模型预估方法中观察角度以及幅值参数对目标RCS预估带来的误差,还能够根据属性参数集快速获得目标任意观察角度、不同频率的RCS值。整个算法流程如图3所示。

图3 基于联合处理的复杂目标RCS估计流程图
4 仿真计算分析
针对复杂目标雷达散射截面积的预估,分别通过文中基于属性散射中心模型预估、物理光学两种RCS估计方法以及所提联合处理方法,并采用FEKO软件仿真为基准计算较为典型的复杂目标二面角的RCS。其中目标雷达散射截面积[1]的最终计算结果为分贝平方米(dBsm),其表达式为
(12)
式中,Ei为入射波电场强度,Es为目标单站回波的电场强度。
针对目标雷达散射截面积的估计问题,本节分别通过基于属性散射中心模型单一方法、物理光学及本文所提方法预估三种典型目标的RCS,并与商业软件FEKO仿真结果对比,结果如下:
平板目标示意图如图4所示,仿真模拟的入射波频率为1 GHz,观察角俯仰角度为90°,方位角度为-90°~90°,不同方法的RCS结果如图5和表1所示。对于平板目标,基于ASC模型预估目标RCS的方法在-30°~30°范围内结果准确,物理光学算法计算结果总体趋势与软件仿真结果一致,仅在部分结果特别小的观察角度存在较大误差,忽略这些坏值,物理光学方法总体误差较小,但仿真所需时间更长,为基于ASC模型单一方法的3.8倍。本文所提方法提高估计精度的同时所需时间减少,为基于ASC模型单一方法的2.04倍。
图4 平板目标
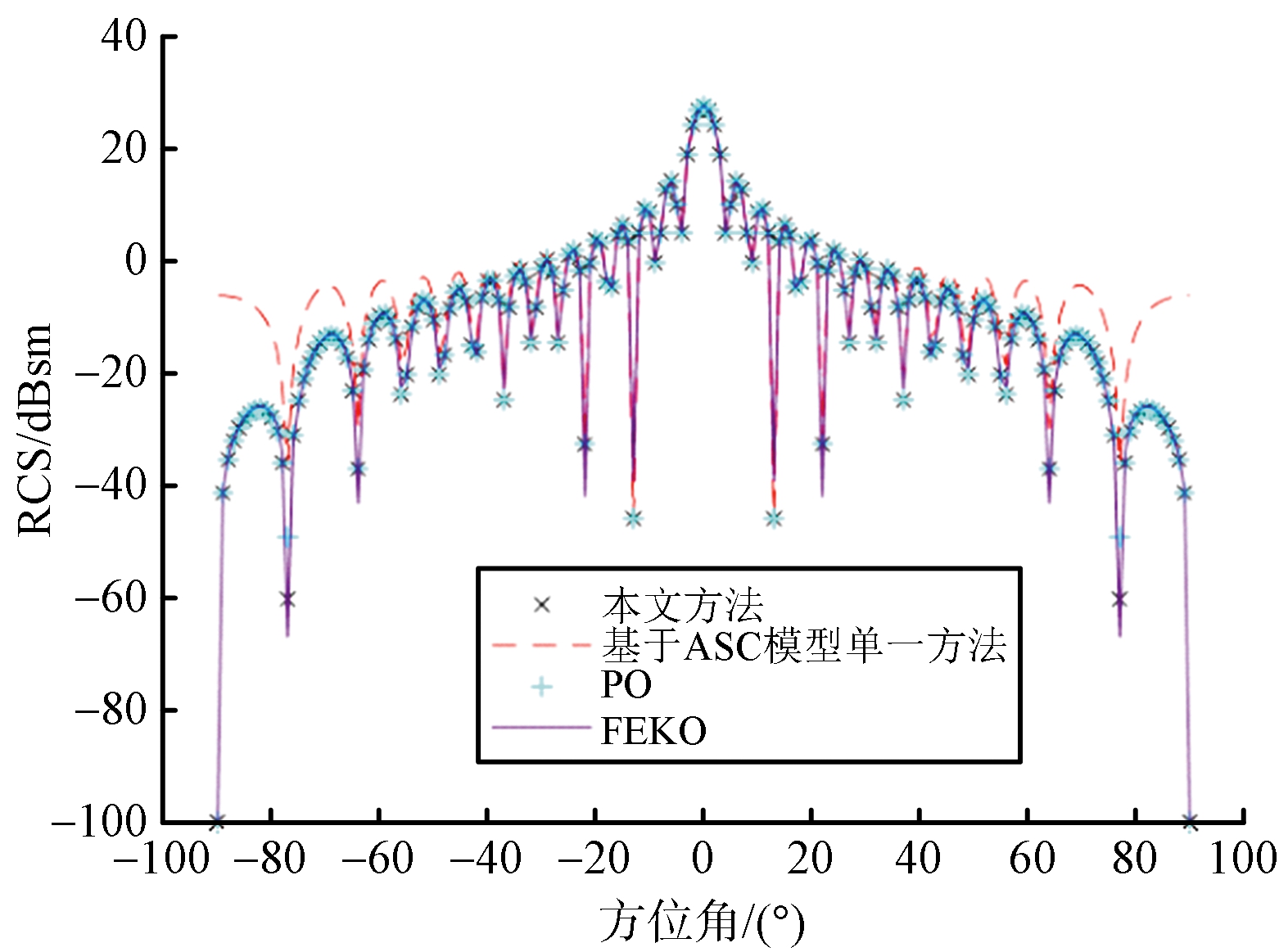
(a) RCS曲线
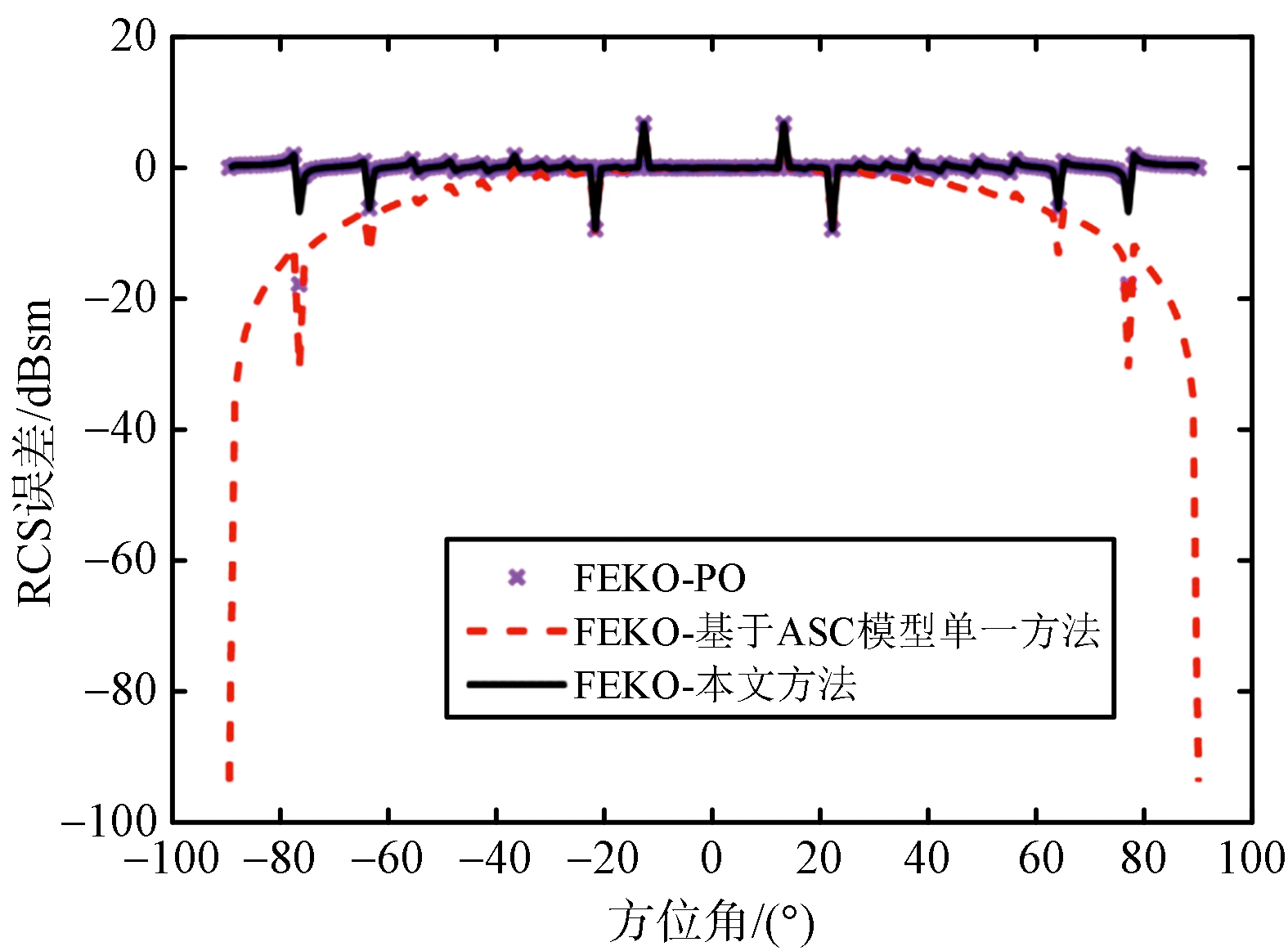
(b) RCS误差曲线
图5 平板目标计算结果
表1 平板目标仿真时间表
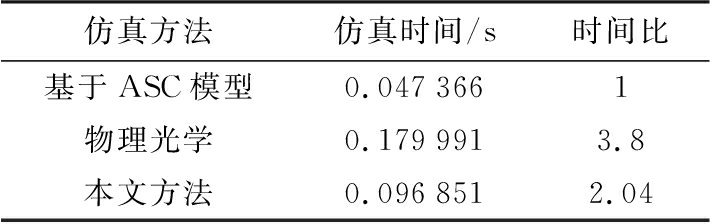
仿真方法仿真时间/s时间比基于ASC模型0.0473661物理光学0.1799913.8本文方法0.0968512.04
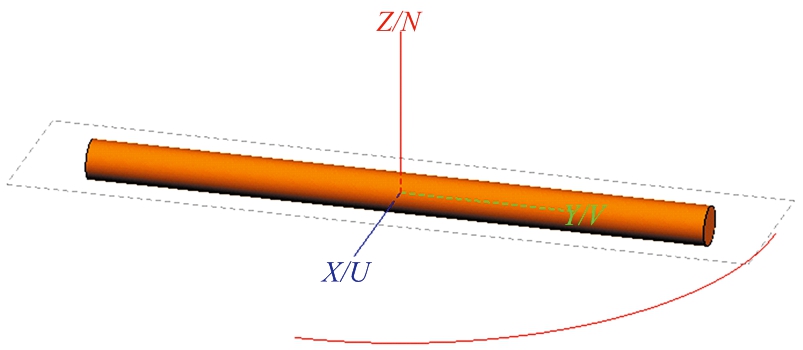
图6 圆柱目标
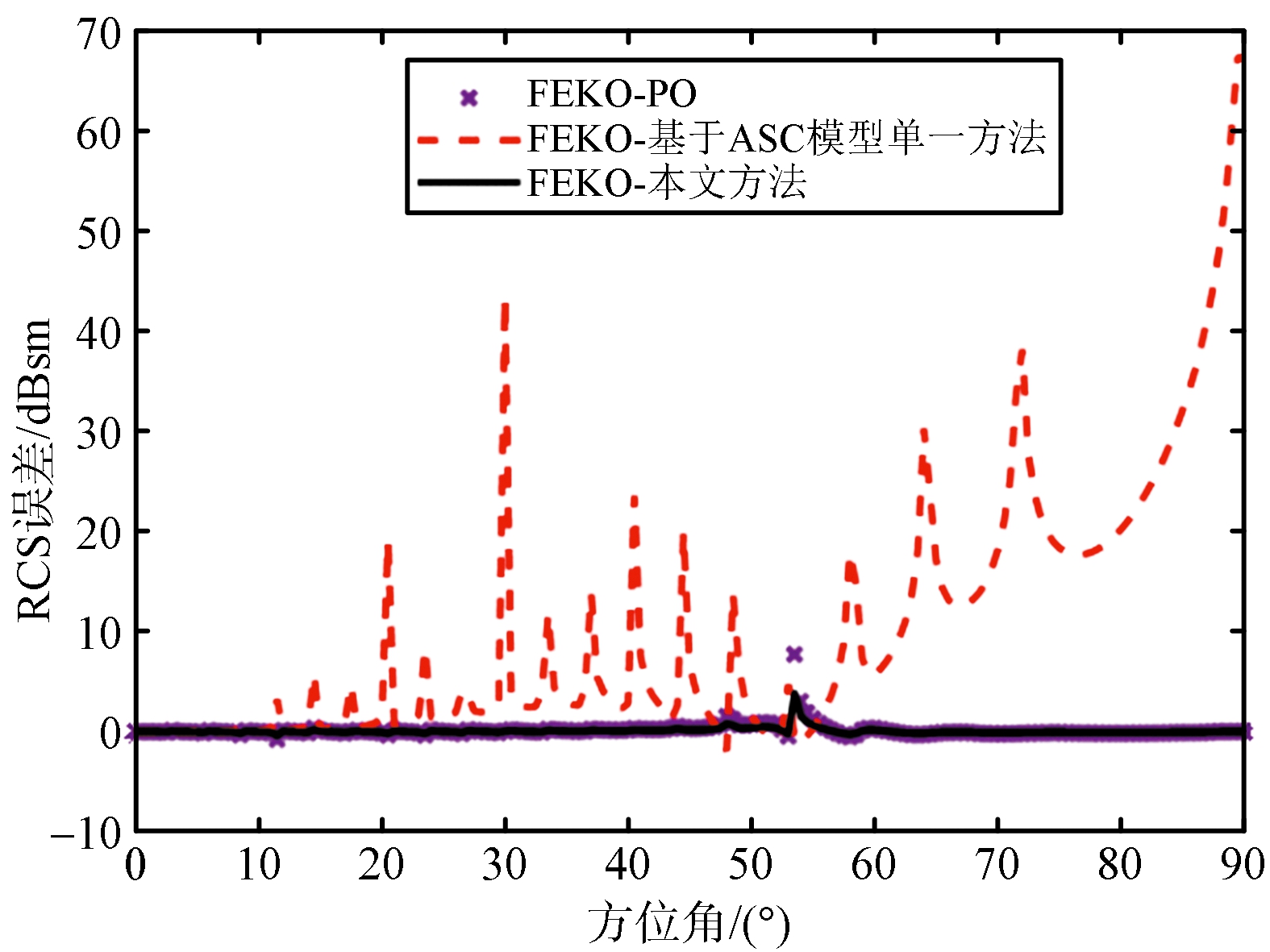
圆柱目标示意图如图6所示,仿真模拟的入射波频率为1 GHz,观察角俯仰角度为90°,方位角度为0°~90°,不同方法的RCS结果如图7和表2所示。基于ASC模型预估圆柱目标RCS的方法在0°~40°范围内结果准确,物理光学算法计算结果总体趋势与软件仿真结果相差较小,但仿真所需时间更长,为基于ASC模型单一方法的4.05倍。而本文方法在更短的时间内较准确得到估计结果,所需时间为基于ASC模型单一方法的2.17倍。
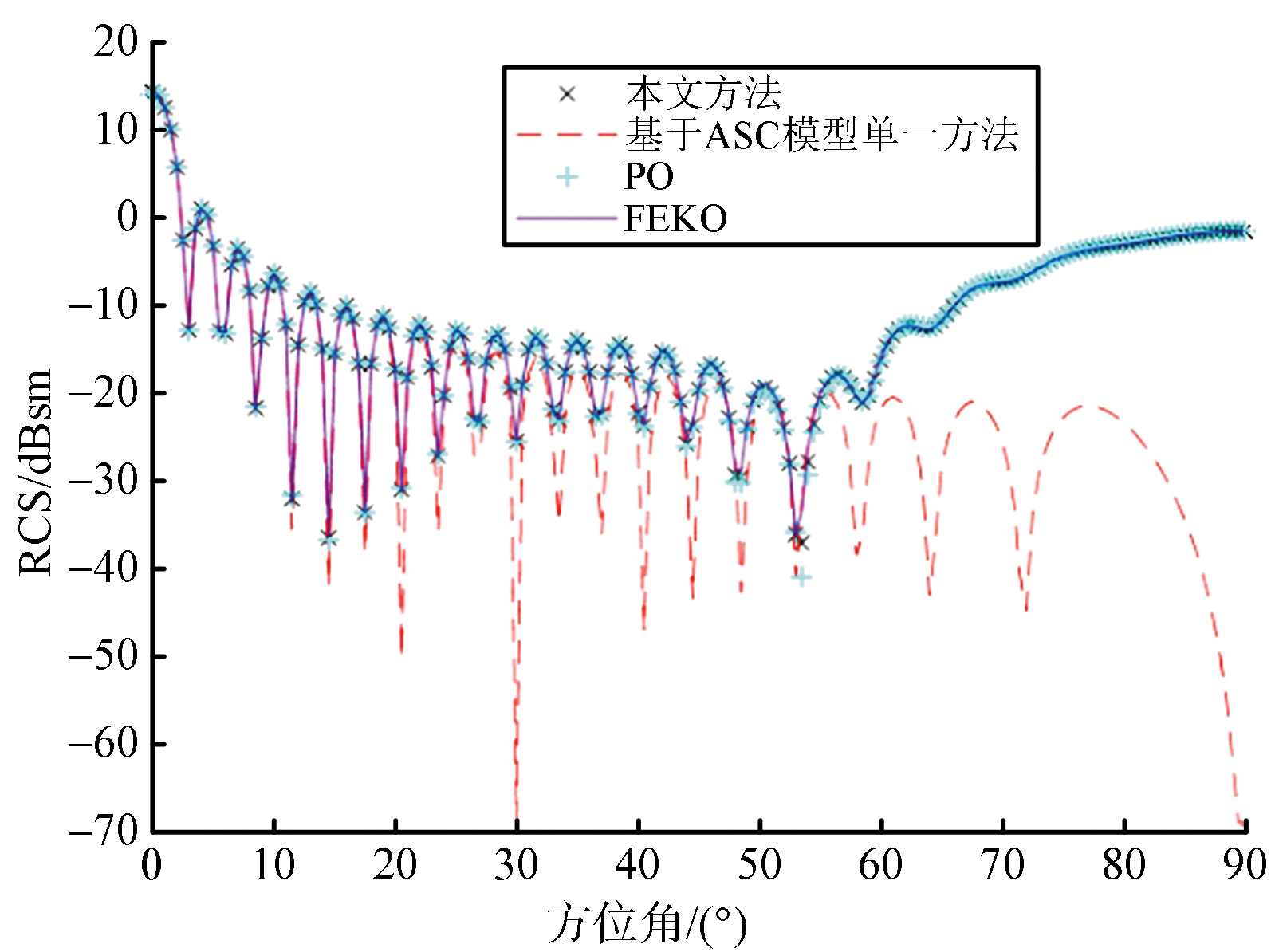
(a) RCS曲线
(b) RCS误差曲线
图7 圆柱计算结果
表2 圆柱目标仿真时间表
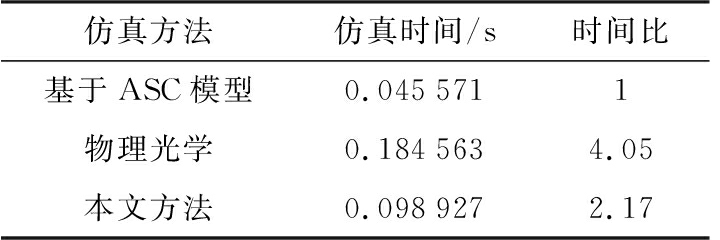
仿真方法仿真时间/s时间比基于ASC模型0.0455711物理光学0.1845634.05本文方法0.0989272.17
二面角目标示意图如图8所示,仿真模拟的入射波频率为2 GHz,观察角俯仰角度为45°,方位角度为-45°~45°,不同方法的RCS结果如图9和表3所示。当目标结构复杂时,基于ASC模型预估目标RCS的方法只在±3°范围内与软件仿真结果相差较小。物理光学算法计算结果总体趋势与软件仿真结果一致,误差较小,但仿真所需时间增加,为基于ASC模型单一方法的8.3倍。本文所提方法所需时间减少且误差较小,所需时间为基于ASC模型单一方法的5.53倍。
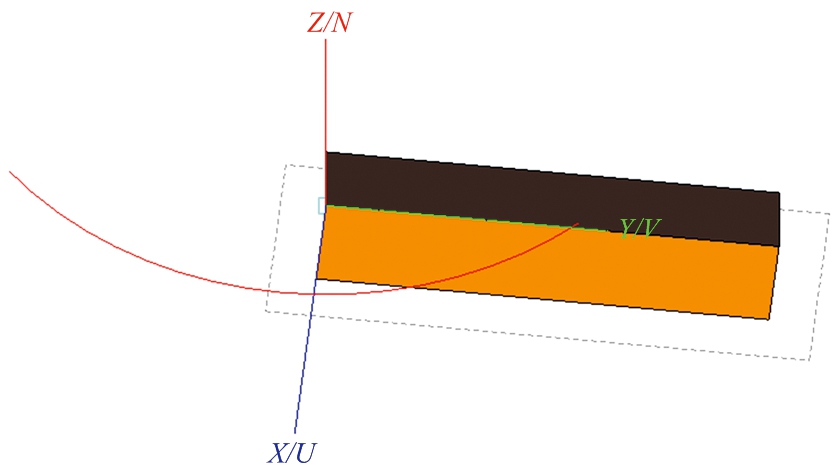
图8 二面角目标及观察角度示意图
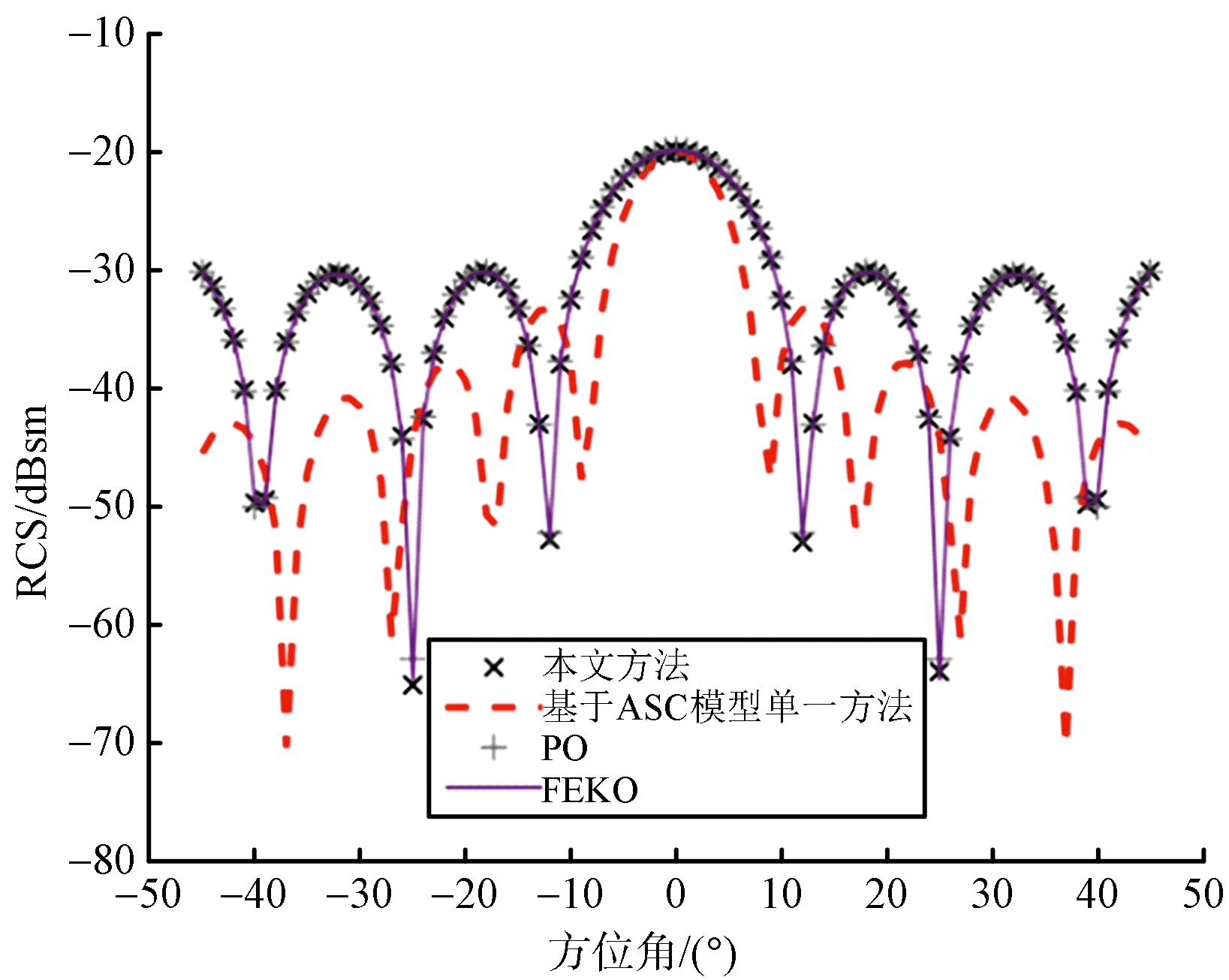
(a) RCS曲线
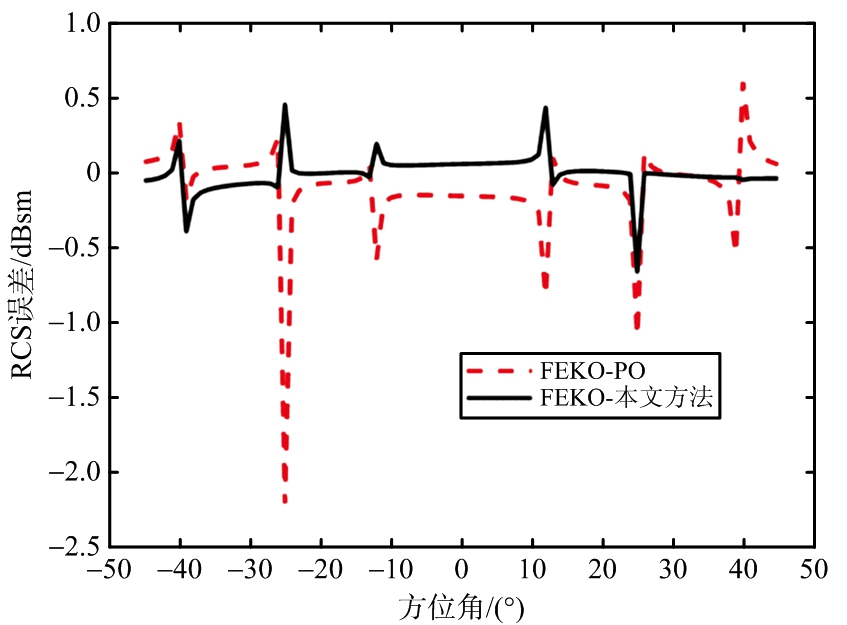
(b) RCS误差曲线
图9 二面角结果对比
表3 二面角目标仿真时间表
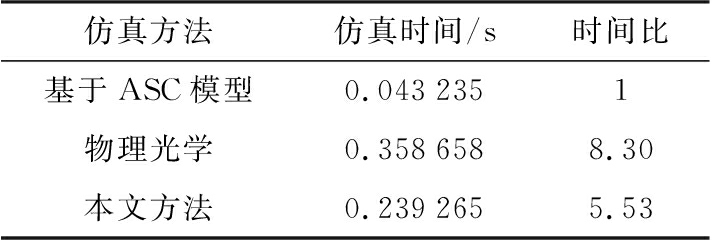
仿真方法仿真时间/s时间比基于ASC模型0.0432351物理光学0.3586588.30本文方法0.2392655.53
从上述三种模型RCS计算结果与仿真时间可以看出,本文所提方法能够准确地得到目标的RCS,并且仿真时间比物理光学方法更短,这是因为该方法只对一部分角度进行了面元遮挡的判别,减少了计算量。且对于结构复杂的二面角结构,基于ASC模型的RCS预估方法准确的方位角度小。而PO计算的回波RCS在全方位角度内与仿真结果差距都在允许误差范围内,只有在极个别回波能量特别小时存在较大差距。相比于基于ASC模型的RCS预估方法和PO方法,所提联合处理方法,能在两者达到一个期望值,时间上优于PO方法且性能上优于ASC模型方法。
5 结束语
本文介绍了基于属性散射中心模型以及物理光学两种预估目标RCS测量方法,联合FEKO软件仿真结果对比分析了两种预估方法的优缺点。最后提出了一种结合两种方法的基于联合模型处理的复杂目标RCS估计方法,这种方法能够快速准确地得到目标在任意观察角度、任意频段的RCS。后续相关工作可根据更深层的电磁学计算理论,建立准确的电磁模型,高效的正向确定目标在不同观察角度下强散射中心及属性参数,能够更加快速准确地估计全波段、全角度下目标的RCS。
[1] 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京:电子工业出版社, 2005.
[2] LIU Yang , HU Weidong, ZHANG Wenlong, et al. Radar Cross Section Near-Field to Far-Field Prediction for Isotropic-Point Scattering Target Based on Regression Estimation[J]. Sensors, 2020, 20(21):6023.
[3] 周亮, 匡华星, 王玲玲. 基于抛物方程法的主动雷达探测威力评估方法[J]. 雷达与对抗, 2020,40(1):12-16.
[4] 陈海青,汪刘应,刘顾,等. 基于GRECO与GO-PO算法的复杂目标RCS计算与分析[J]. 舰船电子工程, 2020, 40(10):168-172.
[5] 王永春. 隐身目标电磁散射特性研究[D]. 西安:西安电子科技大学, 2017.
[6] 冯卫永, 刘孟孟. 舰船RCS测量方法研究[J]. 科技风, 2017(15):18.
[7] LI Tingli , DU Lan. SAR Automatic Target Recognition Based on Attribute Scattering Center Model and Discriminative Dictionary Learning[J]. IEEE Sensors Journal, 2019, 19(12):4598-4611.
[8] 谢意远, 高悦欣, 邢孟道,等. 跨谱段SAR散射中心多维参数解耦和估计方法[J]. 电子与信息学报, 2020, 43(3):632-639.
[9] KNOTT E F, TULEY M T, SHAEFFER J F. Radar Cross Section [M]. Raleigh NC: SciTech Publishing Inc,2004:124-125.
[10] 徐灿, 李智. 基于改进Gordon方程的RCS快速算法[J]. 装备学院学报, 2016,27(5):85-89.
[11] 吴志威, 徐乐. 腔体目标的SBR算法研究[C]∥2019年全国微波毫米波会议论文集(上册),广州:中国电子学会微波分会,2019:317-319.

