0 引言
生物雷达可以实现非接触式人体体征监测,在不影响人体正常活动的情况下获取生命体征信息,可以应用于医疗监护、睡眠监测、驾驶员疲劳检测等场景[1-3]。常用雷达的发射信号形式有连续波(Continuous Wave,CW)雷达,超带宽(Ultra Wideband,UWB)雷达以及FMCW雷达。CW雷达不需要很大的发射功率,但是不具备测距能力,UWB雷达可以探测较远的目标,但发送信号需要很大的峰值功率[3]。FMCW雷达系统具有探测目标距离远、功率低、系统集成度高且成本低等优点[4]。因此,本文采用FMCW毫米波雷达进行人体生命体征信号的采集和处理。
国内外的研究中,利用生物雷达进行人体生命信号的提取主要对静止被测人员距离维处的生命信号进行带通滤波后作快速傅里叶变换(Fast Fourier Transformation,FFT)得到呼吸、心跳的频率[1],但该方法不能有效地处理局部非平稳信号。文献[5]利用两个FMCW雷达设置在被测人员前后位置同时检测,对前后雷达采集到的生命信号相加处理,消除人体随机移动的影响,对于特殊场景下该方法具有局限性。对于处理局部非平稳信号,经验模态分解[6]( Empirical Mode Decomposition,EMD) 是Huang 等人提出的一种自适应信号处理方法,将非平稳信号分解成若干个IMF分量,但EMD 分解后得到的IMF分量存在模态混叠以及端点效应问题。文献[7]提出一种改进经验模态分解方法提取生命信号,并对提取的呼吸、心跳频带信号进行分类、重构,进行两次经验模态分解,能够有效地滤除杂波得到正常状态下的呼吸和心跳频率,但算法整体分解时间较长。
针对上述问题,本文在提高雷达距离分辨率的基础上对被测人员的距离维检测,消除人体抖动及环境噪声的影响,引入IFCEEMD算法用于生命信号提取,保证算法处理的实时性并且提取的生命信号具有真实的物理意义,结合相关性分析和FFT进行处理,提取不同身体状态下的呼吸和心跳信号。
1 FMCW雷达生命信号探测原理
FMCW雷达系统具有平均发射功率低、结构简单等优点。发射信号通常为三角波或锯齿波,图1为本文选用锯齿波作为发射波形用于人体生命信号提取的发射信号与接收信号的频域图。图2为一帧数据中发射信号示意图。
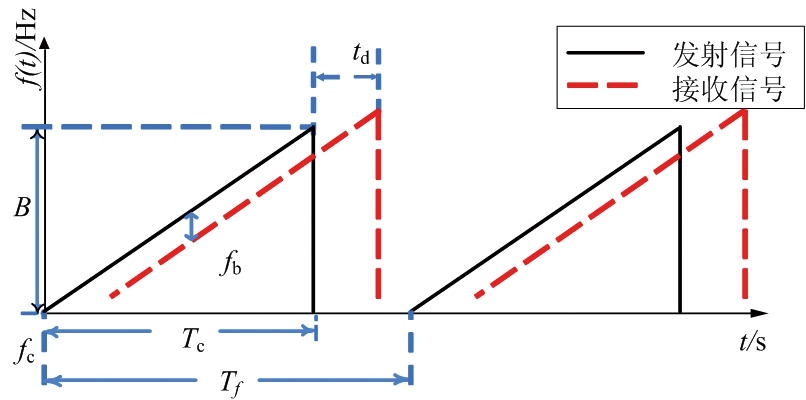
图1 FMCW发射信号与接收信号
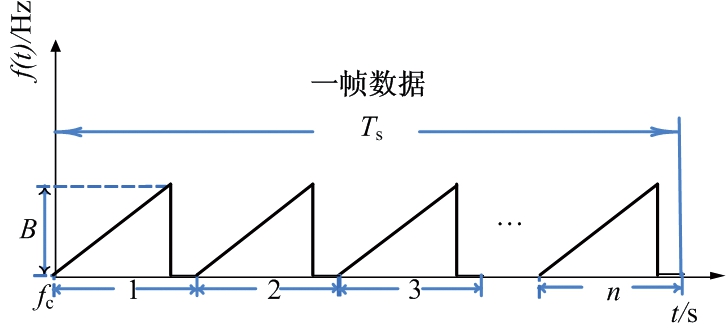
图2 一帧发射信号数据
FMCW雷达发射波形信号[8]可以表示为
(1)
式中,ATX为发射信号幅值,fc为雷达发射信号起始频率,B/Tc为锯齿波斜率,φ为发射信号初始相位。雷达发射信号照射到人体胸腔后反射的接收信号可以表示为
SRX(t)=ARXSTX(t-td)
(2)
td=2R1(τ)/c
(3)
式(2)中ARX为接收信号幅度,td为物体在径向距离处与距离相关的回波延时,式(3)中c为光速,R1(τ)包含着胸腔的位移信息,其中
R1(τ)=d0+R(τ)
(4)
式中,d0为雷达天线到目标胸腔运动中心的距离。通过雷达接收信号与本振信号混频得到中频信号:
ATXARXexp(j(2πfbt+φb))
(5)
(6)
(7)
最终得到的中频信号中具有关于人体胸腔位移相关的频率fb以及相位φb。
2 自适应生命信号提取算法
2.1 距离维FFT
由于雷达对扫频范围的物体都进行检测,通过对发射信号进行连续采样,运用距离维FFT确定人体的位置,提取人体目标位置处中频信号的相位信息进行处理,可以有效地滤除环境中其他距离处物体带来的干扰信息。
以图2中一帧持续时长Ts作为慢时间轴的时间单元,将雷达接收信号距离FFT结果按照慢时间轴排列得到如图3所示的距离维与慢时间轴关系图。
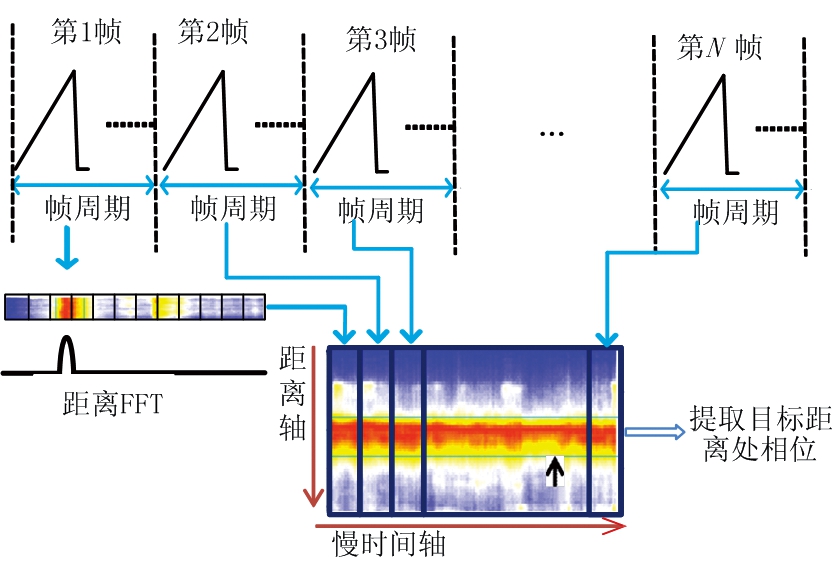
图3 距离维与慢时间轴关系图
选定固定的慢时间轴观测窗口,对距离FFT结果统计判断被测人员位置,提取目标距离位置处关于慢时间轴窗口的相位信息,作连续的相位差运算,消除相位漂移,得到含有呼吸和心跳的生命信号。
2.2 改进的FCEEMD算法
对距离维提取的生命信号r(t)进行EMD分解得到若干个IMF分量,得到的IMF分量由高频到低频排列,可以滤除相应的高频信号、杂波信号以及呼吸谐波。具体步骤如下:
1)求出r(t)信号全部极大值和极小值,用三次样条函数做出极大值和极小值对应的包络线。计算出上、下包络线的均值用m1(t)表示:
h1(t)=r(t)-m1(t)
(8)
式(8)得到第一个IMF分量的第一次分解结果,重复上述筛选操作k次后,如果任一时间点t上的均值为0,即满足第一个IMF分量的停止要求,得到首个IMF分量,记为IMF1(t)。
2)得到的IMF1(t)中包含了接收信号中的最高频信号部分,将IMF1(t)从接收信号r(t)中去除,得到r1(t)=r(t)-IMF1(t),将r1(t)作为原始信号重复上述步骤1)的操作得到第二个IMF分量IMF2(t)。通过如此反复操作n次后得到:
r2(t)=r1(t)-IMF2(t)
(9)
⋮
rn(t)=rn-1(t)-IMFn(t)
(10)
3)在rn(t)成为单调函数时结束循环,可以得到n个IMF分量,有
(11)
式中rn(t)为残余分量,代表信号的平均趋势。
由于EMD分解存在模态混叠以及端点效应问题,得到的IMF分量无法表达准确的物理意义。EMD的改进算法EEMD(Ensemble Empirical Mode Decomposition)[9]在EMD的基础上每次分解添加了随机噪声解决EMD分解后各IMF分量的模态混叠问题,但进行分解后还会有残余噪声,影响结果的精度且运算量大。
互补集合经验模态分解(Complete Ensemble Empirical Mode Decomposition,CEEMD)[10]在EMD基础上向r(t)分解时加入正负相反的两对高斯白噪声消除EEMD分解时加入的新的噪声:
(12)
式中S为r(t)信号,N为加入的白噪声。将加入一对正负白噪声后的信号M1,M2作为新的接收信号进行上述EMD分解,将每组分解的结果求均值得到最终的各IMF分量。本文在CEEMD算法基础上,将IMF分量分解停止准则设置为将筛选操作次数k固定为10次[11]保证算法的实时性。
r(t)在EMD分解时信号存在端点效应会造成提取的生命信号失真,为避免信号两端无法确定处于极大值还是极小值,导致包络线失真造成整个分解后的序列结果发散。本文在考虑算法复杂性与实时性上将线性延拓法[12]引入IFCEEMD分解中,解决分解后带来的端点效应,提高分解后信号的正交性。具体步骤如下:
选取离边界最近的两个极大值点A、B,将两个极大值点连接并延长至边界取交点D与原边界端点C比较,如交点D小于端点C值,则选择C作为边界处的极大值,否则选取D作为边界处的极大值点,如图4(a)所示。
对于极小值点,如果交点D大于端点C值,则C值作为极小值,否则选取交点D作为极小值,如图4(b)所示。
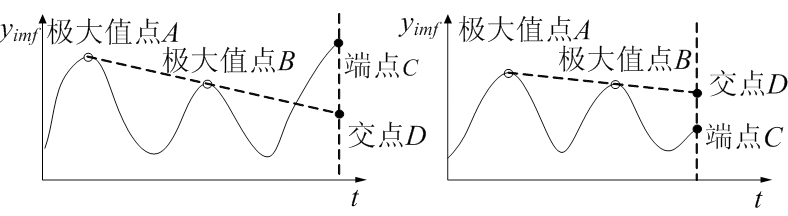
(a) 极大值点延拓
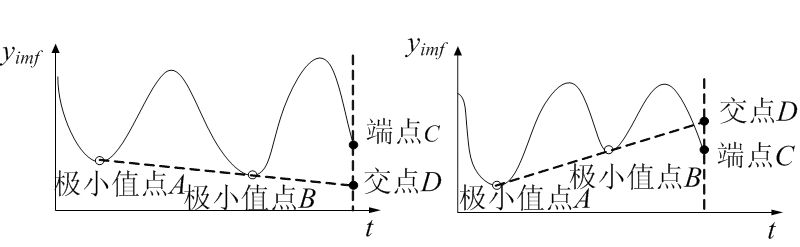
(b) 极小值点延拓
图4 线性延拓法
从IFCEEMD分解后得到的IMF分量由高频到低频排列,人体正常每分钟呼吸次数在6~50次,取呼吸频带为0.1~0.83 Hz,心跳频率在60~120次每分钟,取心跳频带为1~2 Hz。对于呼吸次数缓慢或急促时通过能量阈值法[13]会导致结果选取高于实际呼吸频率的IMF分量,考虑算法提取呼吸和心跳信号自适应性,本文将滤波后的呼吸信号与FFT后频率峰值在呼吸频带内的IMF分量利用相关性分析法提取出正确的生命信号结果。
3 实验结果与分析
3.1 实验环境参数
本文实验使用天线中心频率为60.5 GHz,最大频率带宽为6.8 GHz的FMCW雷达系统进行数据采集。数据采集环境为人体胸腔正面面对雷达系统0.5 m距离处,FMCW雷达采集参数如表1所示。
表1 FMCW雷达参数

参数参数值起始频率fc57.1 GHz带宽B6.8 GHz采样率2.5 MS/s锯齿波周期Tc55 μs帧周期Ts10 ms一帧内发射锯齿波个数n1
对每个锯齿波做128点的FFT运算得到频率峰值,慢时间轴采用20.48 s的窗口观测信息。
3.2 实验结果
3.2.1 目标静止测量结果
根据FMCW雷达参数可以得到距离分辨率为 2.36 cm,通过如图5的静止目标距离-慢时间轴关系图可知被测目标在距离单元22即51.92 cm处。
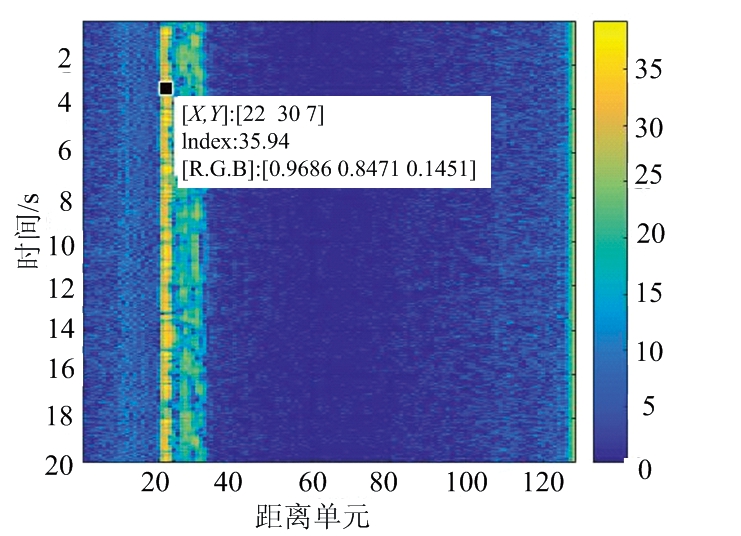
图5 静止目标距离维与慢时间轴关系
利用接触式脉搏测量仪与小米手环测得心跳频率为80次/分钟(1.33 Hz),呼吸频率为19次/分钟(0.32 Hz)。图6为雷达提取的静止目标原始生命信号以及呼吸、心跳频带内的时域和频谱图。
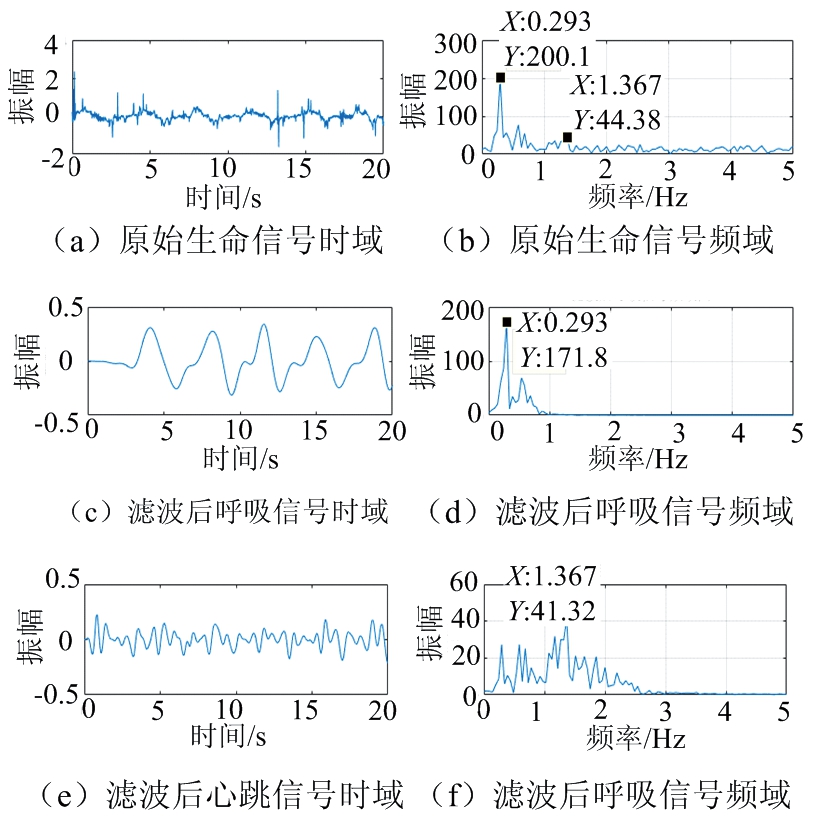
图6 静止目标生命信号时域与频谱图
为验证算法的实时性与准确性,用EMD、CEEMD、IFCEEMD分别分解雷达提取的生命信号得到图7(a)、(b)和图8的时域分解结果。
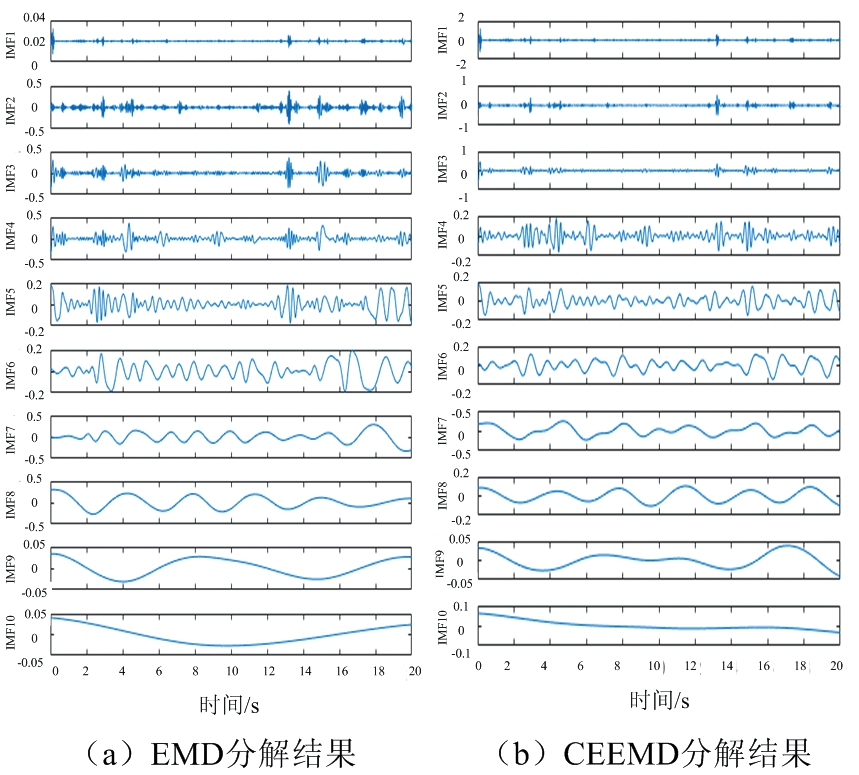
图7 静止目标EMD和CEEMD分解结果

图8 静止目标生命信号IFCEEMD结果
IFCEEMD分解后第5~10个分量对应的频域图结果如图9所示。
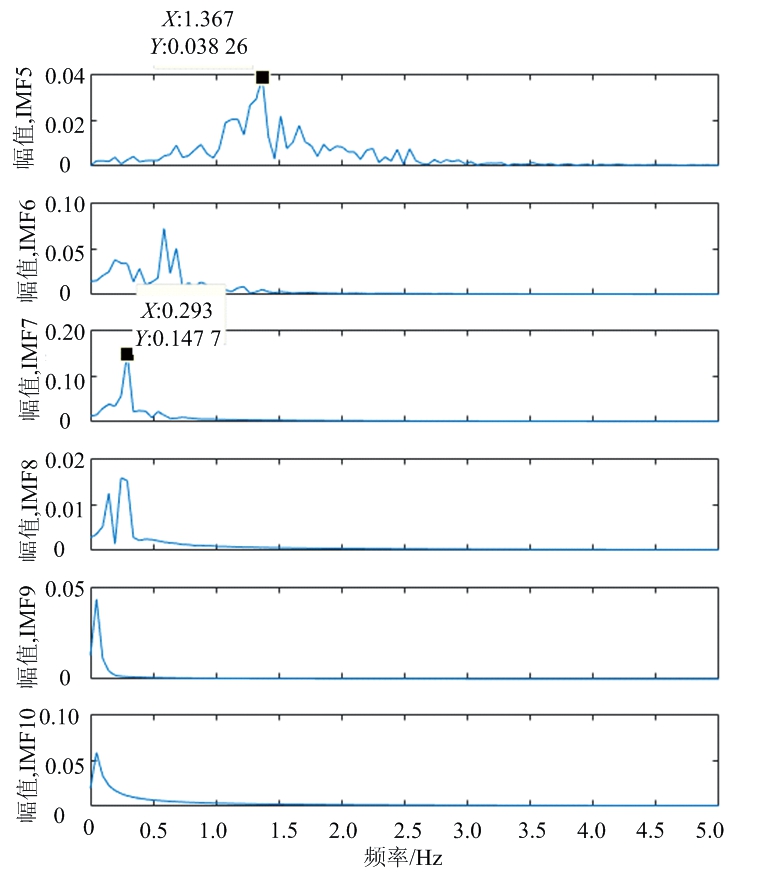
图9 IFCEEMD结果频谱
表2为EMD、CEEMD、IFCEEMD分解原始生命信号时的参数以及结果比较。
表2 EMD、CEEMD、IFCEEMD参数
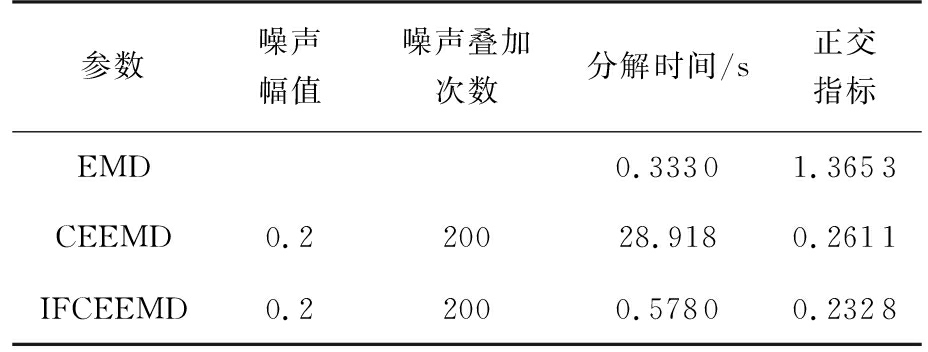
参数噪声幅值噪声叠加次数分解时间/s正交指标EMD0.33301.3653CEEMD0.220028.9180.2611IFCEEMD0.22000.57800.2328
由表2分析可知,IFCEEMD算法比原有的CEEMD算法大幅提高了处理速度,并且分解后的IMF分量正交性也优于CEEMD算法。
对IFCEEMD分解得到的IMF分量分别通过能量阈值法得到10个IMF分量分别在心跳和呼吸频带的能量占比以及本文提出的相关性系数法得到的呼吸信号系数结果如图10所示。
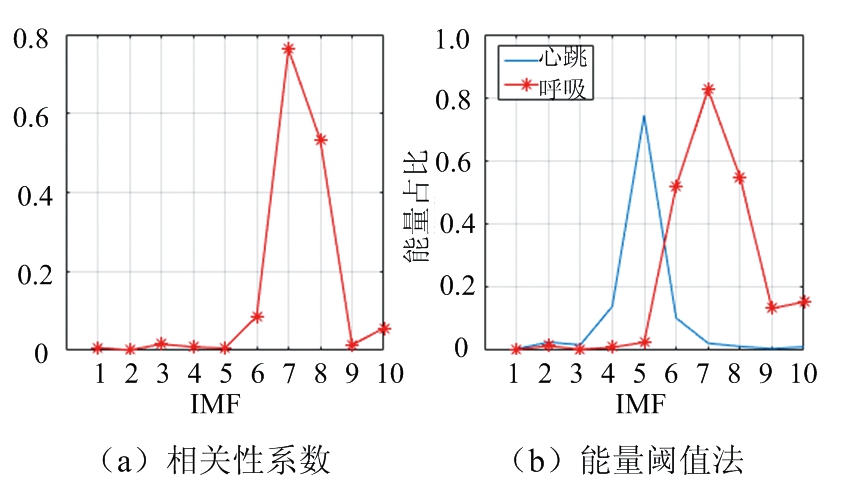
图10 正常呼吸时相关性系数与能量阈值法结果
由图9与图10分析可知,第5个IMF分量和第7个IMF分量分别对应为分解后的心跳和呼吸信号,由图9中IFCEEMD分解的频谱图可以得到心跳的频率为82次/分钟(1.367 Hz),呼吸的频率为18次/分钟(0.293 Hz),与实际预先测量结果一致。相关性系数结果以及能量阈值法对于正常状态下的呼吸信号都可以准确地从IMF分量中提取出来。
3.2.2 不同呼吸状态测量结果
运用能量阈值法选取呼吸信号时对于呼吸急促与缓慢状态下不能准确地提取呼吸信号。为适应被测目标在不同呼吸状态下,从IFCEEMD分解得到的IMF分量中选取与实际相符的呼吸信号,本文提出一种筛选方法将滤波后的呼吸心跳信号与FFT后频率峰值在呼吸频带内的IMF分量利用相关性分析提取出正确的生命信号结果。
对于呼吸急促状态下,预先测得呼吸频率为36次/分钟(0.6 Hz)。图11为雷达提取的生命信号以及呼吸、心跳频带内的时域图。
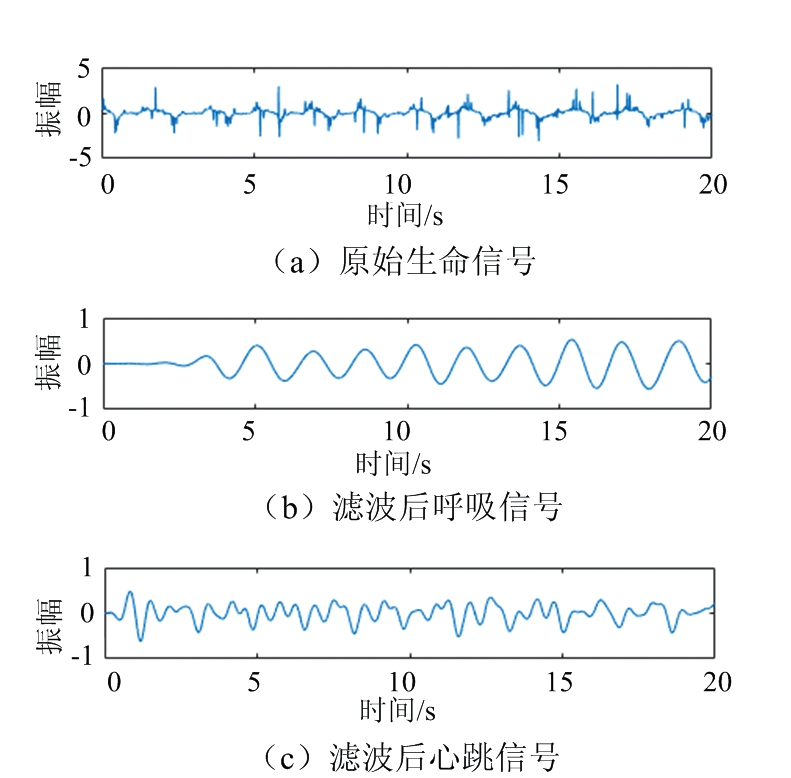
图11 呼吸急促时生命信号时域图
图12为IFCEEMD分解后各分量时域图,分解后第5~10个分量对应的频域图结果如图13所示。
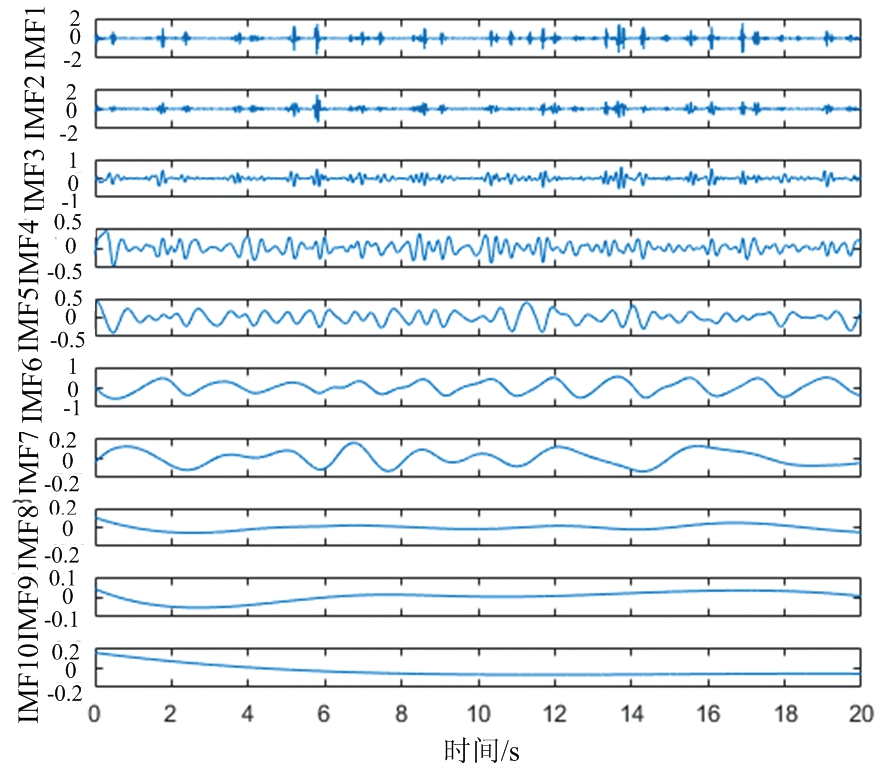
图12 呼吸急促时生命信号IFCEEMD结果
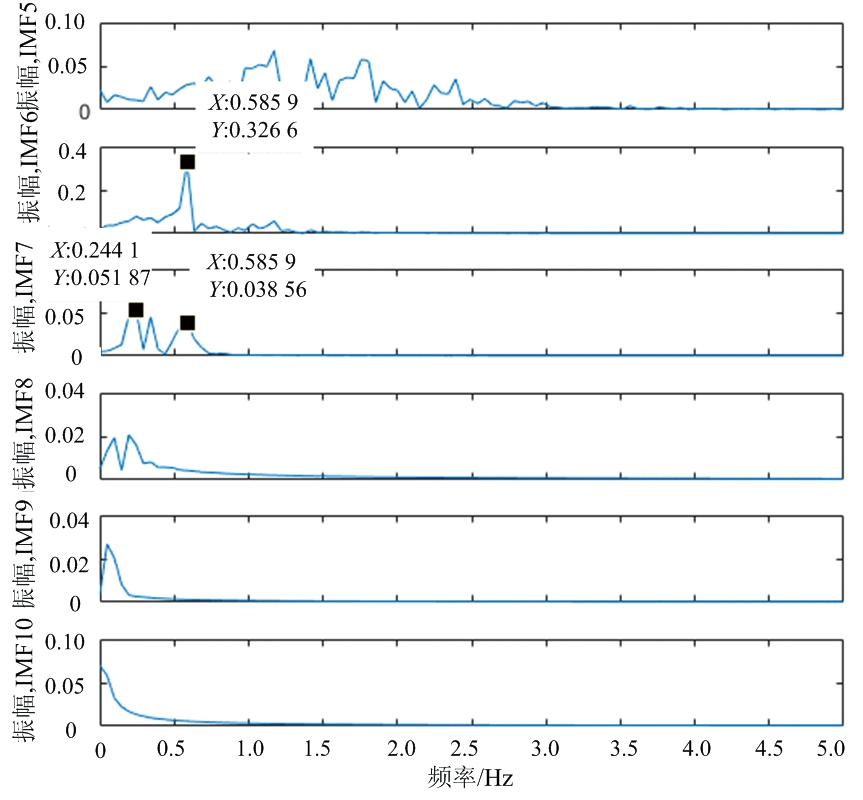
图13 呼吸急促时生命信号IFCEEMD结果频谱
图14为对所有IMF分量通过能量阈值法得到对应呼吸和心跳频带的能量占比以及呼吸信号通过相关性分析法计算后的结果。
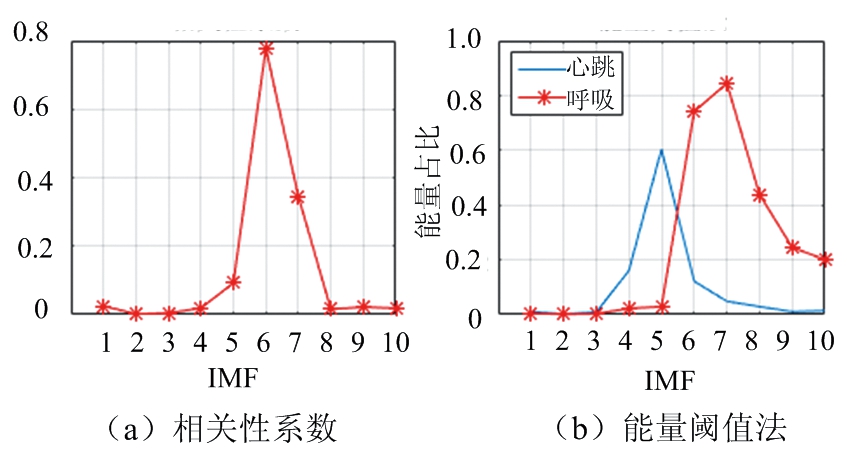
图14 呼吸急促时相关性系数与能量阈值法结果
由图13结果分析可知,IMF6与IMF7的频谱峰值都处于呼吸频带内。由图14可知,对于呼吸信号存在两个能量占比大于0.7的分量,而IMF7还存在呼吸频带内的其他低频信号能量占比更高,与实际结果相比较IMF6才是实际的呼吸信号,利用相关性分析后的结果能够正确地选取呼吸信号。
对于呼吸缓慢状态下,预先测得呼吸频率为9次/分钟(0.15 Hz)。图15为相关性系数法与能量阈值法对各IMF分量计算后的结果。图16为提取的生命信号经过IFCEEMD分解后第5~10个分量的频谱图。
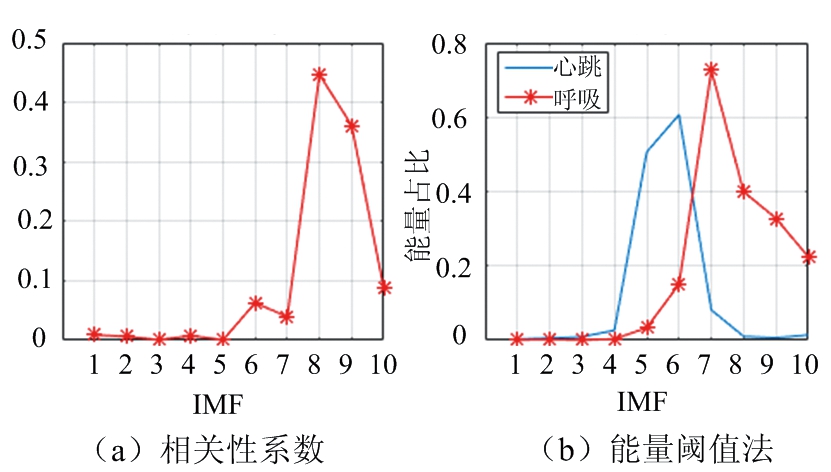
图15 呼吸缓慢时相关性系数与能量阈值法结果
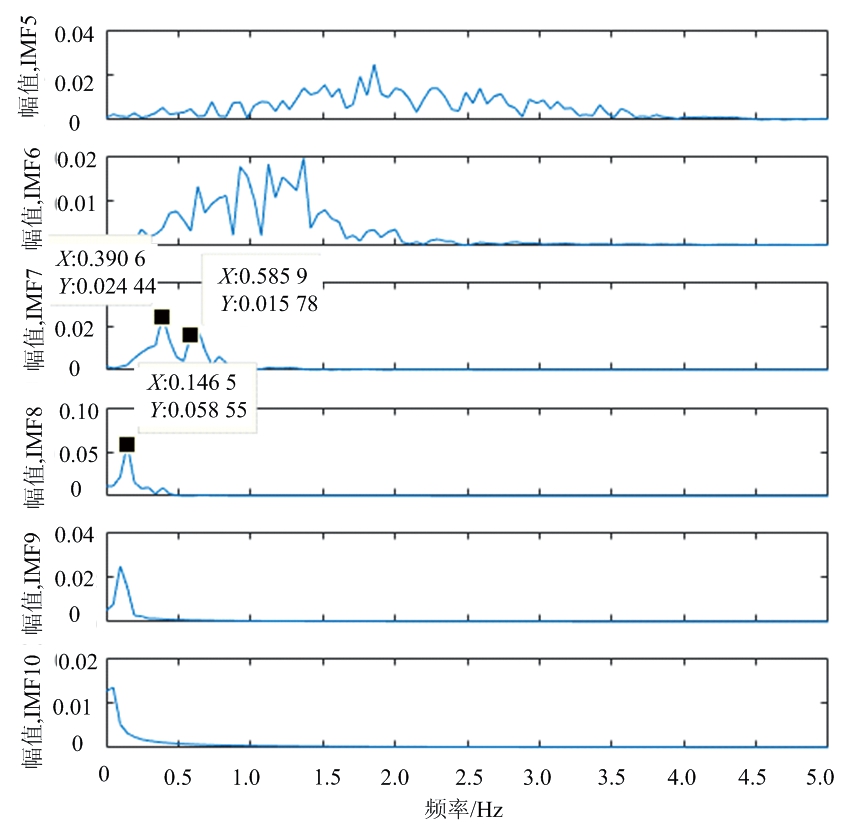
图16 呼吸缓慢时生命信号IFCEEMD结果频谱
对于呼吸缓慢状态下,由于IMF7中含有呼吸频带内的频率能量更高,能量阈值法计算后的结果为IMF7的呼吸频带能量占比更高,而实际的呼吸信号为IMF8,本文提出的方法对呼吸缓慢情况下同样也能准确地提取呼吸信号。
3.2.3 目标身体抖动测量结果
目标身体抖动会造成目标在距离维的检测结果波动,但人体抖动时胸腔部位还是基本保持在能量最集中的距离单元内。为适应被测目标的身体状态,提高FMCW雷达系统的发射带宽能够实现更精确的距离分辨率,捕获到实际人体胸腔距离处的原始生命信号。将FMCW雷达系统分别在4 GHz以及6.8 GHz下对于人体处于抖动状态下的生命信号以及提取的结果进行分析。
将表1中的FMCW雷达参数中带宽B调整为4 GHz。在4 GHz带宽下距离分辨率为3.92 cm,图17为发射信号带宽为4 GHz时距离-慢时间轴关系图, 0~20 s内被测人员保持静止,20~40 s内目标身体伴随着随机抖动,由于距离分辨率相比较6.8 GHz带宽下降,被测目标在静止状态下距离集中在14个距离单元即54.88 cm处。随机抖动环境下的距离信息集中在14~15个距离单元之间,导致提取的连续相位信息丢失。预先测得心跳频率为80次/分钟(1.33 Hz),呼吸频率为24次/分钟(0.4 Hz)。
提取图17中20~40 s内目标随机抖动状态下主要距离维的生命信号,提取的生命信号以及呼吸心跳频带内的时域和频谱图如图18所示。IFCEEMD分解生命信号后得到的IMF分量如图19所示。根据图18中FFT后的频谱与图19中IFCEEMD后的频谱图,结果均表明在4 GHz带宽下由于身体抖动对呼吸心跳结果与实际存在较大误差。
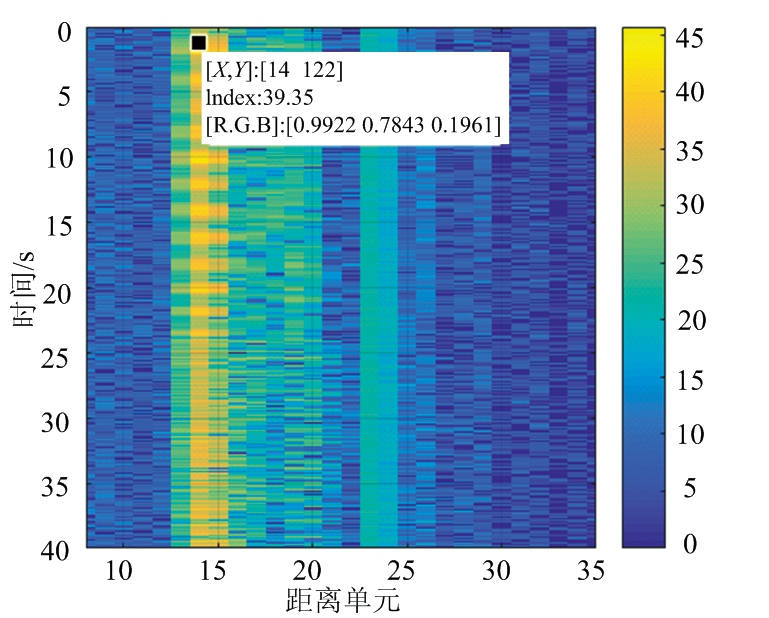
图17 4 GHz带宽距离-慢时间轴关系图
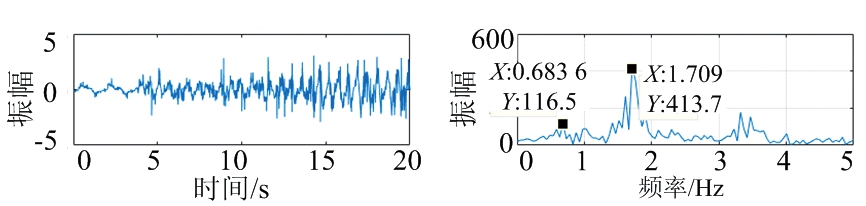
(a) 原始生命信号时域 (b) 原始生命信号频域
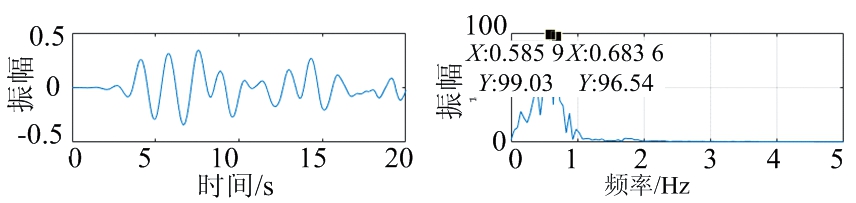
(c) 滤波后呼吸信号时域 (d) 滤波后呼吸信号频域
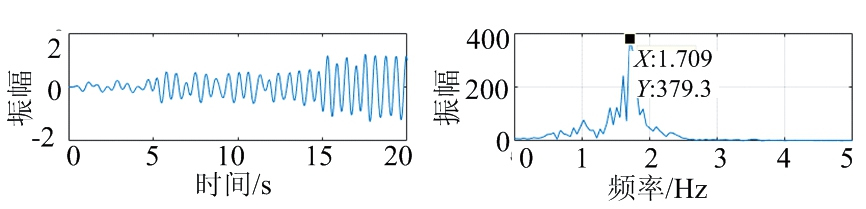
(e) 滤波后心跳信号时域 (f) 滤波后呼吸信号频域
图18 4 GHz带宽下身体随机抖动生命信号时域与频谱图
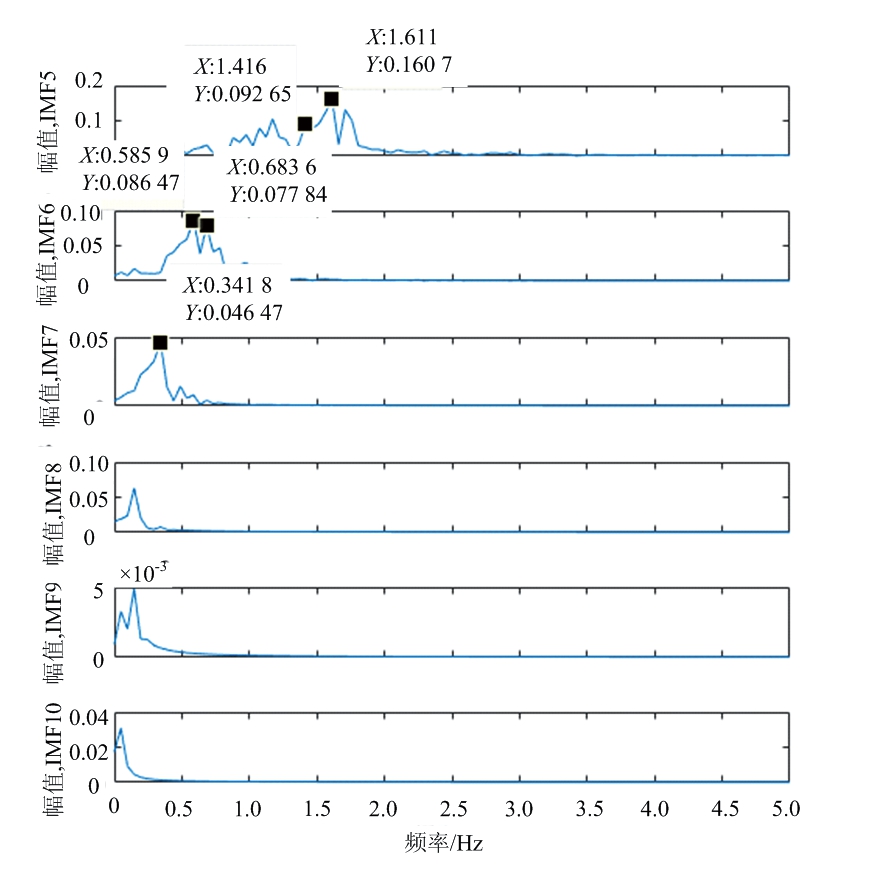
图19 4 GHz带宽下生命信号IFCEEMD结果频谱
将FMCW雷达系统发射信号带宽提高到6.8 GHz带宽后,预先测得身体随机抖动下人体心跳频率为80次/分钟(1.33 Hz),呼吸频率为33次/分钟(0.55 Hz)。提取被测目标20 s内呼吸时伴随着身体抖动的生命信号,对应生命信号时域与频域图如图20所示。IFCEEMD分解后第5~10个分量分频谱图如图21所示,通过图22中相关系数与能量阈值法的结果分析可知,相关性分析法能够准确提取出IMF6为呼吸信号,得到呼吸频率为0.585 9 Hz(35次/分钟)与实际呼吸频率相差2次/分钟,得到心跳信号为1.416 Hz(85次/分钟)与实际人体呼吸频率80次/分钟的结果相差在误差范围内。
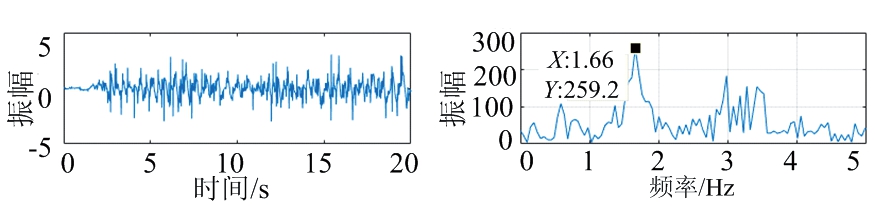
(a) 原始生命信号时域 (b) 原始生命信号频域
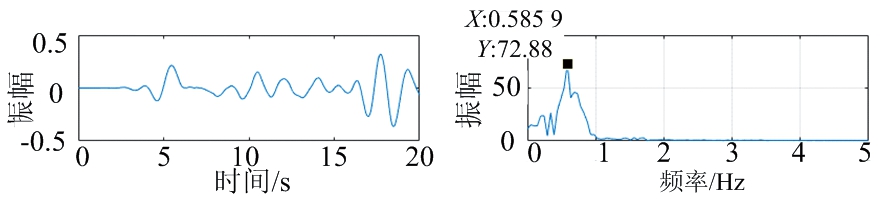
(c) 滤波后呼吸信号时域 (d) 滤波后呼吸信号频域
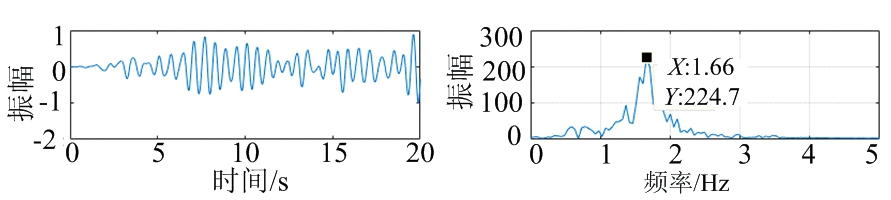
(e) 滤波后心跳信号时域 (f) 滤波后呼吸信号频域
图20 6.8 GHz带宽身体随机抖动时生命信号时域与频谱图
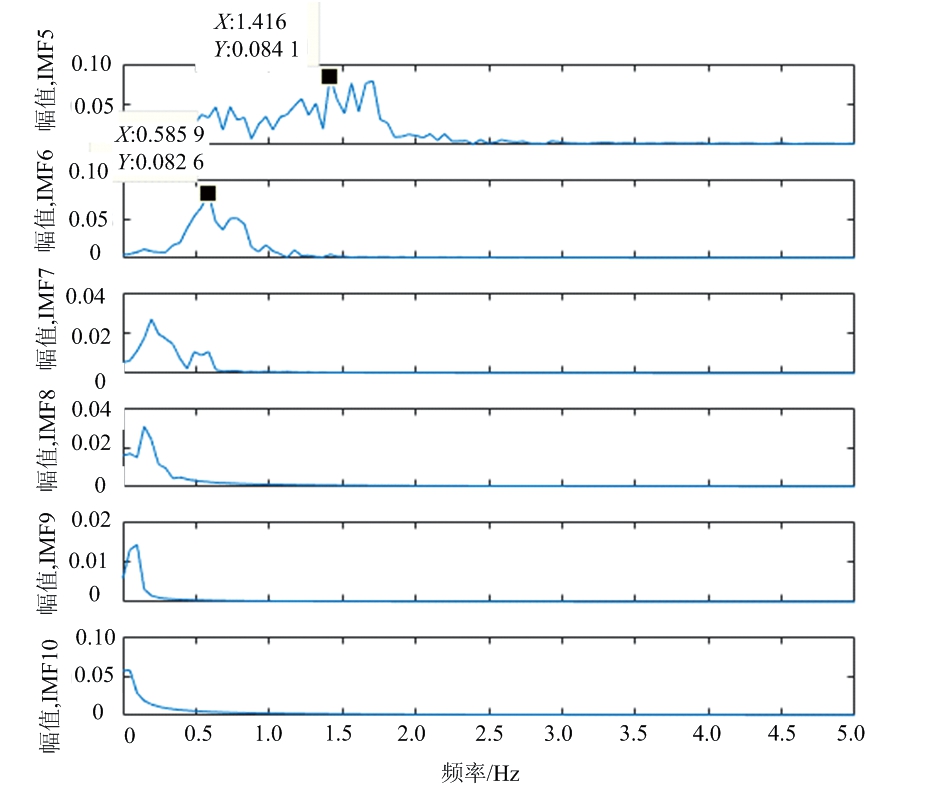
图21 6.8 GHz带宽下生命信号IFCEEMD结果频谱
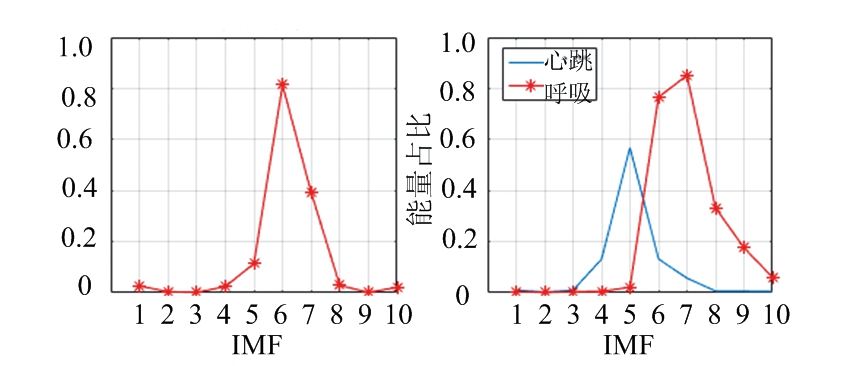
(a) 相关性系数 (b) 能量阈值法
图22 6.8 GHz带宽身体抖动时相关性系数与能量阈值法结果
通过6.8 GHz与4 GHz带宽下测量的比较,提高距离分辨率后能够有效消除人体身体抖动对呼吸和心跳信号提取的影响,并且提高算法对于复杂环境下的适应性。
4 结束语
本文利用高带宽的FMCW雷达系统提高雷达距离分辨率,对探测距离内的对象提取生命信号。实验结果分析表明:IFCEEMD算法能够在满足计算实时性的基础上具有较好的分解效果,并且提高距离分辨率后能够有效消除身体抖动以及环境噪声对生命信号的干扰,最后利用相关性筛选方法自适应地提取各种呼吸状态下的生命信号提取,能够适应更多复杂场景下的非接触式人体生命体征监测。
[1] MUNOZ-FERRERAS J M, WANG Jing, PENG Zhengyu, et al. FMCW-Radar-Based Vital-Sign Monitoring of Multiple Patients[C]∥ IEEE MTT-S International Microwave Biomedical Conference, Nanjing, China:IEEE,2019:1-3.
[2] ALIZADEH M , SHAKER G , DE ALMEIDA J C M, et al. Remote Monitoring of Human Vital Signs Using mm-Wave FMCW Radar[J]. IEEE Access, 2019,7:54958-54968.
[3] LIANG X , ZHANG H , YE S , et al. Improved Denoising Method for Through-Wall Vital Sign Detection Using UWB Impulse Radar[J]. Digital Signal Processing, 2018, 74:72-93.
[4] AHMAD A , ROH J C , WANG D , et al. Vital Signs Monitoring of Multiple People Using a FMCW Millimeter-Wave Sensor[C]∥2018 IEEE Radar Conference,Oklahoma City,OK,USA:IEEE, 2018:1450-1455.
[5] MUNOZ-FERRERAS J M, PENG Z Y, GOMEZ-GARCIA R, et al. Random Body Movement Mitigation for FMCW-Radar-Based Vital-Sign Monitoring[C]∥ IEEE Topical Conference on Biomedical Wireless Technologies, Networks & Sensing Systems, Austin, TX, USA:IEEE, 2016:22-24.
[6] HUANG N E , SHEN Z , LONG S R , et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454:903-995.
[7] 刘震宇, 陈惠明, 陆蔚, 等. 基于改进经验模态分解的雷达生命信号检测[J]. 仪器仪表学报, 2018, 39(12):171-178.
[8] WANG Y , WANG W , ZHOU M , et al. Remote Monitoring of Human Vital Signs Based on 77-GHz mm-Wave FMCW Radar[J]. Sensors, 2020, 20(10):2999.
[9] WU Zhaohua, HUANG N E. Ensemble Empirical Mode Decomposition: a Noise Assisted Data Analysis Method [J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41.
[10] YEH J R, SHIEH J S, HUANG N E. Complementary Ensemble Empirical Mode Decomposition: a Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2):135-156.
[11] WANG Y H ,YEH C H , YOUNG H W V , et al. On the Computational Complexity of the Empirical Mode Decomposition Algorithm[J]. Physica A Statistical Mechanics & Its Applications, 2014(4):159-167.
[12] 杨贤昭. 基于经验模态分解的故障诊断方法研究[D].武汉:武汉科技大学, 2012.
[13] 冯久超,潘水洋.基于经验模态分解的生命信号提取算法[J].华南理工大学学报(自然科学版), 2010, 38(10):1-6.
