0 引言
随着通信、互联网技术以及各种智能化系统的飞速发展，车联网成为智能交通系统的重要组成部分，自动驾驶也成为全球研究的热点，更在“中国制造2025”中上升为国家战略之一[1]。而通信和雷达探测作为无线电技术最典型的两个应用场景，从硬件结构到软件算法处理的差距都在逐渐减小，使得频谱资源日益紧缺，雷达通信一体化因为其在硬件资源利用率、共享频谱等方面的优势成为缓解频谱资源紧缺的解决方案。
早期的一体化系统理念主要停留在设备层面上的集成，不同系统仍占据不同的频段资源。基于维度复用的一体化比如时分、频分、码分方式，并没有提高资源的利用率[2-4]。为了通信与雷达能更好地同时工作且减小彼此间的干扰，一体化的研究重心逐渐放在波形共用上，共用波形一体化的设计思路是采用同一种波形能够同时完成雷达和通信功能，所以并不存在资源竞争的问题。现有的一体化研究主要基于两个方向：
一是，在通信OFDM的基础上加上雷达功能。如文献[5]将多个OFDM符号作为一个一体化信号，通过调节多个符号的相位来优化OFDM的模糊函数，但通信信息只能通过对OFDM符号整体加载相位调制。文献[6]采用直接序列扩频调制优化整体信号的模糊函数，这类方法虽然能够获得较好的模糊函数性能，但并没有考虑峰均比的问题，且对数字接收端的要求太高，不适合实际运用。
二是，在现有的雷达波型上加载通信信息。常见的LFM、FMCW等波形因具有恒包络特性，所以不必担心峰均比的问题。文献[7-8]介绍的PCFM波形采用CPM调制通信以保证不影响频谱效率以及恒包络特性，但这种调制方式会对距离旁瓣产生调制作用，导致主旁瓣比下降。且由于距离旁瓣调制与调制信息有关，所以调制波形具有随机性，进而会对多普勒维的脉冲主旁瓣造成影响[9]。文献[10]提出在一个LFM信号内部选择一小段时间进行MSK+LFM调制，这样的设计对主旁瓣比影响较小，但调制效率很低。文献[11-12]提出了频带重叠的OFDM-FMCW，采用FRFT-OFDM信号结构通过不同初始频率子LFM信号加载通信信息，并利用最大似然求解目标参数或通过调节幅度，虽有较高的调制效率，但是也存在很严重的峰均比问题。文献[13]提出了多斜率键控调制的FMCW一体化系统，该系统采用差拍处理后的频率值来估计目标信息，通信信息加载在不同的斜率上，接收端通过不同斜率的相关处理来解调数据。该类方法的问题在于斜率的改变会造成信号带宽改变，损失系统频带利用率。文献[14]采用不同初始频率的跳频Chirp(FHC)MIMO雷达波形，通过在每个跳频码上嵌入PSK通信实现一体化，这种方案将产生距离旁瓣(RSM)的问题，且采用匹配滤波的方式处理大时带宽积信号，接收端需要的滤波器较长，资源损耗大。
为了避免FMCW一体化波形存在的RSM问题，本文设计了一种新颖的MFSK-FMCW一体化波形，以雷达常用的FMCW波作为通信信息的载波，通过对每一个一体化符号的单独处理，避免了RSM的出现。同时其通信接收机可等效为LoRa接收机，具有恒定包络特性以及低功耗和抗衰落等优点。并且针对所设计的一体化波形，因通信数据调制而导致的频率相干积累困难的问题，本文给出了多普勒尺度变换的方法，通过改变信号相干积累的核函数，使得不同符号间的多普勒频率能在同一频点处完成积累。
1 MFSK-FMCW一体化信号设计
1.1 信号模型
图1为本文设想的应用场景图，车A、B、C上都载有一体化信号收发机，车B与车C主要使用其通信接收功能，行驶过程中，车A发送经过调制的一体化信号，车B与车C都能接收并解调得到其中包含的通信信息，同时车A能接收来自车B的回波信号，经处理后可得出车B的距离及速度信息。
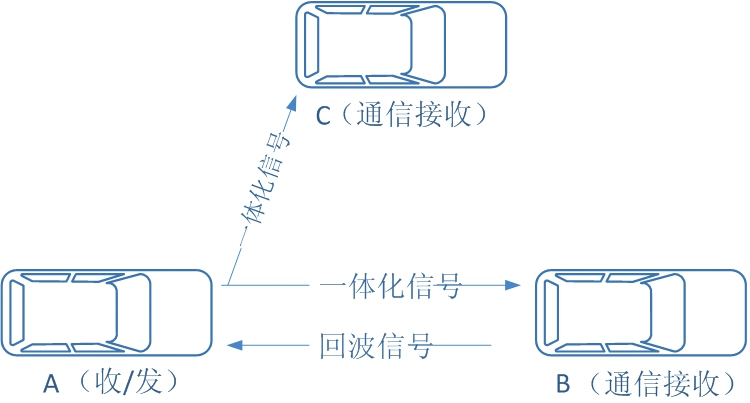
图1 应用场景图
以FMCW信号作为MFSK信号的载波，每一个斜率上调制一个MFSK符号，如图2所示，B为带宽，T为符号时长，f0为射频载波频率，Δf为频移间隔，m为随机调制的K进制通信符号，m∈[0,1,…,K-1]。如图3为一体化发射信号的调制流程图。
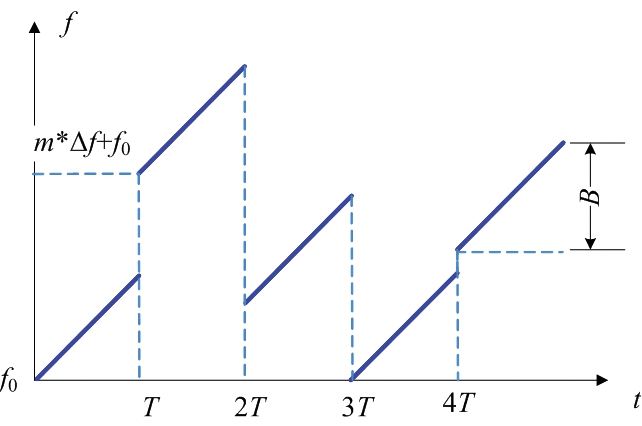
图2 MFSK-FMCW时频结构图
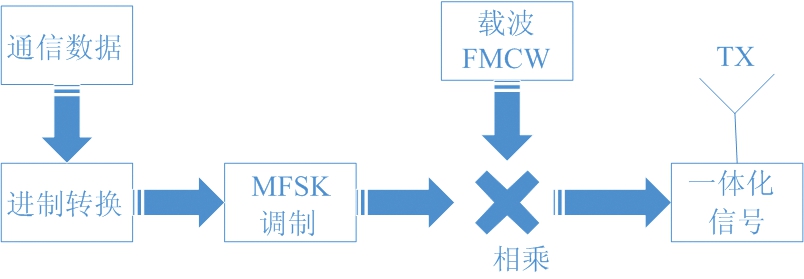
图3 发射信号调制流程图
作为载波的FMCW信号可以表示为
SLFM=
jπμ(t-iT)2]·rect(t-iT)
(1)
式中，
μ为调频斜率，N为符号数。调制后的发送信号可由下式表示：
Tx=
jπμ(t-iT)2]·rect(t-iT)
(2)
假设信号经过目标反射后的回波时延为τ，则其幅度归一化的回波信号可表示为
Rx=
(t-iT-τ)+jπμ(t-iT-τ)2]·
rect(t-iT-τ)+n(t)
(3)
式中，mi为第i个符号上随机调制的通信信息，n(t)为杂波干扰。
1.2 信号处理
图4为LoRa信号处理流程图，本文通信接收端的处理方式与LoRa相同，采用FMCW作为通信载波不会影响通信性能[15]。图5为常规FMCW雷达回波信号处理流程图。
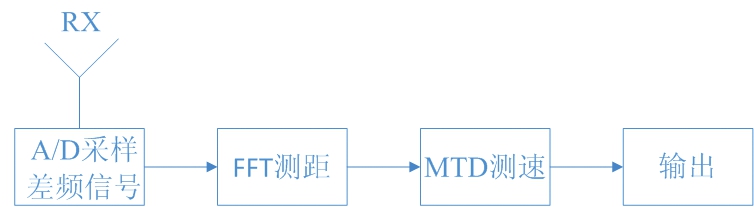
图5 FMCW信号处理流程图
图4 LoRa信号处理流程图
将发送信号与接收的一体化回波信号进行差拍处理(也称dechirp处理)，再经过FFT处理后可得目标的距离信息，下面给出第i个符号差拍处理的结果：
sdechirp(t)=Tx·Rx*=exp[j2π(Δf·mi+f0)·
τ+jπμ[2(t-iT)τ-τ2]]·
(4)
记t′为信号的快时间，则
可表示为从发送第一个符号开始至第i个符号到达目标所用的时间。因此回波时延τ可以表示为
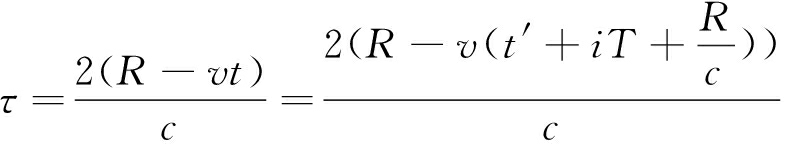
(5)
将式(5)代入式(4)并化简可得
sdechirp(t′)=
f0))·t′]·exp[j2π(Δf·mi+f0)·
(6)
φ(t′)中的值与载波无关且2R/c≪1，2v/c≪1，故可忽略不计。为了便于FFT处理，对信号进行离散化，时间t对应的采样点数为nTs，0≤n≤N-1，N为信号的采样点数，M为一个符号的采样点数，Ts为采样间隔。则dechirp后的回波信号的离散形式为
sdechirp(n′)=
iMTs)]·exp[j2π(Δf·mi+f0)·
(7)
经过dechirp处理后的回波信号是一个单频信号，可以通过对其进行FFT处理得到目标的距离信息，与脉冲压缩相比，dechirp与FFT组合的方式对信号采样的要求更低，即对系统模数转换器的要求更低，更方便处理信号。经FFT处理后的信号表示如下：
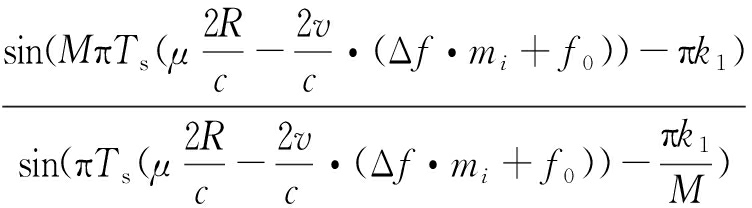
(8)
由公式(8)可知，Sdechirp(k1)的包络为一个sinc函数，当
时，可取得包络的峰值点，此时的k1所对应的距离即为所求目标的距离信息。对每一个符号作FFT处理后采样所得的峰值难以保持在同一频点，这是因为k1的值不是定值，受载波增量影响会出现频谱扩展现象。
2 多普勒尺度变换及相位补偿的影响
2.1 问题说明
目标的速度信息以多普勒的形式加载在每一个回波符号上，可以通过对信号作MTD获得目标的速度。由公式(8)所示，相位项
中不包含速度信息，可视作含有目标距离信息的干扰项，又于公式(8)中已经测得目标的距离信息，故可对每个符号的峰值点相位作对应的相位补偿处理，消除干扰项，此时的相位项可表示为
P(i)=
iMTs)]
(9)
对相位P(i)作MTD可得下式：
SMTD=
f0)+k2)]
(10)
式中的采样点k2对应的速度即为所求目标速度。
此时所求得的速度受两个方面的影响：1)相位补偿问题，已测得的目标距离信息受距离分辨率的限制，不一定为目标的真实距离，这将使得式(9)中的相位补偿不能完全消除干扰项，会有残留；2)多普勒相干积累问题，调制的通信信息会使一体化信号上各符号间的相位发生跳变，做多普勒相干积累时的频率难以保持在同一频点处，导致测速受到干扰。
针对这两个问题，本文提出了多普勒尺度变换来解决多普勒相干积累问题，并对相位补偿后的影响进行分析。图6为本文所用方法的一体化信号回波处理流程图。
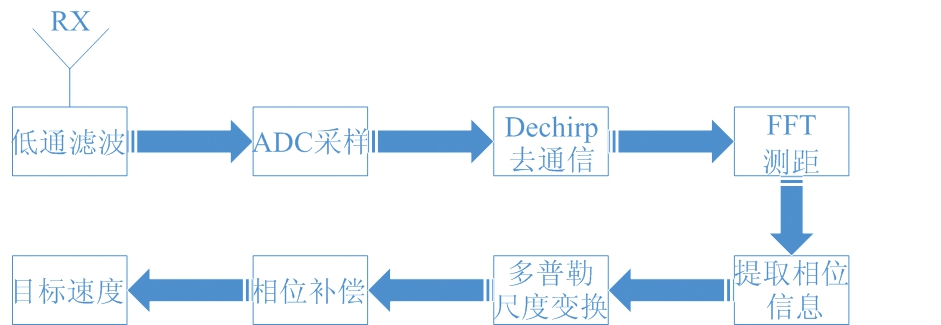
图6 一体化信号回波处理流程图
2.2 多普勒尺度变换处理
因通信信号的随机调制导致MTD的结果不能在同一频点积累的问题，具体表现在公式(10)中k2的值将随着载波增量项Δf·mi改变，这将导致有不同程度的旁瓣产生，削弱甚至淹没主瓣，最大值幅度值对应的采样点位置可能并非为目标速度所对应的位置，影响测速。
基于尺度变换思想，本文提出一种消除符号间多普勒扩展的方法，通过在傅里叶变换核函数中引入尺度变换因子达到不同符号间多普勒对齐的效果，将核函数
变换为
此时的式(10)重写为
SMTD=
(11)
修正的傅里叶变换核与载波增量相关，由式(11)可知，第i个符号的峰值位于
处，这意味着经过尺度变换处理后的结果与载波增量Δf·mi无关。也就是说，不同符号上的目标多普勒可以在固定频点k2的位置获得积累。
2.3 相位补偿与误差分析
式(9)中所述消除目标相位中带有距离信息的干扰项时，所用的目标距离信息为已测得的目标距离，此距离受到系统的距离分辨率ΔR的限制，并不一定为目标的实际位置，若要保证测距的准确性，应使测得的目标距离与真实距离R之间的差距在半个距离分辨率内：
(12)
从公式
可以看出，k1为速度距离耦合项，包括目标实际距离R以及由载波增量和速度共同影响的距离走动，n为真实距离对应的采样位置。将
与k1的表达式代入式(12)并化简可得
(13)
其中
由于距离走动项与载波增量为正相关，故mi取为mmax，继续代入并化简可得速度v的取值范围：
(14)
系统受距离分辨率的限制，对所测量的目标速度有此上限值。
假设在一次雷达测速(一个CPI持续时间内)过程中，目标的位移很小，则可认为在此次测量中目标的距离走动eR为固定值。公式(9)的相位补偿处理可重新表示为
P(i)=
(15)
对补偿后的相位作MTD，可得
SMTD=
(16)
式中，
为补偿残留项，因为mi为随机调制的通信信息，故mi服从离散均匀分布，则补偿残留项可视为信号的乘性噪声，取值离散且等概率。当eR取值
时噪声对信号的影响最大，此时噪声均值为
噪声方差为
3 仿真实验
本文按照表1所给的参数进行了仿真实验，添加信噪比为-10 dB的高斯白噪声，预先在场景中设置了一个径向速度为7 m/s，距离为15 m的运动目标。仿真中采用的频移间隔为最小频移间隔1/T的整数倍。
表1 一体化系统仿真参数表
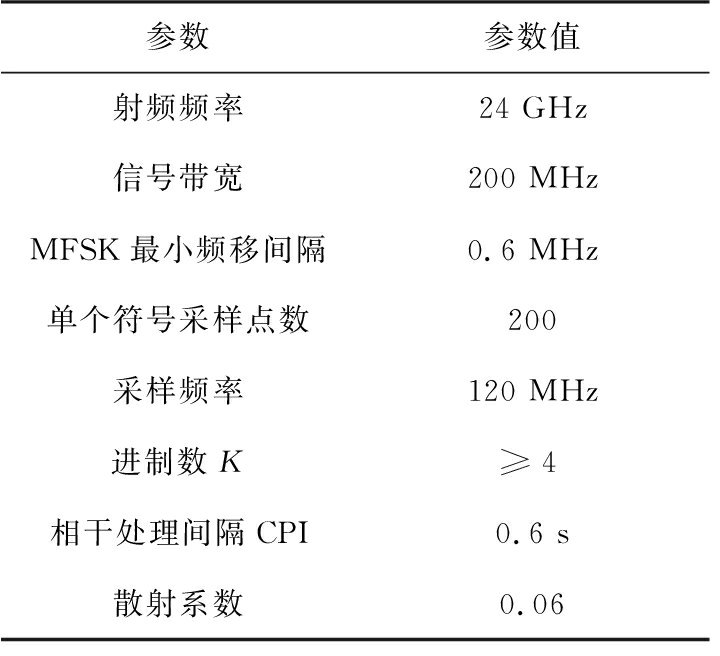
参数参数值射频频率24 GHz信号带宽200 MHzMFSK最小频移间隔0.6 MHz单个符号采样点数200采样频率120 MHz进制数K≥4相干处理间隔CPI0.6 s散射系数0.06
如图7(a)所示，为对已去除通信信息的回波信号作FFT处理的等高线图，未经过尺度变换处理，可以看到受载波增量影响，峰值频率不在一条直线上，存在频率扩展现象，若对此时的信号作MTD处理将会有幅值较高的旁瓣出现，图7(b)为尺度变换处理之后的等高线图，此时的频率保持在一条直线上，即目标多普勒能在同一频点积累。
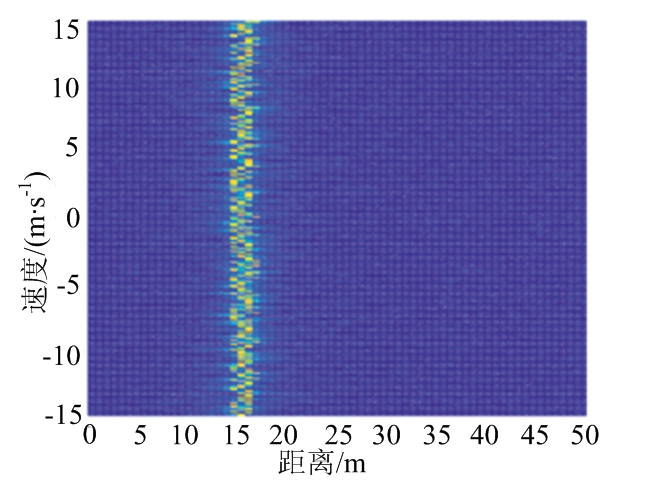
(a) 未经处理的多普勒扩展图
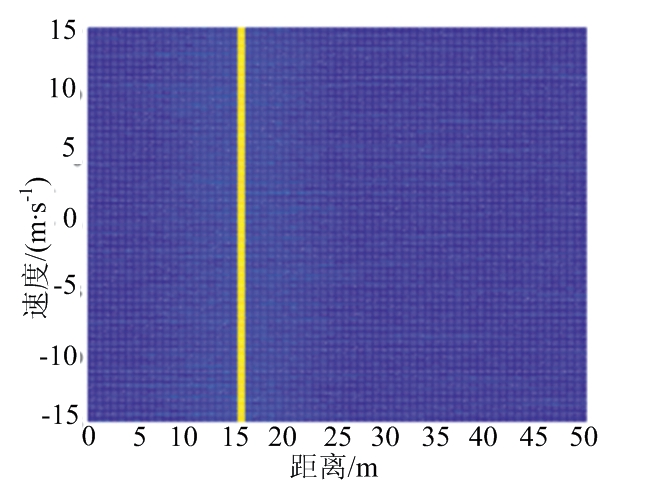
(b) 尺度变换后的多普勒扩展图
图7 尺度变换前后对比图
图8(a)、(b)分别给出了经4FSK调制的信号，在1倍最小频移间隔的条件下，采用本文方法前后所得到的距离多普勒图，图8(b)中的能量更为集中。图8(c)、(d)分别给出了8倍最小频移间隔条件下的距离多普勒图。可以看到随着频移间隔的增大，乘性噪声对目标测速的影响也在变大，采用传统MTD检测方法，MTD后的能量较为分散，不能集中在同一个频点处，故如图8(c)所示会有很多旁瓣。且在频移间隔为8倍最小频移间隔的情况下，传统方法已经不能正常测量目标速度，而采用本文提出的多普勒尺度变换与相位补偿处理过后，与未经处理相比，对旁瓣的抑制效果显著，MTD后的能量更加集中，目标速度更为明确。图8(b)与图8(d)同样也会有较小干扰出现，这是由于系统距离分辨率的限制，干扰项不能完全消除而导致的乘性噪声影响，文中公式(15)已有说明。
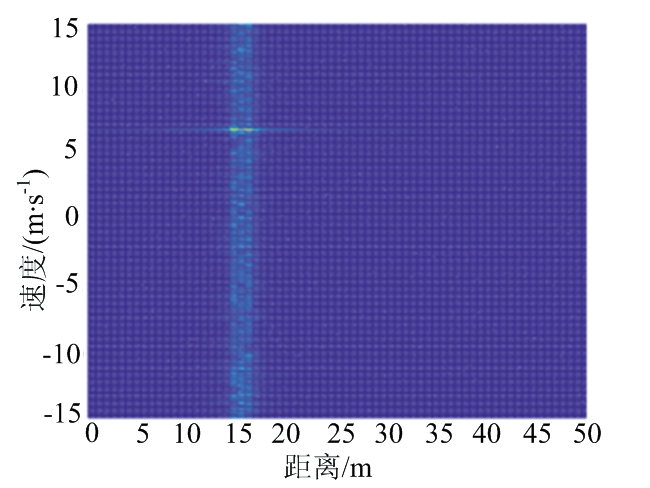
(a) 传统MTD方法的距离多普勒图
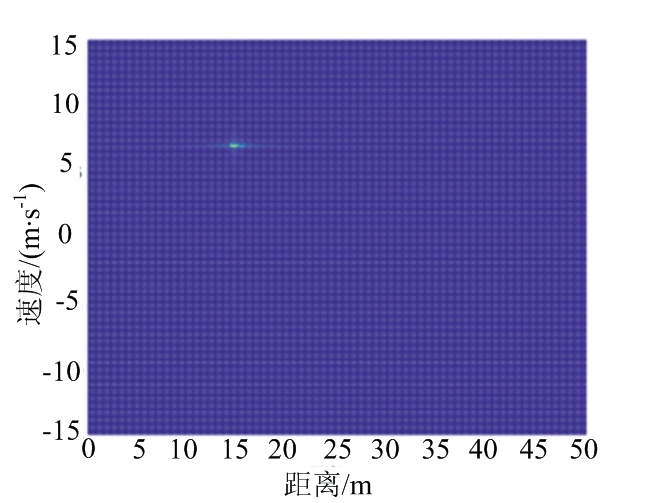
(b) 尺度变换后的距离多普勒图
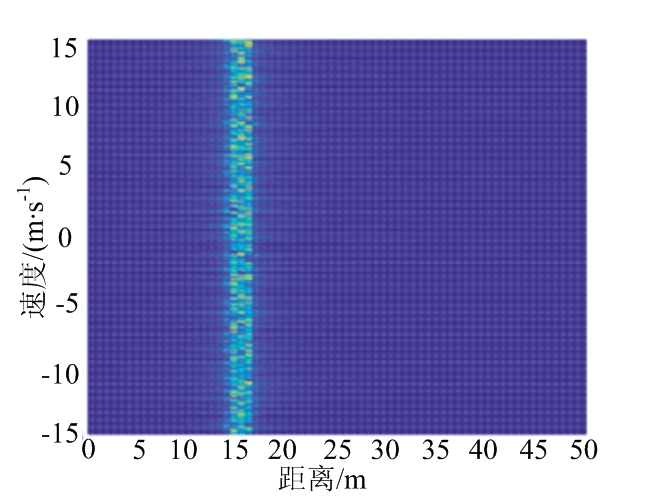
(c) 传统MTD方法的距离多普勒图
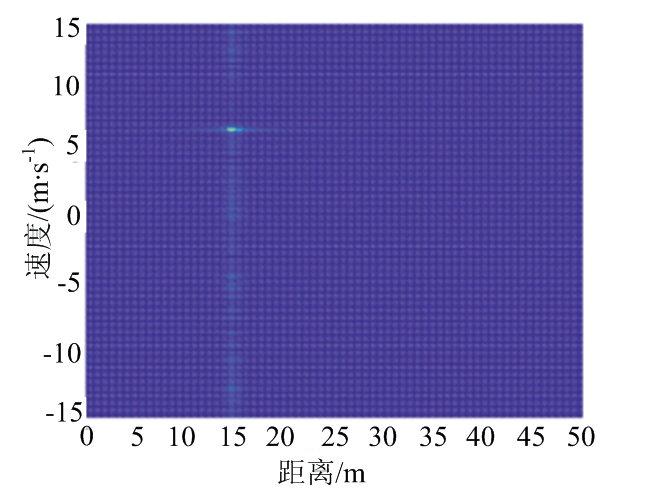
(d) 尺度变换后的距离多普勒图
图8 传统MTD方法与本文方法对比
由式(16)可知，频移间隔一定时，乘性噪声的大小只与通信调制进制数相关，进制数越高对相位项的影响也就越大。为更好地了解乘性噪声对测速的影响，图9为采用本文方法后，进制数与多普勒主旁瓣比趋势图。此处的主旁瓣比可以理解为图8(c)中MTD后测得速度的峰值幅度最大值与旁瓣值的比值，随着进制数的增加，多普勒主旁瓣比在减小，即测速受到的干扰变大，难分辨出真实的速度信息，当比值趋于1时，已经不能正常测速。
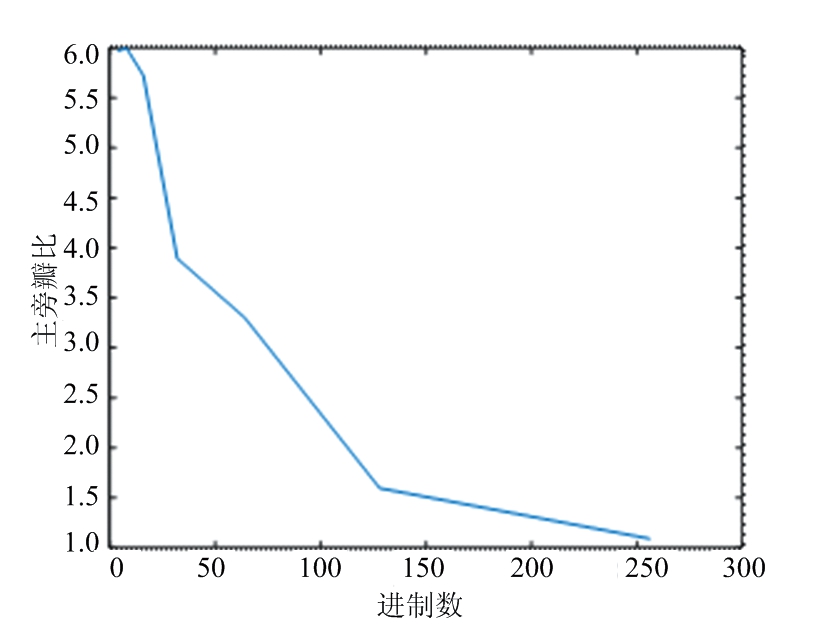
图9 进制数与主旁瓣比趋势图
4 结束语
本文设计了一种基于MFSK-FMCW的雷达通信一体化波形，在车载FMCW波形的基础上引入了频移键控，从而加载通信信息，将FMCW作为MFSK调制的载波，对FMCW体制的改动不大，保留了原有FMCW雷达的优势，具有良好的通信与雷达性能。相比于现有的MSK,2FSK通信，MFSK-FMCW有更好的频带利用率以及较高的扩频增益。具有良好的恒包络特性及较高的距离分辨率。本文通过多普勒尺度变换处理，很好地解决了因加载通信信息而导致的相干积累不能在同一频点的问题，但因系统距离分辨率的限制，测速会受到一个与通信载波增量相关的乘性类噪声项影响，此影响与通信进制数成正相关，因此需要在通信调制效率与雷达测速性能之间做出权衡。
[1] 朱伏生. 车载雷达通信系统综述[J]. 中兴通讯技术, 2018, 24(3):32-38.
[2] MOGHADDASI J, WU K . Unified Radar-Communication (RadCom) Multi-Port Interferometer Transceiver[C]∥ 2013 European Radar Conference, Nuremberg, Germany:IEEE, 2013:1791-1794.
[3] TAKASE H, SHINRIKI M. A Dual-Use System for Radar and Communication with Complete Complementary Codes[C]∥ International Radar Symposium, Gdansk, Poland:IEEE, 2010:1-4.
[4] 杨慧婷,周宇,谷亚彬,等.参数调制多载波雷达通信共享信号设计[J].雷达学报,2019,8(1):54-63.
[5] LEVANON N. Multifrequency Complementary Phase-Coded Radar Signal[J]. IEE Proceedings- Radar, Sonar and Navigation, 2002, 147(6):276-284.
[6] HU L, DU D C, XUE G R. Radar-Communication Integration Based on OFDM Signal[C]∥ IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China:IEEE, 2014:442-445.
[7] BLUNT S D, COOK M, JAKABOSKY J, et al. Polyphase-Coded FM (PCFM) Radar Waveforms, Part I: Implementation[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50(3):2218-2229.
[8] BLUNT S D, JAKABOSKY J, COOK M, et al. Polyphase-Coded FM (PCFM) Radar Waveforms, Part II: Optimization[J]. IEEE Trans on Aerospace and Electronic Systems, 2014. 50(3):2230-2241.
[9] MCCORMICK P M, SAHIN C, BLUNT S D, et al. FMCW Implementation of Phase-Attached Radar-Communications (PARC)[C]∥ IEEE Radar Conference, Boston, MA, USA:IEEE, 2019:1-6.
[10] ALABD M B, NUSS B, WINKLER C, et al. Partial Chirp Modulation Technique for Chirp Sequence Based Radar Communications[C]∥16th European Radar Conference,Paris,France:IEEE,2019:173-176.
[11] 谷亚彬, 张林让,周宇.采用FRFT-OFDM的雷达通信功能共享方法[J].西安电子科技大学学报(自然科学版), 2017,44(6):48-52.
[12] CHEN R , YANG B , WANG W , et al. Range and Velocity Estimation for DFRFT-OFDM-Based Joint Communication and Sensing Systems[C]∥ 2019 IEEE 90th Vehicular Technology Conference, Honolulu, HI, USA:IEEE, 2019:1-5.
[13] FAN Y W, BAO J C , ALJUMAILY M S, et al. Communications via Frequency-Modulated Continuous-Wave Radar in Millimeter Wave Band[C]∥ IEEE Global Communications Conference,Waikoloa, HI, USA:IEEE, 2019:1-7.
[14] NUSENU S Y , WANG W Q , CHEN H . Dual-
Function MIMO Radar-Communications Employing Frequency-Hopping Chirp Waveforms[J]. Progress In Electromagnetics Research M, 2018, 64:135-146.
[15] VANGELISTA L. Frequency Shift Chirp Modulation: The LoRa Modulation[J]. IEEE Signal Processing Letters, 2017, 24(12):1818-1821.
