0 引言
组网雷达系统通常是由多部空间位置分离的雷达组成,这些雷达协同工作以完成目标检测、目标定位、目标跟踪等不同类型的探测任务[1-5]。与传统的单基地雷达相比,多个工作方式不同,工作频段各异且空间覆盖范围互不重叠的雷达组网具有多成员雷达之间的信息互通和资源共享[6-7]等优势。组网雷达系统体现的体制多样性、频段多样性以及空间分散性有利于其在电磁干扰环境中实现反侦察、干扰抑制以及隐身目标探测等任务[8]。因此,组网雷达系统具有更好的探测性能和抗干扰性能[7-10]。
组网雷达系统复杂多样的组网特性使得传统干扰方式难以获得理想且有效的干扰效果 [11-12]。传统电子干扰技术主要包括单干扰机“独立工作”,其干扰敌方组网雷达能力有限,或者是多部干扰机间缺乏智能的协同机制,干扰资源分散,且资源利用率低。为了解决上述问题,多站协同干扰技术[13-17]逐渐发展起来。协同干扰系统通常是由多个干扰机进行组网,然后通过合理配置干扰资源(如:干扰时间、干扰功率、干扰样式等),形成与敌方组网雷达系统工作维度相当的对抗系统,并最大程度发挥己方干扰系统的作战能力。
近年来,干扰系统资源调度问题已受到了众多学者的广泛研究和关注[12,15-19]。文献[12]中,敌方组网雷达的检测概率和定位精度被推导并作为评估指标,然后结合隶属度函数建立干扰资源优化问题。文献[15]提出一种模糊评价方法以综合评估协同干扰效果。文献[16]中,建议了一种包含干扰效益、损失代价和飞行距离代价的多目标函数优化模型,以解决无人机群协同干扰资源调度的问题。文献[18]建立了一种新的干扰资源分配模型,通过雷达分组操作实现单干扰机对敌方多部雷达的干扰。文献[19]提出了一种基于agent分布式协同拍卖的多平台雷达干扰资源分配算法。在该干扰资源优化算法中,敌方雷达威胁系数和抑制概率作为干扰资源优化配置问题的性能指标。
上述研究成果为解决干扰资源调度问题提供了思路[12,15-19]。但是,大多数成果中建立的干扰资源分配模型较简单,且干扰频率匹配问题未被关注。因此,针对敌方组网雷达难以被有效干扰的问题,本文提出了一种随队支援干扰系统协同压制组网雷达系统的干扰波束和功率资源联合分配方法。首先,基于干扰信号模型以及敌方组网雷达系统和己方随队支援干扰系统的几何位置关系,构建压制干扰环境中敌方雷达回波信号模型;然后,利用K-N融合准则[20]获得组网雷达系统对目标的检测概率;接着,建立干扰频率隶属度函数[12]以评估己方干扰机和敌方雷达的频率匹配程度;最后,依据频率匹配结果,建立并求解带有干扰资源约束条件的干扰波束和功率联合优化问题,实现干扰资源合理分配。
1 系统模型1.1 干扰系统配置
假设敌方预警组网雷达系统由N个空间位置分离的相控阵雷达组成,其中雷达n位于(xn,yn)∈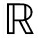 2(n=1,…,N)。组网雷达系统中的每个雷达节点均采用单站工作模式,即每个雷达产生聚集波束检测目标,然后仅能接收自身发射的信号。
2(n=1,…,N)。组网雷达系统中的每个雷达节点均采用单站工作模式,即每个雷达产生聚集波束检测目标,然后仅能接收自身发射的信号。
假设在k时刻有一个己方目标在敌方组网雷达监视区域内运动以执行侦察任务,目标的位置为(xk,yk),其速度为![]() 为了保护目标不被敌方组网雷达探测,目标自身配备干扰设备,同时多个干扰机组成随队支援干扰编队[21]对敌方组网雷达系统实施协同压制干扰。通常,干扰系统对组网雷达系统实施协同干扰的前提是获得雷达的特征参数(如雷达位置、脉冲载频和脉冲宽度等),并将其作为先验信息。这些特征参数可通过电子侦察系统截获、识别和分析敌方雷达发射的电磁信号获得[21-24]。
为了保护目标不被敌方组网雷达探测,目标自身配备干扰设备,同时多个干扰机组成随队支援干扰编队[21]对敌方组网雷达系统实施协同压制干扰。通常,干扰系统对组网雷达系统实施协同干扰的前提是获得雷达的特征参数(如雷达位置、脉冲载频和脉冲宽度等),并将其作为先验信息。这些特征参数可通过电子侦察系统截获、识别和分析敌方雷达发射的电磁信号获得[21-24]。
假设包括目标装载的干扰设备在内共有M个己方干扰机,其中干扰机m(m=1,…,M)的位置和速度分别为![]() 和
和![]() 为了实现最优的干扰性能,需要优化随队支援干扰系统的两种干扰资源:干扰机对雷达的波束指向分配和干扰波束发射功率。首先,定义一个二元变量矩阵以描述干扰机对雷达的波束指向分配关系,如下:
为了实现最优的干扰性能,需要优化随队支援干扰系统的两种干扰资源:干扰机对雷达的波束指向分配和干扰波束发射功率。首先,定义一个二元变量矩阵以描述干扰机对雷达的波束指向分配关系,如下:
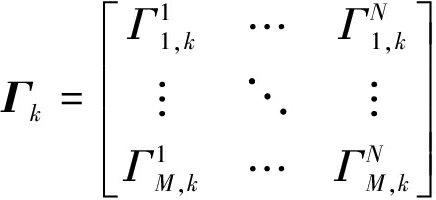
(1)
式中,矩阵元素![]() 描述了干扰机m是否分配了干扰波束用以干扰雷达n:
描述了干扰机m是否分配了干扰波束用以干扰雷达n:
(2)
然后,定义干扰功率分配矩阵以衡量随队支援干扰系统的功率资源分配情况,如下:
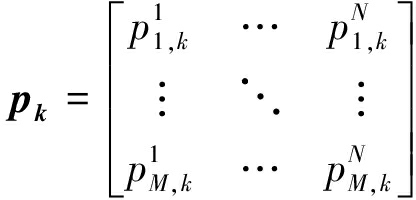
(3)
式中,![]() 表示干扰机m用于干扰雷达n的干扰功率。
表示干扰机m用于干扰雷达n的干扰功率。
为了清楚地展现随队支援干扰系统压制敌方组网雷达系统的工作机制,图1给出了己方随队支援干扰系统掩护目标飞机侦察敌方组网雷达系统的示意图。在k时刻,干扰资源调度的目的是获得下一扫描周期中最优的干扰机-雷达的干扰波束调度和干扰功率分配结果(Γk+1,pk+1),以实现在系统干扰资源设置下的最优干扰性能。具体地,第2节将推导出能够准确量化随队支援压制干扰性能的目标函数。第3节将给出干扰资源配置优化问题的详细表述及其快速两步求解。通过求解优化问题,寻找系统干扰资源变量的最佳配置(Γk+1,pk+1),使以目标函数为特征的干扰性能最大化。
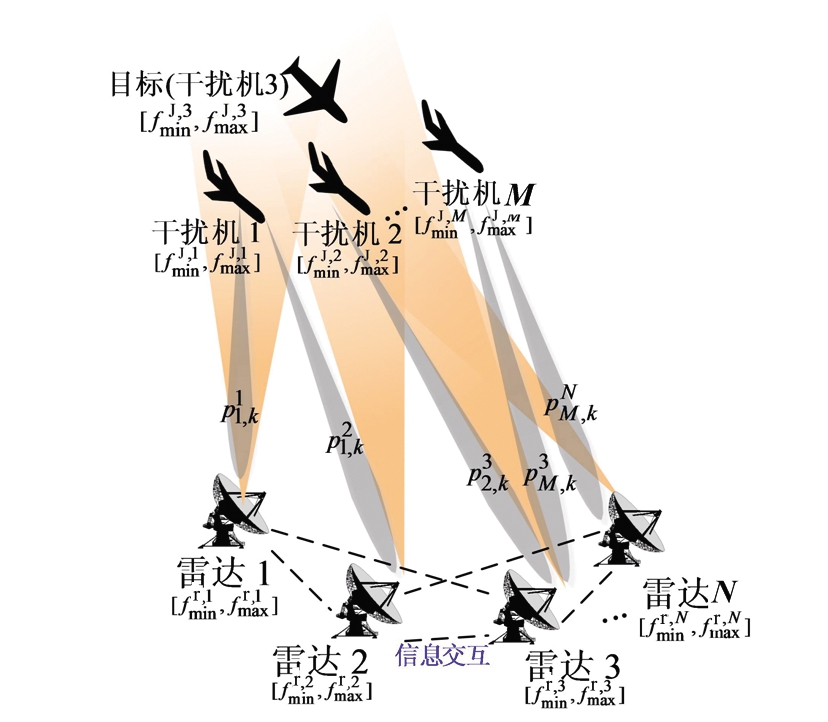
图1 己方随队支援干扰系统掩护目标飞机侦察敌方组网雷达系统
1.2 干扰信号模型
随队支援干扰系统通过发射大功率宽带的噪声干扰信号降低目标在敌方雷达接收天线处的信干噪比[21,23]。当敌方雷达主瓣接收到干扰信号时,干扰信号可以遮盖目标回波信号。在现代雷达电子对抗中存在着多种压制干扰样式(如:射频噪声干扰、噪声调幅干扰、噪声调频干扰等),且相关研究也已非常成熟[21,23]。本文以噪声调频干扰信号[21,23]为例说明随队支援干扰系统资源调度的工作原理。己方干扰机m对敌方雷达n施加的噪声调频干扰信号如下:
![]()
![]()
2πKFM![]() u(t′)dt+φ}
u(t′)dt+φ}
(4)
式中:![]() 和KFM分别表示噪声调频信号的幅度、中心频率和调频斜率;u(t)为零均值平稳随机分布的调制噪声;φ为干扰信号的初始相位,且在[0,2π)内满足均匀分布。
和KFM分别表示噪声调频信号的幅度、中心频率和调频斜率;u(t)为零均值平稳随机分布的调制噪声;φ为干扰信号的初始相位,且在[0,2π)内满足均匀分布。
1.3 压制干扰环境中的雷达回波信号模型
在k时刻,敌方雷达n接收到的回波信号基带形式如下[4]:
(5)
式中,νn,k(t)是均值为零的复高斯噪声,sn,k(t)表示目标回波信号[25-26]:
sn,k(t)=![]()
exp(-j2πfn,kt)
(6)
式中,Sn(t)是雷达信号的归一化复包络,hk是目标的雷达横截面积,且τn,k=2Rn,k/c是由于雷达n与目标之间的距离Rn,k导致的时延,fn,k是多普勒频移。此外,![]() 是雷达n接收到的目标回波信号功率,具体如下[5]:
是雷达n接收到的目标回波信号功率,具体如下[5]:
(7)
式中,![]() 和λ分别表示敌方雷达n的发射功率、天线增益和工作波长。
和λ分别表示敌方雷达n的发射功率、天线增益和工作波长。
回顾式![]() 是雷达n接收的压制干扰信号。敌方雷达接收到的压制干扰信号的基带形式是发射干扰信号
是雷达n接收的压制干扰信号。敌方雷达接收到的压制干扰信号的基带形式是发射干扰信号![]() 的衰减延时版本,有如下形式:
的衰减延时版本,有如下形式:
(8)
式中,![]() 是由于敌方雷达n与己方干扰机m之间的距离
是由于敌方雷达n与己方干扰机m之间的距离![]() 导致的时延,
导致的时延,![]() 是雷达n接收的干扰信号功率[5]:
是雷达n接收的干扰信号功率[5]:
(9)
式中,![]() 为干扰机m的发射天线增益,
为干扰机m的发射天线增益,![]() 表示敌方雷达n在己方干扰机m方向
表示敌方雷达n在己方干扰机m方向![]() 的天线增益,λf是己方干扰机的工作波长,γ为极化失配损失。
的天线增益,λf是己方干扰机的工作波长,γ为极化失配损失。
2 随队支援干扰系统的干扰性能指标
压制干扰信号能有效降低目标在敌方雷达接收天线处的信干噪比[21,23,27],而目标的检测概率是其信干噪比的函数。当目标信干噪比减小时,检测概率也会随之减小。此外,检测概率可以评估敌方组网雷达系统的检测性能。因此,本文推导了组网雷达的检测概率,并将其作为干扰性能指标。
2.1 干扰频率隶属度函数
随队支援干扰系统通过发射大功率宽带噪声干扰信号来压制敌方组网雷达系统。然而,单个干扰机的工作频带难以覆盖敌方组网雷达系统的整个工作频带。因此,保证压制干扰有效实施的关键是己方干扰机与敌方雷达的工作频率需保持一致。
己方干扰机有效干扰敌方组网雷达系统的前提是己方干扰机与敌方雷达的工作频率重合。通常,干扰频率隶属度函数可以评估干扰机与雷达工作频率的重合程度。因此,干扰频率隶属度函数![]() 被用来描述敌方雷达n是否会受到干扰机m的干扰,隶属度函数由下面形式[12]给出:
被用来描述敌方雷达n是否会受到干扰机m的干扰,隶属度函数由下面形式[12]给出:
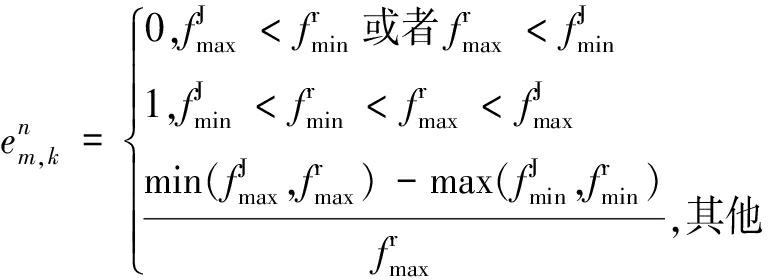
(10)
式中,![]() 和
和![]() 分别表示干扰机的最大和最小工作频率;
分别表示干扰机的最大和最小工作频率;![]() 和
和![]() 分别表示敌方雷达的最大和最小工作频率。
分别表示敌方雷达的最大和最小工作频率。
2.2 压制干扰下组网雷达系统检测模型
多干扰机实施协同压制干扰后,雷达n接收到的信干噪比表示为[5,28]
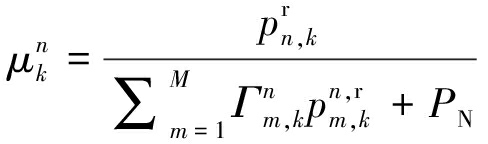
(11)
式中,![]() 和
和![]() 分别是在式(7)和式(9)中定义的目标回波功率和干扰功率,PN表示雷达接收机内部噪声功率。
分别是在式(7)和式(9)中定义的目标回波功率和干扰功率,PN表示雷达接收机内部噪声功率。
本文以Swerling-I型目标为例计算目标的检测概率。雷达n对目标的检测概率计算公式如下[25,28]:
(12)
式中,VT是检测门限。
考虑组网雷达系统采用K-N融合准则[20],其表示当N个雷达中至少有K(K≤N)个雷达检测到目标时,假设检验一定有效。该融合准则可以由下式给出:

(13)
式中,vn∈{0,1}表示雷达n对目标的判决结果,v0表示组网雷达的判决结果。
基于单雷达对目标的检测概率![]() 组网雷达系统对目标的检测概率为
组网雷达系统对目标的检测概率为
PD,k=![]()
(14)
3 干扰波束和功率联合分配策略3.1 协同干扰系统约束
从数学上讲,多干扰机协同干扰敌方组网雷达系统的波束和功率联合分配算法可以表征为一个优化问题,其目的是在干扰资源约束下,最小化敌方组网雷达的检测性能。这些限制应予以考虑和拟订。首先,假设每个干扰机最多能产生L(L≤N)个波束干扰多部雷达:
(15)
此外,雷达与干扰机的对应关系满足下面约束:
(17)
约束式(16)表示每个干扰机最多只能分配一个干扰波束干扰同一个雷达。约束(17)表示每个雷达最多被S个干扰机干扰。对于干扰功率pk,对应的约束条件为
(18)
(19)
约束式(18)表示被分配的干扰波束的辐射功率![]() 受到最大值pmax和最小值pmin的约束,同时保证己方干扰机和敌方雷达的频率是匹配的。在式(18)中,ε表示预设的干扰隶属度阈值。约束式(19)表示己方随队支援干扰系统的总干扰功率PT是有限的。
受到最大值pmax和最小值pmin的约束,同时保证己方干扰机和敌方雷达的频率是匹配的。在式(18)中,ε表示预设的干扰隶属度阈值。约束式(19)表示己方随队支援干扰系统的总干扰功率PT是有限的。
3.2 干扰资源优化分配问题
在式(14)中计算的目标检测概率能够量化敌方组网雷达系统的检测性能,因此检测概率可以被用作干扰资源联合优化分配问题的优化准则。本文工作的目的是满足己方干扰机与敌方雷达的工作频率匹配的同时,通过优化己方随队支援干扰系统的干扰波束和功率资源配置使得敌方组网雷达系统的检测概率最小化。多干扰机协同干扰敌方组网雷达系统的资源分配策略可表示为
![]() 若
若![]()
![]() 其他
其他
(20)
在优化问题式(20)中的资源约束由式(15)~(19)描述。这些约束分别表示,当己方干扰机与敌方雷达的工作频率匹配且相应的干扰波束分配确定后,干扰波束的辐射功率被一个功率区间[pmin,pmax]限制;干扰机m最多仅能分配一个干扰波束干扰雷达n;每个干扰机最多产生L个干扰波束;每个雷达最多被S个干扰机干扰;随队支援干扰系统的总辐射功率是有限的。
值得注意的是,本文的干扰波束与功率联合优化模型是在精确侦察敌方组网雷达系统特征参数的理想假设上构建的。然而,在实际电磁环境中,电子侦察系统精确感知敌方雷达特征参数是十分困难的,仅能通过参数估计技术粗略获得敌方雷达特征参数的大致范围。在这样的情况下,受参数估计精度的影响,后续计算的随队支援干扰系统干扰性能指标与真实干扰性能指标之间存在泛化误差。这将误导干扰资源的合理分配,并降低随队支援干扰系统的整体协同干扰性能。通常,资源稳健调度可解决因参数估计不精确而造成的泛化误差问题[29-30]。
3.3 优化问题的快速两步求解
在式(20)中建立的多干扰机协同干扰敌方组网雷达系统的资源联合优化函数包含了两个变量,即用于描述干扰机-雷达的干扰波束分配的整数变量Γk和描述辐射干扰资源的连续变量pk。由于两个干扰资源参数是耦合的,且干扰波束分配变量是离散的,因此式(20)中的优化问题是非凸的NP-hard问题[31-32]。在实际应用中,需要在每个跟踪区间实时获得资源分配方案。一种直接的求解方法是拆分二元波束分配变量Γk和功率变量pk。为了解决这个问题,参考文献[29,33]中的求解方法,通过分解式(20),本文提出了一种快速两步求解方法以获得干扰资源分配结果(Γk,pk)。具体的步骤如下:
1)基于干扰功率平均分配的干扰波束调度:首先,假设每个干扰机每时刻产生N个干扰波束,且每个干扰波束的辐射功率是相同的。由此产生的干扰功率平均分配矩阵为puni=1M×N·PT/MN。然后,非凸约束![]() 被凸约束
被凸约束![]() 替换以获得干扰波束分配问题的凸松弛解[34]。优化问题式(20)可以转换为如下的子问题:
替换以获得干扰波束分配问题的凸松弛解[34]。优化问题式(20)可以转换为如下的子问题:
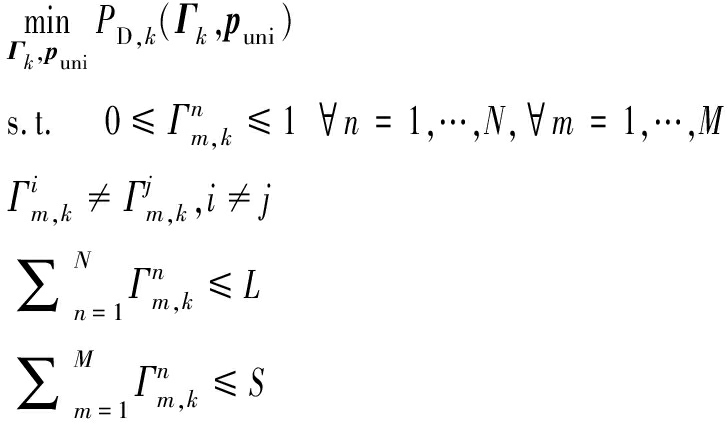
(21)
由于无法保证目标函数二次偏导的正定性,因此优化子问题式(21)也是非凸的[31]。为了求解干扰波束调度优化子问题式(21),本文采用粒子群优化算法。粒子群优化算法不依赖于优化问题的凸性和发散性。近年来,它已被广泛应用于寻找高维优化问题的最优解[35]。
值得注意的是,松弛优化问题式(21)并不等价于原始优化问题式(20),因为松弛优化问题式(21)通过粒子群算法获得的干扰波束调度结果是小数。尽管如此,松弛优化问题的最优目标值是原始优化问题的一个下界。这是因为松弛问题的可行集包含了原问题的可行集[33]。因此,我们可以根据松弛优化问题的解![]() 产生一个原始优化问题的次优解
产生一个原始优化问题的次优解![]() 原始优化问题的次优解的具体操作过程如表1所示。
原始优化问题的次优解的具体操作过程如表1所示。
表1 基于PSO的波束指向![]() 求解方法
求解方法

步骤1 初始化puni,Γ0k=0M×N步骤2 PSO求解式(21),得到松弛结果Γ0k;步骤3 循环l=1,…,L×M寻找最大值 [ml,il]=argmax{Γ0k};更新Γ0k(ml,il)=1,且Γ0k(ml,il)=0;判断Γ0k是否满足式(20)中约束条件,若不满足,Γ0k(ml,il)=0; 循环结束步骤4 输出波束指向结果Γ0k。
2)基于干扰波束调度结果![]() 的功率分配:给定干扰波束调度结果
的功率分配:给定干扰波束调度结果![]() 优化问题式(20)可以转化为
优化问题式(20)可以转化为
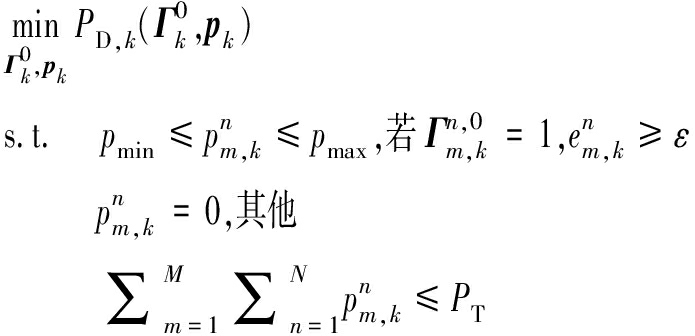
(22)
如前所述,功率分配子优化问题式(22)仍是非凸问题。针对该优化问题,由于功率变量是连续型变量,因此仍可以采用粒子群算法获得干扰功率分配结果![]()
4 仿真结果与分析
为了突出本文提出的干扰波束和功率联合优化算法的有效性与优越性,将其与干扰资源平均分配算法进行对比。考虑组网雷达系统由N=5个雷达节点组成,每部雷达在频段[0,10]GHz内随机跳频。组网雷达系统的融合中心采用K-N融合准则,其中K=3。在图2所示的随队支援干扰掩护单目标飞机侦察敌方组网雷达系统场景中,1个目标和2个干扰机执行对敌方组网雷达的侦察任务。假设目标携带压制干扰设备,并且与2个干扰机组成了随队支援干扰编队。每个干扰机的初始状态如表2所示。
随队支援干扰系统的总辐射功率为300 W,每个干扰波束辐射的最大功率和最小功率分别为pmax=0.9PT和pmin=0.01PT。每个干扰机可产生的最大波束数量为L=2。连续间隔之间的持续时间设置为T0=1 s,帧数设置为30,蒙特卡洛次数设置为Mc=300。
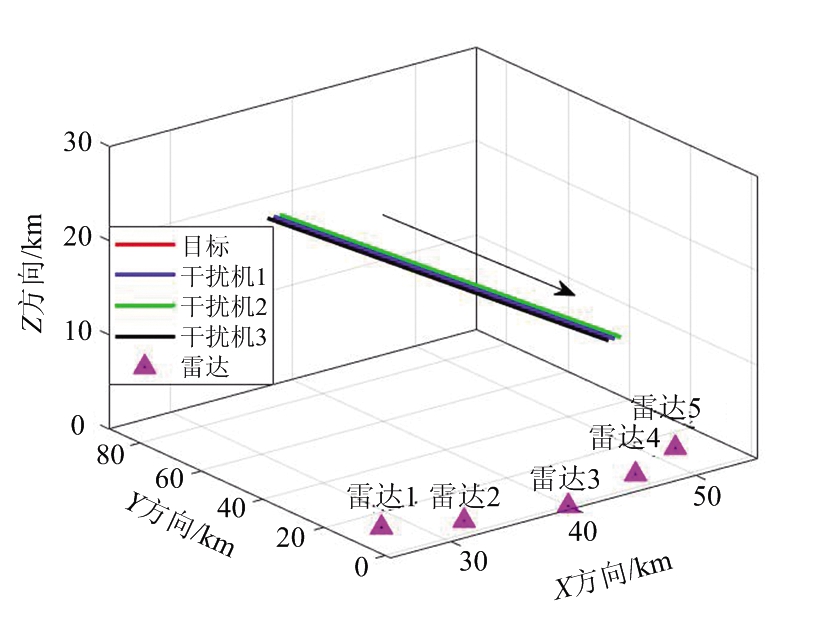
图2 随队支援干扰系统掩护目标飞机侦察敌方组网雷达场景图
表2 干扰机工作参数
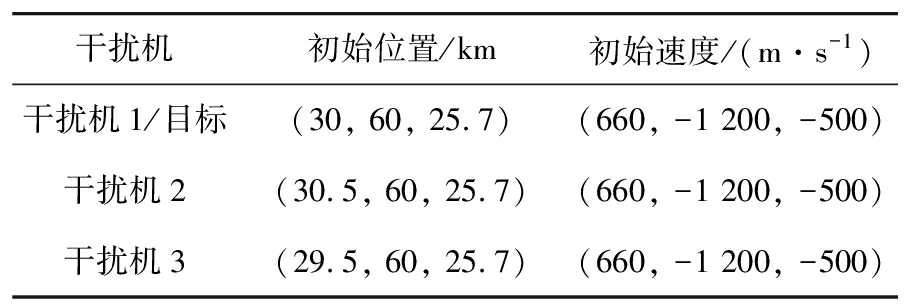
干扰机初始位置/km初始速度/(m·s-1)干扰机1/目标(30, 60, 25.7)(660, -1 200, -500)干扰机2(30.5, 60, 25.7)(660, -1 200, -500)干扰机3(29.5, 60, 25.7)(660, -1 200, -500)
本文提出的干扰波束与功率联合优化算法与干扰资源均匀分配算法获得的目标检测概率如图3所示。从图中可以看出,本文提出的优化算法通过合理分配干扰系统资源,可以获得更低的检测概率。与干扰资源均匀分配算法相比,本文的优化算法使组网雷达系统的检测性能整体下降了约28%。这意味着本文提出的优化算法能有效地压制敌方组网雷达系统,且具有更好的压制干扰性能。在整个运动过程中,由于随队支援干扰系统逐渐靠近敌方组网雷达系统,因此检测概率呈现增长趋势。
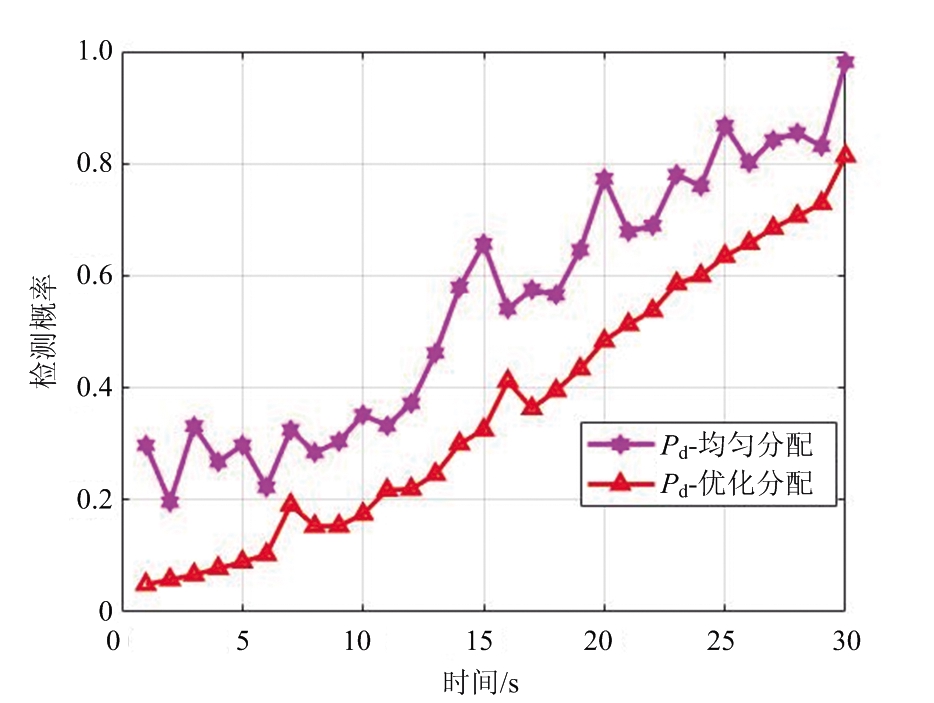
图3 不同干扰资源分配策略下的目标检测概率对比
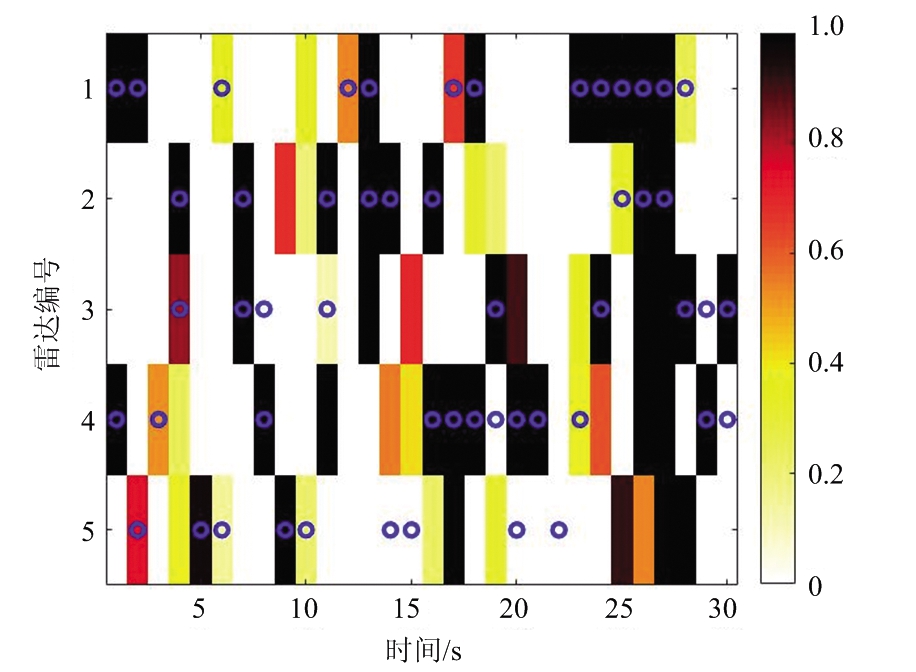
(a) 干扰机1与5个雷达的干扰隶属度以及干扰波束调度结果
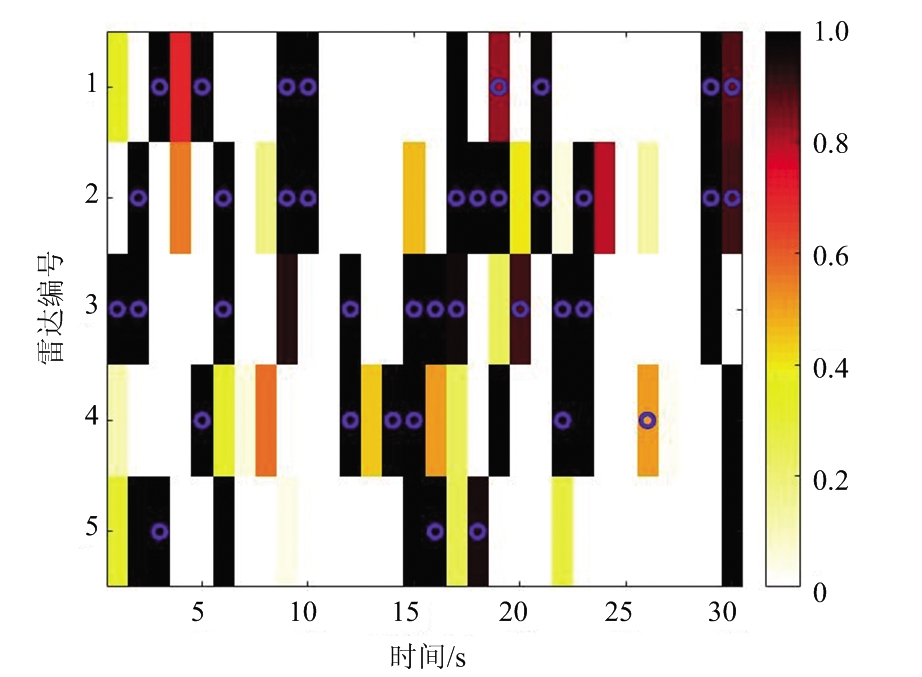
(b) 干扰机2与5个雷达的干扰隶属度以及干扰波束调度结果
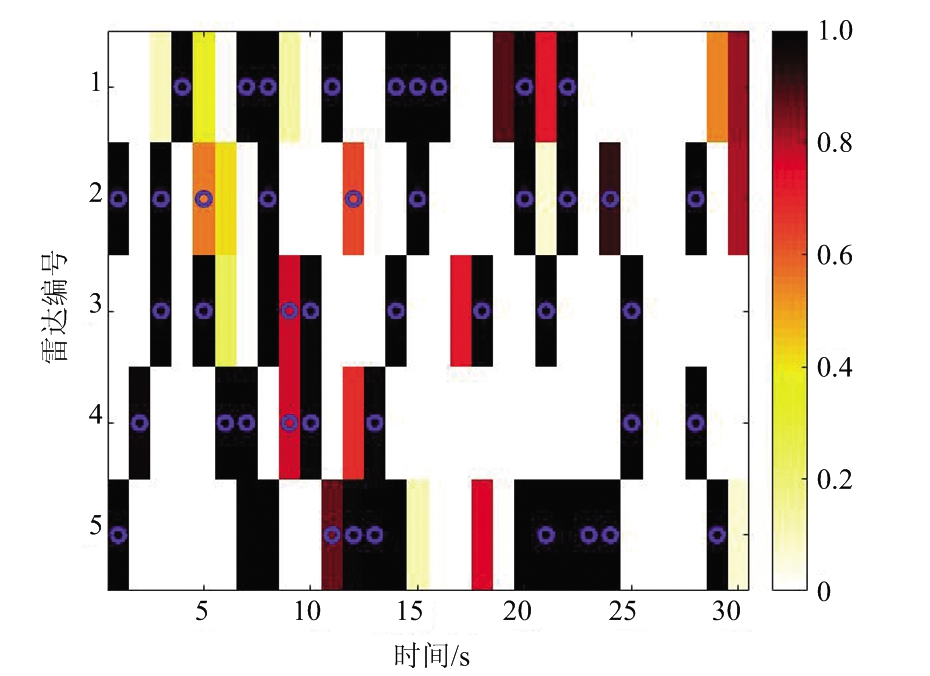
(c) 干扰机3与5个雷达的干扰隶属度以及干扰波束调度结果
图4 干扰频率隶属度函数与干扰波束调度结果
图4给出了每个干扰机与所有雷达的干扰频率隶属度函数,以及相应的干扰波束调度结果。网格颜色表示干扰机与雷达间的干扰频率隶属度函数值。蓝色的圆圈表示在该时刻干扰机m发射干扰波束干扰雷达n。结合图4(a)、(b)和(c),可以看出随队支援干扰系统每次优化确定较高隶属度函数值对应的干扰机-雷达对分配关系,这种贪婪的优化准则保证每次确定波束分配关系时实施最优的分配决策[30]。
干扰波束与功率联合优化算法对所有雷达的干扰功率分配结果如图5所示。网格颜色表示随队支援干扰系统压制特定雷达所分配的干扰功率。从图中可以看出,雷达2~4被分配更多的干扰功率。这是因为与雷达1和雷达5相比,雷达2~4与随队干扰系统形成的方位角较小,雷达天线增益相对较大。

图5 随队支援干扰对所有雷达的干扰功率分配结果图
5 结束语
为了掩护己方目标不被敌方组网雷达系统发现,本文提出了一种多干扰机协同敌方干扰组网雷达系统的干扰资源调度方法。在压制干扰环境中,基于K-N融合准则,敌方组网雷达系统的检测概率被推导并被用作性能指标以量化随队支援干扰系统的压制干扰性能。然后,在干扰资源有限的条件下,考虑随队支援干扰系统与敌方组网雷达系统之间的干扰频率匹配问题,通过优化分配各干扰机的波束和功率资源,最小化敌方组网雷达系统对己方突防目标的检测概率。仿真结果表明,与干扰资源均匀分配方法相比,本文所提的干扰波束与功率资源联合调度方法具有优越的干扰性能。
[1] 王经鹤. 组网雷达多帧检测前跟踪技术研究[D]. 成都:电子科技大学, 2019.
[2] 时晨光, 汪飞, 周建江, 等. 基于低截获概率优化的雷达组网系统最优功率分配算法[J]. 雷达学报, 2014, 3(4):465-473.
[3] LI Jian, STOICA P. MIMO Radar with Colocated Antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5):106-114.
[4] HAIMOVICH A M, BLUM R S, CIMINI L J. MIMO Radar with Widely Separated Antennas[J]. IEEE Signal Processing Magazine, 2007, 25(1):116-129.
[5] CHERNYAK V S. Fundamentals of Multisite Radar Systems:Multistatic Radars and Multi-Radar Systems[M]. UK:Routledge, 2018:2-24.
[6] CHARLISH A, HOFFMANN F, DEGEN C, et al. The Development from Adaptive to Cognitive Radar Resource Management[J]. IEEE Aerospace and Electronic Systems Magazine, 2020, 35(6):8-19.
[7] SHI Chenguang, WANG Fei, SELLATHURAI M, et al. Low Probability of Intercept-Based Optimal Power Allocation Scheme for an Integrated Multi-Static Radar and Communication System[J]. IEEE Systems Journal, 2019, 14(1):983-994.
[8] ZHENG Gaoqian, ZHENG Ying. Radar Netting Technology & Its Development[C]∥Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu, China:IEEE, 2011:933-937.
[9] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial Diversity in Radars—Models and Detection Performance[J]. IEEE Trans on Signal Processing, 2006, 54(3):823-838.
[10] YAN Junkun, LIU Hongwei, PU Wenqiang, et al. Joint Beam Selection and Power Allocation for Multiple Target Tracking in Netted Colocated MIMO Radar System[J]. IEEE Trans on Signal Processing, 2016, 64(24):6417-6427.
[11] 段先华, 孙庆国, 蔡丹. 基于改进遗传算法的协同干扰资源优化分配[J]. 江苏科技大学学报(自然科学版), 2016, 30(5):466-472.
[12] MA Jing, SHI Bin, CHE Fei, et al. Research on Evaluation Method of Cooperative Jamming Effect in Cognitive Confrontation[C]∥International Conference on Artificial Intelligence for Communications and Networks, Springer, Cham:IEEE, 2019:40-51.
[13] 谯梁, 杨帅, 王鑫, 等. 雷达干扰效果评估与协同干扰策略分配算法研究[J]. 航天电子对抗, 2019, 35(3):27-32.
[14] 步雨浓, 袁健全, 池庆玺. 智能协同干扰技术作战应用分析[J]. 战术导弹技术, 2019(5):71-76.
[15] XING Huaixi, WU Hua, CHEN You, et al. A Cooperative Interference Resource Allocation Method Based on Improved Firefly Algorithm[J]. Defence Technology, 2021, 17(4):1352-1360.
[16] QIN Qingwen, DONG Wenfeng, LIN Meiqing, et al. Cooperative Jamming Resource Allocation of UAV Swarm Based on Multi-Objective DPSO[C]∥2018 Chinese Control and Decision Conference, Shenyang, China:IEEE, 2018:5319-5325.
[17] GAO Yang, LI Dongsheng. Electronic Countermeasures Jamming Resource Optimal Distribution[J]. Information Technology and Intelligent Transportation Systems, Cham, 2017(11):113-121.
[18] 郭小一, 袁卫卫, 黄金才. 雷达干扰资源一对多分配方法[J]. 火力与指挥控制, 2008, 33(12):22-25.
[19] LV Mingshan, LIU Dongli, JIANG Ning, et al. Radar Jamming Resources Assignment Algorithm for EW Real-Time Decision Support System of Multi-Platforms[C]∥2010 International Conference on Intelligent Control and Information Processing, Dalian, China:IEEE, 2010:83-86.
[20] ANDARGOLI S M H, MALEKZADEH J. LPI Optimization Framework for Search Radar Network Based on Information Fusion[J]. Aerospace Science and Technology, 2017(4):206-214.
[21] 赵国庆. 雷达对抗原理[M]. 西安:西安电子科技大学出版社, 1999:122-143.
[22] JIANG Haiqing, ZHANG Yangrui, XU Hongyi. Optimal Allocation of Cooperative Jamming Resource Based on Hybrid Quantum-Behaved Particle Swarm Optimisation and Genetic Algorithm[J]. IET Radar, Sonar & Navigation,2017, 11(1):185-192.
[23] 张永顺,童宁宁,赵国庆.雷达电子战原理[M]. 北京: 国防工业出版社,2010:19-25.
[24] 胡新宇, 张铁军, 王昀. 低截获概率雷达信号侦察技术[J]. 航天电子对抗, 2020, 36(5):40-43.
[25] VAN TREES H L. Detection, Estimation, and Modulation Theory, part III[M]. USA:John Wiley & Sons, 1971:252-286.
[26] STOICA P, LI Jian, XIE Yao. On Probing Signal Design for MIMO Radar[J]. IEEE Trans on Signal Processing, 2007, 55(8):4151-4161.
[27] DAI Huanyao, WANG Xuesong, LI Yongzhen. Main-Lobe Jamming Suppression Method of Using Spatial Polarization Characteristics of Antennas[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(3):2167-2179.
[28] RICHARDS M A. Fundamentals of Radar Signal Processing[M]. USA:McGraw-Hill Education,2005:256-262.
[29] ZHANG Dalin, SUN Jun, YI Wei, et al. Joint Jamming Beam and Power Scheduling for Suppressing Netted Radar System[C]∥2021 IEEE Radar Conference, Atlanta, GA, USA:IEEE 2021:1-6.
[30] 谢明池. 分布式组网雷达资源自适应管控算法研究[D]. 成都:电子科技大学, 2019.
[31] BOYD S, VANDENBERGHE L. Convex Optimization. Cambridge[M].UK: Cambridge University Press, 2013:75-80.
[32] GODRICH H, PETROPULU A P,POOR H V. Sensor Selection in Distributed Multiple-Radar Architectures for Localization: A Knapsack Problem Formulation[J]. IEEE Trans on Signal Processing, 2012, 60(1):247-260.
[33] XIE Mingchi, YI Wei, KIRUBARAJAN T, et al. Joint Node Selection and Power Allocation Strategy for Multitarget Tracking in Decentralized Radar Networks[J]. IEEE Trans on Signal Processing, 2018, 66(3):729-743.
[34] JOSHI S, BOYD S. Sensor Selection via Convex Optimization[J]. IEEE Trans on Signal Processing, 2009, 57(2):451-462.
[35] YANG Yichuan, YI Wei, ZHANG Tianxian, et al. Fast Optimal Antenna Placement for Distributed MIMO Radar with Surveillance Performance[J]. IEEE Signal Processing Letters,2015, 22(11):1955-1959.


