0 引言
极化雷达通过发射和接收一组正交的极化电磁波，可以获得完整的目标极化散射矩阵[1]。这有利于完整地描述目标散射机理，为准确解译目标散射机理提供了可能。目前，极化雷达的应用越来越广泛，已成为地球观测和海洋遥感的主流传感器[1-2]。通过对散射机理的建模和解译，可以挖掘和提取极化散射矩阵中丰富的目标散射信息。极化目标分解是典型的目标解译方法，包含相干和非相干分解两大类[3]。基于获取的极化散射信息，具有不同物理属性的目标可以被区分出来。相关的应用涉及土地覆盖分类[4]、人造目标检测和识别[5]以及灾害评估[3]。此外，极化信息的表征与极化基的选择有关。其中，水平和垂直极化基是常用的。然而，研究表明其他极化基在某些应用上也可能有更好的表现。在文献[6]中，表面粗糙度在圆极化基上比在线极化基上对相干值更敏感。理论上，如果获得了一个极化基上的极化散射矩阵，那么不同极化基上的极化散射矩阵可以通过酉变化得到。这种极化基的变换通常是通过改变极化椭圆率角和极化方向角来完成[1]。
雷达目标的后向散射信息敏感于目标姿态与雷达视线之间的相对几何关系，这被定义为目标散射多样性[7]。同一目标的散射机理可能随雷达视线位置的变化发生明显改变。因此，通常认为目标散射多样性会给雷达信息解译增加困难。文献[7]引入极化旋转域的概念，并对目标散射多样性进行了挖掘和利用。极化旋转域表征了极化特性随极化方位角的变化，为了实现可视化表征，文献[8-9]又相继提出了极化相干和极化相关方向图解译工具，并导出一系列具有明确物理意义的极化旋转不变特征量。这些特征已经被成功应用于人造目标增强和检测[9-11]，地物识别和分类[12]，以及灾害评估领域[13]。
极化方位角和极化椭圆率角可以完备地表征极化响应，由此可以构建极化特征图。共极化和交叉极化特征图由Zyl等人提出，并用于分析地面物体的散射特性[14]。为了区分不同的极化特征图，还从中导出了一系列特征：基座高度特征[14]以及线性共极化的标准偏差(SDLP)特征[15]。这些共极化和交叉极化特征已被应用于海上浮油监测[16]和地物分类[17]等。值得注意的是，这些极化特征图侧重于接收和发射天线的极化状态，并且两者的极化状态定义相同，这可能会导致极化信息的丢失[18]。
值得注意的是，极化方位角实际上表明了目标与雷达视线之间的相对几何关系。也就是说，极化旋转域表征了极化椭圆率角固定的情况下，目标绕雷达视线旋转的极化响应。考虑到信息的完备性，通过研究极化旋转域在不同极化椭圆率角度上的变化，有望挖掘出更多能够解译目标机理的特征。对此，本文提出了一种三维极化相关方向图。通过特征图的形式表征极化相关值随极化方位角和极化椭圆率角的变化情况。通过进一步的数学推导，本文得到了3种独立的极化相关方向图，然后选择了4种典型的散射体：平板、二面角、偶极子和螺旋体结构进行了研究。实验结果表明它们的三维极化相关方向图的形态结构存在显著差异。接着文中分析了这些三维极化相关方向图中的极值点分布和曲率情况。在此基础上，提出了高斯曲率最大值这一新的极化特征。结合星载极化SAR实测数据验证了高斯曲率最大值特征能够有效地区分舰船和海杂波，有望用于提高舰船目标检测性能。
在极化SAR的应用中，舰船目标检测是一个重要的方向，无论是在军事和民用领域。目前的舰船检测方法，主要分为两类：基于统计学的方法[19]和基于散射特性的方法[9,20]。其中，恒虚警率检测(Constant False Alarm Ratio, CFAR)方法被广泛使用，它能够根据统计模型自适应地确定阈值。最近，为了提高检测性能，超像素[11,21-22]等计算机视觉的方法也被引入舰船检测中。然而，随着雷达图像分辨率的提高，目标的分布不能被忽视，相干斑的强度也在增强，这导致了传统CFAR检测器性能的下降[21]。此外，如何从极化SAR数据中挖掘有用的特征量也是一个需要思考和解决的问题。为此，本文基于挖掘出的高斯曲率最大值特征量，提出了一种新的舰船检测方法，并对检测方法的性能进行了讨论。
1 二维极化旋转域解译工具
二维极化旋转域解译工具将目标极化矩阵拓展到绕雷达视线的旋转域[7-8]。其中，为了将繁杂的数学表达式进行可视化处理，文献[9]提出了极化相关方向图的概念。下面从极化基变换的角度对这种二维极化相关方向图进行说明。
1.1 极化矩阵的极化基变换
以水平和垂直极化基为例，极化雷达获取的全极化信息可由极化散射矩阵表征为
(1)
式中，下标HV代表垂直发射和水平接收，其他下标可类似定义。
在满足互易性条件SHV=SVH的情况下，Pauli矢量kP和Lexicographic矢量kL能够被表征为
(2)
(3)
进一步，任一极化基下的Pauli矢量kP(θ,τ)和Lexicographic矢量kP(θ,τ)可以通过酉变化得到[1]。以Pauli矢量为例，kP(θ,τ)和kP之间可以通过酉矩阵U3p(θ,τ)进行转换：
式中，θ为极化方位角，τ为极化椭圆率角。酉矩阵U3p(θ,τ)可以表示为极化方位角酉矩阵U3p(θ)和极化椭圆率角酉矩阵U3p(τ)的乘积。
另一方面，极化相干矩阵T定义为
(5)
式中，上标†表示矩阵的共轭转置操作，符号〈·〉代表样本平均。因此，任一极化基下的极化相干T(θ,τ)能够表示为
(6)
极化协方差矩阵的极化基变换能够利用特殊酉矩阵UT-C对变换后的极化相干矩阵T(θ,τ)进行矩阵变换得到：
(7)
(8)
1.2 极化相关方向图
对于Pauli矢量或者Lexicographic矢量中的任一两个不同的元素k1和k2，极化相关值
定义为[9]
(9)
式中，
为k2的共轭转置。极化旋转域解译工具中的极化相关方向图研究了不同极化方位角下的极化相关值演化规律。根据公式(4)，如果固定极化椭圆率角为0，可以得到任一极化方位角下的Pauli矢量kP(θ)和Lexicographic矢量kL(θ)。同样，对于kP(θ)或者kL(θ)中的任一两个不同的元素k1(θ)和k2(θ)，极化相关方向图[9]的数学表达式为
(10)
2 三维极化旋转域解译工具
本文将极化相关方向图沿极化椭圆率角维度进行了拓展，研究其在不同极化椭圆率角上的变化情况，导出了三维极化相关方向图
其数学表达式为
(11)
式中，k1(θ,τ)和k2(θ,τ)为极化基变换后的Pauli矢量kP(θ,τ)或者Lexicographic矢量kL(θ,τ)中的任一两个不同的元素。由此可以得到6种三维极化相关方向图：
和
通过进一步的数学推导，有以下三个关系式成立：
(12)
因此，在研究中只需要考虑以下三种独立的三维极化相关方向图：
和
可视化工具能将繁杂的数学表达式进行直观的表征。三维极化相关方向图表征了不同极化椭圆率角下的相关方向图。以偶极子的三维极化相关方向图
为例，其在图 1 (a)中进行展示。图形表面颜色的深浅表示取值的大小。一个坐标轴为极化椭圆率角τ，另外两个坐标轴为极化相关值。这种可视化可以看作是将三维极化相关方向图
在柱坐标系下进行表征。不同极化椭圆率角下的二维极化相关方向图在图1(b)中展示。这种二维的切片在本文中定义为极化椭圆率角平面。可以看到不同极化椭圆率角平面的形状不相同，下节中将从极值点分布和曲率两个角度进行详细分析。
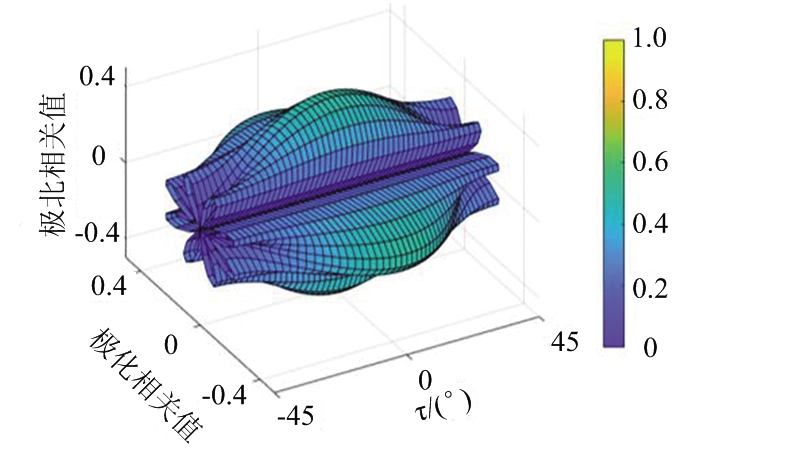
(a) 偶极子三维极化相关方向图示意图
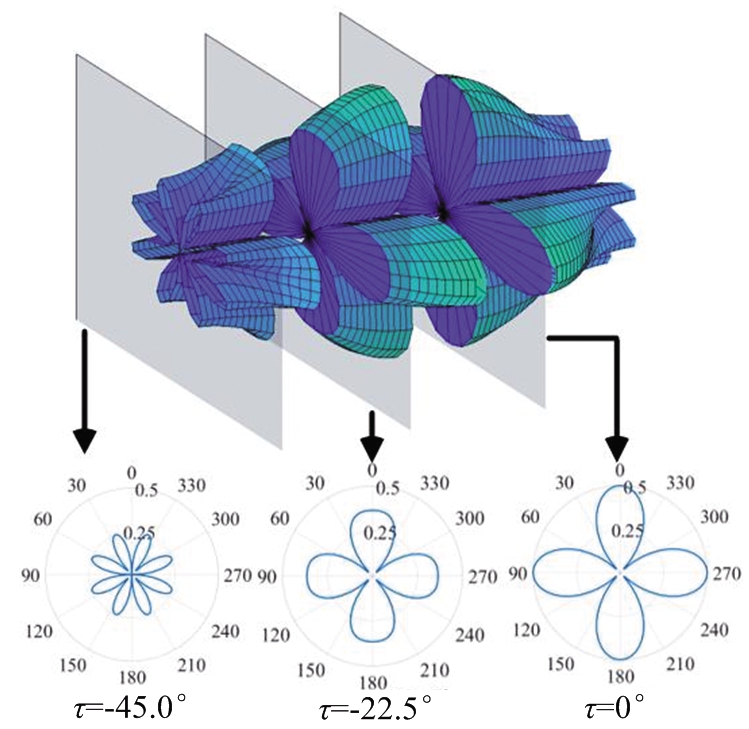
(b) 不同极化椭圆率角下的二维极化相关方向图
图1 三维极化相关方向图示意图
3 典型散射体的三维极化相关方向图分析
本文选取典型散射体：平板、二面角、偶极子和螺旋体结构进行分析。这些散射体对应的极化散射矩阵如表 1所示，对应的三维极化相关方向图如图 2所示。图形表面颜色的深浅代表取值的大小，颜色范围与图1(a)保持一致。从图中可以观察到不同散射体不同类型的三维极化相关方向图的形状、表面的起伏程度存在显著差异。这种差异性有利用区分不同的散射结构。本文以
类型的三维极化相关方向图为例进行分析和说明。
表1 典型散射体的极化散射矩阵和
三维极化相关方向图的数学表达式
三维极化相关方向图的数学表达式平板1001[]12sin(4τ)二面角100-1[]|cos(2τ)sin(2θ)cos2(2θ)+sin2(2θ)sin2(2τ)|偶极子1000[]12sin2τ()sin2θ()+cos2θ()cos2τ()[]cos22τ()sin22θ()+sin22τ()螺旋体121jj-1[]cos(2τ)sin(2τ)-1[]4
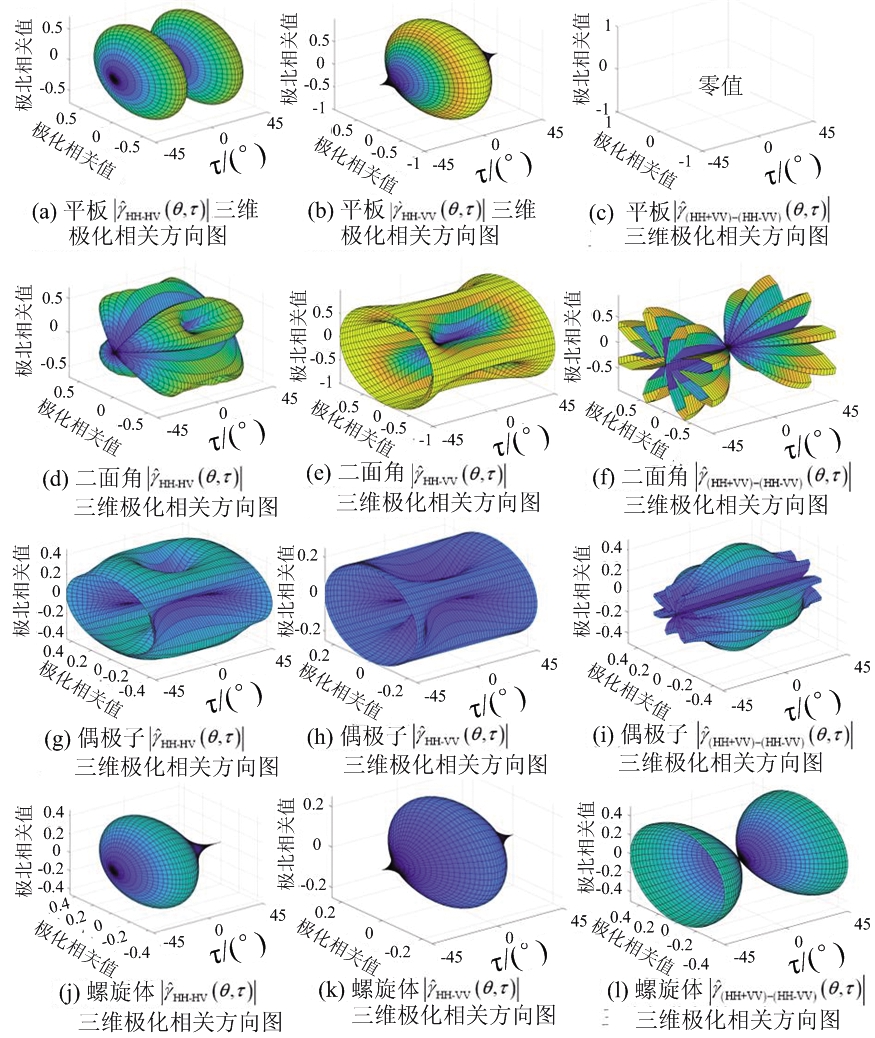
图 2 典型散射结构的三维极化相关方向图
3.1 极值点分析
本文首先对三维极化相关方向图的极值点分布进行分析。在分析之前，4种典型散射体的三维极化相关方向图的数学表达式在表 1中进行总结。注意到典型散射体的极化椭圆率角平面具有周期性，如图 1(b)所示。其主值周期为θ∈[-90°,90°]，后面的分析也将在主值周期范围内。对于平板结构，其最大值点分布在τ=± 22.5°位置处的圆上，最小值点位于τ=0°,±45°位置处。对于二面角结构，最小值点位于τ=±45°平面上的任一位置以及τ=0°并且θ=0°,±45°,±90°的位置上。最大值所在曲线的解析表达式很难进行求解，但是从图2(d)中可以观察到，其位于凹口上方的椭圆线上。对于偶极子结构，最大值所在曲线的解析表达式同样很难进行求解，但是从图2(g)中可以观察到，其位于凹口上方的椭圆线上。最小值点位于τ=0°并且θ=0°,±90°的位置处。对于螺旋体结构，其最大值点位于τ=-15°的圆上，最小值点位于τ=±45°位置处。
综上所述，不同散射结构三维流形中极值点的分布存在显著差异。值得注意的是，当τ=±45°时，除了偶极子外，其他三种散射体的极化相关值为0。在τ=0°条件下，平板结构的极化相关值
都为0。
3.2 曲面曲率分析
从图 2可以观察到不同散射体三维极化相关方向图表面的起伏程度存在显著差异。在一些位置处存在向里凹陷的谷结构，而另一些地方向外凸起形成脊的结构。这也反映了极化相关值随极化椭圆率角和极化方位角的变化对不同的散射体是不相同的。因此，本文引入微分几何中的高斯曲率(Gaussian Curvature, GC)来描述曲面的性质[23]。它能够衡量曲面在一个点局部沿各个方向是否有弯曲，以及弯曲的方向。仅当某点处曲面沿各个方向都有弯曲，高斯曲率值不为0。这里设定欧式空间中的坐标系向量为
曲面S的法向量n能够表示为
(13)
式中，符号×表示向量的叉积。这样微分几何中的第一基本形式F和第二基本形式D可以定义为
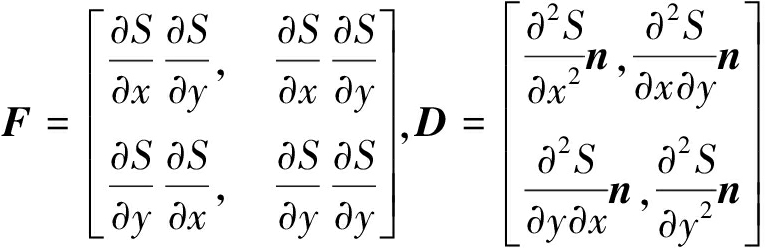
(14)
高斯曲率GC可以相应地定义为GC=det(D)/det(F)[23]。因此，4种典型散射体的极化相关值在(θ,τ)参数空间中的高斯曲率值分布情况如图 3所示。可以观察到，对于平板和螺旋体结构而言，高斯曲率值始终为0。实际上，从图2(a)中可以看出，对于某一固定极化椭圆率角下的切面，其极化相关值恒为定值，不随极化方位角的变化而变化。因此，其在参数空间中各点的高斯曲率值恒为0。对于二面角结构，可以观察到两个峰值分别位于θ=±45°并且τ=0°的两个位置，该位置也对应于图2(d)中三维极化相关方向图的凹口位置。对于偶极子结构，也可以观察到一个峰值点，这也与图2(g)中三维极化相关方向图的凹口位置相对应。
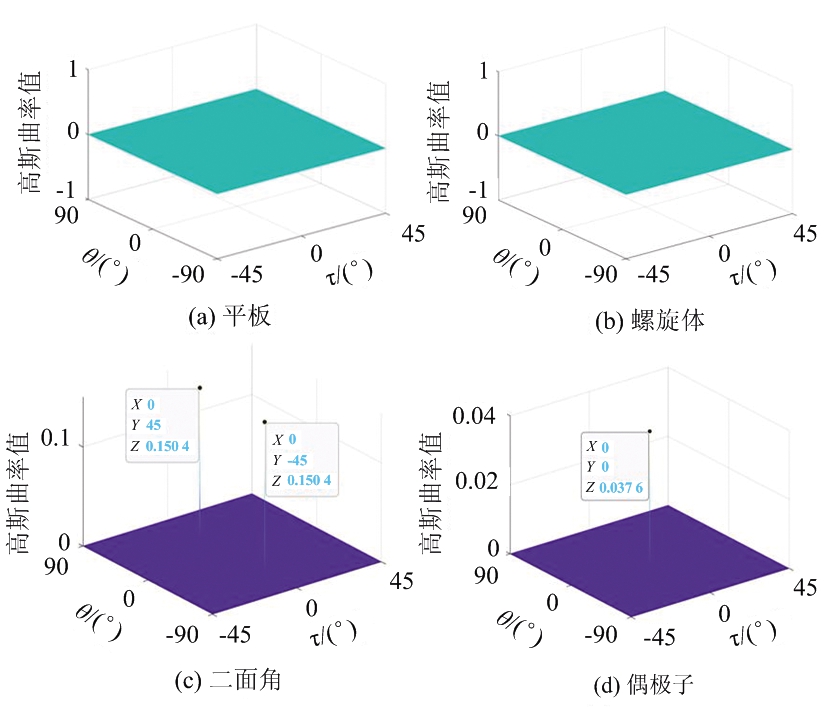
图 3 4种典型散射体三维极化相关方向图 
的高斯曲率值分布情况
综上所述，三维极化相关方向图的弯曲程度存在显著差异，对应的曲率值也不相同。与平板和螺旋体结构相比，二面角和偶极子结构三维极化相关方向图的高斯曲率值在参数空间中存在峰值，与它们三维极化相关方向图图形中的凹口位置相对应。峰值的大小和位置能为散射机理的解译提供可能。对此，本文定义了高斯曲率最大值特征GCmax这一新的极化特征，其数学表达式为
GCmax=max(|GC|)
(15)
在极化SAR应用中，舰船目标检测是一个重要的方向，无论是在军事还是民用领域。其中，海面通常以奇次散射为主，舰船目标通常以偶次散射和体散射为主。图 3所示的结果显示出平板结构与二面角和偶极子结构的GCmax特征值差异明显。因此，GCmax特征有望用于舰船检测中，下节将结合实测数据进行进一步说明。
4 基于三维极化相关方向图特征的舰船检测4.1 数据介绍
本文选取两景C波段的Radarsat-2数据进行实验验证。一景位于中国香港海域，在2008年12月16日拍摄获取。距离向和方位向的像素间隔分别为4.82 m和4.73 m。另外一景数据于2016年1月1日拍摄于直布罗陀海峡区域。距离向和方位向的像素间隔分别为4.60 m和4.73 m。从中国香港海域区域中选取两个感兴趣区域(Region of Interest, ROI)进行分析，区域的Pauli伪彩色图分别如图4(a)和(c)所示，真值图分别如图4(b)和(d)所示。从直布罗陀海峡区域选取一个ROI进行分析，区域的Pauli伪彩色图和真值图分别如图4(e)和(f)所示。3个ROI的详细信息如表 2所示。舰船的真值由专家借助AIS辅助数据进行标注。
表 2 3个ROI区域详细信息
ROI区域大小(像素数目) 舰船数目香港海域密集区域300×500142香港海域稀疏区域500×1 00012直布罗陀区域700×1 30037
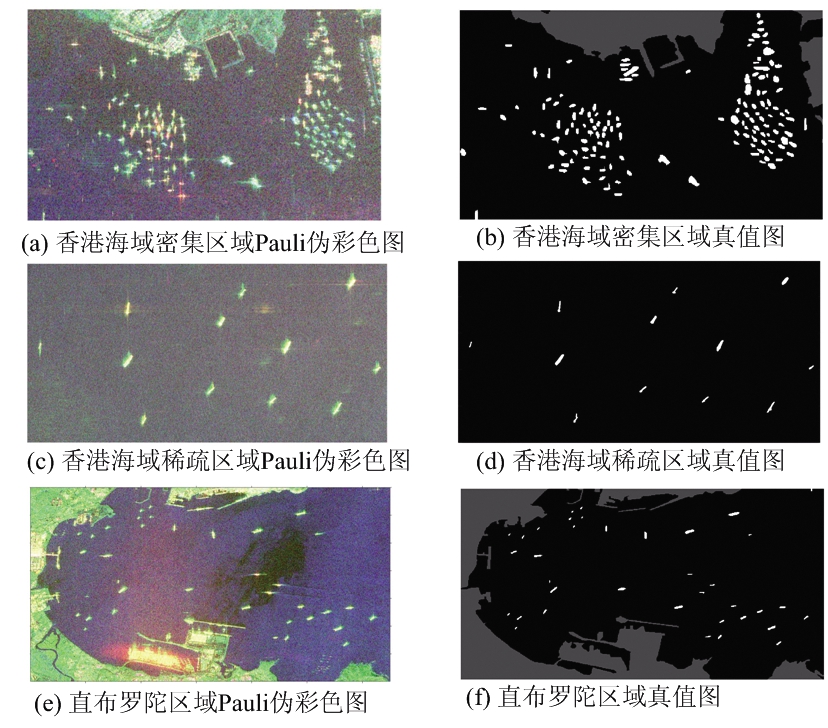
图4 ROI区域Pauli 伪彩色图和真值图
4.2 舰船和海杂波的三维极化相关方向图分析
本文以场景中随机选取的3个位于舰船区域的像素和3个位于海域区域的像素为例进行说明。由于篇幅的限制，本文选取三维极化相关方向图进行分析。6个像素的三维极化相关方向图如图 5所示，其中第一行为舰船像素的三维极化相关方向图，第二行为海域像素的三维极化相关方向图。特征图表面的颜色代表极化相关值的大小。尽管相比于图 2所示的理论结果，实测数据的三维极化相关方向图在形状上有所改变，但是，三维流形的一些特征仍有保留。例如图5(d)～(f)中海域像素的三维极化相关方向图与图2(a)相似，都表现为两个圆饼状的结构。图 5中第一行舰船像素的三维极化相关方向图的结果都表现出图2(d)和(g)所示的凹口结构，这在图 5第一行中用红色箭头进行标识。
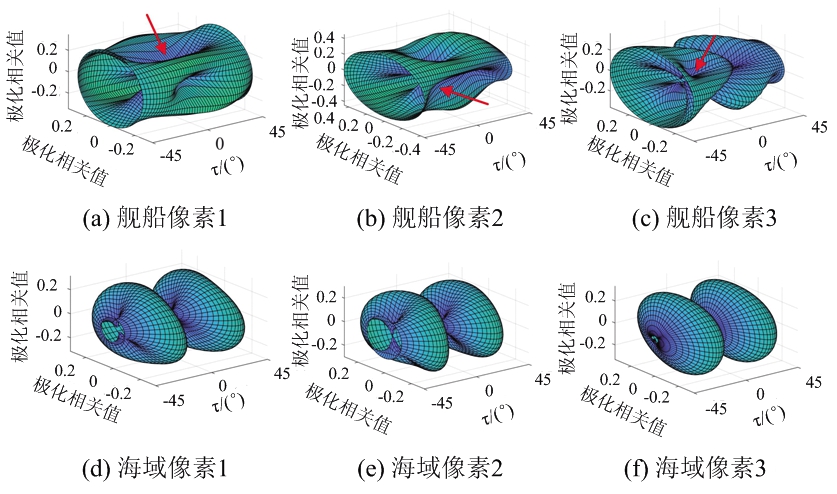
图 5 舰船和海域像素的
三维极化相关方向图
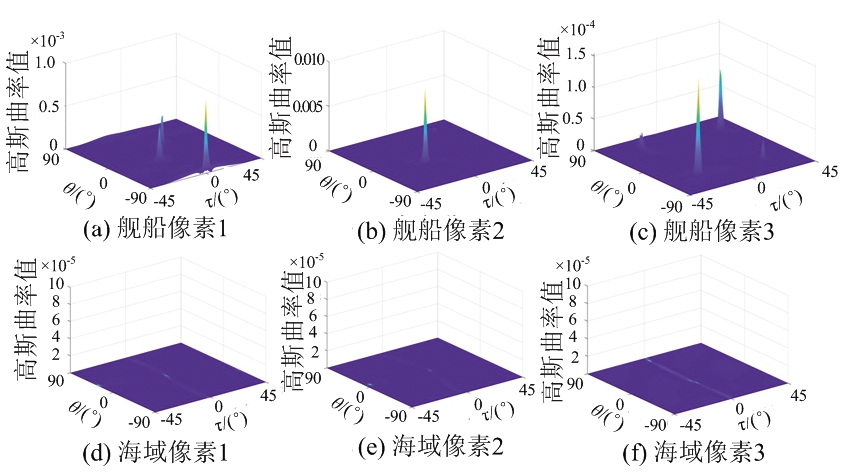
图6 舰船和海域像素高斯曲率分布情况
这两种类型像素的高斯曲率结果如图 6所示，其中第一行为舰船像素的结果，第二行为海域像素的结果。可以观察到海域像素的三维极化相关方向图的高斯曲率结果都趋近于0，与图 3第一行所示的平板和螺旋体结构的结果相似。而对于舰船像素，其高斯曲率结果中有峰值点的存在。因此，对于实测数据而言，本文提出的高斯曲率最大值特征GCmax有望有效地区分舰船和海杂波。
对此，本文选取从三维极化相关方向图中导出的高斯曲率最大值特征
用于舰船检测。3个ROI中
特征的直方图结果如图 7所示。蓝色的柱状图表示海域部分，橘色的柱状图表示舰船部分，横坐标为高斯曲率最大值，纵坐标为概率值。从3个ROI的结果中可以看出船海两部分的特征分布差异明显，通过简单的阈值分割有望将舰船部分检测出来。对此，本文根据三组直方图的结果，选取10-5作为阈值分割的门限。
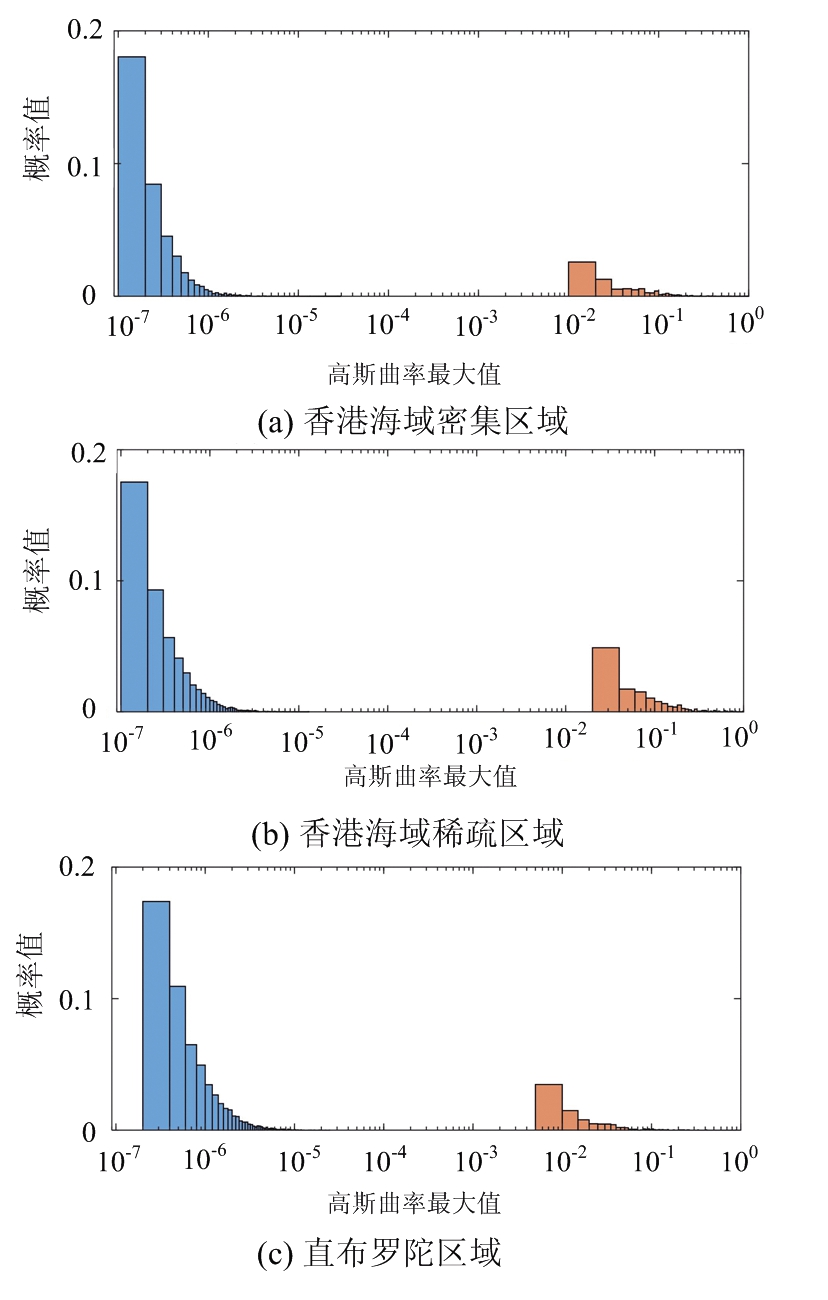
图7 高斯曲率最大值特征直方图(蓝色表示海域部分，橘色表示舰船部分)
4.3 基于三维极化相关方向图特征的舰船检测
根据以上分析，本文基于提取的高斯曲率最大值特征
提出了一种新的检测方法，算法流程图如图 8所示。阈值分割的门限已在上一节中进行了分析。为了减少阈值分割后孤立小区域所带来的虚警，本方法采用形态学处理的手段，滤除区域面积小于最小舰船所占像素数目50%的目标。二值化的检测结果采用定量指标FoM(Figure of Merit)进行评估，其表达式如下所示：
(16)
式中，NC，NFA和NM分别代表正确检测数目、虚警数目和漏检数目。对于一个目标而言，如果其中超过α%的像素数目被检测到，则认为该目标被正确检测。系数α从10到50都被验证过，当α=10时对比方法的性能能够达到最优。如果目标中的任一像素都与真值没有重合，则认为该目标为虚警。除了以上两种情况外的目标为漏检。
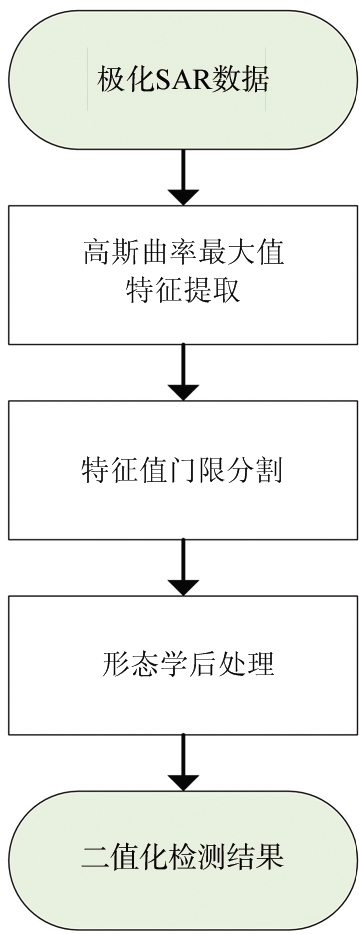
图8 算法流程图
为了进行对比实验，本文选取SO-CFAR检测器[24]和新近提出的NPNF舰船检测器[25]进行对比。对于SO-CFAR方法，后向散射总功率特征SPAN被选取用于舰船检测。根据区域中最大和最小船只所占像素数目，香港海域密集区域、香港海域稀疏区域和直布罗陀区域中目标-保护-背景窗的大小分别设置为3-9-19、3-21-31和3-9-19。此外，3个ROI中虚警率都设置为10-3。对于NPNF方法，由于其需要海域样本的先验信息，从每个ROI中各随机选取了一块50×50像素大小的海域样本。同样地，由于该方法中也用到了CFAR方法，3个ROI中的虚警率同样设置为10-3。
3个ROI中的舰船检测结果分别如图 9、图 10和图11所示，定量化的检测结果如表 3所示。对于香港海域密集区域，本文提出的方法优于对比方法，FoM指标比性能最佳的NPNF方法高出1.27%，同时本文提出方法的结果中虚警目标更少。对于直布罗陀区域，所提方法同样具有最好的性能，FoM指标比最好的SO-CFAR对比方法高出5.27%，虚警和漏检目标相比对比方法同样也更少。对于舰船稀疏的区域，所提方法同样能保持与对比方法相同的性能。值得注意的，相比于SO-CFAR方法，本文所提方法和NPNF方法能够检测到更多的舰船像素，舰船的轮廓也更加完整，例如图10红圈所标识的舰船目标。
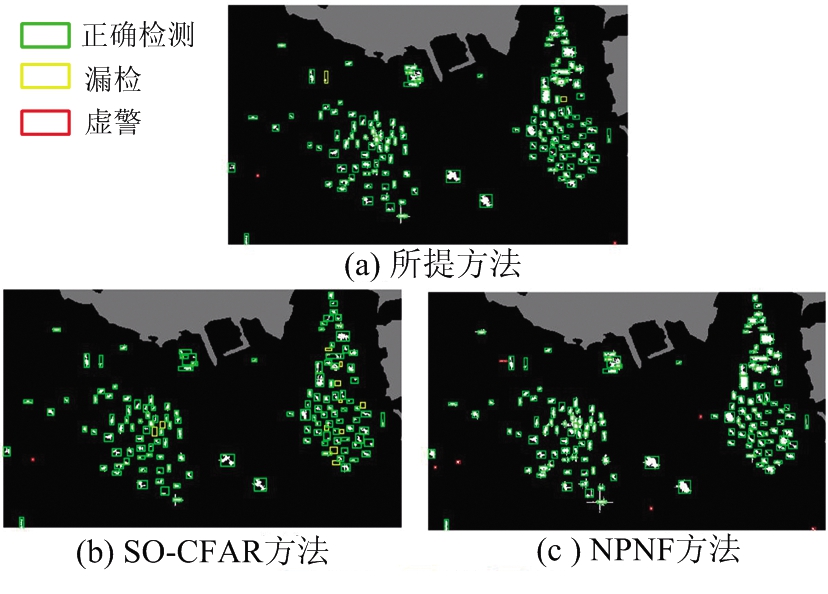
图9 香港海域密集区域舰船检测结果
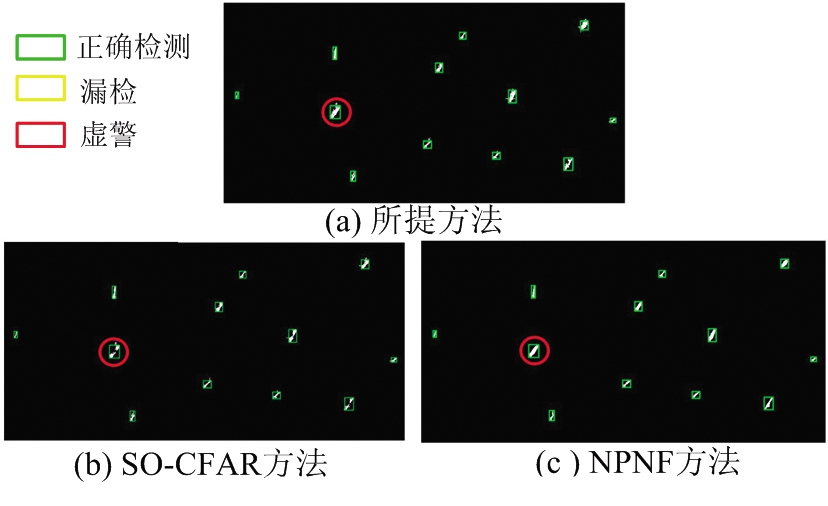
图10 香港海域稀疏区域舰船检测结果
图11 直布罗陀区域舰船检测结果
表3 3个区域舰船检测定量化结果
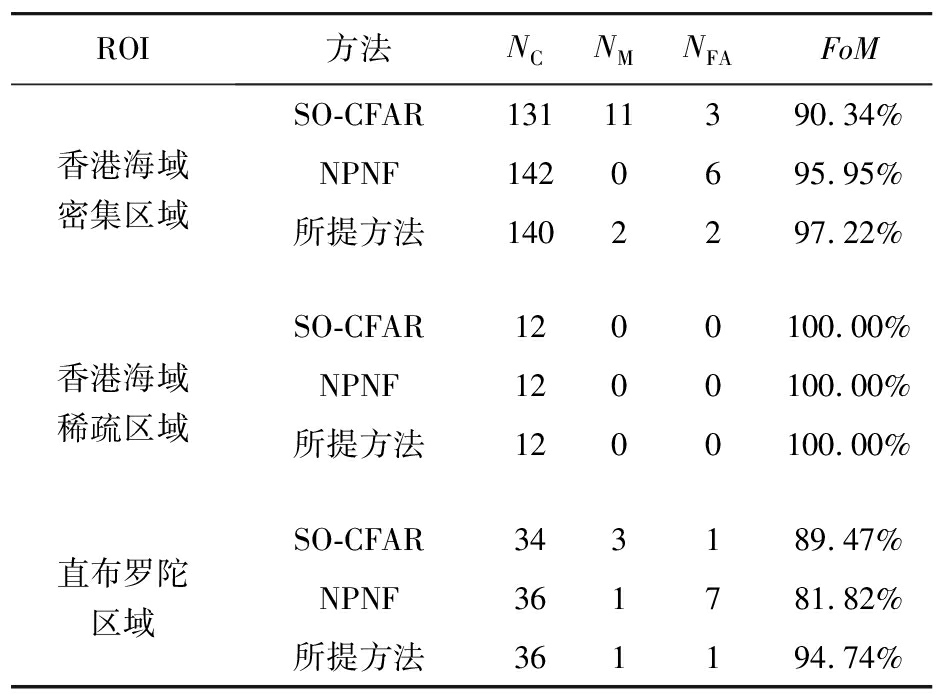
ROI方法NCNMNFAFoM香港海域密集区域SO-CFAR13111390.34%NPNF1420695.95%所提方法1402297.22%香港海域稀疏区域SO-CFAR1200100.00%NPNF1200100.00%所提方法1200100.00%直布罗陀区域SO-CFAR343189.47%NPNF361781.82%所提方法361194.74%
4.4 实验结果的讨论
综合上一节的定量化的实验结果，可以看到本文提出的方法对于近岸密集舰船区域有很好的检测性能，性能都优于对比方法，漏检和虚警目标更少。同时对于远岸舰船稀疏区域，本方法也能够保持与对比方法相同的检测性能，同时检测出的舰船轮廓更为完整。虽然对比方法中的NPNF方法在稀疏区域中所检测出的舰船轮廓也较为完整，但是该方法需要海域样本的先验知识，这在某些情况下可能是很难获取的。
本文所提方法对舰船检测性能的提升来自于所提取的高斯曲率最大值特征量。海面通常以奇次散射为主，而舰船目标通常以体散射与二次散射为主。本文借助提出的三维极化相关方向图可视化工具，发现奇次散射与体散射和二次散射类型散射体的三维极化相关方法图的一个明显的区别是是否有凹口，而高斯曲率最大值特征能够很好地反映凹口的有无以及凹口凹陷的程度。所以，本文提取的高斯曲率最大值特征能够很好地区别海杂波和舰船目标，实测数据的高斯曲率结果和直方图结果也很好地验证了本文提出的高斯曲率最大值特征的有效性。最后通过简单的阈值分割方法就能将舰船目标检测出来。3个区域中的舰船检测结果也同样表明了所使用阈值的鲁棒性。
值得注意的是，所提方法中在香港海域密集区域有两个虚警目标，在直布罗陀区域有一个虚警目标。这三个虚警目标在图12所示的Pauli伪彩色图中用红圈进行标识。可以观察到图12(a)中红圈标识的虚警出现的位置处有两个红色的亮斑，散射机理以二次散射为主。这可能是受到周围密集舰船的影响所形成的。图12(b)中红圈标识的虚警出现的位置由于受到陆地的影响，海面部分偏红，导致所标识的海域二次散射成分偏高，最终导致了虚警的产生。
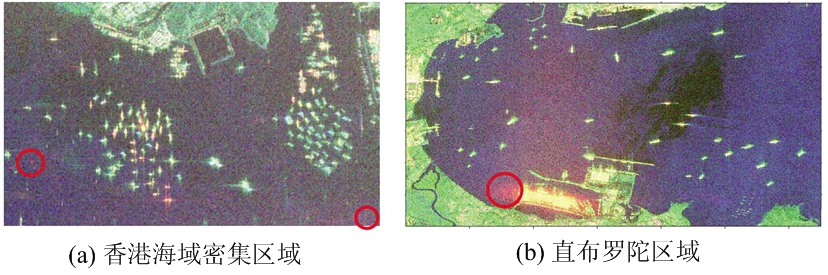
图12 所提方法舰船检测结果中虚警区域标识
5 结束语
本文提出了一种三维极化旋转域解译工具，能够表征极化相关值随极化方位角和极化椭圆率角的变化情况。实验表明不同典型散射体的三维极化相关方向图存在显著差异，着重表现在极值点的分布和曲面起伏程度的不同。为了刻画这些三维流形，本文引入了微分几何中的高斯曲率，提出了高斯曲率最大值这一新的极化特征。结合星载极化SAR实测数据验证了高斯曲率最大值特征能够有效区分舰船和海杂波。结合该特征，本文提出了一种阈值分割的舰船检测方法。与传统的CFAR方法和新近提出的NPNF舰船检测方法相比，本文方法表现出更好的舰船检测性能。尤其是在近岸舰船密集区域，检测结果得到明显提升。
[1] LEE J S, PORRIER E. 极化雷达成像基础与应用 [M]. 北京:电子工业出版社, 2013:1-296.
[2] CHEN S W, WANG X S, XIAO S P, et al. Target Scattering Mechanism in Polarimetric Synthetic Aperture Radar[M]. Singapore: Springer, 2018:1-225.
[3] 王雪松, 陈思伟. 合成孔径雷达极化成像解译识别技术的进展与展望[J]. 雷达学报, 2020, 9(2):259-276.
[4] GUI R, XU X, YANG R, et al. Generalized Zero-Shot Domain Adaptation for Unsupervised Cross-Domain PolSAR Image Classification [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15:270-283.
[5] LI H L, LI M D, CUI X C, et al. Man-Made Target Structure Recognition with Polarimetric Correlation Pattern and Roll-Invariant Feature Coding [J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19:1-5.
[6] SCHULER D L, LEE J S, KASILINGAM D, et al. Surface Roughness and Slope Measurements Using Polarimetric SAR Data [J]. IEEE Trans on Geoscience and Remote Sensing, 2002, 40(3):687-698.
[7] CHEN S W, WANG X S, SATO M. Uniform Polarimetric Matrix Rotation Theory and Its Applications [J]. IEEE Trans on Geoscience and Remote Sensing, 2014, 52(8):4756-4770.
[8] CHEN S W. Polarimetric Coherence Pattern: A Visualization and Characterization Tool for PolSAR Data Investigation [J]. IEEE Trans on Geoscience and Remote Sensing, 2018, 56(1):286-297.
[9] CUI X C, TAO C S, SU Y, et al. PolSAR Ship Detection Based on Polarimetric Correlation Pattern [J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(3):471-475.
[10] XIAO S P, CHEN S W, CHANG Y L, et al. Polarimetric Coherence Optimization and Its Application for Manmade Target Extraction in PolSAR Data [J]. IEICE Trans on Electronics, 2014, 97(6):566-574.
[11] 崔兴超, 粟毅, 陈思伟. 融合极化旋转域特征和超像素技术的极化SAR舰船检测 [J]. 雷达学报, 2021, 10(1):35-48.
[12] TAO C S, CHEN S W, LI Y Z, et al. PolSAR Land Cover Classification Based on Roll-Invariant and Selected Hidden Polarimetric Features in the Rotation Domain [J]. Remote Sensing, 2017, 9(7):660.
[13] 王雪松,陈思伟.合成孔径雷达极化成像解译识别技术的进展与展望[J].雷达学报,2020,9(2):259-276.
[14] ZYL J J V, ZEBKER H A, ELACHI C. Imaging Radar Polarization Signatures: Theory and Observation [J]. Radio Science, 1 987, 22(4):529-543.
[15] CHOE B H, OSINSKI G R, NEISH C D, et al. Polarimetric SAR Signatures for Characterizing Geological Units in the Canadian Arctic [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(11):4406-4414.
[16] NUNZIATA F, MIGLIACCIO M, GAMBARDELLA A. Pedestal Height for Sea Oil Slick Observation [J]. IET Radar, Sonar & Navigation, 2011, 5(2):103-110.
[17] VERMA A, DEY S, BHOGAPURAPU N, et al. Polarimetric SAR Signature for Crop Characterization [C]∥Proceedings of the IGARSS 2021 - 2021 IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium:IEEE, 2021:1-6.
[18] TOUZI R, OMARI K, SLEEP B, et al. Scattered and Received Wave Polarization Optimization for Enhanced Peatland Classification and Fire Damage Assessment Using Polarimetric PALSAR [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(11):4452-4477.
[19] LIU T, JIANG Y N, MARINO A, et al. The Polarimetric Detection Optimization Filter and Its Statistical Test for Ship Detection [J]. IEEE Trans on Geoscience and Remote Sensing, 2022, 60:1-18.
[20] CUI X C, SU Y, CHEN S W. A Saliency Detector for Polarimetric SAR Ship Detection Using Similarity Test [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(9):3423-3433.
[21] LI M D, CUI X C, CHEN S W. Adaptive Superpi-xel-Level CFAR Detector for SAR Inshore Dense Ship Detection [J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19:1-5.
[22] LIN H, CHEN H, JIN K, et al. Ship Detection with Superpixel-Level Fisher Vector in High-Resolution SAR Images [J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(2):247-251.
[23] GONG Y. Spectrally Regularized Surfaces[D]. Zürich, Switzerland; ETH-Zürich, 2015.
[24] TRUNK G V. Range Resolution of Targets Using Automatic Detectors [J]. IEEE Trans on Aerospace and Electronic Systems, 1978, 14(5):750-755.
[25] LIU T, YANG Z Y, ZHANG T, et al. A New Form of the Polarimetric Notch Filter [J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19:1-5.
