0 引言
目前，传统的针对阵列模型或导向矢量失配等问题提出的稳健算法为：空间谱估计算法、稀疏矩阵重构算法、对角加载(Diagnoal Loading，DL)算法、特征子空间算法(Eigenspace-based，ESB)和不确定集约束算法[1]。对角加载波束形成算法[2-4]通过在协方差矩阵上添加载平衡因子使得自适应和鲁棒性达到最佳平衡，但是因子大小的不易估计，改善效果不明显。特征子空间算法[5-6]和投影方法[7]本质上相同，已知期望和干扰信号导向矢量和特征向量，将所需信号投影到干扰互补子空间，从而得到最优的加权矢量，更好地消除了导向矢量失配的误差，但是在低信噪比时，信号功率和噪声功率大小非常接近，通过特征值大小分辨出信号和噪声子空间十分困难。稀疏矩阵算法是利用矩阵信号干扰空间的稀疏性，对信号的接收矩阵进行了重构，利用较低的快拍数恢复出原来的信号，以此降低算法计算量。不确定集约束[8]的方法不同与以上对协方差矩阵的改进，可看成是对权值的优化约束问题。当采样协方差矩阵中包含了期望信号时，会出现信号“自消”现象，传统的稳健自适应算法在期望导向量严重失配或高信噪比时，性能会下降[9]。
为了提高自适应波束算法的稳健性，文献[10]指出期望信号在空域中的功率分布中有残留噪声，消除残留噪声可以重构出更加精确的期望导向矢量和干扰加噪声矩阵协方差，但随着信噪比的提高，干扰抑制减弱，算法性能变差。文献[11-12]提出了对传统的波束形成算法进行加权，形成改进算法，虽然相比传统算法副瓣电平大大降低，小样本情况下方向图稳定性也得到了极大的改善。但是由于没有有效地提取出干扰噪声信号协方差矩阵，故容易产生“自消”。文献[13]在基于标准Capon波束形成器对期望矢量先进行波束预处理，降低了导向矢量失配的影响，但是对干扰移动和低样拍等情况下的算法性能没有改善。文献[14]在文献[13]的基础上展宽了干扰零陷，但是展宽干扰零陷引入的计算误差会影响算法的性能，并且算法需要对所有空域进行积分，运算量大。文献[15]基于Capon的空间谱估计算法，重构出精度较高的干扰噪声协方差矩阵和期望信号，降低了失配对算法的影响。为了降低小样本对波束性能的影响，文献[16]提出了一种基于稀疏干扰矩阵的稳健波束算法，该算法利用信号在空域的稀疏性，仅设置扰动参量对干扰方向的谱估计进行修正并重构，性能良好且计算复杂度低。文献[17-18]提出了缺少先验信息的协方差矩阵重构算法，在未知阵列结构的情况下性能良好，但是在估计期望信号导向矢量的时候不确定约束集的大小很难选择，增大了算法的复杂性。文献[19]使用去相关性算法得到新的干扰噪声协方差矩阵，有效地降低了干扰和期望信号的相关性，但该算法提高波束形成的性能效果有限。文献[20]针对干扰运动的抑制问题提出了一种零陷加宽的方法。
本文利用残留噪声功率消除重构期望导向矢量和干扰协方差矩阵减小算法计算量，再基于改进的MVDR算法有效地降低了副瓣和样本对算法性能的影响，最后在干扰方向展宽零陷解决了干扰波动的问题。
1 阵列信号模型
一般假设远场回波信号为数量低于阵元数的非相干点源窄带信号，其中期望点源在θ0方向，干扰点源在θi(i∈1,2,…,p)方向上，且M>P+1，接收端放置M个单元的均匀线阵列，阵元间距d为半波长，相邻元件之间路径长度的差异会导致相位差为
则阵列接收信号经过理想化处理后的采样矩阵为
X(k)=AS(k)+N(k)=
xs(k)+xi+n(k)
(1)
式中，A=[a(θ0),a(θ1),…,a(θp)]T为M×(P+1)维阵列流型矩阵，[]T为矩阵转置；S(k)为采样信号波形，k为快拍数；a(θ0)为期望导向矢量，a(θi)为干扰导向矢量，n(k)为独立同分布的高斯白噪声向量。
M元均匀线阵列天线的接收信号协方差矩阵为
R=E[x(k)x(k)H]=
Rs+Ri+n=
(2)
式中，Rs为期望信号协方差矩阵，Ri+n为干扰加噪声协方差矩阵，
为噪声功率，I为M维单位矩阵。
根据最大化输出信干噪比(MSINR)准则，即
(3)
标准Capon波束形成[1]可以表示期望信号无失真响应下，阵列输出功率最小的最优化问题，即最小方差无失真响应：
(4)
由此可得最优权值为
(5)
但在实际应用中，回波信号总是会包含期望信号，采样拍数也不可能无限，因此通常会用T次快拍下的采样协方差矩阵
来替代， 得到标准Capon波束形成的权值为
(6)
2 本文提出的算法2.1 期望信号矢量估计
根据文献[6]，MUSIC谱估计算法功率谱表示为
(7)
由文献[9]所提出的理论，假设单个信源在θi1方向、功率为σ2，则理想协方差矩阵为
将其代入式(7)，令θ=θi1，可得
(8)
式(8)可表明，每个回波信号辐射区域中的功率是有用信号功率与空域噪声功率之和，并且回波信号中包含的噪声功率为自然噪声功率的1/M。所以可推出空域噪声功率可以利用功率谱在非信号区间进行估计：
(9)
式中，Θn为非期望信号角度区域，θt为在Θn的采样点，T为采样点个数。根据式(8)、式(9)，可获得实际的噪声功率和噪声协方差矩阵：
(10)
为了降低计算量，可先结合文献[13]对波束预处理，然后消除空域噪声成分后重构期望信号，其最大特征值对应的特征矢量等于期望信号导向矢量。
2.2 干扰噪声协方差矩阵估计
由2.1节得到期望信号的协方差矩阵
故将
进行特征分解，特征值降序重排，取较大特征值构成其信号子空间B。根据信号和噪声空间的正交特性，因此对每一个快拍信号x(t)，都可用Q=I-BBH构造投影矩阵来消除期望成分，故
QH(xs(t)+xi+n(t))≈QHxi+n(t)
(11)
由式(11)可得
QHRQ≈
(12)
又因为Q为信号子空间的正交投影补矩阵，而
包含的主要是信号导向矢量，根据独立不相干的矢量正交性，Q矩阵不会改变导引矢量模值，所以
近似等于
故
(13)
根据式(13)可得，干扰协方差矩阵
由于式(12)的近似有误差，所以的估计也不够精确，但中最主要包含的信息还是干扰信号。通过目前求得的干扰协方差矩阵和干扰导向矢量就可得到干扰功率
结合功率协方差矩阵表达式构造出干扰加噪声协方差矩阵：
(14)
式中，
为干扰信号的导向矢量，
为实际噪声功率，I为单位矩阵。综上可知，用干扰功率估计的干扰噪声协方差矩阵比直接用投影法估计协方差矩阵更加准确。
2.3 低副瓣加权和特征干扰相消
虽然重构了导向矢量和干扰噪声协方差矩阵，传统的RCB算法在导向矢量失配的情况下具有稳健性，但是当小样本和副瓣较高时，接收矩阵出现低秩和奇异解，从而导致算法产生较大的误差。本文利用类似输出方向图加窗的方法，对最优权值进行加窗，使其随单元分布成锥形减弱，从而达到副瓣电平降低的目的。现在采用Dolph-Chebyshev加权函数对W1加窗，加窗后的期望信号方向矢量为
aT(θ0)=W1·a(θ0)
(15)
另外，通过文献[12]提出的特征干扰相消器，本文对干扰信号矢量建立新的线性约束，这样提高干扰信号抑制和噪声抑制自由度，优点是在小样本数下，减小噪声的不稳定对方向图主瓣形成的影响。对应线性最小方差约束(LCMV)算法，特征干扰相消器可称为线性特征干扰相消器(LCEC)。
LCEC的准则为
(16)
式中，Ui为干扰子空间矩阵，C为约束矩阵,f为对应的约束响应矢量。干扰噪声协方差矩阵
为噪声空间，Λi、Λn均为对角阵，对角元素与子空间中的特征值一一对应，代表信号功率，并且
当M×R维的C矩阵为期望方向矢量a(θ0)时，对应的约束值f为常数，既是MVDR算法的改进。
由拉格朗日乘子法求得式(16)的最佳权值为
WDREC= UnUna(θ0)(aH(θ0)UnUna(θ0))-1
(17)
2.4 干扰零陷展宽
本文结合了文献[12]算法对权值WDREC进行修正并对干扰输出功率进行参数约束，实现干扰区域零陷加宽。
要使上一节得到的权值WDREC更加接近最终权值W，对权值进行二次约束，可得约束方程如下：
(18)
式中，ε为极小的自定义约束且保证ε>0。利用Lagrange乘子法求解式(18)得目标函数为
(19)
式中，λ为拉格朗日乘数。
对式(19)关于W求偏导并使偏导等于零解得
(20)
最优拉格朗日乘子λ可以通过求解约束方程获得，将式(20)代入约束条件式(19)中，可得关于λ的方程：
(21)
从式(14)可知理想干扰协方差矩阵表达式为
(22)
式中：
为干扰信号矢量；
为其矢量对应的特征值并表示干扰功率，且有
式(22)可以改写为
g(λ)=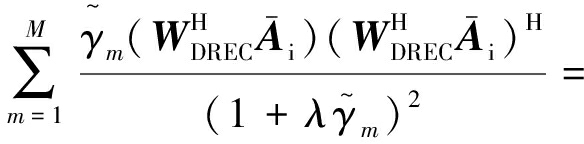
(23)
式中，
1) 当λ>0时，g(λ)是关于λ的单调递减函数，并且当λ=0时，g(0)>ε；当λ→∞时，有
因此，λ∈(0,+∞)内必有唯一的一个解满足约束方程g(λ)=ε。同时，g(λ)关于
的单调递减函数，为了减少计算量，缩小λ的取值范围，将式(23)中的用
代替，令
则有如下不等式：
(24)
可得λ的取值范围为
(25)
由于g(λ)为λ的单调递减函数，g(λ)=ε取值越小越好，因此最优λ乘数取值越大为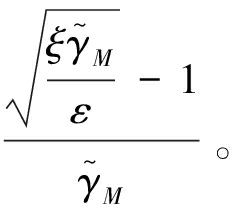
2) 同样，当λ<0时，g(λ)关于λ的单调递增函数，显然有
因此，必有唯一解λ∈(-∞,0)满足约束方程g(λ)=ε。式(25)变为
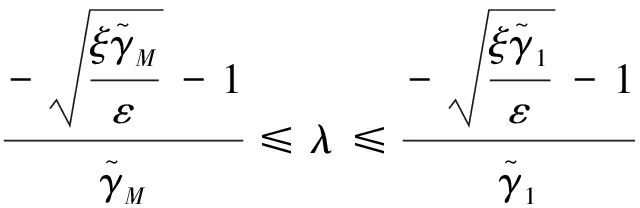
(26)
又因为g(λ)为λ的单调递增函数，因此最优λ乘数取值为
综上可知，由于约束参数ε取值越小越好，所以得到正负最优λ关于零点对称。
3 仿真实验分析
为了证实本文算法的可行性，实验将和理想MVDR算法、文献[10]残留噪声功率消除算法、文献[12]的特征干扰相消算法、文献[14]谱估计和零陷展宽结合算法、文献[20]基于二次约束的零陷加宽算法进行分析对比。假设阵元数M=16，期望信号的真实角度θ0=10°，本文算法和比较波束算法为非盲算法，在波束形成前用分辨率较低的DOA粗略估计得期望信号角度为
回波信号存在估计失配情况。干扰信号的真实方位角为θ1=-40°和θ2= 50°，所有结果均由100次独立的蒙特卡洛实验统计得到。
实验1： 不同约束参数ε正负拉格朗日乘数的算法分析
当输入SNR=10 dB，干噪比均为30 dB，采样拍数N=50。图1、图2的约束参数分别取较大ε= 10-2和较小ε= 10-12时波束对比。
图1 ε=10-2的方向图差异
图2 ε=10-12的方向图差异
从图1可以看出，当ε取值较大时，正负λ乘数都能实现期望导向失配修正和零陷变宽，且主瓣和副瓣吻合比较一致，波动较小。随着ε取值越来越小，即约束参数精度越高时，如图2所示，干扰零陷的深度会加深，功率转移到主波束方向，导致主瓣相应变宽和副瓣上升，算法性能略有下降。综上可知，约束参数变化对算法性能虽然有影响，但该算法仍然拥有良好的抗干扰运动和抗系统误差的鲁棒性。
实验2： 导向矢量失配时不同算法的波束图分析
当期望信号和两个干扰信号的实际回波方向为θ0=10°，θ1=-40°和θ2= 50°。预估方向偏离5°为
在ε= 10-12下，图3、图4、图5为各种算法在导向矢量失配时，变量为单一条件的归一化波束方向图对比。
当期望信号真实方向为θ0=10°，预估方向为
输入为高信噪比SNR=60 dB，干噪比均为30 dB，快拍数N=50。
图3 导向矢量失配下的归一波束图
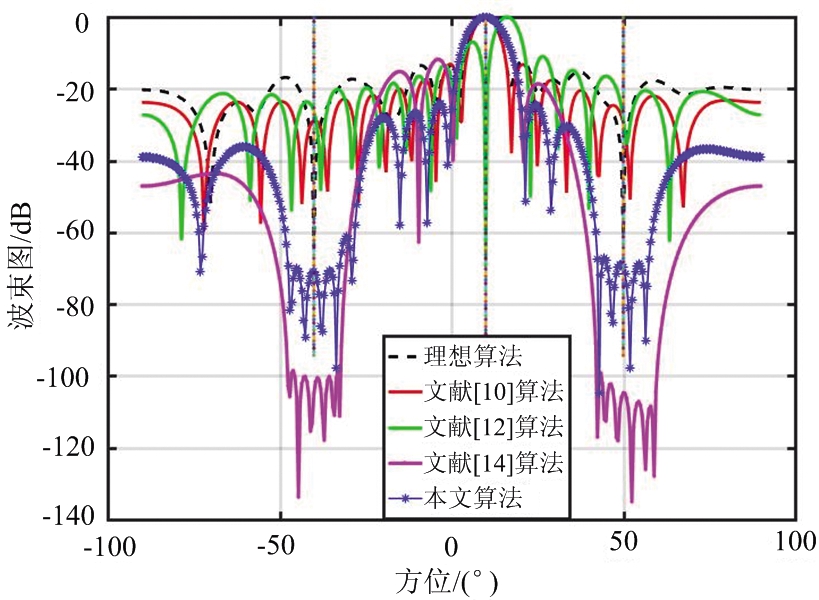
图4 高信噪比下的归一波束图
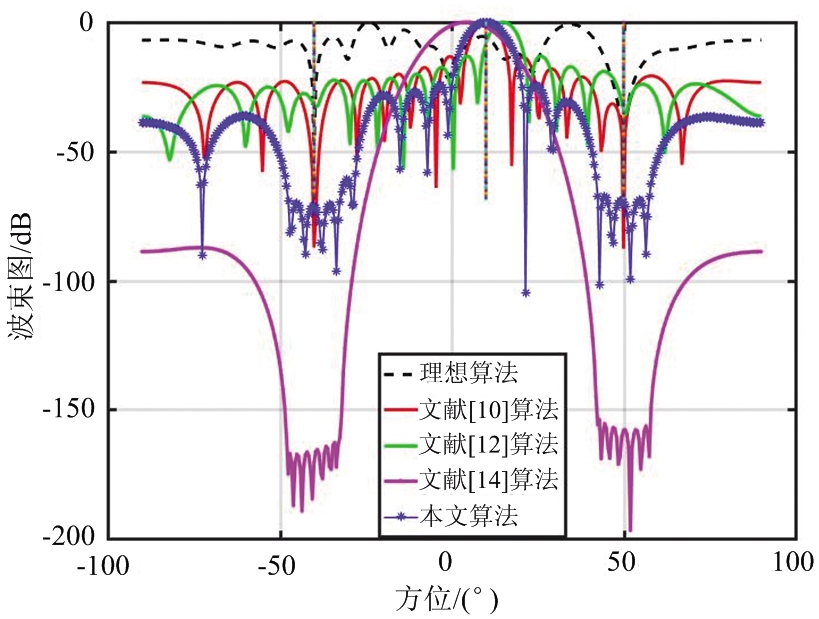
图5 低样拍数下的归一波束图
当期望信号真实方向为θ0=10°，估计方向为
输入信噪比SNR=10 dB，干噪比均为30 dB，快拍数N=15。
从图3可以看出，在期望矢量失配时，几种稳健算法都能够满足失配下的校准和干扰抑制，深度有所差别。文献[14]和本文的算法不仅在干扰位置产生较深的零陷，并且对零陷有效的展宽，有利于抗干扰移动。但是从计算量来说，前者进行空间谱估计时使用了大量积分运算，而后者的计算主要是矩阵分解，计算量大大减小，所以本文算法更有利于实际应用。并且，由于本文使用了副瓣控制加权，在主瓣宽未发生大的扩展的前提下副瓣高度明显比其他算法低，大大地提高了算法的性能。随着信噪比的提高，如图4可知文献[10]算法由于信噪比过大，使x(t)的近似估计误差会增大，干扰信号无法正常抑制，性能急剧下降。在低样拍数的情况下，如图5所示，文献[14]算法的样拍数低于阵元数后性能急剧的恶化，导向矢量发生偏移，这是因为在低样拍数下接收信号协方差矩阵发生误差，无法再近似为实际信号计算。综上分析，本文算法解决了在高信噪比和低样拍数的情况下性能恶化的问题。
实验3： 不同输入SNR下的输出SINR分析
当期望信号和两个干扰信号的实际回波方向为θ0=10°，θ1=-40°和θ2= 50°。预估方向为在快拍数N=50固定不变时，SNR从-10 dB到30 dB逐渐变化，每种情况均由100次独立的蒙特卡洛实验统计得到。图6为输入SNR对SINR的影响。
图6 不同输入信噪比下的输出信干噪比
从图6可以看出，本文算法使用的展宽零陷算法带来了约束计算的误差，会导致性能的下降，但是用副瓣加权的算法可以优化旁瓣，从而弥补性能的下降，使其远远优于其他算法。并且，本文算法利用特征干扰相消算法重构干扰矩阵从根本上解决了在高信噪比下干扰抑制下降的问题，使输出SINR与理论情况相差很小。
实验4： 不同采样拍数下的输出SINR分析
当期望信号和两个干扰信号的实际回波方向为θ0=10°，θ1=-40°和θ2=50°。预估方向为在信噪比SNR=10 dB固定不变时，观察快拍数在N=[5:10:105]范围内，SINR随快拍数的曲线对比。图7为不同快拍数下的输出信干噪比。
图7 不同快拍数下的输出信干噪比
从图7可知，本文算法明显降低了快拍数对算法稳健性的影响，在极低的样本数下就能快速达到收敛，并且输出SINR接近理论值。相比本文算法，文献[14]达到性能收敛时样本数至少需要20。文献[12]和文献[20]都只考虑了单方面的因素，性能一般。理论波束算法在低样拍数时无法得到完整的样本协方差矩阵，所以算法性能出现急剧变化，直到快拍数为50才趋于收敛。综上可得，本文算法在不降低算法性能的前提下，大大提高了算法收敛的速度。
实验5： 随失配角度变化的输出SINR分析
当快拍数N=50，输入SNR=10 dB，JNR=30 dB固定不变。图8表示期望信号的失配角度在[-12:1:12]范围内，输出SINR的曲线对比。
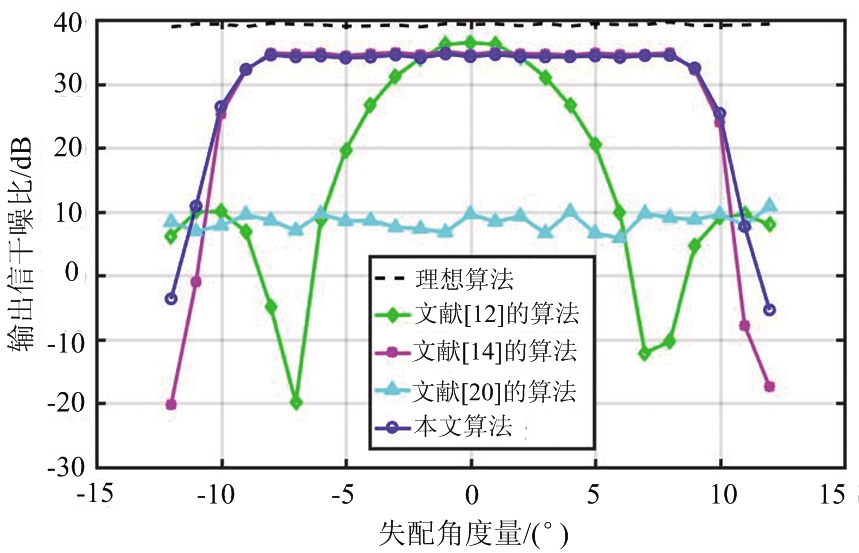
图8 不同失配角度下的输出信干噪比
由图8可得，本文的算法失配角度在[-8:1:8]有着良好的稳健性，使用了矩阵相消算法的文献[12]由于未对期望信号矢量进行估计，所以在角度失配方面稳健性差。文献[20]在期望信号失配时输出SINR发生了剧烈起伏，并且远离性能最优值。本文算法在导向矢量失配的情况下稳健性与空间谱估计算法近似，且宽度略宽。
实验6： 不同算法的复杂度对比分析
算法的运算速度是数字波束形成器实际应用的关键，为了减少FPGA和AD采样的压力，快速的自适应算法是对雷达工作性能的保证，所有算法在MATLAB上进行仿真，性能配备主频为3.79 GHz-CPU。在其他仿真条件不变的情况下，快拍数N=100，输入SNR=10 dB，干扰噪声比为JNR=30 dB。当将期望回波信号和强干扰信号预估范围设置为10°，L为信号空域内的总采样点数，N为阵元个数，M为空域回波信号总数。算法总运行的时间由100次独立的蒙特卡洛实验累计得到。
由表1可知，本文算法和文献[10]算法主要的运算是矩阵特征分解，因此处于同一个量级，文献[12]主要是矩阵求逆运算，而文献[14]算法在重
表1 不同算法的复杂度对比
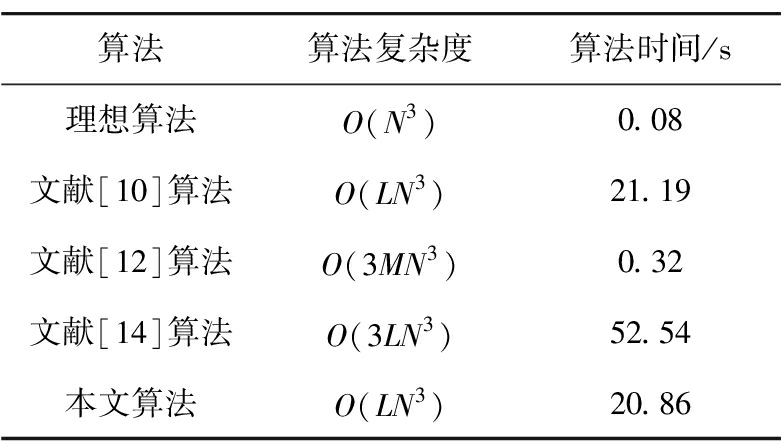
算法算法复杂度算法时间/s理想算法O(N3)0.08文献[10]算法O(LN3)21.19文献[12]算法O(3MN3)0.32文献[14]算法O(3LN3)52.54本文算法O(LN3)20.86
构干扰噪声矩阵时比本文算法增多了特征分解和空间积分运算，由于L≫N，所以当阵列数较小时，L的影响远远大于N，故大大地增加了算法的运算时间。
综上所述，本文算法在阵元数较大的时候，保证了算法的复杂度，在阵元数较小的情况下，减少算法的计算量。
4 结束语
本文算法首先基于残留噪声消除算法对期望信号矢量进行了估计，然后利用干扰功率估计算法构造了新的干扰噪声协方差矩阵，此算法较空间积分算法而言，性能更优，且计算量更小；接着为了降低零陷展宽算法误差对波束性能的影响，对最优权值进行副瓣加权降低波束的旁瓣；并结合特征干扰相消，消除快拍数对波束形成算法的影响；最后在构造干扰矩阵零陷之后，使用二次约束准则实现零陷加宽，虽然干扰区域展宽会使得零陷深度降低，但是提高了算法的鲁棒性，更有利于实际应用。仿真结果证明了该方法在降低协方差矩阵构造计算量的同时，克服了比较算法在高信噪比和低样拍数的情况中性能下降的问题，提升了导向矢量失配和抗运动干扰的能力。本文算法在高信噪比和强干扰等恶劣环境中都拥有良好的鲁棒性，通过降低快拍数的影响和减少计算量，使算法在雷达休止期拥有更快的波束校准和波束形成。
[1] 夏翔. 有限快拍与导向矢量误差两种情况下鲁棒波束形成的研究[D]. 南京:南京信息工程大学, 2020.
[2] MASELE M P, WU Xing, WANG Lijiao. A Robust Adaptive Beamforming with Diagonal Loading and Steering Vector Estimation [C]∥2019 IEEE 2nd International Conference on Electronic Information and Communication Technology (ICEICT), Harbin:IEEE, 2019:253-257.
[3] 崔琳, 张熠鑫, 焦亚萌. 一种导向矢量失配的鲁棒波束形成算法[J]. 西安工程大学学报, 2021, 35(1):24-29.
[4] LI Wenxing, YANG Bin, ZHAO Yu. Low-Complexity Non-Uniform Diagonal Loading for Robust Adaptive Beamforming[C]∥2017 International Applied Computational Electromagnetics Society Symposium(ACES), Suzhou:IEEE, 2017:1-2.
[5] 刘晓军, 刘聪锋, 廖桂生. 子空间投影稳健波束形成算法及其性能分析[J]. 系统工程与电子技术, 2010, 32(4):669-673.
[6] 李鹏, 夏翔, 俞传富, 等. 基于导向矢量估计的鲁棒波束形成[J]. 雷达科学与技术, 2020, 18(1):21-26.
LI Peng，XIA Xiang，YU Chuanfu，et al. Robust Beamforming Based on Steering Vector Estimation[J]. Radar Science and Technology, 2020, 18(1):21-26.(in Chinese)
[7] 杨航. 快速稳健的自适应天线波束形成算法研究[D]. 哈尔滨:哈尔滨工程大学, 2019.
[8] LI Peng, WANG Liyan, SUN Zeyu, et al. Robust Adaptive Beamforming with Sidelobe Controlled Based on Improved Objective Function[C]∥2019 International Applied Computational Electromagnetics Society Symposium-China(ACES), Nanjing:IEEE, 2019:1-2.
[9] ZHANG X, LIU S, YAN F, et al. Robust Adaptive Beamforming Based on Covariance Matrix Reconstruction Against Steering Vector Mismatch[C]∥2019 IEEE/CIC International Conference on Communications in China(ICCC), Changchun: IEEE, 2019:283-286.
[10] ZHU Xingyu, YE Zhongfu, XU Xu, et al. Covariance Matrix Reconstruction via Residual Noise Elimination and Interference Powers Estimation for Robust Adaptive Beamforming [J]. IEEE Access, 2019, 7:53262-53272.
[11] YANG Jie, YANG Yixin, LEI Bo. An Efficient Robust Adaptive Beamforming Method Using Steering Vector Estimation and Interference Covariance Matrix Reconstruction [C]∥2018 OCEANS-MTS/IEEE Kobe Techno-Oceans(OTO), Kobe, Japan: IEEE, 2018:1-4.
[12] HAIMOVICH A. The Eigencanceler: Adaptive Radar by Eigenanalysis Methods[J].IEEE Trans on Aerospace and Electronic Systems, 1996, 32(2):532-542.
[13] 王昊, 马启明. 协方差矩阵重构的稳健自适应波束形成算法[J]. 声学学报, 2019, 44(2):170-176.
[14] 沈肖雅, 葛俊祥, 王奇. 一种稳健自适应波束形成算法[J]. 中国电子科学研究院学报, 2019, 14(4):373-380.
[15] GU Yujie, ZHANG Yimin. Adaptive Beamforming Based on Interference Covariance Matrix Estimation [C]∥ 2019 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA USA:IEEE, 2019:619-623.
[16] 鹿玉泽, 王玉玺, 郑家毅, 等.一种基于稀疏干扰协方差矩阵重构的稳健自适应波束形成算法[J]. 电子设计工程, 2017, 25(16):51-55.
[17] 闵仁江. 基于干扰噪声协方差矩阵重构的稳健自适应波束形成算法[D]. 南宁：广西大学, 2017.
[18] 郭云舟, 贾维敏, 金伟,等. 基于协方差矩阵锥化和导向矢量估计的鲁棒自适应波束形成算法[J]. 电光与控制, 2020, 27(10):57-61.
[19] 王宁章, 闵仁江, 许慧青. 基于干扰加噪声协方差矩阵重构的稳健自适应波束形成[J]. 微型机与应用, 2016, 35(23):62-64.
[20] 王金博， 孙青， 唐宏. 一种干扰零陷加宽的静态波束控制方法[J]. 微波学报, 2007(S1):230-233.
