0 引言
反导预警与空间监视雷达为了能够同时具有长时宽和大带宽，一般采用脉冲压缩体制。脉冲压缩在匹配滤波时会产生与多普勒频移成正比的附加延时，即距离多普勒耦合现象[1]。距离多普勒耦合现象对信号脉压、脉冲积累、距离检测及宽带回波开窗有较大影响，有效处理耦合带来的误差对于提升雷达高精度测距具有重要意义[2-7]。
距离多普勒耦合的修正量由雷达工作参数(脉宽、频率、带宽)及目标径向速度计算得到，其中雷达工作参数为系统输入量。因此，有效处理距离多普勒耦合的核心是目标的径向速度估计。目标径向速度则需要通过测速波形测量获取或目标滤波估计[8]。专用测速波形需要额外占用雷达的时间资源，且存在测速误差和误关联；而航迹滤波速度仅依赖距离探测精度及滤波模型的精确建模。综合考虑处理效果和工程应用，航迹滤波估计径向速度具有较好的测距精度和相关稳定性，是解决该问题的最优选择。
距离多普勒耦合的修正一般在脉冲压缩前进行，修正残差会传递到航迹滤波器下一帧的量测距离中。如果对量测距离进行反修，并在航迹输出前利用当前滤波速度再次修正，能够防止误差传递，但影响滤波效果；且在波形切换时反修后的量测距离会发生跳变，会导致滤波器速度估计异常及无法关联[9]。
文献[10]提出通过信号脉压前的相位修正及脉冲积累前的延时修正来消除距离多普勒耦合对脉压和相参积累的影响，但是其修正效果依赖于速度估计的准确性，也存在耦合修正残差传递的情况。文献[11]提出在极坐标系中进行滤波并修正距离多普勒耦合，但极坐标系无法正确建模高机动目标的运动模型，其处理一般只能针对匀速目标。
针对上述问题，本文对弹道目标的高精度距离测量进行了深入研究：首先分析了距离多普勒耦合的影响；对典型的弹道目标观测模型和运动模型进行建模；提出了一种针对弹道目标的精确测距方法；通过仿真实验对该方法进行对比验证。实验结果表明该方法对于处理机动目标距离多普勒耦合有较好的效果，这对于提升雷达的整体性能具有重要意义。
1 距离多普勒耦合的影响
对于脉冲压缩雷达，当目标存在径向运动时，就会发生多普勒失配现象，即匹配滤波器输出的回波峰值位置会产生与多普勒频移成比例的偏差。对于脉冲宽度为τ，载频为fc，带宽为B的矩形脉冲，目标径向运动v引起的距离耦合误差为
(1)
定义耦合系数kc为
(2)
耦合系数的符号由线性调频信号的调频斜率决定，当斜率为正时，耦合系数为正，反之为负。不同频率、波形参数下的耦合系数及耦合误差见表1。可以得到，当雷达工作频段高且脉宽大时，耦合误差会对距离测量产生较大影响，此时径向速度的精度将直接关系到雷达测距的精度。
表1 工作参数与耦合误差对应关系
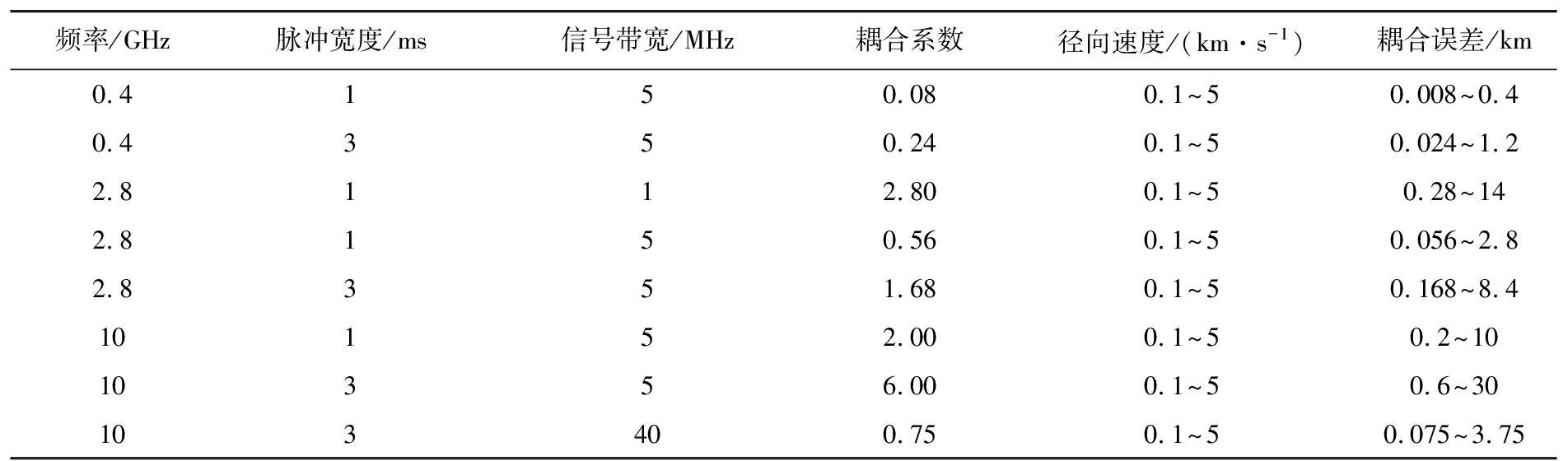
频率/GHz脉冲宽度/ms信号带宽/MHz耦合系数径向速度/(km·s-1)耦合误差/km0.4150.080.1～50.008～0.40.4350.240.1～50.024～1.22.8112.800.1～50.28～142.8150.560.1～50.056～2.82.8351.680.1～50.168～8.410152.000.1～50.2～1010356.000.1～50.6～30103400.750.1～50.075～3.75
2 雷达跟踪建模2.1 雷达量测模型
雷达观测数据包括距离r，方位a，仰角e，其坐标系为以阵面为中心的极坐标系。
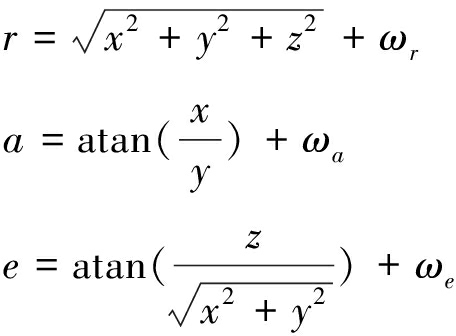
(3)
式中，[x,y,z]为地面直角坐标系下的坐标，ωr,ωa,ωe为量测噪声，其中ωr包括信号处理对距离多普勒耦合修正的残差。
2.2 目标运动模型
典型弹道目标飞行过程，包括主动段、自由段及再入段。目标在主动段受力包括发动机推力、重力、空气阻力及地球自转产生的离心力等。假定目标状态为[x y z vx vy vz]，在地心地固坐标系下对弹道目标建立运动模型，则目标在主动段的运动模型为[12]
(4)
式中：aT为导弹发动机推力对应的加速度；ρ(h)为根据空气密度计算的空气阻力系数；β为弹道目标面阻比；μG为地球引力常量；r=
为地球自转速度。而目标在自由段和再入段时没有主动段助推力，即公式(4)中aT为零。
3 高精度测距算法设计3.1 算法流程设计
距离多普勒耦合处理的难点在于：利用滤波器预测速度进行耦合修正时，残差会传递到下一帧的量测数据中。当耦合系数大于一定范围时，误差会随着迭代次数的增长不断放大。
解决残差传递的关键是增加解耦所需的测速旁路进行速度估计。测速旁路采用独立的滤波器对目标速度进行滤波,测速滤波器采用Singer算法，能够有效处理弹道目标等高机动目标。该方法的主要步骤为：
第一步，返修已解耦距离测量。首先根据公式(2)计算耦合系数kc。信号处理产生的量测数据Zk中量测距离rk已解耦，利用信号处理在脉压前用来解耦的预测径向速度vk|k-1，按公式(5)对rk进行耦合反修，从而得到未解耦量测距离
用r′k替换Zk中的rk得到距离未解耦量测数据Z′k。
r'k=rk-kcvk|k-1
(5)
第二步，径向速度及加速度估计。将未解耦量测距离r′k输入测速滤波器，滤波器的运动模型见公式(8)滤波后得到的滤波值X′k包含径向速度滤波值V′k及径向加速度滤波值a′k。
第三步，耦合修正。利用第一步中的r′k及第二步中的V′k及a′k按公式(6)对未解耦的距离测量r′k进行修正，得到修正后的距离测量r″k。将r″k替换Z′k中的r′k得到弹道滤波器的观测输入Z″k。
r″k=r'k+kc(v'k+kca'k)
(6)
第四步，弹道滤波。将解耦后的Z″k输入测速滤波器，滤波器中目标运动模型见公式(4)。滤波后得到的当前滤波值Xk，进行状态估计后，得到目标预测状态及弹道面阻比。根据公式(7)计算预测径向速度Vk+1|k用于下一帧信号处理修正距离多普勒耦合。
(7)
在算法的第三步中，v′k及a′k是利用未解耦的距离量测计算的，因此修正残差不会传递到下一轮修正中。距离多普勒耦合处理整体流程图如图1所示。下面对算法中第二步和第四步进行详细论述。
图1 距离多普勒耦合处理流程图
3.2 径向速度及加速度估计
算法的第一步完成了返修已解耦距离测量，此时利用得到的未解耦量测距直接估计目标的径向速度和加速度。通常高机动目标一般处于变加速状态，因此测速旁路采用Singer算法对目标径向速度及加速度进行估计。
(8)
对方程离散化，并考虑地球引力后得到
Xk+1=ΨXk+Qwk+Γg
(9)
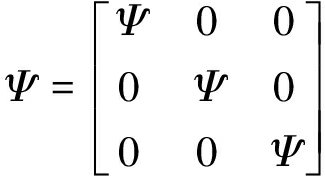
(10)
(11)
式中：ω(t)为过程噪声，α为机动时间常数τ的倒数，Q为Singer模型的过程；考虑重力对弹道目标的固定作用，Γ=[0 0 0 0 0 0 0 0 -1]′为控制项矩阵；g为重力加速度常量。
3.3 弹道滤波
算法的第三步完成距离测量耦合修正后，采用IMM-UKF滤波器进行弹道滤波。结合弹道目标运动非线性的特点，我们采用不敏卡尔曼滤波(UKF)，并结合能动态切换弹道飞行阶段的交互多模型(IMM)作为弹道滤波器[12]。
UKF通过选取一组均值和协方差与原状态分布一致的采样点，能够很好地反映状态的分布[6]，具有较好的非线性滤波性能。这里，弹道目标状态向量
向量维数为n =7。首先采用不敏变换进行Sigma采样点选取，在已知非线性函数的均值
和Pk-1/k-1时，选择2n+1个采样点。
目标状态预测为
(12)
χk/k-1=f(χk/k-1,k-1)
(13)
目标预测协方差矩阵为
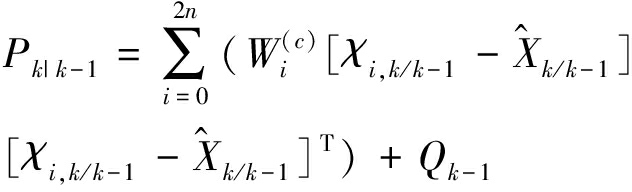
(14)
更新量测为
(15)
ζk/k-1=h(χk/k-1,k)
(16)
弹道目标全阶段跟踪本质上是一个混合过程估计问题，如采用多种运动模型就能够对全弹道运动过程合理建模[13]。
因此，采用的IMM算法将其中所有滤波器的估计结果的加权平均，权重由各滤波器的模型概率决定，其中目标运动阶段的模型概率[14]可以正确地反映目标飞行的阶段，算法流程如图2所示。
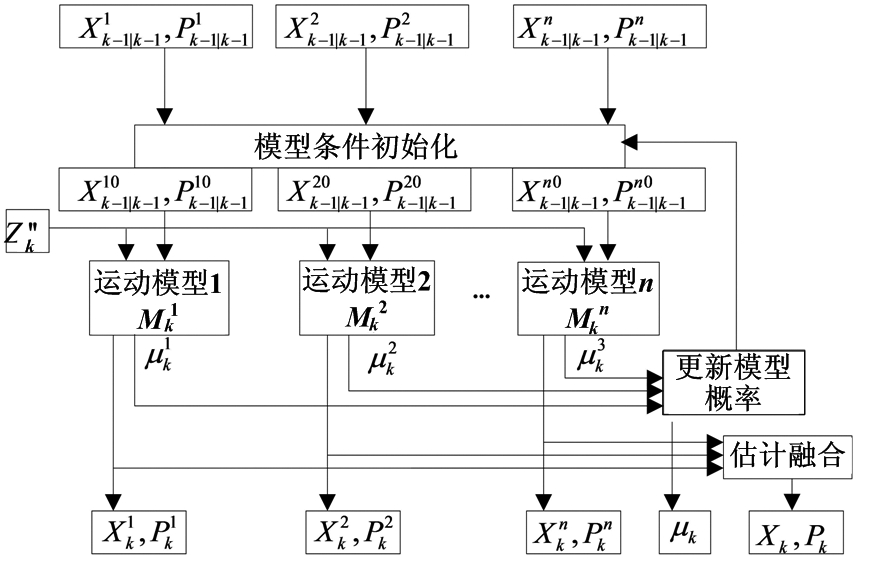
图2 IMM算法结构图
4 仿真分析
仿真实验对弹道目标全弹道进行仿真，弹道运动模型见2.2节。雷达位于距导弹发点100 km，能够观测导弹主动段加速到再入的全过程。仿真雷达量测数据包含伪随机高斯噪声，噪声最大值为3σ。具体仿真参数如表2所示。
表2 仿真场景参数设置
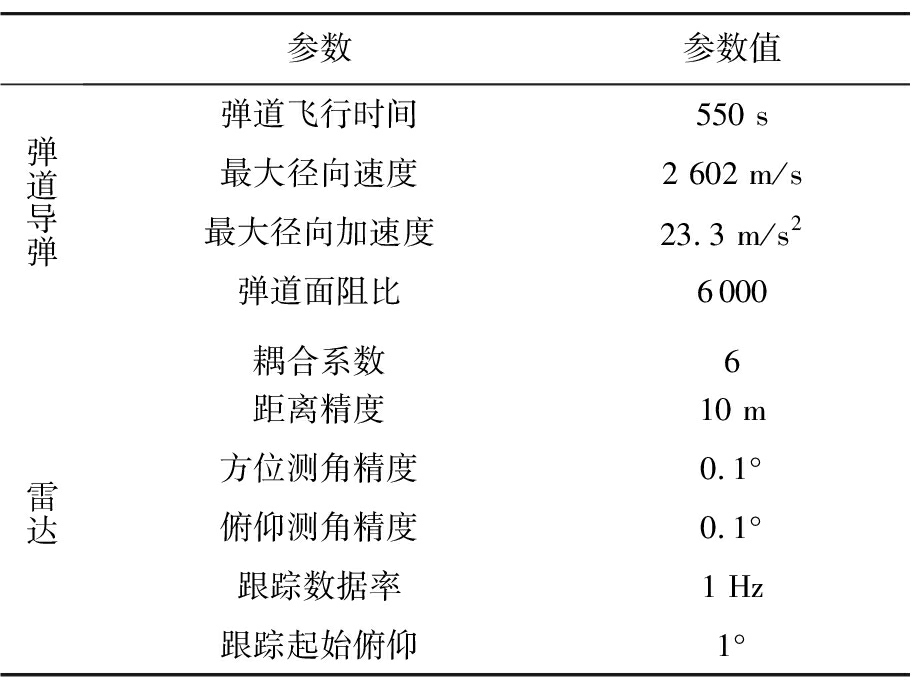
参数参数值弹道导弹弹道飞行时间550 s最大径向速度2 602 m/s最大径向加速度23.3 m/s2弹道面阻比6000 雷达耦合系数6距离精度10 m方位测角精度0.1°俯仰测角精度0.1°跟踪数据率1 Hz跟踪起始俯仰1°
目标径向速度及径向加速度变化曲线如图3所示。
实验中采用蒙特卡罗仿真(独立运行200次)进行仿真，并与传统的单路处理方法对比。单路处理与测速旁路方法对于弹道滤波采用相同的IMM滤波器，其全弹道残差修正效果比对如图4(a)所示。为了验证加速度补偿的效果，修改测速旁路方法不对加速度进行修正，其修正对比效果如图4(b)所示。
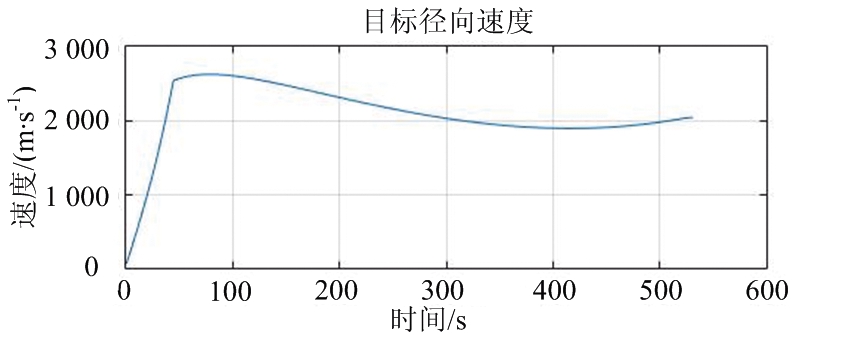
(a) 全弹道时间-径向速度
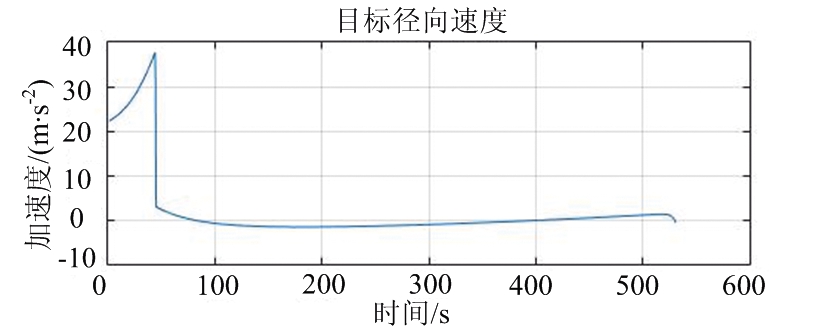
(b) 全弹道时间-径向加速度
图3 目标径向速度及径向加速度
(a) 单路处理与测速旁路对比
(b) 加速度修正与加速度未修正对比
图4 距离多普勒耦合修正残差比对
对独立运行的所有仿真结果进行残差(无符号)均值及残差均方根统计，统计结果如表3所示。
表3 修正残差均值与均方根对比
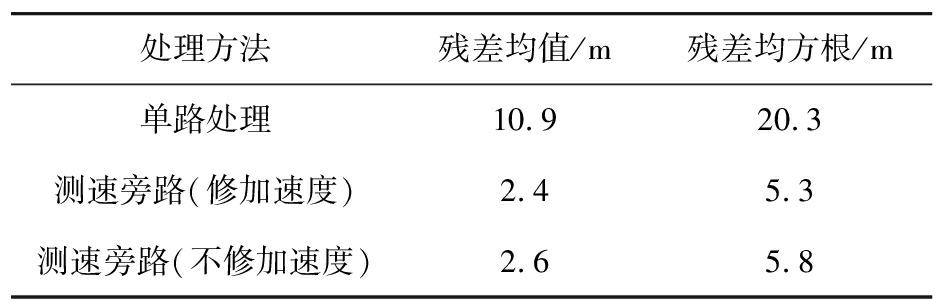
处理方法残差均值/m残差均方根/m单路处理10.920.3测速旁路(修加速度)2.45.3测速旁路(不修加速度)2.65.8
通过仿真结果可以得出：测速旁路对弹道目标的距离多普勒耦合修正精度相较于单路处理有着较大提升；特别地，在主动段及再入段等加速度变化较大的飞行阶段，修正加速度能够进一步提升距离估计的精度。
5 结束语
多普勒耦合的处理对目标跟踪、目标关联、目标检测都具有重要影响，有效处理该问题是能否发挥雷达效能的前提。本文提出了基于多普勒耦合估计的弹道目标高精度测距方法，该方法具有以下优势：
1) 针对传统方法会导致距离多普勒耦合修正残差传递的问题，文中方法添加了测速旁路，能够消除当前帧修正残差对下一帧的影响。
2) 传统方法采用滤波器上一帧预测的速度修正当前帧的耦合，会引入一定误差。文中方法利用当前帧估计目标当前的径向速度和加速度，提高了耦合修正的精度。
3) 相较于传统方法只利用径向速度进行修正，文中的处理方法在修正距离多普勒耦合时，考虑径向加速度因素，进一步提高了修正精度。
仿真分析中对弹道目标全弹道数据进行跟踪处理，对比了传统的单路处理与测速旁路的修正残差，并且验证了采用加速度修正对算法具有增量得益，特别是目标处于机动段时，实验结果显示本文方法相比于传统方法具有更高精度的距离估计。今后的工作重点在于考虑该方法在群目标跟踪下的应用，特别是对群目标跟踪关联稳定性的提升。
[1] RICHARDS M A，SCHEER J A，HOLM W A. Principles of Modern Radar，Vol.I: Basic Principles[M]. Edison，NJ:SciTech Publishing，2010.
[2] BLACKMA S. Design and Analysis of Modern Tracking Systems[M]. Norwood，MA:Artech House，1999.
[3] 李攀. 多普勒频移对脉冲压缩雷达的影响及其补偿研究[D].武汉：华中科技大学，2017.
[4] 李国君,赵栋华,赵永铁.距离多普勒耦合对雷达滤波精度影响分析[J].舰船电子工程,2018,38(4):51-53.
[5] 庄俊，杨沛，王鹏.波形切换对雷达距离测量的影响[J].舰船电子对抗，2019，42(4)；16-19.
[6] 鞠荣华，纪永刚，黎明，等. 高频地波雷达船只目标距离参数估计与评价[J]. 中国海洋大学学报(自然科学版),2019,49(1):128-133.
[7] TILLY J F, HAAG S,SCHUMANN O，et al. Detection and Tracking on Automotive Radar Data with Deep Learning[J]. 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa:IEEE, 2020:1-7.
[8] LEVANON N. Radar Principles[M]. New York :John Wiley & Sons, 1988.
[9] FANG Xin, XIAO Guoqing, CAO Zongjie, et al. Migration Correction Algorithm for Coherent Integration of Low-Observable Target with Uniform Radial Acce-leration [J]. IEEE Trans on Instrumentation and Measurement, 2021，70:1-13.
[10] CHO H W, CHOI S, CHO Y R,et al. Deep Complex-Valued Network for Ego-Velocity Estimation with Millimeter-Wave Radar[C]∥2020 IEEE Sensors，Rotterdam, Netherlands:IEEE,2020:1-4.
[11] TROFIMENKO M A, FARBER V E. Estimation of Speed-Error Influence on Stability Boundaries of Algorithms Estimating Range and Radial Velocity in Radar Stations Using LFM Signal[J].Radiotehnika，2015(10):7-16.
[12] 钮俊清，单奇，任清安,等. 跟踪弹道导弹全阶段的可变多模型方法[J ]. 雷达科学与技术，2011，9(3)：224-231.
NIU Junqing, SHAN Qi, REN Qingan, et al.A New Algorithm with Variable-Structure Multiple Model for Tracking Ballistic Missile at Entire Flight Stages[J]. Radar Science and Technology, 2011,9(3):224-231.(in Chinese)
[13] LANGEL S，CRESPILLO O G，JOERGER M. Overnbounding the Effect of Uncertain Gauss-Markov Noise in Kalman Filtering[J]. Navigation，2021(5):259-276.
[14] WANG Yu，WANG Xiaogang，CUI Naigang. Robust Decentralized State Estimation for Formation Flying Spacecraft[J]. IET Radar, Sonar & Navigation，2019, 13(5)：814-823.
