0 引言
我国的气候条件复杂而多变,气象灾害种类繁多且发生频率较高[1],若不能准确探测天气条件,容易造成严重的气象损失。相较于传统气象雷达,双偏振气象雷达[2]获取到的气象粒子大小、形状、空间位置[3]等信息更加精准,因此在定量估计降水、获知粒子相态、预警灾害等[4]方面具有重要意义。
目前,实现双偏振气象雷达降水粒子分类算法的主要思路有两种,一种是模糊逻辑算法,另一种是机器学习类方法。Straka (1996年)[5]首次在降水粒子分类领域应用了模糊逻辑算法。之后大部分专家研究了该算法在不同波段雷达中的应用[6],以及输入参量的选取[7]和隶属度函数的选择[8]等问题。虽然模糊逻辑算法能够有效对降水粒子进行分类,但是由于隶属度函数参数的确定、函数的形状以及权值的选择主要依靠专家经验值,具有很强的主观性,因此容易造成分类误差。近二十年来,K-近邻算法[9]、决策树算法[10],以及聚类算法[11]等机器学习热度再次燃起。K-近邻算法方法简单且适用于多分类,但K值的选取往往需要依靠专家经验值,数据量大时计算量也会增加;决策树算法运行速度快,对于缺失属性的样本包容性强,但不仅容易造成过度拟合还会忽略数据属性间的联系;聚类的方法简单且无需训练数据集,但是对非规则形状的降水粒子分类性能较差。2008年Marzano等[12]将贝叶斯分类算法与降水粒子分类结合在一起。由于贝叶斯分类算法能够充分地应用先验信息,并且能够随着属性特征的增减调整算法的结构,在降水粒子分类算法中更具优势。
虽然朴素贝叶斯算法原理简单,但是在实际应用中需要为其提供数量大、质量高的训练数据集。训练数据集内数据最可靠的获取方法是使用带有粒子检测系统的探测器深入到云层中进行采集,然而此方法成本较高、获取数据量少。这致使贝叶斯算法的分类效果很大程度上受限于训练数据集样本的数量。不仅如此,训练数据集一成不变易致使分类器泛化性不足,而重新训练分类器以大量时间为代价。为了解决这一问题,学者们提出了一种增量学习方法[13],即在接受过训练的系统或者算法的基础上,追加包含有用信息的数据样本至原有数据集,提取出的有用信息会对分类器进行更新而无需重新训练分类器,以此实现在扩充旧知识的同时逐步动态地掌握新信息的过程。在充分利用与发挥朴素贝叶斯理论适应性前提下,合理应用增量学习实现动态调节算法的过程,能够在增加样本数量的同时增强算法的分类效果,提高其适应性。
因此,本文提出了一种基于增量贝叶斯的双偏振气象雷达降水粒子分类方法。该方法首先对偏振参量数据进行离散化处理,然后由带标签数据计算得到的偏振参量条件概率表来构建离散属性朴素贝叶斯分类器,接着使用朴素贝叶斯分类器分类无标签数据,将符合条件的数据追加到训练数据集中,最后修正朴素贝叶斯分类器完成增量学习,得到增量贝叶斯分类器实现降水粒子分类。
1 增量贝叶斯降水粒子分类算法
增量贝叶斯降水粒子分类算法首先对数据进行离散化,之后利用有标签的训练数据集D计算出条件概率表实现朴素贝叶斯分类器的构造,结合贝叶斯公式实现无标签的增量数据集Dz的分类,使其成为有标签数据,并将符合阈值门限的新的有标签数据加入到原始训练数据集中,更新朴素贝叶斯分类器得到增量贝叶斯分类器,最后利用增量贝叶斯分类器进行降水粒子分类。
1.1 数据离散化
双偏振气象雷达通过发射和接收水平以及垂直方向电磁波获取到的偏振参量分别为雷达反射率因子、差分反射率因子、互相关系数以及差分相移率(分别简记为ZH,ZDR,ρHV,KDP)。朴素贝叶斯分类器使用离散属性的条件概率表描述雷达偏振参量与不同降水粒子之间的关系,而增量贝叶斯分类器是在朴素贝叶斯分类器的基础上得到的,因此两者都需要对偏振参量数据样本进行离散化处理以进行后续条件概率值的计算,区别在于朴素贝叶斯分类器使用了有标签的训练数据集D,增量贝叶斯分类器使用了无标签的增量数据集Dz。离散化过程如图1所示(以![]() 为例)。首先删去ZH样本中重复出现的项,再将其余数据从小到大排列得到
为例)。首先删去ZH样本中重复出现的项,再将其余数据从小到大排列得到![]() 接着设置采样间隔δ并对ZH′ 进行等间隔数据取样,得到离散化标准
接着设置采样间隔δ并对ZH′ 进行等间隔数据取样,得到离散化标准![]() 将ZH内数值元素
将ZH内数值元素![]() 一一与离散化标准对比,并将
一一与离散化标准对比,并将![]() 替换成与其数值最接近的离散化标准值
替换成与其数值最接近的离散化标准值![]() 即令
即令![]() 由此可得到ZH的离散化数据集
由此可得到ZH的离散化数据集![]() 以相同方法离散化其余偏振参量数据样本用于后续的计算。
以相同方法离散化其余偏振参量数据样本用于后续的计算。

图1 离散化流程图
1.2 朴素贝叶斯分类器
将离散化处理后的偏振参量数据作为属性节点输入到朴素贝叶斯分类器中。除属性节点外,朴素贝叶斯分类器的结构还包括类节点C以及有向线段,如图2所示。类节点C的取值对应分类器输出的9类降水粒子(视地杂波为一种降水粒子类别),如表1所示。

图2 朴素贝叶斯结构
表1 类标签取值及降水粒子输出结果
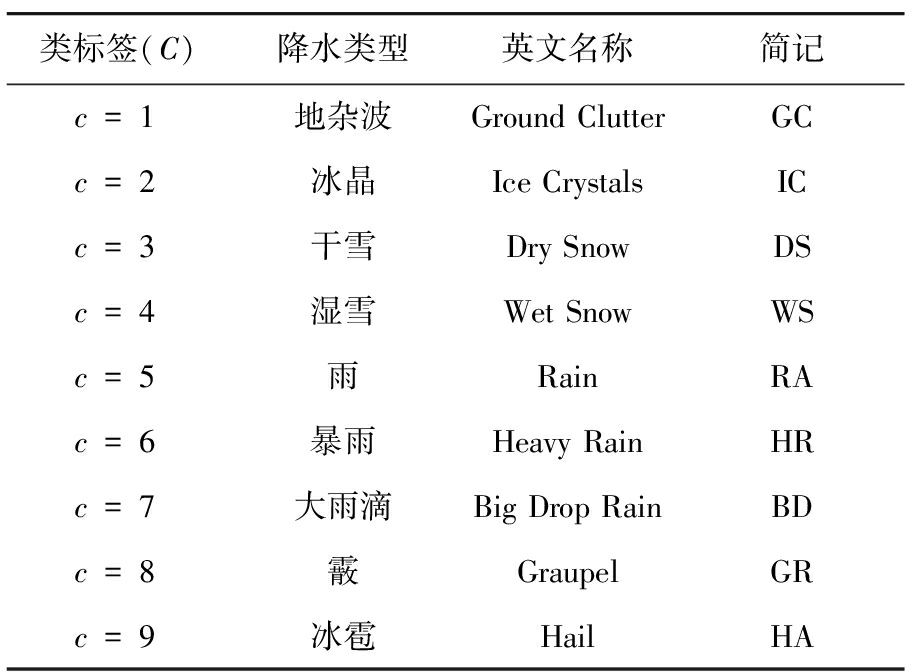
类标签(C)降水类型英文名称简记c=1地杂波Ground ClutterGCc=2冰晶Ice CrystalsICc=3干雪Dry SnowDSc=4湿雪Wet SnowWSc=5雨RainRAc=6暴雨Heavy RainHRc=7大雨滴Big Drop RainBDc=8霰GraupelGRc=9冰雹HailHA
构建朴素贝叶斯分类器的关键就是算得贝叶斯结构中每个属性节点的条件概率表,由朴素贝叶斯结构可知,每个属性节点仅与类节点有关,因此需要利用离散化后数据获取每个属性节点与类节点之间的条件概率表。下面以属性节点ZH为例介绍条件概率表的计算方法。统计![]() 中为同一个离散化标准值
中为同一个离散化标准值![]() 且携带的类节点标签值也相同的数据个数,即同时满足
且携带的类节点标签值也相同的数据个数,即同时满足![]() 以及c=j的数据个数,并记为
以及c=j的数据个数,并记为![]() 其中j=1,2,…,9。则离散化标准值
其中j=1,2,…,9。则离散化标准值![]() 的条件概率值为
的条件概率值为
(1)
式中,Nh为ZH样本总个数。根据这种计算方式,计算出每个离散化标准值关于降水粒子种类的条件概率值,即可得到属性节点ZH关于类节点C的条件概率表,如图3所示。同理,依次得到其余属性节点与类节点之间的条件概率表,即可完成朴素贝叶斯分类器的构建。
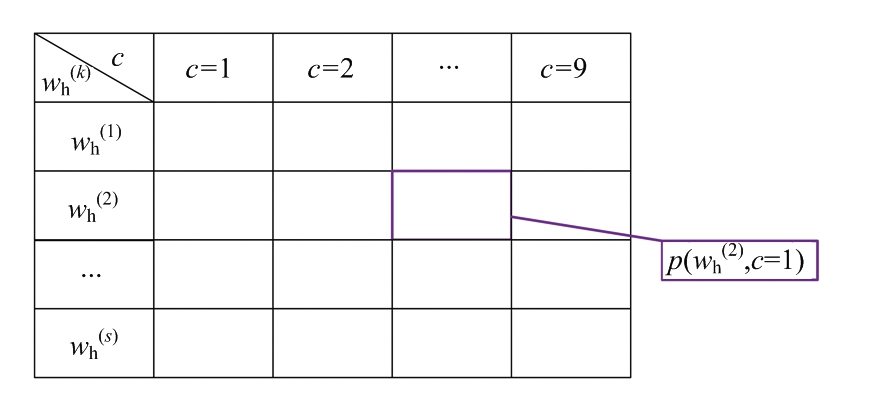
图3 属性节点ZH关于类节点C的条件概率表
1.3 增量贝叶斯分类器
将朴素贝叶斯分类器进行增量学习,即可得到增量贝叶斯分类器。增量学习是指将无标签数据经过朴素贝叶斯分类器分类后,通过严格的判断过程将满足条件的新的有标签数据扩充到训练数据集D中,并且修正朴素贝叶斯分类器。将全部的无标签数据学习完毕,即完成增量贝叶斯分类器的构建。
(a) 扩充训练数据集
将离散化后的无标签数据输入到朴素贝叶斯分类器中进行分类判断,即可得到有标签数据。用x1,x2,x3,x4分别表示朴素贝叶斯分类器的属性节点ZH,ZDR,ρHV,KDP,则该分类判断过程可由下式描述:
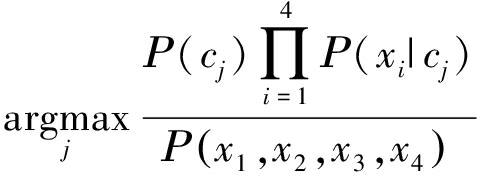
(2)
式中,j∈{1,2,…,9}表示降水粒子的标签类别数,xi表示第i个属性节点,i∈{1,2,3,4},Ρ(x1,x2,x3,x4)为常数。公式(2)转化为式(3):
(3)
式中,属性节点的类条件概率Ρ(xi|cj)以条件概率表的形式存在,类先验概率的P(cj)计算公式为:![]() 表示降水粒子类别为j的样本个数,N为样本总个数。式(3)输出的结果j就是朴素贝叶斯分类器为无标签数据赋予的类别标签。
表示降水粒子类别为j的样本个数,N为样本总个数。式(3)输出的结果j就是朴素贝叶斯分类器为无标签数据赋予的类别标签。
然而并非所有新带标签数据都适合用来扩充训练数据集。本文借鉴了罗福星等人[14-16]提出的类置信度的概念,即设定一个阈值,通过判断经过朴素贝叶斯分类器分类后的数据样本是否达到阈值条件来决定其能否进行下一步的增量学习。因此,数据样本属于某种降水粒子cj的类置信度θj定义为
(4)
令θt=max{θj,1≤j≤9},判断该数据样本是否达到阈值的条件:如果θt满足![]() 即θt的值不小于其他类别置信度之和的a(a∈[0,1])倍,则认为该数据样本属于类别cj的结果是可信的,否则认为该样本不可信。文献[14]指出,当a∈[1/2,1]时,能够取得比较好的分类结果。
即θt的值不小于其他类别置信度之和的a(a∈[0,1])倍,则认为该数据样本属于类别cj的结果是可信的,否则认为该样本不可信。文献[14]指出,当a∈[1/2,1]时,能够取得比较好的分类结果。
(b) 修正朴素贝叶斯分类器
当新带标签数据样本加入到训练数据集D中时,朴素贝叶斯分类器的类先验概率值和各个属性节点的类条件概率会发生变化,需要对概率公式进行修正。类先验概率值公式如式(3)所示,其修正公式如下:

(5)
式中,P(cj)′表示新加入数据样本后的类先验概率值,j∈{1,2,…,9},P(cj)表示未加入前的类先验概率值,N为未加入数据样本前的样本总数,cz为新加入的样本数据的降水粒子类别。通过执行公式(5)中不同公式,实现对分类器类先验概率值的修正。
类条件概率值公式如式(1)所示,其修正公式如下:
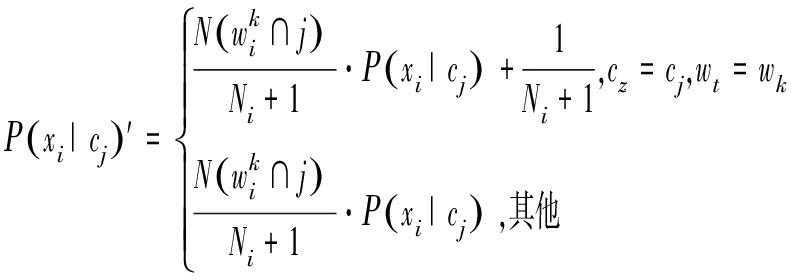
(6)
式中,P(xi|cj)′表示新加入数据样本后第i种属性节点的类条件概率值,i∈{1,2,3,4},j∈{1,2,…,9},Ρ(xi|cj)表示未加入数据样本的类条件概率值,Ni为第i种属性节点的样本总数,![]() 表示未加入新样本前第i种属性节点中离散化标准值等于
表示未加入新样本前第i种属性节点中离散化标准值等于![]() 且降水粒子类别恰好为j的数据个数,wt为新加入数据样本离散化后得到的离散化标准值。通过对条件概率表中每个类条件概率值进行调整,实现属性节点的类条件概率的修正过程。
且降水粒子类别恰好为j的数据个数,wt为新加入数据样本离散化后得到的离散化标准值。通过对条件概率表中每个类条件概率值进行调整,实现属性节点的类条件概率的修正过程。
对于投入到训练数据集D中的一个新带标签数据样本,完成类先验概率值以及属性节点的类条件概率的修正即可完成一次对朴素贝叶斯分类器的增量学习过程,此时训练样本集D中增加一个降水粒子数据样本,增量样本集Dz中减少对应的数据样本。之后再取增量样本集Dz中一个新的无标签降水粒子数据样本,利用经过更新后的朴素贝叶斯分类器给该无标签数据赋予标签,并进行阈值计算及判断,概率值修正等,重复上述过程,直到增量样本集Dz为空,结束朴素贝叶斯分类器的增量学习过程,如图4所示。对朴素贝叶斯分类器增量学习完毕,即完成增量贝叶斯分类器的构建。
1.4 降水粒子分类过程
完成增量学习的朴素贝叶斯分类器即为增量贝叶斯分类器,之后利用构造好的增量贝叶斯分类器分类测试数据来验证算法性能。由于增量贝叶斯分类器是在朴素贝叶斯分类器的基础上得到的,因此两者判断降水粒子类别的方式本质相同,同样将降水粒子分类问题转变为公式(2)的最大后验概率问题,最后化简为公式(3)。区别在于,进行降水粒子分类使用的P(cj)为修正后的先验概率值,使用的Ρ(xi|cj)为修正后的类条件概率值。公式(3)输出的结果j就是最终得到的降水粒子种类。

图4 增量学习流程图
2 算法流程
结合前文,基于增量贝叶斯的双偏振气象雷达降水粒子分类方法流程图如图5所示。
具体实现步骤如下:
步骤1 利用训练数据集D训练朴素贝叶斯分类器,初始化取样次数t=1;
步骤2 利用朴素贝叶斯分类器对![]() 分类,得到相应的类别标签ct;
分类,得到相应的类别标签ct;
步骤3 依据式(5)判断是否满足阈值条件,若满足则进行步骤4,否则执行步骤5;
步骤4 扩充训练数据集,即![]() 同时修正朴素贝叶斯分类器的类先验概率值和类条件概率值;
同时修正朴素贝叶斯分类器的类先验概率值和类条件概率值;
步骤![]() 判断Dz是否为空,若结果为空,执行步骤6,否则令t=t+1并且返回步骤2;
判断Dz是否为空,若结果为空,执行步骤6,否则令t=t+1并且返回步骤2;
步骤6 结束增量贝叶斯分类器的构造过程,并进行降水粒子分类。

图5 基于增量贝叶斯的双偏振气象雷达降水粒子分类方法流程图
通过上述步骤即可实现对增量贝叶斯分类器的构造过程,经此得到的训练数据集数据得到扩充,得到的增量贝叶斯分类器具有更高的分类准确率以及更强的泛化性。
3 实验算法验证
实验数据集取自NOAA(National Oceanic and Atmospheric Administration,美国国家海洋和大气管理局)官方网站,选取WSR-88D雷达网中坐落于俄克拉荷马市(OKLAHOMA)的一部双偏振气象雷达KTLX,该雷达位于35.1958N° 97.1640W°,波长为10 m,脉冲重复频率为250~1 200 Hz,仰角为0.5°。
实验一:首先采集了KTLX雷达在2019年9月13日11:46时刻的雷达回波数据作为测试数据测试算法性能,然后分别给出了朴素贝叶斯分类器,增量贝叶斯分类器,以及模糊逻辑算法(NOAA官方提供分类结果)的降水粒子分类结果,如图6所示。3种算法分类结果的不同类别降水粒子数量统计如表2所示。由于本文分类结果以图像形式呈现,因此引入灰度共生矩阵定量的分析分类结果图像的特征。主要使用了其中3个特征[17]:1) 能量 指灰度共生矩阵元素值平方和,是衡量图像灰度分布的均匀性的重要指标。2) 同质性 一幅图像对角元素间的相紧密度,同质性与图像像素间的相同度成正比,当图像中所有元素全部相同时有最大同质性。3) 熵 图像中纹理信息的多少反映了图像中所包含的信息量的大小。

(a) 朴素贝叶斯算法分类结果图

(b) 增量贝叶斯算法分类结果图
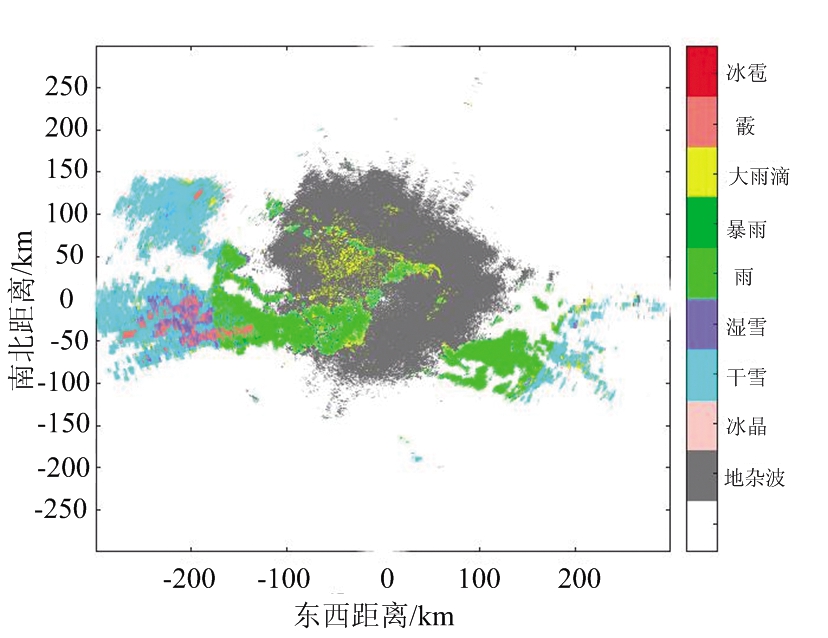
(c) 模糊逻辑算法分类结果图
图6 不同方法所得分类结果对比图 (2019/09/13 11:46)
表2 各类粒子数量及占比(2019/09/13 11:46)
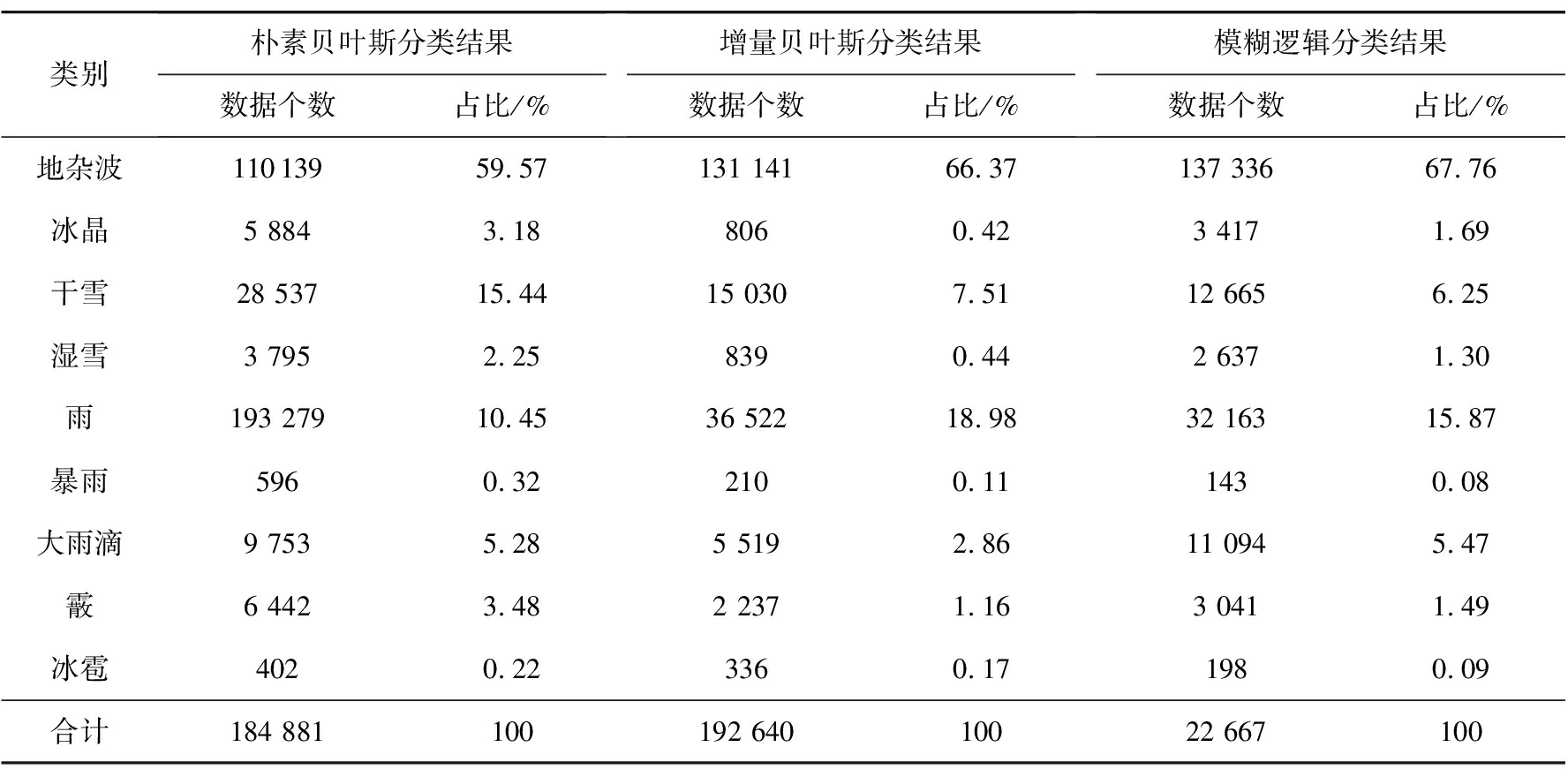
类别朴素贝叶斯分类结果数据个数占比/%增量贝叶斯分类结果数据个数占比/%模糊逻辑分类结果数据个数占比/%地杂波11013959.57131 14166.37137 33667.76冰晶5 8843.188060.423 4171.69干雪28 53715.4415 0307.5112 6656.25湿雪3 7952.258390.442 6371.30雨193 27910.4536 52218.9832 16315.87暴雨5960.322100.111430.08大雨滴9 7535.285 5192.8611 0945.47霰6 4423.482 2371.163 0411.49冰雹4020.223360.171980.09合计184 881100192 64010022 667100
通过图6可以看出3种分类器都能够很好地完成降水粒子分类过程。比较图6(a)、(b)、(c)三组分类结果图易知:该地区的当日气候主要以雨、干雪以及大雨滴为主,混合少量的湿雪,且相邻降水粒子种类连续性较强。从图6可知,暴雨与大雨滴周围一般存在雨这种降水粒子,这是由于降雨一般由对流云或者层状云形成,不同物理过程决定了雨的形状大小以及粒子的浓度密度等特征,即暴雨与大雨滴是在雨的基础上增加粒子的大小、浓度等形成的。冰雹、冰晶是由于水蒸气的温度急速下降,水蒸气凝华形成冰团导致的,当过冷的水滴聚集在下落的雪花上时,就会形成了称为软冰雹的霰,因此在雨雪交界的地方多存在此三者降水粒子。图6(b)中分类结果图相较于图6(a)图像展现出较强的物理聚类特征,这表明所提方法对降水粒子的分类能力更强;且图像更加清晰凝实,这是由于每一个样本在图中都以不同颜色点的形式存在,结合表2的数据可知增量贝叶斯比朴素贝叶斯算法识别出更多的测试数据,因此增量贝叶斯分类器的算法结果图中点数更加密集,展现出的图像更加清晰。此外,观察易知三组分类结果图的主要区别集中在中间以及左侧居中区域,在此区域内增量贝叶斯分类算法比朴素贝叶斯分类器识别出了更多的雨,与模糊逻辑算法分类结果相近,由此说明相较于朴素贝叶斯分类器而言,增量贝叶斯算法具有更好的分类准确性。通过表2能够发现,相较于朴素贝叶斯算法,增量贝叶斯算法识别出了更多的地杂波,而分类结果为大雨滴的数据量较少,这是因为地杂波中存在未知点,而朴素贝叶斯算法性能有限,容易误将地杂波判断为大雨滴。表3中的方位角表示的是图像纹理方向,例如0°表示水平纹理特征,90°表示的是垂直纹理特征。从表3可知,增量贝叶斯算法的能量与同质性皆高于朴素贝叶斯算法,而熵值却小于朴素贝叶斯算法。这说明图6(b)中图像的连续性与集中性优于图6(a),更符合降水粒子在空间中连续的特征。
表3 灰度共生矩阵统计量特征(2019/09/13 11:46)
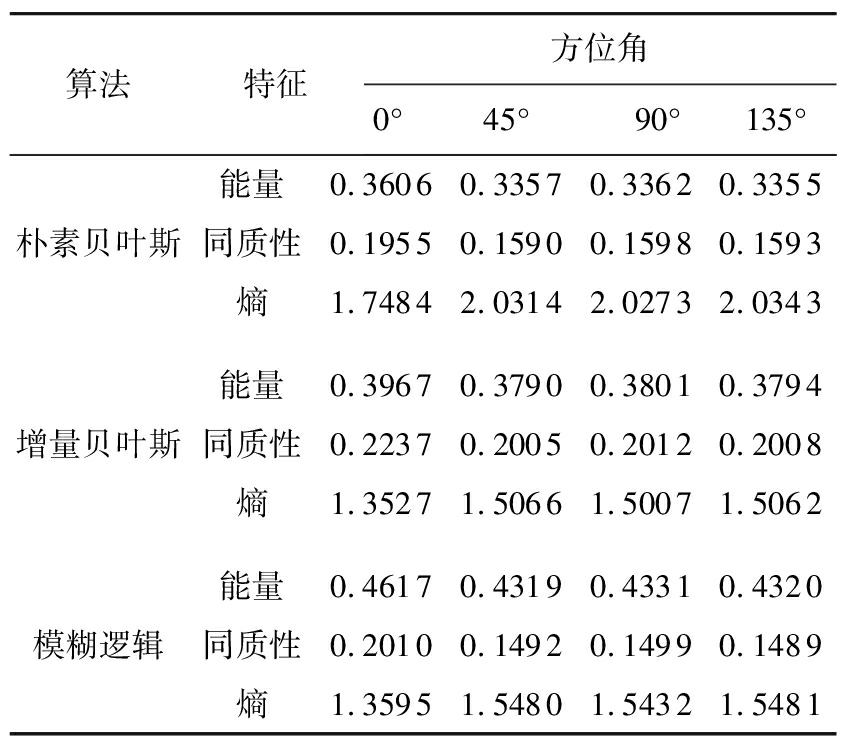
算法特征方位角0° 45° 90°135°朴素贝叶斯能量0.36060.33570.33620.3355同质性0.19550.15900.15980.1593熵1.74842.03142.02732.0343增量贝叶斯能量0.39670.37900.38010.3794同质性0.22370.20050.20120.2008熵1.35271.50661.50071.5062模糊逻辑能量0.46170.43190.43310.4320同质性0.20100.14920.14990.1489熵1.35951.54801.54321.5481
实验二:选取2020年4月22日5:06时刻的雷达回波数据继续验证算法性能。

(a) 朴素贝叶斯算法分类结果图

(b) 增量贝叶斯算法分类结果图

(c) 模糊逻辑算法分类结果图
图7 分类结果对比图(2020/04/22 5:06)
雪是云层中水汽冷凝形成的固态降水粒子,根据密度可将雪分为干雪和湿雪,其中干雪的重量轻,密度小,含水量不足,而湿雪的重量重,密度高,含水量充足。从图7能够看出,雪雨多相连存在。通过表3中的各类粒子数量占比以及图7中(a)、(b)朴素贝叶斯与增量贝叶斯算法的对比图来看,增量贝叶斯能够区分出更多的降水粒子数据样本,对雨的识别明显高于朴素贝叶斯分类器,而朴素贝叶斯分类器更多的将数据判定为暴雨,相同区域模糊逻辑的分类结果判定结果同为雨,由此可知增量贝叶斯分类器的分类结果更加准确。从表4中降水粒子识别数量来看,相较于朴素贝叶斯分类算法、增量贝叶斯分类器与模糊逻辑算法分别识别出了44 638、62 843、87 481个地杂波数据,易知增量贝叶斯算法比朴素贝叶斯算法分辨出了更多的地杂波,且从其他数据易知增量朴素贝叶斯分类算法识别出的降水粒子更接近于模糊逻辑算法,因此对气象信息的分类具有更高的准确性。表5中的方位角同样表示图像纹理方向,且从表中能够看出增量贝叶斯算法的能量与同质性皆高于朴素贝叶斯算法与模糊逻辑算法,而熵值却小于后两者。这说明增量朴素贝叶斯识别的降水粒子具有更好的空间连续性,与降水粒子空间连续的真实分布情况更吻合。
表4 各类粒子数量及占比(2020/04/22 5:06)

类别朴素贝叶斯分类结果数据个数占比/%增量贝叶斯分类结果数据个数占比/%模糊逻辑分类结果数据个数占比/%地杂波44 63825.5162 84335.3287 48141.41冰晶10 4555.971 0251.067 6463.62干雪34 89419.9416 5519.3020 1859.56湿雪8 0744.615930.462 9711.41雨33 02018.8779 02644.2468 10732.24暴雨10 3195.908 7514.927 9693.77大雨滴18 03810.318 5584.8113 9586.61霰11 0356.313930.286310.30冰雹4 5142.581 2960.732 2951.09合计174 987100179 036100211 243100
表5 灰度共生矩阵统计量特征(2020/04/22 5:06)
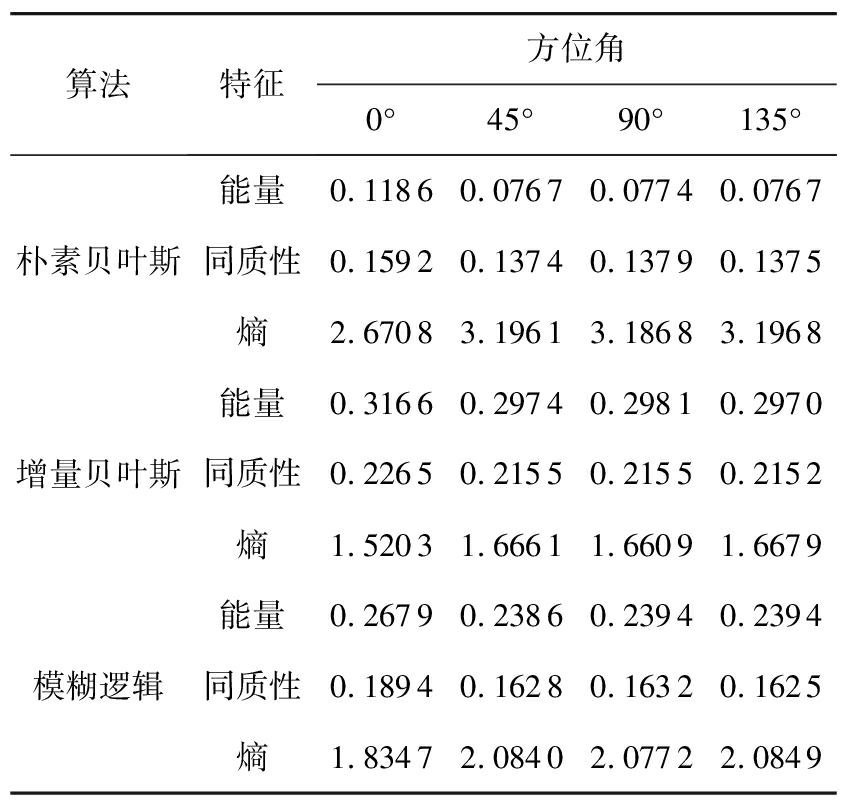
算法特征方位角0°45°90°135°朴素贝叶斯能量0.11860.07670.07740.0767同质性0.15920.13740.13790.1375熵2.67083.19613.18683.1968增量贝叶斯能量0.31660.29740.29810.2970同质性0.22650.21550.21550.2152熵1.52031.66611.66091.6679模糊逻辑能量0.26790.23860.23940.2394同质性0.18940.16280.16320.1625熵1.83472.08402.07722.0849
4 结束语
本文提出了一种基于增量学习的朴素贝叶斯双偏振气象雷达降水粒子分类算法,首先对雷达的偏振参量进行离散化处理,利用有标签的训练数据集构建朴素贝叶斯分类器;最后对分类器进行增量学习。通过实验能够证明经过增量学习后分类器有所增益,主要体现在两个方面:1)通过增量学习过程增加了训练数据集的数据样本,且数据经过阈值判断可信度更高,利用可信度高的数据样本训练出的分类器分类结果更加准确;2)对分类器进行增量学习时需要根据输入的新带标签样本不断修正分类器,由此实现及时调整分类器,动态地完成降水粒子分类的过程,使得分类器具有更好的适应性以及泛化性。因此基于增量贝叶斯的双偏振气象雷达降水粒子分类算法在数据量不足、气候条件复杂、地杂波干扰等情况下有重要的研究意义。
[1] 李柏,古庆同,李瑞义,等.新一代天气雷达灾害性天气监测能力分析及未来发展[J]. 气象, 2013, 39(3):265-280.
[2] ECCLES P J, ATLAS D. A Dual-Wavelength Radar Hail Detector[J]. Journal of Applied Meteorology, 1973, 12(5):847-854.
[3] SELIGA T A, BRINGI V N. Differential Reflectivity and Differential Phase Shift: Applications in Radar Meteorology[J]. Radio Science, 1978, 13(2):271-275.
[4] 张磊. C波段双线偏振雷达数据处理及其在粒子分类和降水估测中的应用[D]. 南京:南京信息工程大学, 2017.
[5] STRAKA J M. Hydrometer Fields in a Supercell Storm as Deduced from Dual-Polarization Radar[C]∥Preprints, 18th Conf on Severe Local Storms, San Francisco,CA:Amer Meteor Sco,1996:1-5.
[6] MATROSOV S Y, CLARK K A, KINGSMILL D E. A Polarimetric Radar Approach to Identify Rain, Melting-Layer, and Snow Regions for Applying Corrections to Vertical Profiles of Reflectivity [J]. Journal of Applied Meteorology and Climatology, 2007, 46(2):154-166.
[7] CHANDRASEKAR V, KERANEN R, LIM S, et al. Recent Advances in Classification of Observations from Dual Polarization Weather Radars [J]. Atmospheric Research, 2013,119:97-111.
[8] AL-SAKKA H, BOUMAHMOUD A A, BEATRICE F, et al. A New Fuzzy Logic Hydrometeor Classification Scheme Applied to the French X-C, and S-Band Polarimetric Radars[J]. Journal of Applied Meteorology & Climatology, 2013, 52(10):2328-2344.
[9] WANG A G, AN N, CHEN G L, et al. Accelerating Incremental Wrapper Based Gene Selection with K-Nearest-Neighbor[C]∥ Proceedings of 2014 IEEE International Conference on Bioinformatics and Biomedicine, Belfast,UK:IEEE, 2014:2-5.
[10] AGRAWAL R, IMIELINSKI T, SWAMI A. Database Mining: A Performance Perspective[J]. IEEE Trans on Knowledge and Data Engineering, 1993,5(6):914-925.
[11] GRAZIOLI J, TUIA D, BERNE A. Hydrometeor Classification from Polarimetric Radar Measurements: A Clustering Approach[J]. Atmospheric Measurement Tech-niques, 2015, 8(1):149-170.
[12] MARZANO F S, SCARANARI D, MONTOPOLI M, et al. Supervised Classification and Estimation of Hydrometeors from C-Band Dual-Polarized Radars: A Bayesian Approach[J]. IEEE Trans on Geoscience and Remote Sensing, 2008, 46(1):85-98.
[13] 张智敏. 基于增量学习的分类算法研究[D]. 广州:华南理工大学, 2010.
[14] 罗福星. 增量学习朴素贝叶斯中文分类系统的研究[D].长沙:中南大学, 2008.
[15] 高洁,吉根林.一种增量式Bayes文本分类算法[J].南京师范大学学报(工程技术版), 2004(3):49-52.
[16] 王小林,镇丽华,杨思春,等.基于增量式贝叶斯模型的中文问句分类研究[J].计算机工程, 2014, 40(9):238-242.
[17] 葛静祥.
图像纹理特征提取及分类算法研究[D]. 天津: 天津大学, 2010.


