0 引言
海上目标的监测是高频地波雷达重要应用之一,传统的监测指标主要是目标的径向速度和距离,除此之外,横向速度同样可以为运动目标的监测提供重要的信息。若可以同时获取目标的横向速度和径向速度,则可以合成目标的真实速度矢量,极大提高目标检测跟踪的准确度[1]。
许多文章提出过提取横向速度的方法。根据目标横向运动时回波信号的时变特征,可以估计出目标的横向速度[2]。但要求其横向速度较大,使得目标的径向距离发生变化,若横向速度较小,则无法得到横向速度。根据移动物体上的不同反射点的回波信号的多普勒频率的关系可以推算出横向速度的大小[3],但此方法需要强的反射回波和准确的目标方位角使得该方法的使用有较大限制。双基地雷达可以用来获取海流的横向和径向运动分量[4],但若将其应用在目标横向速度反演上,成本较高,便携性差。更为新颖的方法还有利用GPS和神经网络算法来反演横向速度[5],但其仅适合于车辆横向速度的估计,无法应用于海上船只目标。
为实现海上目标横向速度的测量,可以使用电波干涉法来进行横向速度的提取[6],但传统的处理过程是对各个通道回波信号解调和匹配滤波后直接进行干涉,无法很好地应对低信噪比信号的情况。文献[1]提出使用广义S变换来对噪声进行抑制,但其提升目标回波信号信噪比的能力有限,无法很好地应用于实际情况。
为此,本文提出了一种适用于高频地波雷达低信噪比信号横向速度提取的方法。该方法首先将通道中的信号进行相干积累,提高回波信号信噪比,然后选取两通道中积累后的目标信号相位相减得到相位差,最后通过多个积累后目标信号得到相位差变化率,进而反演横向速度。仿真分析表明,该方法可以有效提高低信噪比信号反演出的横向速度的准确度,并通过实测数据的处理验证了该方法在实际应用当中的有效性。
1 横向速度的提取原理
应用电波干涉法实现横向速度提取的原理如图1所示,双通道的两根接收天线相距为D,以两根接收天线位置为焦点可以分别画出椭圆簇和双曲线簇。当目标沿双曲线运动时,目标到两焦点的距离差r2- r1为一常数。由于同焦点的椭圆与双曲线正交,目标沿椭圆的运动导致距离差r2- r1的变化最大。定义干涉体制下目标沿双曲线运动为径向运动,沿椭圆运动为横向运动,则目标横向速度vl与两接收通道信号相位差变化率kp间关系为[7]
(1)
式中, λ为波长,r0为目标两天线中心位置距离,φ0为目标方位角。

图1 横向速度测量原理图
在实际应用中,目标到天线阵的距离r0由雷达可以得到,对雷达阵列信号作DOA估计则可以获得方向角φ0的大小。kp则可以由两通道多帧目标回波信号相位相减形成的相位差序列得到。
2 信噪比对横向速度提取的影响
实际工程中回波信号总是存在噪声,这些噪声会降低回波相位提取的准确度。下面对不同信噪比影响横向速度提取准确度的程度进行仿真分析。仿真中设定横向速度为5 m/s,目标距离为15 km,干涉天线距离为140 m,扫频周期为0.125 s,载波频率为7.5 MHz,扫频带宽为30 kHz。在不加噪声时,对回波信号进行匹配滤波得到的信号幅度如图2(a)所示,选取目标信号在不同通道中相位相减得到两通道信号的相位差,由多帧信号得到相位差随时间的变化如图2(b)所示,此相位差时间变化率为0.007 3 rad/s,将其代入公式(1)中,可得到横向速度为5 m/s。与设定的横向速度完全一致,验证了电波干涉法用于提取横向速度的可行性。
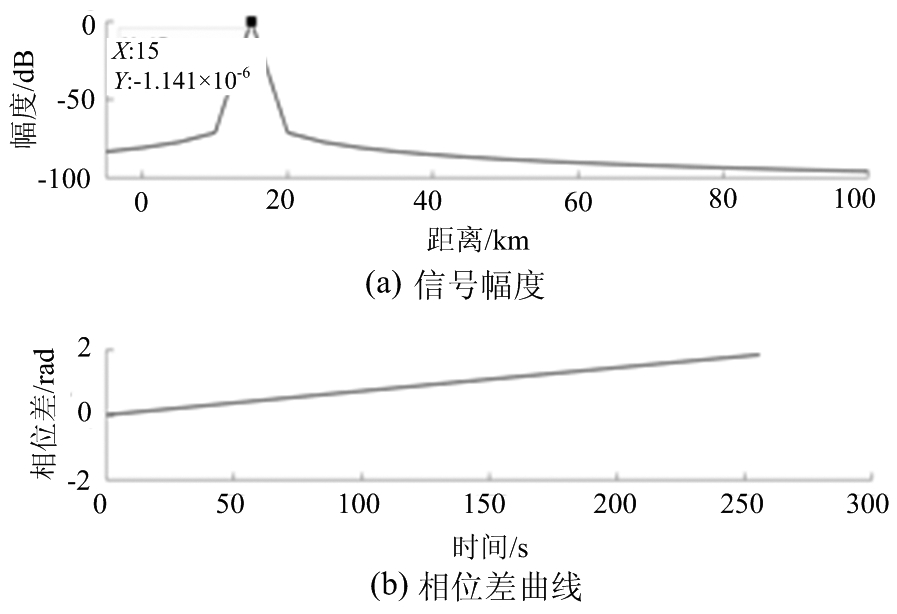
图2 无噪声信号仿真结果
下面逐渐降低信号信噪比,分别对原始回波信号信噪比分别是0 dB和-25 dB的情况进行仿真,对0 dB的回波信号进行匹配滤波得到的信号幅度如图3(a)所示,由图3(a)可以看出在15 km处仍可明显看出目标信号,利用多帧信号得到的相位差随时间的变化如图3(b)所示,由此相位差曲线进行直线最小二乘拟合得到相位差随时间变化率为0.007 2 rad/s,将其代入公式(1)中,得到横向速度为4.95 m/s。保持信号信噪比为0 dB,其他仿真条件不变,做200次随机实验,计算反演出的横向速度的RMSE(均方根误差)仅为0.041 2 m/s,说明对于信噪比较高的回波信号,使用匹配滤波处理后的两通道信号进行干涉,可以反演出较为准确的横向速度。
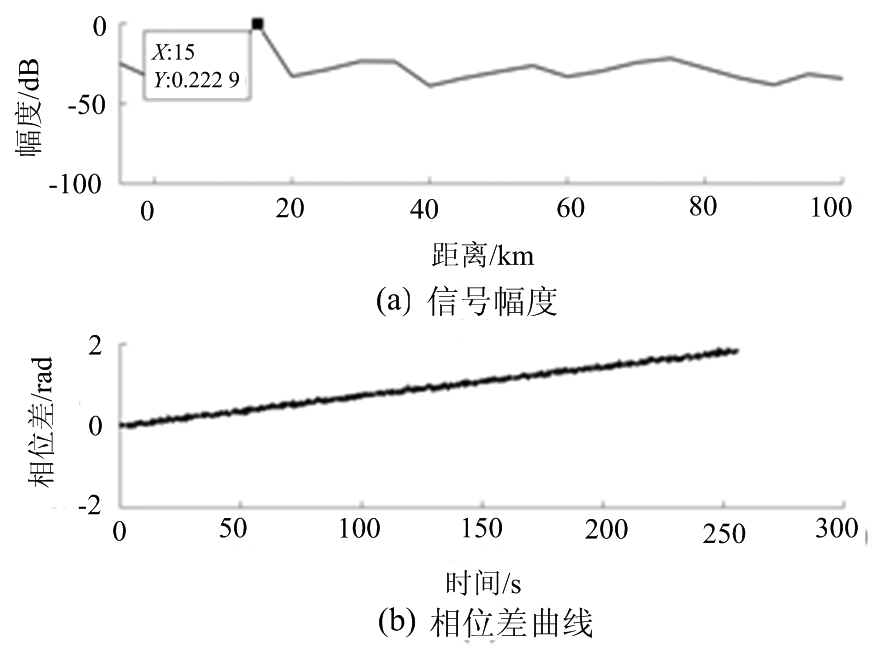
图3 0 dB信号仿真结果
降低回波信号信噪比为-25 dB,处理后所得目标信号幅度如图4(a)所示,从图中可以看出,在15 km处已经看不到目标信号,此时若进行干涉处理,得到相位差随时间的变化如图4(b)所示,可以看到相位差曲线的噪声较大。利用该相位差曲线拟合得到相位差变化率为0.005 rad/s,将其代入式(1)得到横向速度大小为3.38 m/s。保持信号信噪比为-25 dB,其他仿真条件不变,做200次随机实验,计算反演出的横向速度的RMSE为1.20 m/s,与设定值偏差较大。在实际情况中,目标的原始回波信号往往会低于-25 dB,为能够继续应用干涉法提取目标横向速度,需要在不影响通道间相位差的前提下,进一步提高目标信号的信噪比,从而减弱相位差曲线的噪声,来提高反演横向速度的准确度。

图4 -25 dB信号仿真结果
3 相干积累后提取横向速度
为使干涉模型可以用于反演实际的低信噪比目标信号的横向速度,可以将多帧目标回波信号进行相干积累,使用积累后的目标回波信号进行干涉来反演横向速度。下面从公式出发说明相干积累后反演横向速度的基本原理。
设雷达的发射信号为线性调频连续波,发射信号表达式如下:
(2)
式中,A为幅度,f0为载波频率,k=B/T为调频的斜率,B为信号的带宽,T为扫频周期。天线1中回波信号如下:
sr1(t,m)=A0exp{j2π[f0(t-τ)+
(3)
式中,A0为回波信号幅度,τ为回波时延。经解调和匹配滤波处理后,输出信号so1为
so1(t,m)=Ag1exp{j[-2π(r0m+r1m)/λ]}
(4)
同样对于天线2中的输出信号为
so2(t,m)=Ag2exp{j[-2π(r0m+r2m)/λ]}
(5)
式中,r0m,r1m,r2m是第m帧扫频周期目标到发射天线、接收天线1、接收天线2的距离。Ag1,Ag2为处理后的信号幅度。使用式(4)的相位减去式(5)的相位即可得到通道间的相位差um:
(6)
此时相位差变化率的大小kp为
(7)
由第1节讨论可知,横向速度和径向速度是互不影响的,故径向距离的改变只依赖于径向速度vr的大小而不受横向速度的影响。由于目标这样的运动特征,使得我们可以利用目标的径向速度进行相干积累增强信号信噪比,同时由于横向速度不受径向速度的影响,所以不会破坏横向速度带来的相位变化,使得积累后两天线中信号相位相减后仍可以得到正确的相位差曲线。
对天线1中的数据,若选取初始的扫频周期距离为r10,则后续的扫频周期时间对应的目标径向距离r1m为
r1m= r10+mTvr
(8)
对于目标到天线2和发射天线的径向距离,同理可有
r2m= r20+mTvr
(9)
r0m= r00+mTvr
(10)
将式(8),(9),(10)分别代入式(4),(5)中,可得
so1(t,m)=Ag1exp{j[-2π(r00+r10+
2mTvr)/λ]}
(11)
so2(t,m)=Ag2exp{j[-2π(r00+r20+
2mTvr)/λ]}
(12)
分别选取M帧扫频周期中式(11),(12)对应的谱点,各自形成M点序列,将序列视为-MT/2到MT/2时间上的连续信号,对其作傅里叶变换即进行相干积累,得到积累后的目标信号So1,So2为
So1=AgmAg1exp{j[-2π(r00+ r10)/λ]}
(13)
So2=AgmAg2exp{j[-2π(r00+ r20)/λ]}
(14)
Agm是经过M帧信号积累后的增益,而噪声由于并不具备相干性,无法因为积累而提高幅度,因此可以有效提高目标信号信噪比。同时可以看到在提高信噪比的同时,并未影响回波信号的相位,故使用式(13)相位减去式(14)相位可以获得相位差u0。
每间隔N帧扫频周期,重复上述操作,即可得相位差序列u0,uN,u2N,…… 此时相位差变化率大小为
(15)
为验证上述推导的正确性,取相干积累的扫频周期数M为100帧。相干积累后的信号幅度如图5(a)所示,选取两通道中多个积累后的目标信号的相位相减得到相位差随时间的变化如图5(b)所示,此相位差随时间变化率同样为0.007 3 rad/s,与不加噪声的匹配滤波后的结果相同,所以同样可以得到设定的5 m/s的横向速度,说明了相干积累用于反演横向速度的可行性。
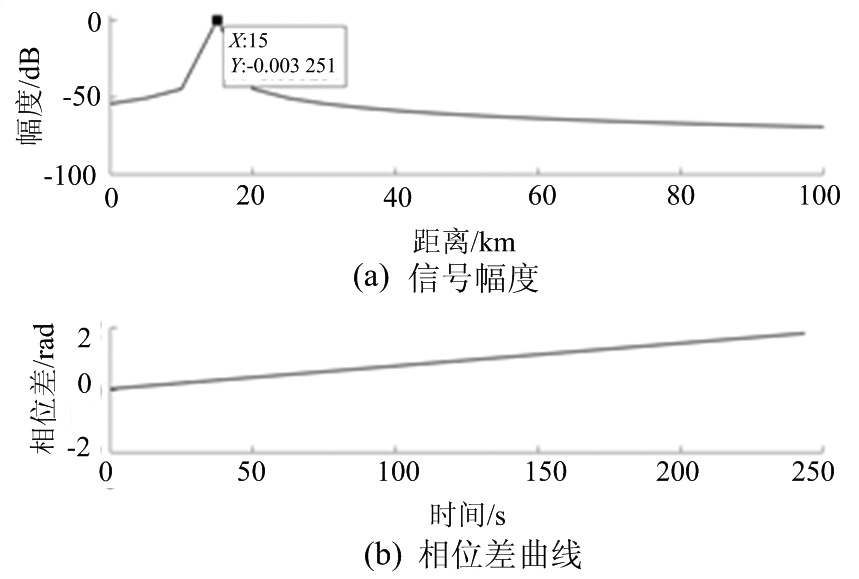
图5 无噪声信号100帧相干积累仿真结果
为验证相干积累提升信号的信噪比后,可以提高低信噪比信号的横向速度反演的准确度,我们设定原始回波信号信噪比分别为-25 dB和-35 dB,对其进行相干积累处理。首先设定信号信噪比为-25 dB,相干积累帧数为100帧,得到积累后的信号幅度和相位差曲线如图6所示,从图6(a)可以看到,相较于图4(a)的目标信号,积累后的目标信号信噪比有明显提升。使用每个通道中的积累后的目标信号进行干涉,得到的相位差曲线如图6(b)所示,对该相位差曲线进行直线最小二乘拟合,得到相位差变化率为0.007 2 rad/s,代入式(1)计算得到横向速度为4.95 m/s。保持仿真条件不变,进行200次随机实验,得到反演出的横向速度的RMSE仅为0.16 m/s,远小于未进行相干积累时的1.20 m/s,由此可见相干积累提高目标回波信号信噪比后,反演出的横向速度比匹配滤波后直接干涉得到的横向速度具有更高的准确度。
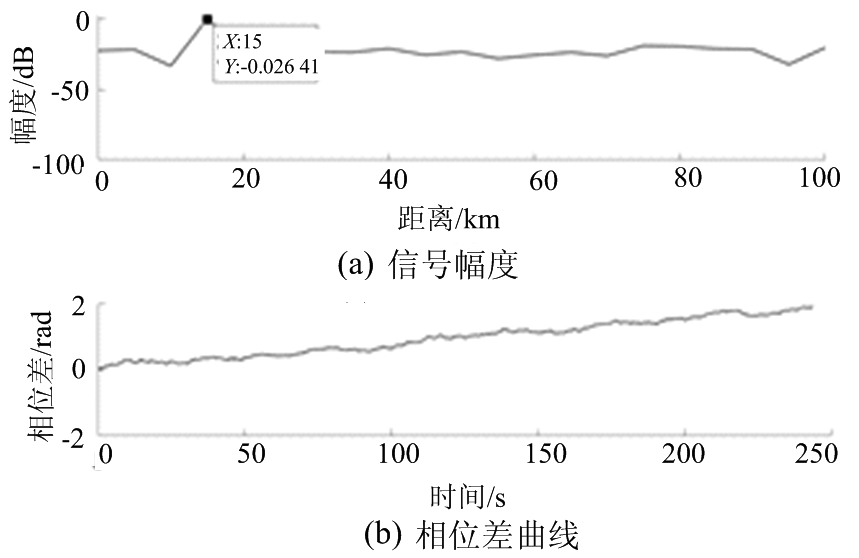
图6 -25 dB信号100帧相干积累仿真结果
接下来将信号信噪比降低为-35 dB,相干积累帧数仍为100帧,得到图7所示的信号幅度和相位差曲线,从图中可以看出由于原始回波信号信噪比较低,积累后的目标回波信号信噪比也相应降低,致使得到的相位差曲线的噪声较大。通过直线最小二乘拟合得到的相位差变化率为0.007 8 rad/s,将其代入式(1)计算横向速度为5.3 m/s。在此仿真条件下进行200次随机实验,得到反演出的横向速度的RMSE为0.63 m/s。

图7 -35 dB信号100帧相干积累仿真结果
为进一步减小反演出横向速度的RMSE,将相干积累的帧数提高到500帧,进行相干积累,得到如图8所示的目标信号幅度和相位差曲线,从图中可以看到在增加积累窗长后,目标信号信噪比进一步提升。相对于100帧信号相干积累后的相位差曲线,此时的相位差曲线变得更为平滑,由该曲线拟合得到的相位差变化率为0.007 1 rad/s,代入式(1)中计算得到横向速度大小为4.8 m/s。保持仿真条件不变,进行200次随机实验,得到反演出的横向速度的RMSE为0.51 m/s, 相对于100帧相干积累时反演出的横向速度的RMSE减小了0.1 m/s,进一步提高了横向速度反演的准确度。值得注意的是由于总的数据点数一定,在提高了积累窗长后,会使得积累后的信号数据点数变少,从而降低拟合的准确度,若想保证较大的积累窗长,需要保证较大的采样频率,使得在观测时间内能够采集到足够多的数据点。

图8 -35 dB信号500帧相干积累仿真结果
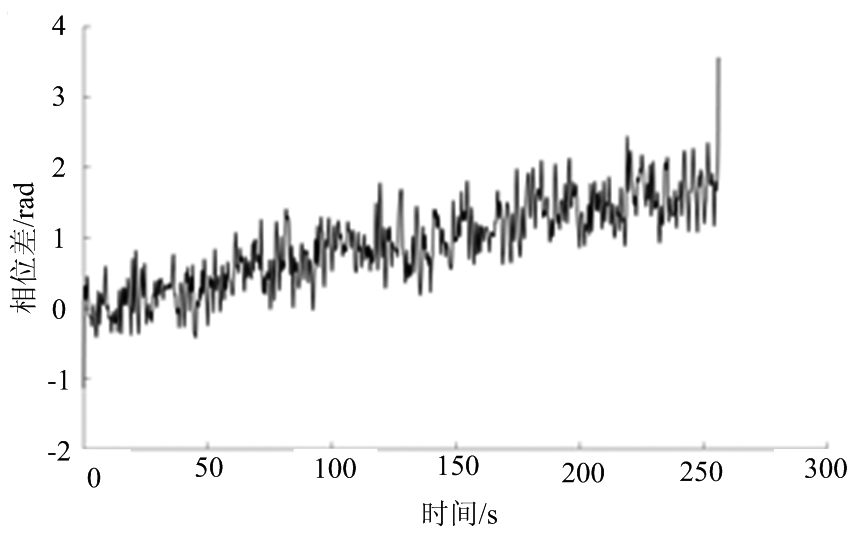
图9 S变换处理后的相位差曲线
最后给出-25 dB信噪比的信号经S变换处理后得到的相位差曲线如图9所示,可以看到相对于图6(b)相干积累后的相位差曲线,S变换处理后得到的相位差曲线的噪声仍是比较大的,不利于斜率的提取。从这里可以看出相较于其他抑制噪声的方法,相干积累不仅操作简单,同时由于充分利用了目标横向速度和径向速度互不影响的运动特征,其效果是优于其他方法的。
4 实测数据分析
为检验相干积累用于反演实际目标横向速度的效果,对真实雷达数据进行处理分析。雷达数据来源于武汉大学研制的高频地波雷达,时间地点为2015年1月17日龙海雷达站,该雷达站有6根接收天线是间距18 m的均匀线阵,工作频率为7.8 MHz,扫频周期为0.25 s,扫频带宽为30 kHz。

图10 1月17日目标积累后信号幅度

图11 1月17日目标对应的相位差曲线
在距离雷达站5 km处探测到一船只目标,其位置位于天线阵列法向方向上,用于干涉的两根天线间距为90 m,相干积累的窗长为500帧扫频周期。进行相干积累后目标回波信号的幅度如图10所示,选取两通道目标信号的相位进行相减得到相位差,由多个窗中的信号干涉得到相位差随时间的变化如图11所示,对该相位差曲线进行直线最小二乘拟合得到相位差变化率大小为0.009 8 rad/s,将其代入公式(1)中计算其横向速度大小为3.32 m/s,由AIS数据计算其横向速度大小为3.3 m/s,两者仅相差0.02 m/s。
另一实测数据同样来自于武汉大学研制的高频地波雷达,其时间地点为2019年10月23日龙海雷达站,该雷达同样有6根接收天线是间距18 m的均匀线阵,两发八收,其中我们关注的工作频率为7.5 MHz,扫频周期为0.125 s,扫频带宽为30 kHz。
在与雷达站相距5 km处,探测到一船只目标,目标与雷达站的连线和天线阵列夹角为100°,用于干涉的两根天线间距为90 m,相干积累的窗长仍选取500帧扫频周期。相干积累后的回波信号幅度如图12所示,选取的两通道中积累后的目标信号进行干涉,得到相位差曲线如图13所示,对该曲线进行直线最小二乘拟合,得到相位差变化率大小为0.008 7 rad/s,将其代入式(1)中,计算得到横向速度为3.8 m/s,由AIS提供的数据计算得到横向速度大小为3.62 m/s,两者相差仅为0.18 m/s。由上述两个反演横向速度的实例可以看出,相干积累用于提取目标横向速度是可行的。
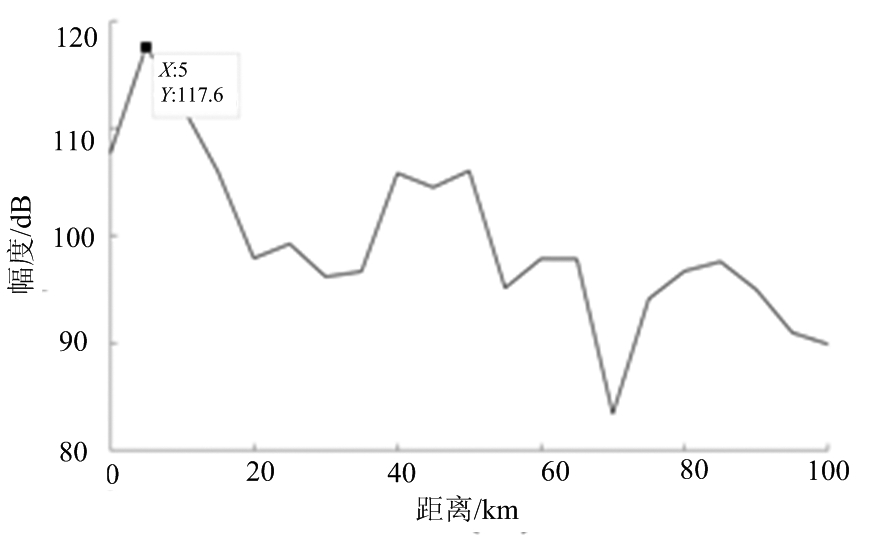
图12 10月23日目标积累后信号幅度
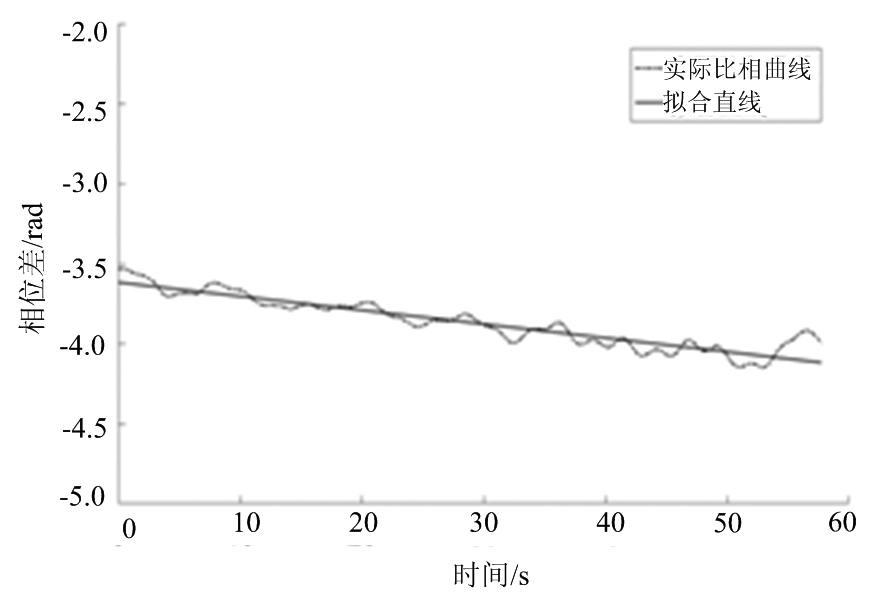
图13 10月23日目标对应的相位差曲线
5 局限性分析
在上面的讨论中,已经证实了相干积累用于提取横向速度的有效性,但都是基于横向速度和径向速度不变的前提条件下进行分析。但当目标移动距离很大时,尽管目标是匀速直线运动,在上述分析的曲线坐标系中,目标的横向速度和径向速度都会发生改变,使得提取的结果发生错误。为此,有必要找出目标横向速度和径向速度保持不变的横向距离移动范围,以此来控制不同横向速度目标的观测时间。
为此我们设定一径向距离为5 km的目标,为排除噪声的影响,不加噪声。画出相位差随目标的横向移动距离的变化曲线,如图14所示,可以看到当目标横向运动1.2 km后,实际相位差曲线与理想的相位差曲线发生了偏差,说明在目标径向距离5 km的条件下,目标的横向移动距离不应超过1.2 km,否则得到的相位差曲线是有偏差的,无法用于提取横向速度。

图14 径向距离5 km时的相位差曲线
对于其他径向距离的目标,可以按照比例关系来得到目标的最大横向移动距离,若知目标的横向速度,则可以得到对应的观测时间如下:
![]()
(16)
式中r为目标径向距离。在实际应用中可以针对观测目标的运动特征估计vl大小范围,得到合适的观测时间。例如船只目标横向速度一般不会超过20 m/s,所以对于5 km处的目标,其观测时间不应超过60 s。若目标速度较大,对应的观测时间会非常短,此时为保证积累的周期数,需要有较大的信号采样率。
另一个会给结果带来误差的因素是目标的加速度,若目标具有加速度,则相位差曲线不再为一直线,此时使用直线拟合则会带来误差。设定横向速度大小为5 m/s,相干积累的帧数为100帧,表1给出了不同加速度下反演出的横向速度,从表中可以看到当加速度不大于0.015 m/s2时,反演出的横向速度与真实值仍是较为接近的。但当加速度大小大于0.015 m/s2时,与真实值的偏差会超过1 m/s。
表1 不同加速度反演出的横向速度

加速度/(m·s-2)速度/(m·s-1)0.0055.300.0105.600.0156.020.0206.350.0256.74
6 结束语
本文针对高频地波雷达反演横向速度准确度差的问题,提出对目标信号相干积累后再提取相位差变化率的方法。通过仿真得到了该方法在反演-25 dB信噪比信号的横向速度时,其结果的RMSE仅为0.16 m/s左右,在反演-35 dB信噪比信号的横向速度时,其RMSE也仅为0.5 m/s左右。并通过雷达实测数据处理验证了该方法在实际场景下提取横向速度的可行性。同时对该方法的局限性进行了分析,给出了不同距离下,不同速度目标所对应的观测时间范围公式,并通过仿真分析得到目标加速度不超过0.015 m/s2时,该方法仍能保证一定的准确度。
[1] LI Miao , WU Xiongbin , CHEN Zhangyou , et al. A Scheme for Multitarget Lateral Velocity Measurement with High-Frequency Monostatic Radar[J]. IEEE Journal of Oceanic Engineering, 2019, 45(4):1427-1438.
[2] QIANG Mengye , BAI Yechao , ZHANG Xinggan . Lateral Velocity Measurement and Error Analysis[J]. The Journal of Engineering, 2019(1):7796-7799.
[3] 弗洛里安·弗斯特尔,海尔曼·罗林.城市交通情况下的横向速度估计(英文)[J].雷达科学与技术,2007,5(3):161-166.
FÖLSTER Florian, ROHLING Hermann. Lateral Velocity Estimation in City Traffic Scenarios [J]. Radar Science and Technology, 2007,5(3):161-166.
[4] ROARTY H , KERFOOT J , KOHUT J,et al. Improving the Measurements of High Frequency Radar: Reduced Averaging Times and Bistatics[C]∥ 2013 MTS/IEEE OCEANS - Bergen, Bergen, Norway :IEEE, 2013:1-6.
[5] ZHANG Bo , ZHAO Wanzhong , ZOU Songchun , et al. A Reliable Vehicle Lateral Velocity Estimation Methodology Based on SBI-LSTM During GPS-Outage[J].IEEE Sensors Journal,2021,21(14):15485-15495.
[6] 张健,陈章友. 电波干涉法测量运动目标横向速度仿真分析[C]∥第十二届全国电波传播学术讨论会,青岛:中国电子学会,2013:254-256.
[7] LI Chuan , CHEN Zhangyou , WU Xiongbin . A Scheme to Measure Lateral Velocity by Radio Interfe-rometry[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(2):127-131.
