0 引言
外辐射源雷达是利用第三方辐射源信号(如广播电视台)进行目标探测定位的双/多基地雷达,具有覆盖性能好、生存能力强、部署灵活等优点[1-2]。传统外辐射源雷达在工作中,单个接收站一般只与一个发射站配对,通过参考通道接收该发射站的直达波以及通过监测通道接收目标反射回波,对获取信号进行处理后,可以得到目标双基地距离差、双基地速度与到达角等量测值[3-4]。但由于发射站不可控,外辐射源雷达这种系统配置与工作方式很难保证目标的跟踪连续性与定位精度[5]。
采用多个发射站的不同频率目标回波进行联合探测,可以大幅度提升定位精度并扩大探测覆盖区域[6-7]。因此,在尽量减小系统规模与复杂度的前提下,采用外辐射源雷达分时多频工作模式,通过周期性切换工作频率,单个接收站可以与多个发射站配对,在不同时刻接收来自不同发射站的目标回波,获取目标的空间分集信息,以此提高监测与跟踪性能。
收发站位置信息是外辐射源雷达工作的前提,接收站可根据需要灵活部署,其准确的位置信息可实时获取,而不可控的第三方发射站位置信息通常需要提前获得。但在实际工作中,发射站往往会发生变化而无法预先获取其位置,尤其是分时多频外辐射源雷达需要利用多个发射站,因此,对分时多频系统中的发射站进行实时定位是首先需要解决的问题。
目前,关于外辐射源雷达的发射站定位研究并不多,文献[8]通过合作目标的双基地距离差从而得到多个含有发射站位置信息的椭圆方程,多个椭圆间的交点即为发射站位置。文献[9]利用合作飞行器的笛卡尔坐标信息,将坐标变换到双基地坐标系下后通过匹配双基地距离与速度得到发射站位置。文献[10]针对多目标情况下关联的复杂性,通过坐标变换,建立距离和多普勒的代价函数,正确稳定关联双基地雷达目标观测值与真实信息,从而实现对发射站的定位。上述文献提及方法都是针对传统外辐射源雷达工作模式的单个发射站进行定位,且都需要合作目标配合,通过获取足够多的合作目标精确位置信息来实现定位,其应用场景往往受到局限性较大。
分时多频外辐射源雷达系统本质上是一个异步多传感器系统,在对未知位置的发射站设置位置初值后,则发射站的位置估计就可以转换成求解传感器系统固有偏差,从而将定位问题转化成多传感器误差配准过程。这样就可以在目标探测跟踪过程中实现对发射站的实时现场定位,可以提高外辐射源雷达的环境适应性与布设灵活性。
关于多传感器系统的误差配准问题,主要方法有基于加权最小二乘(Weighted Least Squares, WLS)理论[11-14]、基于最大似然(Maximum Likelihood, ML)准则[15-19]以及基于卡尔曼滤波器的空间配准算法[20-24]。其中,文献[11]提出一种基于快坐标下降的最小二乘方法,在异步量测中估计传感器系统误差。文献[14]针对多辐射源系统的双基地距离差量测存在固定偏差的情况,基于最小二乘算法,同时求解目标位置与系统偏差。文献[15-16]基于最大似然估计的空间配准算法,通过使似然函数达到最大值,从而实现对目标状态和系统误差的联合估计。文献[22]提出一种带配准误差的增广状态高斯混合滤波器(Gaussian Mixture Hypothesis Density, GM-PHD)来提高量测关联的正确率。文献[23]讨论了全局传感器的无偏情况下,局部传感器误差配准问题,提出了采用两步扩展卡尔曼滤波算法估计量测偏差。
上述文献方法均仅用于估计量测层面的较小偏差,并不适用于分时多频外辐射源雷达量测异步且量测函数非线性情况的发射站坐标误差求解问题。
本文针对分时多频外辐射源雷达系统的发射站定位问题,通过各自收发对量测估计完成时间配准,同时,通过设置发射站位置初值构造参数为发射站坐标偏差的伪量测,完成空间配准,采用卡尔曼滤波器对两个发射站进行定位。此方法无需合作目标所提供的位置信息,而是仅利用接收站获得的量测值便可对发射站进行定位,并且可以达到较高定位精度。
1 探测定位模型
分时多频外辐射源雷达二维探测示意图如图1所示:场景中有2个第三方发射站和1个接收站,发射站工作频率分别为f1、f2,接收站周期性切换中心工作频率分别与两个发射站形成收发对,其周期通常为相干积累时间长度T。接收站包含监测天线与参考天线,分时接收两个发射站的直达波和目标反射回波,若收发对1在kT时刻开始目标探测,则收发对2在(k+1)T时刻开始目标探测(k=2n,n=0,1,2,…)。
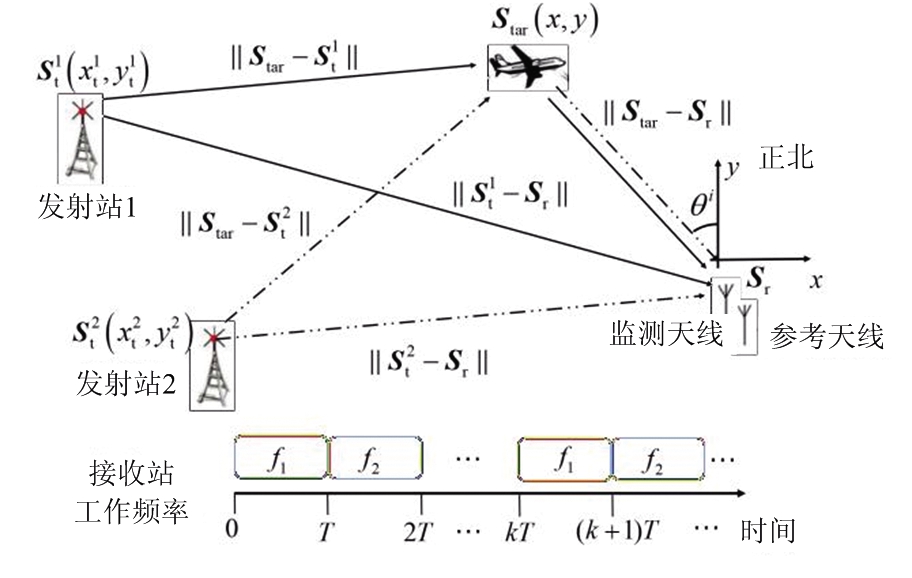
图1 分时多频外辐射源雷达二维探测示意图
图中Sr=[xr,yr]为接收站位置,![]() 为收发对i(i=1, 2)所对应的发射站的位置坐标、Star=[x,y]为目标位置。目标到接收站距离R=‖Star-Sr‖、目标到收发对i所对应的发射站的距离为
为收发对i(i=1, 2)所对应的发射站的位置坐标、Star=[x,y]为目标位置。目标到接收站距离R=‖Star-Sr‖、目标到收发对i所对应的发射站的距离为![]() 收发对i基线距离为
收发对i基线距离为![]() 为2-范式。收发对i通过反射回波与直达波时延获取双基地距离差量测为
为2-范式。收发对i通过反射回波与直达波时延获取双基地距离差量测为![]() 通过多普勒频移获得双基地速度量测为
通过多普勒频移获得双基地速度量测为![]() (双基地距离差的时间变化率),通过到达角的估计来获取目标方位角量测为θi(目标与接收站连线与正北方向角度)。
(双基地距离差的时间变化率),通过到达角的估计来获取目标方位角量测为θi(目标与接收站连线与正北方向角度)。
在探测目标位置未知情况下,无法通过单个收发对自身量测值来定位发射站位置,因此需要获取两个收发对同一时刻的目标量测值。由于两个收发对采用分时切换方式对目标进行异步量测,故需要对每个收发对中缺失的量测值分别进行估计,从而得到在时间上完整的量测序列,完成时间对齐。
对于收发对1,没有获取到目标(k+1)T时刻量测,我们假设目标双基地坐标系下的运动为匀加速运动模型,结合收发对1的kT时刻与(k+2)T时刻目标量测值,通过内插方法得到收发对1的(k+1)T时刻双基地距离差量测估计值![]() 为
为
![]()
![]()
(1)
同理,双基地速度量测估计值为
(2)
由于接收站位置固定,收发对1的(k+1)T时刻方位角量测估计值可用收发对2该时刻方位角量测值替代。
(3)
同理,对收发对2也使用相同方式对其未获取时间周期内的量测值进行估计,从而使得两个收发对的目标量测在时间上对齐。
由于两个收发对在时间上对齐的量测值都是各自收发对的双基地量测,需进一步统一到公共笛卡尔坐标系下。以接收站为原点,建立北东地(North East Down, NED)坐标系,各自收发对结合所获得的量测值进行单站定位,便可得到目标在该公共笛卡尔坐标系下的位置信息。
对于收发对i,根据双基地距离差量测值![]() 在发射站位置已知时,可得到一个以接收站、发射站为焦点的椭圆。结合椭圆方程与方位角量测,可得到目标与接收站距离估计值
在发射站位置已知时,可得到一个以接收站、发射站为焦点的椭圆。结合椭圆方程与方位角量测,可得到目标与接收站距离估计值![]() 如下:
如下:
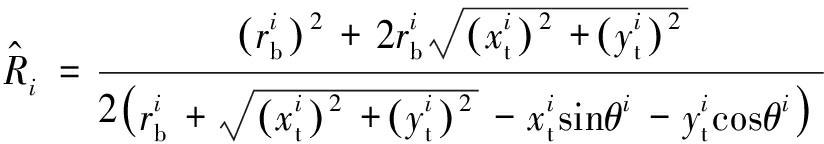
(4)
进一步,将![]() 乘以收发对i方位角量测θi的正弦值、余弦值,得到公共笛卡尔坐标系下目标位置估计值为
乘以收发对i方位角量测θi的正弦值、余弦值,得到公共笛卡尔坐标系下目标位置估计值为
(5)
若已知发射站准确位置,单站定位可以得到目标在公共笛卡尔坐标系下的位置信息。但若发射站位置未知,对两个发射站分别设定为带有偏差的初值后,各自进行单站定位,发射站坐标存在固定偏差导致得到的目标位置信息存在误差,利用各自收发对得到的该目标不准确位置信息求解发射站坐标固定偏差,从而可将发射站定位问题转换为多传感器固定系统偏差下的空间配准问题。
2 基于伪量测构造的发射站定位
发射站坐标所设初值情况下,将两个收发对单站定位得到的目标位置估计值之差定义为目标观测误差的伪量测,分别是目标与接收站距离估计![]() 之差
之差![]() 目标横坐标估计
目标横坐标估计![]() 之差
之差![]() 目标纵坐标估计
目标纵坐标估计![]() 之差
之差![]() 将发射站坐标初值表示为真值与偏差的组合,对单站定位方程一阶泰勒展开处理可完成目标真实状态与发射站坐标偏差的解耦,公共笛卡尔坐标系下,目标真实状态相互抵消,构造出参数为发射站坐标偏差的线性化伪量测方程。根据伪量测方程进行卡尔曼滤波并随着滤波过程不断修正更新该参数来求解发射站坐标偏差,进而实现发射站定位,具体过程如下:
将发射站坐标初值表示为真值与偏差的组合,对单站定位方程一阶泰勒展开处理可完成目标真实状态与发射站坐标偏差的解耦,公共笛卡尔坐标系下,目标真实状态相互抵消,构造出参数为发射站坐标偏差的线性化伪量测方程。根据伪量测方程进行卡尔曼滤波并随着滤波过程不断修正更新该参数来求解发射站坐标偏差,进而实现发射站定位,具体过程如下:
设定收发对i (i=1, 2)对应发射站的位置初始值为![]() 可表示为
可表示为
(6)
式中,![]() 为发射站的真实位置坐标,
为发射站的真实位置坐标,![]() 为发射站位置初值与发射站的真实坐标间的偏差。
为发射站位置初值与发射站的真实坐标间的偏差。
在kT时刻,根据收发对i的目标量测![]() 与发射站初值
与发射站初值![]() 得到发射站坐标存在固定偏差情况下的目标位置估计值,分别为
得到发射站坐标存在固定偏差情况下的目标位置估计值,分别为![]() 实际应用中,考虑到方位角量测θi存在噪声且目标与接收站距离往往较远,根据式(5)可知,所求目标坐标估计
实际应用中,考虑到方位角量测θi存在噪声且目标与接收站距离往往较远,根据式(5)可知,所求目标坐标估计![]() 相较于目标与接收站距离
相较于目标与接收站距离![]() 会进一步放大方位角量测误差,因此,只保留目标与接收站的距离估计值
会进一步放大方位角量测误差,因此,只保留目标与接收站的距离估计值![]() 进行后续处理。
进行后续处理。
将式(6)代入式(4)中结合量测值得到![]() 对
对![]() 在
在![]() 处一阶泰勒展开,
处一阶泰勒展开,![]() 可表示为发射站坐标偏差ζi的线性化模型:
可表示为发射站坐标偏差ζi的线性化模型:
(7)
式中,![]() 为目标与接收站真实距离。
为目标与接收站真实距离。
将两个收发对得到的目标与接收站距离估计值![]() 相减,则可构造目标观测误差的伪量测z(k),表示为
相减,则可构造目标观测误差的伪量测z(k),表示为
(8)
将式(7)代入式(8)中,R(k)相互抵消,得到k时刻,发射站坐标偏差ζi(k)为参数的伪量测方程。
定义发射站坐标偏差的状态转移方程与伪量测方程z(k)如下:
β(k)=F(k|k-1)β(k-1)
(9)
z(k)=B(k)β(k)+wz(k)
(10)
式中,B(k)=[-C1(k),C2(k)],β(k)=[ζ1(k),ζ2(k)]T,wz(k)为伪量测方程噪声误差项,假设其为均值为零的高斯白噪声,协方差为![]() 考虑发射站位置固定,状态转移矩阵F(k|k-1)为单位矩阵。
考虑发射站位置固定,状态转移矩阵F(k|k-1)为单位矩阵。
根据构建的伪量测方程采用卡尔曼滤波器进行递推,多场滤波更新结果即为所求发射站坐标偏差β(k)。卡尔曼滤波递推过程如下:
首先进行一步预测
β(k|k-1)=F(k|k-1)β(k-1|k-1)
(11)
P(k|k-1)=F(k|k-1)·
P(k-1|k-1)FT(k|k-1)
(12)
z(k|k-1)=B(k)β(k|k-1)
(13)
随后计算滤波增益K
(14)
最后完成更新
β(k|k)=β(k|k-1)+K(z(k)-z(k|k-1))
(15)
P(k|k)=P(k|k-1)-
(16)
利用停止卡尔曼递推后得到的结果β(k|k)对初值进行修正,即得到发射站坐标估计值。
由于一阶泰勒展开过程往往会带来较大的线性化误差,利用所得到发射站坐标估计值,通过牛顿迭代方法,利用相同量测值再次进行上述伪量测构造与卡尔曼滤波过程,多次迭代后,即可得到最优修正估计值,迭代修正公式如下:
(17)
式中![]() 为第i个发射站第n次迭代得到的估计值。设定阈值μ,两个发射站均满足
为第i个发射站第n次迭代得到的估计值。设定阈值μ,两个发射站均满足![]() 时迭代终止,
时迭代终止,![]() 为第i个发射站位置最终估计值。
为第i个发射站位置最终估计值。
3 克拉美罗下界(CRLB)分析
为了后续验证算法性能性,本节将分析所求参数β的克拉美罗下界(Cramer-Rao Lower Bound, CRLB)。假设量测噪声为独立同分布的零均值高斯白噪声,收发对i的量测噪声项wi(k)=[nr(k),nθ(k)]T的噪声协方差矩阵V(k)为
(18)
式中σr、σθ为双基地距离差量测和方位角量测的噪声标准差,得到k时刻伪量测的噪声方差![]() 为
为
(19)
式中,
(20)
定义![]() 为参数估计值,β为参数真值,则该参数均方误差为
为参数估计值,β为参数真值,则该参数均方误差为
(21)
式中,J(β)是关于所求参数β的Fisher信息矩阵(Fisher Information Matrix, FIM)。具体可表示为

(22)
其中,
(23)
4 仿真实验
本节通过仿真测试评估所提算法性能,仿真场景设置如下:两个未知位置的发射站,一个已知位置的接收站,接收站坐标Sr=[0,0] km,发射站的坐标分别为[8.3,2.6] km、[-5.4,6.6] km。接收站周期性切换工作频率,异步接收来自不同发射站的回波信号,接收站频率切换周期T=1 s。假设两个收发对所有量测噪声为独立同分布的零均值高斯白噪声。目标在两个收发对共同探测区域内匀加速运动,目标运动起点为[9.2,5.4] km,沿横纵坐标轴正方向上的初始速度vx0=120 m/s、vy0=100 m/s,加速度为ax0=0.3 m/s2、ay0=-0.8 m/s2,运动时间为100 s。
算法性能评价指标采用发射站位置估计的均方根误差(Root Mean Squared Error, RMSE),其定义如下:
(24)
式中,RMSEi为第i个发射站位置估计的均方根误差,![]() 为第i个发射站的第mc次蒙特卡洛仿真位置估计结果,
为第i个发射站的第mc次蒙特卡洛仿真位置估计结果,![]() 为第i个发射站真实位置,N为蒙特卡洛仿真次数,设置为1 000。
为第i个发射站真实位置,N为蒙特卡洛仿真次数,设置为1 000。
4.1 不同量测噪声标准差下发射站定位结果
双基地距离差量测、方位角量测的噪声标准差表示为σw=[σr,σθ]。设定迭代终止阈值μ=0.01 m。表1给出了发射站位置在不同量测噪声标准差时的位置估计RMSE。其中CRLBi表示第i个发射站位置估计克拉美罗下界。由表1可知,第i个发射站,得到的定位结果RMSEi接近对应σw下的CRLBi,且当量测噪声标准差为零时,可以得到发射站位置坐标的无偏估计。
另外,量测噪声标准差相同时,RMSE1与RMSE2不一致,根据定位方程式,分析可知,如果两个发射站与接收站、目标之间的几何关系不同,那么伪量测构造过程会对目标量测进行不同的非线性处理,由式(4)可以看出:基线距离越长,双基地距离差量测噪声误差带来的影响会加大,同时,方位角量测噪声影响会变小,几何关系不同导致了各自位置估计RMSEi的不一致。
表1 不同量测噪声标准差发射站位置估计RMSE
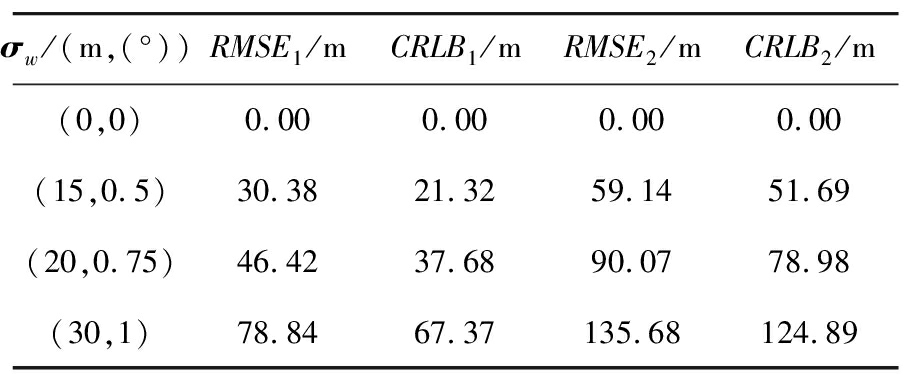
σw/(m,(°))RMSE1/mCRLB1/mRMSE2/mCRLB2/m(0,0)0.000.000.000.00(15,0.5)30.3821.3259.1451.69(20,0.75)46.4237.6890.0778.98(30,1)78.8467.37135.68124.89
4.2 不同伪量测对所提算法性能影响
为了测试不同伪量测的对所提算法的性能影响,本节对比分析了所提算法与文献[24]中传统算法的性能差异。在传统算法中,多传感器系统进行空间配准时,通过目标坐标(x,y)构造伪量测。由于这种配准方法目前主要应用于主动雷达领域估计量测固定偏差,故本文重新实现了该传统方法构造伪量测在外辐射源雷达中的进行发射站定位的实验;设置双基地距离差、双基地速度、方位角量测噪声标准差分别为30 m、1.5 m/s、1°。不同伪量测对所提算法性能的影响如图2所示。

(a) 不同伪量测对应的定位结果(发射站1)
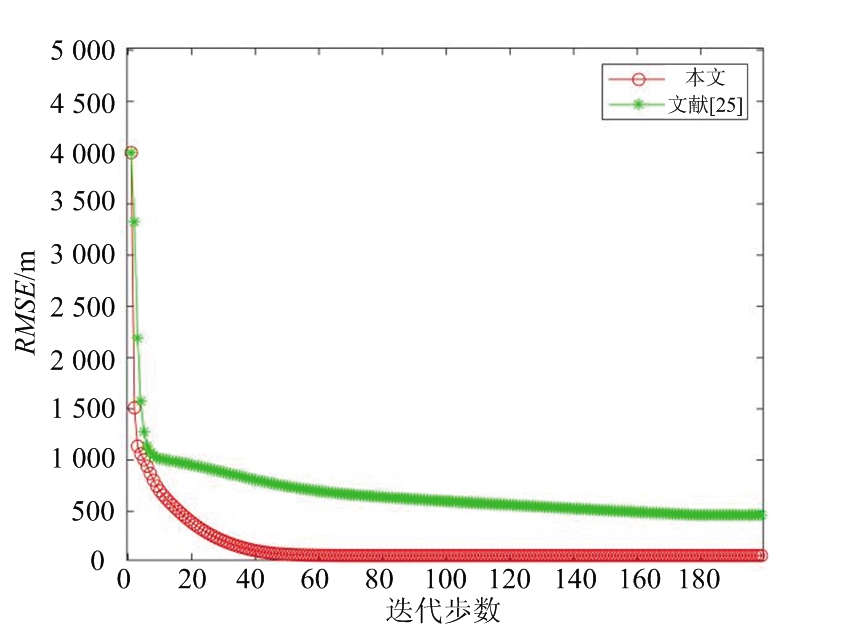
(b) 不同伪量测对应的定位结果(发射站2)
图2 不同伪量测对所提算法性能的影响
由图2分析得出发射站定位结果RMSEi在开始迭代时快速下降,然后下降变缓,最后收敛于一个稳定值。收敛速度方面,要满足两个发射站位置估计RMSEi均达到收敛,采用本文伪量测处理需要50步迭代,而采用文献[24]方法构造的伪量测处理需要进行180步迭代,这是由于伪量测矩阵维数不同导致收敛速度有所差别。定位精度方面,本文所得到发射站位置估计RMSEi足够小,可以满足精度要求,而文献[24]方法得到的发射站位置估计依然存在较大误差。以上结果与分析表明采用本文方法构造伪量测最后得到发射站位置估计精度更高且收敛速度更快,可以大幅降低计算量。
4.3 发射站初始值对所提算法性能影响
在本文算法开始,需要对发射站坐标设置一个初始值。实际应用中,根据发射站直达波到达角度,可以得知发射站的大致方位信息,以此作为依据,根据距离发射站位置的远近对发射站设置三种初始值情况分别进行仿真。情况1:对两个发射站设置初始坐标分别为[2,0.7] km、[-1.5,1.7] km;情况2:初始坐标设置为[4,1.4] km、[-3,3.4] km;情况3:初始坐标设置为[6,2.1] km、[-4.5,5.1] km。发射站初值对所提算法性能影响如图3所示,其中量测噪声与上一小节相同。
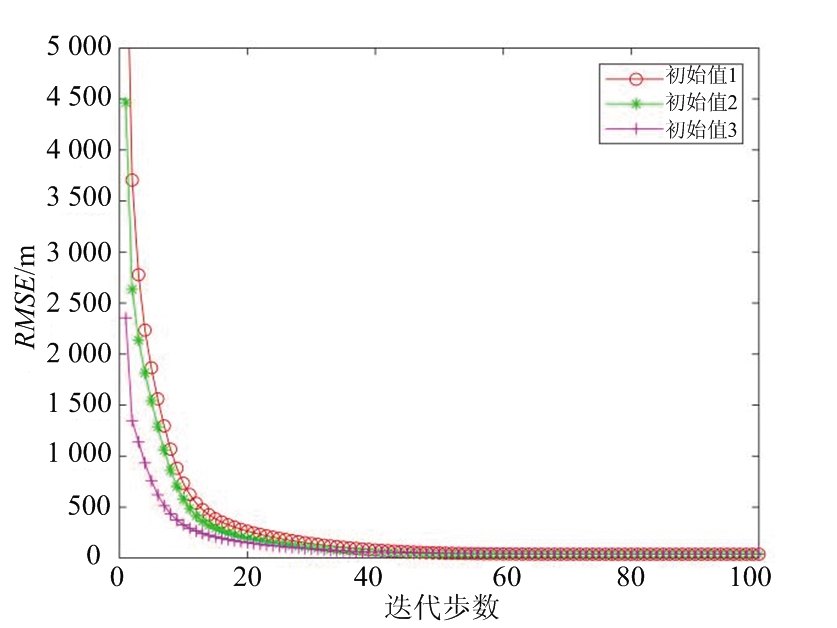
(a) 不同初始值对应的定位结果(发射站1)

(b) 不同初始值对应的定位结果(发射站2)
图3 发射站初值对所提算法性能影响
由图3分析得出设定不同发射站坐标初始值,RMSEi经过数次迭代,在近似相同迭代步数处收敛于一个稳定值,且最后结果并无明显区别,说明本文所提算法对发射站初始值不敏感,具有一定的鲁棒性。
5 结束语
针对分时多频外辐射源雷达发射站实时定位问题,本文构建了时间同步后的发射站坐标空间配准模型,将两个收发对目标笛卡尔坐标系状态差值与发射站坐标偏差组合在同一量测方程中,给出了基于伪量测构造的扩展迭代卡尔曼滤波发射站定位算法,该方法无需获得合作目标信息,便可有效处理多个发射站定位问题。仿真结果表明,此方法均方根误差接近克拉美罗下界,且收敛速度快。
[1] 万显荣.基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势[J].雷达学报,2012,1(2):109-123.
[2] BLASONE G P, COLONE F, LOMBARDO P, et al. Passive Radar DPCA Schemes with Adaptive Channel Calibration[J]. IEEE Trans on Aerospace and Electronic Systems, 2020, 56(5):4014-4034.
[3] 赵勇胜, 赵拥军, 赵闯. 联合角度和时差的单站无源相干定位加权最小二乘算法[J]. 雷达学报, 2016, 5(3):302-311.
[4] GAO X F, LI P, HAO X H, et al. A Novel DOA Estimation Algorithm Using Directional Antennas in Cylindrical Conformal Arrays[J]. Defence Technology, 2021, 17(3):1042-1051.
[5] STEJSKAL V, KUSCHEL H, BRENNER T, et al. DETOUR Trials: the Mission and Its Results[C]∥ 2017 18th International Radar Symposium, Prague, Czech Republic: IEEE, 2017:1-14.
[6] 李飞, 江胜利, 皇甫流成,等. TNR型调频广播外辐射源雷达探测实验[J]. 雷达科学与技术, 2019, 17(2):191-197.
[7] 顾昌浩, 万显荣, 吕敏,等. 多频外辐射源雷达无人机探测实验研究[J]. 雷达科学与技术, 2019, 17(6):591-596.
[8] YI J, WAN X, YAN F, et al. ADS-B Information Based Transmitter Localization in Passive Radar[C]∥ URSI General Assembly and Scientific Symposium,Beijing, China:IEEE, 2014:1-4.
[9] MALANOWSKI M, KULPA K, ZYWEK M, et al. Estimation of Transmitter Position Based on Known Target Trajectory in Passive Radar[C]∥2020 IEEE International Radar Conference,Washington, DC, USA:IEEE, 2020:506-511.
[10] KRUECKEMEIER M, SCHWARTAU F, PAUL S, et al. Passive Radar Transmitter Localization Using a Planar Approximation[J]. IEEE Trans on Aerospace and Electronic Systems, 2021, 57(5):3405-3415.
[11] PU Wenqiang, LIU Yafeng, YAN Junkun, et al. Optimal Estimation of Sensor Biases for Asynchronous Multi-Sensor Data Fusion[J]. Mathematical Programming, 2018, 170:357-386.
[12] 左燕, 陈志猛, 蔡立平. 基于约束总体最小二乘的单站DOA/TDOA联合误差校正与定位算法[J]. 电子与信息学报, 2019,41(6):1317-1323.
[13] 孙顺, 董凯, 齐林, 等. 基于TDOA与GROA的多运动站误差配准算法[J]. 电子与信息学报, 2017, 39(6):1439-1445.
[14] YI J, WAN X, LEUNG H, et al. Noncooperative Registration for Multistatic Passive Radars[J]. IEEE Trans on Aerospace Electronic Systems, 2016, 52(2):53-65.
[15] GINI F, FORTUNATI S, GIOMPAPA S, et al. On the Application of the Expectation-Maximisation Algorithm to the Relative Sensor Registration Problem[J]. IET Radar Sonar & Navigation, 2013, 7(2):191-203.
[16] WANG Jun, MA Shuheng, ZHANG Yuxi, et al. EMLR for Multiple Radars on a Mobile Platform[J]. The Journal of Engineering, 2019(20):6494-6498.
[17] SHANG Juan, YAO Yuan. Approach of System Error Registration for Two-Station Coast Radars for Sea Surface Monitoring[J]. The Journal of Engineering, 2019(21):7721-7725.
[18] 崔亚奇, 熊伟, 何友. 基于MLR的机动平台传感器误差配准算法[J]. 航空学报, 2012, 33(1):118-128.
[19] WU W H, JIANG J. Maximum Likelihood Registration for Passive Sensors of Multiple Airborne Platforms in WGS-84[J]. Systems Engineering and Electronics, 2014, 37(2):304-309.
[20] 王鼎, 尹洁昕, 刘瑞瑞, 等. 同步时钟偏差存在下的时差定位性能分析及改进的定位方法[J]. 电子学报, 2018, 46(6):1281-1288.
[21] NABAA N, BISHOP R H. Solution to a Multisensor Tracking Problem with Sensor Registration Errors[J]. IEEE Trans on Aerospace & Electronic Systems, 1999, 35(1):354-363.
[22] WU W, JING J, LIU W, et al. Augmented State GM-PHD Filter with Registration Errors for Multi-Target Tracking by Doppler Radars[J]. Signal Processing, 2016, 120:117-128.
[23] GE Quanbo, CHEN Tianxiang, DUAN Zhansheng, et al. Relative Sensor Registration with Two-Step Method for State Estimation[J]. Cognitive Computation and Systems, 2019,1(2):45-54.
[24] 董云龙, 黄高东. 一种基于SSR-TSEKF的多雷达误差配准算法[J]. 电光与控制, 2020, 27(6):27-31.




