0 引 言
在合成孔径雷达(Synthetic Aperture Radar, SAR)领域,高分辨率和宽测绘带成像一直是其发展目标,也是未来SAR的发展趋势。然而对于单通道SAR,高分辨率和宽测绘带对脉冲重复频率(Pulse Repeat Frequency, PRF)的要求是矛盾的,也即经典的最小天线面积限制[1]。即使应用了诸如聚束模式、混合聚束模式、扫描模式、TOPSAR、马赛克模式等方法[1-3],也只能在高分辨率和宽测绘带中进行取舍,不可兼得。因此,多通道SAR设计已成为目前实现高分宽幅成像的主流方案[4],并已得到RADARSAT-2[5]、TerraSAR-X[6]、ALOS-2[7]、高分三号[8]等星载SAR的验证。
方位多通道SAR利用相位中心偏置天线技术,通过增加接收天线来增加方位向采样率,接收的信号经均匀化处理和重新排列后可满足奈奎斯特采样定律,从而达到抑制方位模糊的目的。这样可以在使用低PRF采样的情况下获得方位向高分辨率的图像,实现高分宽幅。如果想要获得更高分辨率或者更大的测绘幅宽,可以将多通道与波束扫描模式结合,相关的处理方法及结果在文献[9]和[10]中给出。
斜视SAR可以实现灵活观测,在每次飞行期间可以对一个区域进行多次观测,而且可以在多个角度观测目标的后向散射信息得到目标的表面结构信息。因此斜视SAR也是如今发展的一个热点方向[11]。
一个很自然的想法就是将多通道波束扫描模式与斜视工作方式相结合,这样可以实现灵活的高分宽幅对地观测,但是一些问题也应运而生。由于斜视的工作模式,信号的多普勒中心频率在二维频域是随着距离向频率的变化而变化的,这会产生额外的多普勒带宽。当斜视角很大时,甚至会出现由于多普勒中心在信号距离向带宽范围内变化过大而造成方位频谱混叠的现象。因此,相对于正侧视时的多通道波束扫描模式,斜视多通道波束扫描模式的信号多普勒带宽又进一步增加了,这样在使用文献[9]中的方法时,会使得信号在方位去斜之后的多普勒带宽仍然大于通道数与采样率的乘积,导致后续的重构处理仍然无法进行。
针对上述斜视多通道波束扫描模式的问题,在结合传统斜视SAR成像处理的基础上,本文提出了一种基于方位向去斜加方位重采样的方法。在本方法中,首先对每个通道的信号分别进行线性距离走动校正(Linear Range Walk Correction,LRWC)处理,去除由于斜视引起的多普勒带宽,使得信号等效于正侧视时的情况。其次,再对各个通道线性距离走动校正后的信号分别进行方位Dechirp处理,去除由于波束扫描引起的多普勒带宽,此时信号的多普勒带宽小于通道数与方位采样率的乘积,可以对各个通道的信号进行重构处理得到重构后的信号。接着使用两步式的第一步对信号进行等效的升采样处理得到等效的方位过采样的单通道波束扫描模式的信号。值得注意的是,由于在第一步进行了线性距离走动校正处理,SAR信号的方位时不变关系被破坏,需要进行方位重采样处理。方位重采样之后便可以使用传统单通道波束扫描模式的处理方法进行成像处理。
1 斜视多通道波束扫描模式
为了更好地说明问题,本节首先给出正侧视下的多通道波束扫描模式的信号特性,接着引出斜视情况下相对于正侧视情况下的不同,最后通过对斜视多通道波束扫描模式信号特性的分析说明对于该模式信号现有处理方法所存在的问题。
图1所示为斜视多通道波束扫描模式的示意图(以斜视多通道滑动聚束模式为例)。图中所示的是前斜视的情况,后斜视情况下的分析与前斜视相同。在这个系统中,通道1发射雷达信号,所有通道接收回波信号。Tx为发射通道,Rx为接收通道。不失一般性,假设通道1为参考通道,则通道1发射信号,所有通道接收信号。红色箭头表示发射方向,黑色箭头表示接收方向。其中,雷达平台运动速度为vs,而波束足迹在地面的运动速度为vg。如图所示,在成像中心时刻,波束并不是指向雷达运动轨迹的法线方向,而是与轨迹的法线方向有一个夹角θsq,也就是SAR系统工作的斜视角。
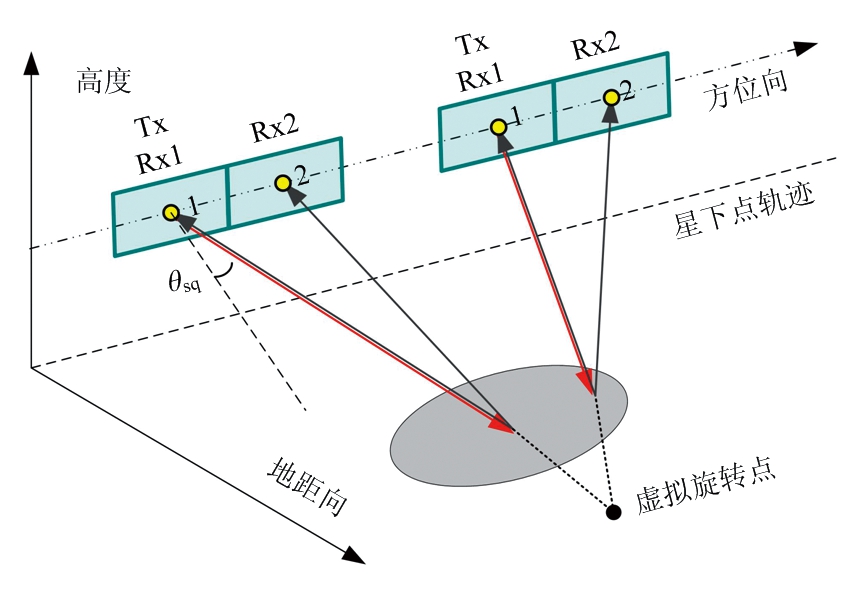
图1 斜视多通道波束扫描模式SAR系统成像几何示意图(以双通道为例)
假设场景中有一点目标P,其最近斜距为R0,则正侧视多通道波束扫描模式时,该点所经历的双程天线方向图为
Ga(ta)=![]()
(1)
式中, ta为方位时间,G0为常数增益, La为天线长度,λ为信号波长,ωr为波束扫描的角速度。
可以看出,就单点目标来说,可以将波束扫描模式下的双程天线方向图等效为条带模式的方向图,等效天线长度为条带模式下的![]() (称之为滑动因子)倍,因此,此时的单点信号的多普勒带宽为
(称之为滑动因子)倍,因此,此时的单点信号的多普勒带宽为
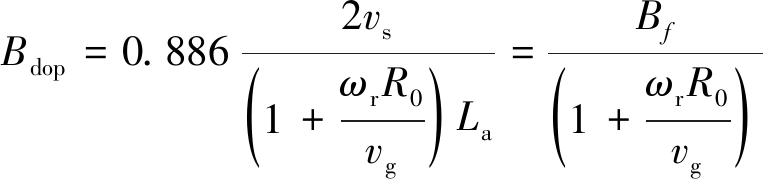
(2)
式中,
(3)
为条带模式下的单点目标多普勒带宽,θbw为方位向波束宽度。
对于方位向有多点目标的情况,正侧视的多通道波束扫描模式的时频关系图如图2所示。可以看出,此时信号总的多普勒带宽为
Btotal=Bs+Bf
(4)
式中,Bs为由于波束扫描引起的多普勒带宽,Krot为由于波束扫描引起的多普勒中心变化的调频率,Ka为信号的多普勒调频率。可以看出,由于波束的扫描,方位向不同位置点目标的多普勒中心不同,产生了额外的多普勒带宽。使得此时通道数与PRF的乘积远小于场景信号的多普勒带宽,即
M·PRF<Btotal
(5)
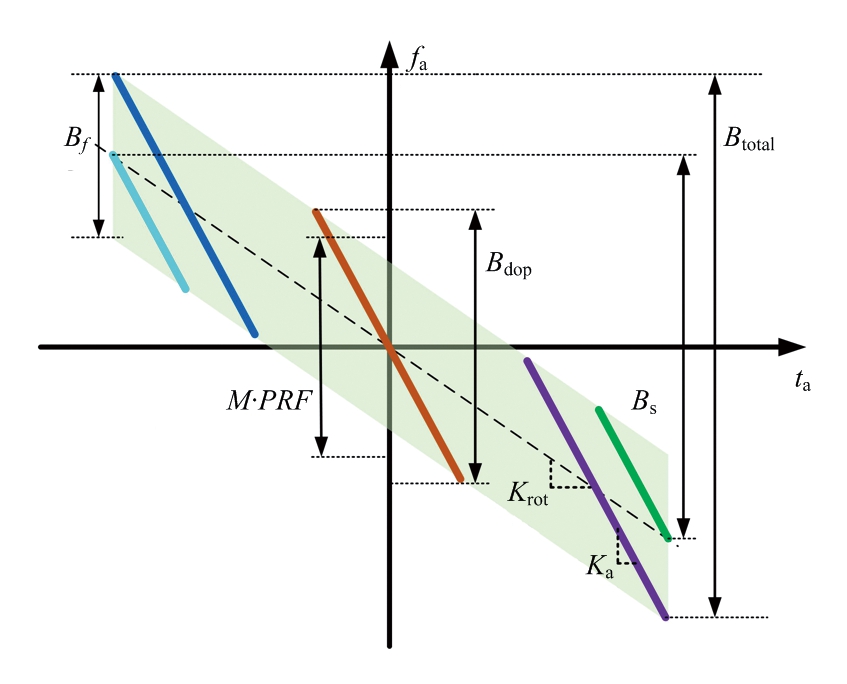
图2 正侧视多通道波束扫描模式信号时频关系图
在传统多通道信号中,第m个通道的回波信号在多普勒域的表达式为
Sm(τ,fa)=![]()
(6)
(7)
式中τ为距离向时间,fa为方位频率,N为信号的模糊数,Δxm为第m个通道的相位中心与参考通道相位中心的距离。
上式成立的条件是通道数与PRF的乘积大于场景信号的多普勒带宽,并且上式也是传统滤波器组重构方法的基础。因此,此时是无法直接使用传统的多通道信号的处理方式的。但是通道数与PRF的乘积大于条带模式下的信号多普勒带宽:
M·PRF>Bf
(8)
此时可以利用文献[9]中的方法进行处理,解决传统多通道信号重构不能应用于多通道波束扫描模式的情况。
当处于斜视模式情况下,由于信号多普勒中心随着距离频率的变化而变化,会产生额外的多普勒带宽,因此在斜视情况下,公式(4)可以改为
Btotal=Bs+Bf_squint
(9)
式中Bf_squint为斜视条带模式下的单点信号多普勒带宽。
(10)
当斜视角大到一定的程度时,可能会出现图3所示的通道数与PRF的乘积小于信号多普勒带宽的情况,即
M·PRF<Bf_squint
(11)
此时,即使是首先去除由于波束扫描引起的多普勒带宽,信号也是无法重构的。
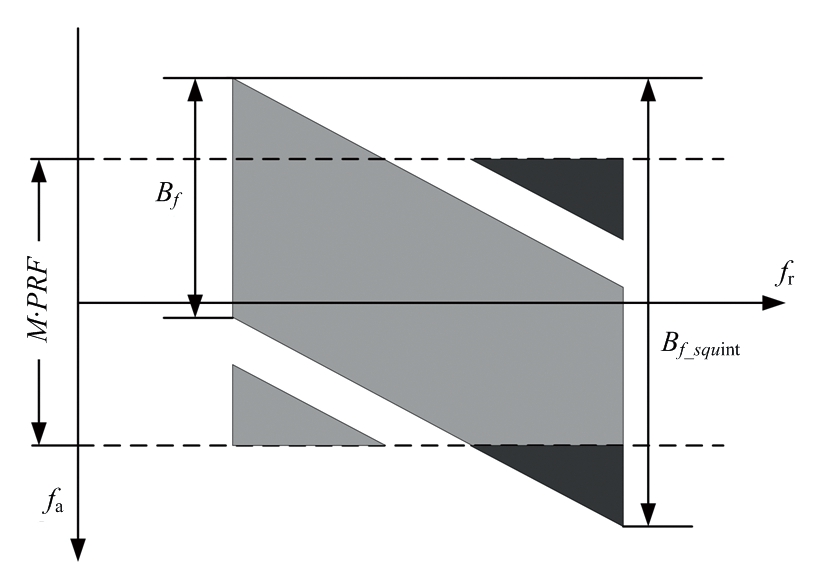
图3 斜视模式下频谱混叠示意图
可见,当多通道波束扫描模式工作在斜视情况时,又会出现新的问题,即场景信号的多普勒带宽即使去除由于多普勒中心变化导致的多普勒带宽后,其值仍然大于通道数与PRF的乘积,导致现有文献的处理方法失效。
2 斜视多通道波束扫描模式处理方法
本节将基于第2节分析的结果,结合现有文献的研究,提出一种基于方位去斜加方位重采样的斜视多通道波束扫描模式的信号处理方法。
斜视多通道扫描模式下参考通道的回波信号可以表示为
ss(τ,ta)=![]()
(12)
式中,ωr(·)为脉冲信号的包络,ωa(·)为公式(1)所示的双程天线方向图,R(ta)为等效的单程距离历程,Kr为距离向信号调频率,tc为场景中心目标点的波束中心穿越时刻, c为光速, λ为信号波长。则第m个通道的回波信号可以表示为
(13)
首先,如前所述,由于系统工作在斜视情况下,信号的多普勒中心频率在二维频域会随着距离频率的变化而变化,产生额外的多普勒带宽。因此,可以使用线性距离走动校正的方法去除斜距历程中的线性部分,使得信号等效于正侧视时获得的回波信号。LRWC所使用的校正函数为
![]()
(14)
式中,f0为信号载频,fτ为距离向频率,下标m表示的是第m个通道。需要注意的是,对于每个通道信号而言,其LRWC的函数是不一样的,不同通道信号的LRWC函数有一个不同的时延,这是因为不同接收通道的等效相位中心位于不同的位置,如公式(14),这样可以保持多通道信号的特性。
线性距离走动校正之后,雷达平台的运动轨迹可以等效于图4中的绿色虚线。
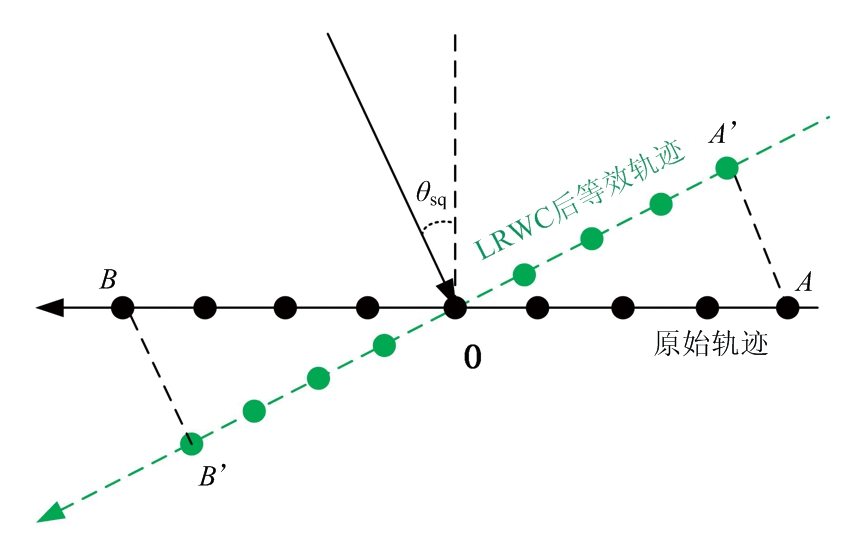
图4 LRWC示意图
由于LRWC之后,因斜视引起的多普勒带宽被消除了,此时信号等效于正侧视情况下的回波信号,可以使用文献[9]中所使用的方法进一步进行方位带宽的压缩,使得信号总的多普勒带宽小于通道数与PRF的乘积。于是,接下来选取方位Dechirp函数:
(15)
式中Rrot为虚拟旋转点的最近斜距。和LRWC函数一样,该Dechirp函数也是针对各个通道设置的,有一个与通道位置相关的时延。
经过LRWC和方位Dechirp之后,信号在距离频域方位时域可以表示为
S sm(fτ,ta)=![]()
(16)
可以将上式简写为
(17)
可以看出,此时信号仍然保持着多通道信号的特性,但是方位信号的带宽已经被压缩至M·PRF以内了,可以进行多通道信号重构处理,重构后的二维频域的信号为
SSa(fτ,fa)=[SS1(fτ,fa),…,SSM(fτ,fa)]P(fa)
(18)
式中P(fa)为重构矩阵,其表达式可参考文献[9]的公式(34)。注意,重构之后需要对信号进行逆Dechirp操作恢复由于波束扫描引起的多普勒带宽,逆Dechirp函数为
(19)
后面可以看出,该操作其实可以和两步式操作中的去斜相互抵消而直接进入两步式的后续操作。
信号重构之后,便可以将信号看作等效的正侧视单通道滑动聚束模式信号。但是此时需要注意的是,由于之前的LRWC处理,使得信号的方位“时不变”特性被破坏,可以发现,原本同一距离门相同的多普勒参数(如等效速度)变得不再相同。因此,为了解决方位“时不变”特性被破坏的问题,需要进行方位重采样恢复方位“时不变”特性[12]。方位重采样是将LRWC后的方位频谱映射到等效的正侧视信号的方位频谱以实现等效正侧视的效果,并使得信号具有方位“时不变”特性的方法,该方法需要在方位频域将方位频谱进行重采样。
方位重采样操作需要在方位频域信号和方位时域信号都不混叠的情况下操作,于是首先需要对信号进行“两步式”解混叠预处理操作[13]。“两步式”处理之后,便可以进行方位重采样处理。
等效阵列原理将斜视情况下经过LRWC后的信号等效于正侧视情形下的信号,通过比较两者的方位信号特性,得到两种情形下的信号之间的关系,之后便使用方位重采样的方法将经过LRWC处理之后的信号重采样为等效正侧视的情形。
经过LRWC处理后的信号方位频谱与等效正侧视信号在二维频域中的映射关系为
![]() cosθsq(fa+fdc)-
cosθsq(fa+fdc)-
(20)
式中![]() 为等效正侧视的信号方位频率,fa为经过LRWC处理后的信号方位频率,fdc为二维频域中的多普勒中心频率,且
为等效正侧视的信号方位频率,fa为经过LRWC处理后的信号方位频率,fdc为二维频域中的多普勒中心频率,且
(21)
通过求解公式(20),可以得到新的方位频率轴映射到旧频率轴的映射关系为
fa=![]()
(22)
式中,θsq>0时,K=1;θsq<0时,K=-1。
利用上式进行二维频谱的方位重采样之后,还有一步重要的操作就是乘以一个补偿相位函数,以消除两步式预处理的卷积操作引入的相位。补偿相位函数如下:
(23)
需要注意的是,补偿函数中的fa对应于公式(22)中的fa,而不是公式(20)中的![]() 因为两步式操作引入的相位中使用的是旧的时间轴,对应于旧的频率轴。补偿相位之后就可以进行成像处理[14]。整个的处理流程如图5所示。
因为两步式操作引入的相位中使用的是旧的时间轴,对应于旧的频率轴。补偿相位之后就可以进行成像处理[14]。整个的处理流程如图5所示。
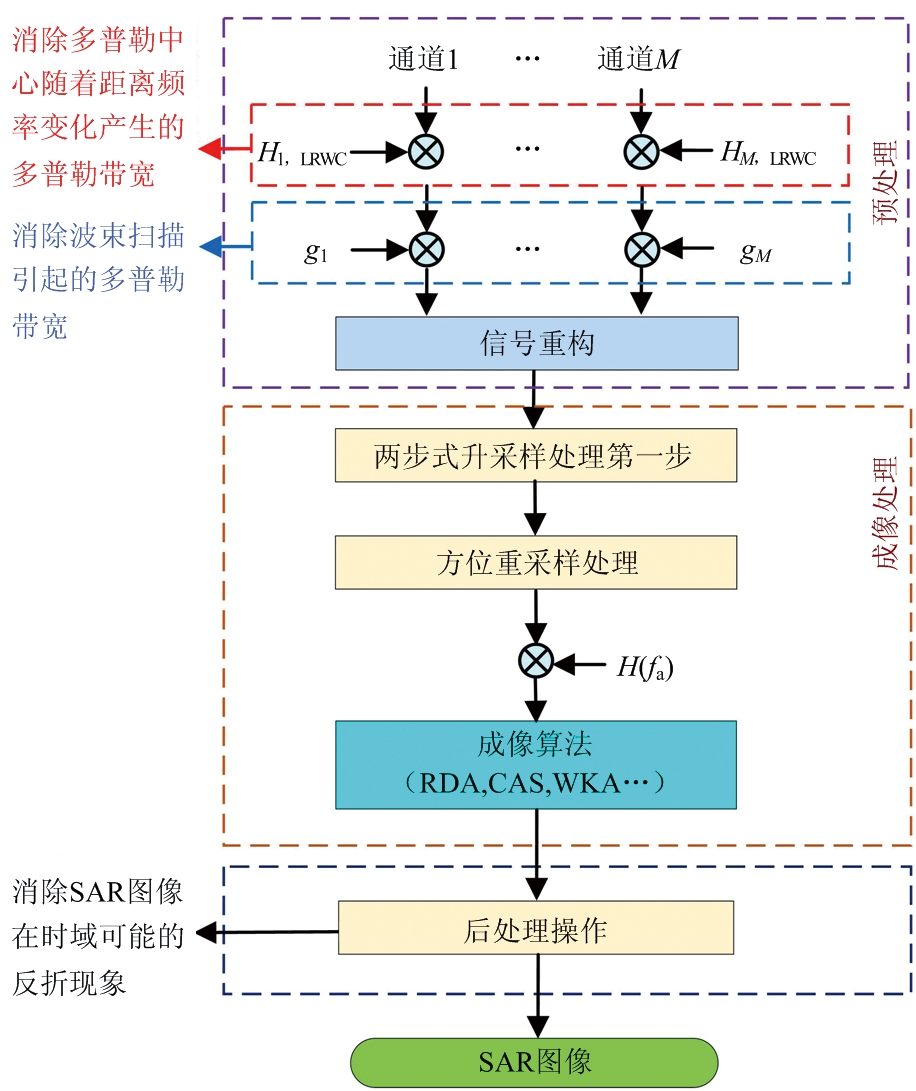
图5 斜视多通道波束扫描模式SAR信号处理流程图
3 实验分析
为了验证本文方法对于斜视多通道波束扫描模式SAR信号处理的有效性,本节将进行点目标仿真实验,对包含9个目标的3×3矩形点阵目标进行成像仿真分析。不失一般性,本节还是以斜视多通道滑动聚束模式为例。
仿真实验采用的SAR系统参数具体见表1。其中,天线的方位向长度是3 m,系统的滑动因子为0.6,天线的方位向通道数为2。此时,对于单点信号来说,对应的正侧视多通道滑动聚束模式的多普勒带宽为Bdop=214.13 Hz,对应的正侧视多通道条带模式下的带宽为Bf=128.48 Hz,而公式(10)中的斜视多通道条带模式下的带宽为Bf_squint=263.81 Hz。PRF设置为83.51 Hz,可以发现,此时通道数与PRF的乘积小于单点信号斜视条带模式下的多普勒带宽,但是大于对应的正侧视多通道条带模式下的带宽。实验结果分别如图6和图7所示。
表1 系统仿真参数

参数参数值载频f09.65 GHz速度vs120 m/s高度H10 km下视角θview60°脉冲重复频率PRF83.51 Hz天线长度La3 m斜视角θsq25°距离带宽Br400 MHz采样频率Fs480 MHz脉冲宽度Tr2 μs场景大小(距离×方位)2 km×2 km通道数2滑动因子0.6
图6(a)所示为斜视多通道条带模式下的二维频谱,使用的是2×PRF的采样率(即通道数与PRF的乘积)。可以发现,由于斜视,信号的二维频谱在方位向发生了混叠。因此,在本节的实验中,当直接使用文献[9]的方法进行重构后,由于不满足滤波器组重构方法的条件,重构失败,重构后的二维频谱是混叠的,如图6(b)所示。本文在重构之前同时使用了LRWC和方位Dechirp,使得信号的多普勒带宽限制在通道数与PRF的乘积之内。在本文方法中重构后的二维频谱如图6(c)所示,重构之后的频谱是正确、不混叠的。
实验对点阵中的3个目标进行了分析,分别是左上(P1)、中心(P5)和右下(P9)的点目标,成像结果如图7所示。可以看出,3个点目标均聚焦良好,无散焦现象。成像质量评估结果汇总在表2中,可以看出3个点目标的峰值旁瓣比(Peak Sidelobe Ratio, PSLR)、积分旁瓣比(Integrated Sidelobe Ratio, ISLR)均能达到理想值-13.26 dB和-10 dB。对于分辨率/脉冲响应宽度(Impulse Response Width,IRW),可以通过对比理论值与实验结果来评价。可以计算出点目标的理论分辨率为
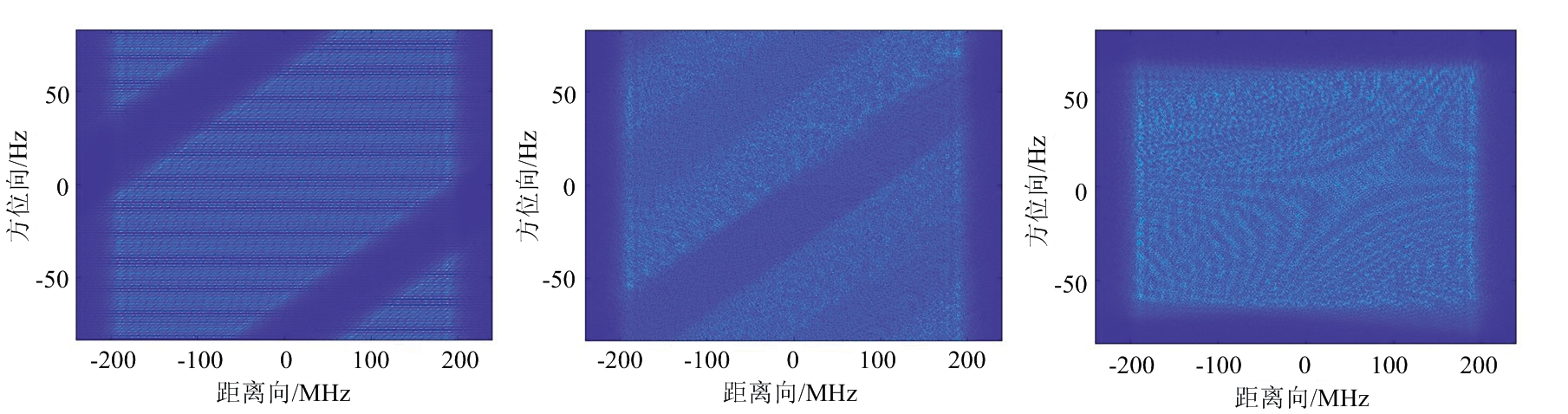
(a) 斜视单通道条带模式二维频谱 (b) 文献[9] 的方法得到的二维频谱 (c) 本文方法得到的二维频谱
图6 不同情况下点阵目标的二维频谱(所有频谱已搬到基带)
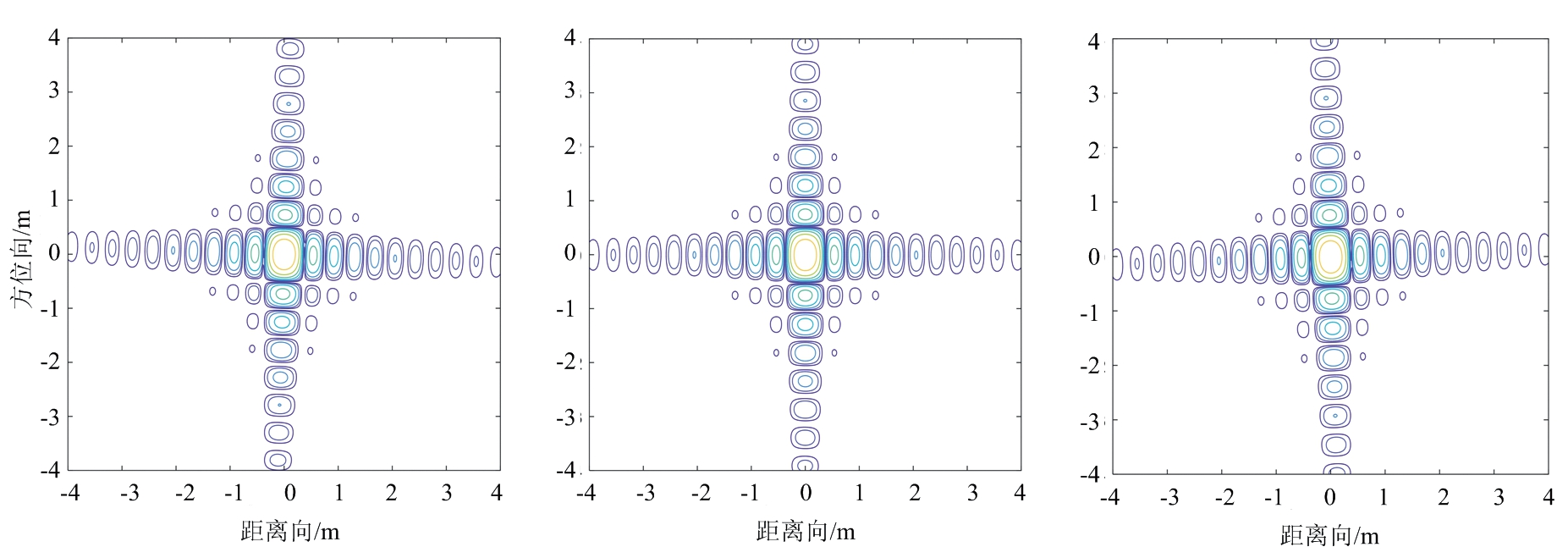
(a) 点目标P1成像轮廓图 (b) 点目标P5成像轮廓图 (c) 点目标P9成像轮廓图
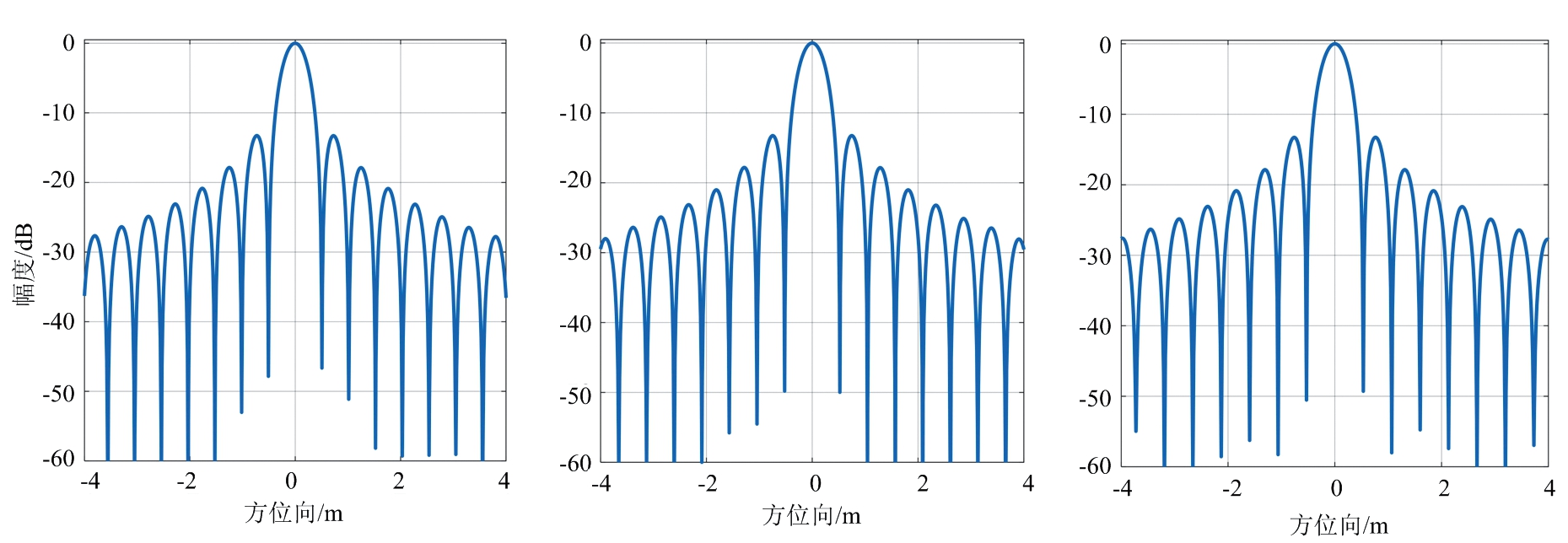
(d) 点目标P1方位向剖面图 (e) 点目标P5方位向剖面图 (f) 点目标P9方位向剖面图
图7 点目标成像结果
表2 成像质量结果
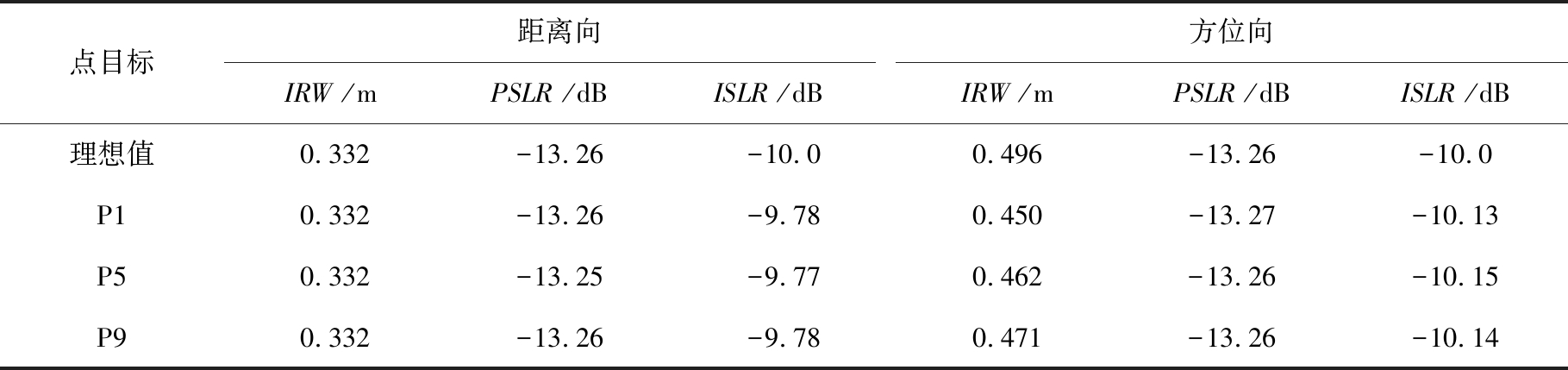
点目标距离向IRW /mPSLR /dBISLR /dB方位向IRW /mPSLR /dBISLR /dB理想值0.332-13.26-10.00.496-13.26-10.0P10.332-13.26-9.780.450-13.27-10.13P50.332-13.25-9.770.462-13.26-10.15P90.332-13.26-9.780.471-13.26-10.14
方位向:![]()
距离向:![]()
对比表2中的数据可以发现,实验结果的分辨率与理论值一致,说明了本文方法在斜视多通道波束扫描模式下的有效性。
4 结束语
方位多通道在现在的高分宽幅SAR系统中发挥着重要作用,而波束扫描模式的方位多通道模式可以在进一步提高方位向分辨率的同时保持距离向测绘幅宽不变。SAR工作在斜视情况下可以实现灵活的对地观测,因此斜视多通道波束扫描模式有实用价值。本文首先介绍了斜视多通道波束扫描模式下的问题,即由于斜视会引起多普勒中心频率在距离向信号的频带内变化,进而使得各通道信号去斜后的带宽仍然大于通道数与PRF的乘积。接着本文基于现有文献,提出了一种基于方位去斜加方位重采样的方法,该方法首先对各个通道的信号分别进行LRWC处理,去除由于多普勒中心频率随着距离频率的变化而变化引起的带宽;其次,使用方位去斜加重构的方法得到重构后的信号;最后使用方位重采样的方法将经过LRWC之后的重构信号等效为正侧视信号,然后补偿相位之后即可进行成像处理。在文章的最后,给出了3×3点阵目标的仿真实验结果,并取3个点目标进行分析,可以看出,使用本文方法处理后,点目标均聚焦良好,质量参数也能达到理想数值,证明了本文所提出方法的有效性。本文的方法使得多通道波束扫描模式下的SAR系统的灵活观测成为可能。
[1] 邓云凯, 禹卫东, 张衡, 等. 未来星载SAR技术发展趋势[J]. 雷达学报, 2020, 9(1):1-33.
[2] 韦维,朱岱寅,吴迪. 机载SAR多模式统一化成像处理技术研究[J]. 雷达科学与技术, 2020, 18(6):625-632.
[3] SUN G C, LIU Y B, XIANG J X, et al. Spaceborne Synthetic Aperture Radar Imaging Algorithms: An Overview[J]. IEEE Geoscience and Remote Sensing Magazine, 2021(10):2-25.
[4] MOREIRA A, PRATS-IRAOLA P, YOUNIS M,et al. A Tutorial on Synthetic Aperture Radar[J]. IEEE Geoscience and Remote Sensing Magazine, 2013,1(1):6-43.
[5] MOON W M, STAPLES G, KIM D J, et al. RADARSAT-2 and Coastal Applications: Surface Wind, Waterline, and Intertidal Flat Roughness[J]. Proceedings of the IEEE, 2010, 98(5):800-815.
[6] WERNINGHAUS R, BUCKREUSS S. The TerraSAR-X Mission and System Design[J]. IEEE Trans on Geoscience and Remote Sensing, 2010, 48(2):606-614.
[7] KARVONEN J, RINNE E, SALLILA H, et al. On Suitability of ALOS-2/PALSAR-2 Dual-Polarized SAR Data for Arctic Sea Ice Parameter Estimation[J]. IEEE Trans on Geoscience and Remote Sensing, 2020, 58(11):7969-7981.
[8] 孙吉利, 禹卫东, 邓云凯. 高分三号卫星SAR工作模式与载荷设计[J]. 航天器工程, 2017, 26(6):61-67.
[9] FANG T Z, DENG Y K, LIANG D, et al. Multichannel Sliding Spotlight SAR Imaging: First Result of GF-3 Satellite[J]. IEEE Trans on Geoscience and Remote Sensing, 2021, 60(1):1-16.
[10] FANG T Z, ZHANG H, LIANG D, et al. A Channel Phase Error Estimation Method for Multichannel TOPS and Multichannel Sliding Spotlight SAR Imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2021,19:1-5.
[11] LUO Y, ZHAO F J, LI N, et al. A Modified Cartesian Factorized Back-Projection Algorithm for Highly Squint Spotlight Synthetic Aperture Radar Imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(6):902-906.
[12] XING Mengdao, YU Feng, et al. Azimuth Resampling Processing for Highly Squinted Synthetic Aperture Radar Imaging with Several Modes[J]. IEEE Trans on Geoscience and Remote Sensing, 2014, 52(7):4339-4352.
[13] LANARI R, TESAURO M,SANSOSTI E, et al. Spotlight SAR Data Focusing Based on a Two-Step Processing Approach[J]. IEEE Trans on Geoscience and Remote Sensing, 2001,39(9):1993-2004.
[14] LIANG D , ZHANG H , FANG T Z , et al. A Modified Cartesian Factorized Backprojection Algorithm Integrating with Non-Start-Stop Model for High Resolution SAR Imaging[J]. Remote Sensing, 2020, 12(22):3807.


