0 引 言
自适应旁瓣对消是一种常见的雷达抗有源干扰的技术,其原理是在雷达主天线附近安装(或全数字合成)若干个弱方向或无方向的辅助天线,当存在副瓣干扰时,主天线与辅助天线接收的干扰信号幅度相当,利用各辅助天线接收的干扰信号,通过一定的自适应算法,得到加权系数,辅助天线信号经加权求和后与主天线接收的信号对消,达到干扰对消的目的。近年来随着雷达电子对抗问题的凸显,自适应旁瓣对消技术得到广泛应用[1-4]。
文献[5-7]探讨了影响旁瓣对消性能的主要因素。影响自适应旁瓣对消实际应用效果一个重要的因素就是正确采集干扰信息的样本数据,能否在辅助天线中采集到与主天线高度相关的干扰数据,一定程度上决定着旁瓣对消技术实施的成败。在常规的应用中往往通过采集远距离端不包含杂波信息的回波数据来实现,但是对于工作在复杂杂波环境的中近程雷达来说,回波信息可能包含大量乃至全距离段的杂波数据,有时杂波能量相当于甚至强于干扰信号能量。如果错误地选取了强杂波干扰数据作为干扰样本进行旁瓣对消处理,不仅达不到对消效果,甚至可能影响任务目标的正常检测。
对于杂波环境下干扰样本的提取问题,一种解决思路是在条件允许的情况下先进行滤波处理,然后采用杂波滤除后的数据提取干扰样本进行旁瓣对消。这种方法可以有效地在杂波环境下进行样本提取,但又引入了新的问题。由于有源噪声压制干扰数据在多个脉冲之间不具备相参性,使得经过滤波处理后的干扰能量在多个频道中分散,从而降低了信号的干噪比,对于包含较少杂波的数据来说,这样做的后果就是使得对消性能下降。本文尝试提出一种能兼顾杂波环境和对消性能的方法,通过采集样本并统计辅助波束与主波束数据的相关性,确定样本数据是否包含于主波束强相关的干扰信息,如果相关度高则进行旁瓣对消处理;反之则说明强杂波环境已经影响到干扰样本的正确采集,对数据滤波并再次进行相关统计,从而对有效抑制了杂波的数据进行旁瓣对消处理。将雷达放置在同时包含山区和平坦地形的环境下进行试验,对本文提出的方法进行验证。
1 基于相关性的杂波环境自适应旁瓣对消方法
1.1 自适应旁瓣对消
自适应旁瓣对消权值计算主要有开环法和闭环法两种[8-9]。闭环法对实现元器件要求低,适合模拟实现,但收敛速度受到很大限制;开环法直接求解干扰协方差,不存在收敛问题,近年来随着数字器件性能的不断提高而广泛采用。
X表示主天线接收的信号;Y=[Y1,Y2,…,YN]T表示辅助天线接收的信号;W=[W1,W2,…,WN]T表示加权系数;V0表示对消输出,则有
(1)
式(1)表明,对消剩余就是由主天线信号减去权矢量和辅助天线信号的内积,而对消的目的是使对消剩余功率最小,用统计表示为E{|V0|2},即
ξ=![]()
E[(X-WHY)(X*-WTY*)]=
(2)
式中,E[·]表示统计期望,RYX表示辅助通道和主通道的互相关矩阵,RYY表示辅助通道的自相关矩阵。均方误差的梯度可通过对权矢量进行微分得到,即
∇=![]()
-2RYX+2RYYW
(3)
若∇=0,就可得到最佳权矢量Wopt,即![]()
对消剩余功率最小时的剩余干扰信号为(V0)min=X-WoptY,由此可求出最优权值保证干扰对消的剩余功率最小。
1.2 子区域最小最大法干扰样本提取
实际工程应用中,对于脉冲重复周期较短的中近程雷达,当雷达波束指向复杂杂波环境时,杂波数据在回波数据中的分布往往不具备明显的规律性,除了近距离杂波较强外,任意距离段都可能出现强杂波的情况,因此简单地选取固定距离段数据作为样本难以规避杂波影响。这里给出一种子区域最小最大法提取样本点,该方法的原理是均匀的噪声及压制干扰起伏较小,而叠加了杂波的区域不仅能量更大且具有较大起伏,通过局部幅值最小可以规避杂波干扰,而在该子区域内选择能量最大的点可以提取到更强的干扰信息;方法简单易实现,既可以较为有效地规避杂波干扰,又有助于选择干扰能量较大的样本点,具体方法如下所示:
1) 将完整的统计区域均匀分成若干子区域,计算每个子区域的幅度均值avg1;
2) 在所有的子区域中,选取幅度均值最小的子区域,记录最小幅度值avgmin并记录该区域内的所有统计点位置;
3) 对上面选取的子区域的统计点按照能量大小进行排序;
4) 选择该子区域中能量最大的N个点作为样本点。
1.3 相关性统计
自适应旁瓣对消实现的原理要求雷达主波束与辅助波束之间存在强相关的干扰信息,而对于杂波信息,由于天线方向图、波束指向等差异,主波束和辅助波束之间的相关性要低得多。干扰样本提取后,通过统计二者之间的相关性并设定阈值,可以判断当前辅助波束数据受杂波影响的程度,决定是否适合进行旁瓣对消处理,相关系数计算公式如下:

(4)
式中,b0为主波束,bm为辅助波束,N为样本点数,M为辅助波束个数。依次计算主波束与每个辅助波束的相关性,并取最大值作为相关性统计结果。
主波束和辅助波束的相关性统计根据需要分两次进行,第一次在时域进行,确定当前提取样本数据是否已经受杂波严重影响,导致无法进行有效的对消;如果相关系数达不到阈值要求,则在滤波后针对不同的频道数据再次进行相关性统计,进一步确定滤波后该频道数据中残留杂波对对消样本提取影响情况。相关系数阈值较低时,可以提高对干扰的灵敏度,但同时带来计算量的提高,实际应用中需根据抗干扰指标的具体要求以及试验数据进行分析得到。
1.4 方法实现流程
方法具体实施时,为保证处理效率,可以嵌入常规的数字信号处理脉冲压缩、相参滤波中进行,除相关性统计外,不需要额外增加计算负荷;在初步判断回波数据是否需要进行自适应旁瓣处理后,根据需要依次在时域和多普勒频域(以下简称频域)进行处理。如果在时域进行相关性统计后满足对消要求,则在频域不再进行对消相关处理,以保证弱杂波区域更好的干噪比及对消效果;反之则标记该方位指向的回波数据不宜在时域进行对消处理,并在相参滤波处理结果后在频域进行相关性统计,如果满足相关性要求即在频域进行对消处理,反之则该回波数据在时域、频域均不采取对消处理。本文提出的基于相关性的杂波环境自适应旁瓣对消方法流程如图1所示。
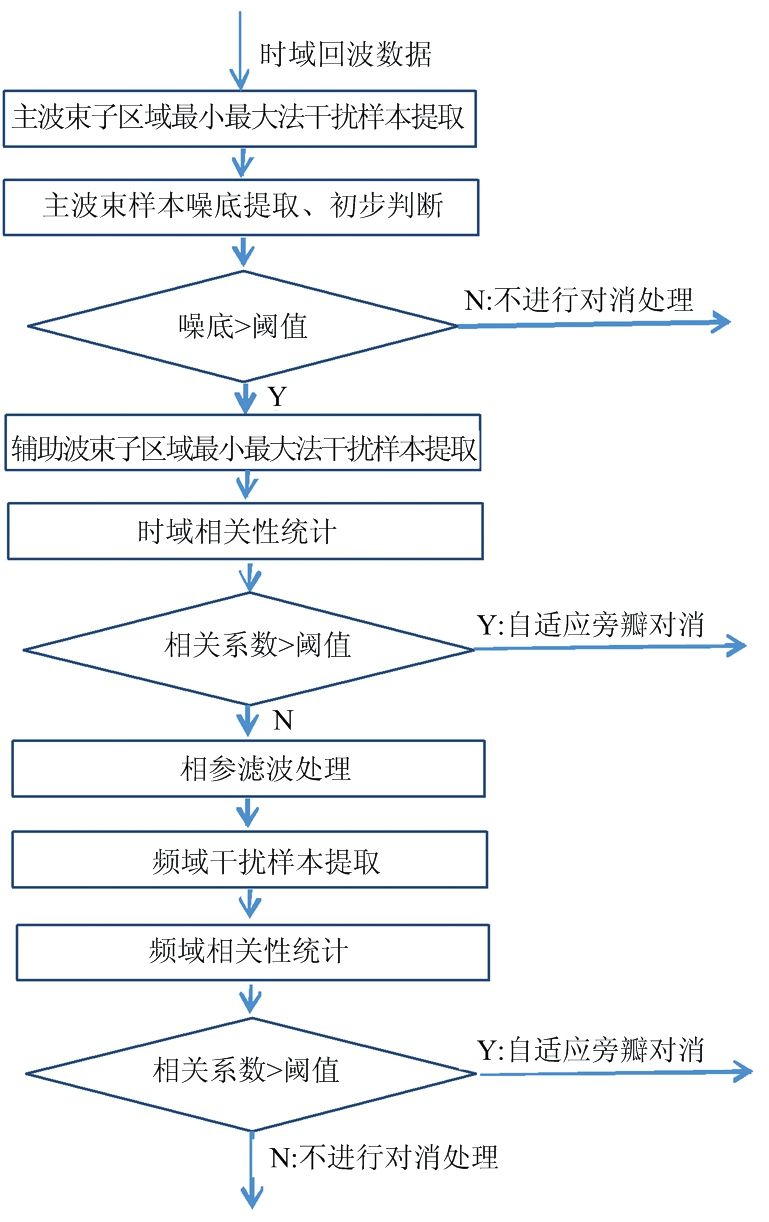
图1 方法流程图
1.5 方法实现步骤
方法具体实现步骤如下:
1) 时域回波中对主波束采用子区域最小最大法提取干扰样本,然后计算样本噪底At。
2) 设无干扰情况下噪底幅度为A0,设置阈值δ1=A0+σ1,如果At>δ1,说明样本中有干扰或存在杂波,需要进一步判断;而如果At<δ1,则认为样本中干扰强度没有达到阈值,不再进行对消处理以提高处理效率。
3) 采用子区域最小最大法提取辅助波束干扰样本数据并与主波束样本数据进行相关性统计,得到相关系数λt,如果λt>δ2,其中δ2为时域相关性阈值,说明时域回波数据中,主波束与辅助波束干扰信息强相关,可以进行对消处理;反之λt<δ2,则说明干扰信息相关度低,样本提取过程可能受杂波影响,需要进一步分析处理。
4) 对时域回波数据进行相参滤波处理,得到频域回波数据。
5) 对频域数据再次提取干扰样本并进行频域相关性统计,得到相关系数λf。对于某个频道的样本数据,如果λf>δ3,其中δ3为频域相关性阈值,说明频域回波数据中,主波束与辅助波束干扰信息强相关,可以进行对消处理;反之λf<δ3,则说明干扰信息相关度仍然较低,不再进行对消处理。
2 试验及结果分析
采用仿真试验平台进行实测试验验证本文方法有效性。雷达方位扫描范围内同时包含有祁连山脉和较平坦的沙漠戈壁环境。在满足远场条件下放置干扰机释放噪声有源压制干扰,共设置8个辅助波束,采集干扰后的回波数据进行分析。根据经验取σ1=5 dB,时域相关系数阈值δ2=0.9,频域相关系数阈值δ3=0.8。试验环境设置如图2所示。
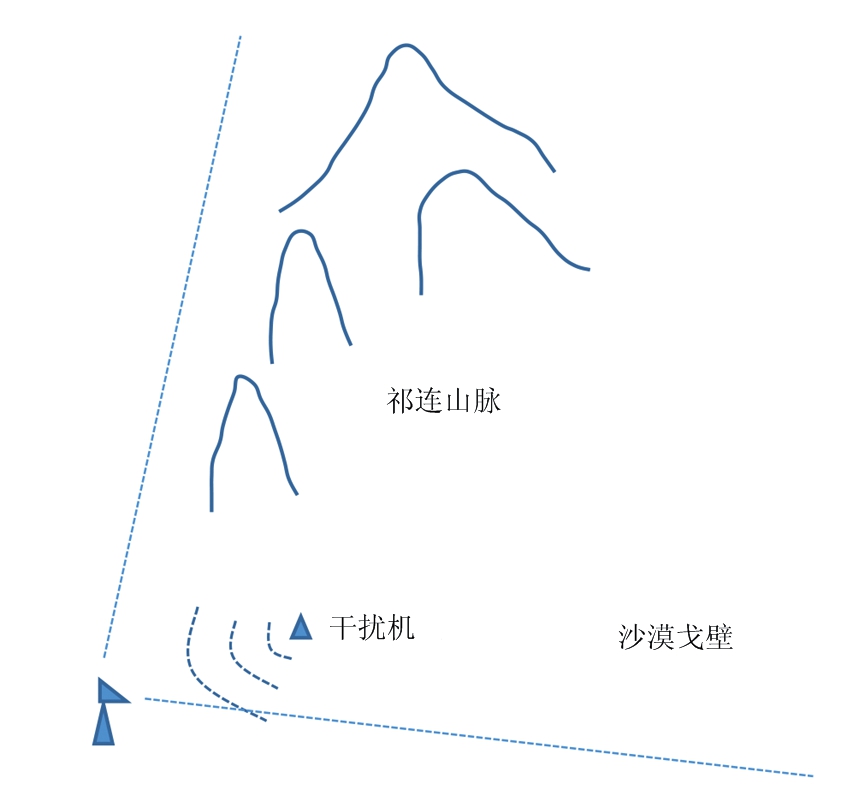
图2 试验环境示意图
试验采用对消比CG来衡量旁瓣对消的性能,定义为
(5)
式中n为主天线接收的干扰信号,nr为经过对消处理后的干扰输出,则对消比即对消前和对消后的干扰功率比。
2.1 弱杂波环境试验分析
当方位指向某平坦的沙漠戈壁区域时,计算得到时域相关系数为0.997 8,根据方法流程,系统将自动选择在时域进行自适应对消处理,对消结果如图3所示,可知干扰输出由对消前的117.46 dB降到对消后78.60 dB,对消比为38.86 dB。这里将时域数据不经过对消处理直接进行滤波,然后将频域对消结果与时域进行对比,如图4所示,计算得到的频域相关系数为0.859 5,由于干扰能量在频道间分散,导致主通道与辅助通道干扰信息相关性下降,干扰输出由对消前的106.77 dB经过对消下降到73.92 dB,对消比为32.85 dB。可知本文方法与直接采用滤波后数据对消方法相比,对消效果优化了6.01 dB。从滤波后干扰输出剩余进行横向对比,将时域对消后的数据进行滤波处理如图5所示,与图4中滤波后对消的数据进行对比,前者干扰输出为67.66 dB,比后者优化6.26 dB,与对消比优化结果一致,可见在该弱杂波情况下选用时域对消可以取得更好的结果。

图3 弱杂波环境时域对消结果

图4 弱杂波环境频域对消结果

图5 弱杂波环境时域对消后滤波处理结果
2.2 强杂波环境试验分析
当方位指向祁连山脉区域时,由于工作模式作用距离短,回波数据几乎完全被杂波覆盖,很难提取到合适的干扰样本,如图6所示;此时计算得到时域相关系数很低,为0.367 0,而此时如果采用时域数据直接进行对消处理,则对消效果很差,对消比仅为5.68 dB。采用本文方法,由于时域相关性没有达到阈值δ2要求,系统在滤波后再次进行相关性统计,计算得到中心频道相关系数为0.997 5,满足阈值δ3要求,所以在频域进行对消处理,结果如图7所示;由于区分杂波频道和清洁频道进行处理,清洁频道得到了较好的对消效果,干扰输出由91.52 dB下降到了 60.60 dB,对消比为30.92 dB。从滤波后干扰输出剩余方面进行横向对比,将时域对消后的数据进行滤波处理如图8所示,与图7中滤波后对消的数据进行对比,前者干扰没有得到有效的对消抑制,输出约为94.72 dB,比后者恶化34.12 dB,与对消比结果一致,可见在强杂波环境下选用频域滤波仍然可以有效地对干扰进行对消。

图6 强杂波环境时域对消结果
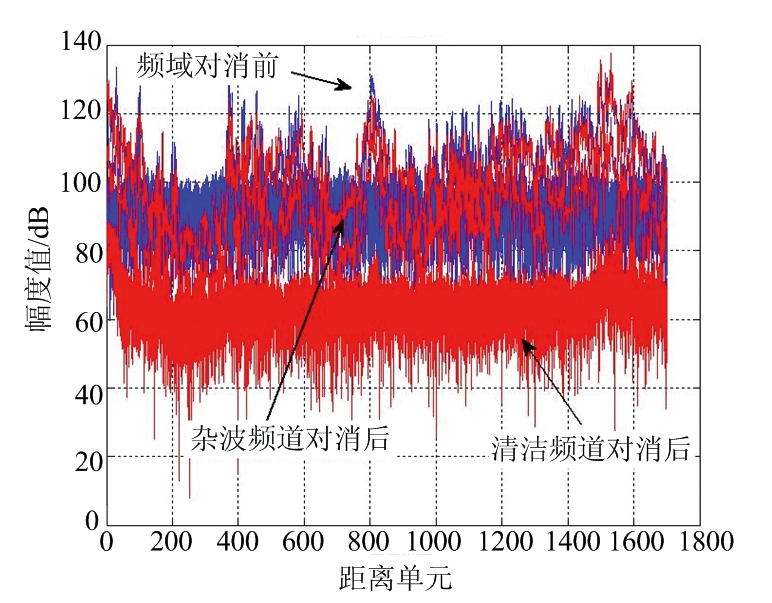
图7 强杂波环境频域对消结果

图8 强杂波环境时域对消后滤波处理结果
2.3 全方位数据对比分析
进行多次较长时间工作,采集多次同时包含强杂波和弱杂波环境的全方位回波数据进行分析。回波数据中方位角度-45°~-17.3°为强杂波山区,-17.3°~45°为弱杂波沙漠戈壁。对比本文方法与单独采用时域对消处理、单独采用频域对消处理的结果,如表1所示(频域对消比仅统计清洁频道),本文方法相比单独采用时域或频域对消都有更好的表现。
表1 全方位数据对比分析
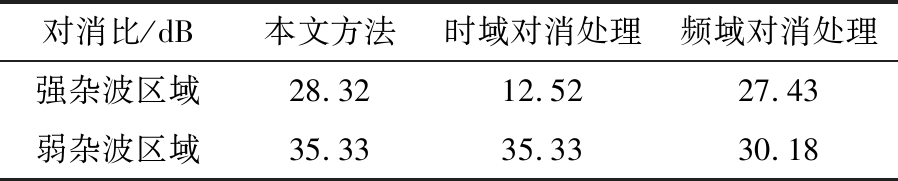
对消比/dB本文方法时域对消处理频域对消处理强杂波区域28.3212.5227.43弱杂波区域35.3335.3330.18
2.4 目标检测情况分析
抗干扰方法在对干扰信息进行有效抑制的同时,不能削弱所需检测的目标能量,对干扰信息的抑制优势应体现在目标信噪比的提高上,通过试验对本文方法目标检测性能进行分析。试验中某方位数据根据本文方法自动选择为时域对消处理,这里将根据本文方法时域后对消而后进行滤波的结果与先滤波而后在频域对消的结果进行比较,如图9、图10所示。二者都是滤波后结果,噪底分别为67.66 dB和73.97 dB,计算得到目标信噪比分别为37.24 dB和31.33 dB,本文方法相比直接采用滤波后对消改善了5.91 dB。

图9 本文方法目标检测结果

图10 直接滤波后对消目标检测结果
3 结束语
本文提出了一种适用于作用距离较短、复杂杂波环境的自适应对消方法。由于这种情况下某些强杂波环境时域采集干扰样本困难,本文通过相关性统计自动选择频域对消处理,可以有效规避强杂波干扰;而在弱杂波环境自动切换到时域对消处理,以避免干扰能量在频道间分散导致对消比下降情况,通过试验对方法有效性进行了验证。本文仅考虑了较为单一的噪声有源压制干扰情况,另外仅针对复杂山区环境进行了试验分析,对于压制、转发干扰组合的复杂干扰及海杂波、气象杂波复杂环境下应用是进一步的发展方向。
[1] 祝飞, 林强, 李飞. 自适应旁瓣对消技术综述[J]. 舰船电子对抗, 2020,43(1):12-18.
[2] 曹运合, 郭勇强, 刘帅, 等. 基于旁瓣对消器的自适应零陷优化设计[J]. 电子与信息学报, 2020,42(3):598-602.
[3] 邱炜, 朱德智, 范明意. 基于AA的多通道雷达自适应抗干扰方法[J]. 火控雷达技术, 2016,45(2):21-25.
[4] 刘亮. 一种相控阵雷达自适应旁瓣对消的工程实现方法[J]. 现代导航, 2019,10(5):375-379.
[5] 祝飞, 林强, 李飞. 雷达自适应旁瓣对消抗干扰性能分析[J]. 舰船电子对抗, 2019,42(5):11-15.
[6] 宋岩, 郭锦鹏, 王长杰,等. 自适应副瓣对消性能影响因素分析[C]∥第十四届全国信号和智能信息处理与应用学术会议论文集, 北京:[出版者不详],2021:70-76.
[7] 彭志刚, 李宝鹏, 李大龙, 等. 一种雷达智能抗干扰评估仿真系统[J]. 雷达科学与技术, 2021,19(3):258-264.
PENG Zhigang,LI Baopeng,LI Dalong,et al. A Simulation System for Radar Intelligent Anti-Jamming Evaluation[J]. Radar Science and Technology, 2021, 19(3):258-264. (in Chinese)
[8] 陈伯孝. 现代雷达系统分析与设计[M]. 西安:西安电子科技大学出版社, 2012:287-295.
[9] BROOKER E, HOWELL J M. Adaptive-Adaptive Array Processing[J]. Proceedings of the IEEE, 1986,74(4):602-604.
