0 引 言
多输入多输出(Multiple Input Multiple Output, MIMO)雷达[1-3]是一种新体制雷达,近年来引起了众多学者的广泛关注。
在发射波形的选择上,MIMO雷达通常发射正交波形[4-5]。文献[6]将完全互补码(Complete Complementary Code, CCC)应用在MIMO雷达系统中,其理想的互补性质可以对静止目标获得良好的检测性能。但完全互补码对多普勒频移十分敏感,即使是较小的多普勒频移也会引入较高的距离旁瓣,因此对于运动目标来说,目标的多普勒频移会破坏这种理想的性质。在多个运动目标存在的情况下,为了解决多普勒敏感性的问题,Calderbank和Pezeshki等人通过选择波形的发射顺序来抑制目标多普勒附近的距离旁瓣[7-8]。针对完全互补码,文献[9]提出了一种广义普洛黑-修-莫尔斯(Generalized Prouhet-Thue-Morse, GPTM)序列设计方法重新排列完全互补码的发射顺序来构造多普勒适应(Doppler Resilient, DR)完全互补码,使其具有较好的多普勒容忍性,在一定的多普勒频移范围内距离旁瓣较低。文献[10]中, Dang针对相控阵雷达中的互补码波形提出了二项式设计(Binomial Design, BD)方法,根据二项式系数在接收端为各个接收脉冲加上不同的权重后进行距离多普勒处理,能够显著地扩大目标多普勒附近的清洁区[11],在清洁区内旁瓣水平较低,可提高目标信噪比(Signal-to-Noise Ratio, SNR)。
上述文献中提到的方法只是单一地在发射端或接收端对信号进行处理,存在旁瓣抑制不完全、多普勒分辨率差等缺点。针对以上存在的问题,本文工作将完全互补码应用于MIMO雷达系统中,并且对发射端和接收端分别处理。在发射端,利用GPTM序列设计方法对完全互补码的发射顺序进行重排;在接收端,将互补码中的二项式方法引入完全互补码中,为各个脉冲加上不同的权重后进行距离多普勒(Range Doppler, RD)处理。经GPTM序列方法处理后得到的RD谱目标多普勒分辨率较高,但旁瓣清洁区较小;经二项式设计方法处理后所得的RD谱具有较大的旁瓣清洁区,但目标多普勒分辨率较低。为结合两种方法的优势,并避免它们各自的不足,采用逐点最小化[12]的方法使得RD谱在获得较大的旁瓣清洁区的同时保持较高的目标多普勒分辨率,并对其进行有序恒虚警(Ordered Statistics-Constant False Alarm Rate, OS-CFAR)目标检测[13-14]。最后,通过仿真验证了本文的信号处理方法在旁瓣抑制和目标检测问题中的有效性。
1 信号模型
1.1 完全互补码
发射信号的相关性直接影响匹配滤波的效果,为了从回波中提取所需信息,提高目标检测性能,发射信号应具有理想的相关特性。完全互补码是一种具备良好自相关特性和互相关特性的码序列。
定义一个包含N个恒模序列集合如下:
(1)
其中,第n个恒模序列![]()
 L×1可以表示为
L×1可以表示为
(2)
若取m=0,1,…,M-1,则由式(1)、(2)可以得到一个更大的序列集合
U={U0,U1,…,UM-1}
(3)
称该集合的维度为(M,N,L),其中M表示天线发射波形的个数,N表示时间维度上的波形脉冲数,L为单个脉冲波形序列长度。
集合U中不同恒模序列间的协方差矩阵可以表示为
(4)
式中l=-L+1,…,L-1表示延迟点数,i,j=0,1,…,M-1,n=0,1,…,N-1,Jl是移位矩阵,定义为
(5)
如果序列集U的协方差矩阵满足
(6)
则序列集U构成了一组完全互补码。其中,i,j=0,…,M-1,l=-L+1,…,L-1,δ(l)为冲激函数;当i=j时表示序列组的自相关,其峰值为NL;当i≠j时表示序列的互相关,其值为0。因此完全互补码具备完美的自相关性能和互相关性能。
1.2 信号发射方式
将完全互补码应用于MIMO雷达中,其互补对内的不同序列在不同时刻发送,不同互补对在不同天线发射。在发射端,不同发射天线发射相互正交的信号;在接收端,利用信号之间的正交性分离来自不同发射天线的回波。
假设在MIMO雷达系统中,发射一组(M,N,L)的完全互补码波形,图1给出了发射方式示意图。图中,假设发射端有M个发射天线,每个发射天线在一个相干处理间隔(Coherent Processing Interval, CPI)内发射了N个脉冲,每个脉冲内都具有L个码元,脉冲重复间隔(Pulse Repetition Interval, PRI)为T。假设在t时刻第m根天线发射了第1个脉冲![]() 那么,在t+(n-1)T时刻天线m将发射第n个脉冲
那么,在t+(n-1)T时刻天线m将发射第n个脉冲![]()

图1 发射示意图
1.3 信号相关性质
图2给出了一组维度为(2,2,16)完全互补码{(A1,A2),(B1,B2)}的自相关函数和互相关函数。其中,图2(a)为序列A1和A2的自相关及自相关之和,图2(b)为序列B1和B2的自相关及自相关之和。由图2(a)、(b)可知,完全互补码每根天线发射的不同序列的自相关具有一定的旁瓣,但其自相关之和为冲激函数,旁瓣等于零,表明CCC码具有理想的自相关特性。图2(c)为此完全互补码的互相关及互相关之和。由图2(c)可知,A,B序列间的互相关旁瓣较高,但两序列的互相关之和全为零,表明CCC码具有理想的互相关特性。

(a) 序列A的自相关

(b) 序列B的自相关

(c) 序列A和序列B的互相关
图2 完全互补码的自相关函数
2 信号处理流程
本文提出的信号处理方法的流程如图3所示,主要包括4个步骤:
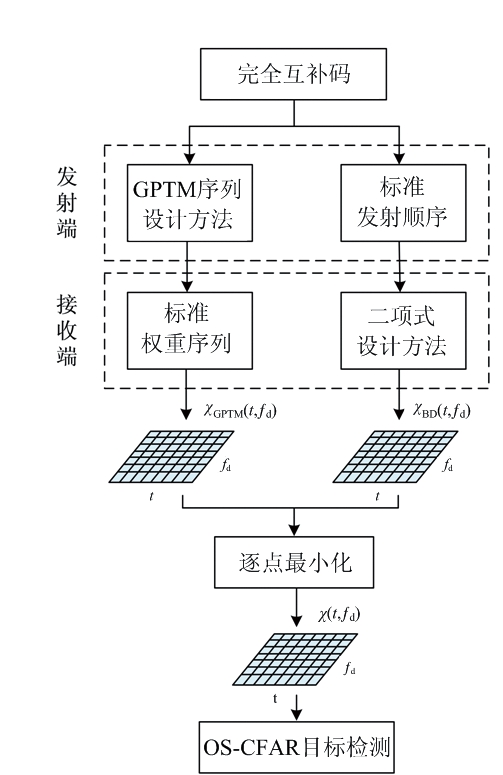
图3 信号处理流程框图
1) 在发射端,以GPTM序列设计方法得到的脉冲发射顺序发射多个脉冲,在接收端脉冲乘上全1的标准权重序列后进行距离多普勒处理,得到GPTM序列设计方法下的距离多普勒谱χGPTM(t,fd);
2) 在发射端脉冲以标准发射顺序进行发射,但在接收端采用二项式设计方法,对不同的接收脉冲乘上不同的权重因子,距离多普勒处理后得到二项式设计方法下的距离多普勒谱χBD(t,fd);
3) 对步骤1)、2)得到的两幅距离多普勒谱作逐点最小化处理,得到最终优化后的距离多普勒谱χ(t,fd);
4) 对步骤3)中逐点最小化处理后的结果χ(t,fd)进行OS-CFAR目标检测。
2.1 GPTM序列方法
GPTM序列设计方法[9]作用于MIMO雷达发射端,通过调整完全互补波形序列的发射顺序,降低由多普勒频率引起的距离旁瓣,构造具有多普勒容忍性的完全互补波形序列。GPTM序列设计方法的步骤如下:
1) 构造一个(M,M,L)的完全互补序列UB=[u0,u1,…,uM-1]作为基本的波形集,其中M表示波形数和脉冲数,L表示序列长度;
2) 选择一个近似阶数P,通过复制UBMP次获得一个(M,MP+1,L)的完全互补序列UE=[UB,UB,…,UB];
3) 利用GPTM序列重新排列UE,并令脉冲数MP+1=N得到另一个(M,N,L)的完全互补序列![]() 即是具有多普勒容忍性的完全互补波形序列。
即是具有多普勒容忍性的完全互补波形序列。
在GPTM序列设计方法中,关键在于步骤3)中对完全互补序列UE的重排,即GPTM序列的获取。令 ={0,1,…,N-1}表示包含UR列序号的集合,UR中有许多由复制产生的重复列,从而集合
={0,1,…,N-1}表示包含UR列序号的集合,UR中有许多由复制产生的重复列,从而集合 可分解为M个子集S0,S1,…,SM-1。其中,
可分解为M个子集S0,S1,…,SM-1。其中,![]() 对UE的重排即可转化为对集合
对UE的重排即可转化为对集合 中元素的划分。在{0,1,…,M-1}范围内的GPTM序列s=(sn)n≥0可由以下递推式得到:
中元素的划分。在{0,1,…,M-1}范围内的GPTM序列s=(sn)n≥0可由以下递推式得到:
(7)
式(7)表示将n用M进制的字符串表示,将该字符串各位相加之和tM(n)对M取余。此时就对集合 里的N个元素进行了划分,将相同列的列号放在同一个子集Sm中。根据此方法即可获知第n个脉冲un发射的为um波形,从而完成对UE的重排。
里的N个元素进行了划分,将相同列的列号放在同一个子集Sm中。根据此方法即可获知第n个脉冲un发射的为um波形,从而完成对UE的重排。
2.2 二项式设计方法
在二项式设计方法[10]中,发射端脉冲以标准发射顺序进行发射,在接收端,利用二项式系数设计一个序列w,为各个脉冲加上不同的权重后再进行距离多普勒处理。通过选择一个合适的w序列可以扩大目标多普勒附近的距离旁瓣清洁区。由文献[12]可知,当加权序列w=[w(1),w(2),…,w(N)]T满足
(8)
二项式设计方法可获得较大的旁瓣清洁区。其中,N表示脉冲总数,![]() 表示从N-1个不同脉冲数目中取出n-1个脉冲数目的组合数,ε表示能量归一化因子,用于保持加权前后各个脉冲的总能量相等,ε可表示为
表示从N-1个不同脉冲数目中取出n-1个脉冲数目的组合数,ε表示能量归一化因子,用于保持加权前后各个脉冲的总能量相等,ε可表示为
(9)
但该方法并没有真正地减少旁瓣,而是通过在接收端为脉冲加权,对旁瓣的能量分布进行位置调整。在距离多普勒谱中将原本位于目标附近的旁瓣转移到远离目标主瓣沿目标多普勒方向的两侧位置,从而在目标主瓣附近获得较大的旁瓣清洁区域,提高目标检测的性能。
2.3 逐点最小化处理
二项式设计方法可以在距离多普勒谱上目标主瓣附近获得较大的清洁区,该区域内旁瓣水平很低,但其缺点在于严重降低了目标的多普勒分辨率。GPTM序列方法虽然无法达到二项式设计方法一样大的旁瓣清洁区,但这种方法具有比二项式设计方法更高的多普勒分辨率。考虑将两者的优点相结合,以提高目标检测的性能。可将两次处理后输出的距离多普勒谱进行如式(10)所示的逐点最小化处理,既能获得较大的旁瓣清洁区,又能保持较高的多普勒分辨率,更有利于下一步对目标的检测。
χ(t,fd)=min[χGPTM(t,fd),χBD(t,fd)]=
(10)
式(10)表示,对距离多普勒上的每一个分辨单元(t,fd),逐点比较GPTM序列方法下的RD谱值χGPTM(t,fd)和二项式设计方法下的RD谱值χBD(t,fd),取两者中较小的值赋给逐点最小化处理后的RD谱χ(t,fd)。
2.4 OS-CFAR检测
在逐点最小化处理后的距离多普勒谱上进一步实现对目标的检测。针对本文的背景,选取适合在多目标场景中使用的OS-CFAR[13]检测方法对目标进行检测。
OS-CFAR检测方法首先应设置保护单元格,防止目标扩展的能量进入到参考窗内对噪声估计值造成污染。其次,对参考窗的设计采取十字参考窗[15]的方法,设定前沿、后沿、上沿和下沿4个参考窗。十字参考窗方法只利用与检测单元处于同一距离和同一多普勒的数据信息,与矩形参考窗相比具有更快的运算速度。
3 仿真结果
为了验证该方法在旁瓣抑制和目标检测问题上的有效性,本文对所提信号处理方法进行仿真。系统参数设计如下:雷达工作频率为fc=1 GHz,带宽为B=10 MHz,采样率fs=10B=0.1 GHz,脉冲重复间隔(PRI)为T=50 μs,每根天线发射的脉冲数目为N=64。发射信号采用一组(2,2,16)的基本完全互补码,每位码元宽度Tc=0.1 μs,具有10个采样点。在仿真场景中一共设置了4个目标,其中,2个强目标(目标1、2)的归一化幅度为0 dB,2个弱目标(目标3、4)的归一化幅度为-20 dB,表1给出了这4个目标的距离及多普勒频移参数。另外接收端接收的噪声为零均值复高斯白噪声,信噪比为SNR=10 dB。
表1 仿真目标参数

目标距离多普勒1r1=1.86 kmfd1=1.3 rad2r2=2.79 kmfd2=-1.1 rad3r3=0.75 kmfd3=-0.7 rad4r4=1.605 kmfd4=-1.8 rad
图4给出了利用GPTM序列设计方法在发射端调整脉冲发射顺序,接收端脉冲以标准权重序列加权,距离多普勒处理后所得的距离多普勒谱。图中,目标的多普勒分辨率较高,且目标附近的距离旁瓣被较好地抑制了,目标能被较明显地分辨出来。但整个距离多普勒谱中仍存在许多旁瓣,将影响目标检测的性能。

图4 GPTM序列设计方法
二项式设计方法是指:发射端脉冲以标准发射顺序发射,再利用二项式设计方法在接收端对各脉冲加上不同权重,然后进行距离多普勒处理得到距离多普勒谱。图5给出了单个目标(目标2)经过二项式设计方法处理后得到的距离多普勒谱。由图5可知,二项式设计方法在目标多普勒附近能获得较大的清洁区,该区域内旁瓣较低,将旁瓣能量移到了目标位置两侧,沿着目标多普勒轴对称分布。因此,二项式设计方法并没有抑制或减少旁瓣能量,而是对旁瓣能量的分布位置进行了调整。
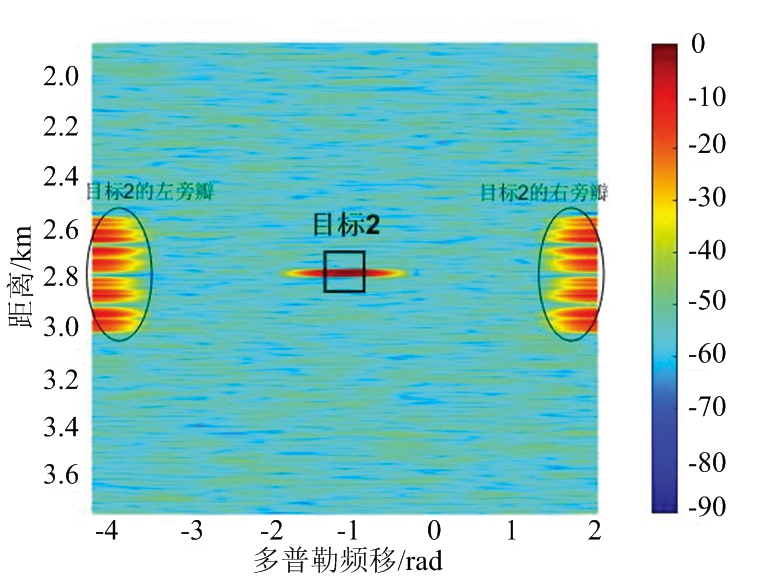
图5 单目标下的二项式设计方法
进一步地,对表1中4个目标的情况进行二项式设计方法处理,得到的距离多普勒谱如图6所示。由图6可知,弱目标4几乎被淹没在强目标1产生的旁瓣中,难以被分辨;并且将图6与图4对比可知,在这种方法下,距离多普勒谱虽然具有更大的旁瓣清洁区,但是目标的多普勒分辨率很低,对目标检测十分不利。
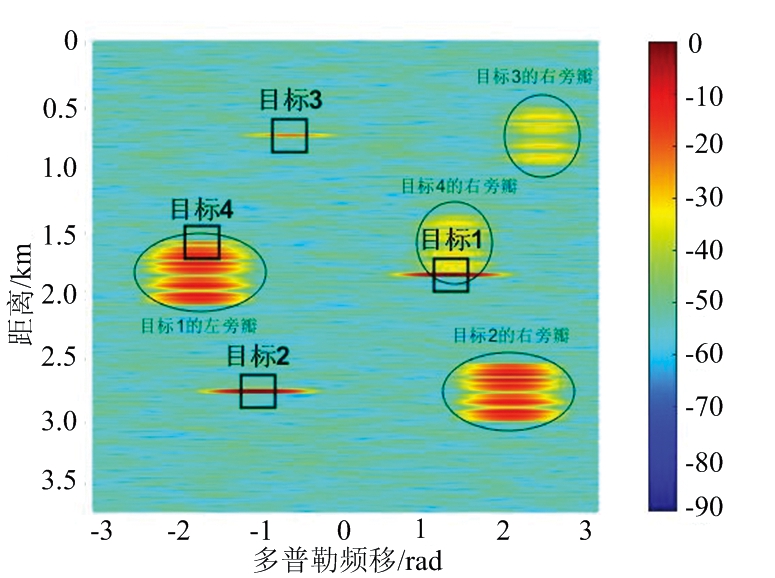
图6 二项式设计方法

图7 逐点最小化处理
利用GPTM序列设计方法和二项式设计方法得到的距离多普勒谱上,目标的位置和幅度是相同的,但旁瓣的分布情况是不同的。图7给出了经逐点最小化处理后的距离多普勒谱。图7与图4对比可知,距离旁瓣所在位置的幅度被明显减弱了,旁瓣抑制性能得到了较好的改善。图7与图6对比可知,各目标的多普勒分辨率均得到了显著提高。由此可知,本文所提的信号处理方法综合了上述两种方法的优势,能保持目标幅度值并有效减少旁瓣,同时具有较大的旁瓣清洁区和较高的目标多普勒分辨率,验证了本文所提的信号处理方法具有良好的目标检测性能。
为进一步验证该信号处理方法对目标检测的有效性,对逐点最小化处理后的距离多普勒谱进行OS-CFAR检测仿真。在检测中采取十字参考窗的设计,多普勒维度的保护单元设置为6个,参考单元设置为36个;时延维的保护单元设置为4个,参考单元设置为40个。虚警率Pfa=10-5,选取第60个参考单元作为样本。
图8给出了OS-CFAR检测的结果。由图8可知,4个非零多普勒目标均能被正确检测出来,验证了该信号处理方法下目标检测的有效性。
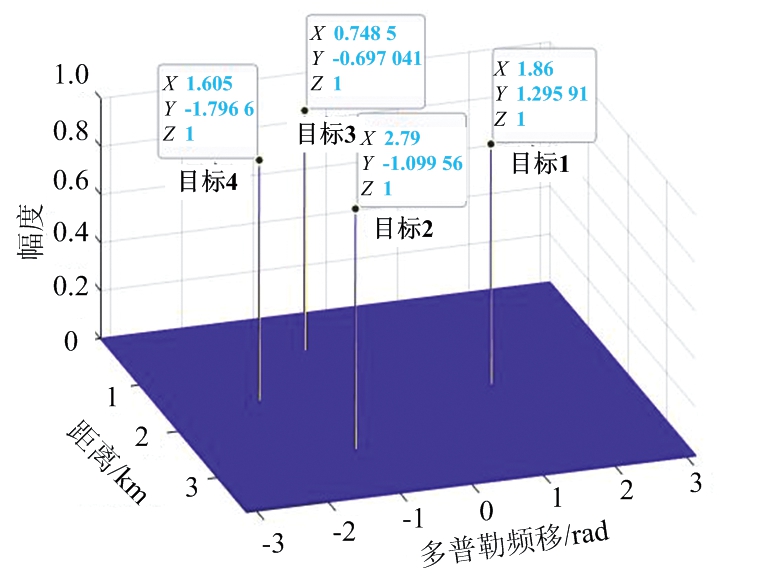
图8 OS-CFAR检测结果
为了更清楚地展现本文所提信号处理方法良好的旁瓣抑制性能和目标多普勒分辨率,针对GPTM序列方法、二项式设计方法及本文方法,将各目标在选定范围内的主瓣旁瓣比值(Mainlobe Sidelobe Ratio, MSR)归纳在表2中,并将各目标主瓣所占据的多普勒单元个数归纳在表3中。
MSR可表示为
(11)
式中,PML表示目标所在距离多普勒单元上的归一化幅度值,PSL表示目标附近(fdh+0.90 rad,fdh+1.34 rad),(rh-0.186 km,rh+0.186 km)范围内旁瓣的归一化幅度平均值。
表2 3种方法下各目标的MSR

方法MSR/dB目标1目标2目标3目标4GPTM41.4341.5940.2524.16BD57.0156.0937.0837.44本文方法58.4757.7044.1140.21
由表2可知,本文方法的MSR相对于GPTM序列方法的MSR得到了大幅提升,旁瓣水平明显降低;相对于二项式设计方法,本文方法的MSR有小幅度的提升,旁瓣水平轻微降低。因此,表2验证了本文提出的信号处理方法能够有效降低GPTM序列方法下目标周围的旁瓣。
表3 3种方法下目标的多普勒分辨率

方法多普勒分辨率目标1目标2目标3目标4GPTM131399BD65654141本文方法131399
由表3可知,本文方法保留了GPTM序列方法较高的多普勒分辨率;相比于二项式设计方法,各目标主瓣所占的多普勒单元个数得到极大的降低,目标的多普勒分辨率得到了明显改善。因此,表3验证了本文提出的信号处理方法能够有效提高二项式设计方法下目标的多普勒分辨率。
由表2和表3可知,本文提出的信号处理方法有效综合了GPTM序列方法和二项式设计方法的优势,既能得到较低的旁瓣水平,也能得到较高的目标多普勒分辨率。
4 结束语
本文针对非零多普勒目标检测问题展开了研究,将完全互补码应用在MIMO雷达中,提出了一种将GPTM序列设计方法和二项式设计方法相结合的信号处理方法。该方法在抑制旁瓣的同时保持了较高的多普勒分辨率,能够提高目标检测的性能。最后,通过仿真验证了该信号处理方法对非零多普勒目标检测的有效性。
[1] 黄志忠. MIMO雷达信号模型及处理方法研究[J]. 信息记录材料, 2021, 22(5):106-108.
[2] BHAMRE P, GUPTA S. Constrained Waveform Designing for MIMO RADAR Using Jaya Optimization[J]. Wireless Personal Communications, 2020, 111(1):331-342.
[3] 池政刚. MIMO雷达波形优化设计技术[D]. 西安:西安电子科技大学, 2020.
[4] 李旭, 安涛, 刘金鹏. 一种优化MIMO雷达波形设计的算法[J]. 舰船电子对抗, 2019, 42(4):66-70.
[5] HONG S, ZHOU F H, DONG Y T, et al. Chaotic Phase-Coded Waveforms with Space-Time Complementary Coding for MIMO Radar Applications[J]. IEEE Access, 2018(6):42066-42083.
[6] LI S F, CHEN J, ZHANG L Q.Optimisation of Complete Complementary Codes in MIMO Radar System[J]. Electronics Letters, 2010, 46(16):1157-1159.
[7] CALDERBANK R, HOWARD S D, MORAN B. Waveform Diversity in Radar Signal Processing[J]. IEEE Signal Processing Magazine, 2009, 26(1):32-41.
[8] PEZESHKI A, CALDERBANK R, MORAN W, et al. Doppler Resilient Golay Complementary Waveforms[J]. IEEE Trans on Information Theory, 2008, 54(9):4254-4266.
[9] TANG J, ZHANG N, MA Z, et al. Construction of Doppler Resilient Complete Complementary Code in MIMO Radar[J]. IEEE Trans on Signal Processing, 2014, 62(18):4704-4712.
[10] DANG W, PEZESHKI A, MORAN W, et al. Coordinating Complementary Waveforms for Sidelobe Suppression[C] ∥ 2011 45th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA:IEEE, 2011:2096-2100.
[11] 李永哲. 基于发射波束域的MIMO雷达信号处理理论与算法研究[D]. 成都:电子科技大学, 2016.
[12] ZHU J H, WANG X Z, HUANG X T, et al. Golay Complementary Waveforms in Reed-Müller Sequences for Radar Detection of Nonzero Doppler Targets[J]. Sensors, 2018, 18(1):192.
[13] YU H X, DIAO L Q, XU S J, et al. Research and Implementation of Orderly Statistical Constant False Alarm Detector[C] ∥ 2019 IEEE International Conference on Signal Processing, Communications and Computing, Dalian, China:IEEE, 2019:1-5.
[14] LEVANON N, DIDI J H. Repeated Sorting on Sliding Window for OS-CFAR[J]. IET Radar Sonar & Navigation, 2019, 13(8):1272-1278.
[15] 黄红平, 张晓玲. 一种改进型二维恒虚警参考窗[J]. 航空兵器, 2011(1):34-37.



