0 引 言
阵列信号处理是现代雷达系统中的热点研究问题，波达方向(Direction of Arrival，DOA)估计技术作为重要分支更是得到广泛应用。为了得到目标精确的角度信息，许多经典算法已经被应用于实际工程中，如多重信号分类法(MUSIC)和旋转不变子空间技术(ESPRIT)。但是随着通信环境的日益复杂，多径传播和同频干扰环境下产生了高度相关和相干信号源，使接收数据协方差矩阵缺秩，噪声子空间与信号子空间不再正交，上述常规算法失效，需要通过诸如空间平滑[1]、矩阵重构[2]和Toeplitz化[3]等解相干操作后才能得到准确的估计结果。均匀圆阵(Uniform Circular Array，UCA)作为最常用的阵列之一，相比均匀线阵(Uniform Linear Array，ULA),不仅能够提供[-180°，180°]的方位角估计，还具备方向图在任何方位都有相同的波束形状、容易共形和导向矢量共轭对称等诸多优势[4]。由于UCA的导向矢量比较复杂，不具备ULA的范德蒙结构，许多常规方法不能直接应用。针对上述问题，文献[5]首次提出模式空间变换的概念，通过构造模式空间变换矩阵，将UCA变为导向矢量具备范德蒙结构的虚拟ULA，学者们由此展开深入研究。文献[6]提出均匀圆阵实值波束空间多重信号分类法(UCA-RB-MUSIC)和均匀圆阵旋转不变子空间法(UCA-ESPRIT)，通过构造实值波束变换矩阵，利用MUSIC和ESPRIT算法估计信号二维角度信息，但是该方法不能估计相干信号；文献[7-8]分别利用阵列平移和划分子阵列的方法解相干，然后利用二维谱峰搜索估计信号角度信息，计算量较大无法满足实时需求；文献[9-10]分别利用Toeplitz化和矩阵重构法估计相干信号，分辨率高实时性好，但只能得到一维角度信息；文献[11-12]提出基于稀疏重构模型下的相干信号二维DOA估计方法，准确性高且对相干信号不敏感，但是涉及复杂的数学优化问题，求解困难；文献[13-14]分别利用双圆阵平移和双圆阵Toeplitz重构方法估计二维相干信号，但损失了一个子阵的阵元。
本文在文献[13]的基础上，采用单一圆阵轴向虚拟平移，通过对平滑后的协方差矩阵去噪处理，利用波达方向矩阵法[15]对俯仰角的稳健性估计出信号的俯仰角；然后将平滑后的协方差矩阵与波束空间变换矩阵相乘得到波束域协方差矩阵，使UCA变为导向矢量具备范德蒙结构的虚拟ULA，最后利用求根MUSIC算法估计信号的方位角。所提方法无需复杂的二维谱峰搜索，方位角和俯仰角自动配对。仿真表明该方法在低信噪比、信号高度相关和相干时仍能得到准确的估计结果，与传统UCA-RB-MUSIC和UCA-ESPRIT算法相比，计算量更小、分辨率更高，可以应用在弹载、机载阵列或其他移动阵列系统中。
1 阵列结构和信号模型
如图 1所示，假设M个各向同性的阵元、均匀分布在半径为r的圆周上，K个远场、窄带、波长为λ的相干信号入射到该阵列。入射信号俯仰角φ∈[0,π]， 定义为入射方向与z轴正向夹角；方位角θ∈[-π,π]， 定义为信号入射方向在xoy平面的投影与x轴正向夹角。在不考虑阵列误差、通道不一致和互耦影响下，阵列接收数据矢量为
X(t)=AS(t)+n(t)
(1)
式中：X(t)=[x1(t),x2(t),…,xM(t)]T为M×1维数据接收矢量,S(t)=[s1(t),s2(t),…,sK(t)]T为K×1维信号矢量；A=[a(θ1,φ1),a(θ2,φ2),…,a(θK,φK)]为M×K维阵列导向矢量，其中
(n=0,1,…,M-1)；n(t)=[n1(t),…,nM(t)]T为M×1维噪声矩阵，假设噪声为空时均白的加性高斯噪声，彼此独立且与信号不相关，噪声功率为δ2。
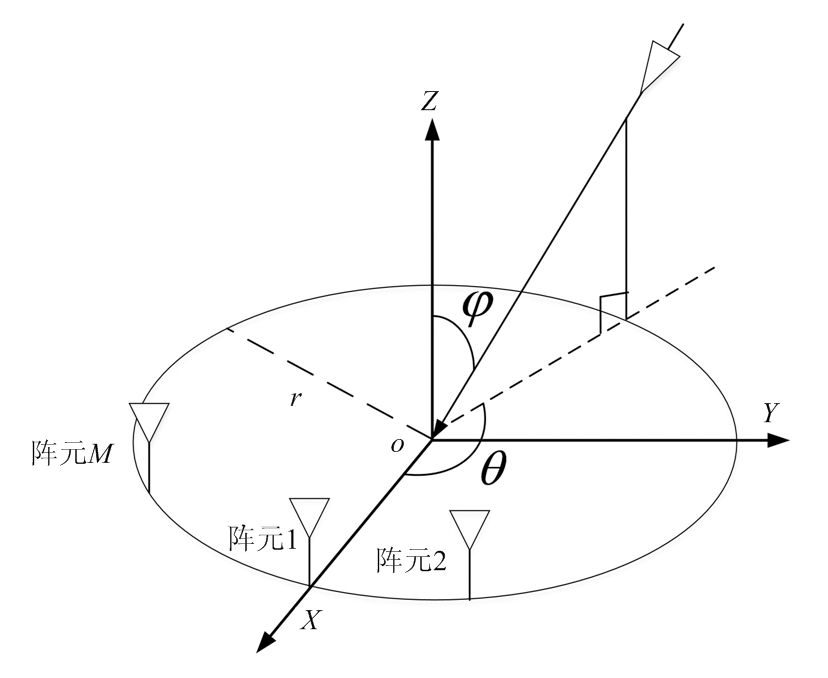
图1 阵列结构图
2 基于波达方向矩阵的波束空间变换法
2.1 波达方向矩阵法
文献[15]首次提出波达方向矩阵法，对于非相干信号源，基于x和y两个平行线阵的数据接收矢量：
(2)
式中，A′为线阵导向矢量，Φ为x阵列与y阵列的相位差对角矩阵，该矩阵只与信号的俯仰角有关。X′(t)的自协方差矩阵为
(3)
X′(t)和Y′(t)的互协方差矩阵为
(4)
式中，Rss=E[S(t)S(t)H]，I为单位矩阵。因为噪声矢量互不相关，互协方差矩阵中不含噪声方差项。定义Rxx的信号部分为
Rxx0=Rxx-δ2I
(5)
对不含噪声方差项的Rxx0作特征分解，得到大特征值ui和对应的特征向量Vi(i∈[1,2,…，K])。利用ui和Vi定义一个新的伪逆矩阵
(6)
然后通过与Ryx相乘构造波达方向矩阵R:
(7)
该文献证明波达方向矩阵R满足如下关系：
RA=AΦ
(8)
即通过对波达方向矩阵R特征分解得到特征值和特征向量，其中非零特征值对应对角阵Φ，非零特征值对应的特征向量与导向矢量A相等，利用此对等关系即可以估计得到俯仰角和方位角。
2.2 俯仰角估计
文献[13]针对相干信号采用双圆阵轴向平移，利用两个子阵的自协方差矩阵和不含噪声方差项的互协方差矩阵构造波达方向矩阵，然后通过特征分解估计出俯仰角和方位角。其相位差矩阵Φ为
(9)
式中， d为两个子阵间距，diag[·]表示对角化。其俯仰角具体求解为
(10)
式中，ηi为R特征分解的非零特征值(i∈[1,…，K])。但是在求解方位角时，由于θ∈[-π,π]，容易出现测向模糊，需要解模糊处理；此外，在对波达方向矩阵进行特征分解时，特征向量并不唯一，需要进行额外处理使特征矢量和导向矢量A对应相等；且在低信噪比时，波达方向矩阵法在求解方位角时对噪声非常敏感，文献[13]采用双圆阵列，消除互协方差矩阵中的噪声方差项，但是却损失了一个子阵的阵元，阵元数较大。
为了解决上述问题，本文针对文献[13]的波达方向矩阵法做出改进，将双圆阵中的第二个子阵由第一个子阵平移得到(即所有子阵均由第一个子阵沿z轴正向虚拟平移得到)，然后分别求取各个子阵的自相关函数和相邻子阵的互相关函数。利用波达方向矩阵法对俯仰角估计的稳健性，通过对互协方差矩阵去噪处理后构造波达方向矩阵R求得俯仰角。假设阵列虚拟平移方向与导弹或其他阵列载体移动方向相同，均沿z轴正向移动，平移次数为p，每次平移距离均为
如图 2所示。
图2 阵列平移图
则虚拟平移阵元接收数据矢量为
X(i)(t)=AΦ(i)S(t)+ni(t)
(11)
式中相位差矩阵Φ如式(9)所示，则对应的子阵自协方差矩阵为
E[X(t)(i)X(t)(i)H]=
AΦ(i)Rss(Φ(i))HAH+δ2I
(12)
相邻子阵间互协方差矩阵为
E[X(t)(i+1)X(t)(i)H]=
AΦ(i+1)Rss(Φ(i))HAH+δ2I
(13)
式中，i∈[0,1,…，p]表示平移次数。根据空间平滑原理，可得平滑后的协方差矩阵
(14)
(15)
式中，
表示平滑后的信号自协方差矩阵：
(16)
只要平移次数p大于相干信源数
为非奇异矩阵，即通过平滑达到了解相干目的。
为了消除互协方差矩阵的噪声方差项，提高算法在低信噪比环境下的估计性能。本文首先采用文献[9]中的去噪方法，利用
特征分解得到的小特征值去除自协方差矩阵和互协方差矩阵的噪声方差项。噪声方差为
(17)
式中，μi为
特征分解后的M-K个小特征值。去噪后的自协方差矩阵为
(18)
去噪后的互协方差矩阵为
(19)
根据2.1节中波达方向矩阵法，利用
构造波达方向矩阵R，由式(10)即可估计出俯仰角。
2.3 方位角估计
在得到俯仰角后，利用波束空间变换理论[5]，直接用波束变换矩阵W乘以平滑后的协方差矩阵
使UCA的导向矢量具备范德蒙结构。波束变换矩阵W为
(20)
式中，ε=[k]为最大相位模式数，[·]表示向下取整，
当阵元数M>2ε时(忽略残差影响)[16]，对
进行波束空间变换：
RT=
(21)
式中：B(θi,φi)=Γ(φi)av(θi)，Γ(φi)=diag[V-ε(φi),…,V0(φi),…,Vε(φi)]，Vm(φi)=jmJm(ksin(φi)),Jm表示阶数为m的第一类贝塞尔函数(m∈[-ε,…,ε])；虚拟线阵导向矢量av(θi)=[e-jεθi,…,e0,…,ejεθi]T。对波束空间自协方差矩阵RT进行特征分解，得到特征值η1>η2,…>η2ε+1和对应的特征向量e1,e2,…,e2ε+1，于是得到信号子空间Us=[e1,e2,…,eK]和噪声子空间Un=[ek+1,ek+2,…,e2ε+1]，因为非奇异，所以UsUn=0。
由波束导向矢量B可以看出，导向矢量的俯仰角和方位角已经分离。在利用波达方向矩阵法求出俯仰角后，可以直接利用求根MUSIC算法估计出方位角信息[17]，求根多项式为
(22)
下面给出本文方法的具体步骤：
步骤1： 获取阵列接收数据矢量X(t)；
步骤2： 采用虚拟平移，分别得到平移后的各个虚拟子阵数据接收矢量X(i)(t)；
步骤3： 计算各个子阵的自协方差矩阵
以及相邻子阵互协方差矩阵
步骤4： 根据空间平滑原理获取平滑后的
然后根据式(18)、式(19)得到去噪后的
步骤5： 根据式(7)利用
和
构造波达方向矩阵R，然后根据波达方向矩阵法，由式(10)估计俯仰角；
步骤6： 根据式(21)对进行波束空间变换得到RT；
步骤7： 对RT进行特征分解得到噪声子空间Un；
步骤8： 根据式(22)，利用求根MUSIC算法估计方位角。
3 仿真实验
为了验证所提方法的正确性、分析所提方法的优缺点，分别做如下仿真实验。实验1为验证本文方法对二维相干信号估计的有效性；实验2为验证本文方法对高度相关信号的有效性，对比算法为文献[6]中的UCA-ESPRIT算法和UCA-RB-MUSIC算法；实验3为验证信号相干情况信噪比对本文方法的影响，对比算法为文献[7]中算法；实验4为验证信号相干情况阵元数对本文方法的影响，对比算法为文献[13]中算法。
实验1 验证本文方法对相干信号的有效性。假设4个窄带等功率相干信号分别从(-100°，60°)、(-50°，50°)、(20°，20°)、(120°，80°)入射到图1所示阵列。阵元数M=12，各相邻阵元间距D=0.5λ，为了减少波束空间变化中的残差影响，取半径r=M*D/(2*π)。仿真的快拍数为128，信噪比SNR=15 dB，独立进行100次蒙特卡罗实验。仿真结果散点图如图 3所示，在4个信号完全相干情况下，所提方法仍能够准确估计出目标信号的二维角度信息，且误差较小准确性较高。
图3 实验1估计结果散点图
实验2 验证本文方法对高度相关信号的有效性。假设4个窄带等功率相关信号分别从(20°，10°)、(120°，40°)、(-50°，50°)、(-100°，60°)入射到图 1所示阵列，各信号相关系数均为0.8，M =15，阵元间距、半径和快拍数与实验1相同。独立进行100次蒙特卡罗实验，仿真得到不同信噪比下本文方法、文献[6]中UCA-ESPRIT算法和UCA-RB-MUSIC算法的估计结果均方根误差变化。均方根误差定义为
RMSE=
(23)
式中，N为蒙特卡罗次数，(θi,φi)为信号i真实值，(θij,φij)为信号i的第j次估计值。
仿真结果如图 4所示，UCA-ESPRIT算法估计性能较差，UCA-RB-MUSIC性能最好，本文方法居中。分析原因主要是因为MUSIC算法用二维谱峰搜索带来的巨大运算量换取了较好的估计性能；而ESPRIT算法直接计算得到二维角度信息，运算量小，估计性能差；本文方法存在多次特征分解，计算量居中，但是性能接近MUSIC算法。显然计算复杂度和估计性能需要折中选择，本文方法估计性能好且计算复杂度不高，可以满足工程实际应用。
图4 实验2均方根误差随信噪比变化图
实验3 验证信噪比对本文方法的影响。假设4个窄带等功率相干信号分别从(20°，20°)、(-50°，50°)、(-100°，60°)、(120°，80°)入射到图1所示阵列。M =12，阵元间距、半径和快拍数与实验1相同。信噪比SNR从0 dB步长为3 dB增加到30 dB，蒙特卡罗实验次数为100，仿真得到本文算法和文献[7]中算法的估计结果均方根误差随信噪比变化情况，如图 5所示。从图中可以看出，信噪比较高时，本文方法性能略低于文献[7]中算法；当信噪比小于5 dB时本文方法性能高于文献[7]中算法，相比二维谱峰搜索带来的巨大计算量，本文所提方法计算量较小实时性更高，且在低信噪比条件下估计性能更好。
图5 实验3均方根误差随信噪比变化图
实验4 验证阵元数对本文方法的影响。假设4个窄带等功率信号分别从(20°，20°)、(50°，40°)、(100°，50°)、(150°，80°)入射到图1所示阵列。阵元间距、半径和快拍数与实验1相同，SNR=20 dB。阵元数从9步长为3增加到24，蒙特卡罗实验次数为100，仿真得到本文算法和文献[13]中算法的估计结果均方根误差随阵元数变化情况，如图 6所示。从图中可以看到两种算法性能无较大差别，4个信号的均方根误差都比较小；本文方法在阵元数小于12性能开始逐渐变差，当阵元数小于9时已经无法准确估计目标结果；且随着阵元数增加，本文所提方法的估计结果均方根误差并非严格单调，这是因为阵元数的奇偶性实际上对波束空间变换的估计结果是有一定影响的[16]。但是文献[13]采用的是双圆阵，损失了一个子阵的阵元，实际阵元数是本文方法的两倍，所需阵元数是比较大的。但是本文方法无子阵列的损失，在阵元数大于9时，分辨性较好，可以满足实际工程应用需求。
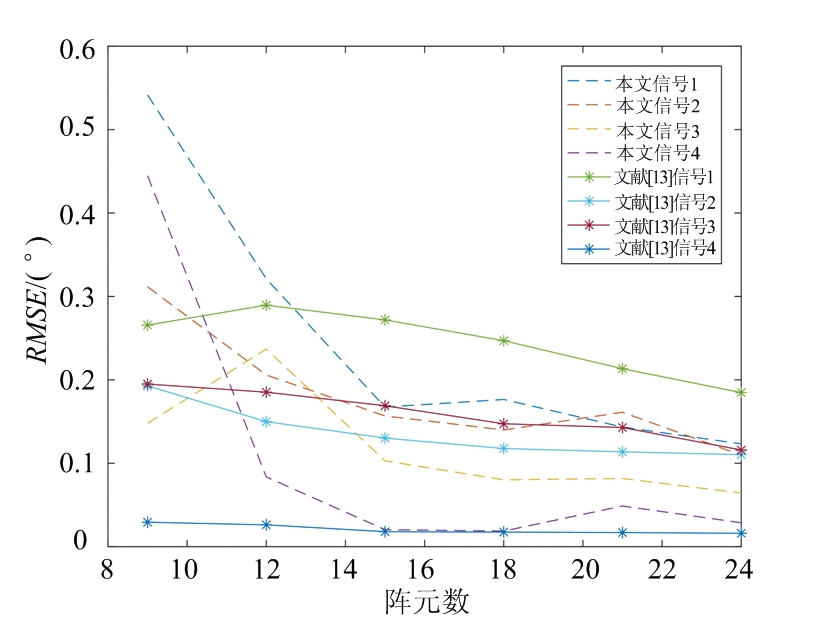
图 6 实验4均方根误差随阵元数变化图
4 结束语
本文通过均匀圆阵的轴向平移，利用波达方向矩阵法对俯仰角估计的稳健性，通过去噪处理后估计得到俯仰角信息；然后通过波束空间变换将导向矢量中方位角和俯仰角分离，使圆阵导向矢量具备范德蒙结构，最后利用求根MUSIC算法估计得到方位角。该方法无需复杂的二维谱峰搜索，俯仰角和方位角自动配对，且不用损失一个子阵的阵元。通过仿真实验可以看出，该方法耗时较少，在低信噪比环境下仍能得到准确结果，分辨率高，满足现代雷达复杂移动阵列场景下测向要求。但本文方法在阵元数较小时(M< 9)性能显著下降，如何将本文所提方法应用到少阵元环境是后续工作重点。
[1] CHEN Zhang, WU Hao, LIU Yongxiang, et al. A Novel ULA-Difference-Coarray-Based DOA Estimation Method for General Coherent Signals[J]. Mathematical Problems in Engineering,2020(11):1-13.
[2] 王宇. 基于阵列重构的空间谱高分辨测向技术研究[D].西安：长安大学,2020.
[3] 唐晓杰,赵迪,何明浩,等.一种基于前后向Toeplitz矩阵重构的相干信号DOA估计算法[J].中国电子科学研究院学报,2019,14(8):823-829.
[4] 熊钊. 基于均匀圆阵的测向与主动反侦察技术研究[D]. 成都：电子科技大学,2020.
[5] DAVIES D E N. A Transformation Between the Phasing Techniques Required for Linear and Circular Aerial Arrays[J]. Proceedings of the Institution of Electrical Engineers,1965,112(11):2041.
[6] MATHEWS C P, ZOLTOWSKI M D. Eigenstructure Techniques for 2-D Angle Estimation with Uniform Circular Arrays[J]. IEEE Trans on Signal Processing,1994,42(9):2395-2407.
[7] 侯碧波. 基于均匀圆阵的2D DOA估计算法研究及实现[D].成都：电子科技大学,2011.
[8] WU Yao, CHEN Hui, CHEN Yongchao. A Method of 2-D DOA Estimation of Coherent Signals Based on Uniform Circular Array via Spatial Smoothing[C]∥ Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu:IEEE, 2011:312-314.
[9] 张薇,韩勇,闫锋刚,等.基于均匀圆阵Toeplitz矩阵集重构解相干算法[J].吉林大学学报(工学版),2020,50(4):1522-1531.
[10] 盘敏容,蒋留兵,车俐,等.基于协方差矩阵重构的互质阵列DOA估计[J].雷达科学与技术,2020,18(1):1-6.
PAN Minrong, JIANG Liubing, CHE Li, et al. DOA Estimation of Coprime Array Based on Covariance Matrix Reconstruction[J]. Radar Science and Technology, 2020, 18(1):1-6.(in Chinese)
[11] SU Xiaolong, LIU Zhen,LIU Tianpeng, et al. A Sparse Representation Method for Coherent Sources Angle Estimation with Uniform Circular Array[J]. International Journal of Antennas and Propagation,2019(10):1-9.
[12] PARK H R, LI Jian. Efficient Sparse Parameter Estimation Based Methods for Two-Dimensional DOA Estimation of Coherent Signals[J]. IET Signal Processing,2020,14(9):643-651.
[13] 毛维平,李国林,谢鑫.均匀圆阵相干信源二维波达方向估计[J].系统工程与电子技术,2013,35(8):1596-1601.
[14] 毛维平,李国林,粘朋雷,等.双圆阵模式空间二维解相干[J].火力与指挥控制,2015,40(1):19-23.
[15] 殷勤业,邹理和, NEWCOMB R W.一种高分辨率二维信号参量估计方法——波达方向矩阵法[J].通信学报,1991(4):1-7.
[16] BELLONI F,KOIVUNEN V. Beamspace Transform for UCA: Error Analysis and Bias Reduction[J]. IEEE Trans on Signal Processing,2006,54(8):3078-3089.
[17] JIANG Guojun, MAO Xingpeng, LIU Yongtan. Reducing Errors for Root-MUSIC-Based Methods in Uniform Circular Arrays[J]. IET Signal Processing,2018,12(1):31-36.
