0 引言
在科学研究和实际应用中,由于在成本、灵活性和机动性能方面的优势,无人机受到了越来越多的关注[1-5]。随着通信与控制技术的发展,无人机集群可以取代单机无人机,带来分工协作、集群智能化等诸多优势。无人机集群规模较大,需要高效的决策指挥无人机执行任务。然而,在复杂动态环境中,传统的任务规划方法很难使大规模无人机集群发挥出执行任务的优势。因此,对无人机集群的高效动态任务规划的需求与日俱增。
真实的战场环境普遍具有动态和不确定的特征[4]。目前,分布式优化方法的研究已获得较大进展,较多有效方法被提出[6-9],可以较好解决真实战场环境的任务分配问题,然而从无人机集群的成本和可靠性方面来说,分布式无人机集群难以在危险多变的战场环境中大规模部署,且分布式优化算法难以求得全局最优解。因此,可有效应对动态战场环境且能求得全局最优解的集中式优化算法是较优的选择。
针对集中式无人机集群任务规划建模,文献[10]构建了约束满足问题(Constraint Satisfaction Problem, CSP)模型,文献[11-12]在CSP基础上以无人机集群的执行任务成本、飞行时间、危险性和数量作为目标函数和以传感器类型、任务顺序和各项时间等作为约束,构建了适合解决静态场景下的无人机集群面对已知确定目标的任务规划模型。第二代非支配排序算法[13]及在其基础上开发的算法[11-12]可以很好地解决CSP。然而,真实战场环境的动态性导致优化问题的目标函数和约束具有动态性,CSP模型难以应对动态优化问题。为有效应对动态战场环境,动态多目标优化问题(Dynamic Multiobjective Optimization Problems, DMOPs)模型被广泛研究[14-19],该模型适合目标函数随时间变化的场景。针对该模型,较多的动态多目标进化算法(DMOEA)已经被提出,例如,基于多样性增强[20-21]、基于种群预测[22-23]和基于记忆机制[24]等动态多目标进化算法。然而,DMOPs仅适配目标函数时变而约束不变的动态场景优化问题,无法适应于动态约束的情况。文献[25]构建了动态约束多目标优化问题(Dynamic Constrained Multiobjective Optimization Problems, DCMOPs)模型,并提出了动态约束多目标进化算法(Dynamic Constrained MOEA, DC-MOEA)。该模型的目标函数和约束都具有时变性,在有效应对时变目标函数的基础上,所提算法引入了自适应惩罚函数机制,合理利用有价值的不可行个体,得以应对动态约束导致的个体进入不可行区域的问题,从而加快种群收敛并求得最优解。
然而,动态环境发生变化还会导致数量的改变,这是更为棘手的难题。目标函数数量的变化将会改变目标函数域的维度,进而使帕累托前沿面发生扩张或收缩,上述动态优化算法很难处理此种类型变化。针对该问题,文献[26]构建了目标函数数量可变的动态多目标优化问题模型,该模型可较好地匹配目标函数数量发生变化的优化问题,提出的动态双档案进化算法(Dynamic Two-Archive EA, DTAEA)在目标函数发生变化时,可重新构建收敛性种群和多样性种群,适应目标域的维度变化,同时维持加速种群收敛。相关研究证明该算法也可同时应对时变目标函数的问题。然而,该算法仅能有效应对目标函数的动态变化,未考虑约束时变和数量动态变化对求解优化问题的影响,导致在环境发生动态变化时,大量先前可行解进入不可行区域,可行解不足,影响优化问题求解速度。
针对以上问题,为有效应对无人机集群协同搜索跟踪的动态场景,本文构建了动态多约束多目标优化问题(Dynamic Multiconstraint Multiobjective Optimization Problems, DMCM-OPs),该模型适用于目标函数与约束的数量动态变化且时变的复杂场景。为有效求解DMCMOPs,本文提出了基于动态自适应惩罚的动态约束双档案进化算法(Dynamic Constraint Two-Archive EA, DCTAEA),该算法同时维持两个种群,平衡种群多样性和收敛性,同时,在收敛性种群更新时引入自适应惩罚函数机制,整合不可行个体的目标函数值和违反约束的惩罚值获得修正目标函数值,并作为不可行个体的选择依据。根据可行个体所占比率动态调整不可行解的约束违反值和目标函数值在修正的目标函数值中所占比重,使得有价值不可行个体获得竞争机会,促使种群进入可行区域并向帕累托前沿面收敛。仿真结果证明,相比第二代非支配排序遗传算法(NSGA-II)的动态版本、基于分解的多目标进化算法(MOEA/D)、约束双档案进化算法(CTAEA)和动态双档案进化算法(DTAEA),本文所提算法能更加有效地解决动态多约束多目标优化问题,实现动态环境下的无人机集群高效任务规划。
1 物理场景描述
1.1 无人机描述
考虑到战场环境的复杂性和危险性,以及无人机负载重量和自身携带的电池能量的限制,无人机装备被动侦察系统,采用测向交叉定位方式对目标进行定位。无人机搜索编队由两架无人机组成,通过被动测向交叉定位方法[27-28]粗略地确定目标位置,如图1(a)所示。搜索编队的有效探测范围可以看作半径为R的圆,如图1(b)所示,在此范围内的目标可以被无人机搜索编队发现。为了简化场景模型,我们把搜索编队的有效探测范围视为半径为R的圆的内接正方形。此外,目标跟踪需要更精确的定位精度,且面临危险性变高,设置无人机跟踪编队由4架无人机组成,如图2所示。
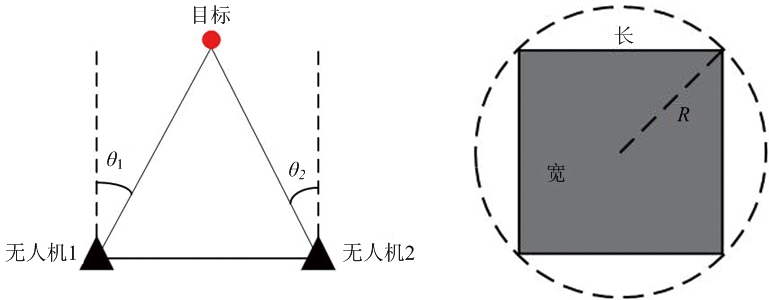
(a) 搜索编队交叉定位示意图 (b) 无人机编队探测范围示意图
图1 无人机编队定位示意图
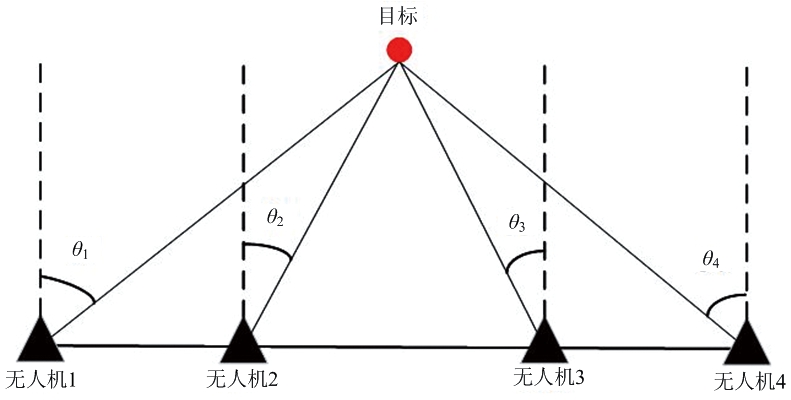
图2 跟踪编队交叉定位示意图
为方便无人机集群协同搜索跟踪任务规划方法设计,本文作出以下假设[7-8]:
1) 集群中无人机是同构的并且每架无人机都能通过编队执行搜索和跟踪任务;
2) 无人机能以固定速度飞行或盘旋在空中,飞行和盘旋状态可以在可忽略的极短时间内转换,且具有相同飞行自持力;
3) 中央控制站覆盖的通信覆盖范围以及与无人机集群的通信带宽可以满足任务要求;
4) 在无人机搜索或跟踪编队到达某个有效探测范围的中心,并悬停一定时间T,则表示对该范围内的目标进行有效搜索和跟踪任务。
1.2 离散任务区域描述
真实战场环境为三维空间区域,但是无人机的运动可以解耦为二维平面和垂直方向上的运动。因此,本文使用水平方向的二维平面来描述战场环境。任务区域被建模为由L*W=M个正方形网格区域构成的战场整体[7],战场环境网格化如图3所示。每个正方形网格区域代表无人机搜索跟踪编队的有效探测范围。因此,有M个搜索任务要执行。无人机的运动可以视为网格离散中心之间的运动[7-8]。
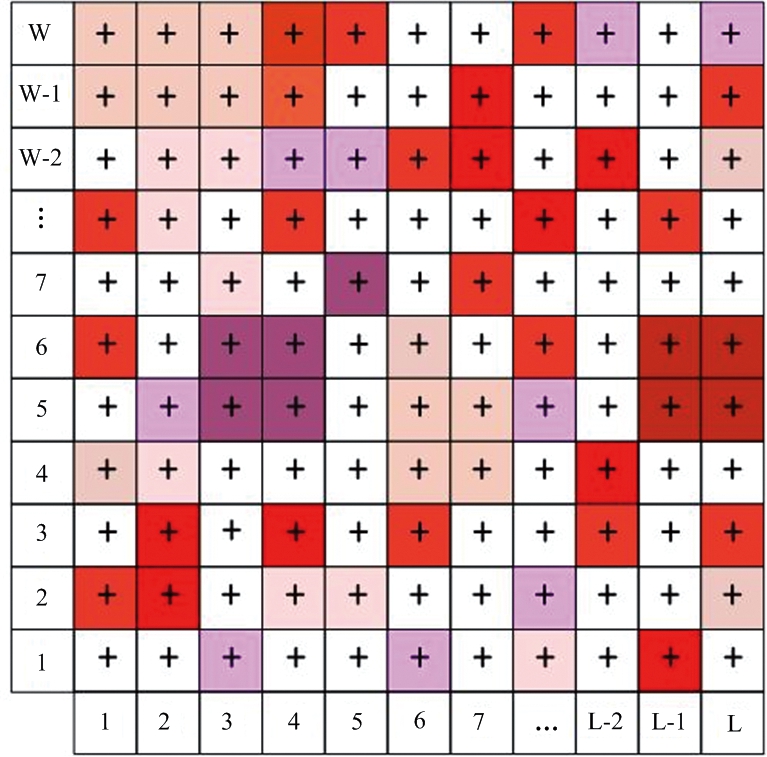
图3 战场离散网格区域及其初始化威胁示意图
由回报函数[29]的启发,本文提出威胁度函数的概念。在无人机集群执行任务前,预警机或卫星可以提供战场的先验信息,根据先验信息,计算出每个网格区域的初始威胁度和威胁度变化函数。网格区域的颜色越深代表该网格区域威胁值越大。
战场网格区域m在t时刻的威胁函数和所有网格在t时刻总威胁值函数表达式分别为
(1)
(2)
式中,wm表示网格m的威胁值的初始化因子,λm表示网格m的威胁等级相关参数,![]() 表示网格区域m的搜索任务在t时刻被编队n执行完毕且网格区域m的威胁值在搜索过后威胁值降低,但是随着无人机搜索编队离开该区域,威胁值随着时间做指数函数增长。发现的目标威胁函数表达式为
表示网格区域m的搜索任务在t时刻被编队n执行完毕且网格区域m的威胁值在搜索过后威胁值降低,但是随着无人机搜索编队离开该区域,威胁值随着时间做指数函数增长。发现的目标威胁函数表达式为
(3)
式中,wk表示目标k的威胁值的初始化因子,λk表示目标k的威胁等级相关参数,γk表示跟踪编队对目标建立跟踪后该目标的常数威胁值。图4表示网格区域和发现目标威胁度随时间的变化情况。其中蓝色线条表示某网格区域在第60 s被无人机搜索编队搜索完毕,根据公式(2),该区域的威胁值降低,而随着搜索编队离开,威胁值上升。红色线条表示在70 s时刻发现的目标并在90 s时刻跟踪编队开始对该目标进行跟踪的威胁值变化情况。
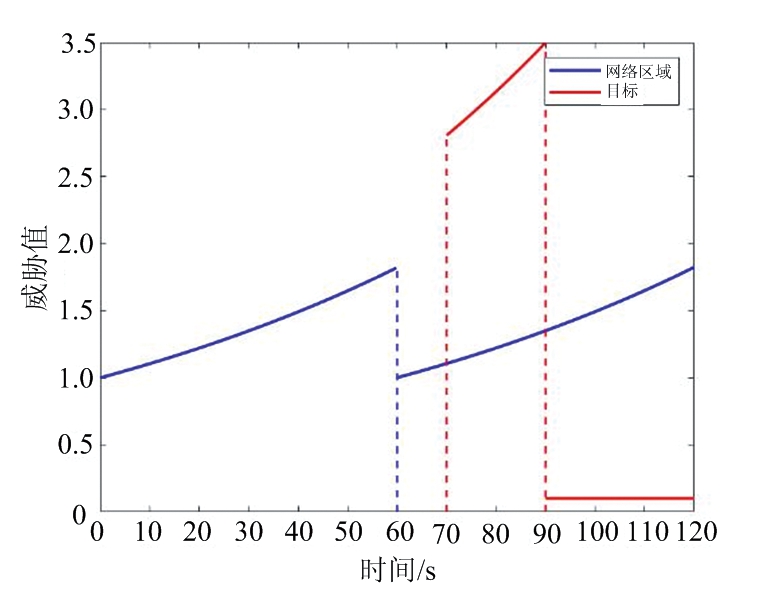
图4 网格区域和目标威胁度随时间变化示意图
1.3 协同搜索跟踪规划描述
战场场景时刻发生动态变化,战场场景所构建的战场离散网格区域威胁值函数是时变的,无人机集群在执行战场覆盖搜索任务的过程中随时会发现不可预测的目标,使无人机集群的任务性质发生改变。由下述2.2、2.3和2.4节可知,上述两大动态变化因素,导致任务规划问题的目标函数和约束发生动态变化,进而使得已求得的任务规划方案在动态变化后的场景中不再是最优解,无人机集群不能高效执行任务。
针对上述问题,本文提出了无人机集群协同跟踪搜索任务规划方法,流程图如图5所示。无人机集群按照初始任务规划方案执行战场覆盖搜索任务,一旦战场环境发生变化,则需要求解新的任务规划方案。该方法的难点在于建立符合真实战场环境的动态任务规划问题模型,以及快速求解最优任务规划方案。因此,下文将对符合战场要求的复杂动态优化问题模型和动态优化问题求解算法展开研究。
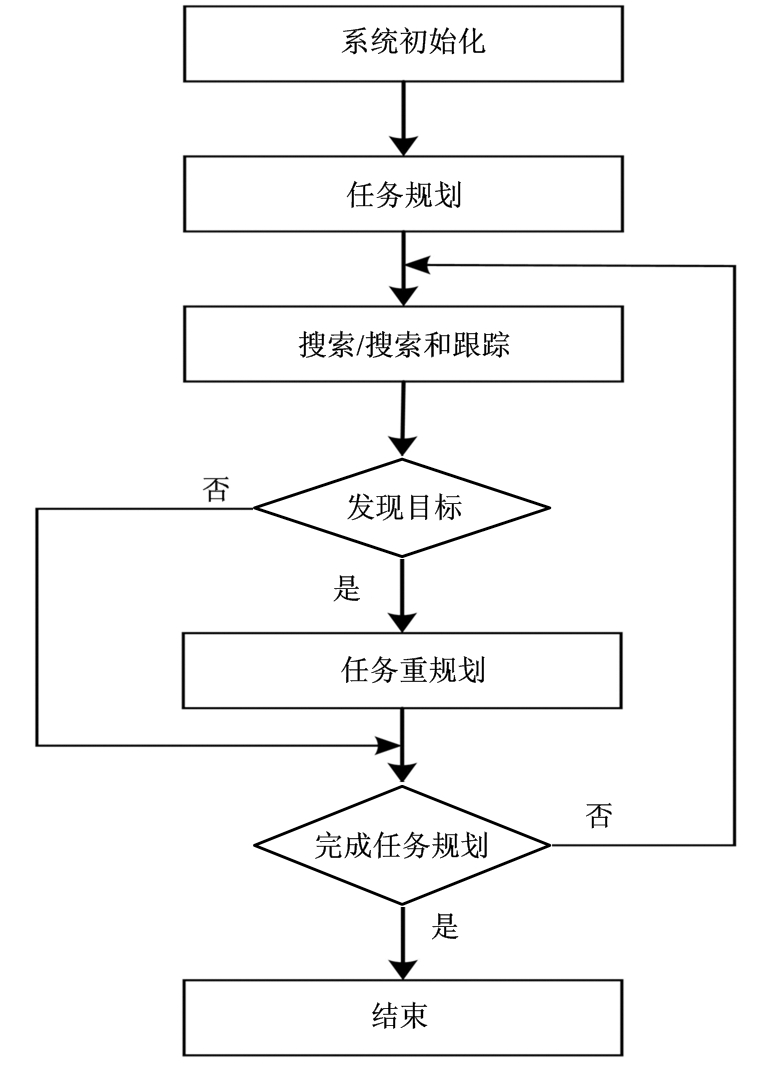
图5 协同搜索跟踪规划流程图
2 协同搜索跟踪任务规划模型
真实的战场环境普遍具有动态和不确定的特征[4],时刻变化的网格区域威胁值函数和发现的威胁目标导致构建的任务规划优化问题模型的目标函数和约束时变且数量变化。然而,CSP、DMOPs、DCMOPs和目标函数可变的动态多目标优化问题等模型不适用于目标函数和约束时变且数量变化的复杂场景。对此,本节构建了DMCMOPs模型,可以有效应对动态战场环境任务规划所面临的目标函数与约束时变且数量变化的难题。下文将详细阐述构成该优化问题模型的决策变量、目标函数和约束。
2.1 任务规划问题的决策变量
决策变量是优化问题中与目标函数和约束有关的变量。在无人机集群协同搜索跟踪任务规划问题中,决策变量决定了无人机编队执行哪些任务和执行任务的顺序,而决策变量的变化影响了任务规划方案的优劣。本文提取的两个决策变量如下所示:
1) 任务分配变量:以两架无人机组成的搜索无人机编队作为基本单位,此变量表示为N*M维的二进制矩阵。当且仅当分配向量assign[m,n]=1时,任务m被分配给了无人机编队n。
2) 任务执行顺序变量:定义了每个无人机编队执行所分配任务的顺序。如果集合{Tm1,Tm2,Tm3,Tm4}是分配给编队n执行的任务,则定义Γn={Tm1,Tm3,Tm4,Tm2}表示编队n执行任务集合{Tm1,Tm2,Tm3,Tm4}的顺序。
2.2 规划问题的目标函数
最优规划方案通过同时优化一组相互冲突的目标函数构成的帕累托最优解驱动。复杂优化问题的目标函数不是唯一的,根据无人机集群协同搜索任务规划问题设置3个评价任务规划方案优劣的目标函数。
1) 战场所有网格区域在任务规划执行期间的最小威胁值定义为
TH= min![]() Stdt
Stdt
(4)
式中,t1和t2分别为执行任务规划起始时刻和结束时刻。
2) 最短飞行时间 规划执行结束的无人机最短飞行时间:
min t2
(5)
3) 最短建立跟踪时间 从发现目标到对该目标建立跟踪的最短时间:
(6)
2.3 规划问题的约束
约束是从现实问题提取的必须满足的条件,同时也决定了任务规划方案是否可行。根据实际问题,本文提取了4个战场和无人机约束条件。
1) 避免碰撞约束 考虑无人机编队之间的安全距离以避免编队之间相互碰撞,编队内的无人机相互之间可视为始终保持安全距离:
dij(t)>dmin i,j=1,…,M;i≠j
(7)
2) 威胁值约束 常数ss,max表示所能接受的网格区域威胁值上限要求:
s(m,t)≤sm,max,m∈M
(8)
3) 飞行时间约束 无人机满足执行完任务安全返回的飞行时间限制:
(9)
其中,![]() 表示无人机最大飞行时间。
表示无人机最大飞行时间。
4) 已发现的目标威胁值约束 常数starget,max表示所能容忍的已发现的目标的威胁值上限。目标在t时刻的威胁值s(k,t)应小于常数starget,max,公式表示如下:
s(k,t)≤starget,max, m∈M
(10)
2.4 搜索跟踪动态任务规划问题数学表征
根据1节和2节所述,在发现目标前,无人机集群需要对战场网格区域进行战场覆盖式搜索,此时建立的优化问题数学表征:
TH=min![]() Stdt
Stdt
min t2
s.t. dij(t)>dmin i,j=1,…,M;i≠j
sm,t≤sm,max, m∈M
(11)
一旦无人机集群搜索编队发现目标,则无人机集群的任务性质发生变化,即从纯粹的战场覆盖式搜索转为在战场覆盖式搜索和对已发现目标进行精确跟踪。无人机集群任务性质的转变导致优化问题数学表征动态调整。无人机集群协同搜索跟踪任务规划的优化问题数学表征为
TH=min![]() Stdt
Stdt
min t2
s.t. dij(t)>dmin i,j=1,…,M;i≠j
sm,t≤sm,max,m∈M
starget,t≤starget,max,m∈M
(12)
相较于单纯的搜索任务规划优化问题数学表征式(11),优化问题数学表征式(12)增加了目标函数公式(6)与约束函数式(10)。其中目标函数式(6)目的在于促使无人机集群尽快对已发现的目标建立跟踪,约束式(10)可以将已发现目标的威胁值限定在安全范围内。由公式(11)到公式(12)的变化本质是DMCMOPs,如下式所示:
minF(x,t)=(f1(x,t),…,fm(x,t),…,fM(t)(x,t))T
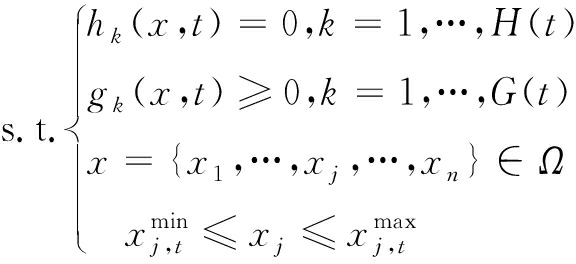
(13)
式中hk(x,t)和gk(x,t)分别为等式约束和不等式约束,M(t)表示目标函数的数量,H(t)和G(t)表示等式约束和不等式约束的数量。
相比CSP、DMOPs、DCMOPs和目标函数可变的动态多目标优化问题模型,公式(13)构建的DMCMOPs模型目标函数和约束发生时变且数量变化。然而,现有算法解决DMCMOP时存在难以应对该模型的复杂动态变化的难题,对此,下一节将提出一种针对目标函数和约束发生时变且数量变化的优化问题的动态优化算法。
3 动态约束双档案进化算法
DMCMOPs模型的目标函数和约束具有时变且数量变化的动态特征,针对目标函数的动态变化,文献[26]提出了DTAEA,然而该方法很难同时应对目标函数和约束的动态变化。目标函数和约束同时发生动态变化时,不仅会导致目标函数域维度和种群收敛性、多样性的变化,还会使大量种群个体落入不可行区域,导致可行个体数量不足,影响种群收敛。本节针对DMCMOPs模型求解难题,提出了一种基于动态自适应惩罚机制的动态双档案进化算法(DCTAEA),该算法核心部分在于维护两个相互协作档案[26,30],即CA和DA,CA起主要作用,在CA更新过程中,当可行性个体不足时,通过引入的动态自适应惩罚机制[25,31]整合不可行个体的目标函数值和违反约束的惩罚值获得修正目标函数值,根据可行个体所占比率动态调整不可行解的约束违反值和目标函数值在修正的目标函数值中所占比重,使得有价值不可行个体获得竞争机会,促使种群进入可行区域并向帕累托前沿面收敛;DA增强种群多样性,更新过程中探索CA未开发区域。算法流程图如图6所示,当环境发生变化时,CA和DA重新构建种群,改变目标域的维度,使得种群更快地适应新环境。环境未发生改变时,直接产生CA和DA子代种群,CA和DA在每次迭代过程中更新各自种群。重复上述过程直到种群收敛获得最优解。
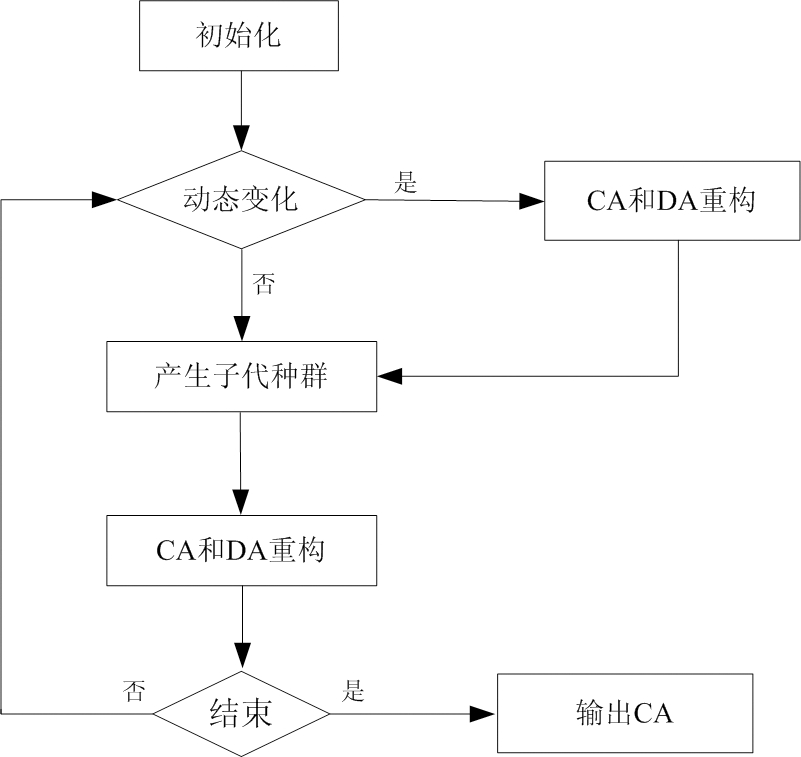
图6 DCTAEA流程图
在公式(13)所示的优化问题模型中,目标函数发生动态变化,导致目标函数域的维度改变,采用文献[26,32]的方法重构种群,改变目标域维度,加快适应新环境。重构的CA和DA产生子代种群后通过迭代更新使种群收敛, CA和DA的侧重点不同。因此本节将分别阐述CA和DA的更新方法。
3.1 CA的更新方法
DTAEA很难应对DMCMOPs模型的约束发生动态变化导致的大量种群个体落入不可行区域的问题。可行个体数量的不足影响了种群的进化,本小节在DTAEA的CA更新方法中引入动态自适应惩罚机制,整合不可行个体的目标函数值和违反约束的惩罚值获得修正的目标函数值,并作为不可行个体的选择依据,充分利用有价值的不可行个体,促使种群进入可行区域并向帕累托前沿面收敛。
CA和子代种群Q的个体数量都为N,结合形成个体数量为2*N的种群HC。由于DMCMOPs模型约束的动态变化,导致部分动态变化前的可行解变为不可行解,CA种群部分个体进入不可行区域,HC中可行个体的集合记为种群SC,此时SC数量往往小于N,可行个体数量的不足严重影响CA的收敛。针对约束动态变化导致可行个体数量的不足影响种群收敛的问题,本小节在CA的更新中引入动态自适应惩罚机制,通过自适应整合归一化目标函数和归一化约束违反值获得不可行解的修正目标函数[25,31]。动态自适应惩罚机制取决于解的价值(即该解的目标函数值和约束违反值的大小)和种群中可行性解的比率。种群中可行性解的比率较低时,不可行解的约束违反值所占权重较大,约束违反值对不可行解的选择起较大作用。种群中可行性解的比率较高时,则目标函数值对不可行解的选择起较大作用。在DMCMOPs发生动态变化时,自适应惩罚机制为具有小目标函数值和小约束违反值的有价值解提供较大参与进化竞争的可能性,进而充分利用可行解和有价值的不可行解共同探索最优解。
不可行解的第i维度归一化修正目标函数值如下式所示:
(14)
其中,第i维目标函数的自适应惩罚值为
(15)
pi(x,t)与x的归一化目标函数值和归一化约束违反值以及种群的可行性个体所占比率动态相关。其中,rf是种群HC中的可行个体的所占比率,![]() 是解x的归一化约束违反值,公式表示如下:
是解x的归一化约束违反值,公式表示如下:
(16)
式中,Gk(x,t)和Hk(x,t)分别为不等式约束和等式约束的约束违反值。
为了挑选有价值的不可行解,需要建立优化问题作为选择标准。依据不可行个体的归一化约束违反值和切比雪夫分解函数值[30]建立二维目标优化问题如下式:
(17)
式中,
gtch-penalty(x(t)|wi(t),z*(t))=
(18)
其中,![]() 和
和![]() 如下文公式(19)和公式(23)~(27)所示。
如下文公式(19)和公式(23)~(27)所示。
依据文献[25]中Pareto支配关系定义,使用快速非支配排序算法[12]把不可行个体划分为若干等级,按照等级由高到低的顺序把该等级个体全部划入CA,直至CA个体数量第一次大于或等于N。若CA个体数量大于N,则把最后放入CA的等级的个体按照归一化约束违反值![]() 排序,
排序,![]() 大的舍弃,直至CA个体数量等于N。若CA个体等于N则无需操作。
大的舍弃,直至CA个体数量等于N。若CA个体等于N则无需操作。
优化问题的目标函数和约束发生动态变化后,随着CA的更新次数增加,HC中可行个体数量也随之增加,可行个体数量不再小于N。如果CA更新时SC中个体数量等于N则CA更新完毕,如果SC中个体数量大于N,参照文献[25,30],执行以下操作。
根据文献[26,33]生成一组均匀分布的权重向量W(t),如下式所示:
W(t)={w1(t),…,wN(t)(t)}
(19)
权重向量W(t)将目标空间划分为N(t)个子空间。图7表示二维目标函数空间的子空间划分和CA个体的分布示意图。图中CA (图7黄色个体)和子代种群Q (图7红色个体) 组成种群HC,在可行空区域的个体集合组成种群SC。每个子空间由唯一的权重向量代表,子空间Δi(t),i∈{1,…,N(t)}如下式所示:
Δi(t)={F(x,t)∈Rm(t)|〈F(x,t),wi〉≤〈F(x,t),wj〉}
(20)
式中,j∈{1,…,N(t)},〈F(x,t),w(t)〉表示F(x,t)与w和原点之间连线的垂直距离。
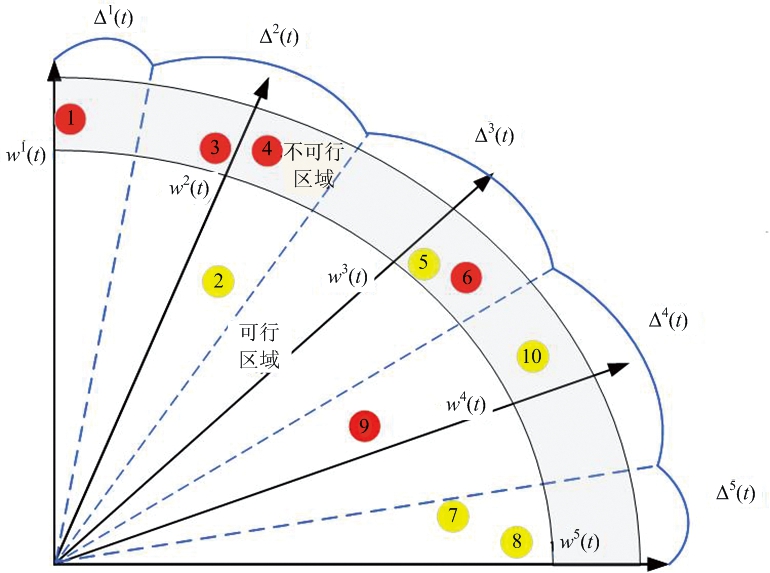
图7 二维目标函数空间的子空间划分和CA个体的分布示意图
CA和子代的所有个体按照子空间分区,个体x与唯一的子区域相关联,其所在的子区域为
(21)
式中,![]() 是F(x,t)的归一化值。
是F(x,t)的归一化值。
F(x,t)=(f1(x,t),…,fm(t)(x,t))T
(22)
并且,
(23)
式中,z*(t)为目标域各维度估计的最小值[26],表示如下:
(24)
式中,
(25)
znad(t)为目标域各维度的最大值,表示如下:
(26)
式中,
(27)
计算每个子空间的个体密度。根据公式(19)~(21) 计算出子空间存在的可行个体数量,得到个体密度最大的子空间Δi。个体之间的相互距离越近,拥挤度越大,种群的多样性也越差。为了提高种群多样性,需要从密度最高子空间中选出相互距离最近的个体集合。计算子空间Δi里个体之间的相互距离:
(28)
相互距离最小的个体存入St中,下一步根据切比雪夫分解方法计算最劣个体并舍弃直至种群SC个体数量等于N。最劣个体表示如下:
(29)
其中,
gtch(x(t)|wi(t),z*(t))=
(30)
优化问题的目标函数和约束发生动态变化后,可行解的数量不足,影响种群收敛。引入动态自适应惩罚机制,充分利用了有价值的具有合适目标函数值和低约束违反值的解,促进不可行解向可行区域移动,加速CA种群收敛。
3.2 DA的更新方法
DA作为CA的辅助角色,不考虑约束导致的个体是否可行。DA 的作用是探索 CA 尚未开发空间,提高了可行区域内 CA 的种群多样性,并且有助于跳过局部最优或局部不可行区域。本小节参照文献[26,30], 给出DA的更新步骤。
同CA的更新机制类似,首先将DA与子代种群Q结合组成种群Hd,然后依次探索每个子空间,找到最优个体。最优个体定义为:将更新的CA作为参考集,在第 ith(1≤ith≤N)次迭代中,如果子空间Δi已经存在ith个及以上的CA个体或 Hd 中没有与当前正在研究的子空间相关的解,则在此迭代期间不再探索该子空间并直接移动到下一个子空间。否则,将选择与当前探索的子空间相关的 Hd 中的最佳非支配解,将其视为在新形成的 DA 中的一员。其中,当前子空间的最佳解xb定义为
(31)
图8表示DA更新过程中的目标域空间CA和DA的父代子代个体分布。其中黄色和红色个体分别为DA种群的父代和子代,黑色方块代表CA种群的个体。在第一次迭代期间,空间Δ1到Δ3和Δ5都存在CA个体,所以直接跳过,对空间Δ4,依据公式(23),选择个体7作为最优解划入CA。在第二次迭代期间,空间Δ2存在CA的两个个体,所以依然跳过该空间,其余空间分别选择个体3,5,10,8作为最优个体划入DA。此时DA数量种群达到要求,DA更新完毕。
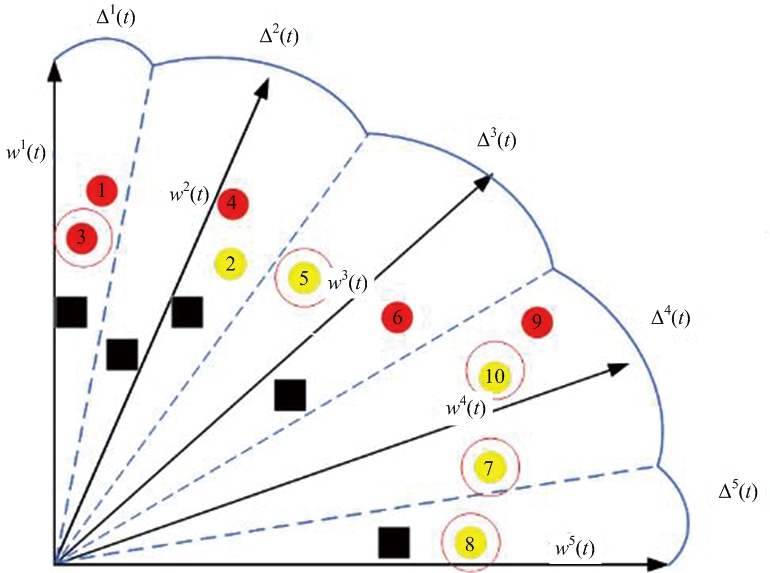
图8 二维目标函数空间的子空间划分和CA及DA个体的分布示意图
以上是本文所提DCTAEA,本文算法针对目标函数和约束的动态变化,通过重建CA和DA种群,增加种群多样性,快速适应新的环境。在CA的更新过程中引入动态自适应惩罚机制,整合不可行个体的目标函数值和违反约束的惩罚者获得修正的目标函数值,充分利用有价值的不可行个体,促使不可行个体向可行区域移动,有利于加快CA收敛,解决了动态约束导致的种群可行个体不足导致的种群难以收敛问题。DA在更新时辅助增强多样性,探索CA未开发的空间,有助于获得最优解。
4 实验设置与结果分析
本文所提算法在解决目标函数和约束时变且数量变化的优化问题能更快适应动态变化,加快种群收敛,获得Pareto前沿面。在发生目标函数和约束的动态变化时,通过CA和DA种群重建增强多样性。在CA的更新过程中,引入动态自适应惩罚机制,整合不可行个体的目标函数值和违反约束的惩罚者获得修正的目标函数值,充分利用有价值的不可行个体,促使不可行个体向可行区域移动,有利于加快种群收敛,求得最优解。本文通过比较所提算法与4种对比算法求解基准测试问题的结果对比证明了所提算法的有效性和优越性。本节将介绍基准测试问题、性能指标以及仿真结果对比分析。
4.1 基准测试问题
为了测试所提算法的有效性和优越性,选取了类型Ⅱ约束测试问题C2-DTLZ2[30]的约束和F2型[26]动态多目标函数测试问题结合组成的基准测试问题DC2-F2,该测试问题同实际问题相似。其中,类型Ⅱ约束表示如下:
c2(x,t)=![]()
r(t)2]}
(32)
F2目标函数表示如下:
![]()
(sin(xm(t)-j+1π/2))fm(t)=(1+g)sin(x1π/2)
(33)
式中,m(t)表示约束和目标函数在时刻t的数量。
4.2 性能指标
在本小节中,介绍了反向世代距离(IGD),和平均反向世代距离(MIGD),可以同时衡量算法所得的Pareto最优解集的收敛性和多样性。
反向世代距离:![]() 是均匀分布在帕累托前沿面上的点集,St是算法得到的近似与帕累托前沿面的解集[31]。
是均匀分布在帕累托前沿面上的点集,St是算法得到的近似与帕累托前沿面的解集[31]。
(34)
由公式(34)可知,所得Pareto最优前沿的IGD值越小,该解集越靠近真实前沿、分布越均匀。
4.3 仿真结果分析
为了验证本文提出的DCTAEA针对DMCMOPs的有效性和优越性,将DCTAEA与以下4种优化算法进行对比:
1) NSGA-II[13]:第二代非支配排序遗传算法;
2) MOEA/D[33]:一种基于分解的多目标进化算法;
3) CTAEA[30]:用于约束多目标优化的双档案进化算法;
4) D-TAEA[26]:动态双档案进化算法。
考虑DMCMOPs面临的主要问题为目标函数和约束的时变和数量变化问题,而时变性已在公式(32)~(33)体现,只需设置目标函数和约束数量m(t)的变化:
(35)
上式表示优化问题以t=1时刻为初始,种群经过300次的迭代进化后,依次经历4次动态变化。动态变化的频率由参数τt决定,τt=25表示种群每进化25代,环境发生一次动态变化。设置种群的个体数量为300,每个算法独立运行31次,求得反向时代距离的平均值,获得种群在整个动态变化过程中的IGD轨迹。
本文提出的DCTAEA及其4种对比算法在τt=25时求解DMCMOPs获得IGD轨迹如图9所示。从图中可以看出,本文所提算法DCTAEA 在大部分时间都显示出最佳性能,能在每次动态变化后经过种群进化获得最小的IGD值,并且其IGD动态变化轨迹最平缓,在每次种群进化过程中IGD保持持续变小趋势,不会发生剧烈变化。所提算法通过动态自适应惩罚机制可以更好地同时应对目标函数和约束时变及数量的变化,因此相比仅针对目标函数动态变化的D-TAEA显示出较大优势。同时,由于CTAEA不能随着变化对CA和DA重构,所以其应对优化问题目标函数和约束的时变及数量动态变化反应较慢。而NSGA-II和MOEA/D作为普通优化问题求解算法,没有动态应对机制,求解DMCMOPs效果较差。这意味着本文所提算法能有效应对动态优化问题的目标函数和约束时变且数量变化带来的影响,特别是引入的动态自适应惩罚机制使得算法增强了应对约束的动态变化的能力,在求解DMCMOPs时能快速收敛,求得的帕累托前沿面更加靠近真实的帕累托前沿面。此外,注意到在第一次动态变化发生后,DCTAEA 的优势并不明显,这是因为此时目标函数数量较少,其他算法也具有较快收敛速度。然而,随着目标函数的增多,DCTAEA优势逐渐显现。
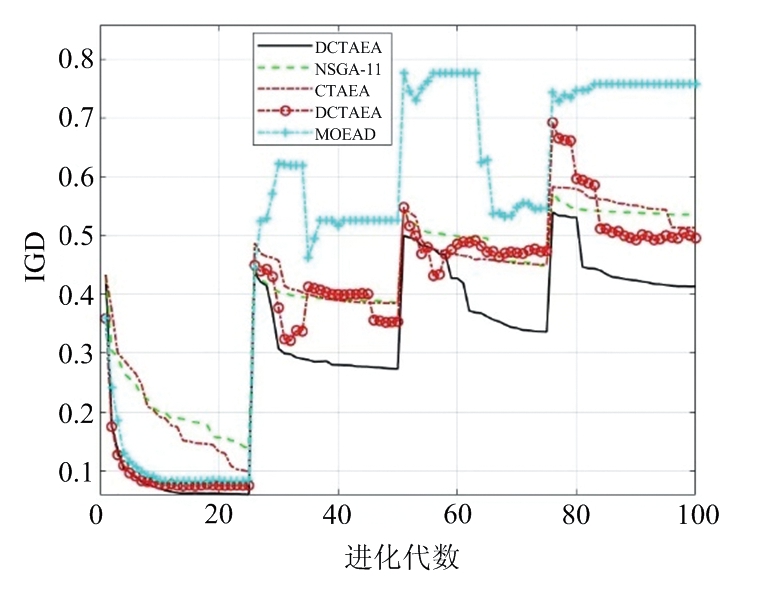
图9 τt=25时整个进化过程IGD的轨迹
图10和图11也显示了所提算法相对其他算法的有效性和优越性。然而,可以发现D-TAEA经过一定的进化步数能达到和所提算法相同的IGD指标值,DCTAEA不再获得全程优势。这是因为随着τt增大,即优化问题发生动态变化的间隔增大,算法有更加充足的时间应对变化。但是本文所提算法依然具有收敛速度最快的优势,从而能更好地应对DMCMOPs。
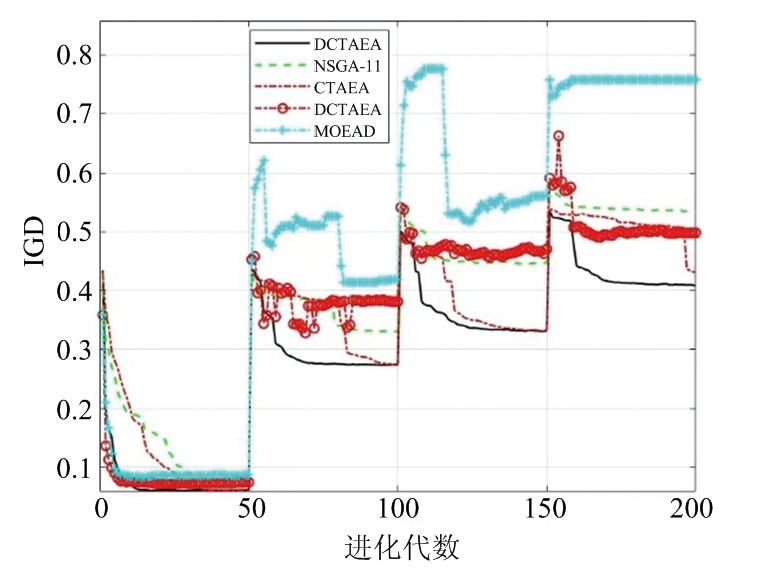
图10 τt=50时整个进化过程IGD的轨迹

图11 τt=100时整个进化过程IGD的轨迹
5 结束语
为了提高无人机集群在复杂动态环境下的执行协同搜索跟踪任务的效率,克服传统优化问题模型面对目标函数和约束存在复杂动态变化不适用的难题,本文构建了目标函数和约束时变且数量变化的动态优化问题模型。为了求解该问题,提出了基于动态自适应惩罚机制的动态约束双档案进化算法所提算法可以随着环境变化自适应重建种群,加快种群适应新的环境,引入自适应惩罚函数机制,整合不可行个体的目标函数值和违反约束的惩罚值获得修正的目标函数值,动态调整不可行解的约束违反值和目标函数的比重,实现有价值不可行解的利用,促使种群进入可行区域并向帕累托前沿面收敛。仿真结果表明,与第二代非支配排序遗传算法的动态版本、基于分解的多目标进化算法、约束双档案进化算法和动态双档案进化算法相比,本文所提算法具有优越性,能使种群在新的环境下更快收敛。
[1] 王超,于德洋,王子强,等.复杂任务环境下多无人机多任务规划技术研究[J].电子技术与软件工程,2021(22):106-109.
[2] WANG N, LI Z, LIANG X, et al. Cooperative Target Search of UAV Swarm with Communication Distance Constraint[J]. Mathematical Problems in Engineering, 2021, 2021:3794329.
[3] 王宇晨,齐文慧,徐立臻.基于区块链的无人机集群安全协作[J].计算机科学,2021,48(S2):528-532.
[4] LIU Z, LIU Y K. Agent-Based Simulation of Multi-UAV Search-Track for Dynamic Targets in Sweep Coverage[J]. Journal of Physics: Conference Series, IOP Publishing, 2021, 1746(1):012033.
[5] 陈浩. 复杂条件下固定翼无人机集群编队控制研究[D].长沙:国防科技大学,2020.
[6] YAO W R , QI N M , WAN N , et al. An Iterative Strategy for Task Assignment and Path Planning of Distributed Multiple Unmanned Aerial Vehicles[J]. Aerospace Science and Technology,2019,86:455-464.
[7] ZHEN Z Y, CHEN Y, WEN L D, et al. An Intelligent Cooperative Mission Planning Scheme of UAV Swarm in Uncertain Dynamic Environment[J]. Aerospace Science and Technology, 2020, 100:105826.
[8] GAO C, ZHEN Z Y, GONG H J. A Self-Organized Search and Attack Algorithm for Multiple Unmanned Aerial Vehicles[J]. Aerospace Science and Technology, 2016, 54:229-240.
[9] ZHEN Z Y, XING D J, Gao C . Cooperative Search-Attack Mission Planning for Multi-UAV Based on Intelligent Self-Organized Algorithm[J]. Aerospace Science & Technology, 2018, 76:402-411.
[10] ART K R, SALIDO M A . Constraint Satisfaction for Planning and Scheduling Problems[J]. Constraints, 2011, 16(3):223-227.
K R, SALIDO M A . Constraint Satisfaction for Planning and Scheduling Problems[J]. Constraints, 2011, 16(3):223-227.
[11] CRISTIAN R A, JAVIER D S, DAVID C. Weighted Strategies to Guide a Multi-Objective Evolutionary Algorithm for Multi-UAV Mission Planning[J].Swarm & Evolutionary Computation,2019,44:480-495.
[12] RAMIREZ-ATENCIA C, BELLO-ORGAZ G, R-MORENO M D, et al. Solving Complex Multi-UAV Mission Planning Problems Using Multi-Objective Genetic Algorithms[J]. Soft Computing, 2017, 21(17):4883-4900.
[13] DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2):182-197.
[14] DEB K, RAO N U B, KARTHIK S. Dynamic Multi-Objective Optimization and Decision-Making Using Modified NSGA-II: A Case Study on Hydrothermal Power Scheduling[C]∥International Conference on Evolutionary Multi-Criterion Optimization, Springer, Berlin, Heidelberg:IEEE,2007:803-817.
[15] JIANG M, WANG Z Z, QIU L M, et al. A Fast Dynamic Evolutionary Multiobjective Algorithm via Manifold Transfer Learning[J]. IEEE Trans on Cybernetics, 2021, 51(7):3417-3428.
[16] WANG F, LIAO F S, LI Y X, et al. A New Prediction Strategy for Dynamic Multi-Objective Optimization Using Gaussian Mixture Model[J]. Information Sciences, 2021, 580:331-351.
[17] LIU R C, YANG P, LIU J D. A Dynamic Multi-Objective Optimization Evolutionary Algorithm for Complex Environmental Changes[J]. Knowledge-Based Systems, 2021, 216:106612.
[18] RONG M, GONG D W, ZHANG Y, et al. Multidirectional Prediction Approach for Dynamic Multiobjective Optimization Problems[J]. IEEE Trans on Cybernetics, 2019, 49(9):3362-3374.
[19] WANG C F, YEN G G, ZOU F. A Novel Predictive Method Based on Key Points for Dynamic Multi-Objective Optimization[J]. Expert Systems with Applications, 2022, 190:116127.
[20] AZZOUZ R, BECHIKH S, BEN SAID L. A Multiple Reference Point-Based Evolutionary Algorithm for Dynamic Multi-Objective Optimization with Undetectable Changes[C]∥2014 IEEE Congress on Evolutionary Computation (CEC),Beijing,China:IEEE,2014:3168-3175.
[21] LI K, KWONG S, CAO J J, et al. Achieving Balance Between Proximity and Diversity in Multi-Objective Evolutionary Algorithm[J]. Information Sciences,2012,182(1):220-242.
[22] PENG Z, ZHENG J,ZOU J. A Population Diversity Maintaining Strategy Based on Dynamic Environment Evolutionary Model for Dynamic Multiobjective Optimization [C]∥2014 IEEE Congress on Evolutionary Computation(CEC),[S.l.]:IEEE,2014:274-281.
[23] LIANG Z P, ZOU Y, ZHENG S X, et al. A Feedback-Based Prediction Strategy for Dynamic Multi-Objective Evolutionary Optimization[J].Expert Systems with Applications, 2021,172:114594.
[24] WANG Y, LI B. Investigation of Memory-Based Multi-Objective Optimization Evolutionary Algorithm in Dynamic Environment[C]∥2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway:IEEE,2009:630-637.
[25] AZZOUZ R, BECHIKH S, SAID L B, et al. Handling Time-Varying Constraints and Objectives in Dynamic Evolutionary Multi-Objective Optimization[J]. Swarm and Evolutionary Computation, 2018, 39:222-248.
[26] CHEN R Z, LI K, YAO X. Dynamic Multi-Objectives Optimization with a Changing Number of Objectives[J]. IEEE Trans on Evolutionary Computation,2017,22(1):157-171.
[27] 林晓烘, 程志锋, 于莹, 等. 海上多无人机协同交叉定位的优化配置方法 [J]. 火力与指挥控制, 2021, 46(12):9-14
[28] YANG Y, ZHENG J B, LIU H W, et al. Optimal Sensor Placement for Source Tracking Under Synchronization Offsets and Sensor Location Errors with Distance-Dependent Noises[J]. Signal Processing, 2022, 193:108399.
[29] OH G, KIM Y, AHN J, et al. Market-Based Task Assignment for Cooperative Timing Missions in Dynamic Environments[J]. Journal of Intelligent & Robotic Systems, 2017, 87(1):97-123.
[30] LI K, CHEN R Z, FU G T, et al. Two-Archive Evolutionary Algorithm for Constrained Multi-Objective Optimization[J]. IEEE Trans on Evolutionary Computation, 2019, 23(2):303-315.
[31] CHEN Q D, DING J L, YANG S X, et al. A Novel Evolutionary Algorithm for Dynamic Constrained Multi-Objective Optimization Problems[J]. IEEE Trans on Evolutionary Computation, 2020, 24(4):792-806.
[32] MCKAY M D, BECKMAN R J, CONOVER W J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code[J]. Technometrics, 2000, 42(1):55-61.
[33] ZHANG Q F, LI H. MOEA/D: A Multi-Objective Evolutionary Algorithm Based on Decomposition[J]. IEEE Trans on Evolutionary Computation,2007,11(6):712-731.




