0 引言
近年来,自动驾驶、智慧交通、区域监控以及安防等领域的需求飙升,这些领域的相关应用场景要求传感器能够探测环境中目标的空间三维信息[1-4]。相比于其他感知环境的传感器如相机、激光雷达来说,商业的毫米波雷达有着独特的优势。不仅因其大小适合安装在汽车的各个位置,能很好地适应汽车和工业领域对雷达设备体积的要求,而且探测距离远,对各种恶劣天气环境的鲁棒性强,在复杂工作环境下能正常运行。而毫米波FMCW MIMO雷达高分辨的3D点云成像技术将有助于提高上述应用中目标检测、分类、预警等功能的效率与准确性。
现有毫米波FMCW MIMO雷达3D点云成像方法包括三维快速傅里叶变换(3D FFT)[5-6]、快速傅里叶变换-二维多重信号分类(FFT-2D MUSIC)[7] 和三维多重信号分类(3D MUSIC)[8]等算法。其中,3D FFT是一种基于快速傅里叶变换算法的三维参数估计方法。FFT-2D MUSIC方法利用FFT估计距离、2D MUSIC估计方位角和俯仰角,与3D FFT相比,提高了空间角分辨能力。3D MUSIC算法在此基础上将2D MUSIC扩展到3D MUSIC,提出一种距离-多普勒-方位角联合估计方法,它通过三维张量构造新的信号模型,并利用前向后向空间平滑技术对数据进行叠加和平滑,获得了三维参数的高分辨。但是,汽车和工业毫米波雷达系统往往方位角的视场(FOV)很大,距离分辨率高,导致划分的方位角网格数和距离单元数多。诸如上述结合MUSIC的点云成像方法,既需要已知源数量和大量的快照,又要对协方差矩阵的奇异值求解,以及联合估计的多层循环搜索,都极大增加了算法复杂度,算法运行的时间往往成倍增加。为了满足实时性的要求,TI公司[9]提出了一种 FFT测距加Capon测角的三维点云成像方法,一方面利用Capon测角没有特征值分解带来的复杂运算,另一方面通过加入CFAR检测算法,检测存在目标的单元,来避免多维循环搜索,这种信号处理框架大大降低了方法运行的时间。
尽管如此,Capon算法的角分辨不足,因而为了改善到达角(DOA)估计的性能,文献[10]提出一种基于渐近最小方差的稀疏迭代方法(SAMV)。该方法在1D角度上划分网格,利用采样数据协方差矩阵与真实协方差矩阵的差异,根据AMV准则,推导出网格功率的迭代公式,从而得到更好的角度谱,有着比Capon和MUSIC更佳的分辨能力。本文在SAMV的基础上,将其扩展至2D,提出一种适用于毫米波FMCW MIMO雷达的三维点云成像方法。首先对差拍信号做FFT,得到1D距离像;然后在每个距离单元的水平方向上划分方位角网格,构造过完备的方向矢量矩阵,从AMV准则的角度出发,得出网格功率的迭代求解公式,由此得到距离-方位角热图;接着对热图的两个维度分别做1D CASO-CFAR,得到目标的距离和方位角单元;最后根据检测出来的单元位置信息,在俯仰角上划分网格,采用SAMV算法估计网格的信号功率,经过检测得到俯仰角。相较于现有方法,该方法在天线数量受限和有限快拍的情况下,能明显提高方位角和俯仰角上的分辨率。
1 信号模型
FMCW MIMO雷达系统模型如图1所示,有3个发射阵元TX1~TX3和4个接收阵元RX1~RX4,其中TX1和TX2的间距为2λ(λ为雷达信号的波长),TX3与TX1和TX2的间距均为λ,并向z轴正方向平移λ/2;RX1到RX4的阵元间距为λ/2。为了方便后续的建模,按照文献[11],将图1的MIMO阵列结构等效为图2的12个虚拟阵元收发共置来进行处理,对应的坐标位置矩阵r=[r11,…,rij,…,r34]∈R12×3,其中r=rTX⊗14+13⊗rRX,rTX∈R3×3和rRX∈R4×3分别是发射阵元与接收阵元的3D坐标矩阵。

图1 MIMO阵列模型

图2 等效虚拟阵列模型
MIMO阵列采用时分发射模式。以TXi为例,假设在一个调频周期内发射的信号为
si(t)=exp[j(2πfct+πβt2)],0≤t≤Tc
(1)
式中,t为信号时间,Tc为每个Chirp的调频周期,β为调频斜率,fc为中心频率。根据图2,RXj接收的回波信号可以表示为
(2)
式中,α为目标的反射系数,τij为发射天线TXi到接收天线RXj的信号传播时延,包括距离和角度时延,即
(3)
式中,R为目标和原点的径向距离,k=[sinθcosφ,cosθcosφ,sinφ]为目标的单位方向矢量。k中的θ和φ为目标的方位角和俯仰角,取值范围为方位角和俯仰角的有效视场角θFOV和φFOV内,即θ∈(-θFOV/2,θFOV/2),φ∈(-φFOV/2,φFOV/2)。
将回波信号与发射信号进行混频,得到差拍信号为
yij(t)=![]()
exp[j2π(βτijat+fcτija+βτijaτija+
(4)
式中,平方项和二次项相对于其他项可以忽略,又因β的值太小,exp[j2π(βτijat)]项也可以忽略,由此改写为
yij(t)=αexp[j2πfc(kT·rij)/c]×
exp[j2π(2βRt/c+2fcR/c)]+
ω(t)
(5)
对yij(t)进行采样得到离散采样序列:
yij(n)=![]()
ω(n)
(6)
式中,fs为采样速率,n=1,2,…,N为采样点数。若将式(6)推广到Q个目标,设目标距离分别为R1,R2,…,RQ,所在的方位角和俯仰角分别为(θ1,φ1),(θ2,φ2),…,(θQ,φQ),则式(6)的信号模型可以进一步写为
yij(n)=![]()
ω(n)
(7)
在一帧的时间内,假设每一个发射阵元均发射M个Chirp,因此有![]() 其中
其中![]() 由式(7)可得
由式(7)可得
![]()
![]()
ωm(n)
(8)
2 算法描述
为了从式(8)得到3D高分辨点云像,需经过一维距离像估计、距离-方位角热图生成、CFAR目标检测和俯仰角估计等一系列的信号处理,具体流程如图3所示。

图3 三维点云成像方法流程框图
2.1 一维距离像估计
如图2所示,就第TiRj个虚拟阵元,先对第
m个Chirp内的N个采样点![]() 作加窗处理,降低旁瓣,并对N个采样点进行点数为K的FFT,即
作加窗处理,降低旁瓣,并对N个采样点进行点数为K的FFT,即
![]()
![]()
k=1,2,…,K
(9)
2.2 距离-方位角热图生成
从式(9)可以看出,若由FFT点数决定的距离单元大小和雷达的距离分辨率一致,则k对应的距离![]() 此时的sinc函数值为1。则式(9)变为
此时的sinc函数值为1。则式(9)变为
(10)
式中,![]() 为目标对应第m个Chirp第k个距离单元上角度为(θq,φq)的散射系数。将所有发射阵元和接收阵元组合的M个Chirp回波数据按照如下形式堆叠和排列,得到
为目标对应第m个Chirp第k个距离单元上角度为(θq,φq)的散射系数。将所有发射阵元和接收阵元组合的M个Chirp回波数据按照如下形式堆叠和排列,得到

令
 则式(10)变为
则式(10)变为
![]()
(11)
式中,![]() 为在距离单元k上的接收信号矩阵,
为在距离单元k上的接收信号矩阵,![]() 为信号的方向矢量矩阵,
为信号的方向矢量矩阵,![]() 为目标在距离单元k上的散射系数矩阵,ω(k)为噪声矩阵。
为目标在距离单元k上的散射系数矩阵,ω(k)为噪声矩阵。
将θFOV和φFOV划分为Qθ,Qφ个网格,2D的网格数为![]() 方位角上网格扫描的顺序为θqθ从-θFOV/2→θFOV/2, 在每一个方位角网格θqθ上进行俯仰角φqφ的扫描,扫描顺序为φqφ从-φFOV/2→φFOV/2,则
方位角上网格扫描的顺序为θqθ从-θFOV/2→θFOV/2, 在每一个方位角网格θqθ上进行俯仰角φqφ的扫描,扫描顺序为φqφ从-φFOV/2→φFOV/2,则
![]()
![]()
qθ=1,…,Qθ,qφ=1,…,Qφ
(12)
将式(11)中的(θq,φq)用![]() 代替,则式(11)可进一步改写为
代替,则式(11)可进一步改写为
Y(k)=Aρ(k)+ω(k)
(13)
式中,![]() 为所有网格的方向矢量矩阵,
为所有网格的方向矢量矩阵,![]() 为对应M个Chirp在第k距离单元上所有网格的散射系数矩阵,Y(k)∈C12×M为在距离单元k处的接收信号矩阵,ω(k)为噪声矩阵。
为对应M个Chirp在第k距离单元上所有网格的散射系数矩阵,Y(k)∈C12×M为在距离单元k处的接收信号矩阵,ω(k)为噪声矩阵。
上述式(13)为用2D SAMV联合方位角和俯仰角估计时的信号模型,将其用于方位角网格功率估计时,需令φqφ=0,而且i等于1和2,j等于1到4。将Y(k)重新组合,得到

(14)
Yazi(k)=Aaziρazi(k)+ω(k)
(15)
式中,k=1,2,…,K,Aazi=[a(θ1,0),…,a(θqθ,0),…,a(θQθ,0)]∈C8×Qθ为俯仰角为零、方位角网格的导向矢量矩阵,![]() 为对应M个Chirp在第k距离单元上俯仰角网格为零处方位角网格的散射系数矩阵,Yazi(k)∈C8×M为“方位角”天线在距离单元k处接收信号矩阵,ω(k)为噪声矩阵。假设信号和噪声之间相互独立,接收信号的协方差矩阵定义为
为对应M个Chirp在第k距离单元上俯仰角网格为零处方位角网格的散射系数矩阵,Yazi(k)∈C8×M为“方位角”天线在距离单元k处接收信号矩阵,ω(k)为噪声矩阵。假设信号和噪声之间相互独立,接收信号的协方差矩阵定义为
(16)
式中,Pazi(k)=diag(pθ1(k),…,pθqθ(k),…,pθQθ(k)),对应的pθqθ(k)为方位角上第qθ个网格上的信号功率,σazi(k)为噪声功率,pθqθ(k)和σazi(k)为待求的参数, 对协方差矩阵Razi(k)矢量化,即
r(pazi(k))=vec(Razi(k))=Sazipazi(k)
(17)
式中,pazi(k)=[pθ1(k),…,pθqθ(k),…,pθQθ(k),σazi(k)],Sazi为系数矩阵,即Sazi=[a*(θ1,0)⊗a(θ1,0),…,a*(θqθ,0)⊗a(θqθ,0),…,a*(θQθ,0)⊗a(θQθ,0),vec(I)],这里的⊗代表Kronecker积。对矩阵Razi(k)的矢量表示可以看作未知的参数矢量pazi(k)中元素的线性组合。由于Chirp数M有限,可以得到采样协方差矩阵为
(18)
同样地,![]()
为了估计式(17)中pazi(k),需要事先得到Razi(k)的渐近一致估计。而文献[12]和[13]的AMV方法则是利用采样协方差矩阵![]() 去估计协方差矩阵的下界,从而渐近地逼近真实协方差矩阵。根据文献[13],估计协方差矩阵的下界为
去估计协方差矩阵的下界,从而渐近地逼近真实协方差矩阵。根据文献[13],估计协方差矩阵的下界为
(19)
式中,![]() 而此下界可以利用AMV准则建立的无约束优化问题求解,即
而此下界可以利用AMV准则建立的无约束优化问题求解,即
(20)
式中,![]() 利用文献[14]的方法求解式(20),进而得到信号功率和噪声功率的迭代式为
利用文献[14]的方法求解式(20),进而得到信号功率和噪声功率的迭代式为
![]()
![]()
(21)
(22)
式中,l为迭代次数。根据Capon波束形成算法对网格功率的估计,有p=1/aHR-1a,则式(21)、式(22)可改写为
(23)
![]()
(24)
在上述迭代过程中,初始值可以通过周期图法来求解,即
(25)
(26)
式中,![]() 对K个距离单元依次处理,可得距离-方位角热图为
对K个距离单元依次处理,可得距离-方位角热图为
prange-azi=[pθ(1),…,pθ(k),…,pθ(K)]∈RQθ×K
(27)
式中,![]()
2.3 CASO-CFAR检测
将式(27)以距离维度Pr和方位角维度Pθ分别送入CASO-CFAR检测器,其中Pr=[pr(θ1),…,pr(θqθ),…,pr(θQθ)],Pθ=[pθ(1),…,pθ(k),…,pθ(K)],对每个方位角网格上θqθ的所有距离单元做1D CASO-CFAR,检测出存在目标的距离单元kd,再对距离单元kd处的所有方位角网格做1D CASO-CFAR,检测出存在目标的距离-方位角网格单元(kd,θdqθ),得到对应的(rd,θd)。由于在应用中我们往往需要将距离较近的值能够检测出来,文献[15]中表明,单元平均选小恒虚警检测(CASO-CFAR)相对于单元平均恒虚警检测(CA-CFAR),使得距离较近的目标检测出来而不出现目标遮蔽的现象。具体处理结构如图4所示。

图4 CASO-CFAR处理结构图
2.4 俯仰角估计
接下来,对检测的距离-方位角网格单元(kd,θdqθ)进行俯仰角估计时,根据式(13),需令k=kd,θqθ=θdqθ,且i等于1到3,j等于1到4,将Y(k)重新组合,得到

(28)
Yele(kd)=Aeleρele(kd)+ω(kd)
(29)
式中,Aele=[a(θdqθ,φ1),…,a(θdqθ,φqφ),…,a(θdqθ,φQφ)]∈C12×Qφ为方位角为θdqθ,俯仰角网格的导向矢量矩阵,![]() 为对应M个Chirp在第kd距离单元上方位角网格为θdqθ处俯仰角网格的散射系数矩阵,Yele(kd)∈C12×M为所有天线的接收信号矩阵,ω(kd)为噪声矩阵。由式(23)、式(24),同理得到式(29)的俯仰角网格功率的迭代公式为
为对应M个Chirp在第kd距离单元上方位角网格为θdqθ处俯仰角网格的散射系数矩阵,Yele(kd)∈C12×M为所有天线的接收信号矩阵,ω(kd)为噪声矩阵。由式(23)、式(24),同理得到式(29)的俯仰角网格功率的迭代公式为

(30)
![]()
(31)
式中,Rele(kd)=AelePele(kd)AeleH+σele(kd)I12为协方差矩阵,![]() 为采样协方差矩阵,Pele(kd)=diag(pφ1(kd),…,pφqφ(kd),…,pφQφ(kd)),pφqφ(kd)为距离单元kd,方位角网格为θdqθ的位置处第qφ个俯仰角网格上的信号功率,σele(kd)为噪声功率。
为采样协方差矩阵,Pele(kd)=diag(pφ1(kd),…,pφqφ(kd),…,pφQφ(kd)),pφqφ(kd)为距离单元kd,方位角网格为θdqθ的位置处第qφ个俯仰角网格上的信号功率,σele(kd)为噪声功率。
3 仿真与实验结果分析
3.1 雷达参数设计
为了对近距离区域内人员等目标的3D位置参数进行探测,需要进行合理的毫米波雷达参数设计。雷达参数主要包括MIMO雷达天线数量及阵列设计、调频起始频率f1、调频斜率β、ADC采样点数N、ADC采样率fs、工作波长λw和每帧的调频周期数M,这些参数由应用场景的最大测量距离Rmax、距离分辨率Rres等指标来确定,以下指标分别满足公式:
Rmax=N×Rres
(32)
(33)
(34)
(35)
雷达硬件支持的参数有上限,将其作为雷达参数设计的先决条件,包括发射功率决定的最大测量距离Rmax、最大的ADC采样率fs-max与最小的ADC采样率fs-min、最大的扫频带宽Bmax、最大的调频斜率βmax与最小的调频斜率βmin、水平及垂直方向最大视场θFOV和φFOV等。具体的参数设置如表1所示。
表1 雷达系统和目标参数

仿真参数数值大小载波频率/GHz60工作带宽/GHz1.7805采样点数N96Chirp数M64距离分辨率/m0.0842θFOV/方位角网格长度/(°)140/1φFOV/俯仰角网格长度/(°)40/1FFT点数96
3.2 仿真结果分析
设置4个点目标,参数设置如表2所示。
表2 仿真目标三维参数

目标距离/ m方位角/(°)俯仰角/(°)14.0416-20-1024.0416-201034.0416-15-1044.04165-10
图5和图6分别为文献[9]方法和本文方法生成的距离-方位角热图以及经过CASO-CFAR检测的结果。从图中可以看出,文献[9]的方法已经无法在分辨出方位角上相差5°的目标1、2和目标3,只在目标1、2的方位角处有亮点,而方位角相差更大的目标4处也有明显的亮点。同时该方法的旁瓣较高,导致经过CFAR检测之后,真实距离-方位角单元的周围许多单元也被检测出来。相比之下,本文方法不仅在4个目标的真实方位角位置处均有明显的亮点,而且旁瓣较低,真实位置周围只有极少的单元被检测出来。图7和图8分别为两种方法在检测单元处估计的俯仰角网格功率谱图。从图中可以看出,文献[9]方法在所有检测单元处都只有一个谱峰,无法分辨出不同俯仰角的目标1和2,而本文方法的俯仰角功率谱在不同的检测单元上有两个不同位置的亮点。图9和图10分别为两种方法在空间直角坐标系中生成的3D点云像。从图中可以看出,文献[9]方法生成的点云像只能分辨出两个目标,而本文方法4个目标的点云都很清晰分辨出来,成像效果很好,只有目标4的俯仰角估计有5°的偏移。由此可见,相比较文献[9]的方法,本文提出的方法不仅在方位角上获得了更好的分辨率,而且在只有两排天线的条件下,俯仰角上依然可以得到一定的分辨率。

(a) 距离-方位角热图

(b) CFAR检测结果
图5 文献[9]方法生成的距离-方位角热图及CFAR检测结果

(a) 距离-方位角热图

(b) CFAR检测结果
图6 本文方法生成的距离-方位角热图及CFAR检测结果

图7 文献[9]方法生成的俯仰网格功率谱图
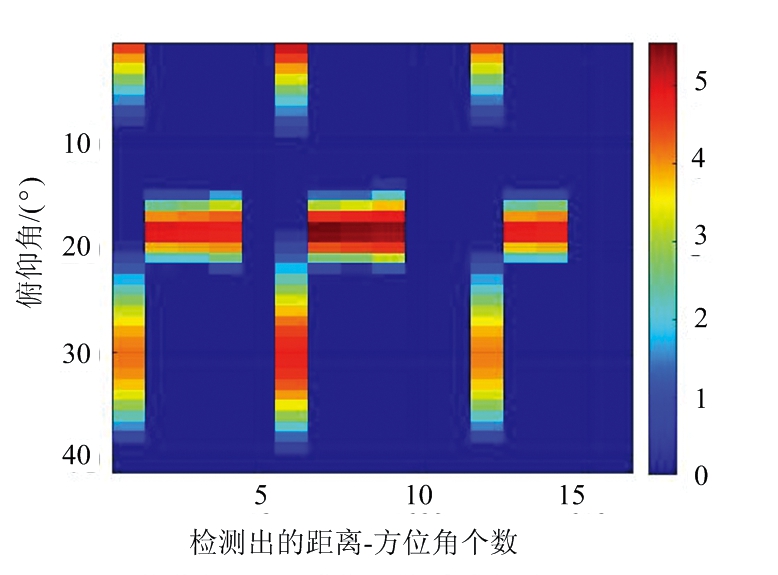
图8 本文方法生成的俯仰网格功率谱图

图9 文献[9]方法生成的3D点云像

图10 本文方法生成的3D点云像
3.3 实测数据处理结果
实验所采用雷达系统由TI(德州仪器)公司的毫米波雷达IWR6843ISK评估板卡、毫米波传感器承载卡平台MMWAVEICBOOST和数据采集卡DCA1000组成。评估板卡可以设置雷达系统参数,天线系统如图1所示,将差频信号在设置的采样率下进行I/Q采样,之后将采样好的信号通过工业载板传输给DCA1000,DCA1000将处理好的差频采样复信号打包成二进制文件通过网口传输给电脑。
实验时的场景如图11所示,在距离雷达5 m处的两个人体目标,人体目标的高度大约为1.7 m,人体的宽度大约为0.5 m,厚度大约为0.2 m,两人相距为1 m,雷达的高度为1 m,图12和图13分别为两种方法生成的距离方位热图及CFAR检测结果。从图中可以看出,文献[9]中的方法,已无法分辨在方位角上相差5°的两个人体目标,而本文方法依然能够清晰地分辨出两个目标。图14和图15分别为两种方法在检测单元处估计出来的俯仰角网格功率谱图。从图中可以看出,文献[9]方法由于Capon测角算法的分辨率有限,且雷达在俯仰维上只有两排天线,无法有效地估计目标所在的俯仰角范围,而本文方法依然在目标的俯仰角范围有明显的亮斑。图16和图17分别为两种方法的三维点云成像结果。从图中可以看出,文献[9]方法只能分辨出一个目标的点云像,且因俯仰角上分辨率很低,只能取峰值位置,导致点云成像结果和目标轮廓相差很大。而本文方法能清晰地生成两个目标的点云,同时由于SAMV方法估计出来的是网格的真实功率,经过检测算法后,三维点云结果和目标的轮廓十分相似。

图11 实验场景

(a) 距离-方位角热图

(b) CFAR检测结果
图12 文献[9]方法生成的距离-方位角热图及CFAR检测结果

(a) 距离-方位角热图

(b) CFAR检测结果
图13 本文方法生成的距离-方位角热图及CFAR检测结果

图14 文献[9]方法生成的俯仰网格功率谱图

图15 本文方法生成的俯仰网格功率谱图

图16 文献[9]方法生成的3D点云像

图17 本文方法生成的3D点云像
4 结束语
本文提出一种毫米波FMCW MIMO雷达高分辨三维点云成像方法,通过毫米波雷达的大带宽,得到高分辨的距离信息,引入SAMV方法,提升雷达的测角能力,结合CASO-CFAR算法,减少点云成像的时间。通过仿真和实验结果表明,相对于现有方法,该方法即使在天线数目有限的商业毫米波雷达上,依然有着更高的分辨率,兼顾了实时性的要求。本方法生成的近距离人体目标三维点云像,点云轮廓更加清晰、准确,便于后续基于点云的目标分类、姿势识别和计数等雷达应用的开发。
[1] AHMAD A, ROH J C, WANG D, et al. Vital Signs Monitoring of Multiple People Using a FMCW Millimeter-Wave Sensor[C]∥2018 IEEE Radar Conference, Oklahoma City, OK, USA:IEEE, 2018:1450-1455.
[2] GAO Teng, LAI Zhichao, MEI Zengyang, et al. Hybrid SVM-CNN Classification Technique for Moving Targets in Automotive FMCW Radar System[C]∥2019 11th International Conference on Wireless Communications and Signal Processing, Xi’an, China:IEEE, 2019:1-6.
[3] BHATTACHARYA A, VAUGHAN R. Deep Learning Radar Design for Breathing and Fall Detection[J]. IEEE Sensors Journal, 2020, 20(9):5072-5085.
[4] HAN Kawon, HONG Songcheol. Detection and Localization of Multiple Humans Based on Curve Length of I/Q Signal Trajectory Using MIMO FMCW Radar[J]. IEEE Microwave and Wireless Components Letters, 2021, 31(4):413-416.
[5] GAO Xiangyu, XING Guanbin, ROY S, et al. Experiments with mmWave Automotive Radar Test-Bed[C]∥2019 53rd Asilomar Conference on Signals, Systems, and Computers,Pacific Grove, CA, USA:IEEE, 2019:1-6.
[6] 肖中平. 基于AWR1642的车载防撞雷达设计与实现[D]. 成都:电子科技大学, 2019.
[7] WITTEMEIER J, AHMED A M, TRAN T N, et al. 3D Localization Using a Scalable FMCW MIMO Radar Design[C]∥2020 German Microwave Conference, Cottbus, Germany:IEEE, 2020:100-103.
[8] GURCAN Y, YAROVOY A. Super-Resolution Algorithm for Joint Range-Azimuth-Doppler Estimation in Automotive Radars[C]∥2017 European Radar Conference, Nuremberg, Germany:IEEE, 2017:73-76.
[9] Instruments Texas. People Tracking and Counting Reference Design Using mmWave Radar Sensor [EB/OL]. [2020-04-27]. https://www.ti.com/lit/ug/tidue71d/tidue71d.pdf.
[10] ABEIDA H, ZHANG Q, LI J, et al. Iterative Sparse Asymptotic Minimum Variance Based Approaches for Array Processing[J]. IEEE Trans on Signal Processing, 2013, 61(4):933-944.
[11] SANDEEP Rao. MIMO Radar[EB/OL]. [2018-07-26].http:∥www.ti.com/cn/cn/lit/an/swr554a/swr554a.pdf.
[12] DELMAS J P. Asymptotically Minimum Variance Second-Order Estimation for Noncircular Signals with Application to DOA Estimation[J]. IEEE Trans on Signal Processing,2004,52(5):1235-1241.
[13] 张翔宇,孙俊,曹欣荣,等.基于稀疏近似最小方差的宽带DOA估计算法[J].现代雷达,2018,40(1):30-35.
[14] 陈沛,赵拥军,刘成城.基于稀疏重构的共形阵列稳健自适应波束形成算法[J].电子与信息学报,2017,39(2):301-308.
[15] 汪洋. 毫米波雷达目标检测及恒虚警处理研究[D].广州:广东工业大学,2019.

