0 引言
多输入多输出(Multiple-Input Multiple-Output,MIMO)技术给雷达系统性能带来了全新的突破。与传统雷达相比,MIMO雷达在目标分辨与参数估计、低截获以及杂波抑制等方面有潜在的优势[1-2]。波达方向角(Direction of Arrival,DOA)估计是MIMO雷达目标参数估计中的重要组成部分,主要有子空间类[3-5]和稀疏表征类[6]等DOA估计方法。在实际应用中,由于元器件长时间使用老化和恶劣环境的影响会导致天线阵元物理性损坏。由于失效阵元无法正常发射和接收信号,因此MIMO雷达经匹配滤波处理后所形成虚拟阵列中存在大量失效虚拟阵元,则其输出数据矩阵中存在大量整行缺失元素,破坏了阵列数据的完整结构,导致现有DOA估计方法精度下降甚至完全失效。
针对均匀线性阵列阵元失效下DOA估计精度下降的问题,文献[7]将单快拍阵列接收信号变换成一个等效低秩矩阵,利用矩阵填充(Matrix Completion,MC)方法求解核范数最小化问题对缺失数据进行填充,但由于该方法仅利用单快拍接收数据,DOA估计精度较低。文献[8]将阵列接收数据构造成二重块Hankel矩阵,并利用不定增广拉格朗日乘子法(Inexacted Augmented Lagrange Method,IALM)对失效阵元的缺失数据进行恢复。文献[9]针对冗余阵元失效场景下利用虚拟差分阵列中的冗余阵元对协方差矩阵中缺失数据进行填充,但当非冗余阵元失效时,虚拟差分阵列存在空洞,利用虚拟差分阵列无法有效恢复缺失数据,DOA估计性能有待提升。文献[10]提出冗余虚拟阵元和非冗余虚拟阵元失效场景下的阵元失效DOA估计方法,当冗余虚拟阵元失效时,利用差联合阵对失效阵元缺失数据进行填充;非冗余虚拟阵元失效时利用阵列冗余度结合MC算法对缺失数据进行恢复。针对存在阵元失效下MIMO雷达DOA估计问题,文献[11]提出一种基于差分共阵处理的协方差矩阵重构方法,但该方法要求发射阵元的间距为接收阵元间距的N倍(其中N为接收阵元数),因此并不能适用于任意结构的MIMO雷达,具有一定的局限性。文献[12]提出了一种基于块Hankel矩阵填充的MIMO雷达失效阵元缺失数据恢复方法,该方法利用MIMO雷达虚拟阵列协方差矩阵构造具有四重Hankel结构的低秩块Hankel矩阵,并利用MC方法填补块 Hankel矩阵中的缺失数据,得到完整的虚拟阵列协方差矩阵。然而在实际应用中,目标信号只占据空域少量角度分辨单元,目标相对于整个空间来说是稀疏的[6]。因此,MIMO雷达虚拟阵列的采样数据矩阵不仅具有低秩性且还具有稀疏特性,联合利用低秩和稀疏先验,不仅能挖掘矩阵行间或列间元素的相关性,而且还能充分利用行内或列内元素的相关性,这为恢复阵元失效下MIMO雷达采样数据矩阵中的整行缺失元素提供了可能。
本文将MIMO雷达的阵元失效分为冗余虚拟阵元失效和非冗余虚拟阵元失效两种情况。当冗余虚拟阵元失效时,对空间上相同位置的正常工作冗余虚拟阵元数据取均值来填充失效阵元的缺失数据。当非冗余虚拟阵元失效时,针对利用虚拟阵列冗余度进行降维填充后的数据矩阵中仍存在整行缺失的数据问题,建立带有低秩和稀疏二重先验约束的矩阵填充模型,利用增广拉格朗日交替方向乘子法(Augmented Lagrange Method-Alternating Direction Method of Multipliers,ALM-ADMM)进行求解得到完整的降维数据矩阵。最后利用root-MUSIC算法估计目标DOA。仿真实验证明,本文方法能够有效提高阵元失效下MIMO雷达DOA估计精度。
1 阵元失效下MIMO雷达信号模型
假设MIMO雷达系统具有M个发射阵元和N个接收阵元,发射和接收阵列均为阵元间隔为半波长的均匀线阵。各发射阵元和接收阵元的归一化坐标分别记为{uT,m=m-1}和{uR,n=n-1},m=1,2,…,M,n=1,2,…,N。假设远场存在K个非相干目标,它们的DOA分别为θ1,θ2,…,θK,第
个发射阵元失效和第
个接收阵元失效,其中ΩT和ΩR分别为失效发射和接收阵元位置集合,则阵元失效下Q个脉冲周期的回波信号经匹配滤波后的MIMO雷达虚拟阵列输出数据矩阵![]() 为
为
(1)
式中: ⊙为Khatri-Rao积;S=[s1,s2,…,sQ]∈ K×Q为目标系数矩阵;
K×Q为目标系数矩阵;![]()
 MN×Q为阵元失效下的高斯白噪声矩阵;
MN×Q为阵元失效下的高斯白噪声矩阵;![]() 和
和![]() 分别为发射阵列和接收阵列存在失效阵元时的流形矩阵,分别表示为
分别为发射阵列和接收阵列存在失效阵元时的流形矩阵,分别表示为
(2)
(3)
其中,![]() 和
和![]() 分别表示矩阵
分别表示矩阵![]() 的第m行元素和矩阵
的第m行元素和矩阵![]() 的第n行元素, At=[at(θ1),at(θ2),…,at(θK)]为正常发射阵列的流形矩阵,at(θk)=[e-juT,1πsin(θk),e-juT,2πsin(θk),…,e-juT,Mπsin(θk)]T,Ar=[ar(θ1),ar(θ2),…,ar(θK)]为正常接收阵列的流形矩阵,ar(θk)=[e-juR,1πsin(θk),e-juR,2πsin(θk),…,e-juR,Nπsin(θk)]T。
的第n行元素, At=[at(θ1),at(θ2),…,at(θK)]为正常发射阵列的流形矩阵,at(θk)=[e-juT,1πsin(θk),e-juT,2πsin(θk),…,e-juT,Mπsin(θk)]T,Ar=[ar(θ1),ar(θ2),…,ar(θK)]为正常接收阵列的流形矩阵,ar(θk)=[e-juR,1πsin(θk),e-juR,2πsin(θk),…,e-juR,Nπsin(θk)]T。
2 不同阵元失效场景下的DOA估计方法
2.1 冗余虚拟阵元失效下DOA估计
MIMO雷达冗余虚拟阵元失效情形如图1所示,假设接收阵列第2个阵元失效。由图1可知,空间上同一位置处具有多个冗余虚拟阵元,即使出现失效虚拟阵元仍有正常冗余虚拟阵元能够输出数据。因此,可以利用正常工作的冗余虚拟阵元对信号进行降维,将具有MN个虚拟阵元的虚拟阵列转换成具有M+N-1个有效虚拟阵元的等效阵列,实现对失效阵元缺失数据的填补。
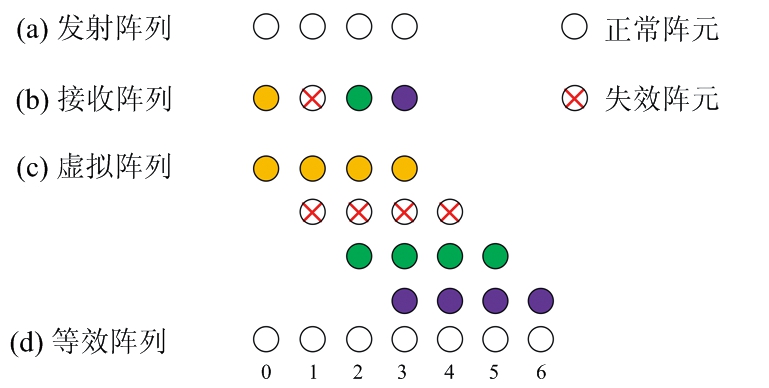
图1 冗余虚拟阵元失效场景
MN个虚拟阵元输出信号可以看成一个等效阵列的接收信号,则该等效阵列的阵元坐标可表示为
{ud=uT,m+uR,n|m=1,2,…,M;n=1,2,…,N}
(4)
定义集合Γd表示位于空间上相同位置ud的冗余虚拟阵元编号集合,如下所示:
Γd={(m,n)|uT,m+uR,n=ud}
(5)
为了降低计算复杂度,本文在降维过程中首先剔除失效虚拟阵元的零元素数据,然后对空间上位置为ud的正常工作的冗余虚拟阵元数据取均值处理,即
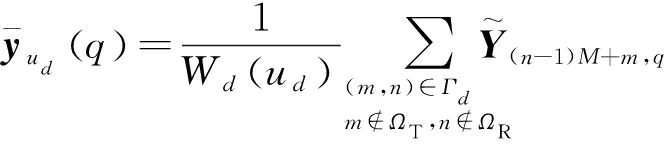
(6)
式中,![]() 为降维后空间上位置为ud的等效虚拟阵元在第q个脉冲周期内的输出信号;Wd(ud)表示空间位置ud的正常冗余虚拟阵元个数;
为降维后空间上位置为ud的等效虚拟阵元在第q个脉冲周期内的输出信号;Wd(ud)表示空间位置ud的正常冗余虚拟阵元个数;![]() 为矩阵
为矩阵![]() 中第{(n-1)×M+m,q}个元素。
中第{(n-1)×M+m,q}个元素。
经过上述处理,不但能够利用虚拟阵列的冗余度对虚拟阵列输出信号进行降维,而且能对失效阵元的缺失数据进行填充,等效阵列的输出数据矩阵为
(7)
式中:![]()
 (M+N-1)×Q为等效阵列输出数据矩阵;
(M+N-1)×Q为等效阵列输出数据矩阵;![]()
 (M+N-1)×K为降维后的线性阵列流形矩阵,其中,
(M+N-1)×K为降维后的线性阵列流形矩阵,其中,![]()
 (M+N-1)×Q为降维后的高斯白噪声矩阵。等效阵列协方差矩阵在Q个脉冲周期内的最大似然估计为
(M+N-1)×Q为降维后的高斯白噪声矩阵。等效阵列协方差矩阵在Q个脉冲周期内的最大似然估计为![]() 由于在理想情况下等效阵列协方差矩阵
由于在理想情况下等效阵列协方差矩阵![]() 具有Toeplitz特性,因此可将
具有Toeplitz特性,因此可将![]() 中每一条对角线上的元素值替换为该对角线上元素的均值,从而增强对噪声的鲁棒性[12]。最后利用root-MUSIC算法估计DOA。
中每一条对角线上的元素值替换为该对角线上元素的均值,从而增强对噪声的鲁棒性[12]。最后利用root-MUSIC算法估计DOA。
2.2 非冗余虚拟阵元失效情况下DOA估计
MIMO雷达非冗余虚拟阵元失效情况如图2所示,假设接收阵列第1个阵元失效。由图2可知,在空间位置{ud=0}上只存在一个失效虚拟阵元即无正常冗余虚拟阵元,因此利用2.1节方法对失效阵元缺失数据进行填充时所形成的等效阵列中仍然存在等效阵元空洞。与冗余虚拟阵元失效不同,当非冗余虚拟阵元失效时,等效阵列中输出数据矩阵![]() 中仍然某些行元素全为零。
中仍然某些行元素全为零。
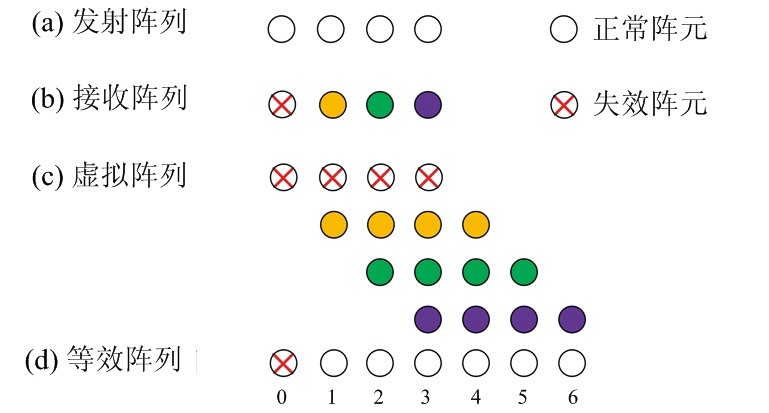
图2 非冗余虚拟阵元失效场景
根据式(7),在理想无噪声和无失效阵元情况下等效阵列输出的完整数据矩阵可以表示为![]() 可以得到矩阵的秩
可以得到矩阵的秩![]() 由于目标个数k
由于目标个数k![]() 为低秩矩阵。由于来波信号在空域具有稀疏性,将目标可能入射角范围按等角度间隔划分得到P个角度网格
为低秩矩阵。由于来波信号在空域具有稀疏性,将目标可能入射角范围按等角度间隔划分得到P个角度网格![]() 则P≫K,过完备字典Φ可以表示为Φ=[φ0,φ1,…,φM+N-2]T∈
则P≫K,过完备字典Φ可以表示为Φ=[φ0,φ1,…,φM+N-2]T∈ (M+N-1)×P,其中,
(M+N-1)×P,其中,![]()
 P×1,则
P×1,则![]() 可以在一个过完备字典Φ下稀疏表示,即
可以在一个过完备字典Φ下稀疏表示,即![]() 其中
其中![]() 与S具有相同的行支撑,即
与S具有相同的行支撑,即![]() 是K行稀疏矩阵,
是K行稀疏矩阵,![]() 中的非零行元素对应冗余字典中目标的DOA。联合利用矩阵的低秩先验和稀疏先验建立如下矩阵填充模型:
中的非零行元素对应冗余字典中目标的DOA。联合利用矩阵的低秩先验和稀疏先验建立如下矩阵填充模型:
(8)
式中,![]() 为待恢复矩阵,γ为正则化参数,‖·‖*和‖·‖1分别为核范数和l1范数,E为辅助变量矩阵来补偿矩阵
为待恢复矩阵,γ为正则化参数,‖·‖*和‖·‖1分别为核范数和l1范数,E为辅助变量矩阵来补偿矩阵![]() 中缺失元素,Ψ为矩阵
中缺失元素,Ψ为矩阵![]() 中已知非零元素位置的集合,PΨ(·)表示投影到集合Ψ的投影算子。
中已知非零元素位置的集合,PΨ(·)表示投影到集合Ψ的投影算子。
利用增广拉格朗日乘子法(ALM)[13]并结合ADMM[14]算法可以有效地求解式(8)中的优化问题。式(8)的增广拉格朗日函数可以表示为
(9)
式中:R1,R2为拉格朗日乘子矩阵;μ1,μ2为惩罚因子;〈·〉表示两个矩阵的内积。
上式中含有多个未知变量,不易直接求解,因此采用ADMM算法将多变量优化问题分解为多个单变量优化问题,来交替估计最优变量![]() 即通过固定其他变量不变的情况下求解其中一个变量,通过固定
即通过固定其他变量不变的情况下求解其中一个变量,通过固定![]() 不变,迭代求解
不变,迭代求解![]() 的子问题可以表述为
的子问题可以表述为
![]()
![]()
(10)
由于求解![]() 的子问题不存在闭式解,于是采用加速近端梯度法(Accelerated Proximal Gradient, APG)[15]方法来近似求解
的子问题不存在闭式解,于是采用加速近端梯度法(Accelerated Proximal Gradient, APG)[15]方法来近似求解![]() 令
令![]() 其中
其中![]() 引入近端变量W,定义如下函数:
引入近端变量W,定义如下函数:
![]()
![]() ∇
∇![]()
(11)
式中,∇![]() 是一个常数,保证对于所有W都有
是一个常数,保证对于所有W都有![]() 即可将问题转化成求解
即可将问题转化成求解![]() 的最小值来近似得到
的最小值来近似得到![]() 的最小值如下所示:
的最小值如下所示:
![]()
![]()
(12)
式中,![]() ∇f(Wj),其中,j表示第j次迭代。式(12)可以用软阈值函数来求解,
∇f(Wj),其中,j表示第j次迭代。式(12)可以用软阈值函数来求解,
(13)
式中,soft(x,λ)=sign(x)max{|x|-λ,0}为软阈值算子。近端变量Wj的迭代如下:
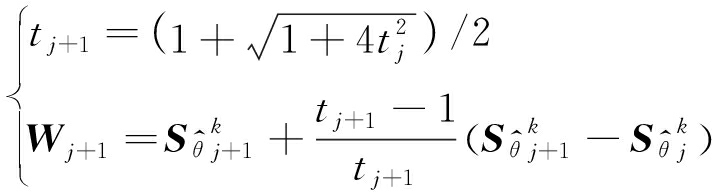
(14)
通过固定S,E,R1,R2不变,迭代求解![]() 的子问题可以表述为
的子问题可以表述为
![]()
![]()
(15)
式(15)可以转化为求解如下优化方程:
(16)
式中,![]() 上述核范数最小化问题可以用SVT算法[16]求解得
上述核范数最小化问题可以用SVT算法[16]求解得
(17)
式中,Uk,Vk分别为Hk的左奇异向量和右奇异向量,Σk为由奇异值组成的对角矩阵,即Hk=UkΣk(Vk)H。
由于E是一个辅助变量矩阵用来补偿等效阵元空洞所对应缺失数据,它在索引集Ψ中元素为零,即PΨ(E)=PΨ(0)。定义Ψ的补集为![]() 因此只需更新迭代矩阵E在
因此只需更新迭代矩阵E在![]() 中元素而保持在Ψ中元素为零。固定
中元素而保持在Ψ中元素为零。固定![]() 不变,E的迭代求解问题可以表述为
不变,E的迭代求解问题可以表述为
Ek+1=![]()
(18)
则E的完整迭代解为
Ek+1=![]()
(19)
拉格朗日乘子矩阵R1,R2的迭代为![]() 其中,
其中,![]() 和ρ2为大于1的常数,能够保证每次迭代中
和ρ2为大于1的常数,能够保证每次迭代中![]() 两个惩罚因子一直递增。
两个惩罚因子一直递增。
通过求解式(8)所表示的优化模型即可获得完整的数据矩阵![]() 将
将![]() 中的缺失数据由矩阵
中的缺失数据由矩阵![]() 中相同位置的元素来替换,则得到等效阵列完整输出数据矩阵Yc,按照与2.1节相同方法从Yc中估计出目标DOA。
中相同位置的元素来替换,则得到等效阵列完整输出数据矩阵Yc,按照与2.1节相同方法从Yc中估计出目标DOA。
2.3 计算复杂度分析
当冗余阵元失效时,本文方法的计算复杂度约为![]() 其中N1为未失效的阵元个数;文献[10]方法的复杂度约为
其中N1为未失效的阵元个数;文献[10]方法的复杂度约为![]() 文献[12]的复杂度约为
文献[12]的复杂度约为![]() 其中K1为迭代的次数。当非冗余阵元失效时,本文方法计算复杂度为O(K2((2J+1)(M+N-1)QP+2J(M+N-1)P2+(M+N-1)Q2+(M+N-1)Q)),其中K2为外部迭代次数,J为内部迭代次数;文献[10]方法的复杂度约为
其中K1为迭代的次数。当非冗余阵元失效时,本文方法计算复杂度为O(K2((2J+1)(M+N-1)QP+2J(M+N-1)P2+(M+N-1)Q2+(M+N-1)Q)),其中K2为外部迭代次数,J为内部迭代次数;文献[10]方法的复杂度约为![]() 文献[12]的复杂度约为
文献[12]的复杂度约为![]() 由此可知,当冗余阵元失效时,本文方法复杂度与文献[10]方法相当,远小于文献[12]方法的复杂度;当非冗余阵元失效时,本文方法计算复杂度高于文献[10]的方法,但小于文献[12]方法的计算复杂度。
由此可知,当冗余阵元失效时,本文方法复杂度与文献[10]方法相当,远小于文献[12]方法的复杂度;当非冗余阵元失效时,本文方法计算复杂度高于文献[10]的方法,但小于文献[12]方法的计算复杂度。
3 仿真实验
为了验证本文方法在MIMO雷达阵元失效时的DOA估计性能,设计以下仿真实验,以阵元正常时利用RD-root-MUSIC[3-4]进行DOA估计的性能作为参照,同时在阵元失效下将本文方法和RD-root-MUSIC、文献[10]的方法以及文献[12]的方法进行对比。假设MIMO雷达发射阵元数为M=5,接收阵元数为N=15,脉冲周期数为Q=100。3个目标DOA分别为θ1=20°,θ2=-15°,θ3=0°。DOA估计均方根误差定义为![]() 其中,
其中,![]() 为第k个目标在第mt次蒙特卡罗实验中目标DOA的估计值,MT为蒙特卡罗次数,信噪比定义为
为第k个目标在第mt次蒙特卡罗实验中目标DOA的估计值,MT为蒙特卡罗次数,信噪比定义为![]() 在本文方法中,构造冗余字典所使用的角度间隔为
在本文方法中,构造冗余字典所使用的角度间隔为![]() ∞/2,其中,‖·‖∞为无穷范数。
∞/2,其中,‖·‖∞为无穷范数。
3.1 冗余虚拟阵元失效时DOA估计性能对比
假设发射阵列中第3个阵元失效,接收阵列中第2,5,9,11,14个阵元失效,快拍数为100,信噪比变化范围为-30~0 dB,进行100次蒙特卡罗实验,DOA估计均方根误差随信噪比变化如图3(a)所示。由图3(a)可知,当阵元失效时RD-root-MUSIC算法的目标角度估计误差明显大于阵元正常时的估计误差,表明MIMO雷达的传统降维预处理方法[6]无法对失效阵元缺失数据进行有效填补。本文方法DOA估计性能要优于文献[10]方法和文献[12]方法,低信噪比时与阵元正常时的DOA估计性能接近,而在高信噪比时精度高于阵元正常的DOA估计精度。
假设信噪比为-10 dB,快拍数由50~350变化,其余参数与上述仿真实验一致,仿真结果如图3(b)所示。由图3(b)可知,随着快拍数的不断增加,所有方法的DOA估计性能都有所提升,在不同快拍数的情况下本文方法始终能保持最优,且DOA估计精度高于阵元正常时的估计精度。
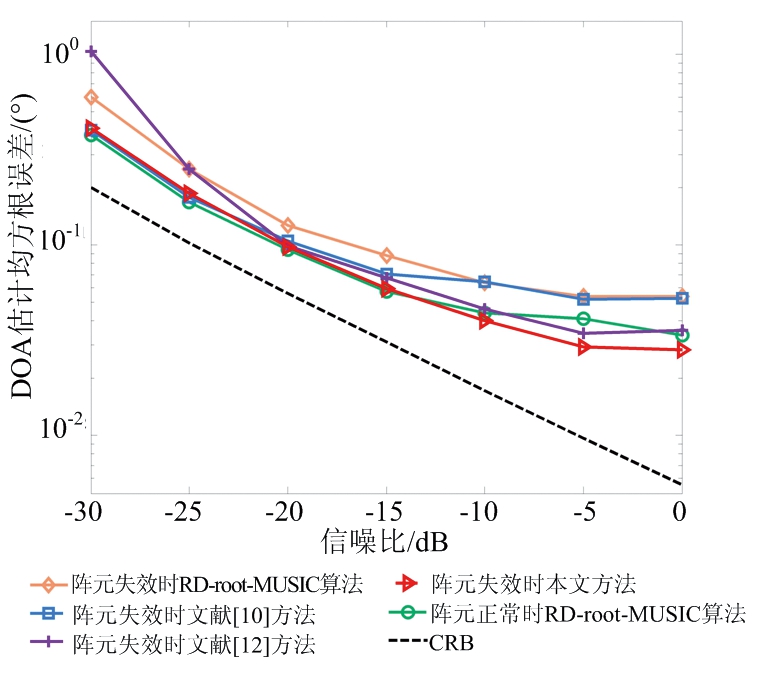
(a) DOA估计均方根误差随信噪比变化
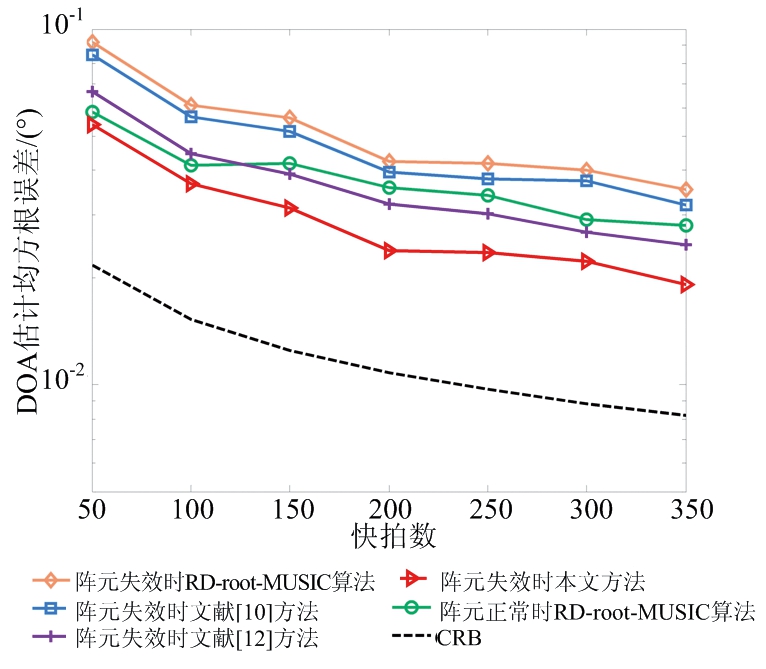
(b) DOA估计均方根误差随快拍数变化
图3 冗余虚拟阵元失效时DOA估计性能对比
3.2 非冗余虚拟阵元失效时DOA估计性能对比
假设MIMO雷达发射阵列第3个阵元失效,接收阵列第3,4,8,11,15个阵元失效,快拍数为100,仿真结果如图4(a)所示。由图4(a)可知,随着信噪比的增加,各种方法的DOA精度也随之提高,但本文方法估计的DOA更加趋近于阵元正常时的DOA,并且DOA估计性能明显优于文献[10]和文献[12]方法。图4(b)为目标角度估计均方根误差与快拍数的变化关系图,其中信噪比为-10 dB,快拍数由50~350变化,其余参数与上述实验一致。图4(b)中可以看出,本文方法的目标角度估计性能在不同快拍数下始终保持最优。
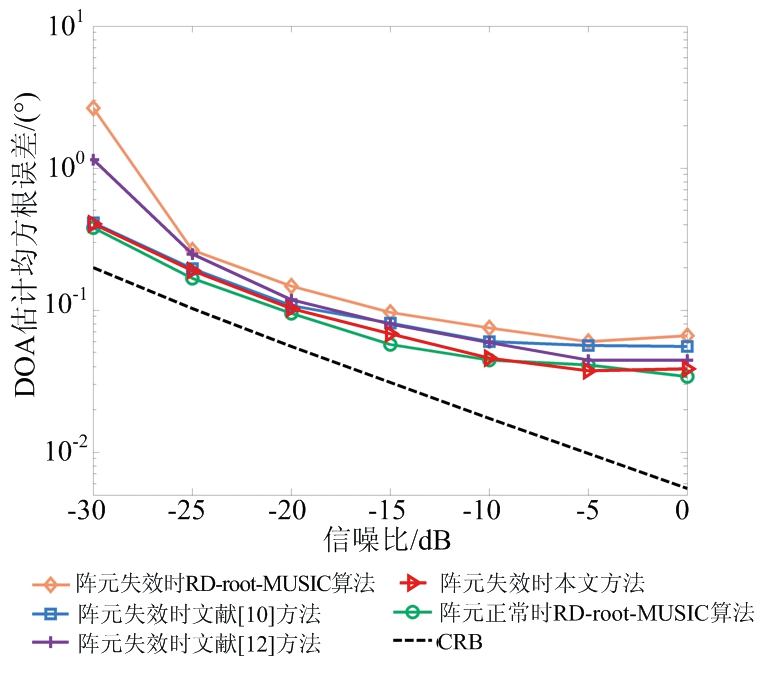
(a) DOA估计均方根误差随信噪比变化
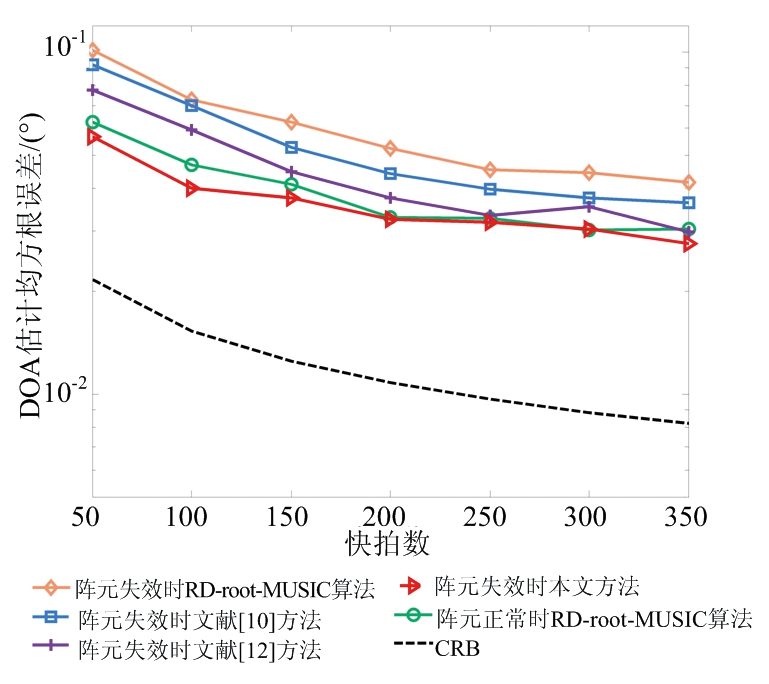
(b) DOA估计均方根误差随快拍数变化
图4 非冗余虚拟阵元失效时DOA估计性能对比
4 结束语
当MIMO雷达阵列存在阵元失效时,虚拟阵列采样数据矩阵出现大批整行目标数据缺失,导致现有DOA估计算法性能下降甚至失效。针对此问题,本文提出了一种基于采样数据矩阵重构的MIMO雷达DOA估计方法。当冗余虚拟阵元失效时,利用空间上相同位置的虚拟阵元的冗余性对失效阵元缺失数据进行填充;当非冗余虚拟阵元失效时,由于利用阵列冗余度进行填充后采样数据矩阵中仍有整行元素缺失,因此构造带有低秩和稀疏先验约束的矩阵重构问题,利用ALM-ADMM算法进行求解实现对缺失元素的恢复。本文方法能有效避免因阵元失效带来的DOA估计性能下降的影响,具有较高的目标DOA估计精度。
[1] BAIDOO E, HU Jurong, ZENG Bao, et al. Joint DOD and DOA Estimation Using Tensor Reconstruction Based Sparse Representation Approach for Bistatic MIMO Radar with Unknown Noise Effect[J]. Signal Processing, 2021, 182:107912.
[2] SALARI S, CHAN F, CHAN Y T, et al. Joint DOA and Clutter Covariance Matrix Estimation in Compressive Sensing MIMO Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2019, 55(1):318-331.
[3] ZHANG Xiaofei, XU Lingyun, XU Lei, et al. Direction of Departure (DOD) and Direction of Arrival (DOA) Estimation in MIMO Radar with Reduced-Dimension MUSIC[J]. IEEE Communications Letters, 2010, 14(12):1161-1163.
[4] NI Zhengwei, LUO Yinan, MOTANI M, et al. DoA Estimation for Lens Antenna Array via Root-MUSIC, Outlier Detection, and Clustering[J]. IEEE Access, 2020, 8:199187-199196.
[5] LIAO Yanping, ZHAO Ruigang, GAO Lipeng. Joint DOD and DOA Estimation in Bistatic MIMO Radar with Distributed Nested Arrays[J]. IEEE Access, 2019, 7:50954-50961.
[6] WANG Xianpeng, WANG Wei, LIU Jing, et al. A Sparse Representation Scheme for Angle Estimation in Monostatic MIMO Radar[J]. Signal Processing, 2014, 104:258-263.
[7] 杨东, 廖桂生, 朱圣棋, 等. 阵列信号降采样低秩矩阵的恢复方法[J]. 西安电子科技大学学报, 2014, 41(5):30-35.
[8] 张永顺, 葛启超, 丁姗姗. 阵元缺损下的波达方向估计算法[J]. 电子科技大学学报, 2017, 46(4):501-504.
[9] ZHU Chenglong, WANG Wenqin, CHEN Hui, et al. Impaired Sensor Diagnosis, Beamforming and DOA Estimation with Difference Co-Array Processing[J]. IEEE Sensors Journal, 2015, 15(7):3773-3780.
[10] SUN B G, WU Chenxi, SHI Junpeng, et al. Direction-of-Arrival Estimation Under Array Sensor Fai-lures with ULA[J]. IEEE Access, 2020, 8:26445-26456.
[11] ZHANG Weiyu, VOROBYOV S A,GUO L. DOA Estimation in MIMO Radar with Broken Sensors by Difference Co-Array Processing[C]∥IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Cancun, Mexico:IEEE, 2015:321-324.
[12] CHEN Jinli, ZHANG Tingxiao, LI Jiaqiang, et al. Joint Sensor Failure Detection and Corrupted Covariance Matrix Recovery in Bistatic MIMO Radar with Impaired Arrays[J]. IEEE Sensors Journal, 2019, 19(14):5834-5842.
[13] LIN Zhouchen, CHEN Minming, MA Yi. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices[J]. Eprint Arxiv, 2010, 9:1-19.
[14] XIE Y, SHANBHAG U V. SI-ADMM: A Stochastic Inexact ADMM Framework for Stochastic Convex Programs[J]. IEEE Trans on Automatic Control, 2020, 65(6):2355-2370.
[15] TANG Wengen, JIANG Hong, ZHANG Qi. Range-Angle Decoupling and Estimation for FDA-MIMO Radar via Atomic Norm Minimization and Accelerated Proximal Gradient[J]. IEEE Signal Processing Letters, 2020, 27:366-370.
[16] CAI J F, CANDES E J, SHEN Z. A Singular Value Thresholding Algorithm for Matrix Completion[J]. SIAM Journal on Optimization, 2010, 20(4):1956-1982.
