0 引言
海杂波信号作为一类典型的雷达干扰回波，它是指海面雷达的后向散射回波，易受到各种外部自然因素影响，如风、潮汐、浪涌等，其物理机理复杂多变，非高斯、非线性和非平稳特性显著，容易对雷达目标检测造成干扰。研究海杂波背景下的混沌小信号检测方法，对建立海洋安全观测监测、海面目标检测系统具有重要的理论研究和应用价值。
小信号检测方法研究除了考虑信号与噪声间的差异性来验证小信号的存在之外，还可以从噪声本身入手，利用随机共振手段将噪声能量转移到小信号上以增强小信号，从而实现小信号的检测。随机共振理论由Benzi等[1-2]在研究冰河时代周期性变化的气候问题而提出，用于定性描述太阳公转偏心率周期变化引起的地球冷暖气候期交替的现象。此后，随机共振理论大放异彩，被应用到物理、化学、信号处理等各类领域，国内外研究学者在微弱信号检测领域也取得了丰富的研究成果。1998年，Barnes[3]在研究弱电场和磁场信号时，利用随机共振理论，通过增加弱信号的混沌功率谱密度来提高信噪比实现弱信号的检测；Saha等[4]于2003年提出了一种量化的随机共振检测器，适用于检测噪声中的弱正弦信号，且其检测性能优于匹配滤波器的检测性能；温熙森等[5]在2009年提出了基于随机共振的机械故障早期检测方法，对故障诊断及预测理论发展具有深远的影响；2018年，行鸿彦等[6]在研究海杂波背景下的微弱信号检测方法时，提出了一种自适应随机共振微弱信号检测方法，实现了对Duffing振子随机共振系统的多参数调优的工作，提升了检测性能。
分析传统随机共振系统的缺陷，结合变种差分进化算法，提出一种新的海杂波背景下的随机共振混沌小信号检测方法。基于变种差分进化算法和随机共振理论建立海杂波混沌小信号检测模型，利用变种差分进化算法的快速收敛性对Duffing振子的a,b,k进行寻优，以系统输出信噪比为目标函数，完成变种差分进化算法的变异、交叉、选择操作，最大化地增强小信号，保证在系统输出信号的时频特性分析中检测到小信号的存在。对实测海杂波数据进行仿真实验，以验证变种差分进化算法优化随机共振系统的实用性。
1 随机共振理论分析
1.1 Duffing振子的双稳态随机共振系统
Duffing振子的随机共振系统利用其混沌状态下小信号、背景噪声及系统本身发生的匹配协同关系，实现混沌小信号的检测[7-8]。
对于一个混沌小信号f(t)和噪声信号u(t)共同作用的Duffing振子随机共振方程组为
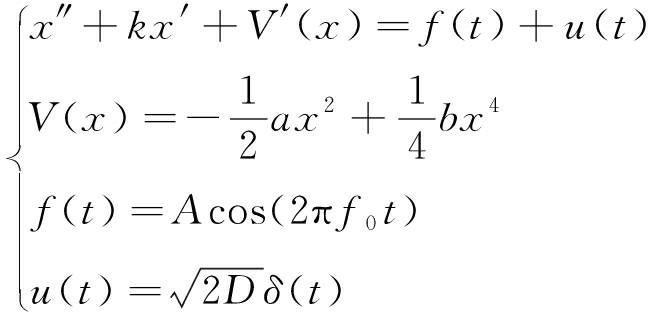
(1)
式中，x为系统输出信号，k为阻尼比，V(x)为势函数，f(t)为系统输入信号，u(t)是均值为0、噪声强度为D的高斯白噪声。而根据一元二次方程求解公式可以计算出，势函数V(x)包含的3个极值点，分别为
定义势函数势垒高度为
若势函数的极点等于其拐点(即函数的二阶导数在该点两侧异号或不存在)时，推算出此时的系统临界值为
当且仅当输入信号幅值A>Ac时，信号、噪声及系统三者达到匹配协同关系，噪声信号的部分能量迁移到信号上，实现信号增强即进入随机共振状态，此时公式(1)可简化成
x″+kx′-ax+bx3=f(t)+u(t)
(2)
公式(2)是典型二阶Duffing振子的随机共振系统，通过分析公式得出，参数a，b，k为决定Duffing振子随机共振系统的核心参数，为接下来的寻优算法作铺垫。
1.2 随机共振基本理论
1.2.1 绝热近似理论
随机共振现象可通过加入适宜的噪声或者调整系统参数来实现，从而达到增强小信号的目的[9]。为了方便科学计量分析，本节只考虑调整系统参数a，b，k的手段。将公式(2)转化为动力学方程表达式：
(3)
利用福克·普朗克方程[10]求解上述随机过程中随机变量(x,y)的概率分布函数可得
ax-bx3+Acos(2πf0t))·
(4)
式中
由于不存在关于变量y的函数，导致无法分析该函数解的准确表达式，这时就需要借助数学分析理论中的各类近似求解手段来处理，比如绝热近似理论、线性响应理论等。
假设系统输入信号f(t)和背景噪声u(t)的信号强度都很小时，即A≪1，D≪1，概率分布函数存在两个解
分别对应两个吸引域(-∞,0)和(0,+∞)，此时各个吸引域中的概率总量为
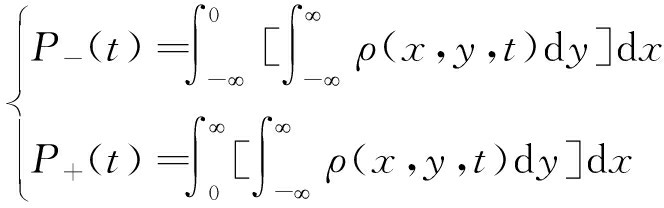
(5)
对于低频输入信号f(t)而言，此时两个吸引域各自达到平衡所花费的时间远小于两者整体趋于稳定的时间。换言之，可以认为吸引域各自趋于平衡稳定的操作是瞬间完成的，这一近似过程便称为绝热近似理论。
1.2.2 线性响应理论
线性响应理论最早就是为了解释随机共振现象而被提出，可以弥补绝热近似理论不能解决的情形。对于输入周期小信号f(t)，经Duffing振子的随机共振系统后输出的信号也包含该周期项，设系统敏感函数为χ(t)，根据涨落耗散定理计算的幅值a和相位φ分别为
a=A|χ(ω)|, φ=-arctan[Imχ(ω)/Reχ(ω)]
(6)
式中：
(7)
Imχ(ω)=πωS0(ω)/D
(8)
(9)
χ(ω)是系统敏感函数χ(t)的傅里叶变换，S0(ω)是系统输出信号零时刻的功率谱密度函数，依据公式(9)可以推导出线性响应理论分析的系统输出信噪比为
(10)
对于线性响应理论下的随机共振系统而言，当t→+∞时，<x(t)x(0)>的值无限接近<x(t)><x(0)>，然而在实际计算操作中远远不能实现；此外，对于绝热近似理论中不能研究的高频输入信号随机共振，线性响应理论适用任意频段的输入信号，但是关于其时间尺度ω/vk，vk为克莱莫斯逃逸速率，会随着零时刻的系统势垒函数U0及噪声强度D呈指数级减少，容易出现ω/vk≪U0/D不成立的情况，该情形下的随机共振理论分析便又不能进行。
1.3 外差式随机共振
绝热近似理论是随机共振分析理论中最主要、最常见的手段，它的局限性也十分明显，需要满足输入信号和噪声的强度均较小且输入信号频率较低的苛刻条件。对于研究海杂波背景下的混沌小信号而言，往往有时候包含其中的混沌小信号频率较高，为了将绝热近似理论运用到高频段输入信号的信号检测中，可以考虑使用外差式随机共振，其实现流程如图1所示。
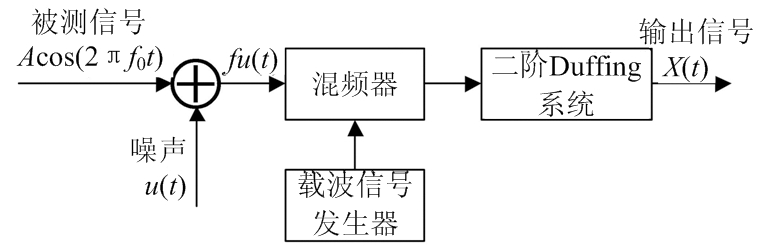
图1 外差式随机共振流程图
根据图1可知，外差式随机共振原理就是利用混频将低频输入信号迁移到高频段中，得到一对中心频率为载波信号频率fc的信号：
fu(t)*c(t)=[Acos(2πf0t)+u(t)]*cos(2πfct)=
f0)t)+u(t)*cos(2πfct)
(11)
经混频后产生一高频信号(fc+f0)和一低频信号(fc-f0)，中心载波频率将二者划分为高低频信号，所以低频信号频率远小于高频信号频率，相应地，两者的频谱大小恰恰相反，即
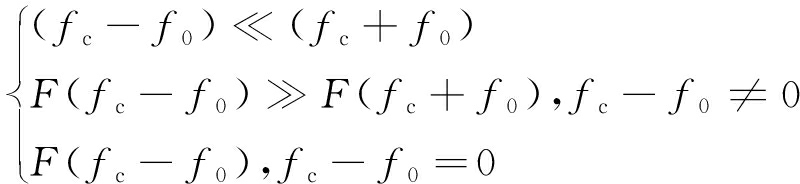
(12)
其中，F(fc-f0)是随机共振系统的输出信号频谱，当fc≠f0时，外差式随机共振系统会增强低频(fc-f0)处的信号，通过在输出信号频谱图中清晰看到该处的尖峰。然而当fc=f0时，输出信号频谱中的尖峰便会消失，可以利用这一点，灵活调节载波频率fc来获取输入信号的频率f0。
2 变种差分进化算法
差分进化算法是一种基于遗传算法基本思想改变编码方式、种群迭代方式、淘汰方式的改进型寻优算法[11-12]。由于其大胆的劣者绝对淘汰方式不仅提升了算法的收敛速度、全局优化搜索能力，同时还保证了较强的鲁棒性[13]。差分进化算法使用浮点矢量完成编码，采用父系差分向量完成变异，并与父系交叉生成子代，较遗传算法收敛更快且效果更加显著。但是这样的操作背后，带来的问题便是容易出现过早收敛，降低了全局搜索能力[14-15]。针对这一问题，提出了一种变种差分进化算法。变种差分进化算法通过加入自适应变异算子，迭代初期能够保证变异发生概率，维持种群多样性，防止过早收敛；迭代后期能够保护最优解，提高全局搜索能力。
为了解决传统随机共振系统独立调参寻优效果差的问题，利用变种差分进化算法实现对二阶Duffing振子随机共振系统多参数的同步寻优，将系统输出信号的信噪比作为寻优算法的目标函数，它能够反映随机共振系统对混沌小信号的增强水平，当目标函数取最大值时寻优过程结束。变种差分进化算法优化随机共振系统多参数的具体步骤如下：
步骤1: 初始化参数，设置初始种群数量为NP，最高迭代次数为G次，空间变量维度为D，创建初始种群
随机产生第0代第i个个体第j维度的取值：
(13)
式中，
代表第i个个体取值的上下限，rand(D,NP)代表在(D,NP)区间内均匀分布的随机数。
步骤2: 目标函数计算，对于一个二阶Duffing振子的随机共振系统而言，输出信号的信噪比随着系统参数的变化而变化，它能够反映该系统对混沌小信号的增强水平，目标函数为
Obj(a,b,k)=SNRout(sc(a,b,k))
(14)
式中，sc(a,b,k)为随机共振系统输出信号，SNRout(sc(a,b,k))为系统输出信号的信噪比。
步骤3: 变异操作，采用差分策略进行对个体的变异操作，是区别于遗传算法的标志之一。随机选取两个区别于待变异的父系个体进行差分缩放后并与该个体进行合成，得到
Hi(g+1)=xp1(g)+F·(xp2(g)-xp3(g)),
i≠p1≠p2≠p3
(15)
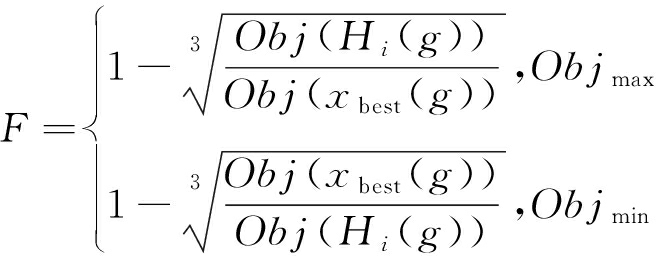
(16)
式中，F代表自适应变异算子，xi(g)代表迭代g次后的第i个个体，Obj(xbest(g))为最优个体的目标函数值，Obj(Hi(g))为当前个体的目标函数值，Objmax为最大目标函数值，Objmin为最小目标函数值。在整个变异过程中种群所有个体的取值均要求满足边界条件，即
<
(17)
步骤4: 交叉操作，对迭代g后的第i个个体xi(g)和变异个体Hi(g+1)进行交叉计算：
(18)
式中，cr为交叉因子，jrand为[1,2,…,D]的随机整数。差分进化算法的交叉不同于遗传算法中对每个个体进行交叉，它只对同一维度的个体进行交叉。
步骤5: 选择操作，差分进化算法利用贪婪算法进行选择操作
(19)
步骤6: 更新目标函数值，根据当前迭代次数优化的系统参数计算系统输出信号信噪比，对比上一次迭代输出的信噪比，如果较小则重新进行一轮迭代寻优；否则输出寻优参数a,b,k。
步骤7: 输出最优随机共振，当迭代次数达到最高迭代次数G时，输出满足最大目标函数值对应的二阶Duffing振子的随机共振系统参数a,b,k，根据所获最优参数值对输入信号进行随机共振输出，分析输出信号的频谱特性。
基于变种差分进化算法的随机共振混沌小信号检测方法流程如图2所示。
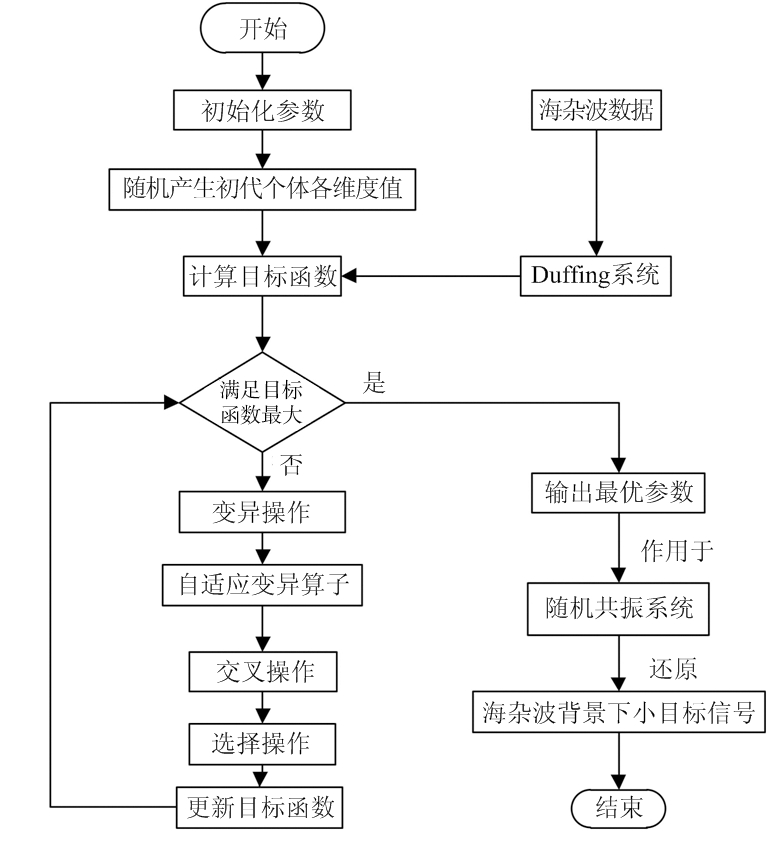
图2 基于变种差分进化算法的随机共振混沌小信号检测方法流程图
3 实验仿真分析
为了验证变种差分进化算法优化随机共振系统混沌小信号检测的实用有效性，本节进行三组仿真实验：前两组实验分别将低频小信号和高频小信号混合噪声作为Duffing振子随机共振系统的输入信号，经变种差分算法优化系统参数后，得到系统输出信号并分析其时频特性验证混沌小信号检测效果；第三组实验则是将实测海杂波数据作为背景噪声输入随机共振系统，分析经优化后系统输出信号的时频特性判断混沌小信号是否能被检测。
3.1 低频小信号检测
二阶Duffing振子的随机共振系统参数a,b,k直接影响系统的输出效果，其中k值与克莱莫斯逃逸速率vk密切相关，二者呈反比例关系；分析公式(1)可知，系统参数a,b直接影响势垒高度和系统临界值Ac，a的取值与两者呈正比例关系，b却相反，根据图3分析a,b分别取值为1时势垒函数发生的变化。
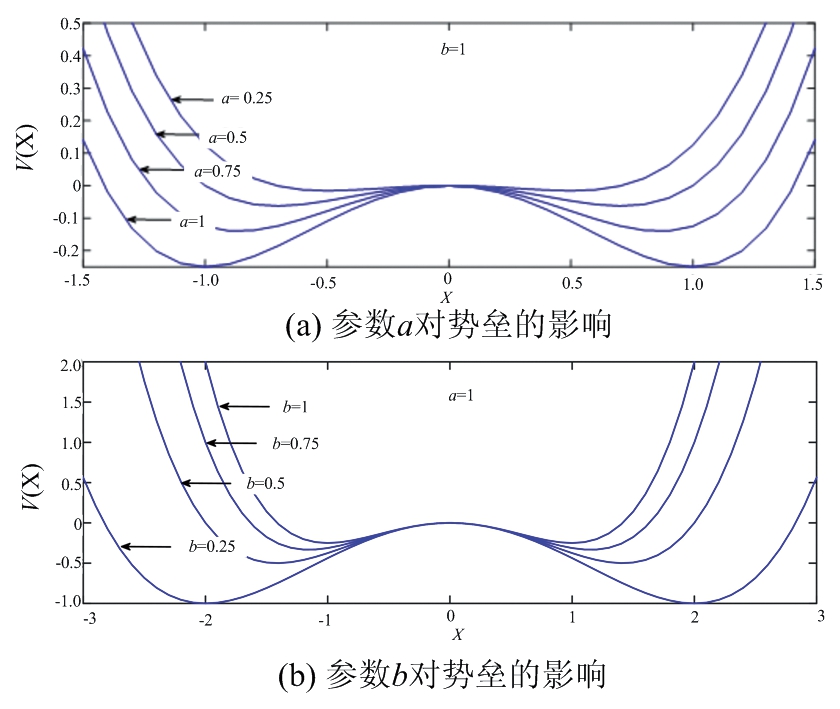
图3 参数a,b对势垒函数的影响
考虑到发生随机共振时系统参数较小，设置种群数量NP为50，变量维度D为10，初始变异算子F0为0.4，交叉因子cr为0.1，最大迭代次数G为200。输入如下的低频小信号：
(20)
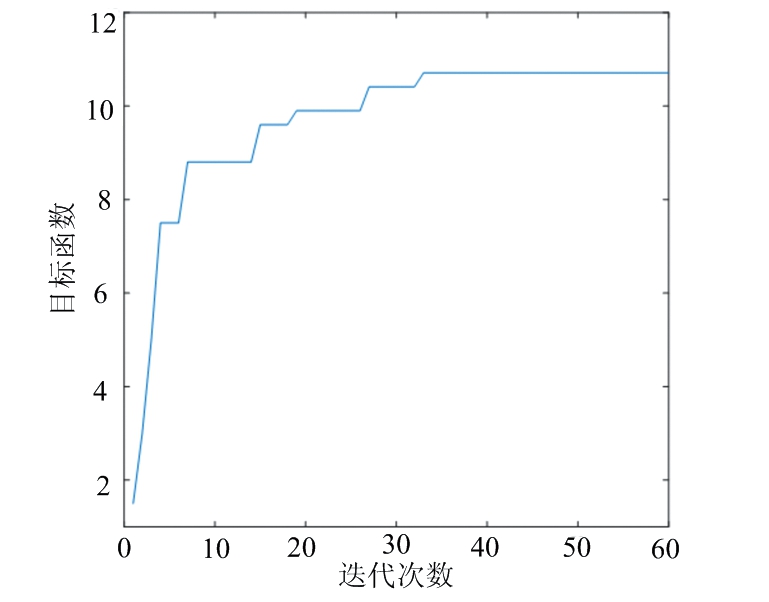
图4 变种差分进化算法优化随机系统参数收敛图
式中，小信号频率为0.01 Hz，采样频率为5 Hz，采样点数为800个。设定低频信号幅值A=0.1，0.08，0.06，0.04，0.02，对应噪声强度D=0.15，0.3，0.45，0.6，0.75，形成5组信噪比逐次递减的输入信号1，2，3，4，5，设置优化输出系统参数寻优范围为[0.001，2]，参数精度为0.001。以输入信号幅值A=0.1，噪声强度D=0.15为例进行详细描述，利用变种差分进化算法，寻找当前输入信号特性下Duffing振子随机共振系统的输出信噪比最大时对应的系统参数a,b,k。如图4所示，变种差分进化算法经过33次迭代寻优获得系统当前输入信号的最优参数，分别为a=0.226，b=0.315，k=0.691，该情形下输出信号的信噪比最大为10.710 dB，对比输入信噪比(-18.681 dB)提升了29.391 dB。图5为变种差分进化算法在最优参数下的随机共振图，图5(a)为输入信号图，可以看到混沌小信号被淹没在噪声中，如图5(b)分析其频谱特性也未能看出端倪。然而分析其输出信号图5(c)能够简约看出信号的轮廓，再分析其频谱特性图5(d)，能够明显观察到小信号被增强，直接判断出0.01 Hz处存在小信号。
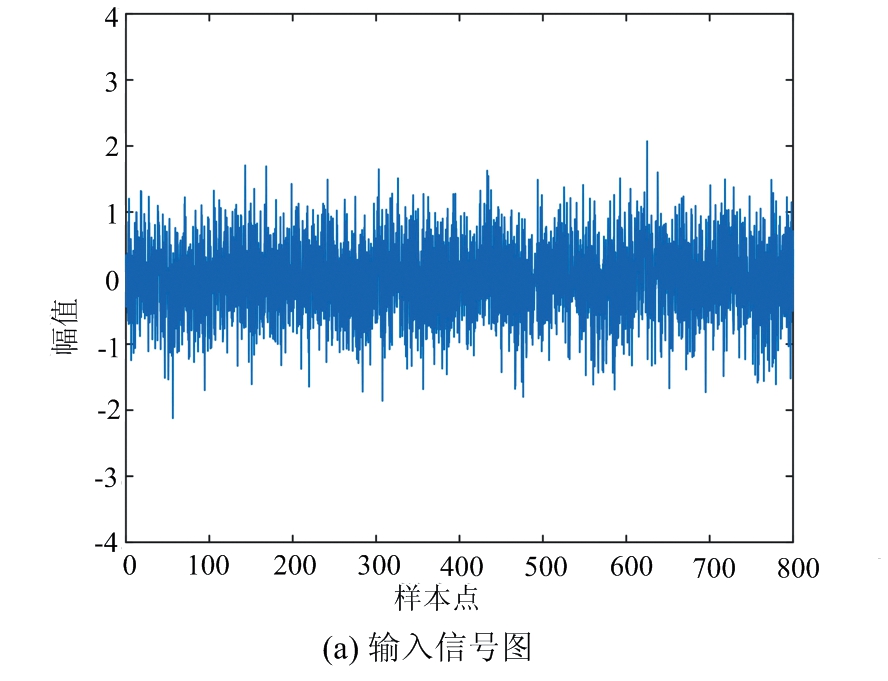
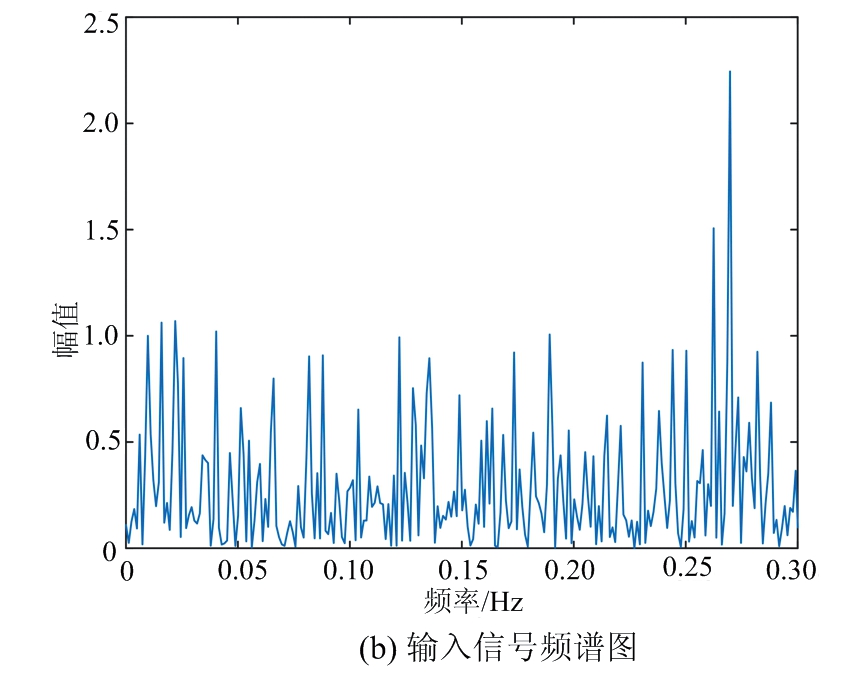
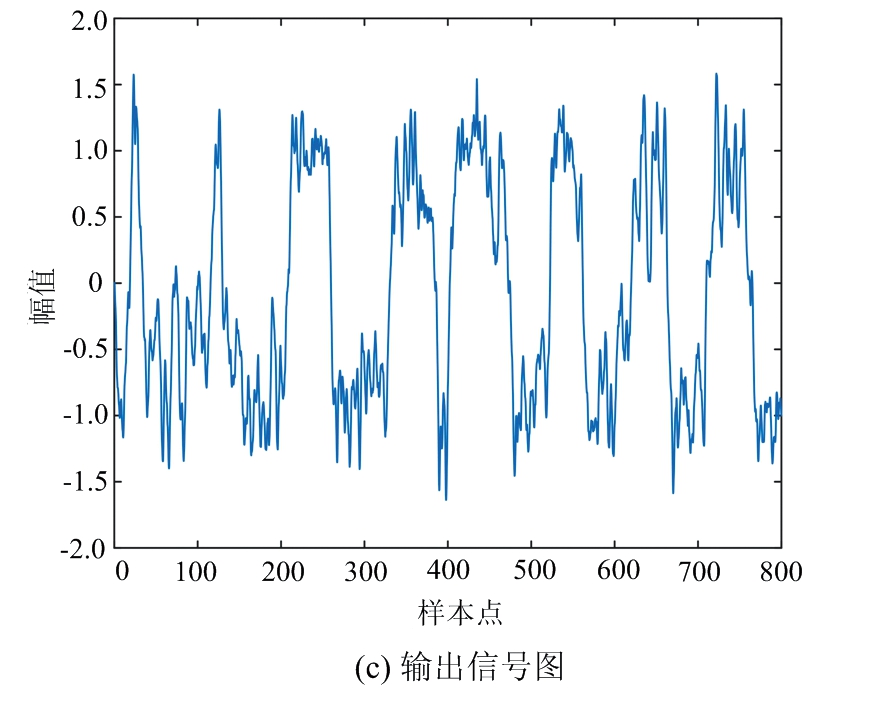
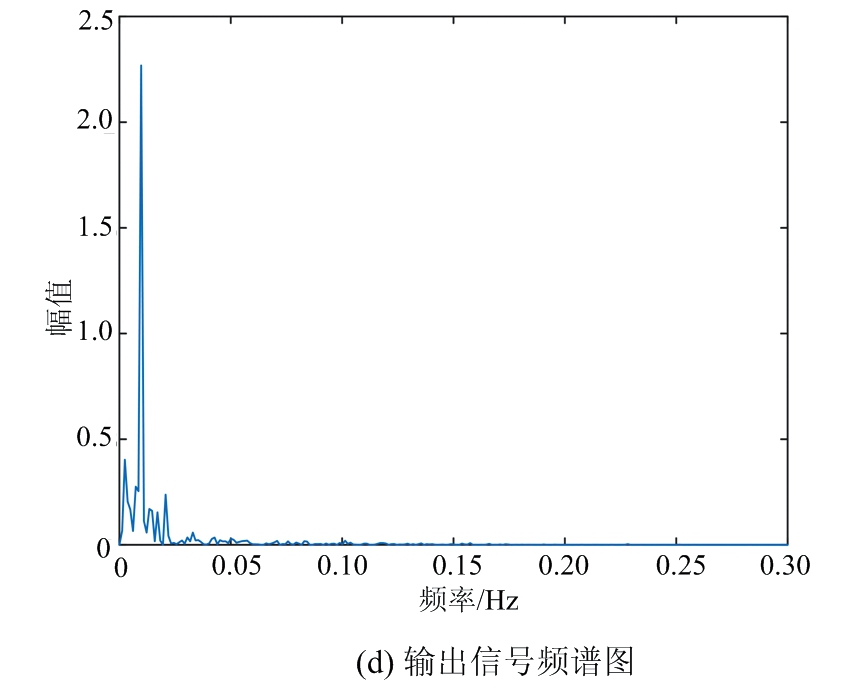
图5 低频小信号变种差分进化算法随机共振系统参数分析图
为了验证变种差分进化算法优化随机共振系统参数的可靠性，表1给出5组输入信号的参数寻优及输出信号的信噪比结果。
从表1分析可知，对于输入低频小信号而言，差分变种进化算法优化的Duffing振子随机共振系统能够显著地提升输出信号的信噪比，换言之，该方法能增强淹没在噪声背景下的小信号，实现随机共振系统中的小信号检测。较混沌变长萤火虫算法优化随机共振系统，迭代收敛速度更快，信噪比增益平均提高1.98 dB，提取淹没在强噪声背景下的低频小信号效果更好。
表1 5组输入信号的参数寻优及输出信号的信噪比结果
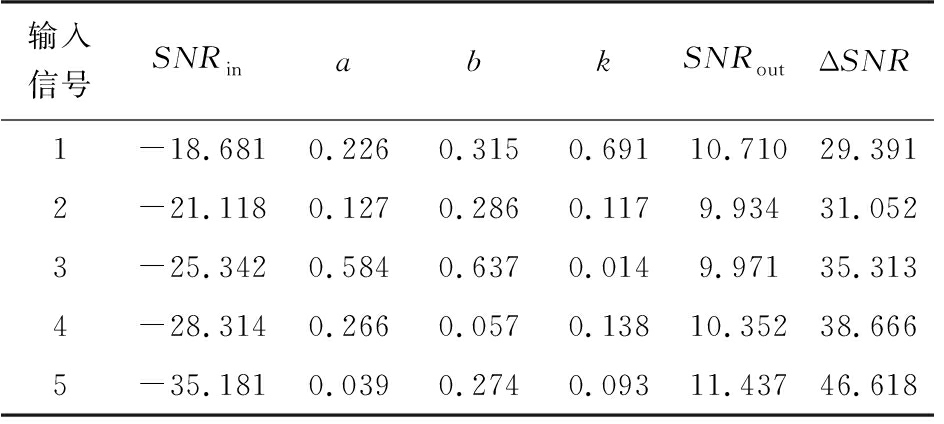
输入信号SNRinabkSNRoutΔSNR1-18.6810.2260.3150.69110.71029.3912-21.1180.1270.2860.1179.93431.0523-25.3420.5840.6370.0149.97135.3134-28.3140.2660.0570.13810.35238.6665-35.1810.0390.2740.09311.43746.618
3.2 高频小信号检测
在绝热近似理论中，要求输入信号的幅值低、频率低，噪声强度低，但是实际工程应用中的输入信号往往可能是频率。针对这一难题，可以利用外差式随机共振来解决。为了进一步验证变种差分进化算法优化随机共振的小信号检测方法的可行性，输入信号幅值A=0.2，噪声强度D=2.1，信号频率f0=20 Hz的高频小信号，采样频率fs=5 Hz，采样点数为800个，结合外差式随机共振理论设定载波频率fc=20.01 Hz经混频后输出的低频信号分量满足绝热近似理论要求，进行高频小信号检测实验。
利用变种差分进化算法对随机共振系统下的高频小信号进行检测，得到输出信号信噪比最大对应的系统参数a,b,k，分别为a=0.146，b=0.419，k=0.304，输出当前情形下最大的信噪比3.54 dB，较输入信噪比(-23.22 dB)提升了26.76 dB。图6为输入高频小信号情形下的优化随机共振图，从图6(a)、(b)分析，输入信号的时频特性图中均未能观测出淹没在强噪声背景下的高频小信号。然而在图6(c)输出信号图中能够较清晰地看出输入信号的轮廓，对其进行频率分析得到图6(d)的输出信号频谱图，能够明显看出小信号被增强，判断f=0.01 Hz处存在小信号，依据外差式随机共振恢复原理，计算得出f0=fc-0.01=20 Hz，进一步推断出增强的频率代表输入频率为20 Hz，表明变种差分进化算法优化的Duffing振子随机共振系统能检测出高频小信号。
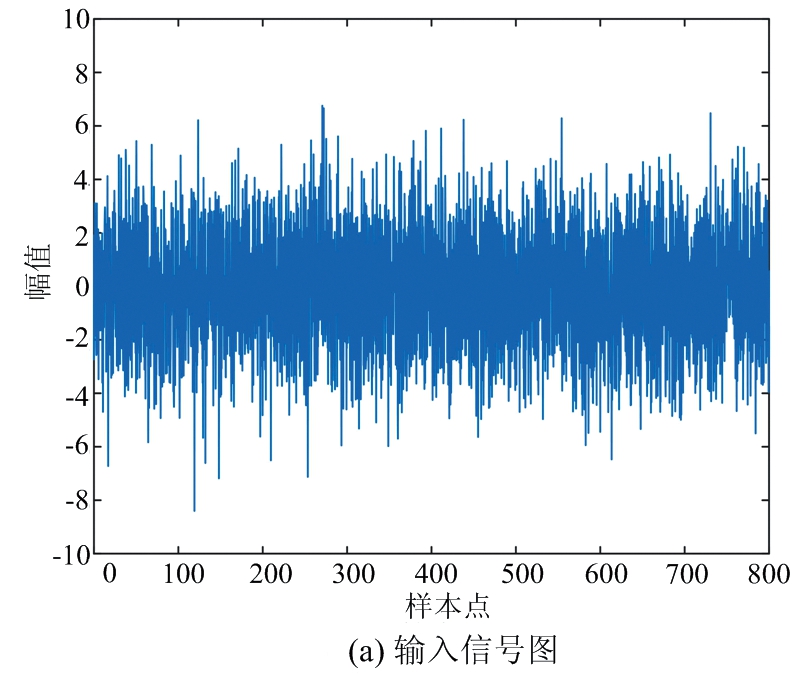
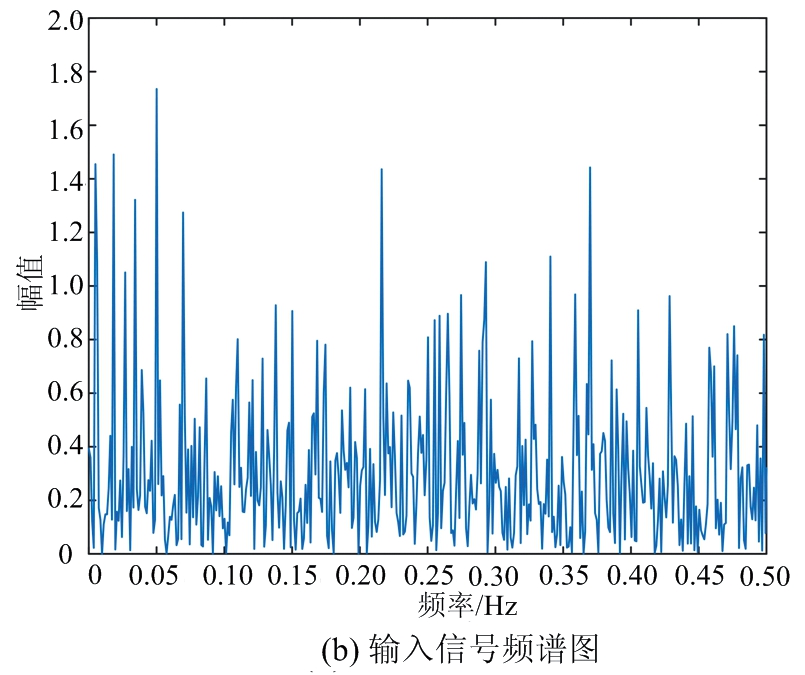
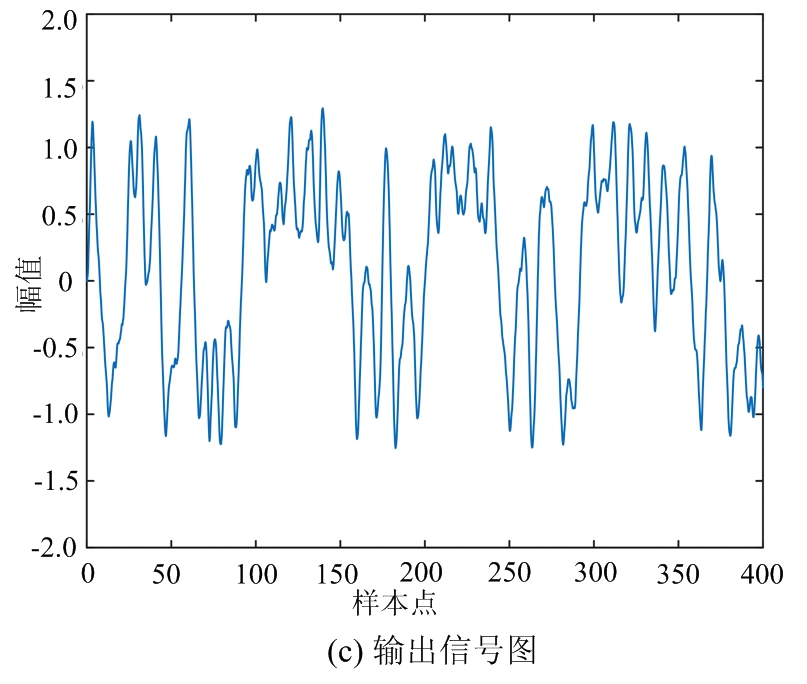
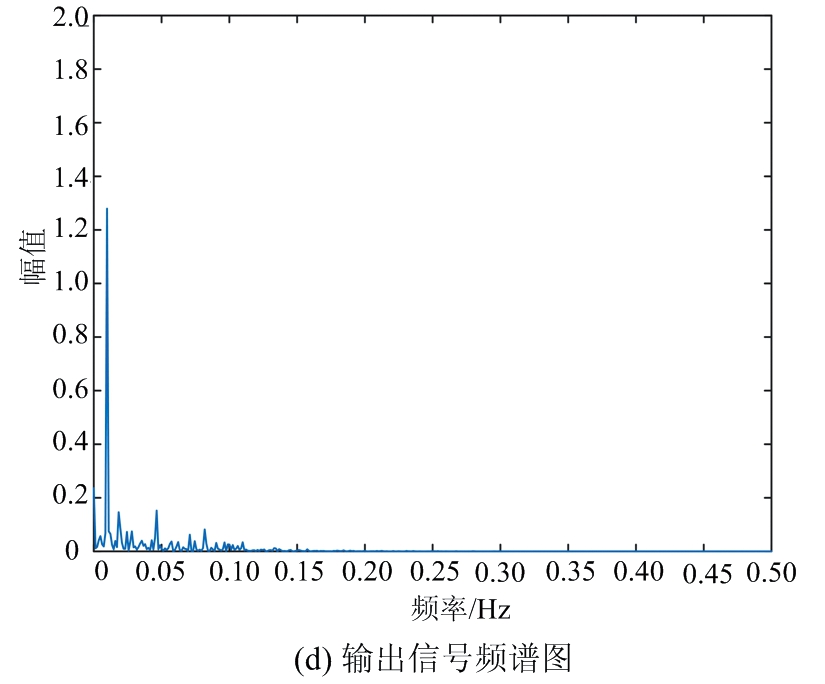
图6 高频小信号变种差分进化算法随机共振系统参数分析图
3.3 海杂波背景下的混沌小信号检测
为了验证变种差分进化算法的实用性，进行基于随机共振理论的海杂波背景下的混沌小目标检测实验，选用的是IPIX雷达收集的#54海杂波含目标信号数据，目标数据区间：主目标为8，次目标为7∶10。将含目标的海杂波数据取代Duffing振子的随机共振系统的输入信号，经变种差分进化算法优化后的系统，输出信噪比最大对应的系统参数a,b,k，分别为a=0.973，b=0.738，k=0.034，输出信噪比为22.47 dB，较输入信号的信噪比(-55.03 dB)提升了83.50 dB，海杂波背景下的随机共振混沌小信号检测效果如图7所示，其中图7(a)、(b)为输入信号时频特性图，均不能分析出混沌小信号的存在，经优化后的随机共振系统后，图7(c)能够隐约勾勒出淹没在海杂波背景下的混沌小信号轮廓，图7(d)能清晰地辨认出在频率为0.016 32处出现频谱尖峰，代表该处存在混沌小信号，达到实验研究的效果。
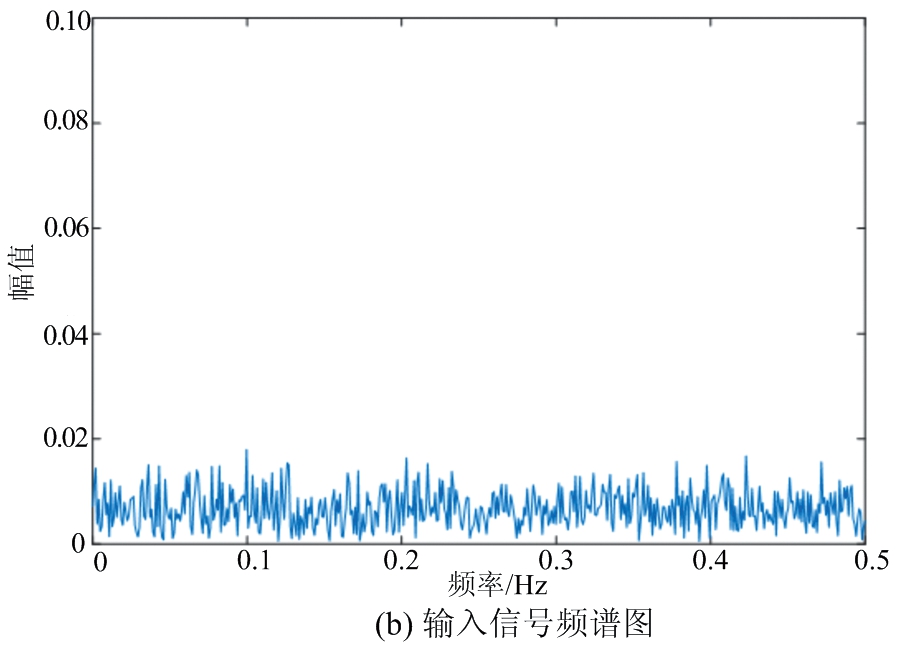
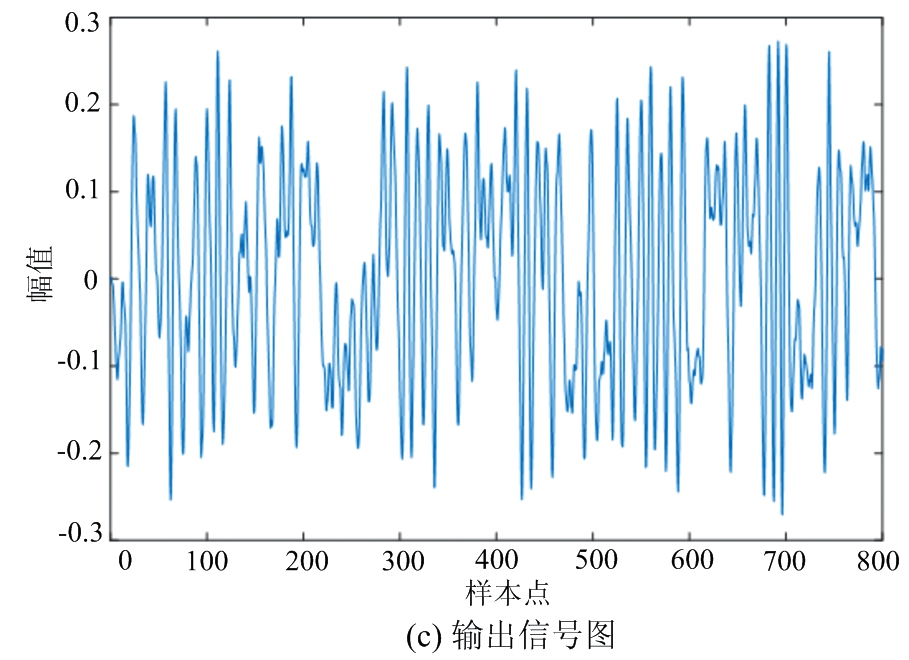
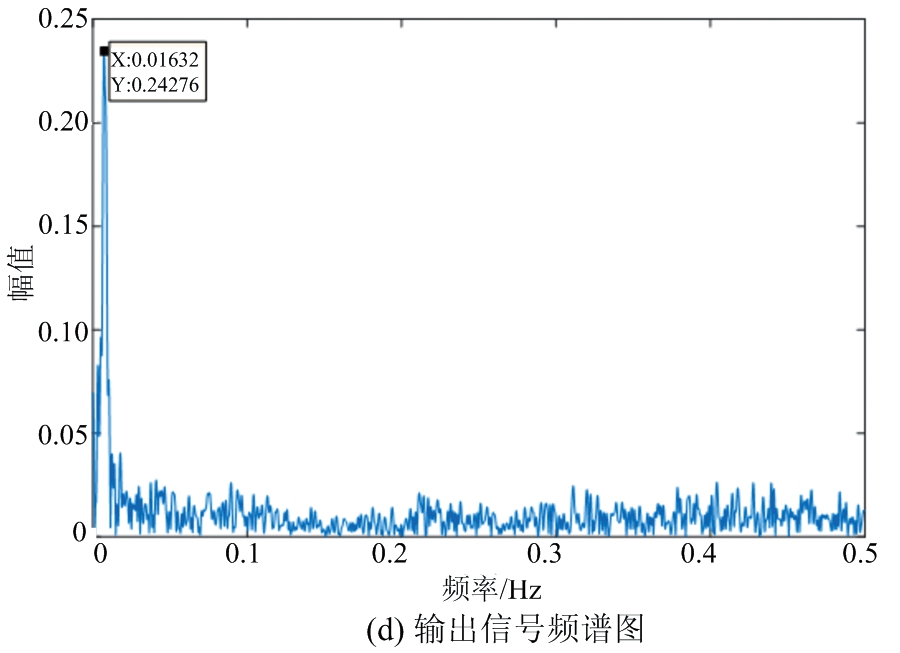
图7 海杂波背景下的随机共振混沌小信号检测效果图
4 结束语
针对传统随机共振小信号检测无法对多参数进行同步寻优的缺陷，本文提出了一种基于变种差分进化算法的随机共振混沌小信号检测方法，利用变种差分进化算法中加入自适应变异算子提升全局寻优搜索能力的同时避免了过早收敛，对Duffing振子的随机共振系统参数a,b,k进行寻优，选用系统输出信号的信噪比作为目标函数，完成变种差分算法的变异、交叉、选择操作。对低频小信号输入进行仿真实验，与混沌变步长萤火虫优化算法作对比，输出信噪比平均提升1.98 dB，小信号检测效果提升显著；对高频小信号输入进行仿真实验，结合外差式随机共振理论能够准确恢复出高频小信号对应低频段处的小信号，进一步推导出高频小信号的存在；对实测海杂波数据进行仿真实验，实验结果表明该方法能够有效地检测出淹没在海杂波背景下的混沌小信号。
[1] BENZI R, SUTERA A, VULPIANI A. The Mechanism of Stochastic Resonance[J]. Journal of Physics A: Mathematical and General, 1981, 14:453-457.
[2] BENZI R, PARISI G, SUTERA A, et al. A Theory of Stochastic Resonance in Climatic Change[J]. SIAM Journal on Applied Mathematics, 1983, 43(3): 565-578.
[3] BARNES F S. A Model for the Detection of Weak ELF Electric and Magnetic Fields[J].Bioelectroche-mistry and Bioenergetics,1998,47(2):207-212.
[4] SAHA A A, ANAND G V. Design of Detectors Based on Stochastic Resonance[J].Signal Processing,2003,83(6):1193-1212.
[5] 温熙森，杨定新，胡茑庆. 基于随机共振的机械故障早期检测方法研究[Z]. 湖南省:解放军国防科学技术大学,2009-01-01.
[6] 行鸿彦,卢春霞,张强.自适应随机共振微弱信号检测[J].系统仿真学报,2018,30(2):587-594.
[7] 刘广凯,全厚德,康艳梅,等.一种随机共振增强正弦信号的二次多项式接收方法[J].物理学报,2019,68(21):32-42.
[8] 戴荣,于海涛,王权.基于Duffing系统的谐振式微悬臂梁传感器微弱谐振信号检测[J].机械工程学报,2020,56(13):50-59.
[9] JIANG Xiaolin, DIAO Ming. A New Type Double-Threshold Signal Detection Algorithm for Satellite Communication Systems Based on Stochastic Resonance Technology[J]. Wireless Networks,2019(5):259-272.
[10] 葛江华,王岩,王亚萍,等.基于QGA和随机共振的轴承微弱故障信号检测方法[J].哈尔滨理工大学学报,2020,25(3):94-101.
[11] ZHAO Taifei,LIU Longfei, LIU Le,et al. Differential Evolution Particle Filtering Channel Estimation for Non-Line-of-Sight Wireless Ultraviolet Communication[J]. Optics Communications,2019(11):80-85.
[12] 陈挺,胡兵轩,任庭昊,等.基于差分进化优化RBF网络的小电流接地多判据选线方法[J].自动化技术与应用,2020,39(8):97-102.
[13] VIKRAM A,KARNA D,KUMAR A, et al. An Analytical Approach of Integrating Automated Load Scheduling to a Smart Energy Meter Using Differential Evolution Algorithm[C]∥2020 4th International Conference on Information Processing and Control Engineering University of California,Berkeley,USA:IEEE,2020:1-5.
[14] 段伟,徐斌.基于改进差分进化算法的压力机杆系参数优化[J].机械设计与研究,2021,37(3):1-5.
[15] 孙凤山,范孟豹,曹丙花,等.基于混沌映射与差分进化自适应教与学优化算法的太赫兹图像增强模型[J].仪器仪表学报,2021,42(4):92-101.
