0 引言
欺骗性干扰是指干扰机将截获到的信号经过部分复制后转发给雷达，使得对方雷达跟踪到虚假目标，从而保护真实目标，同时雷达系统还可能因为要处理的假目标太多而无法正常工作。现代雷达可通过发射正交波形来降低各子脉冲之间的互相关性，同时利用信号的随机性和不确定性使干扰信号脉压后的输出尽可能小，从而降低信号的截获概率，以此来抑制欺骗干扰。此外，多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达也要求发射正交波形，因此对正交波形的优化设计具有重要意义。
常用的正交波形形式是相位编码信号。文献[1-5]以自相关旁瓣最大值、互相关最大值、自相关旁瓣能量和互相关能量等的加权和为目标函数，设计具有良好正交性能的相位编码；文献[6]和[7]则以自相关和互相关函数的峰值旁瓣电平比(Peak Sidelobe Level Ratio, PSLR)以及积分旁瓣电平比(Integrated Sidelobe Level Ratio, ISLR)构建代价函数优化多相正交序列。但随着现代雷达技术的不断发展，单一的调制信号形式已不能满足现代信息化战争的新要求，从脉内、脉间多个维度设计复合调制波形可以提高信号的随机性和复杂度，从而降低雷达的截获概率，提升雷达的抗干扰能力。FSK-PSK信号就是一种常见的复合调制信号形式。唐璐[8]对跳频信号进行相位调制得到具有良好的随机性和低截获特性的FSK-PSK复合调制信号，Chang等[9]设计了比传统离散频率编码波形具有更好的正交性和更低的旁瓣的离散频率/相位编码波形(Discrete Frequency and Phase Coding Waveform, DFPCW)，张洋[10]通过优化信号捷变频率和脉内相位编码分别改善了信号的多普勒旁瓣水平和距离旁瓣水平，但这些文献并没有对欺骗干扰的抑制展开研究。
本文在以上研究的基础上，以脉内切片转发干扰(Intrapulse Slice Repeater Jamming , ISRJ)为例，设计脉内相位编码、脉间跳频编码的FSK-PSK正交波形来对抗压制干扰，以最小化子脉冲的自相关旁瓣电平和各个子脉冲之间的互相关函数电平加权和为准则，用0-1离散变量表示跳频和相位，将原优化问题转化为0-1整数规划问题，构造增广拉格朗日函数，对所有0-1变量求导，采用拟牛顿法求解优化问题模型，从而对FSK-PSK复合调制信号的跳频和相位进行联合优化。
1 信号形式和优化问题模型
1.1 FSK-PSK复合调制下的ISRJ
将一个脉宽为T的宽脉冲分为M个彼此相接的子脉冲，每个子脉冲的脉宽Tc=T/M，采用跳频编码序列对子脉冲进行调制。每个子脉冲中用长度为N的相位编码序列进行调制，每个码元的宽度Tp=Tc/N,为了提高信号的随机性和复杂度，每个子脉冲的相位编码序列均不相同。FSK-PSK复合调制信号模型如图1所示。
图1 FSK-PSK复合调制信号模型
那么信号的复包络可写为如下形式：
(1)
式中，um(t)表示第m个子脉冲信号：
(2)
其中，fm=σm/TP,m=1,2,…,M为频点，σm∈[1,2,…,M]为第m个子脉冲的跳频系数，本文假设每个子脉冲的跳频系数均不相同；cm(n)=ej2πdm(n)/K，n=0,1,…,N-1表示第m个子脉冲的相位编码序列，dm(n)∈[0,1,…,K-1]为相位离散值，K表示离散相位个数，pn(t)为宽度TP的理想矩形脉冲。
脉内切片转发干扰即部分脉冲转发干扰，是指干扰机对截获到的雷达发射信号按照预先设定的次数进行采样并转发形成的干扰，是一种典型的欺骗干扰形式，采样周期和采样时长的不同决定了不同的干扰形式。脉内切片转发干扰比脉间转发干扰的功率利用率更高，干扰形式也更加多样。
假设干扰机对所截获的FSK-PSK复合调制信号，在一个码元内采样NS点，即以TS=TP/NS为周期进行采样(切片)，随后将切片信号转发出去，形成脉内切片干扰信号，其信号形式如图2所示。
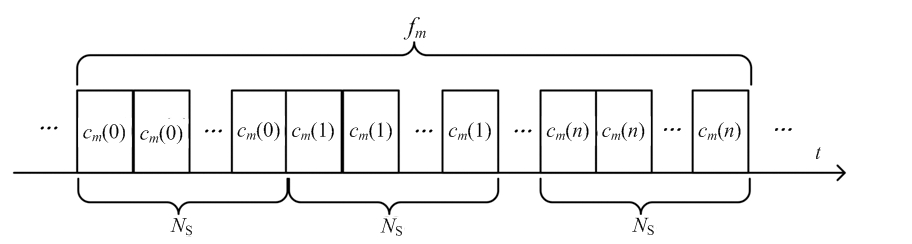
图2 ISRJ信号模型(第m个子脉冲)
那么整个脉冲共采样N′=NM·NS个点，采样后的第m个子脉冲信号可表示为
(3)
式中，
表示第m个子脉冲信号采样后的相位编码序列，
为宽度TS的理想矩形脉冲。
1.2 优化问题模型
利用式(3)计算第m个子脉冲和第l个子脉冲的互相关：
χml(τ)=
(4)
取τ=kTS,-(N′-1)≤k≤N′-1有
χml(kTS)=
(5)
将χml(kTS)简写为χml(k)，并定义：
表示克罗内克函数。
Hml,k=qml·rml,k·Jk·Dml
那么第m个子脉冲和第l个子脉冲的互相关函数的离散形式可表示为
(6)
当m=l时，式(6)表示第m个子脉冲的自相关函数的离散形式：
(7)
此时
为对抗ISRJ信号，可设计FSK-PSK脉内正交波形，以最小化子脉冲的自相关旁瓣电平和各个子脉冲之间的互相关函数电平加权和为准则建立目标函数，优化FSK-PSK复合调制信号。该问题的目标函数可表示为
f=
(8)
式中，Ψ=[k|NS≤|k|≤N′-1]表示自相关的副瓣范围，Ω=[k|0≤|k|≤N′-1]表示互相关函数范围；α∈[0,1]为加权系数，当α=1时，只抑制自相关函数副瓣部分即f1，而α=0时，只抑制互相关函数电平部分即f2。
考虑跳频系数σm和相位部分离散值dm(n)的整数约束以及各子脉冲跳频系数两两不同的约束条件，可建立如下优化问题模型：
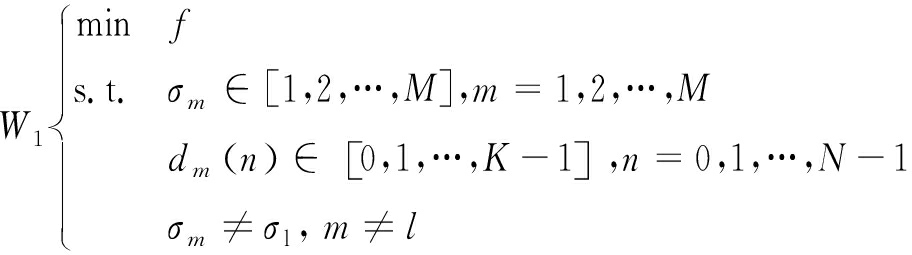
(9)
2 抗ISRJ的FSK-PSK正交波形优化方法
2.1 0-1整数规划模型
设
变量
，前M个变量组成向量bm=[δ1m,δ2m,…,δMm]T确定第m个子脉冲的跳频系数σm，后NK个变量组成向量em=[δ(M+1)m,δ(M+2)m,…,δ(M+NK)m]T确定第m个子脉冲相位部分离散值序列dm。这样δm=[bm;em]，σm=P·bm，dm(n)=L·[δ(M+nK+1)m,δ(M+nK+2)m,…,δ(M+nK+K)m]T，dm=IN⊗L·em，c′m=cm⊗FNS=ej2πdm/K⊗FNS，所有确定子脉冲的变量δm组合成待优化变量δ=[δ1;δ2;…;δM]M(M+NK)×1。
对于0-1离散变量δij，需要利用如下光滑处理的NCP(Nonlinear Complementarity Problem)函数[11]，将其转化成为连续问题：
(10)
式中u为极小的正数。问题W1可改写为如下形式：
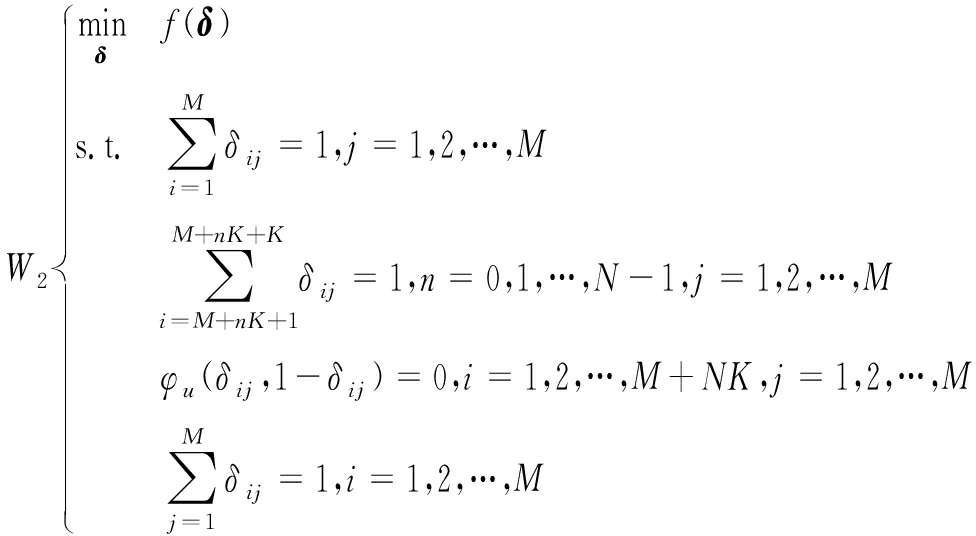
(11)
式中第一项约束条件是对跳频系数的整数约束，共M个，第二项约束条件是对相位部分离散值的整数约束，共MN个，第三项约束条件是关于0-1离散变量的NCP函数，共M(M+NK)个，第四个约束条件表示各子脉冲跳频系数两两不同，共M个。将所有约束条件进行如下描述：
hj(δ)=0,j=1,2,…，J
J=M+MN+M(M+NK)+M
(12)
通过增广拉格朗日乘子法将该优化问题转化为无约束优化问题可得
L(δ,λ,γ)=
(13)
式中λ=[λ1,λ2,…,λJ]T为拉格朗日乘子λj组成的向量，γ=[γ1,γ2,…,γJ]T为惩罚因子γj组成的向量。采用拟牛顿法求解无约束优化问题得到：δ=argminL(δ,λ,γ)。这一方法需要对变量求导。
首先对目标函数表达式(8)作如下转换：
f(δ)=
(14)
式中
而yml,k=χml(k)。增广拉格朗日函数对变量δm求导时可将δm拆分成跳频部分变量bm和相位部分变量em分别求导。本文求导时采用分子布局。
2.2 优化跳频
2.2.1 目标函数求导
对于自相关函数f1(δ)，根据求导链式法则得
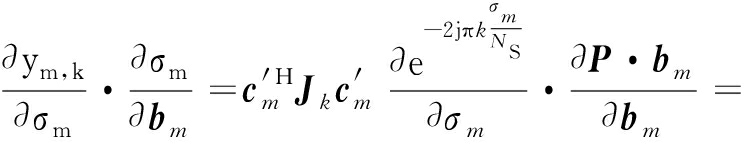
(15)
对于互相关函数f2(δ)：
(16)
求式(16)中各项：
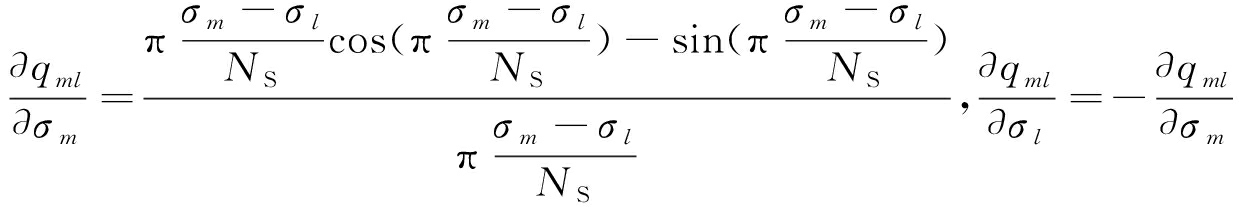
(17)
那么函数f1(δ)、f2(δ)分别对跳频部分变量求导得
(18)
则目标函数对跳频部分求导得
(19)
2.2.2 约束条件求导
约束条件对变量δim(1≤i≤M,m=1,2,…,M)求导，此时δim∈bm。
(20)
式中vm=M(N+1)+(m-1)(M+NK)。
2.3 优化相位
2.3.1 目标函数求导
自相关函数对相位部分求导：
(21)
计算式(21)中各项：
=j2π/K·diag[cm(n)(n=0,
1,…,N-1)]
(22)
将式(22)代入式(21)并化简可得
(23)
互相关函数对相位部分变量求导得
(24)
根据式(22)可求式(24)并化简：
(25)
那么函数f1(δ)、f2(δ)分别对相位部分变量求导得
(26)
则目标函数对相位部分变量求导得
(27)
2.3.2 约束条件求导
约束条件对变量δim(M+1≤i≤M+NK,m=1,2,…,M-1)求导，此时δim∈em。
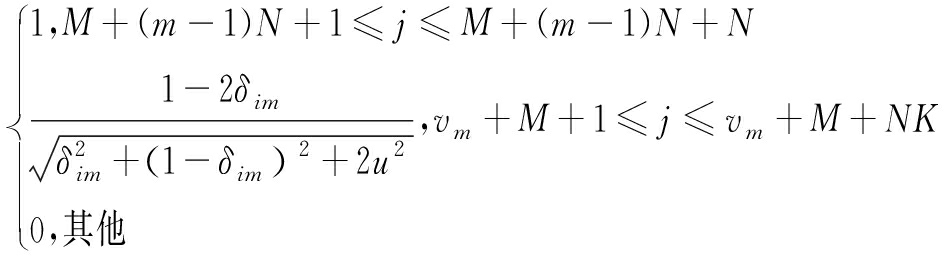
(28)
式中vm=M(N+1)+(m-1)(M+NK)。
2.4 抗ISRJ的FSK-PSK正交波形优化算法
根据式(19)和(27)，可得目标函数对第m个子脉冲的所有变量组成的向量δm的求导公式：
(29)
目标函数和约束条件分别对变量δ进行求导可用如下公式表示：
(30)
那么增广拉格朗日函数对变量δ的求导公式可表示为
(31)
得到增广拉格朗日函数对变量的求导公式后，通过增广拉格朗日乘子法将原优化问题转化为一个无约束的优化问题，可采用拟牛顿法进行求解。
基于FSK-PSK复合调制的抗ISRJ波形优化算法步骤如表1所示。
表1 基于FSK-PSK复合调制的抗ISRJ波形优化算法步骤
算法:抗ISRJ的FSK-PSK正交波形设计Step0:随机产生初始的跳频系数和相位编码序列,由此确定初始的δ(0),初始化λ(0)、γ(0),设迭代次数t=0;Step1:采用拟牛顿法求解δ(t+1)=argminLδ,λ(t),γ(t) ;Step2:设收敛门限为ε,若∑Jj=1hj(δ(t+1))<ε则算法终止,否则转到Step3;Step3:更新惩罚因子,若∑Jj=1|hj(δ(t+1))|∑Jj=1|hj(δ(t))|>θ则γ(t+1)j=2γ(t)j,否则γ(t+1)j=γ(t)j;Step4:更新拉格朗日乘子λ(t+1)j=λ(t)j+γ(t)jhj(δ(t));Step5:令t←t+1,返回Step1。
3 仿真结果与分析
定义脉内子脉冲信号的自相关平均副瓣电平(Auto-correlation Average Sidelobe Level, AASL)、互相关平均电平(Cross-correlation Average Level, CCAL)如下：
(32)
式中，Ψ=[k|NS≤|k|≤N′-1]表示自相关函数的副瓣范围，Ω=[k|0≤|k|≤N′-1]表示互相关函数范围。
对于一组子脉冲数目M=4，跳频系数σm={2,1,4,3}，相位编码码长N=50，离散相位数分别为K=2/4/8的FSK-PSK信号，其相位编码序列与PSK信号完全相同，两种信号的AASL和CCAL值如表2所示。
表2 PSK和FSK-PSK信号对比
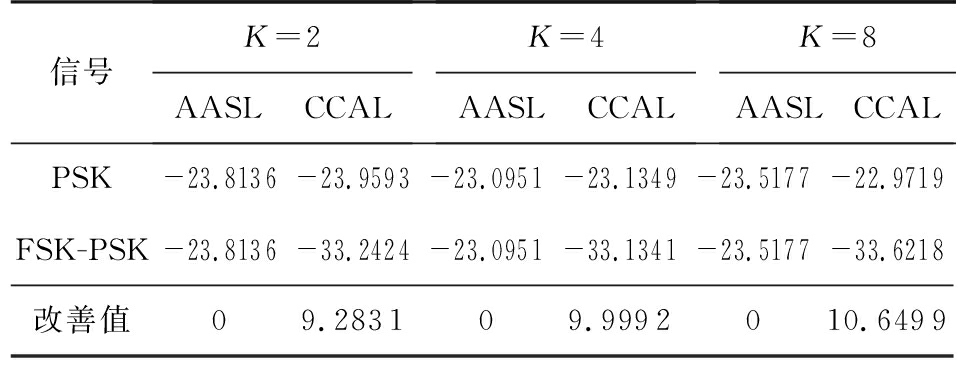
信号 K=2AASLCCALK=4AASLCCALK=8AASLCCALPSK-23.8136-23.9593-23.0951-23.1349-23.5177-22.9719FSK-PSK-23.8136-33.2424-23.0951-33.1341-23.5177-33.6218改善值09.283109.9992010.6499
由表中数据可知，FSK-PSK信号相对于PSK信号，其子脉冲的自相关平均旁瓣电平是相当的，但其子脉冲互相关平均电平比PSK信号低了10 dB左右。
设置一组子脉冲数目M=4，跳频系数σm={1,2,3,4}，相位编码码长N=50，离散相位数为K=4的FSK-PSK信号，其各子脉冲的自相关模糊函数图如图3所示，从图中可以看出， FSK-PSK复合调制信号自相关旁瓣较低，且随着多普勒频移增大，其自相关主峰依然保持较高水平，具有较好的多普勒频移容忍度。
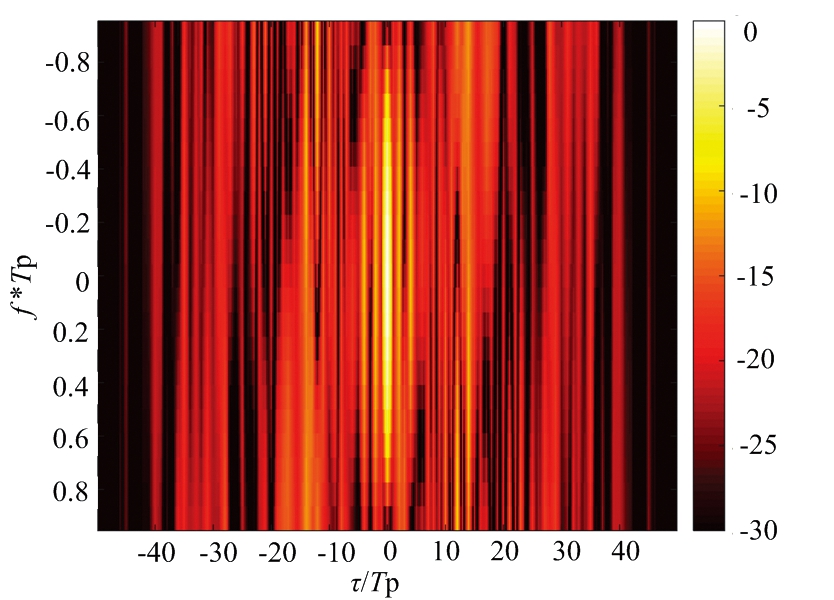
(a) 子脉冲1自相关模糊函数
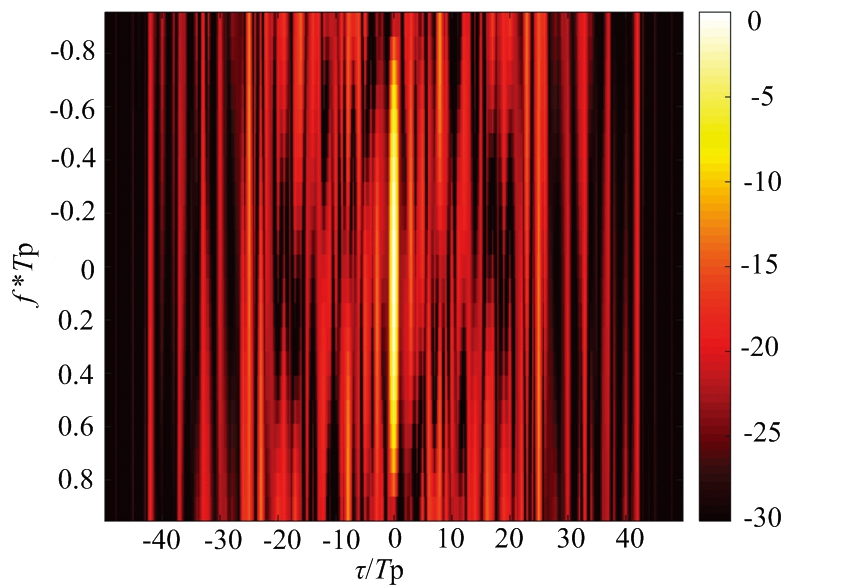
(b) 子脉冲2自相关模糊函数
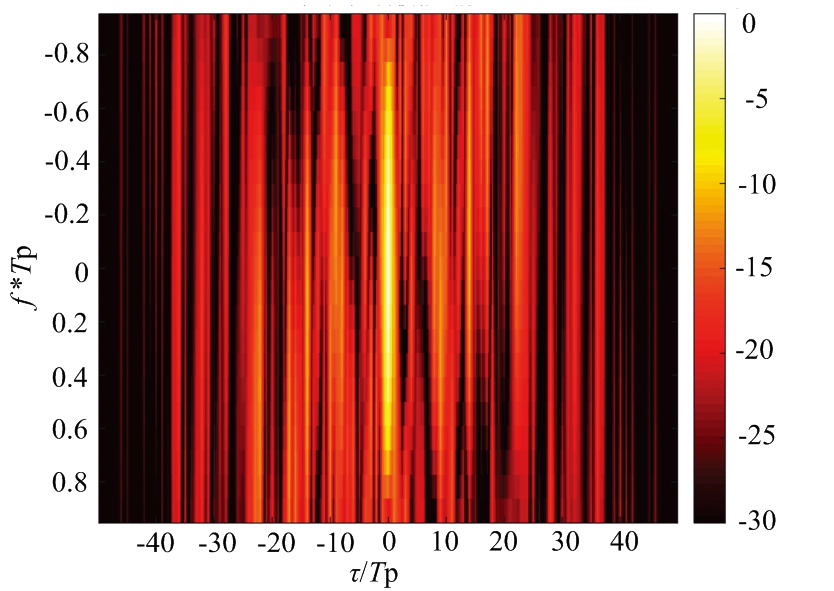
(c) 子脉冲3自相关模糊函数
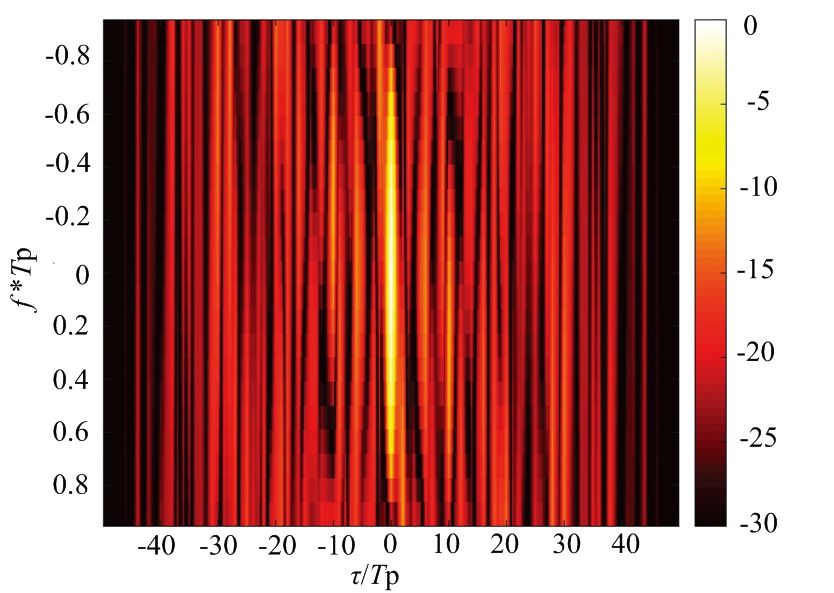
(d) 子脉冲4自相关模糊函数
图3 FSK-PSK复合调制信号自相关模糊函数
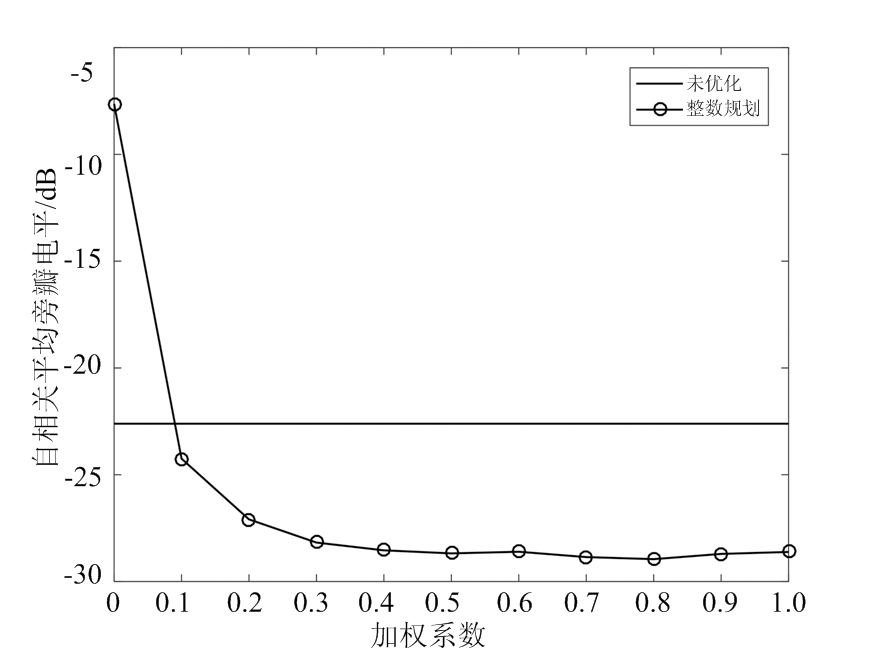
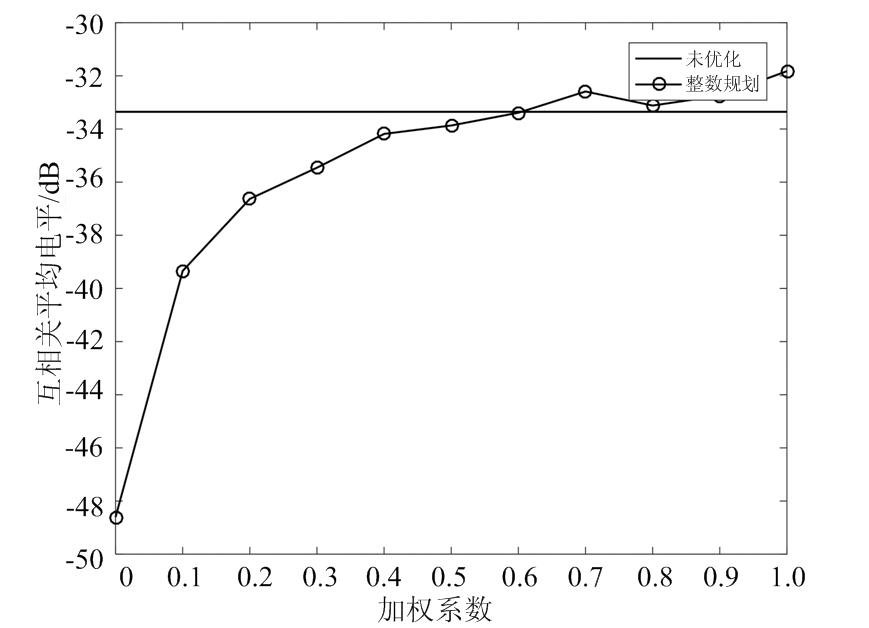
设计FSK-PSK信号的子脉冲数目M=4，子脉冲信号的初始跳频系数分别对应了σm={1,2,3,4}，子脉冲信号的相位编码码长N=50，离散相位数K=4。设置优化模型的加权系数分别为α={0,0.1,…,1}，固定跳频系数仅优化相位的FSK-PSK信号和跳频相位联合优化的FSK-PSK信号，其自相关和互相关优化前后结果对比如图4所示, 具体优化数据结果如表3所示，其中初始波形AASL=-22.610 8 dB，CCAL=-33.353 8 dB。
(a) 自相关结果对比
(b) 互相关结果对比
图4 FSK-PSK信号的自相关和互相关优化前后对比
表3 优化后的跳频序列和AASL、CCAL值
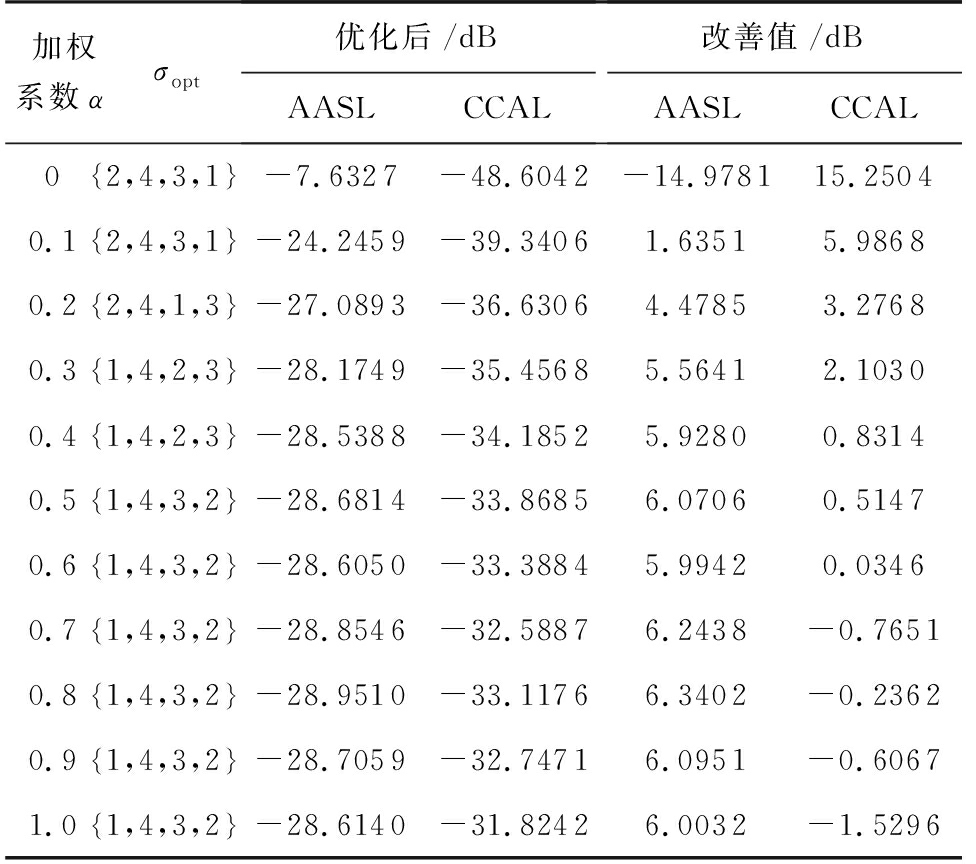
加权系数ασopt优化后/dBAASLCCAL改善值/dBAASLCCAL02,4,3,1 -7.6327-48.6042-14.978115.25040.12,4,3,1 -24.2459-39.34061.63515.98680.22,4,1,3 -27.0893-36.63064.47853.27680.31,4,2,3 -28.1749-35.45685.56412.10300.41,4,2,3 -28.5388-34.18525.92800.83140.51,4,3,2 -28.6814-33.86856.07060.51470.61,4,3,2 -28.6050-33.38845.99420.03460.71,4,3,2 -28.8546-32.58876.2438-0.76510.81,4,3,2 -28.9510-33.11766.3402-0.23620.91,4,3,2 -28.7059-32.74716.0951-0.60671.01,4,3,2 -28.6140-31.82426.0032-1.5296
从图4和表3可以看出，随着加权系数的增加，对自相关部分的优化比重增加，而对互相关部分的优化比重相应降低，因此优化后的AASL值整体呈下降趋势、CCAL值整体呈上升趋势，加权系数α∈[0.1,0.6]时优化后的波形相较于初始信号，其自相关旁瓣和子脉冲互相关均能得到抑制。
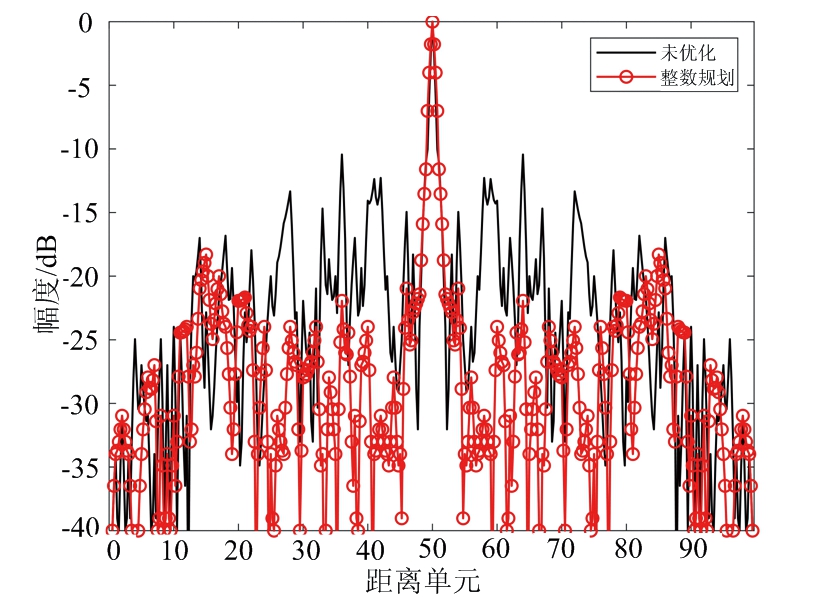
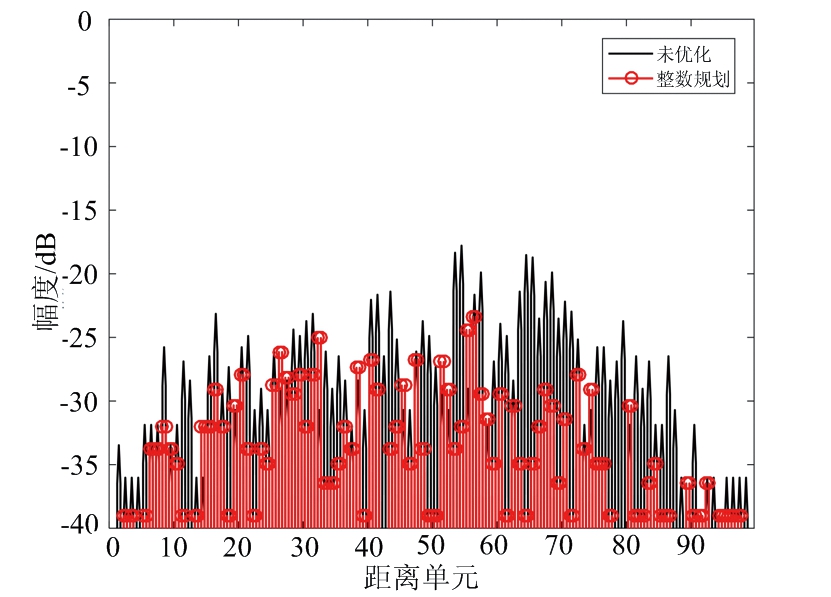
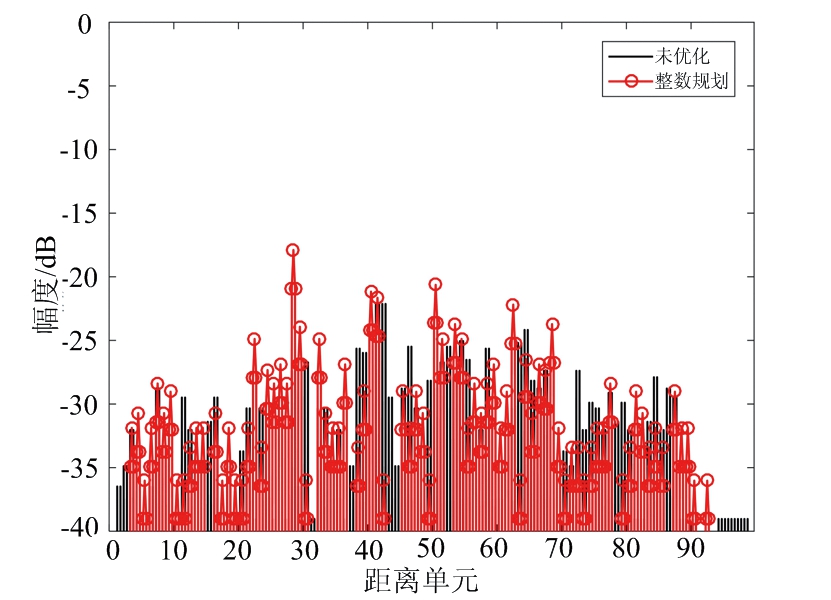
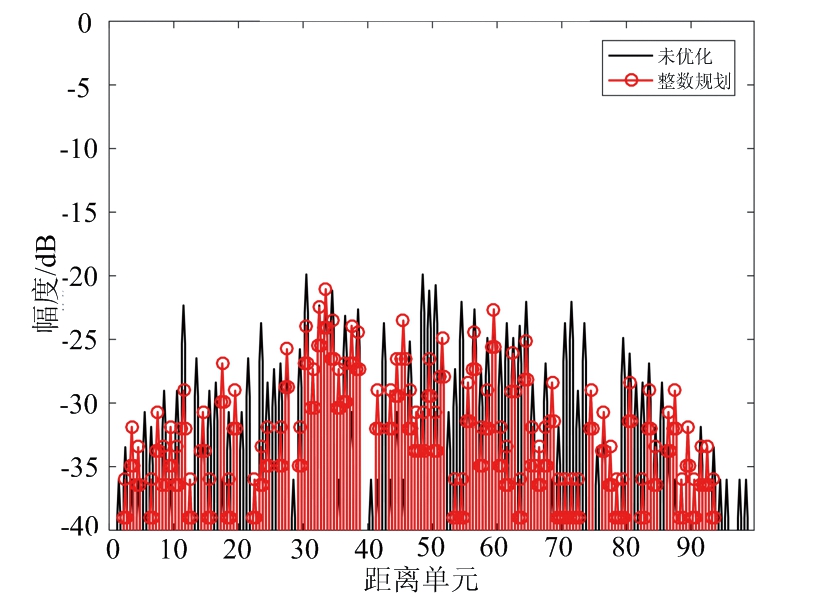
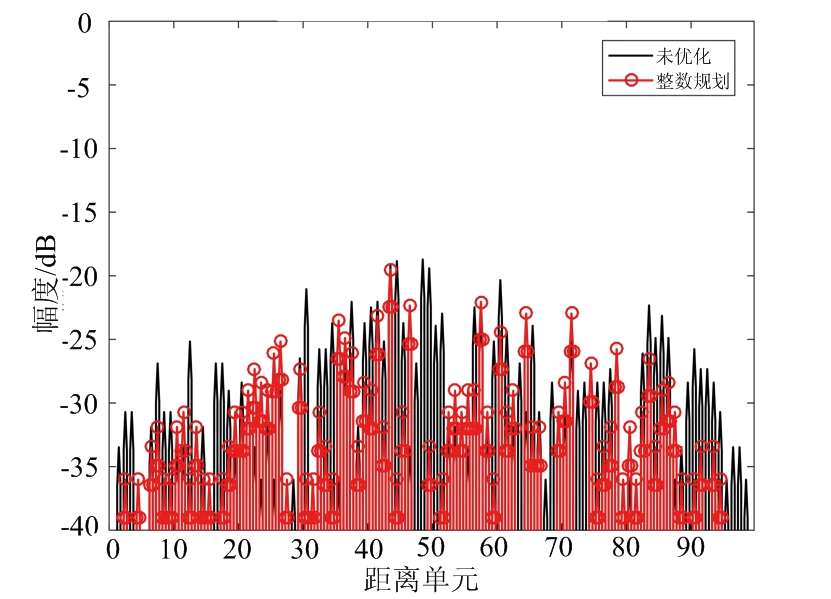
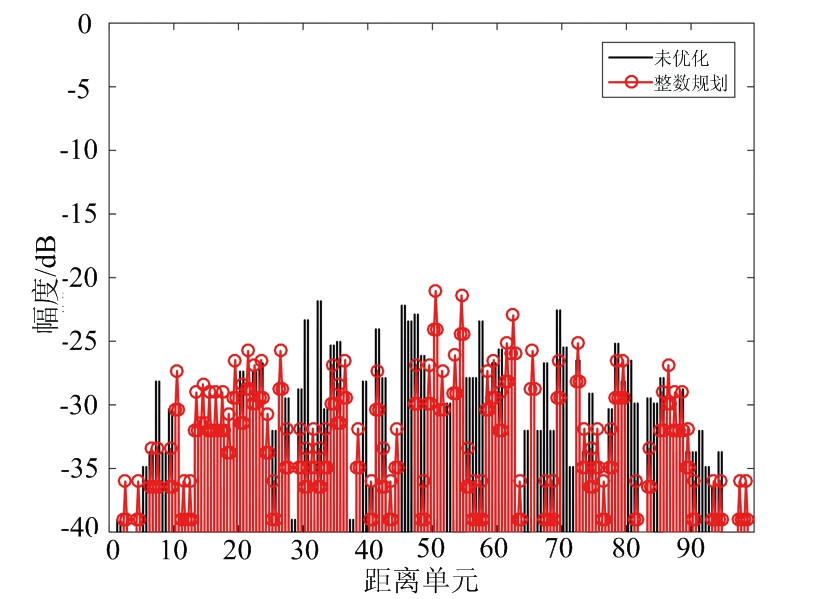
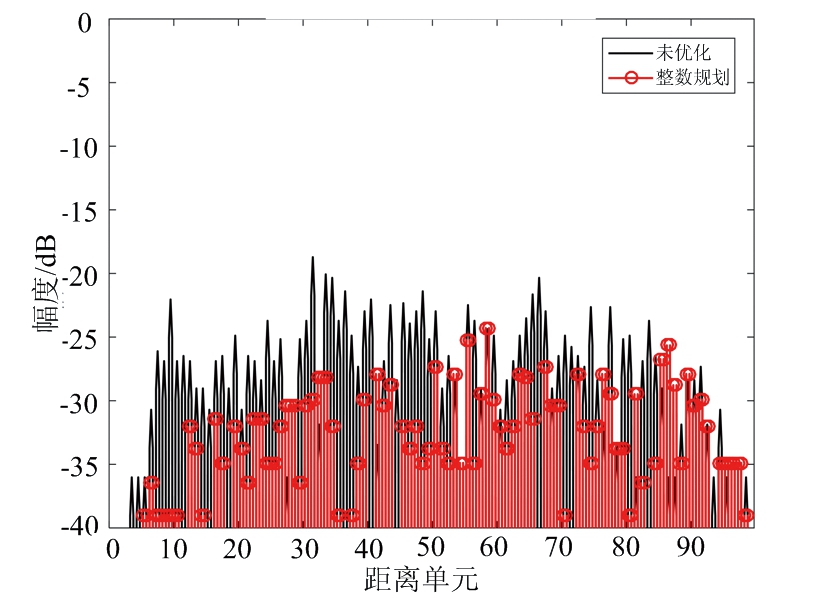
设置加权系数α=0.2，FSK-PSK信号的子脉冲数目M=4，子脉冲信号的相位编码码长N=50，离散相位数K=4，初始跳频系数设为σm={1,2,3,4}，优化后各子脉冲跳频系数和相位编码信息如表4所示，各个子脉冲的自相关和互相关结果如图5所示。从图5可以看出，优化波形的自相关和互相关均明显低于未优化波形。
表4 优化后的正交FSK-PSK复合调制信号
子脉冲跳频系数相位编码122,2,1,3,2,3,3,0,0,3,1,0,0,3,1,1,0,2,2,3,0,0,0,3,2,1,1,0,3,3,3,2,1,1,1,1,0,3,0,3,3,3,3,2,3,3,2,2,3,3242,2,3,3,0,0,0,2,2,2,3,3,3,0,3,3,3,3,2,3,2,1,2,3,3,2,1,2,2,0,0,0,0,3,0,0,0,2,1,2,1,1,2,2,1,0,3,3,3,2311,1,1,1,1,2,1,3,3,2,1,1,3,3,0,0,0,0,0,0,3,3,3,3,2,0,1,1,3,0,1,2,3,0,0,0,0,1,0,0,2,3,1,2,1,0,3,0,2,1433,1,3,0,2,3,0,3,3,3,2,3,3,1,2,2,2,2,2,2,2,2,3,3,0,0,0,3,3,0,1,2,2,2,0,0,0,0,1,1,1,3,3,3,2,1,1,1,0,3
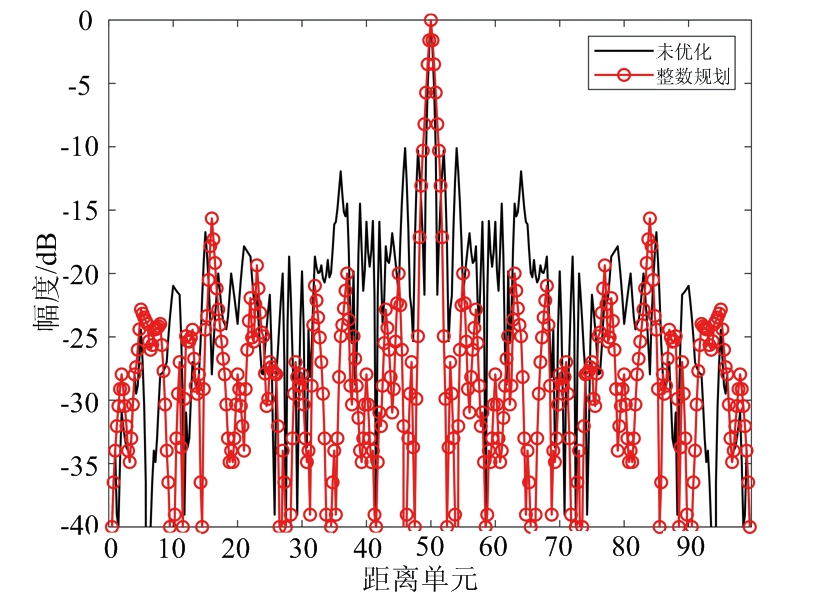
(a) 子脉冲1自相关
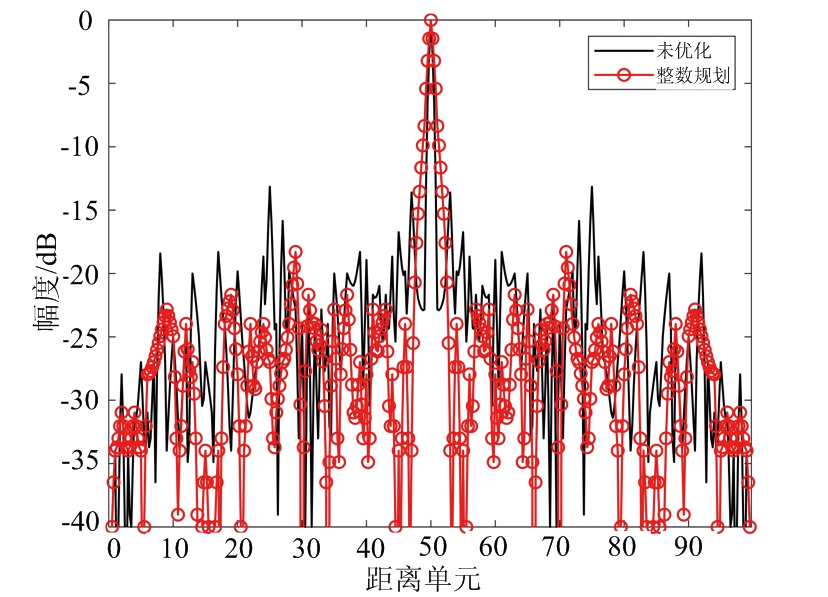
(b) 子脉冲2自相关
(c) 子脉冲3自相关
(d) 子脉冲4自相关
(e) 子脉冲1、2互相关
(f) 子脉冲1、3互相关
(g) 子脉冲1、4互相关
(h) 子脉冲2、3互相关
(i) 子脉冲2、4互相关
(j) 子脉冲3、4互相关
图5 优化前后自相关和互相关对比
对一组子脉冲数M=4的FSK-PSK复合调制信号，设置加权系数α=0.2，子脉冲信号的相位编码离散相位数K=4，码长N分别为40、60、80，初始跳频系数σm={1,2,3,4}，优化后的跳频系数σopt以及优化前后的AASL和CCAL如表5所示。
表5 不同序列长度波形优化前后性能对比
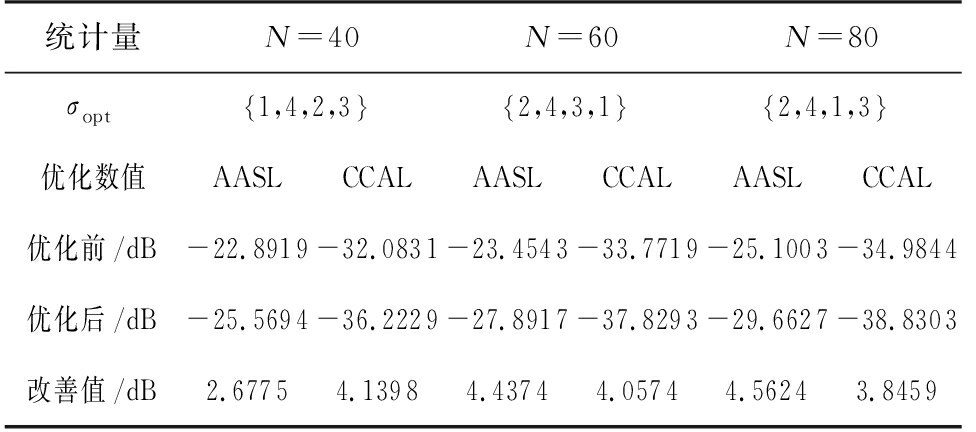
统计量N=40N=60N=80σopt1,4,2,3 2,4,3,1 2,4,1,3 优化数值AASLCCALAASLCCALAASLCCAL优化前/dB-22.8919-32.0831-23.4543-33.7719-25.1003-34.9844优化后/dB-25.5694-36.2229-27.8917-37.8293-29.6627-38.8303改善值/dB2.67754.13984.43744.05744.56243.8459
从表中数据可知，对不同长度的FSK-PSK信号序列经优化后其自相关旁瓣和互相关均能被抑制，且子脉冲序列越长，优化后的AASL和CCAL值越小，抗脉内切片转发干扰的能力越强。
4 结束语
FSK-PSK复合调制信号比PSK信号的抗干扰性能更好，因此本文采用FSK-PSK复合调制信号作为发射波形，以最小化子脉冲的自相关旁瓣电平和各个子脉冲之间的互相关函数电平加权和为准则，用0-1离散变量表示跳频和相位，考虑子脉冲跳频和相位编码序列的相位离散值的整数约束以及各子脉冲跳频两两不同的约束条件，构建抗脉内切片转发干扰的FSK-PSK正交波形设计优化问题模型，进行0-1整数规划。将约束条件写入增广拉格朗日函数，通过增广拉格朗日乘子法将原优化问题转化为无约束优化问题，对变量求导，采用拟牛顿法求解。
本文通过仿真验证了FSK-PSK复合调制信号与简单形式的PSK信号相比，其子脉冲的自相关平均旁瓣电平是相当的，但其子脉冲互相关平均电平比PSK信号显著降低，用FSK-PSK信号设计正交波形能够提升雷达的抗干扰性能。在选取合适的加权值时，本文设计的FSK-PSK复合调制信号能够同时有效抑制子脉冲的自相关旁瓣和互相关电平，并且其子脉冲序列长度越长，性能越好。
[1] 谢雷振, 陈怡君, 康乐, 等. 遗传-和声搜索算法下的MIMO雷达正交多相码设计[J]. 电光与控制, 2018, 25(8):23-27.
[2] XIE Leizhen, LI Kaiming, LI Wangyang, et al. Design of MIMO Radar Orthogonal Polyphase Code Based on Improved Artificial Bee Algorithm[C]∥ 2019 IEEE 2nd International Conference on Electronic Information and Communication Technology,Harbin,China:IEEE, 2019:507-511.
[3] PEI Bingnan, PEI Tengda, ZHANG Haosheng. Orthogonal Waveform Design of MIMO Radar Based on Niche Genetic Algorithm[C]∥ 2020 IEEE International Conference on Signal Processing, Communications and Computing, Shanghai, China:IEEE, 2020:1-6.
[4] 扈月松, 史小斌, 马兰. 一种基于遗传算法的正交波形设计方法[J]. 火控雷达技术, 2021, 50(1):8-14.
[5] ZHANG Lei, WEN Fangqing. A Novel MIMO Radar Orthogonal Waveform Design Algorithm Based on Intelligent Ions Motion[J]. Remote Sensing, 2021, 13(10):1968.
[6] REDDY B R, KUMARI M U. Polyphase Orthogonal Waveform Using Modified Particle Swarm Optimization Algorithm for MIMO Radar[C]∥2012 IEEE International Conference on Signal Processing, Computing and Control, Solan, India: IEEE, 2012:1-6.
[7] RAMARAKULA M, RAMANA V. Optimization of Polyphase Orthogonal Sequences for MIMO Radar Using Genetic Algorithm with Hamming Scan[C]∥ 2019 IEEE International Conference on Advanced Networks and Telecommunications Systems, Goa,India:IEEE, 2019:1-5.
[8] 唐璐. 低截获概率信号及其低副瓣脉压技术研究[D]. 西安:西安电子科技大学, 2015.
[9] CHANG G H, YU X, YU C. Discrete Frequency and Phase Coding Waveform for MIMO Radar[J]. Radioengineering, 2017, 26(3):835-841.
[10] 张洋. 弹载环境下雷达抗干扰波形设计研究[D]. 哈尔滨:哈尔滨工业大学,2019.
[11] RUI S P, XU C X. Inexact Non-Interior Continuation Method for Monotone Semidefinite Complementarity Problems[J]. Optimization Letters, 2012, 6(7):1411-1424.
