0 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种具有全天时、全天候、植被穿透等特点的有源微波遥感设备，通过发射高带宽信号，结合沿航迹运动形成合成孔径，获得距离向和方位向的高分辨率遥感图像，广泛应用于地球科学与遥感领域[1]。但是，由于全球电磁频谱的共享，SAR系统容易遭受来自其他电磁设备的干扰[2-3]。窄带干扰(Narrow-Band Interference, NBI)是SAR系统常见的干扰形式之一，其带宽相比于SAR有用信号更窄(通常小于1%)[4]。由于SAR系统具有较大的相干信号处理增益和一定的抗干扰能力，低功率的NBI对SAR的聚焦成像影响不大。而对于功率更强的NBI，其存在将扰乱SAR信号的脉冲响应，加剧SAR图像的解译难度[5]。因此，有效的抑制干扰对发挥SAR系统的应用效能具有重要的研究意义。
迄今为止，已有多种SAR系统NBI抑制方法相继被提出，根据处理手段的不同可分为参数化、半参数化和非参数化抑制方法。与参数化和半参数化方法相比，非参数化方法不需要复杂的建模和超参数优化，在工程中易于实现[6]。基于经验模态分解(Empirical Mode Decomposition, EMD)的NBI抑制方法是一种非参数化方法，通过EMD将含干扰的SAR信号分解为一系列本征模态函数(Intrinsic Modal Functions, IMF)，分离出代表干扰的分量后重构有用信号，从而达到干扰抑制的目的[7-9]。但是，当原始信号极值点分布不均匀时，EMD方法会存在模态混叠现象，这时NBI与有用信号无法完全分离，并且EMD分解后用以重构有用信号的IMF选择仍然依赖于主观经验，容易造成重构误差，导致NBI抑制后的SAR图像中出现虚影。
为了解决上述问题，本文提出一种基于互补集合经验模态分解(Complementary Ensemble EMD, CEEMD)和排列熵(Permutation Entropy, PE)的NBI抑制方法。CEEMD算法使用正态分布的正负白噪声将信号自动分配到合适的参考尺度，从而解决EMD算法中出现的模态混叠问题[10-11]。在所提方法中，利用矩峰度系数法逐脉冲检测原始回波中是否存在NBI[12]。使用CEEMD将含干扰回波分解为一系列IMF，计算出各IMF的PE，选取阈值去除NBI重构有用信号[13]。
1 基本理论
1.1 NBI信号模型
在复杂的电磁环境中，来自同频段其他电磁设备带来的干扰，为后续的SAR信号处理和图像解译工作带来困难。SAR系统工作时接收到的原始信号通常叠加到距离向快时间和方位向慢时间的二维域中，经正交解调和数字采样后，含NBI的SAR回波数据可表示为
S(tf,tl)=e(tf,tl)+i(tf,tl)+n(tf,tl)
(1)
式中：e(tf,tl)，i(tf,tl)和n(tf,tl)分别表示有用回波信号、NBI信号和系统噪声；tf=1,2,…,Nr和tl=1,2,…,Na分别表示距离向快时间和方位向慢时间；Nr和Na分别表示距离和方位采样数。
通常，NBI可以建模为多个复正弦波之和，其中包含M个频率分量，即
i(tf,tl)=
(2)
式中，Ak(tf,tl)，fk和φk(tf,tl)分别表示第k个NBI信号的幅度、频率和相位。
如前文所述，NBI与有用信号相比应具有足够强的功率才能对SAR系统的成像造成明显的影响。在此假设下，有用信号具有类似噪声的频谱。则式(2)可改写为
(3)
式中，n′(tf,tl)=e(tf,tl)+n(tf,tl)在以下讨论中定义为等效附加噪声。
1.2 EMD算法
EMD是一种自适应信号时频处理方法，其根据数据本身的时标特性进行信号分解，无需预先设置基函数，可以将复杂信号分解为不同的IMF，分解后的任意两个IMF都是相互独立的[8-9]。复信号s(t)的EMD分解步骤如下。
步骤1： 找出信号s(t)的所有极值点，通过三次样条插值连接局部极值点形成上下包络线。上下包络包含所有数据点。
步骤2： 从上包络和下包络的平均值
得到
(4)
若f1(t)满足IMF的条件，则可以认为f1(t)是s(t)的第一个IMF分量。
步骤3： 若f1(t)不符合IMF条件，则将f1(t)作为原始数据，重复步骤1、2，得到上、下包络的均值
通过计算
是否适合IMF分量的必备条件，若不满足，重复如上两步k次，直到满足前提下得到第1个IMF，表示为：c1(t)=fk+1(t)。
步骤4： 将c1(t)从信号s(t)中分离得到r1(t)=s(t)-c1(t)。将r1(t)作为原始信号重复上述三个步骤，得到第二个IMF分量c2(t)。循环n次，直到第n个IMF分量。
步骤5： 重复上述步骤至余项rn(t)为单调函数或其值小于预先给定的阈值，EMD分解结束。所有IMF分量和残余分量之和为原始信号s(t)：
(5)
基于EMD的NBI抑制方法通过将含干扰的SAR原始回波信号经过EMD分解，去除含NBI的IMF分量以重构有用信号[7]。但是当原始信号中含有间歇性干扰、噪声等使信号极值点分布不均匀的成分时，模态混叠问题则会成为EMD方法的明显劣势。经EMD分解后的单个IMF可能同时包含NBI和有用信号，在去除NBI的同时造成有用信号缺失导致成像时图像中产生虚影。
2 基于CEEMD和PE的NBI抑制方法
针对上述问题，本文提出了一种基于CEEMD和PE的NBI抑制方法，具体流程如图1所示。相比于EMD方法，本文所提方法使用CEEMD算法并使用了基于PE分类IMF的处理步骤。
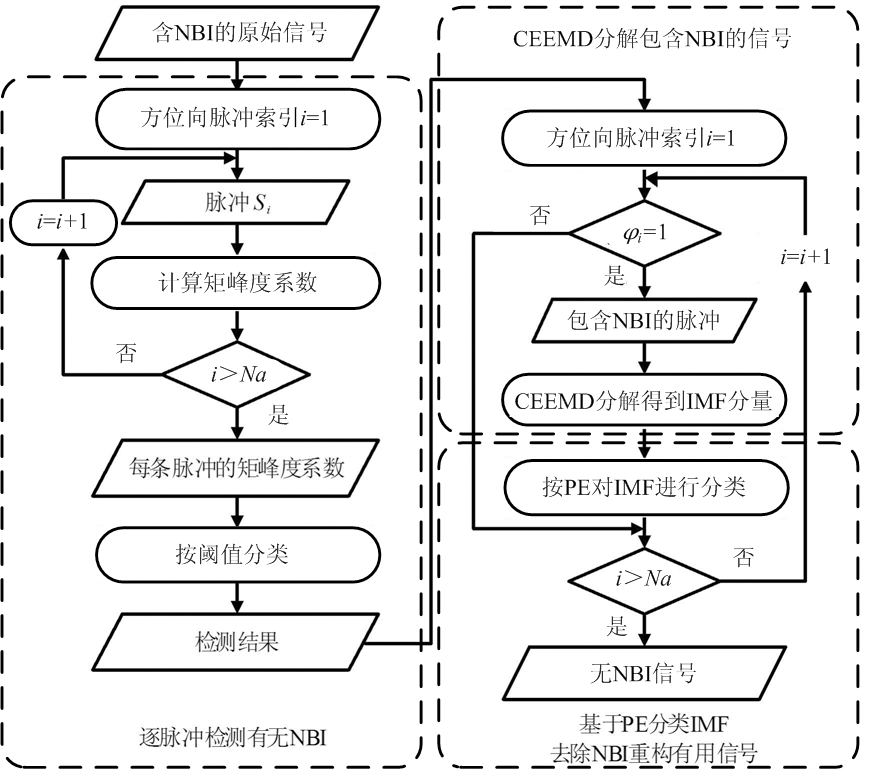
图1 基于CEEMD和PE的NBI抑制方法流程图
2.1 矩峰度系数法检测NBI
为了准确高效地抑制原始信号中的NBI，尽可能保护有用信号，需要在抑制工作前进行干扰检测。不同于频域陷波法需要准确检测NBI在频域中的位置[14]，所提方法只需将包含NBI的回波与不包含NBI的回波分开处理。当NBI功率较强时，会引起整个回波信号的某些特征异常，可以统计这些异常特征进行检测工作。矩峰度系数检测法是一种典型的统计参数法，可以根据回波分布的陡峭程度快速地检测出原始回波是否包含NBI[12]。
假设s为随机变量，均值为u，σ为标准差，矩峰度系数可定义为
(6)
它表征的是分布的陡峭程度，通常是相对于正态分布的统计量。如果峰度大于3，则表示样本具有陡峭的分布，相反，则表示具有平坦的分布。一般来说，SAR回波信号的幅度谱比较平坦，采样数据满足零均值高斯分布，幅度服从瑞利分布。但是，当回波信号中包含强NBI时，SAR回波的分布会变得陡峭。所以阈值分割的操作可以表示为
(7)
式中，
是检测结果，常数1和0分别标记NBI的存在与否。
2.2 CEEMD分解含NBI脉冲
CEEMD算法能够有效克服EMD存在的模态混叠现象，并且由于其分解过程是将原信号加上白噪声和原信号减去白噪声两个信号同时经过EMD之后求均值，可以抵消原信号中加入的噪声。具体算法流程如图2所示。
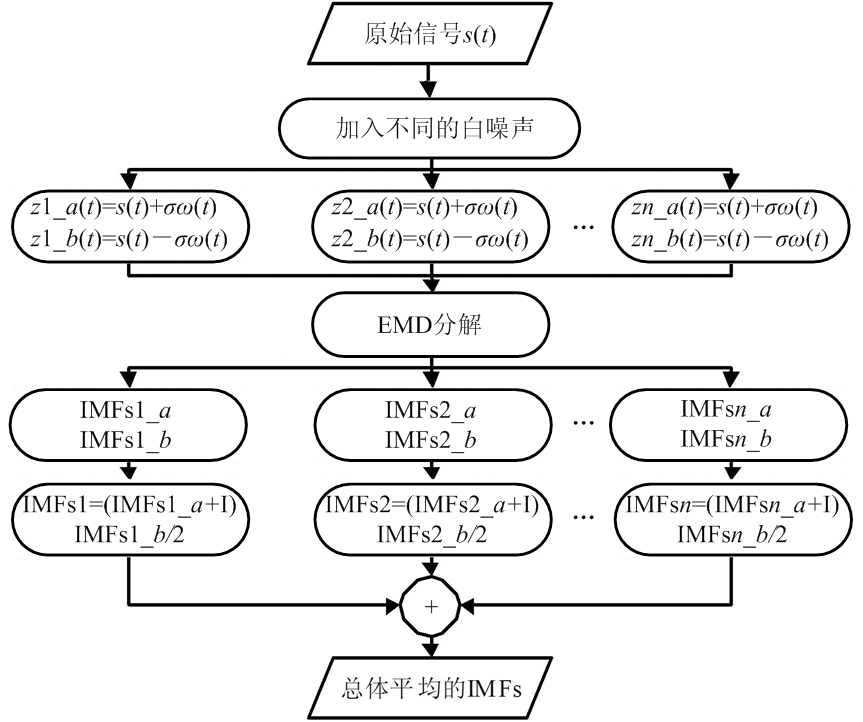
图2 CEEMD算法流程图
步骤1： 在原始信号中加入一对相反的正负白噪声作为辅助噪声，得到
z1,2(t)=s(t)±σω(t)
(8)
步骤2： 将具有正负白噪声的信号分别进行EMD分解，得到两组IMF分量。
步骤3： 重复n次步骤1和步骤2，每次加入一个新的正态分布正负白噪声序列。
步骤4： 计算两组IMF分解后的平均值，然后对n组IMF求平均值，得到最终的IMF分量。
将检测出的含NBI回波信号经上述步骤逐脉冲进行CEEMD分解，可以得到一系列分别含NBI和有用信号的IMF分量。
2.3 基于PE的IMF分类
PE是一种时域信号突变检测方法，能够方便、准确地定位突变发生的时刻[13]。计算CEEMD分解出的每个IMF分量的PE值得到全局阈值以区分NBI和有用信号，去除NBI后对有用信号进行重构，通过传统的成像算法得到聚焦良好的SAR图像。PE计算步骤如下。
步骤1： 重构长度为Nr的时间序列{S(i),i=1,2,…,Nr}得到相空间矩阵X。矩阵的每一行是相空间长度的序列，可以表示为
X=
(9)
式中，m为嵌入维数，τ为延迟时间，L=N-(m-1)τ。
步骤2： 对相空间矩阵X中的第j个重构分量S(j),S(j+τ),…,S[j+(m-1)τ]按照数值大小升序重新排列，j1,j2,…,jm表示重构分量中各元素所在列的索引，即
S[i+(j1-1)τ]≤S[i+(j2-1)τ]≤…≤
S[i+(jm-1)τ]
(10)
步骤3： 若重构分量中存在相等的值，则按照j1,j2的大小排序，任意时间序列S(i)经相空间重构所得的重构矩阵的每一行都能得到一组符号序列，m维相空间映射有m!种不同的符号序列。若将每一种符号序列出现的概率记为P1,P2,…,Pk，按照信息熵的定义，时间序列S(i)的k种不同符号序列的排列熵定义为
(11)
当Pj=1/m!时，HPE(m)达到最大值ln(m!)，此时m阶的PE可以归一化为
HPE=HPE(m)/ln(m!)
(12)
由以上计算步骤可知，HPE的值越大表示时间序列复杂度越高，因此通过阈值选择IMF的操作可以表示为
(13)
式中，
是检测结果，常数1和0分别标记NBI和有用信号。
3 实验结果与分析
为了验证本文所提方法的性能，进行了基于RADARSAT-1星载SAR数据和仿真NBI抑制实验，分别使用频域陷波法[14]、基于EMD的NBI抑制方法[7]和本文所提方法进行对比。主要实验数据及干扰仿真参数如表1所示。
表1 实验数据及干扰仿真参数
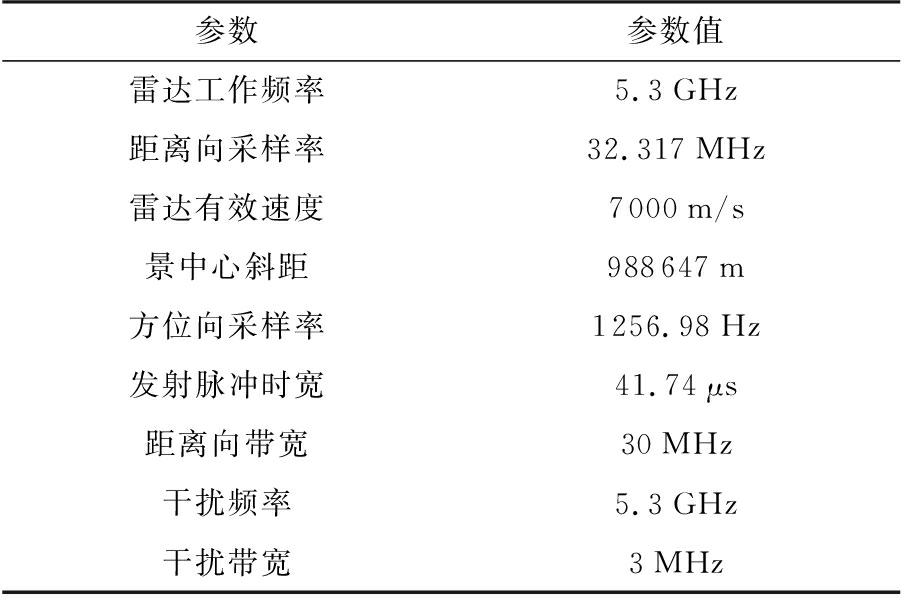
参数参数值雷达工作频率5.3GHz距离向采样率32.317MHz雷达有效速度7000m/s景中心斜距988647m方位向采样率1256.98Hz发射脉冲时宽41.74μs距离向带宽30MHz干扰频率5.3GHz干扰带宽3MHz
图3为实验数据图像和NBI抑制结果。图3(a)为含干扰SAR图像，可以看出由于NBI的存在，场景中出现交错状明亮条纹，并掩盖了部分真实地物及地貌信息。图3(b)～(d)分别为频域陷波法、基于EMD的NBI抑制方法以及本文所提方法NBI的抑制结果。从抑制效果来看，3种方法均能有效抑制图像中的干扰信号。
图3 实验数据及NBI抑制结果
为进一步对比3种干扰抑制方法的性能，在图3中选取4种区域图像(包括港口、河流、城镇和农田)进行详细分析，结果如图4所示。从图4可以看出，频域陷波法在频域进行陷波处理使部分频谱丢失，导致目标响应异常，造成图像散焦；EMD方法由于模式混叠问题，导致图像中出现虚影；相比之下，本文所提方法在去除NBI的基础上，有效保留了地物目标信息，成像效果更好。
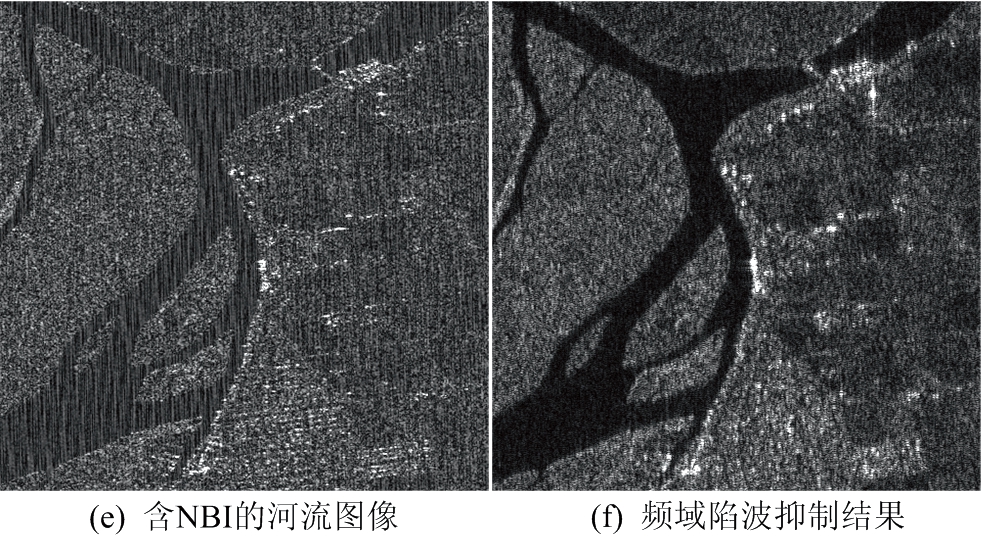
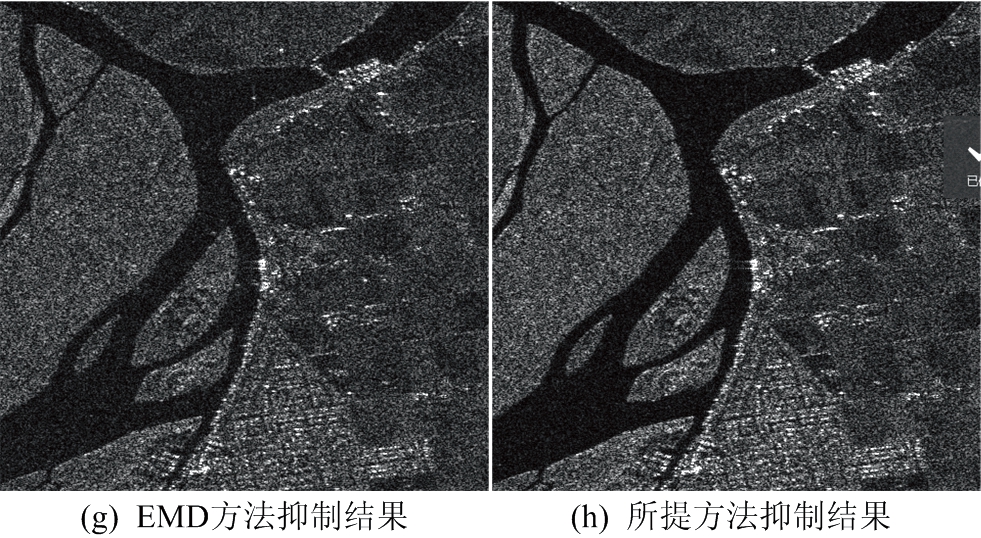
图4 实验数据及NBI抑制结果细节对比
为了定量评估干扰抑制方法的性能，在实验中选取均方根误差(RMSE)作为评价指标对抑制结果进行评价。RMSE定义为
(14)
式中，S表示归一化的SAR原始信号，
表示归一化的恢复信号，而‖·‖F表示矩阵的Frobenius范数。RMSE的值越小表示干扰抑制后信号的恢复性能越好。图5显示了在不同SINR情况下不同NBI抑制方法的RMSE对比，由图中可以看出，本文所提方法的RMSE指标在不同的SINR情况下均小于频域陷波法和基于EMD的干扰抑制方法，表明所提方法恢复性能更佳，进一步验证了所提方法的有效性。
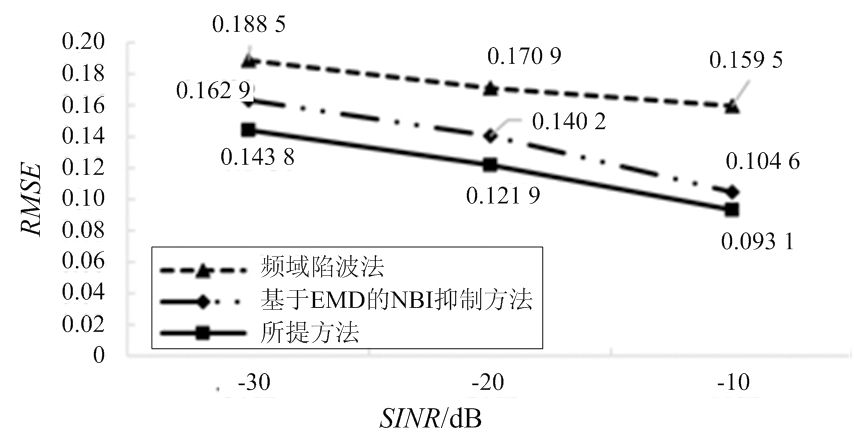
图5 不同SINR情况下抑制方法的RMSE对比
4 结束语
针对EMD方法存在的部分模态混叠问题，本文提出了一种基于CEEMD的SAR系统窄带干扰抑制方法，针对分解后IMF选择问题，采用计算各IMF的PE得出阈值实现NBI和有用信号IMF分量的分割操作。实验结果表明：与EMD和频域陷波滤波相比，所提方法可以有效地抑制NBI并保留目标信息，同时该方法易于实现且不需要复杂的建模，具有较高的实用价值。
[1] 邓云凯, 禹卫东, 张衡, 等. 未来星载SAR技术发展趋势[J]. 雷达学报, 2020, 9(1):1-33.
[2] LV Z, LI N, GUO Z, et al. Detection and Mitigation of Mutual RFI in C-Band SAR: a Case Study of Chinese GaoFen-3[C]∥ 2021 IEEE Radar Conference, Atlanta, GA, USA:IEEE, 2021:1-5.
[3] LI N, LV Z S, GUO Z W, et al. Time-Domain Notch Filtering Method for Pulse RFI Mitigation in Synthetic Aperture Radar[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19(3):1-5.
[4] XU W, XING W D, FANG C H, et al. RFI Suppression Based on Linear Prediction in Synthetic Aperture Radar Data[J]. IEEE Geoscience and Remote Sensing Letters, 2021,18(12):2127-2131.
[5] 李宁, 吕宗森, 郭拯危. 联合变化检测与子带对消技术的SAR图像干扰抑制方法[J]. 系统工程与电子技术, 2021, 43(9):2484-2492.
[6] 黄岩, 赵博, 陶明亮, 等. 合成孔径雷达抗干扰技术综述[J]. 雷达学报, 2020, 9(1):86-106.
[7] ZHOU F, XING M D, BAI X R, et al. Narrow-Band Interference Suppression for SAR Based on Complex Empirical Mode Decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3):423-427.
[8] HUANG N E, SHEN Z, LONG S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998,454(1971):903-995.
[9] RILLING G, FLANDRIN P, GONCALVES P, et al. Bivariate Empirical Mode Decomposition[J]. IEEE Signal Processing Letters, 2007, 14(12):936-939.
[10] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise[C]∥ 2011 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), Prague, Czech Republic:IEEE, 2011:4144-4147.
[11] ZUO L Q, SUN H M, MAO Q C, et al. Noise Suppression Method of Microseismic Signal Based on Complementary Ensemble Empirical Mode Decomposition and
Wavelet Packet Threshold[J]. IEEE Access, 2019, 7:176504-176513.
[12] DE ROO R D. A Simplified Calculation of the Kurtosis for RFI Detection[J]. IEEE Trans on Geoscience and Remote Sensing, 2009, 47(11):3755-3760.
[13] BANDT C, POMPE B. Permutation Entropy: A Natural Complexity Measure for Time Series[J]. Physical Review Letters, 2002, 88(17):174102.
[14] REIGBER A, FERRO-FAMIL L. Interference Suppression in Synthesized SAR Images[J]. IEEE Geoscience and Remote Sensing Letters,2005,2(1):45-49.
