0 引言
外辐射源雷达(Passive Bistatic Radar,PBR)没有发射机,也就不辐射电磁波,其通过接收空间已经存在的电磁波实现目标检测。因为外辐射源雷达工作在静默状态,所以敌方很难实施精确的定向电磁干扰与物理攻击[1-3]。鉴于其卓越的抗干扰、反隐身以及较低的制造成本等特点,近些年吸引了越来越多的研究兴趣。外辐射源雷达的目标检测主要依靠相干积累来实现[4]。相干积累基于双通道实现,这意味着外辐射源雷达至少包含有两个接收通道,参考通道用于接收直达波信号;观测通道用于接收目标回波,当然也会掺杂着杂波干扰。由于辐射信号功率较低、目标波动等因素的影响,观测通道内的目标回波能量远低于直达波和多径杂波[5-8]。因此,杂波消除是外辐射源雷达目标检测的关键步骤。此外,即使在杂波消除之后,目标回波仍然远远比噪声更弱,所以需要对观测信号进行相干积累以提升信号功率,最终实现目标检测[9-10]。
目前广泛使用的调频广播(Frequency Modulation, FM)[11]、电视(Television,TV)[12]、第四代移动通信系统(Long Time Evolution, LTE)[13]、全球定位导航系统(Global Navigation Satellite System, GNSS)[14-16]以及各类商业卫星使用的信号都可以作为外辐射源雷达的信号源。鉴于此类信号的辐射源安装位置海拔比较高且信号覆盖范围广等特点,外辐射源雷达便可以利用这些信号实现隐身低空目标的探测,弥补主动雷达存在探测盲区的不足[17]。在众多的机会辐射源中,GNSS具备建设完整、工作稳定、全球覆盖等特点,是一种非常适合用于目标监视的信号源[18-19]。GNSS主要包括有美国的全球定位系统(Global Position System, GPS)、欧盟的伽利略系统(Galileo System)、俄罗斯的格洛纳斯系统(GLONASS)以及中国的北斗导航系统(Beidou),各方信号都可以被外辐射源雷达利用[20]。因此基于GNSS信号的外辐射源雷达目标检测具备相当的可行性。早在1993年Tsui等人就提出基于GNSS外辐射源的镜面反射目标模型,利用定向天线分别接收直达波和目标回波,然后经过信号处理检测到目标,并估计目标的双基地距离和多普勒频率[21]。
目前已有的外辐射源目标检测方法主要从时域、频域和空域着手解决杂波对目标检测的干扰。Colone等在文献[22]提出的扩展相消算法(Extensive Cancellation Algorithm, ECA)利用参考天线接收直达波信号并构造杂波子空间,基于目标回波空间与杂波空间正交的特征,将观测信号投影于杂波子空间的正交补完成杂波抑制,最后计算投影信号与直达波信号的互模糊函数实现相干积累获得目标检测结果。鉴于GNSS信号互模糊函数多普勒频带较宽的特点,零多普勒频率的固定杂波可能会掩盖低多普勒频率的微弱目标,甚至强目标也会掩盖弱目标,影响该算法的目标检测效果。并且ECA算法需要矩阵求逆,在数据比较长时会带来很大的计算量,难以满足实时信号处理的要求,尤其在较低信噪比(Signal-to-Noise-Ratio, SNR)时,该算法的性能会受到严重影响。Zhao等[23]提出利用观测信号的频域互相关先检测出功率比较强的杂波信号,然后利用估计得到的杂波参数重构杂波信号并将其从观测信号中减除,相比于时域处理方法而言,该算法可有效降低计算量,但是该算法需要主观设置阈值以判定杂波,阈值选择的准确性严重影响到算法的鲁棒性。Zhao等[24]首先分析回波多普勒频率响应,根据多普勒频率将信号分离,并在相应多普勒频率响应的估计过程中消除零多普勒频率信号实现杂波抑制,该算法对数字调频广播信号效果比较明显,但是对其他信号体制不具备普适性。基于空域的杂波抑制方法主要通过降低天线副瓣的方法压制杂波干扰[25],虽然这样可以在信号处理之前从根本上减少杂波的干扰,但这显然增加了外辐射源雷达的系统复杂度。
针对目标反射GNSS回波十分微弱的特点,本文首先根据回波模型分析观测信号的组成成分,然后根据杂波强烈而目标回波微弱的特点,将信号的杂波成分从观测信号中减去。最后利用脉冲压缩实现观测矩阵的相干积累,这样可以在一定程度上避免长时间观测过程中目标运动状态对检测结果的影响。
1 信号模型
GNSS信号是将导航信息调制在周期产生的扩频序列码上产生的,然后再混频到系统所使用的频段之上。其中使用的扩频序列码信号是以1 ms为周期循环产生的,此处为简化数学推导过程忽略调制在其上的导航信息,将GNSS信号建模为简单的以1 ms为周期的扩频序列码信号。
基于GNSS信号的外辐射源雷达目标检测模型如图1所示,在地球轨道飞行的卫星被视为辐射源,雷达接收机放置于参考坐标系的原点处。卫星和目标的坐标分别为Ps(xs,ys,zs)和PT(xT,yT,zT),而且目标速度为VT(vx,vy,vz)。R0表示卫星与雷达之间的直线距离, RTt和RTr则表示目标回波的发射距离和接收距离。β为双基地角,φ表示目标速度与双基地角的平分线之间的夹角。雷达不仅能接收到卫星广播的直达波信号,还会接收到来自目标反射的回波,以及地面反射的回波。此处设置两个接收通道,参考通道负责接收直达波信号,观测通道的波束则指向目标接收观测信号。假设卫星运动已补偿完成,并将信号建模为不含导航信息的扩频序列码,用函数s(t)表示,混频之后的基带观测信号可建模为
Sr(t)=![]()
(1)
式中,λ为载波波长,c为光速,ρ为地杂波的散射系数,σ为目标的散射系数,t为时间,NC和NT分别为杂波路径数和目标数,RCt,RCr分别为地杂波的发射距离和接收距离,Ne(t)表示随时间变化的高斯白噪声。
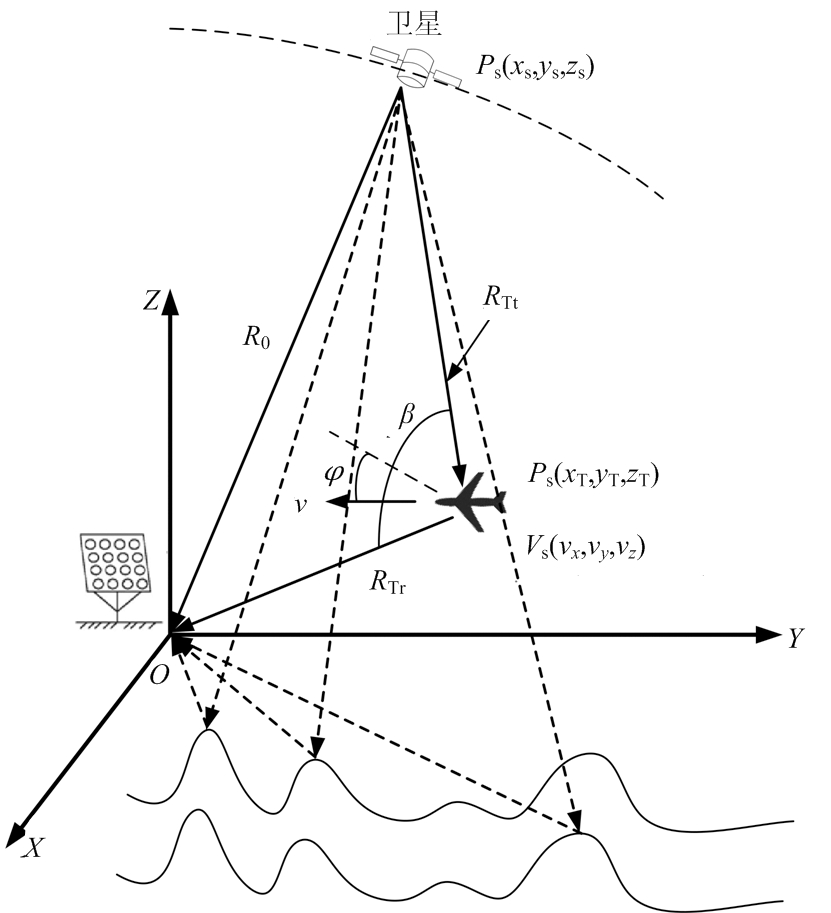
图1 GNSS外辐射源目标检测模型
本文为提高信号处理的效率,将雷达接收的连续波信号按周期Tp=1 ms进行分段截取,并将截取的小段回波信号作为整体进行处理。在忽略导航信号的情况下,可以近似每一段截取的信号在卫星发射的时候都是相同,接收回波的差异主要由目标散射引起,因此可以根据接收回波进行目标特征提取,进而检测并识别目标。
这样可以就将连续波信号重新建模为脉宽为Tp,脉冲重复频率为1 kHz的脉冲信号。鉴于目标相对较低的飞行速度和极高的卫星高度(两万余公里)[17],可近似目标在周期时间Tp内是静止的,而在各周期之间目标是运动的,式(1)所示连续波信号可建模为下列脉冲信号:
Sr(tf,tm)=![]()
(2)
式中,tf,tm分别表示快时间和慢时间,且0<tf<Tp,即目标在快时间域被认为是静止的,而目标的运动状态仅与慢时间tm相关。经上述处理,连续波信号就被分段截取成以Tp为脉宽的观测信号矩阵。那么,数字采样之后的观测信号模型可重写如下:
Sr(n,m)=![]()
(3)
同样,数字采样之后的参考通道信号如下式所示:
Sref![]()
[sref(1) sref(2) … sref(N-1) sref(N)]
(4)
式中,A为参考信号幅度,N为周期时间Tp内直达波信号的长度,与采样率相关。
2 基于迭代对消的外辐射源雷达目标检测
2.1 ECA杂波抑制算法
作为一种经典算法,ECA利用接收回波在杂波正交补空间的投影实现杂波抑制。经上述分析可知,接收回波主要由目标回波和杂波组成,并且目标回波子空间与杂波子空间相互正交。通过将雷达接收回波投影于直达波及其时延信号张成的杂波子空间的正交补,可以实现接收回波的杂波去除。杂波子空间如下式所示:

(5)
式中,L表示距离抑制的阶次,[·]T表示矩阵转置。矩阵中的第一行到第L列分别表示带有0到L-1次平移的多路径样本。
根据目标回波子空间与杂波子空间的正交性[22],ECA算法杂波子空间系数的求解可以转化为下列最优化问题:
(6)
式中,W为子空间系数。
详细考察式(6)可知,该式是一个标准的二阶凹函数。求解该准则的共轭梯度,并令其等于零:
(7)
式中,[·]H表示矩阵的共轭转置。此时,可求得
W=(DHD)-1DHSr
(8)
因此,经过投影之后的剩余目标回波信号如下式所示:
esur=Sr-DW
(9)
2.2 基于迭代对消的杂波抑制
因为卫星较高的飞行高度,图1所示的目标检测模型表明卫星发射的信号需要经历很远的传输路径才能照射到目标,然后经目标散射被雷达接收到,一般认为低于噪声40~50 dB。一方面,由于地面复杂的地理环境,雷达接收到的地杂波不仅强烈,甚至可能包含很多传输路径,即目标散射系数远小于地杂波散射系数σ≪ρ。另一方面,观测通道也会接收到来自卫星发射的直达波,此部分为观测信号中能量最强的分量。
经上述分析,观测信号能量主要被杂波占据,而目标回波很微弱,即信号的主要成分为杂波(非目标回波均为杂波),目标回波可近似归于噪声进行考虑。那么,雷达回波可归纳如下:
Sr(n,m)=![]()
(10)
式中:
![]()
![]()
(11)
重构之后的观测信号矩阵可用S表示:

(12)
式中,![]() 表示单次回波脉冲向量,脉冲内采样点数为N,脉冲数为M。
表示单次回波脉冲向量,脉冲内采样点数为N,脉冲数为M。
观测矩阵的奇异值能有效反映观测回波中各分量的权值,较大的奇异值反映回波中的主要分量,而其余较小的奇异值则反映噪声的功率[26]。如式(10)所示,观测信号由杂波和噪声组成,其中杂波功率强度远大于噪声,可以近似回波的主要分量为杂波。因此,可对观测信号矩阵S进行矩阵分解以获得观测矩阵S的奇异值及相关组成分量,如式(13)所示:
(13)
若矩阵S的秩为P,那么,式中Σ=diag(η1,η2,η3,…,ηP),而ηl(l=1,2,…,P)为观测矩阵S的全部非零奇异值,且满足η1≥η2≥…≥ηQ≥ηQ+1≈…≈ηP。根据奇异值分解理论可知,酉矩阵U由SSH的特征向量(ul,l=1,2,…,N)构成,而酉矩阵D则由SHS的特征向量(dl,l=1,2,…,M)构成。那么,观测矩阵S可进一步分解为
(14)
如前所述,观测信号主要能量由杂波占据,且目标回波功率远低于噪声,因此观测矩阵的前Q个大奇异值(η1,η2,η3,…,ηQ)表示观测矩阵中的杂波分量,将回波矩阵大奇异值对应的主成分消除掉就可以实现杂波消除。虽然已知目标回波功率远低于杂波功率,但是多径杂波数量和目标特性等先验信息是未知的,从而无法在起始阶段即确定上述大特征值个数Q。因此,为有效消除观测矩阵中的杂波成分,在执行杂波消除的过程中,采用式(15)中逐步迭代的方式。
(15)
式中![]() 表示初始观测矩阵。
表示初始观测矩阵。
由上述分析可知,观测信号中的直达波和多径杂波分量比较强烈,而目标和噪声十分微弱,所以杂波的奇异值远远大于噪声或者目标回波的特征值,且上述分解过程得到的奇异值按从大到小排列。为充分消除杂波,此处搜索奇异值比值的最低点所在的位置来确定初始循环次数![]() 具体如式(16)所示,其中的比例系数coe是为了给循环次数充足的裕量,实验中设定coe=2。根据表1的仿真数据,奇异值比值的变化如图2所示,可见,第7个奇异值变化率最小,进而确定初始循环次数可设定为14次。
具体如式(16)所示,其中的比例系数coe是为了给循环次数充足的裕量,实验中设定coe=2。根据表1的仿真数据,奇异值比值的变化如图2所示,可见,第7个奇异值变化率最小,进而确定初始循环次数可设定为14次。
(16)
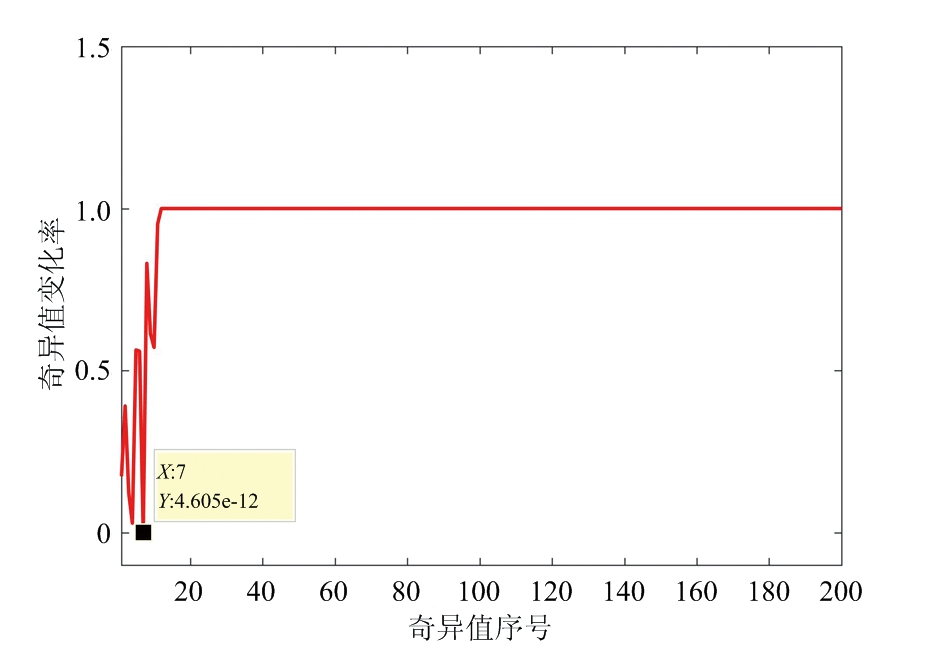
图2 观测矩阵奇异值的比值
如前所述,基于外辐射源的目标回波功率远低于噪声功率,并且可能受剩余杂波的影响。因此,杂波抑制之后仍需对回波进行相干积累以提升目标回波功率,然后才能实现比较稳定的目标检测。将观测矩阵消除杂波之后,分别在距离维和多普勒维进行二维脉冲压缩实现观测矩阵的相干积累,首先用匹配滤波进行距离维的脉冲压缩获取目标的距离信息:
Sr(nl,m)=![]()
DFT(SDirect(n,m),n))
(17)
式中,SDirect(n,m)表示直达波信号。在获得目标距离信息之后,再进行方位向压缩获取目标多普勒维信息,如下所示:
Sr(nl,ml)=DFT(Sr(nl,m),m)
(18)
为获得最佳杂波消除效果,此处利用信息熵来表征相干积累结果的无序或有序状态,相干积累结果杂乱无章而无明显目标显示的时候为无序状态,此时积累结果的熵较大;若相干积累结果为有显著目标显示的状态即为有序状态,且目标峰值高于底噪越多,熵就越小。
考虑到在多目标情况下,随着迭代次数逐渐增加,可能出现某些目标也被消除掉的现象,所以在初始设定的![]() 次迭代条件下,相干积累结果的熵会呈现先下降再上升,然后逐渐稳定的结果。但是此处的关注点是杂波抑制与目标检测,所以重点关注熵减的过程。因为在多目标情况下,消除到只剩下一个目标时熵会减到最小,所以通过最小熵来判定杂波消除完全的可靠性较低。然而,在获得最佳目标检测结果的当次迭代中,相干积累结果由无序状态变化为有序状态,所以在当次迭代过程中,熵减最为剧烈。因此,最佳迭代次数可根据每次迭代之后的相干积累结果熵减的最小值确定。相干积累结果熵的计算和两次迭代之间的熵变分别如式(19)和(20)所示:
次迭代条件下,相干积累结果的熵会呈现先下降再上升,然后逐渐稳定的结果。但是此处的关注点是杂波抑制与目标检测,所以重点关注熵减的过程。因为在多目标情况下,消除到只剩下一个目标时熵会减到最小,所以通过最小熵来判定杂波消除完全的可靠性较低。然而,在获得最佳目标检测结果的当次迭代中,相干积累结果由无序状态变化为有序状态,所以在当次迭代过程中,熵减最为剧烈。因此,最佳迭代次数可根据每次迭代之后的相干积累结果熵减的最小值确定。相干积累结果熵的计算和两次迭代之间的熵变分别如式(19)和(20)所示:
En(l)=-p(nl,ml)lnp(nl,ml)
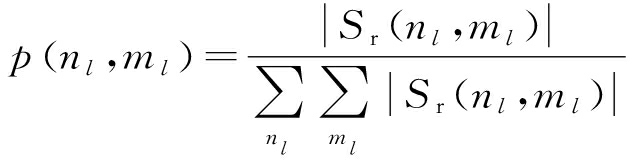
(19)
ΔEn(l)=En(l)-En(l-1)
(20)
其中En(0)表示未进行迭代,而直接对观测矩阵进行相干积累后获得结果的熵。
综上所述,算法执行框图如图3所示,具体包括的步骤有:
1) 采集观测矩阵和直达信号向量;
2) 计算观测矩阵的奇异值、特征向量酉矩阵U和D,并逐步对观测矩阵进行迭代杂波对消;
3) 对杂波对消之后的观测信号进行相干积累获得距离-多普勒(Range Doppler, RD)图谱;
4) 计算迭代过程中相干积累结果熵的变化,熵值下降最剧烈的相应迭代次数为最佳迭代次数,并且利用当次迭代之后的相干积累结果进行目标检测。
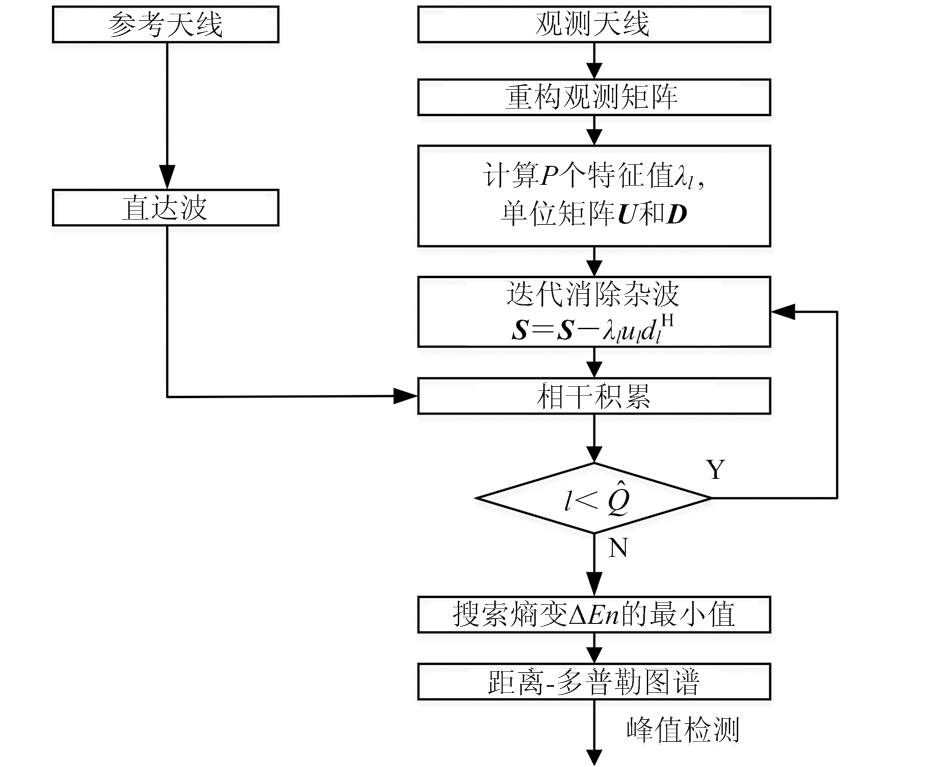
图3 算法执行框架
2.3 算法复杂度分析
如前所述,设定ECA算法的杂波消除阶数为L,并且ECA算法的计算量主要集中于杂波子空间的矩阵求逆。奇异值分解算法经过不断的优化,其精确度及计算速度得到极大提高,这里不再赘述。此处以QR分解为例进行分析,当N>M时,QR分解实现矩阵奇异值分解的计算复杂度为O(M3)[27]。杂波消除过程中需要对观测矩阵进行![]() 次循环对消,每一次对消需要NM2次乘法。此外,相干积累过程主要涉及到三次傅里叶变换(Fast Fourier Transform, FFT)以及一次逆傅里叶变换(Inverse Fast Fourier Transform, IFFT)。具体各算法所需要的乘法数量如表1所示。设定ECA算法的消除阶数为L=250,基于奇异值分解算法的杂波消除循环次数
次循环对消,每一次对消需要NM2次乘法。此外,相干积累过程主要涉及到三次傅里叶变换(Fast Fourier Transform, FFT)以及一次逆傅里叶变换(Inverse Fast Fourier Transform, IFFT)。具体各算法所需要的乘法数量如表1所示。设定ECA算法的消除阶数为L=250,基于奇异值分解算法的杂波消除循环次数![]() 两种算法的计算量如图4所示。图4(a)表示计算复杂度随单脉冲数据长度的变化,图4(b)为计算复杂度随接收回波脉冲数的变化。由图可见,基于迭代对消的杂波消除算法的计算量平均比ECA算法低一个数量级。
两种算法的计算量如图4所示。图4(a)表示计算复杂度随单脉冲数据长度的变化,图4(b)为计算复杂度随接收回波脉冲数的变化。由图可见,基于迭代对消的杂波消除算法的计算量平均比ECA算法低一个数量级。
表1 乘法计算量比较

算法乘法数量ECAO(M(NL2+L2(logL+1)+2NL))迭代对消O(M3+Q^NM2)相干积累O((1.5N+0.5N)Nlog2N+NM)
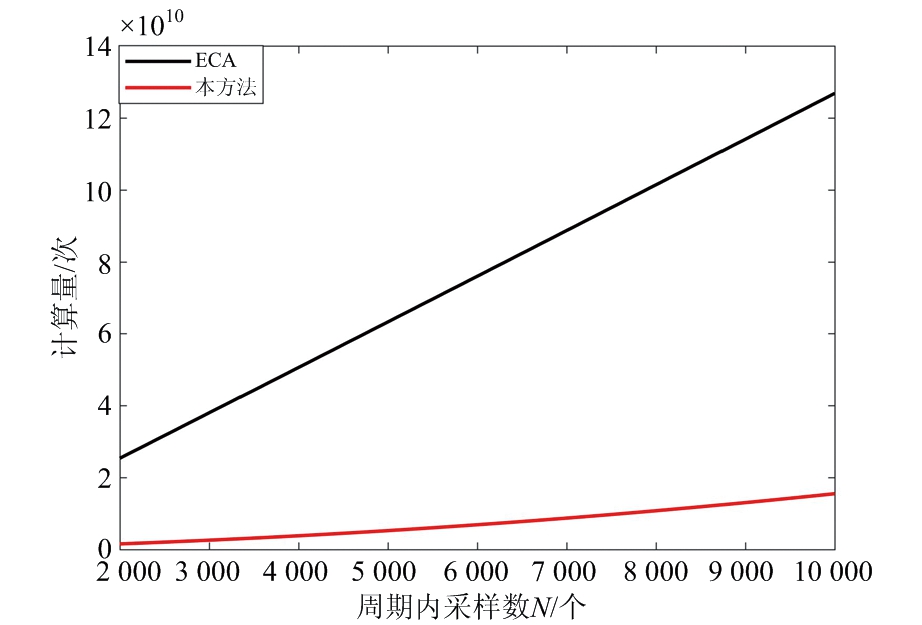
(a) 不同脉冲采样点数条件下的计算量
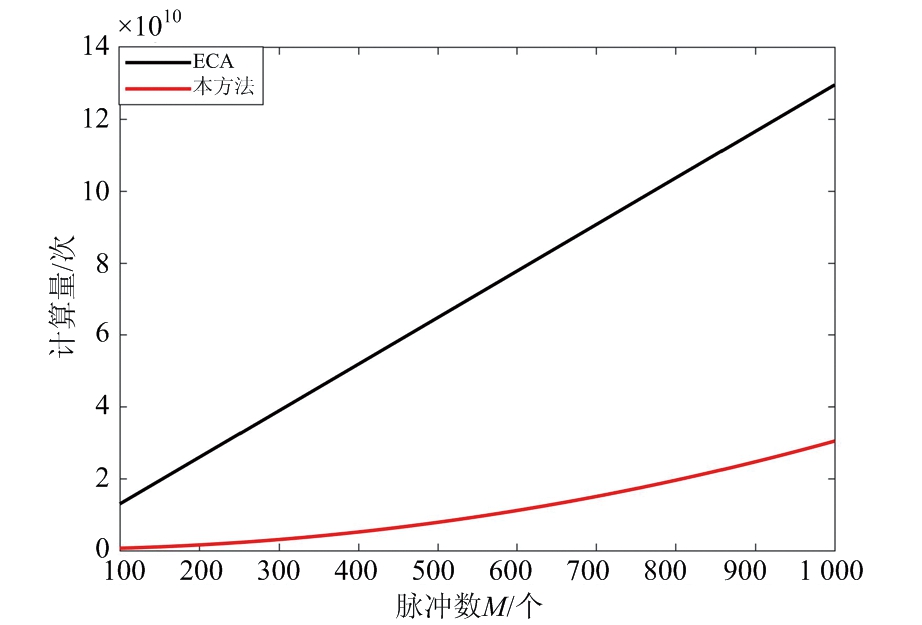
(b) 不同脉冲数条件下的计算量
图4 计算复杂度分析
3 实验结果
此部分利用GPS L1波段仿真信号进行实验,采样频率为2.046 MHz,信号截取长度Tp=1 ms,即1ms的采样点数为2 046,脉冲重复频率为1 kHz,观测时间为200 ms。仿真实验中,观测信号包含一路直达波,五路多径杂波以及三路微弱目标回波,具体仿真参数如表2所示。
表2 相关仿真参数
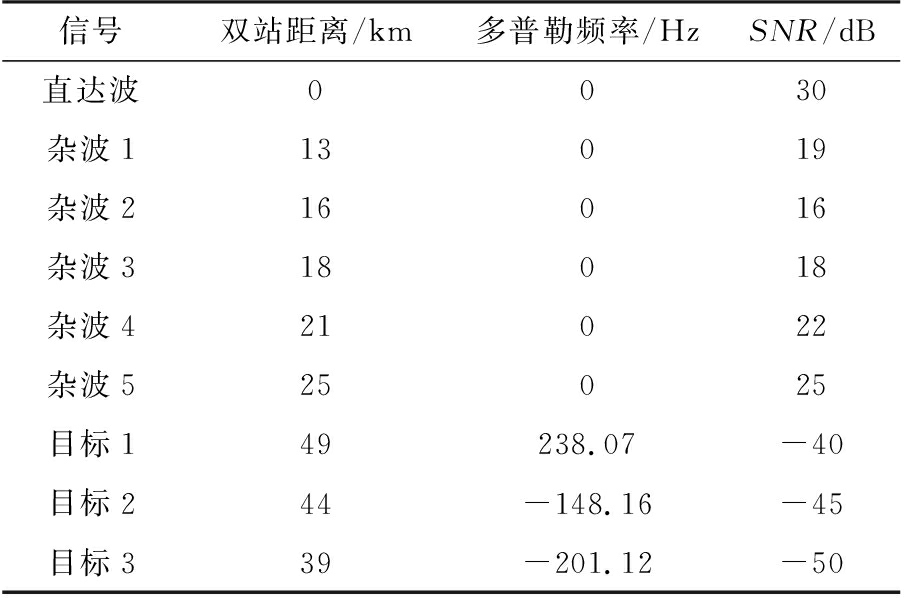
信号双站距离/km多普勒频率/HzSNR/dB直达波0030杂波113019杂波216016杂波318018杂波421022杂波525025目标149238.07-40目标244-148.16-45目标339-201.12-50
3.1 仿真实验效果分析
为有效说明本文所述方法的有效性,实验中不仅对所提方法的目标检测效果进行讨论,并且与经典的ECA方法效果进行比较。
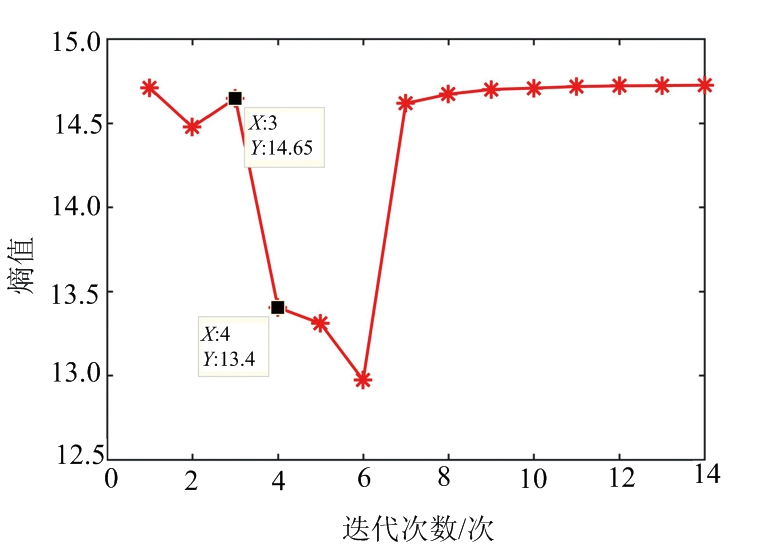
本实验中最佳迭代次数由迭代过程中相干积累结果熵值变化的最小值确定,图5呈现了迭代过程中熵的变化。图5(a)显示迭代过程中熵值的变化,由图可见,随着迭代次数的增加,熵呈现先减后增的趋势,在1~4次迭代之间,相干积累结果的熵逐渐下降,且在第3次和第4次迭代之间熵值减小最为显著,那么,当次迭代可获得最佳目标检测结果;此外,观察熵变的整个过程可见,由于此实验中包含3个目标,在4~6次迭代之间,迭代过程中目标回波也被逐渐对消,到第6次迭代之后,只剩下一个目标回波,所以此时相干积累结果的熵最小;当迭代次数大于6时,3个目标都被完全消除,相干积累无明显峰值出现,所以熵值会逐渐增大到趋于稳定,如图所示。
因为此处迭代对消的目的是消除杂波并实现目标检测,所以熵减的趋势是关注的重点,且在这个过程中熵的变化率小于零。图5(b)则反映了整个迭代对消过程中熵的变化率,可见,第4次迭代造成相干积累结果的熵减最显著,与图5(a)吻合。因此可以判定在本实验中迭代次数为4次即可获得最佳目标检测结果,杂波抑制之后的相干积累结果如图6所示。
(a) 相干积累结果的熵变
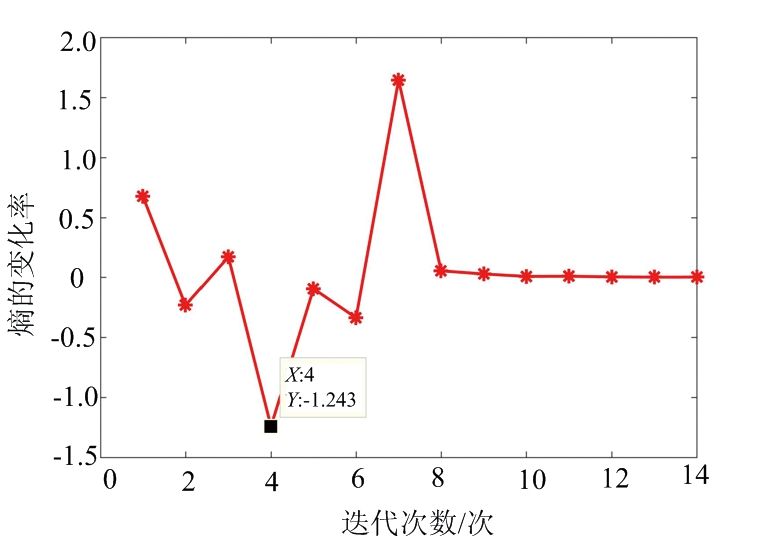
(b) 相干积累结果熵的变化率
图5 迭代过程中相干积累结果熵的变化
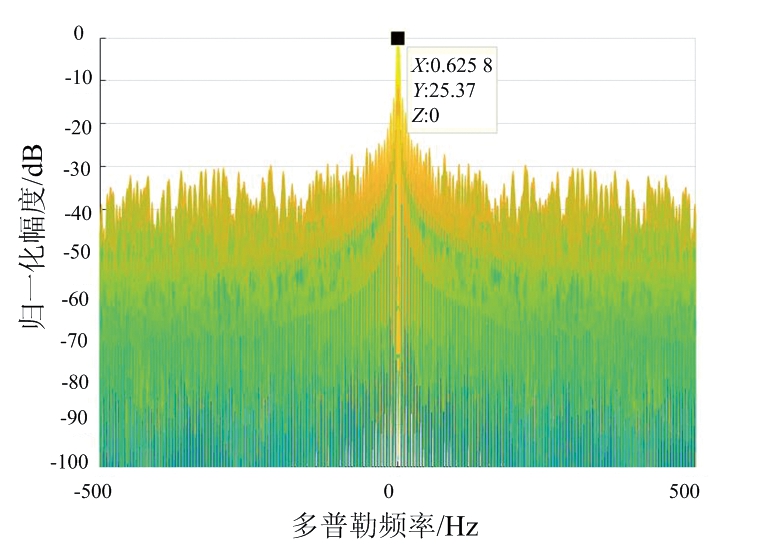
(a) 原始观测矩阵的检测结果
(b) 本方法检测结果
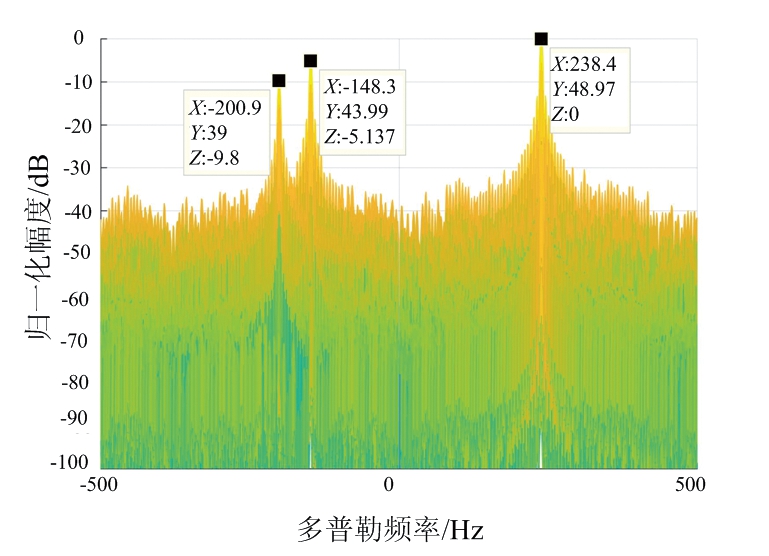
(c) ECA与相干积累的检测结果
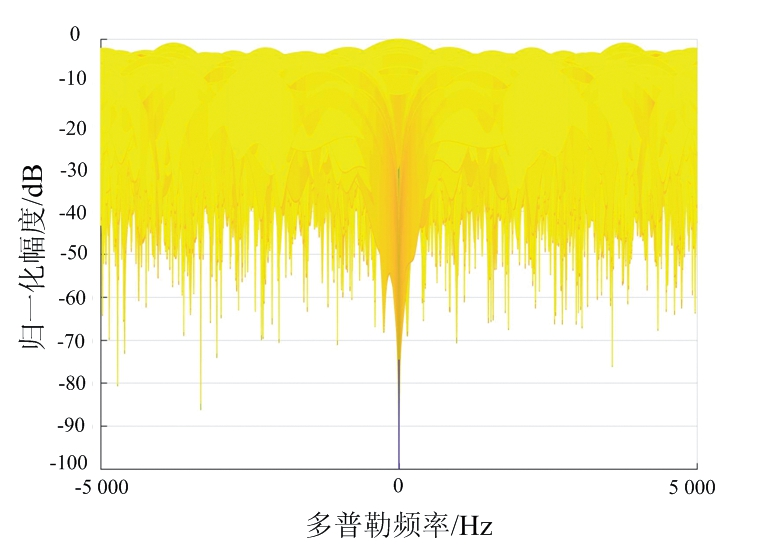
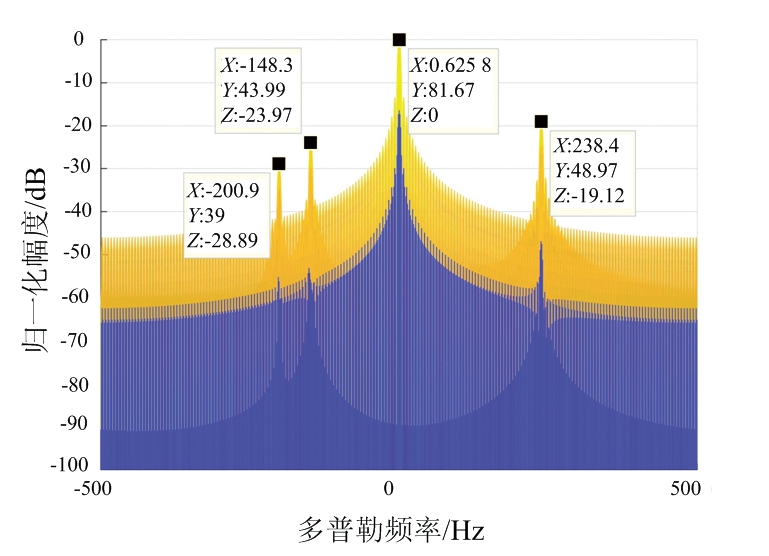
(d) 单脉冲ECA处理之后的互模糊函数
图6 不同方法的目标检测效果
图6给出了本文所提方法的目标检测效果,并与经典的ECA方法进行了比较。图6(a)表示未进行杂波抑制,直接利用观测矩阵进行相干积累的结果,从图中可看到,由于强杂波的存在,相干积累结果的峰值出现在接近零多普勒频率处,即杂波被积累得到很高的功率。因为目标回波本身比较微弱,在相干积累增益相同的情况下,目标自然会被强杂波掩盖,从而无法实现目标检测。但是在利用本文所提方法消除杂波之后就可以有效实现目标检测,如图6(b)所示。在杂波被消除之后,相干积累增强了目标回波功率,目标峰值即出现在相应距离单元和多普勒单元处,而无明显的杂波剩余峰值。从图中读取3个目标的双基地距离和多普勒频率如表3所示。与表2中的参数相比,参数估计精度比较高,可见本文所提方法可以有效实现目标检测,并估计获得比较精确的目标双站距离和多普勒频率参数。
表3 不同方法的目标检测结果
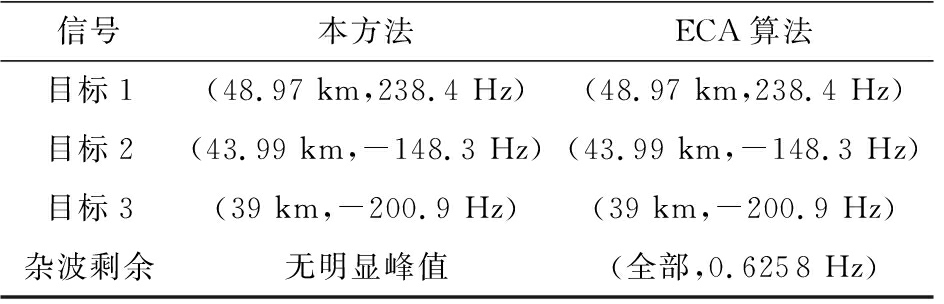
信号本方法ECA算法目标1(48.97 km,238.4 Hz)(48.97 km,238.4 Hz)目标2(43.99 km,-148.3 Hz)(43.99 km,-148.3 Hz)目标3(39 km,-200.9 Hz)(39 km,-200.9 Hz)杂波剩余无明显峰值(全部,0.6258 Hz)
为有效说明所提方法的效果,图6还给出了经典的ECA算法对杂波的抑制性能。图6(c)为分别对200次脉冲进行ECA杂波抑制,然后进行相干积累的结果。图中显示了4个峰值,其中3个多普勒频率远远偏离于零的峰值为目标,在接近零频处的峰值为强烈的杂波剩余,具体4个峰值的参数如表3所示。相比于表2,表3中不仅显示了3个目标的参数估计结果,还给出了ECA算法杂波剩余的相关参数。此处由于数据长度有限,导致相干积累结果的多普勒频谱发生频谱泄露,原本应当位于零频处的杂波偏移到接近零频的0.625 8 Hz处。由图6(c)可见,剩余杂波的峰值强度显然高于目标峰值19 dB以上,因此该杂波剩余将会对后续的目标检测构成严重影响。
图6(d)为利用ECA算法对一次脉冲的观测信号进行杂波抑制之后的互模糊函数,可见模糊函数在零频处存在一个很深的凹口,表明ECA算法可以实现对零频杂波的抑制。然而GNSS信号互模糊函数的多普勒频带较宽,可见在零多普勒频率附近仍然存在较严重的杂波剩余,甚至会淹没目标回波。因此,图6(d)中并无明显目标指示,即无法实现有效的目标检测。
根据表2可知,杂波平均比目标回波强60 dB以上,再综合图6(c)和图6(d)目标检测效果,ECA算法能起到一定的杂波衰减作用,但是其残留的杂波剩余仍然比较强烈,在200 ms的相干积累之后,杂波强度依然远远强过目标回波,导致目标检测效果受到严重影响。
为充分证明本方法对复杂环境的适应性,在不同的信噪比和信杂比(Signal-Clutter-Ratio, SCR)条件下分别做50次蒙特卡洛仿真实验,计算不同的杂波噪声环境下获得最佳检测结果需要迭代的次数的平均值,如图7所示。图7(a)所示为不同信噪比条件下需要的迭代次数,图中横轴为目标2的信噪比,图中标记点处标出的为表1所示实验条件所需的迭代次数。根据结果可知,在该设定的SNR范围内,平均迭代4~5次就可以获得最佳检测结果,因此可以认为本方法在低SNR条件下仍然能获得比较稳健的目标检测效果。图7(b)为不同信杂比(目标2与直达波的功率比值,SCR)条件下的迭代次数,同样,图中标记点处标出的为表1所示实验条件下的所需迭代次数,与图7(a)类似,在该宽泛的SCR范围内,4~5次即可获得目标的检测结果。综上,即使在较强的噪声和杂波干扰条件下,本方法具备较强的鲁棒性。
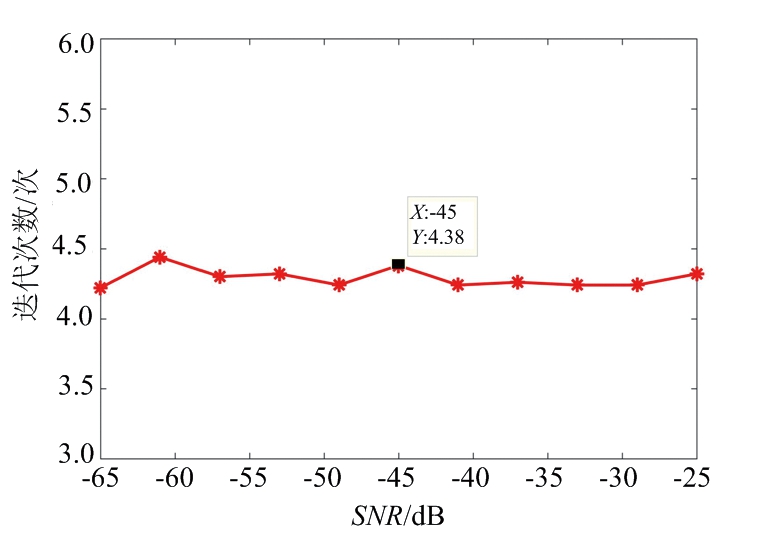
(a) 不同SNR条件所需迭代次数
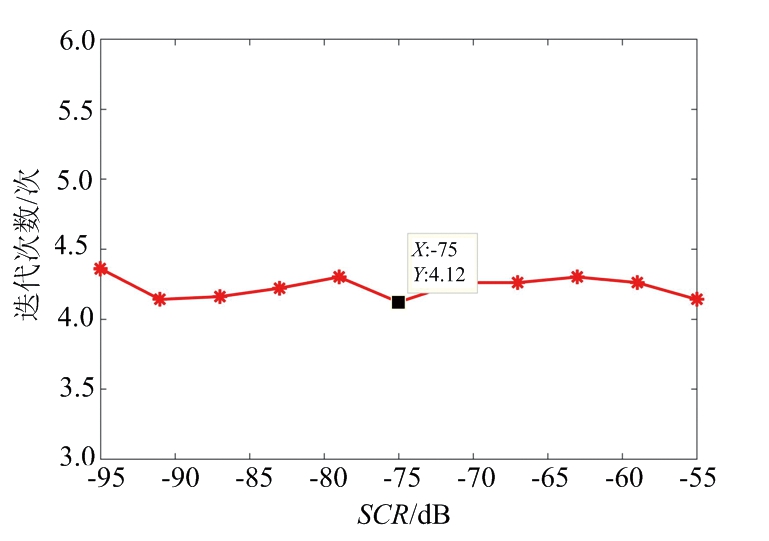
(b) 不同SCR条件所需迭代次数
图7 不同SNR/SCR条件下需要迭代的次数
3.2 算法计算量分析
表4所示为经典ECA算法和本文提出的基于迭代对消的杂波抑制方法对200 ms观测信号处理时间的比较,仿真实验执行处理器为Intel Core(TM)i5-7200U CPU@2.5GHz,仿真软件为MATLAB 2017a。
表4 算法执行时间比较

算法杂波消除阶数/迭代次数执行时间/sECA25019.422本方法143.362
综上所示,本方法执行时间远小于经典的ECA算法,而且本方法对于杂波的衰减量远大于ECA算法,因此本文所提方法更适用于实时外辐射源目标检测。
4 结束语
针对GNSS信号用于机会辐射源的应用,本文提出一种基于迭代对消的外辐射源目标检测算法,该算法针对目标反射回波十分微弱的特征,对构建的观测矩阵进行奇异值分解,将较大特征值对应的杂波成分从中消去进而抑制回波信号中的强烈杂波,然后再对消除杂波后的观测矩阵进行脉冲压缩实现相干积累完成目标检测。在杂波消除过程中,通过搜索每一次迭代之后相干积累结果熵变的最小值判定杂波消除完成,以获得最佳检测结果。最后利用GPS系统L1波段的仿真信号进行实验,证明了本方法可在较宽泛的信噪比和信杂比范围内获得稳定的目标检测效果。
[1] COLONE F, CARDINALI R, LOMBARDO P. Cancellation of Clutter and Multipath in Passive Radar Us-ing a Sequential Approach[C]∥2006 IEEE Conference on Radar, Verona, NY, USA:IEEE, 2006:393-399.
[2] WANG Binbin, CHA Hao, ZHOU Zibo, et al. Clutter Cancellation and Long Time Integration for GNSS-Based Passive Bistatic Radar[J]. Remote Sensing, 2021, 13(4):701.
[3] CHEN Gang, WANG Jun, ZUO Luo, et al. Two-Stage Clutter and Interference Cancellation Method in Passive Bistatic Radar[J]. IET Signal Processing, 2020, 14(6):342-351.
[4] 王顺生. 基于北斗信号外辐射源雷达目标检测与定位方法研究[D]. 西安:西安电子科技大学,2020.
[5] 韦清玉. 基于外辐射源的低慢小目标无源探测研究[D]. 南京:南京理工大学,2020.
[6] 苗铎,杨东凯,许志超,等. GNSS外辐射源雷达低慢小目标探测概率研究[J/OL].北京航空航天大学学报:1-10[2022-06-17].DOI:10.13700/j.bh.1001-5965.2021.0271.
[7] 陈江宁.基于高轨卫星外辐射源微弱目标检测技术研究[D]. 成都:电子科技大学,2021.
[8] 饶云华,周健康,万显荣,等.基于动态有序矩阵的外辐射源雷达CFAR算法[J].电子与信息学报,2021,43(4):1154-1161.
[9] 郭帅.外辐射源雷达干扰与杂波抑制算法研究[D]. 西安:西安电子科技大学,2020.
[10] 钱丽,陈婧.基于小波域KL变换外辐射源雷达杂波抑制算法[J].现代雷达,2021,43(3):44-49.
[11] CARDINALI R, COLONE F, LOMBARDO P, et al. Multipath Cancellation on Reference Antenna for Passive Radar Which Exploits FM Transmission[C]∥IET International Conference on Radar Systems, Edinburgh, UK:IET, 2009:1-5.
[12] ZAIMBASHI A. Target Detection in Analog Terrestrial TV-Based Passive Radar Sensor: Joint Delay-Doppler Estimation[J]. IEEE Sensors Journal, 2017,17(17):5569-5580.
[13] WANG Haitao, WANG Jun, LI Hongwei. Target Detection Using CDMA Based Passive Bistatic Radar[J]. Journal of Systems Engineering and Electronics, 2012,23(6):858-865.
[14] PASTINA D, SANTI F, PIERALICE F, et al. Maritime Moving Target Long Time Integration for GNSS-Based Passive Bistatic Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2018,54(6):3060-3083.
[15] ZAVOROTNY V, GLEASON S, CARDELLACH E, et al. Tutorial on Remote Sensing Using GNSS Bistatic Radar of Opportunity[J]. IEEE Geoscience & Remote Sensing Magazine, 2015, 2(4):8-45.
[16] 万显荣,易建新,占伟杰,等.基于多照射源的被动雷达研究进展与发展趋势[J].雷达学报,2020,9(6):939-958.
[17] CHOW YII P. Large Scale Antenna Array for GPS Bistatic Radar[D]. Australia:The University of Adelaide, 2017.
[18] 鲍庆龙,王森,潘嘉蒙,等.非合作雷达辐射源目标探测系统关键技术分析[J].电波科学学报,2020,35(4):496-503.
[19] SANTI F, PASTINA D, BUCCIARELLI M. Maritime Moving Target Detection Technique for Passive Bistatic Radar with GNSS Transmitters[C]∥2017 18th International Radar Symposium, Prague, Czech Republic: IEEE,2017:1-10.
[20] MA H, ANTONIOU M, PASTINA D, et al. Maritime Moving Target Indication Using Passive GNSS-Based Bistatic Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2017,51(1):115-130.
[21] TSUI J B Y, SHAW R L. Passive Ranging Through Global Positioning System: US05187485A[P] .1993-02-16.
[22] COLONE F , O′HAGAN D W , LOMBARDO P , et al. A Multistage Processing Algorithm for Disturbance Removal and Target Detection in Passive Bistatic Radar[J]. IEEE Trans on Aerospace & Electronic Systems, 2009, 45(2):698-722.
[23] ZHAO Dawei, WANG Jun, CHEN Gang, et al. Clutter Cancellation Based on Frequency Domain Analysis in Passive Bistatic Radar[J].IEEE Access,2020,8:43956-43964.
[24] ZHAO Zhixin, ZHOU Xinhua, WENG Tao, et al. Target Detection Approach for DRM-Based Passive Bistatic Radar[J]. The Journal of Engineering, 2019(2):7868-7871.
[25] FABRIZIO G, COLONE F, LOMBARDO P, et al. Adaptive Beamforming for High-Frequency Over-the-Horizon Passive Radar[J]. IET Radar Sonar & Navigation, 2009, 3(4):384-405.
[26] 张贤达. 矩阵分析与应用[M]. 北京:清华大学出版社, 2013.
[27] DEMMEL J, KAHAN W. Accurate Singular Values of Bidiagonal Matrices[J]. Society for Industrial and Applied Mathematics, 1990, 11(5):873-912.





