0 引言
目前人体动作识别技术应用范围日渐广泛,在医疗探测、安保防护、智能家居等方面都有广泛的应用空间,但目前识别技术大多数依赖于接触式传感器或光学传感器实现[1-2]。其中接触式传感器因需要被监测者佩戴所以对其活动空间产生一定的束缚,而光学传感器因对周围环境光线条件有较高要求通常难以实现全天候工作,同时由于需要在终端采集用户与生活环境的图像或视频,这对被检测者隐私容易造成泄露。雷达因其自身特性可避免以上缺点,近年来被广泛应用于人体动作识别领域的研究工作[3]。基于雷达的人体动作识别方法主要采用连续波多普勒雷达[4]、超宽带脉冲雷达[5-6]与调频连续波(Frequency Modulated Continuous Wave, FMCW)雷达[7-11]三种雷达体制。相比于其他两种,FMCW雷达具有成本低、距离分辨率与速度分辨率更高、抗干扰能力强等优势。
目前在基于FMCW雷达的人体动作识别工作中,微多普勒特征因其对不同目标动作的高区分度特性被应用于人体动作识别。在文献[7]中研究者对微多普勒时频谱图进行分解得到对应躯干和肢体的等8种特征矢量并采用支持向量机对不同动作进行识别。文献[8]通过提取FMCW雷达回波信号中的微多普勒信息并与其他接触式传感器信号进行融合实现对人体活动进行分类。也有研究者通过利用雷达的多个维度特征进行人体动作识别[9-11],文献[9]将时频谱图有效面积的频率上下限、功率密度及能量上下包络和距离多普勒轨迹作为联合特征对危险驾驶行为进行监测。文献[10]提出分别从微多普勒时频谱图中选取频率间隙和从距离多普勒图中选取高功率区域的横纵宽度比值组成联合特征作为人体不同步态的识别依据。文献[11]基于卷积神经网络,通过提取固定帧时间长度拼接的距离-多普勒-时间图特征进行手势动作识别。
以上的动作识别工作都是针对离散化人体动作进行,而现实中人体动作往往为连续式产生,因此单一的离散化人体动作识别方法难以用到实际应用中,对此有研究者提出了连续人体动作识别方法。文献[12]对回波信号进行预处理后提取其微多普勒特征,并采用支持向量机进行分类,但机器学习分类器普遍无法利用一组连续动作中不同动作的前后相关性进行类别判断,因此识别准确率不高。文献[13-16]引入长短期记忆网络作为分类器对连续人体动作进行识别,其中文献[13]提出分别采用微多普勒特征与距离时间特征作为识别依据并对识别结果进行对比,文献[14]将雷达数据与接触式传感器数据进行特征融合得到最后识别结果,文献[15-16]采用连续动作的微多普勒特征作为识别依据,分别搭建双层长短期记忆网络与双层门控循环单元作为分类器进行识别,但文献[15-16]将不同的离散化动作回波信号直接拼接得到模拟的连续动作回波信号,这种模拟的连续动作数据并不能体现人体在不同动作之间的转换过程,因此与真实的人体连续动作数据还存在一定差异,并且只根据微多普勒时频谱图提取动作对应特征作为网络输入特征维度较为单一,动作识别准确率不高。
针对上述问题,本文提出一种基于双流特征融合的人体连续动作识别方法。首先对采集的回波信号进行预处理得到距离时间图与微多普勒时频谱图。之后采用主成分分析法(Principal Component Analysis, PCA)对各个时间段的距离时间图与微多普勒时频谱图进行特征提取得到两组特征向量再将两组特征向量进行并联融合。最后将融合后得到的双流融合特征输入到双向长短期记忆(Bidirectional Long Short-Term Memory,Bi-LSTM) 网络中训练并得到识别结果。
1 连续人体动作识别
本文提出的连续人体动作识别方法主要流程包含回波信号预处理,特征提取与特征融合,Bi-LSTM网络训练与测试。所提人体动作识别方法的整体流程图如图1所示。
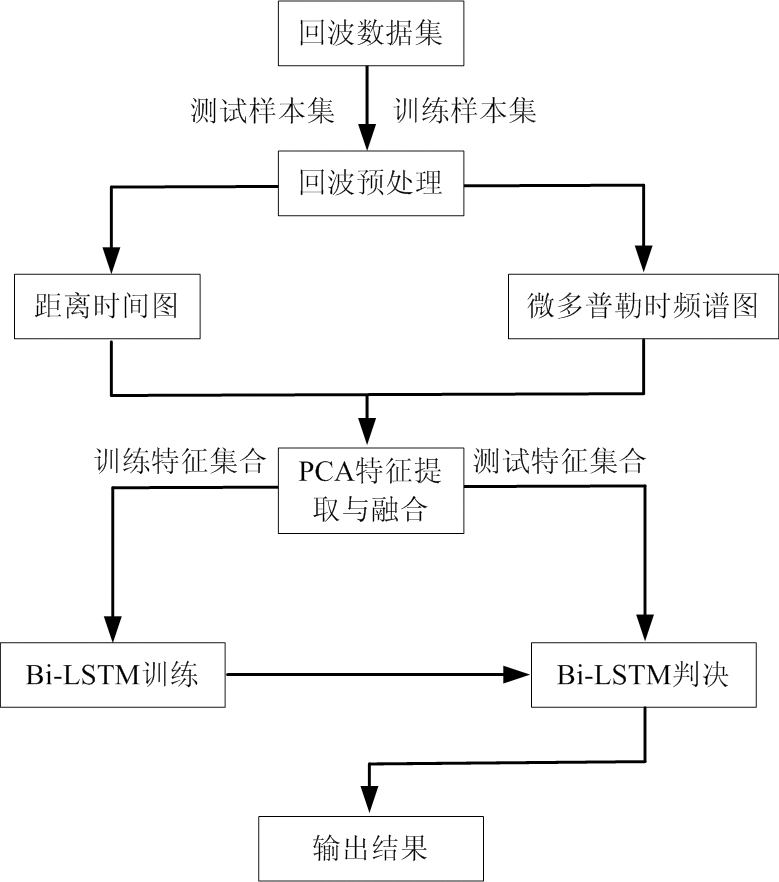
图1 连续人体动作识别方法整体流程图
1.1 回波信号预处理
在回波信号预处理阶段,需要将调频连续波雷达回波信号表示为二维矩阵S(n,m),其中n=0,1,…,N-1,m=0,1,…,M-1,N和M分别是雷达在一个调频周期内的采样点数和总的调频周期个数。对矩阵S(n,m)的每一列进行离散傅里叶变换(Discrete Fourier Transform, DFT)得到
(1)
式中变量k=0,1,…,N-1包含探测目标距离雷达天线的距离信息。FMCW雷达距离分辨率ΔR为
(2)
式中,B为FMCW雷达的信号带宽,c0为电磁波在空气中的传播速度。根据式(1)得到的距离时间图对感兴趣的距离单元信号进行相干叠加得到
(3)
式中k1与k2为目标所在距离单元的最小值与最大值。实验时人体目标距离雷达的距离范围为1.5~4.5 m, K波段雷达回波信号距离分辨率为0.075 m,因此k1与k2取值分别为20与60。之后对D(m)进行短时傅里叶变换(Short-Time Fourier Transform, STFT)得到
(4)
式中g(m)为汉明窗函数,p为窗函数移动的索引值,窗函数每次移动时的重叠率为95%。最后根据T(p,q)可以得到每个时间段内对应动作的微多普勒时频谱图。
1.2 主成分分析
通过回波预处理得到连续人体动作回波的距离时间图与微多普勒时频谱图后,采用PCA进行降维提取特征,具体计算过程如下:
1) 计算训练数据矩阵XnTr的每列平均值,并将矩阵中每行元素与所在列的均值相减得到矩阵![]()
2) 计算协方差矩阵![]()
3) 对协方差矩阵进行特征分解,得到特征值与投影特征向量;
4) 对特征值从大到小排序,选取其中累计贡献率达到95%的前K个特征值将其所对应的投影特征向量以列向量形式排列到一个矩阵An中;
5) 利用式![]() 将原数据投影到An得到降维后的特征矩阵YnTr进而实现对训练集降维。
将原数据投影到An得到降维后的特征矩阵YnTr进而实现对训练集降维。
需指出的是在降维过程中需要保证对所用动作的同一维度图同时进行PCA,即保证所有动作的特征投影到的主成分维度必须一样。将动作的距离时间图与微多普勒特征谱图分别进行PCA后选取前800个主成分作为主成分分析结果,之后将同一时刻动作的距离时间特征与微多普勒特征主成分分析结果并联融合得到该时刻的双流融合特征。
1.3 Bi-LSTM网络
本文搭建了两个Bi-LSTM网络框架,结构图分别如图2(a)与(b)所示,网络中各层尺寸大小见表1。图2(a)为单层Bi-LSTM网络结构图,网络包含一个输入层、一个Bi-LSTM层、一个全连接层与一个softmax输出层,其中输入层大小因需与主成分分析结果一致设置为800,Bi-LSTM层尺寸设置为2 400,表示该层含有2 400个循环单元,全连接层输出大小为6,可以实现6分类。图2(b)所表示的双层Bi-LSTM网络在单层Bi-LSTM网络基础上添加了一个相同尺寸的Bi-LSTM层。首先将每个时刻动作对应的双流融合特征按时间顺序通过输入层输入到网络中,而后经过Bi-LSTM网络层得到时序特征,之后连接全连接与softmax分类器对输入特征进行类别判断,并在最后输出结果。网络所用损失函数为交叉熵损失函数,在梯度优化方面采用Adam算法。Bi-LSTM网络内部层结构图如图3(a)所示,在Bi-LSTM网络层中包含两个双向的LSTM层,每个输入单元对应两个隐藏状态信息,分别为HL(t)与HR(t)。其中HL(t)为从左向右的隐藏层结构,HR(t)为从右向左的隐藏层结构。因此Bi-LSTM网络可以捕获对于当前特定身体动作的前向与后向特征。当人类在连续活动状态时,前后动作在顺序上的相关性有着紧密的联系,例如当人坐下之后就不会发生行走或跳跃等在站立条件下才能进行的动作,但可能会发生喝水、起立等动作或静止无动作。一般的机器学习用作分类器只会局限于利用当前动作本身的特征而无法利用人体动作的顺序相关性进行识别,而长短期记忆网络因其自身特性可以有效地利用当前动作的前向特征作为识别依据,在此基础上采用Bi-LSTM网络作为分类器可以更好地捕捉动作前向与后向特征对连续动作进行识别。
(a) 单层Bi-LSTM网络结构
(b) 双层Bi-LSTM网络结构
图2 整体网络结构图
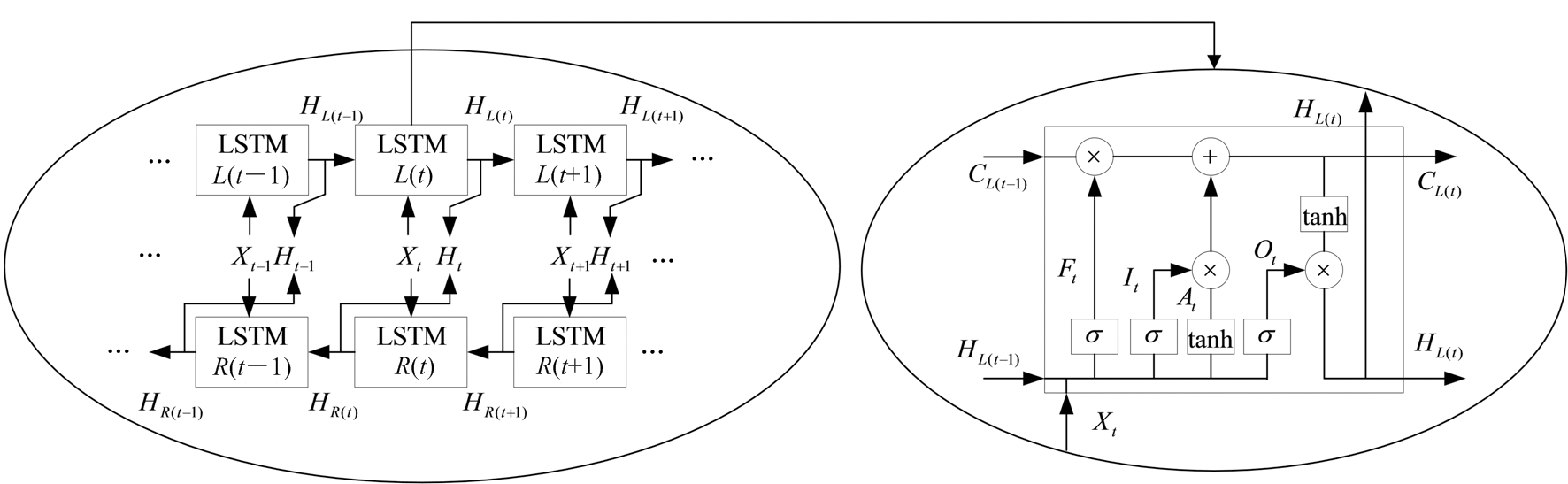
(a) Bi-LSTM网络层结构图 (b) LSTM单元模型图
图3 Bi-LSTM内部结构图
表1 网络各层尺寸大小
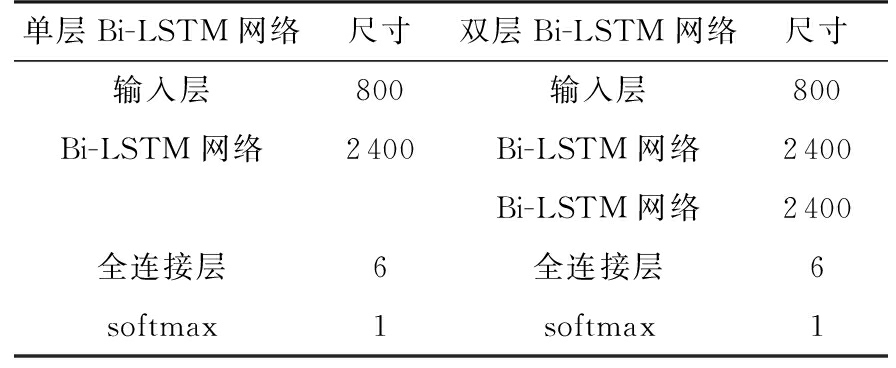
单层Bi-LSTM网络尺寸双层Bi-LSTM网络尺寸输入层800输入层800Bi-LSTM网络2400Bi-LSTM网络2400Bi-LSTM网络2400全连接层6全连接层6softmax1softmax1
通过图3(a)可以看出,Bi-LSTM网络每个层的基本框架是LSTM单元,其内部结构如图3(b)所示。在一个LSTM单元内包含3个门,分别是遗忘门、输入门与输出门。其中遗忘门为数据进入LSTM 单元的第一步,决定该LSTM单元内丢弃什么信息,当前单元的输入序列Xt与上一个单元的隐藏状态HL(t-1)作为它的输入,通过激活函数σ得到遗忘门输出Ft,数学表达式如下:
Ft=σ(WfHL(t-1)+VfXt+Bf)
(5)
式中σ(x)=(1+e-x)-1,Wf和Vf为遗忘门加权系数,Bf为遗忘门偏置。之后的输入门决定该LSTM单元记住的信息。数学表达式如下:
It=σ(WiHL(t-1)+ViXt+Bi)
(6)
At=tanh(WaHL(t-1)+VaXt+Ba)
(7)
式中Wi,Vi,Wa和Va为加权系数,Bi和Ba为偏置,It和At分别是输入门两个输出。下一步对LSTM的细胞状态CL(t)更新:
CL(t)=CL(t-1)⊗Ft+It⊗At
(8)
式中CL(t-1)为上一个单元的细胞状态,Ft,It与At分别为上述计算的遗忘门与输入门的结果。单元内的输出门负责决定该单元需要输出给下一个单元的隐藏状态信息HL(t),计算公式如下所示:
Ot=σ(WoHL(t-1)+VoXt+Bo)
(9)
HL(t)=tanh(CL(t))⊗Ot
(10)
因此可得HL(t)公式表示如下:
HL(t)=σ(WLtHL(t-1)+VLtXt+BLt)
(11)
同理亦可得HR(t)公式为
HR(t)=σ(WRtHR(t-1)+VRtXt+BRt)
(12)
根据HL(t)与HR(t)可得当前时刻的隐藏状态信息也是下一层网络的输入Ht。
Ht=WHLHL(t)+WHRHR(t)+bH
(13)
2 实测数据结果分析
2.1 实验场景
实验采用K波段FMCW雷达对人体所作不同动作回波信号进行采集,雷达具体参数如表2所示,基带采样数据传输到计算机中采用MATLAB 2020a进行数据处理和Bi-LSTM网络训练及测试。实验选定在实验室环境中对3男1女共4人进行数据采集,实验场景如图4所示,每次采集过程中探测目标为一人。观测目标对象从距离雷达3 m处开始活动,当雷达开始工作时,目标对象会按照随机顺序一次性做完弯腰拾东西、坐下、站起、跳跃与举杯喝水这五种动作,每个对象的采集次数为10次,每次采集时间设定为20 s,记录连续动作样本总数共为40组。
表2 K波段FMCW雷达参数

参数参数值载频24GHz带宽2GHz调频周期1ms基带采样频率512kHz

图4 实验场景
2.2 实验结果分析
对回波数据进行回波信号预处理得到连续动作的距离时间图与微多普勒时频谱图如图5所示,图5(a)为一组连续动作的距离时间图,该图反映了探测目标在20 s内与雷达之间的距离变化,图5(b)为图5(a) 对应的微多普勒时频谱图,该图的时间所指的是窗函数g(m)沿着时间轴所对应的时间,也就是式(4)中的变量p,纵轴表示多普勒频率,为式(4)中的变量q。
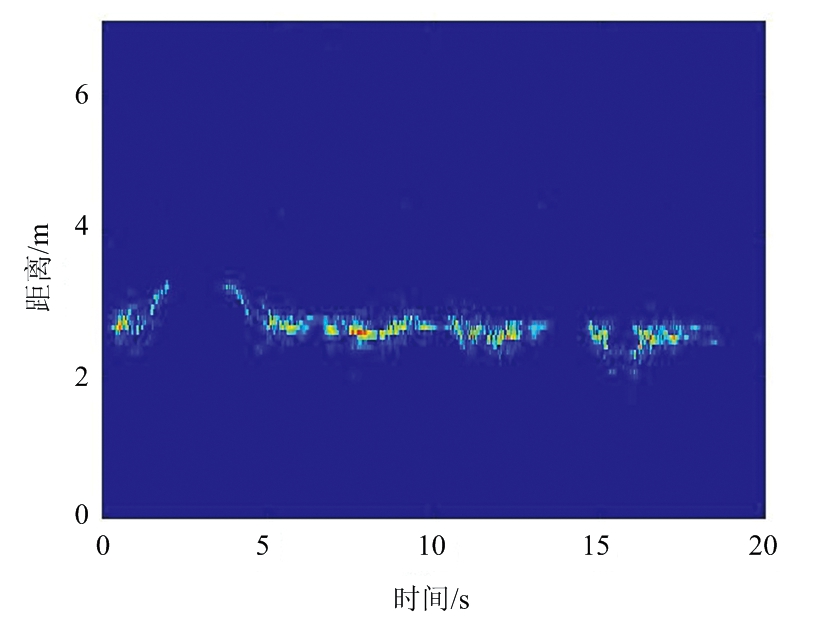
(a) 距离时间图
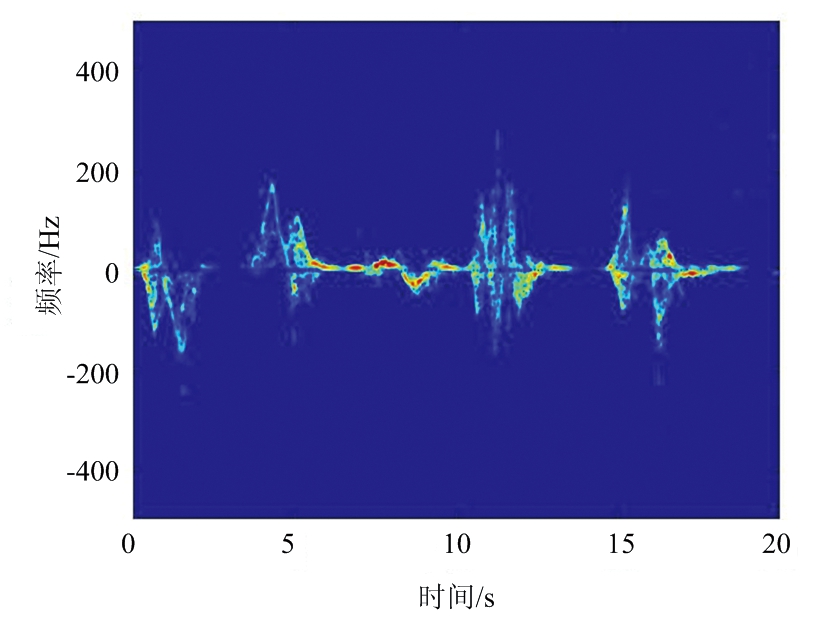
(b) 微多普勒时频谱图
图5 人体连续动作对应的特征图
为了检验本文所提方法对连续人体动作的识别性能,分别将回波信号的距离时间特征、微多普勒特征和双流融合特征向量输入到本文所搭建的两种Bi-LSTM网络中进行训练与测试,考虑到网络一次只能输出一个动作识别结果,因此不可以将一组连续动作的距离时间特征与距离多普勒特征直接进行PCA后并联融合输入网络,而是需要对每组连续动作先进行分割操作。本文对每一组连续动作的距离时间图分割成191个时长为1 s,间隔为0.1 s的距离时间图,并对这些距离时间图分别进行时频分析,每组连续动作经过如上操作会产生191个距离时间图与微多普勒时频谱图,这些图所包含的特征信息对应的是该组连续动作的191个时段内的动作,而每一时段目标所作动作就是当前时段对应特征信息的动作标签类别。在划分训练与测试样本集时首先从收集到的数据样本集中随机抽取一人的所有样本数据作为A组测试样本集,其次将剩余3人的样本数据按照1∶1的比例随机划分为训练样本集与B组测试样本集,共计15组连续动作样本用于训练与25组连续动作样本用于测试。采用连续动作训练样本集经过上述分割操作并标记动作标签类别后对Bi-LSTM网络进行训练,采用B组测试样本经过上述分割操作后进行随机抽样实验测试,采用A组测试样本经过上述分割操作后进行留一法实验测试,网络每0.1 s会对测试样本进行一次动作判定。网络训练过程中学习率设定为0.001,训练迭代次数为100次,梯度下降方式采用小批量随机下降法,批量大小设定为64,实验结果如表3和表4所示。
表3 单层Bi-LSTM网络不同动作识别准确率 %

动作类型随机抽样实验距离时间特征微多普勒特征双流融合特征留一法实验距离时间特征微多普勒特征双流融合特征无动作71.482.786.164.076.175.2坐下72.386.287.765.967.372.6站起74.581.885.367.470.574.4举杯喝水40.169.876.838.456.262.1弯腰捡东西67.079.985.859.974.474.8跳跃47.876.880.551.870.869.9平均识别准确率67.880.684.860.670.575.1
表4 双层Bi-LSTM网络不同动作识别准确率 %
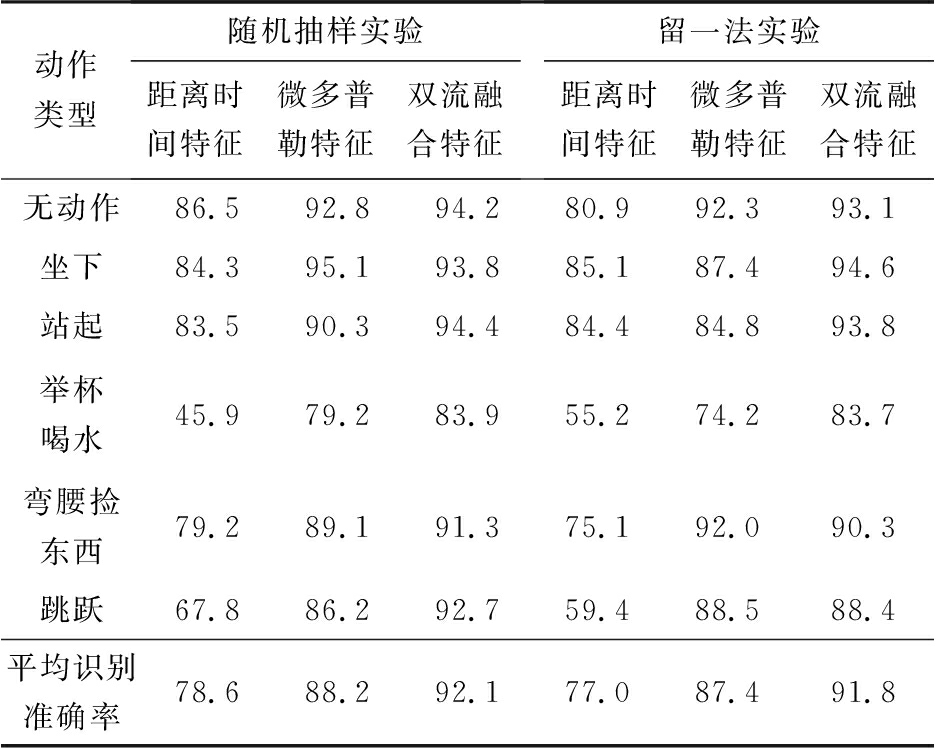
动作类型随机抽样实验距离时间特征微多普勒特征双流融合特征留一法实验距离时间特征微多普勒特征双流融合特征无动作86.592.894.280.992.393.1坐下84.395.193.885.187.494.6站起83.590.394.484.484.893.8举杯喝水45.979.283.955.274.283.7弯腰捡东西79.289.191.375.192.090.3跳跃67.886.292.759.488.588.4平均识别准确率78.688.292.177.087.491.8
对比表3与表4结果可以看出,采用双层Bi-LSTM的网络对比只采用一层Bi-LSTM层可以有效地提高识别准确率,同时观察两种网络模型在3种不同特征情况下对各个不同动作的识别准确率可以看出采用双层Bi-LSTM网络进行留一法实验的平均识别准确率与随机抽样测试的平均识别准确率并无太大差别,在个别动作上的识别准确率互有高低,采用单层Bi-LSTM网络进行的留一法实验结果对比随机抽样实验结果差距较大。因此双层Bi-LSTM网络具有更好的泛化能力,对未知目标样本具有一定的识别能力。
为进一步验证本文所提Bi-LSTM网络对于连续人体动作的识别能力,本文将两种Bi-LSTM网络的双流融合特征识别结果与文献[15]和文献[16]所用方法的识别结果进行对比,对比结果如表5所示。可以看出在随机抽样时间与留一法实验两种不同实验类别情况下,采用双层Bi-LSTM网络对各个不同动作的识别准确率普遍高于其余3种网络结构。
表5 不同方法识别准确率对比 %
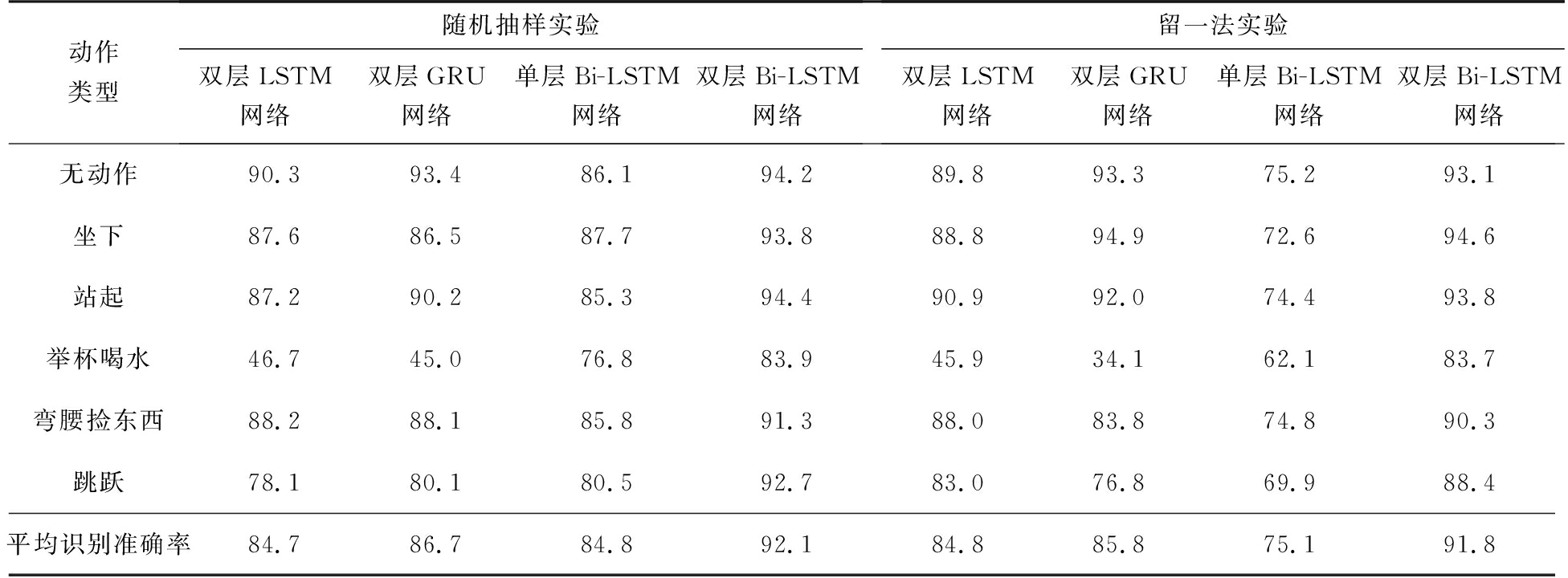
动作类型随机抽样实验双层LSTM网络双层GRU网络单层Bi-LSTM网络双层Bi-LSTM网络留一法实验双层LSTM网络双层GRU网络单层Bi-LSTM网络双层Bi-LSTM网络无动作90.393.486.194.289.893.375.293.1坐下87.686.587.793.888.894.972.694.6站起87.290.285.394.490.992.074.493.8举杯喝水46.745.076.883.945.934.162.183.7弯腰捡东西88.288.185.891.388.083.874.890.3跳跃78.180.180.592.783.076.869.988.4平均识别准确率84.786.784.892.184.885.875.191.8
为进一步研究所提基于双流融合特征的识别效果,本文对随机抽样实验中若干样本数据的识别结果进行对比,结果如图6所示,图6(a)与图6(b)分别展示了在随机抽样实验与同环境留一法实验下采用3种不同特征对共计25个测试样本每个具体的识别准确率情况。从图中可以看出当将融合特征作为网络输入时识别准确率普遍较高,但也有个别数据会出现采用微多普勒特征识别率较高的情况。如图6(a)中的7号、15号样本和图6(b)中的2号、9号样本。
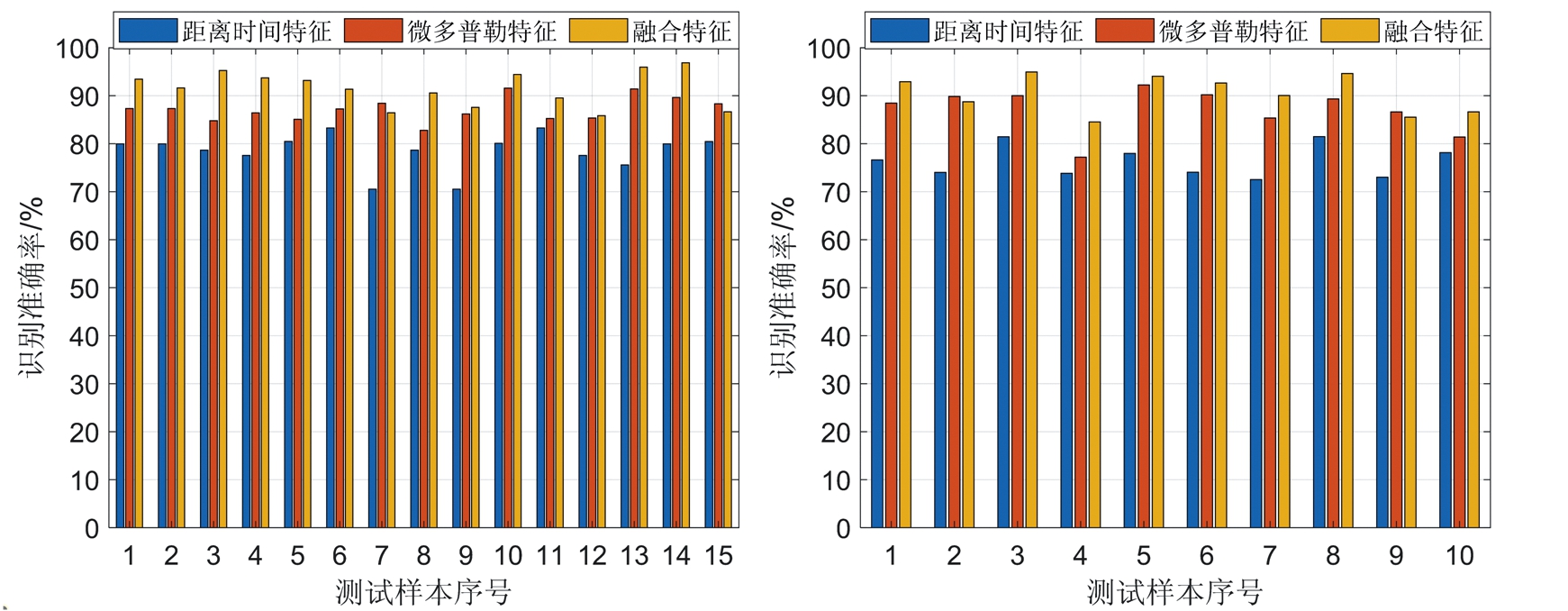
(a) 随机抽样实验 (b) 留一法实验
图6 测试样本识别准确率
为进一步深入研究基于双流融合特征的识别效果,对基于距离时间特征、微多普勒特征与双流融合特征的Bi-LSTM网络判别结果与人体真实动作进行对比,对比结果如图7所示。
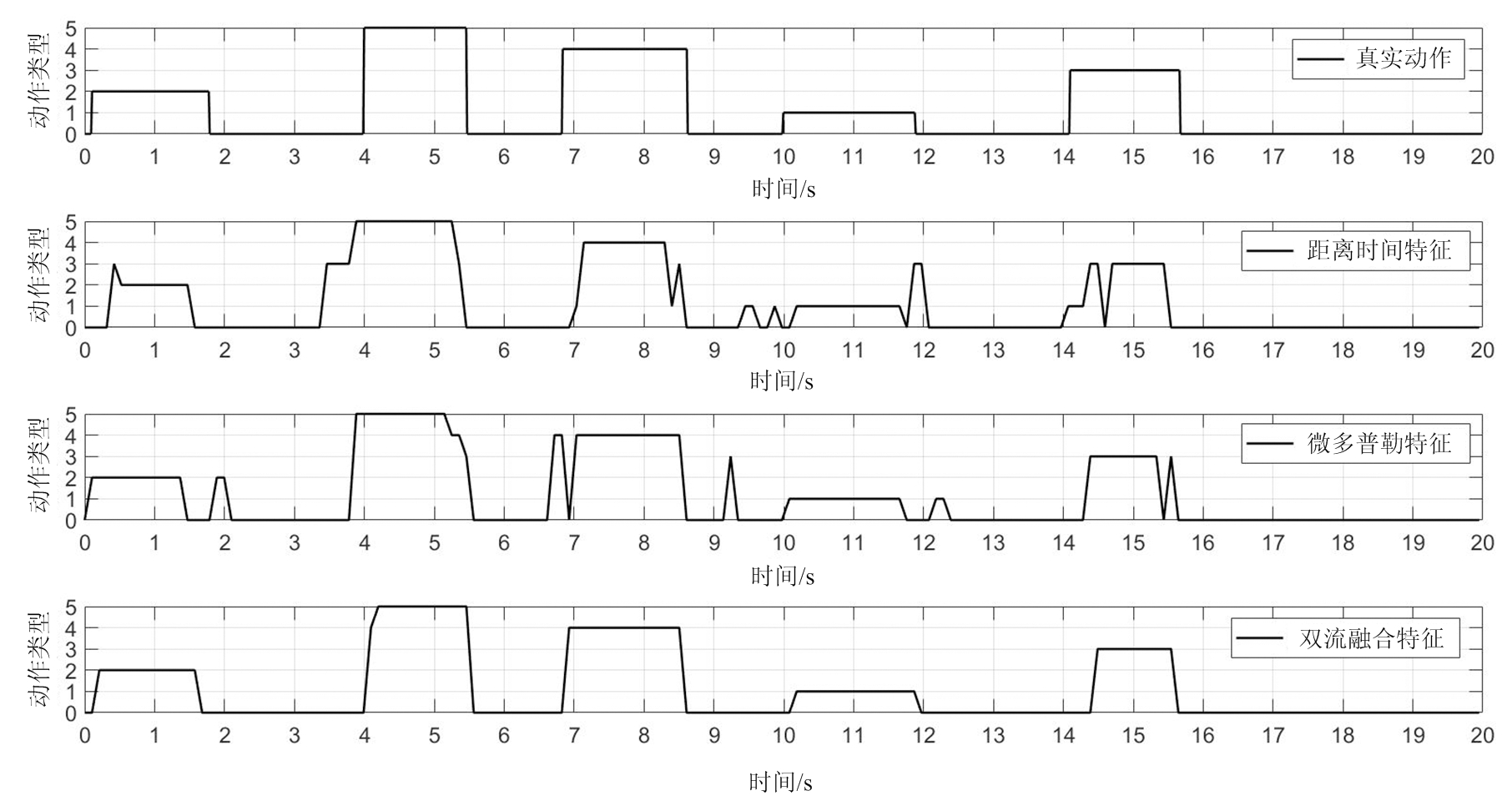
图7 识别结果与真实动作比较图
图7中纵轴为动作类型,数字0~5分别表示无动作、坐下、站立、举杯喝水、弯腰捡东西与跳跃动作,横轴为一组动作的持续时间,动作总时长为20 s。可以看出当采用双流融合特征作为网络输入时识别结果与真实值总体一致,突变较少,在个别动作判别上有少许的延后或提前。当采用单一特征时离散性的突变出现较多,且当采用距离时间特征作为Bi-LSTM网络输入时网络判别值与真实动作差异更加明显。此外在动作变化时特征谱图也会产生急剧的变化,此时这种变化没有对应的动作结果,Bi-LSTM只能根据来自先前时间的实际识别结果或延后时间的实际识别结果来决定此时的动作类型,因此可以发现Bi-LSTM根据融合特征得到的识别结果与真实发生的动作在动作变化时刻存在短暂提前或延迟情况,但这种情况并不会在整体上产生错误的分类。
3 结束语
本文提出了一种基于双流特征融合的FMCW雷达连续人体动作识别方法。基于实测雷达数据处理的结果表明,采用该方法对连续人体动作的平均识别准确率可达到92.1%,对比采用单一维度特征进行识别效果有所提高,且通过留一法实验得出本文所提方法具有一定泛化能力,对未知目标样本具备一定的识别能力。但同时对个别动作识别准确率偏低,在下一阶段工作中将重点提升识别准确率,使得该方法拥有更为广阔的应用前景。
[1] SILVA F H D S, BEZERRA G M, HOLANDA G B, et al. A Novel Feature Extractor for Human Action Recognition in Visual Question Answering[J]. Pattern Recognition Letters, 2021, 147:41-47.
[2] CHACCOUR K, DARAZI R, EL HASSANI A H, et al. From Fall Detection to Fall Prevention: A Generic Classification of Fall-Related Systems[J]. IEEE Sensors Journal, 2017, 17(3):812-822.
[3] KERNEC J L, FIORANELLI F, DING Chuanwei, et al. Radar Signal Processing for Sensing in Assisted Living: The Challenges Associated with Real-Time Implementation of Emerging Algorithms[J]. IEEE Signal Processing Magazine, 2019, 36(4):29-41.
[4] KIM Y, MOON T. Human Detection and Activity Classification Based on Micro-Doppler Signatures Using Deep Convolutional Neural Networks[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(1): 8-12.
[5] SADREAZAMI H, BOLIC M, RAJAN S.CapsFall: Fall Detection Using Ultra-Wideband Radar and Capsule Network[J].IEEE Access,2019,7:55336-55343.
[6] YANG Yang, HOU Chunping, LANG Yue, et al. Open-Set Human Activity Recognition Based on Micro-Doppler Signatures[J]. Pattern Recognition,2019,85:60-69.
[7] 丁晨旭, 张远辉, 孙哲涛, 等. 基于FMCW雷达的人体复杂动作识别[J]. 雷达科学与技术, 2020, 18(6): 584-590.
[8] LI Haobo, SHRESTHA A, FIORANELLI F, et al. Multisensor Data Fusion for Human Activities Classification and Fall Detection[C]∥2017 IEEE Sensors, Glasgow, UK:IEEE, 2017:1-3.
[9] DING Chuanwei, CHAE R, WANG Jing, et al. Inattentive Driving Behavior Detection Based on Portable FMCW Radar[J]. IEEE Trans on Microwave Theory and Techniques, 2019, 67(10):4031-4041.
[10] LI Yiran, PENG Zhengyu, PAL R, et al. Potential Active Shooter Detection Based on Radar Micro-Doppler and Range-Doppler Analysis Using Artificial Neural Network[J]. IEEE Sensors Journal, 2019, 19(3):1052-1063.
[11] 夏朝阳, 周成龙, 介钧誉, 等. 基于多通道调频连续波毫米波雷达的微动手势识别[J]. 电子与信息学报, 2020, 42(1):164-172.
[12] LI Haobo, SHRESTHA A, HEIDARI H, et al. Activities Recognition and Fall Detection in Continuous Data Streams Using Radar Sensor[C]∥2019 IEEE MTT-S International Microwave Biomedical Conference,Nanjing, China:IEEE, 2019:1-4.
[13] SHRESTHA A, LI Haobo, LE KERNEC J, et al. Continuous Human Activity Classification from FMCW Radar with Bi-LSTM Networks[J]. IEEE Sensors Journal, 2020, 20(22):13607-13619.
[14] LI Haobo, SHRESTHA A, HEIDARI H, et al. Bi-LSTM Network for Multimodal Continuous Human Activity Recognition and Fall Detection[J]. IEEE Sensors Journal, 2019, 20(3):1191-1201.
[15] WANG Mingyang, ZHANG Yimin, CUI Guolong. Human Motion Recognition Exploiting Radar with Stacked Recurrent Neural Network[J]. Digital Signal Processing, 2019, 87:125-131.
[16] WANG Mingyang, CUI Guolong, YANG Xiaobo,et al. Human Body and Limb Motion Recognition via Stacked Gated Recurrent Units Network[J]. IET Radar Sonar and Navigation, 2018, 12(9):1046-1051.

