0 引言
在智能交通系统(ITS)中，多目标交通雷达作为道路交通辅助工具，可以监测雷达探测区域内全部车辆的运动状态信息，及时掌握道路车辆信息，有利于交管部门管控道路，减少交通事故的发生，提高道路的安全指数[1]。基于毫米波雷达的交通流量计是典型的用来监测道路状况的装置，可以安装在路侧、路口红绿灯处、天桥等视野较好的高处。雷达通过接收发射出去电磁波的回波信号，获取道路车辆的运动信息，主要包括探测车辆的位置和速度等信息[2-3]，实现对道路车辆运动轨迹的监测。多目标聚类是雷达回波数据处理中关键的一步，快速得到准确的聚类结果可以减小聚类误差在后续处理中产生的影响，减少后续跟踪等高级算法的计算量，提高相关算法的精度。近年来，多种经典聚类算法被应用在交通领域中，包括基于密度的DBSCAN聚类算法[4]，基于分区的K-means算法和模糊C均值(FCM)算法[5]。基于密度峰值的聚类算法。文献[4]中的DBSCAN是基于空间数据点分布密度的算法，但当不同类数据相距较近时聚类效果会略差；基于分区的K-means算法通过确定分类数目K后，将距离作为分类指标，按照簇内的点分布紧密且簇间的距离相对大的规则进行聚类，直至聚类结果不再更新，此方法对K值较敏感，以及随机确定的初始中心，会影响算法的收敛速度和聚类结果；FCM算法是模糊聚类算法[5-6]，用隶属度表示每个数据点属于某簇的程度，通过求解目标函数最优值确定聚类中心和隶属度值。该算法具有较高的精度，但需要设置初始参数，如果参数初始化不合适，可能会影响最终聚类结果的正确性。其次，当数据样本集较大时，算法实时性不佳[7-8]。结合城市道路场景，当道路上车流量较大、车辆相距很近时，雷达采样点分布会更加密集，此时运用传统FCM算法不能准确地识别相邻车辆 [9]。意大利Rodriguez等[10]提出了一种基于密度峰值的快速聚类算法(DPC算法)，该算法主要思想是：1) 聚类中心的密度大于邻域密度；2) 聚类中心与其他高密度点的距离相对较大。DPC算法利用局部密度和相对距离划分样本点，处理过程简单又高效。但DPC算法根据决策图选取初始簇中心，若选取不当，将导致后续样本点聚类错误。
针对以上传统算法中的问题，结合毫米波雷达交通流量计中数据的特点，本文提出一种改进的基于密度峰值的FCM聚类算法：1) 对文献[10]中DPC算法的决策图做出改进，用改进后的决策图确定初始聚类中心。在决策图中使用自适应椭圆距离[11]代替欧式距离，并在图中加入一条自适应函数曲线用以自动确定初始聚类中心；2) 根据步骤1)确定的初始聚类中心计算隶属度矩阵，将聚类中心坐标和隶属度矩阵作为FCM算法的初始条件，使用FCM算法更新聚类中心和隶属度，完成一次模糊聚类；3) 根据一次聚类结果计算各簇样本点的速度中位数，将速度中位数与一次模糊聚类更新的隶属度作为FCM算法初始条件，进行二次模糊聚类，得到最终模糊聚类结果。实验证明，提出的算法最终得到更为精确的聚类结果。
1 基于密度峰值的聚类算法
基于密度峰值的聚类算法核心是认定簇中心满足以下特征：1)簇中心的密度比其周围点的密度大，即簇中心为密度峰值点；2)簇中心之间的距离比簇中心到其他点的距离更大。根据这两个条件即可确定簇中心和簇数目[12]。
用DPC算法处理数据集
时，首先计算任一样本点的局部密度ρi，计算公式如下：
(1)
式中dc为预设的截断距离，dij表示任意两点间的距离，当满足x<0时，χ(x)=1，否则χ(x)=0。式(1)的物理意义为统计以i点为中心，dc为半径的圆内样本点的个数，个数即代表密度大小。除了利用公式(1)中截断核[13]计算局部密度外，还可以用高斯核[14]计算局部点密度，其定义如下：
(2)
由公式(2)可知，高斯核表示的点密度为连续值，不会出现截断核密度中不同数据点具有相同密度值的现象，更有利于后续的数据处理。DPC算法中，在得到任意点的局部密度ρi后，求各点的最小距离δi。最小距离δi由任意点zi与其他高密度点间的最小距离[14-15]确定：
(3)
对于数据集中密度最大的点，其最小距离δi=max(dij)。需要注意的是，对于局部或全局密度最大的点，δi比一般的最小距离大得多。
计算得到任意样本点zi的局部密度ρi和最小距离δi后，以每个点的ρi为横坐标，δi为纵坐标画如图1(a)所示的二维决策图，用户在决策图中，根据分布情况手动选择聚类中心点，通常将同时具有较大ρi和较大δi的点定义为聚类中心，其余点分配到比自身密度高且距离最近的聚类中心所属的簇中[14]。
图1(a)中横坐标为样本点密度，纵坐标为最小距离，红色标记点为选定的初始聚类中心，蓝色点为其他样本点。图1(b)是所有样本点分类后的二维坐标图，不同颜色的点为不同簇，黑色圆点是由二维策略图确定的聚类中心。
DPC算法需要在策略图中手动确定聚类中心，导致算法的运行效率低，在确定聚类中心后，仅根据各样本点到聚类中心的距离进行最终聚类，导致聚类结果准确率低。因此，本文提出的算法对DPC算法中的决策图进行改造，使用自适应椭圆距离代替欧式距离计算dij，进一步计算得到更可靠的ρi和δi，并在决策图中引入自适应函数曲线自动判定聚类中心，提高聚类中心确定的效率。
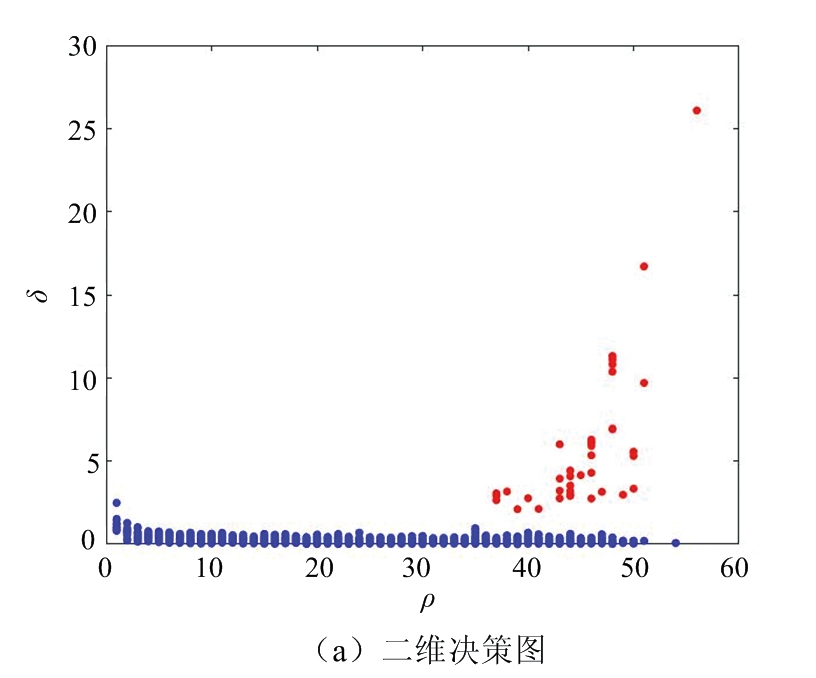
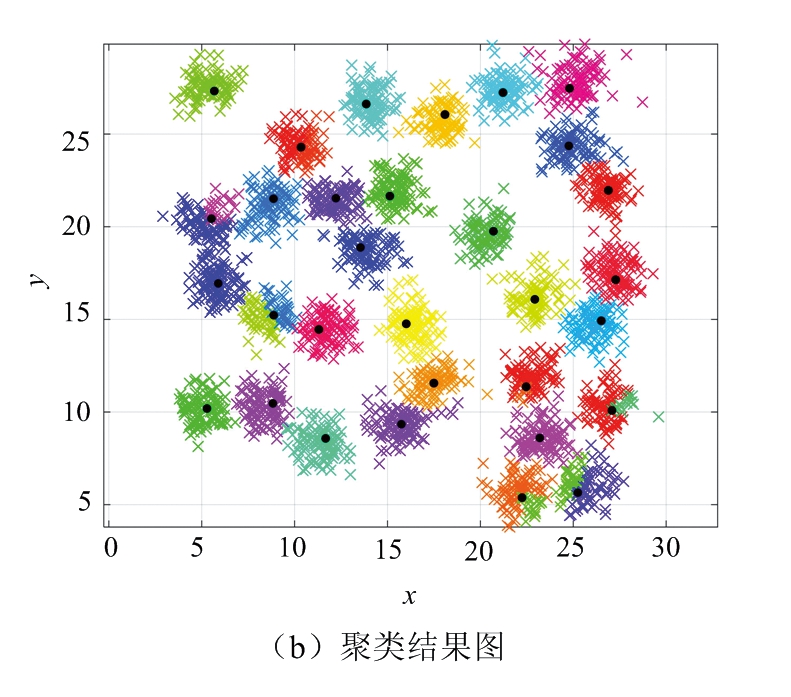
图1 密度峰值聚类算法过程图
2 提出的算法
针对传统DPC算法中聚类中心的确定需要人工操作、聚类仅靠距离这一判定条件，本文对DPC算法进行改造，并使用FCM算法进行模糊聚类。首先，改进DPC算法决策图，使用自适应椭圆距离代替欧氏距离，计算样本点的局部密度和最小距离并将二者作为横、纵坐标，画决策图，在决策图中添加一条自适应函数曲线，以自动确定初始聚类中心；接着，将初始聚类中心信息代入FCM算法，根据距离信息构造目标函数，做一次模糊聚类；最后，在一次模糊聚类结果基础上，根据每簇的速度信息构造目标函数，做二次模糊聚类，以修正一次聚类结果。
2.1 初始聚类中心的确定
对样本点集
进行聚类处理，通常情况下，用欧式距离计算两点之间的间距，本文所处理的样本点坐标由车辆分布确定，当样本数目足够大时，每辆车的采样点应该呈长方形接近椭圆状，因此本文模仿椭圆的一般方程式 [11]计算任意两点k,l间的自适应椭圆距离dkl，其表达式为
(4)
此计算方法设置Mak，Mbk两个变量参数来调整数据之间的距离相关性，用来作为自适应椭圆距离的长轴、短轴参数，其分别为
(5)
式中，Mkl是变化参数，变量间关系满足Mkl=Mklx+Mklx·Mkly，将此关系式代入式(5)可知Mak由Mkly大小决定，Mbk由
和Mak的大小共同决定：
(6)
其中，Mklx和Mkly分别由两点的横、纵坐标差决定：
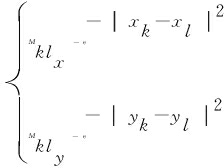
(7)
此式通过自然数e将横、纵坐标差值转化为值域为[0,1]的变量，当横、纵坐标差变化时，Mklx和Mkly成反比例变化，接着公式(6)可自适应地调整Mak和Mbk大小，从而确定长轴、短轴参数。假设纵坐标差值大于横坐标差值，由公式(6)可知此时Mbk为长轴参数，Mak为短轴参数。当横、纵坐标差较大时，由公式(7)可知自适应椭圆距离在计算过程中发生数量级变化，从而增大距离差异性，进一步使得最小距离的差异显著，有利于策略图中聚类中心的准确判断。
本文使用高斯核计算样本点的密度，点集
中任一点的密度计算公式为
(8)
其中，dkl表示式(4)所求的任意两点间的椭圆距离，dc表示截断距离。截断距离[16]需要通过设置一个百分比η来确定，η取值一般为1%～2%，本文中取2%。确定截断距离前，需要先根据式(4)计算得到所有点的椭圆距离dkl，做升序排列，过滤掉前2%的值，此时的最小值定义为截断距离。
计算各点密度后，需要根据密度来确定任意样本点zk的最小距离δk。这里的最小距离[17]指的是，距离样本点zk最近且密度大于ρk的样本点zl，此时两点的椭圆距离dkl为zk的最小距离；若不存在密度大于zk的点，则找出距离zk最远的样本点zl，将此时的dkl标记为最小距离，其数学表示为
(9)
最后，根据所有样本点的密度ρk和最小距离δk，确定初始聚类中心。由DPC算法原理可知，聚类中心同时具有局部密度大、最小距离大的特点。由图1(a)验证可知，聚类中心一般分布在策略图的右上方，结合这一分布特征，引入指数函数f(x)=e1/x，此曲线在第一象限值域为[1,+∞)，函数曲线基本能分隔开聚类中心和非聚类中心样本点。但经实验发现不同样本的策略图分布略有差异，因此为指数函数设置一个自适应参数，设定函数表达式为f(x)=α·e1/x，规定曲线f(x)经过
其中
为某一样本点集的密度均值，
为距离均值，计算式分别为
(10)
(11)
将
代入f(x)表达式中求得α的值。如图2所示，处理的数据为下文实验部分场景一的样本数据，蓝色点由样本数据确定，横坐标为样本点密度，纵坐标为样本点最小距离，红色曲线为自适应指数函数曲线f(x)，曲线上标红的点为
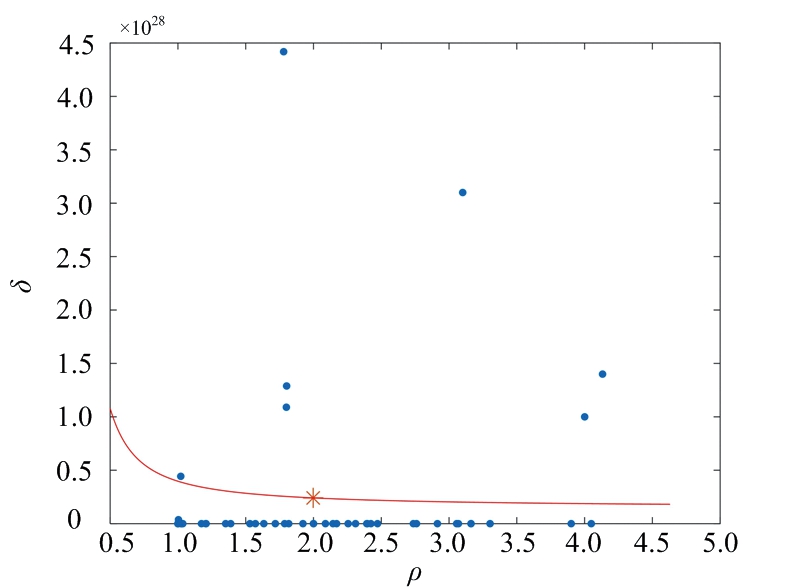
图2 加入幂函数曲线的决策图
由图2可容易确定位于曲线f(x)上方的点满足密度大且最小距离大，即为所求的初始簇中心；位于曲线f(x)下方的点为其他点，需要进一步做聚类处理。
2.2 结合速度的FCM算法
FCM算法是一种基于对目标函数优化的数据聚类算法，其聚类结果是每个样本点关于簇中心的隶属度和更新的簇中心。其中隶属度是一个模糊概念，表示的是某一样本点属于某簇的程度，取值范围为[0,1]，任一样本点关于所有簇中心的隶属度之和为1。在计算过程中隶属度和簇中心会不断更新，直至簇内加权误差平方和最小，得到最终的聚类划分。
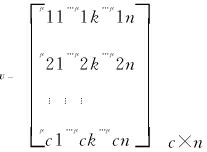
传统FCM算法需要人工确定初始值，运行过程不需人工干预。本节利用上节确定的聚类中心作为FCM算法的初始条件，提高FCM算法运行效率。首先，上节确定的初始聚类中心用集合Ir表示，其中r=1,2,…，c，表示共有c个聚类中心；接着，计算样本点集中所有样本点关于簇中心Ir的隶属度μrk，满足μrk∈[0,1]，μrk表示样本点集的第k个点关于第r个聚类中心的隶属度，U表示由μrk组成的隶属度矩阵：
(12)
由隶属度定义可知，任意样本点k关于聚类中心Ir的隶属度之和为1，即
(13)
将初始聚类中心Ir和隶属度μrk作为FCM算法的目标函数初始条件，根据传统FCM算法构造目标函数为
(14)
式中‖zk-Ir‖表示样本点集中第k点zk到第r个聚类中心Ir的距离；m表示模糊指数，其大小代表模糊程度，值越大表示分类的模糊性越大，反之越小，m范围为[1.5,2.5] ，通常取2，在本文中亦取2。将式(14)结合约束式(13)，构造拉格朗日函数为
(15)
为求取目标函数J的极值，需要将函数分别对μrk和Ir求偏导，并令偏导为0，即
(16)
求解式(16)得到式(17)，由式(17)关系式可知模糊隶属度μrk与聚类中心Ir之间存在一定的相关性，因此FCM算法的μrk和Ir初始值是十分重要的。
(17)
在计算迭代过程中，算法的目标函数值会不断变化，并最终趋于稳定。当更新的目标函数值J与上一次的迭代值满足迭代停止条件时，结束计算，输出此时的μrk、Ir。迭代停止条件：
ε=new J-previous J<ε0
(18)
式中，ε0为设定的最小更新量，本文取0.000 1。最大迭代次数I=1 000，此数值可根据实际情况调整，经实验验证，迭代次数一般在100以内，迭代结束便得到一次聚类结果。
在不断的实验中发现来自同一辆车的不同采样点速度差值极小，而来自不同车的速度差异明显。根据这一特性，结合一次聚类结果，使用模糊聚类的思想进行二次聚类以提高聚类精度。首先，提取每簇样本点的速度信息，确定每簇的速度中位数vr(r=1,2,…，c)。这里采用每簇的速度中位数而不使用均值是因为，经实验发现一次聚类结果中存在误判的点但数目不多，而同一辆车的采样点速度差值极小，因此选用中位数更具有代表性、更合理。利用一次聚类结果更新的μrk，构造目标函数Q如下：
(19)
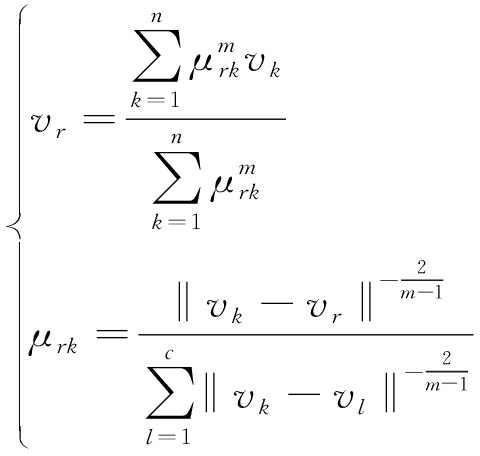
其中，模糊指标m取2，将约束条件式(13)代入目标函数中，与一次聚类相同使用拉格朗日乘子法，解得最优解为
(20)
根据采样点的速度特征，设定此部分的迭代终止条件是，同一簇内任意两点间的速度差值小于σ0，即
|vk-vt|<σ0, ∀k,t且k≠t
(21)
满足式(21)终止迭代后，得到更新的μrk，确定最终的聚类结果。本文实验中σ0取0.5 m/s。最终，由两次模糊聚类得到的是在位置、速度上具有强相关的聚类结果。
综上，本文提出的一种改进的道路行车密度峰值模糊聚类算法具体步骤如下：
输入：样本点集
各样本点坐标(xzk,yzk)、速度vk
输出：更新的μrk
a) 由公式(4)得到dkl，并代入式(7)计算各点的密度ρk，根据式(9)得最短距离δk；
b) 求得
代入曲线f(x)表达式f(x)=α·e1/x确定k值；
c) 以ρk为横轴，δk为纵轴画二维决策图，确定曲线f(x)上方的点为初始簇中心Ir；
d) 计算μrk和各样本点到初始簇中心的距离，将二者作为初始值代入FCM算法进行迭代计算；
e) 迭代更新隶属度μrk和聚类中心Ir；
f) 重复e)，直至满足迭代终止条件式(18)，输出一次聚类结果μrk和Ir；
g) 提取各簇样本点的vk，确定簇内样本点的速度中位数vr；
h) 根据式(20)迭代更新μrk和vr；
i) 重复h)，直至同簇内任意两点的速度满足式(21)时，迭代终止；
j) 输出更新的μrk和vr，得到二次模糊聚类结果。
3 仿真实验
3.1 整体流程
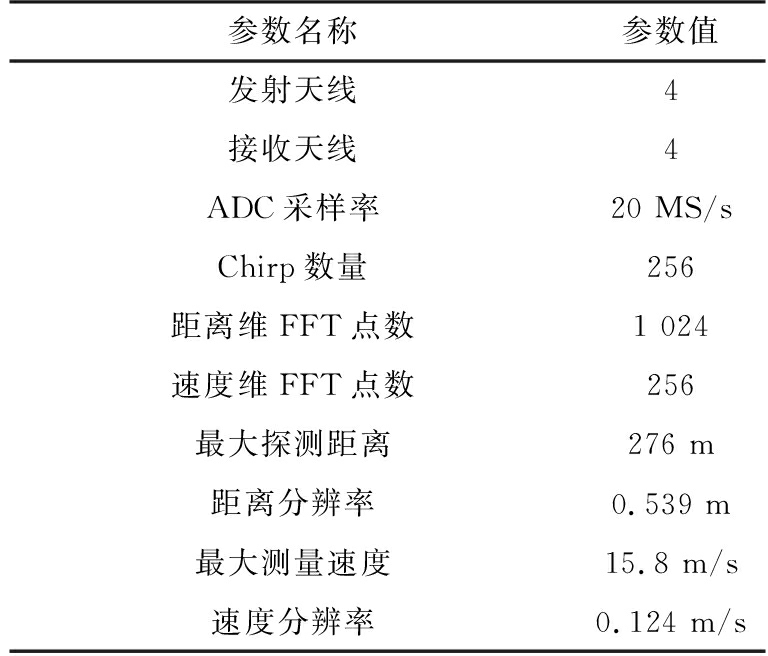
本文采用77 GHz毫米波雷达，工作波形为线性调频连续波，其发射天线和接收天线都为4个，最大可同时探测128个移动车辆目标[18]。采集过程中雷达工作参数如表1所示，每个场景采集10帧ADC原始数据，数据传输速率为20.1 Mbit/s。
表1 雷达工作参数及理论性能
参数名称参数值发射天线4接收天线4ADC采样率20 MS/sChirp数量256距离维FFT点数1 024速度维FFT点数256最大探测距离276 m距离分辨率0.539 m最大测量速度15.8 m/s速度分辨率0.124 m/s
由表1参数可计算出一帧的数据量大小为发射天线×接收天线×距离维FFT点数×速度维FFT点数×2=8 192 Kbit。采集的数据为二进制格式，保存在“.dat”文件中，数据文件大小可以检验采集过程是否存在数据丢失。采集数据过程中有录像可以和算法处理结果进行对比。处理数据的环境为MATLAB R2018b，计算机运算条件为Windows 10， 64-bit，8G内存。
数据处理[19-20]流程如下：
1) 将数据文件读入MATLAB经过傅里叶变换得到样本点的位置、速度信息；
2) 对得到的数据信息做滤波、恒虚警等处理滤除杂波；
3) 将去除杂波后的样本点位置、速度信息代入第三部分提出的算法中，经两次模糊聚类，得到最终高精度的聚类结果。
3.2 实验结果对比
为验证本文提出的算法，用雷达板在城市天桥上采集道路上行驶车辆的数据，对采集的原始数据经预处理后做聚类处理。本部分验证FCM算法、DBSCAN聚类算法和本文提出的聚类算法在3个不同场景下的聚类处理结果。
场景1： 多个小轿车相距较近。
以图3所示的道路场景1为对照，处理相应的雷达数据，图4给出了不同聚类算法对场景1的处理结果。其中，图4(a)给出了经滤波处理后的采样点，共53个。图4(b)为DBSCAN聚类算法处理结果，其中最小半径ε设定为2.2，簇内最小数目为3，共识别出6簇数据。图4(c)为FCM算法处理结果，最终得到7簇数据和各簇中心。图4(d)为DPC算法处理结果，由策略图确定初始聚类中心后，根据各点到聚类中心的距离进行分类，共得到3簇结果。图4(e)为本文提出的算法处理结果，得到7簇数据和各簇中心。
图3 道路场景1
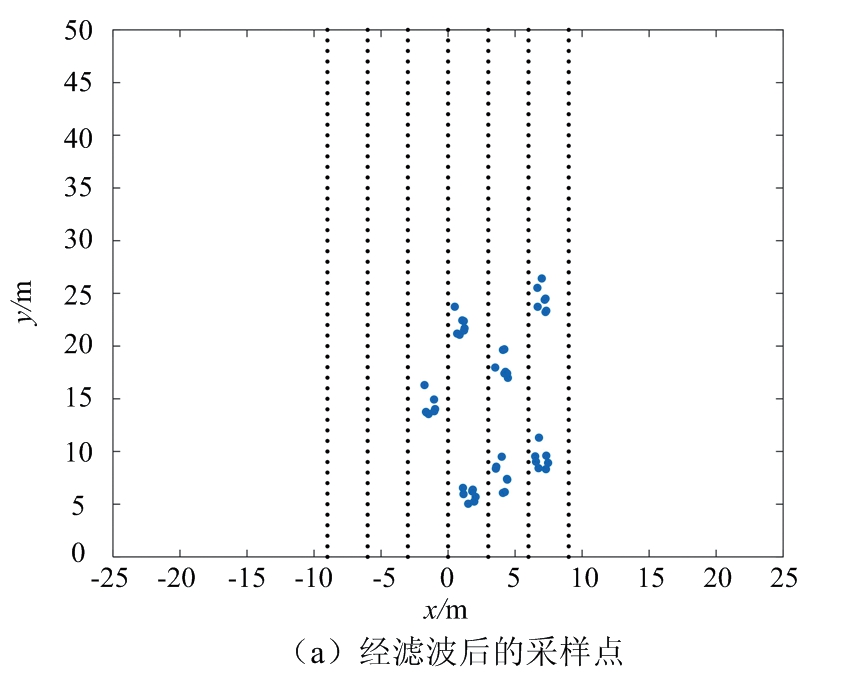
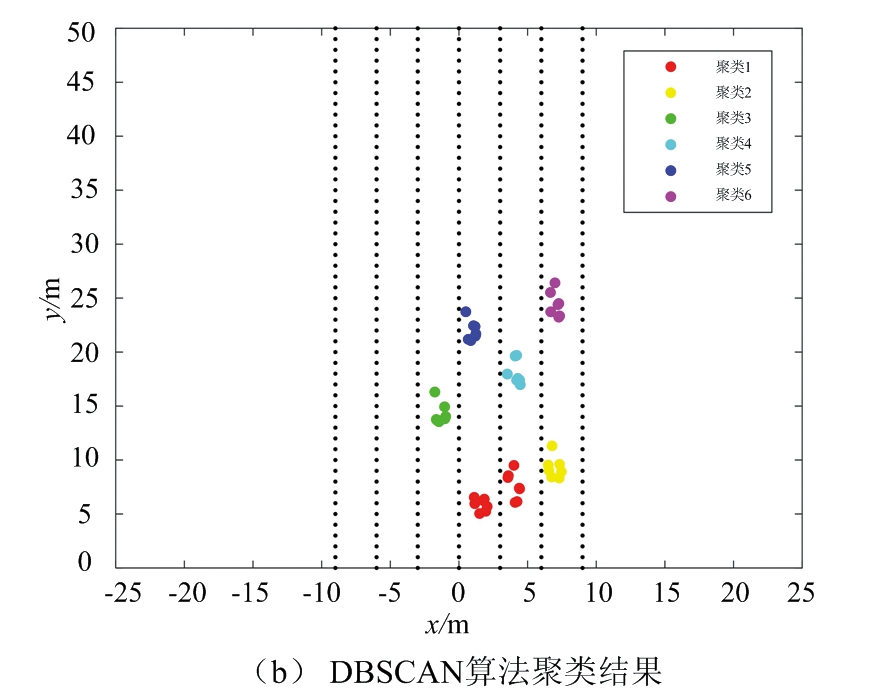
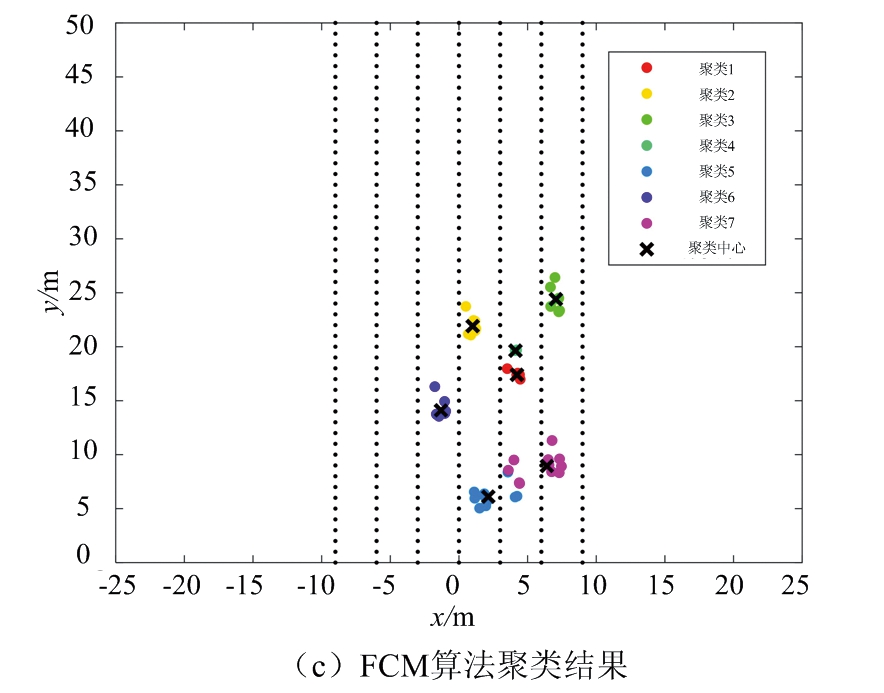
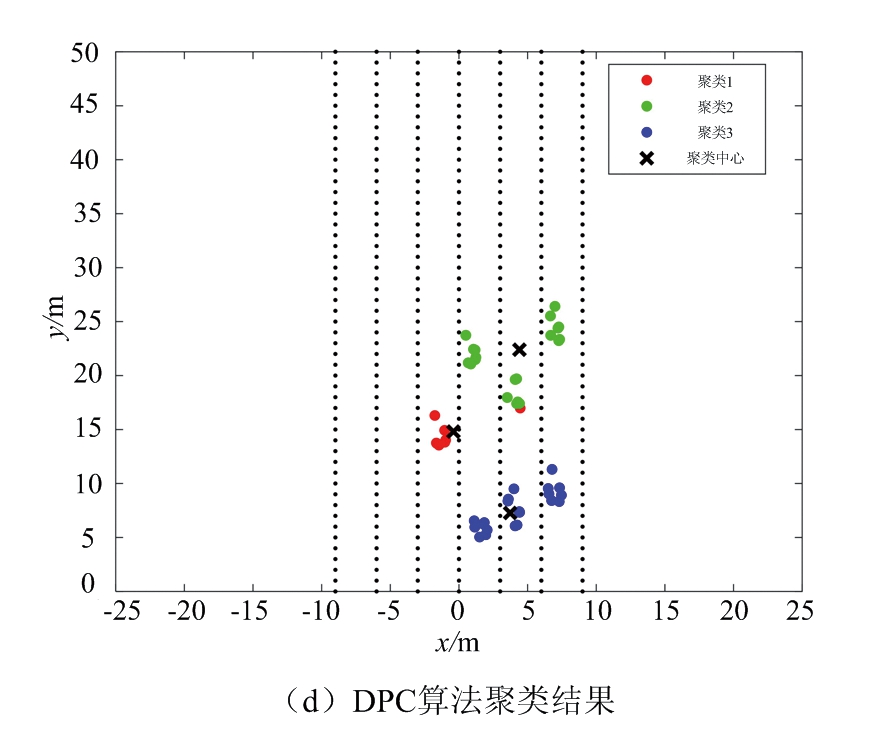
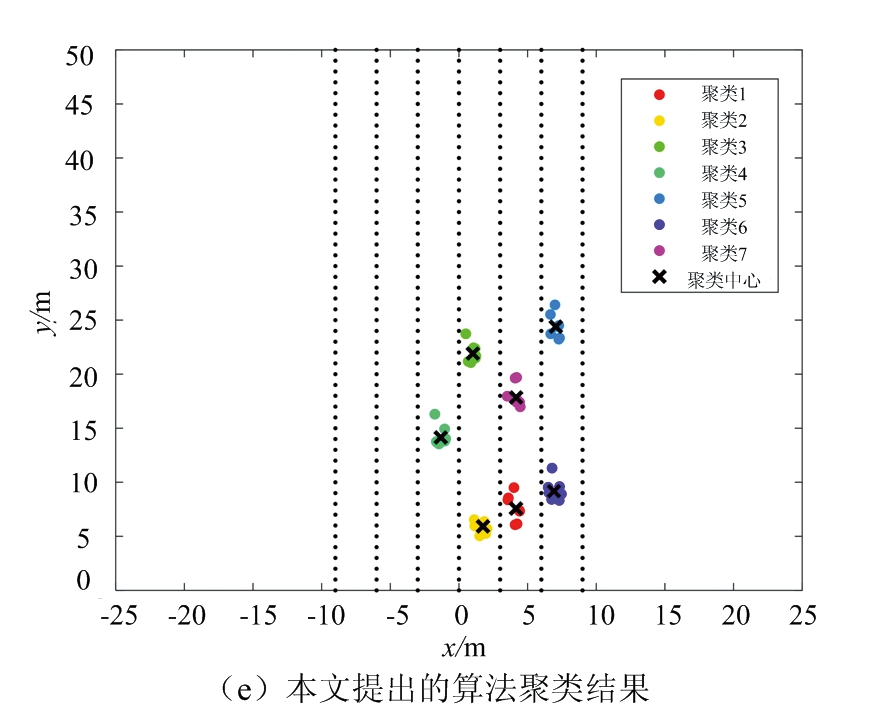
图4 不同聚类算法对场景1的处理结果
对比图4(b)和图4(c)可知，DBSCAN算法和FCM算法能区分大部分车辆目标，但均不能区分位于道路前方相距很近的两辆车。图4(d)由于聚类中心数目误差较大，不能正确聚类道路车辆。由图4(e)可知，本文提出的算法能很好地区分车辆目标，聚类正确。
场景2： 公交车与小轿车相距较近。
以图5所示的道路场景2为对照，处理相应的雷达数据。图6给出不同聚类算法对场景2的处理结果。其中，图6(a)是经滤波处理后的采样点，共39个。图6(b)为DBSCAN聚类算法处理结果，最小半径设定为2.5，簇内最小数目为3，共识别出5簇数据。图6(c)为FCM算法处理结果，最终得到6簇数据和各簇中心。图6(d)为DPC算法处理结果，共识别出3簇数据。图6(e)为本文提出的算法处理结果，得到5簇数据和各簇中心。
图5 道路场景2
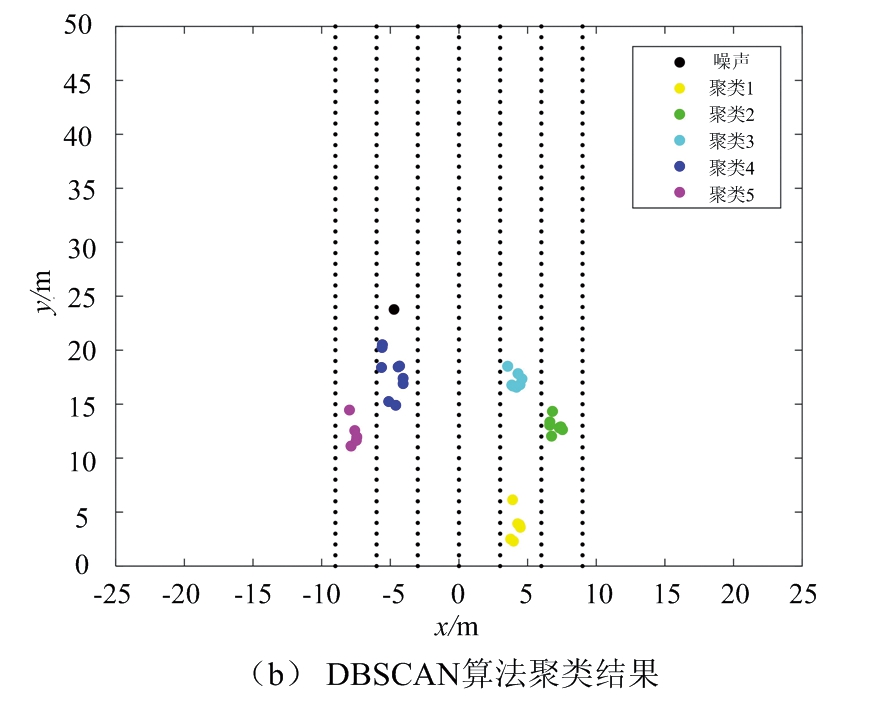
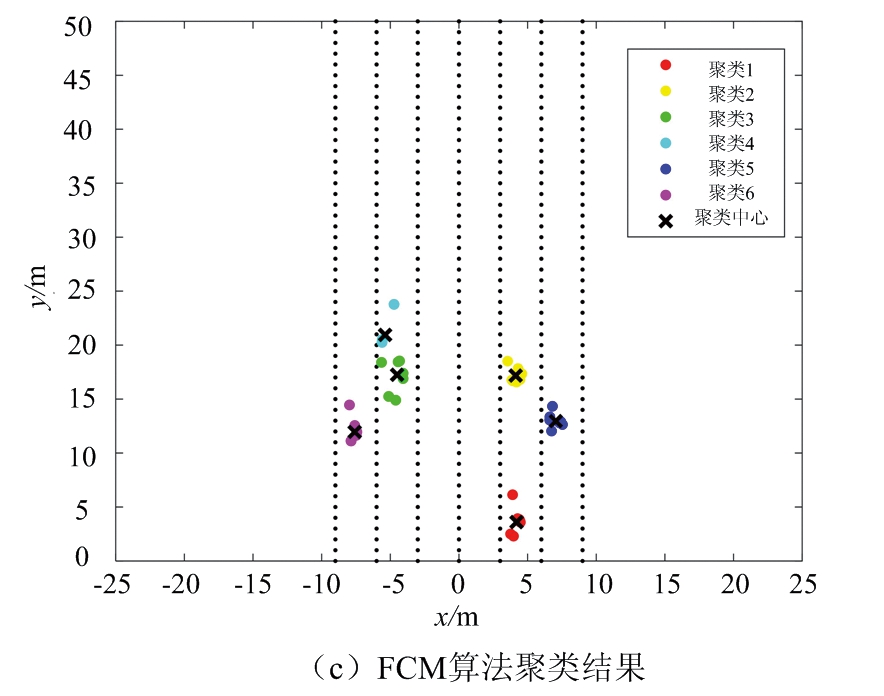
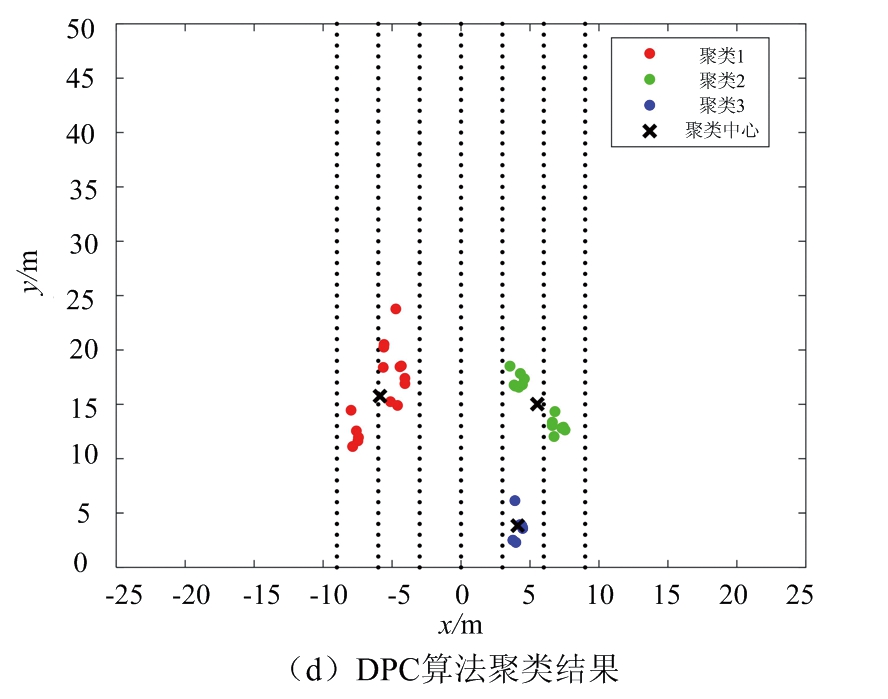
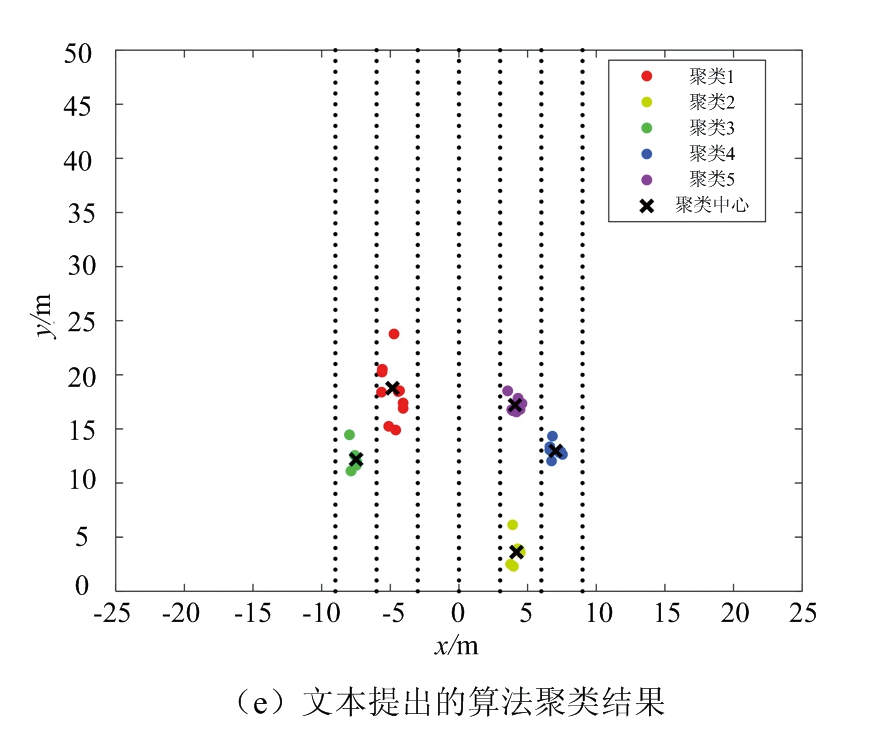
图6 不同聚类算法对场景2的处理结果
图6(b)中DBSCAN聚类算法的参数ε比场景1中参数大，是为了兼顾大目标，但从聚类结果可知，由于公交车目标过大，分布稍远的点会被归为噪声点，影响聚类正确率。图6(c)中FCM算法将公交车大目标分为了两个小目标，图6(d)为DPC算法不能正确聚类道路车辆，簇数目相比其他算法误差最大，而本文提出的算法如图6(d)所示，可以做到正确聚类。
场景3： 多个小轿车相距较近，公交车与小轿车相距较近。
以图7所示的道路场景3为对照，处理相应的雷达数据。图8给出了不同聚类算法对场景3的处理结果。其中，图8(a)给出了经滤波处理后的采样点，共58个。图8(b)为DBSCAN聚类算法处理结果，其中最小半径设定为2.5，簇内最小数目为3，共识别出6簇数据。图8(d)为DPC算法聚类结果，共识别出4簇数据。图8(c)和图8(e)分别为FCM算法、本文提出的算法处理结果，均得到8簇数据和各簇中心。
图7 道路场景3
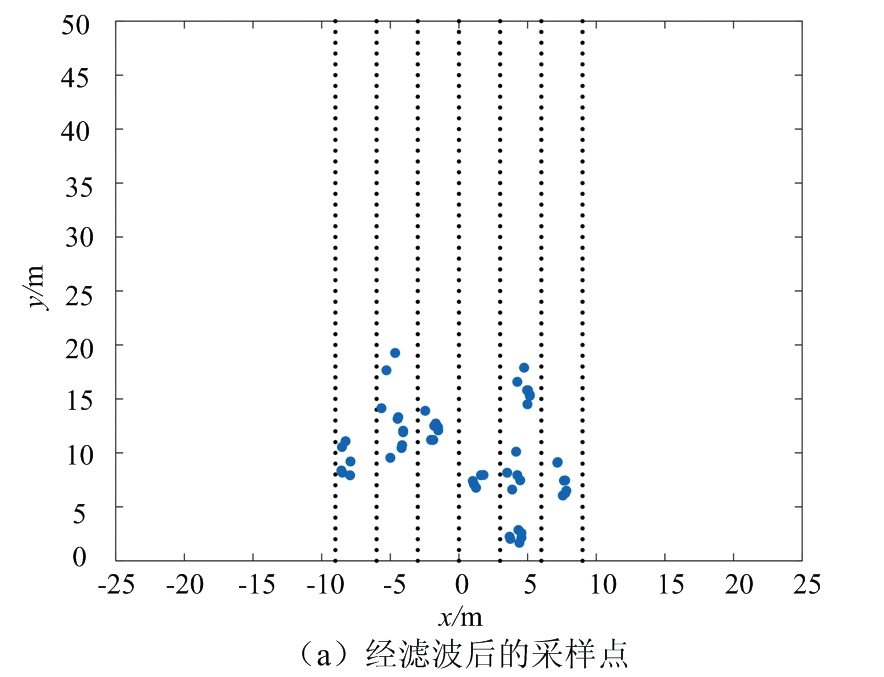
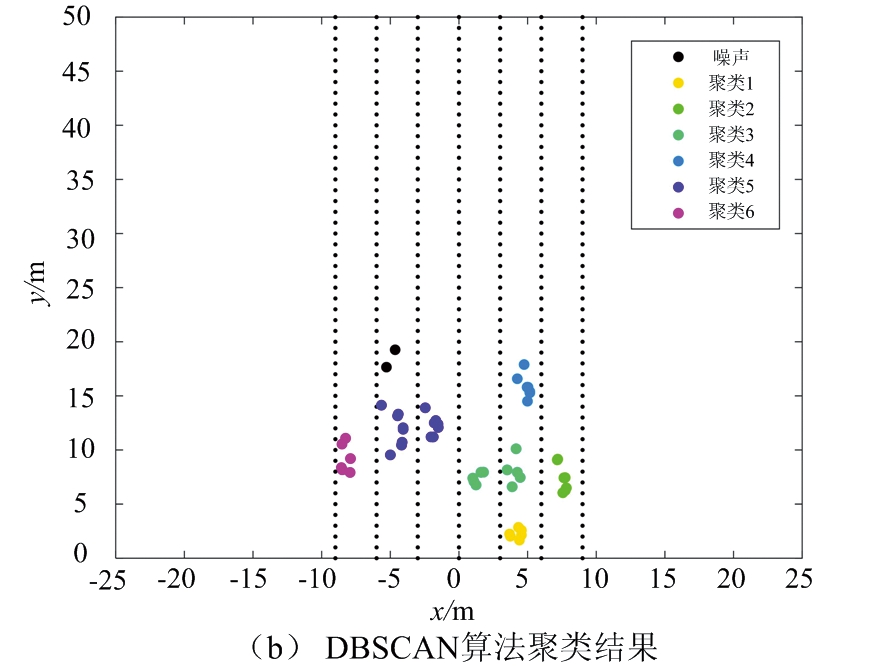
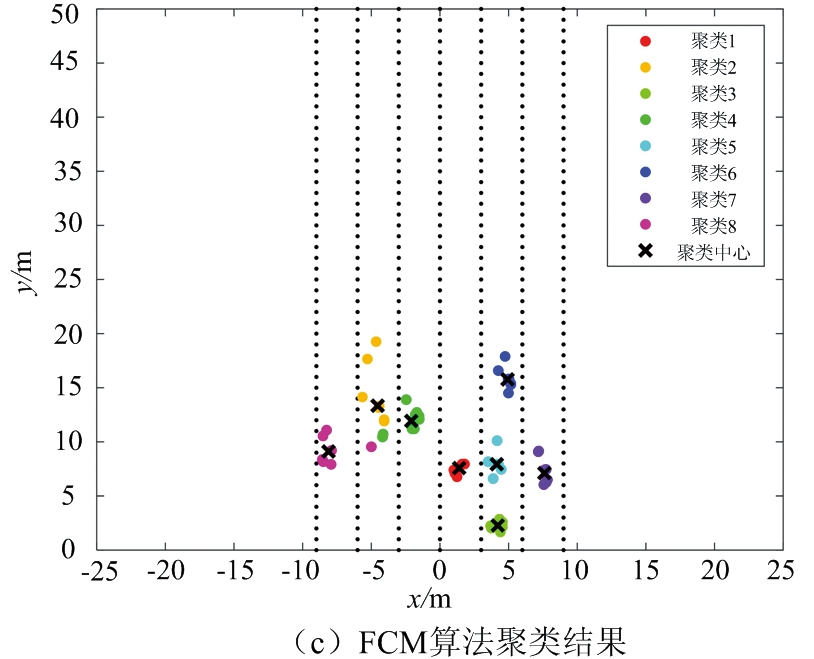
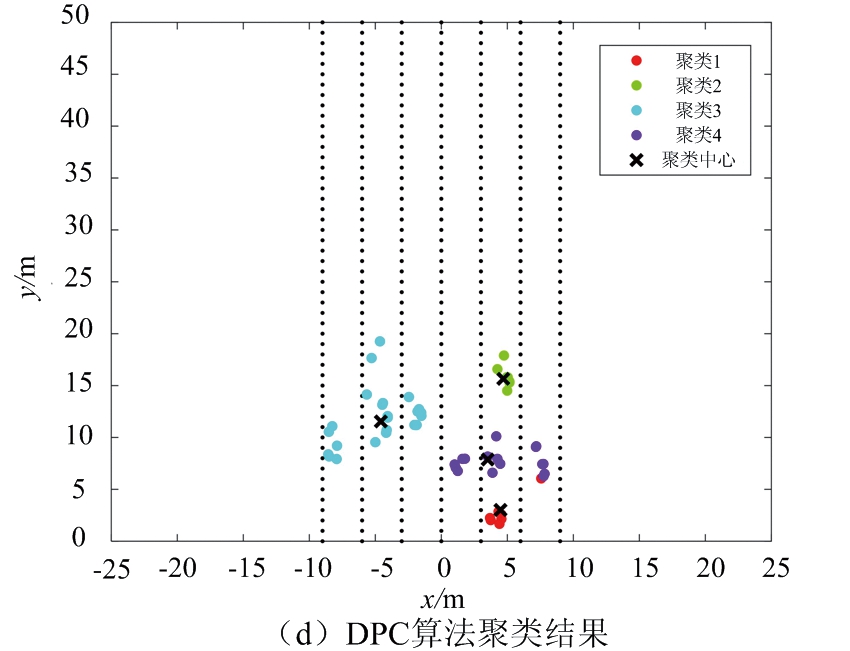
图8 不同聚类算法对场景3的处理结果
对比图8(b)和图8(c)可知，DBSCAN算法和FCM算法能区分大部分车辆目标，但均不能区分位于道路前方相距很近的两辆车。图8(d)的DPC算法由于聚类中心的判断错误，导致最终聚类结果效果差。由图8(e)可知，本文提出的算法能很好地区分车辆目标，聚类正确。
图8(b)中DBSCAN聚类算法对于相距较近的小轿车容易聚类成一个目标，并且由于半径的限制，不能完整识别出场景中的公交车大目标。由图8(c)可知，FCM算法能够识别出各个车辆，但仍存在个别误判的样本点，精确度不够。DPC算法对于相距较近的车辆样本点聚类效果差。本文提出的算法在FCM算法的效果上做出优化，能够识别公交车的全部样本点，减少了误判的样本点。
根据以上3个特殊场景的聚类结果对比可知，DBSCAN聚类算法根据密度分类时，对相距较近和目标较大的车辆聚类效果较差。同时，受半径参数的约束，不能在兼顾小目标的前提下完整识别大目标。传统FCM算法聚类精度较高，能基本识别出道路上的大小车辆目标，但会有个别样本点的误判。DPC算法的初始聚类中心的确定存在误差，导致最终结果误差较大。本文提出的算法在FCM算法的基础上使用速度对数据点再次聚类，明显聚类效果更好。
最后，用Acc指标来衡量各个算法的聚类准确度，Acc [21]定义为
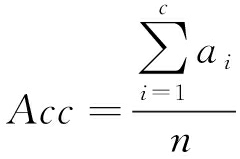
(21)
式中，ai表示第i簇中正确聚类的采样点个数，c表示簇的总个数，n表示处理的原始采样点个数。Acc取值越高说明聚类准确度高，值为1时说明聚类结果完全准确。图9给出了选取的100帧采集数据，使用5种聚类算法的聚类精度比较，其中改进的FCM算法指本文提出的一次模糊聚类算法，即不作二次模糊聚类处理。由图9可以看出，改进的FCM算法比FCM算法聚类精度高，但存在不稳定的问题，本文提出的算法在真实公路场景中聚类精度更高且效果最稳定。
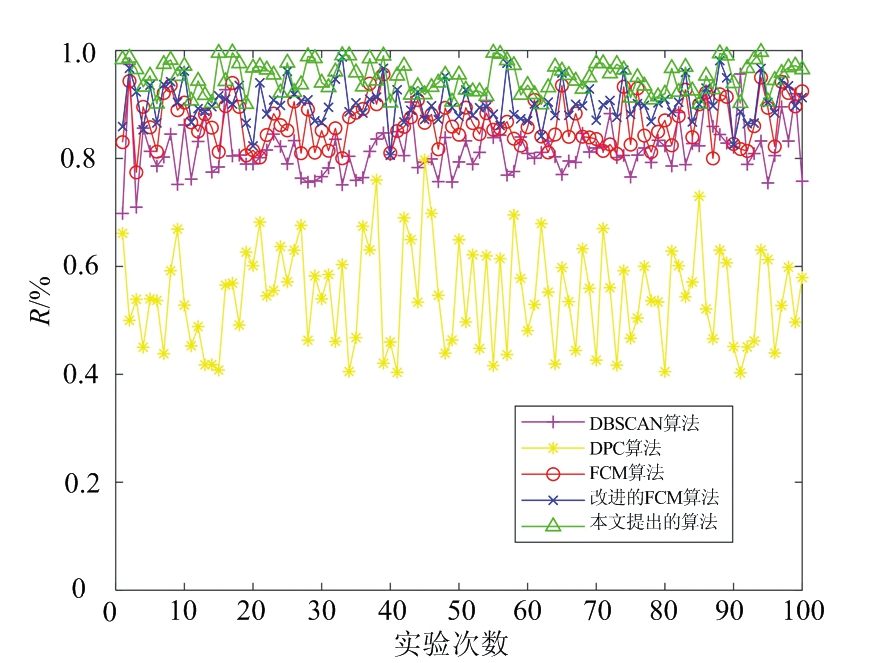
图9 各聚类算法的聚类精度比较
同时对上述实验的3个场景的算法运行时间进行比较，每个场景分别用DBSCAN算法、FCM算法、DPC算法、改进的FCM算法和本文所提算法运行100次，求取运行时间平均值，时间比较如表2所示。
表2 算法运行时间比较
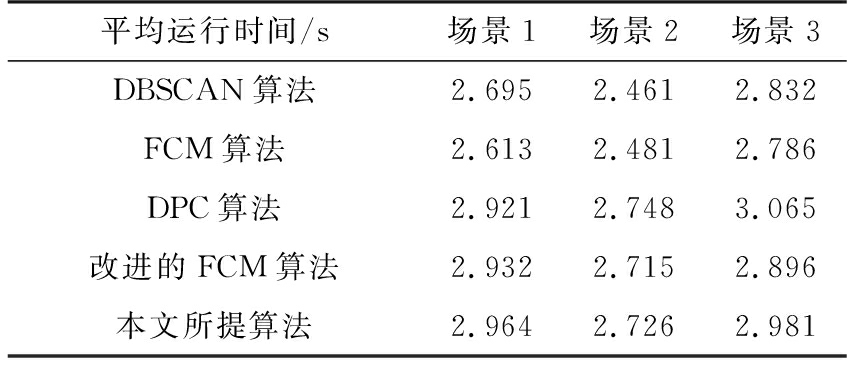
平均运行时间/s场景1场景2场景3DBSCAN算法2.6952.4612.832FCM算法2.6132.4812.786DPC算法2.9212.7483.065改进的FCM算法2.9322.7152.896本文所提算法2.9642.7262.981
由表2可知，本文提出的算法使用DPC算法初始化后再做模糊聚类使得时间复杂度增加，耗时相对较长，但在场景3数据较大的情况下，本文所提算法与各算法处理时间接近。同时，本文采用结合速度信息的二次模糊聚类处理，用较小的时间消耗获取更高、更稳定的聚类正确率。因此本文所提算法可以解决相邻车辆聚类结果不准确的问题，具有更高的准确度，在之后的工作中需要优化算法减少运行时间，使其在时间上具有明显优势。
4 结束语
本文提出的算法根据道路场景的车辆毫米波雷达数据特征，首先，使用改进的DPC算法，采用自适应椭圆距离绘制决策图，找出密度峰值点确定为初始聚类中心。接着，根据初始聚类中心计算初始隶属度矩阵，将二者代入FCM算法中，迭代计算得到一次聚类结果。最后，根据道路中每辆车的速度信息特点，构造关于速度的模糊目标函数，对一次聚类结果进行修正，迭代计算得到最终的聚类结果。实验结果表明，本文算法能有效解决城市道路车辆相距很近导致的目标聚类存在较大误差的问题，具有精度高、鲁棒性强的优点。
[1] MUNOZ-FERRERAS J M, PEREZ-MARTINEZ F, CALVO-GALLEGO J, et al. Traffic Surveillance System Based on a High-Resolution Radar[J]. IEEE Trans on Geoscience and Remote Sensing, 2008, 46(6):1624-1633.
[2] FöLSTER F, ROHLING H. Signal Processing Structure for Automotive Radar[J]. Frequenz, 2006, 60(1-2):20.
[3] 巩朋成, 王兆彬, 谭海明, 等. 杂波背景下基于交替方向乘子法的低截获频控阵MIMO雷达收发联合优化方法[J]. 电子与信息学报, 2021, 43(5):1267-1274.
[4] DENG D. DBSCAN Clustering Algorithm Based on Density[C]∥2020 7th International Forum on Electrical Engineering and Automation, Hefei:IFEEA, 2020:949-953.
[5] TAO Lei, JIA Xiaohong, ZHANG Yanning, et al. Significantly Fast and Robust Fuzzy C-Means Clustering Algorithm Based on Morphological Reconstruction and Membership Filtering[J]. IEEE Trans on Fuzzy Systems,2018, 26(5):3027-3041.
[6] LUO WANG Shengbin,XU Zhenhai,YANG Xiao, et al. Efficient and Unambiguous Two-Target Resolution via Subarray-Based Four-Channel Monopulse[J]. IEEE Trans on Signal Processing, 2020, 68:885-900.
[7] AI Chun, JIA Lijun, HONG Mei, et al. Short-Term Road Speed Forecasting Based on Hybrid RBF Neural Network with the Aid of Fuzzy System-Based Techniques in Urban Traffic Flow[J]. IEEE Access, 2020,8:69461-69470.
[8] BAO D. A Multi-Index Fusion Clustering Strategy for Traffic Flow State Identification[J]. IEEE Access, 2019, 7:166404-166409.
[9] 彭刚，袁晓，刘闻. 雷达辐射源信号聚类分选算法综述[J]. 雷达科学与技术, 2019, 17(5):485-492.
[10] RODRRIGUEZ A, LAIO A. Clustering by Fast Search and Find of Density Peaks[J]. Science, 2014, 344:1492-1496.
[11] CAO Lin, ZHANG Xinyi, WANG Tao, et al. An Adaptive Ellipse Distance Density Peak Fuzzy Clustering Algorithm Based on the Multi-Target Traffic Radar[J]. Sensors, 2020,20(17):4920.
[12] ZHANG Zhiyong, ZHU Qingsheng, FAN Zhu, et al. Density Decay Graph-Based Density Peak Clustering[J]. Knowledge-Based Systems,2021,224:107075.
[13] 毕晓君, 张磊. 基于自适应截断策略的约束多目标优化算法[J]. 电子与信息学报, 2016, 38(8):2047-2053.
[14] CAI Jianghui, WEI Huiling, YANG Haifeng, et al. A Novel Clustering Algorithm Based on DPC and PSO[J]. IEEE Access, 2020,8:88200-88214.
[15] YANG M, NATALIANI Y. A Feature-Reduction Fuzzy Clustering Algorithm Based on Feature-Weighted Entropy[J]. IEEE Trans on Fuzzy Systems, 2018,26(2):817-835.
[16] BAI Xiangzhi, CHEN Zhiguo, ZHANG Yu, et al. Infrared Ship Target Segmentation Based on Spatial Information Improved FCM [J].IEEE Trans on Cybernetics, 2016,46(12):3259-3271.
[17] NIAZMARDI S, HOMAYOUNI S, SAFARI A. An Improved FCM Algorithm Based on the SVDD for Unsupervised Hyperspectral Data Classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2):831-839.
[18] STOLZ M, LI Mingkang, FENG Zhaofei, et al. High Resolution Automotive Radar Data Clustering with Novel Cluster Method [C]∥2018 IEEE Radar Conference, Oklahoma, USA:IEEE, 2018:164-168.
[19] 巩朋成, 刘刚, 黄禾, 等. 频控阵MIMO雷达中基于稀疏迭代的多维信息联合估计方法[J]. 雷达学报, 2018, 7(2):194-201.
[20] 曹孟德，张铖，黄永明，等. FMCW车载毫米波雷达空时码信号处理方案[J]. 雷达科学与技术, 2019, 17(5):493-498.
[21] 谷留全,柴瑞林,王平心. 基于投票理论的三支聚类分析[J]. 计算机科学与应用, 2019,9(12):2349-2356.
