0 引 言
互补序列集[1](Complementary Sets of Sequences, CSS)具备理想的非周期自相关特性，因此被广泛应用于通信[2]、雷达[3]等领域，受到了许多研究学者的关注。
随着雷达系统与通信系统的迅速发展，频谱资源日益紧张，工作在甚高频和超高频雷达会面临同频干扰[4]。针对此问题，雷达稀疏频率序列设计得到了广泛关注，其思想是将雷达序列干扰频带设置为阻带，降低雷达在该频带上的功率。这种设计提高了频带的利用率和雷达系统的抗干扰能力。因此，设计较低旁瓣的稀疏频率序列问题受到了广泛关注。文献[5]利用乘数近似法(Proximal Method of Multipliers, PMM)设计低旁瓣单个稀疏频率序列。但是该文献是基于峰值旁瓣电平(Peak Sidelobe Level, PSL)准则抑制序列自相关旁瓣，在求解自相关函数最大值时难以处理。文献[6]采用循环迭代算法(Cyclic Iterative Algorithm, CIA)设计具备低距离旁瓣的单个稀疏频率序列，并进一步将该算法扩展到具备低旁瓣的正交稀疏频率序列集设计。文献[7-8]提出基于CIA的正交稀疏频率序列设计。同时考虑序列旁瓣性能和稀疏频谱性能，利用CIA迭代求解最优序列的闭式解，并在每次迭代中利用FFT变换，降低了运算的复杂度。文献[9]采用一种结合最速下降方法的迭代算法对单个稀疏频率序列设计和正交稀疏频率序列集设计，该算法通过沿梯度方向搜索，提高了算法的收敛速度。文献[10]将序列集的PSL作为目标函数，频率阻带功率和序列恒模作为约束并建立优化问题。然后利用块逐次最小化(Block Successive Upper-bound Minimization, BSUM)算法求解该问题，并得到具有良好相关特性和稀疏频率特性的正交序列集，该算法每次迭代都可利用FFT计算，收敛速度快。上述文献[5-10]中的研究大都是针对单个稀疏频率序列或正交稀疏频率序列集进行设计，只有少数文献针对互补稀疏频率(Complementary Sparse Frequency, CSF)序列集进行设计。例如，文献[4，11]优化设计了CSF序列集，分别采用功率谱密度(Power Spectrum Density, PSD)为约束、积分旁瓣电平(Integrated Sidelobe Level, ISL)为目标函数以及ISL为约束，PSD为目标函数建立两个非线性优化模型，然后运用MATLAB优化工具箱中“fmincon”函数中的内点法求解。该方法将非线性约束问题近似转化为线性约束问题进行求解，所求取的解为原非线性约束问题的次优解，并且直接提取该次优解的相位以满足恒模约束。而CIA是经典的优化算法，在每次迭代中可直接得到优化变量闭式解。因此，该算法收敛速度快，性能高，被广泛运用于单个序列稀疏频谱优化设计[6]和正交稀疏频率序列集优化设计[6-8]。本文进一步将CIA扩展到CSF序列集的优化设计中。建立针对CSF序列集的加权积分旁瓣电平(Weighted ISL, WISL)数学模型和稀疏频谱数学模型，将二者的加权和作为优化的目标函数，然后采用CIA对该模型进行求解，在每次迭代过程中，给出了满足恒模约束的CSF序列集闭式解。仿真结果表明，相比于文献[11]算法，CIA所优化的序列集具有更好的自相关特性和稀疏频率特性，收敛速度更快，且可灵活控制自相关旁瓣的抑制范围，具有广泛的适应性。
1 优化模型的建立
1.1 WISL优化模型
定义一个复恒模序列集Z，包含M个序列，每个序列长度为N，序列集可以表示为
Z={z1,z2,…,zM}
(1)
其中zm=[zm(1),zm(2),…,zm(N)]T。将序列集Z中的序列按照如下方式进行堆叠：
(2)
式中，0N×1为一个长度为N的全零列向量，q∈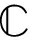
L×1为堆叠后的列向量；显然L=(2M-1)N。按照上述堆叠方式，可得：序列q的非周期自相关函数在时延[-N+1,N-1]的范围内等于序列集{z1,z2,…,zM}各序列的自相关之和。堆叠序列q的自相关函数表示为
(3)
PSL和ISL是目前优化旁瓣的两种主要指标。若以PSL为优化指标，会使序列的旁瓣电平随着序列长度增加而增大，而ISL为优化指标相对较为稳定[7]。本文考虑一般性，选用WISL指标优化序列旁瓣。基于文献[12]讨论，利用Parseval定理可知，序列z的WISL可以表示为
(4)
式中，Φ(wp)表示自相关序列的离散傅里叶变换。Φ(wp)可表示为
(5)
其中γk,k=0,1,…,L-1为自相关序列的加权系数，且γk=γ-k。通常，将γk的取值设为0或1，以对待优化的旁瓣区域进行选择。
因此，为得到自相关旁瓣最小化的恒模序列集，将式(4)中的WISL作为目标函数，使其最小化，并添加序列的恒模约束，可建立序列集旁瓣优化模型如下：
s.t. |zm(n)|=1, n=1,…,N,m=1,2,…,M
(6)
利用傅里叶变换对和卷积变换公式，式(6)中目标函数
可重新改写为[12]
(7)
其中，
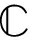L×1，Γ∈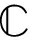L×L，具体定义如下:
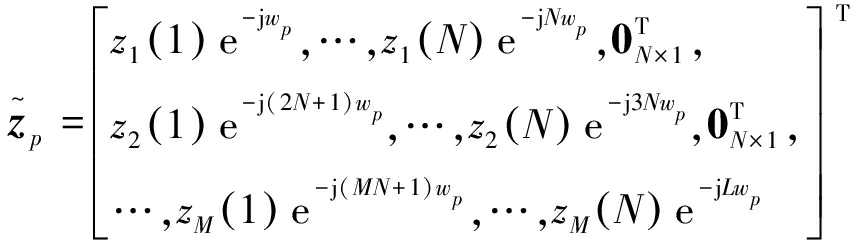
(8)
(9)
为保证矩阵Γ为半正定矩阵，设式(9)中γ0≥λmin，λmin为矩阵γ0Γ中对角元素全为0矩阵的最小特征值[12]。
由文献[12]可知，式(7)中CSF序列集的WISL可进一步近似等价为
OWISL=
(10)
其中，Γ= CTC，C为L×L维矩阵,αp为L×1维辅助向量,
为FFT矩阵，其第m行第n列元素定义为
为矩阵的第p行元素。
表示矩阵C的第k行元素,∘表示哈达玛积。
将式(10)代入式(6)中，序列集的WISL优化模型可重新写成
s.t.|zm(n)|=1, n=1,…,N,m=1,2,…,M
‖αp‖2=MN,p=1,…,2L
(11)
1.2 PSD优化模型
为了使设计的CSS具有稀疏频率特性，本文通过优化序列集以抑制频率阻带内的能量(Energy in the Frequency Stopband, EFS)。
假设序列集Z的频率阻带为
(12)
其中，(fn1,fn2)表示归一化频率(即频率取值范围为从0到1)范围，Ns为频率阻带个数。
对长度为N的序列进行频域变换，考虑正负频率，变换后的频谱序列长度为2N。对序列的频谱序列进行加权，定义频谱序列的加权向量为
wf=[wf(1),…,wf(2N)]T
(13)
假设阻带内的频谱序列加权系数为1，通带内的频谱序列加权系数为0，即
(14)
于是，序列集在频率阻带内的能量EFS可由下式计算：
(15)
式中，
为抑制序列集在频率阻带内的能量，以序列集的EFS为目标函数，使其最小化，并添加序列集的恒模约束，从而建立CSF序列集的频谱优化模型
s.t.|zm(n)|=1,n=1,…,N,m=1,2,…,M
(16)
根据文献[13]的推导，式(16)中的目标函数可以等价为
(17)
式中，
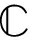表示2N个元素全为1的列向量，bm∈2N×1为辅助变量。
为方便地从堆叠序列q中快速地选择出第m个序列zm，定义选择矩阵
Sm=[0N×(2m-2)N,IN×N,0N×(L-(2m-1)N)]
(18)
从而有
zm= Smq
(19)
将式(19)代入式(17)中，忽略系数
序列集的EFS可等价为
(20)
将式(20)替换式(16)中的目标函数，EFS的优化模型可表示为
s.t.|zm(n)|=1,n=1,…,N,m=1,2,…,M
(21)
1.3 联合优化模型
为了使雷达的发射序列集同时具有低自相关旁瓣和稀疏频谱特性，需对序列集的WISL和EFS进行联合优化。联合式(11)和式(21)，可建立CSF序列集联合优化问题为
s.t.|zm(n)|=1，n=1,…,N,m=1,2,…,M
‖αp‖2=MN,p=1,…,2L
(22)
其中，
为权重因子，用来调节目标函数中EFS和WISL之间的平衡。
2 CIA求解
针对式(22)中的优化问题，本文采用CIA进行求解，其主要思想是交替迭代优化不同的变量。式(22)中的优化问题有3个优化变量q(或{zm}m=1,2,…,M)，{bm}m=1,2,…,M和V，其中变量{bm}m=1,2,…,M和V为辅助变量，且相互独立。交替迭代优化的过程为：首先，固定变量q，求解{bm}m=1,2,…,M和V；然后，利用更新后的{bm}m=1,2,…,M和V，求解变量q。上述两个步骤不断地交替迭代。该两个步骤是每次迭代的主要步骤，具体的求解过程如下：
第一步：固定q，求解{bm}m=1,2,…,M和V。此时，式(22)目标函数可写为
且bm和V可分别根据
和
进行独立求解。由于变量{bm}m=1,2,…,M只与式(22)目标函数中的有关；因此，可进一步化简为
(23)
其中，const1表示与bm无关常数项。
由式(23)可得变量bm的闭式解为
(24)
针对
参考文献[12]的求解过程，可得V的闭式解为
(25)
其中，
(26)
(27)
第二步：固定{bm}m=1,2,…,M和V，求解变量q。此时，式(22)目标函数可写为
其中
可进一步化简为
(28)
式中，
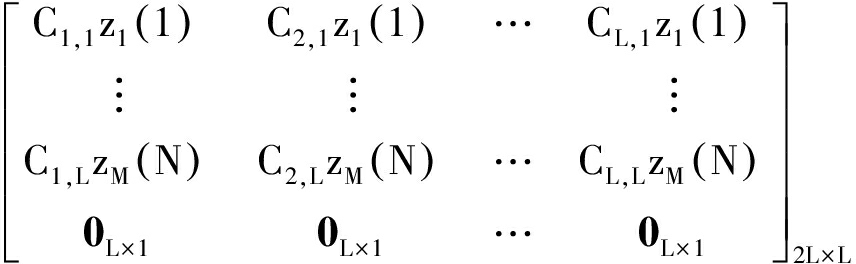
(29)
其中，Cm,n表示矩阵C的第m行第n列元素。
结合式(29)，式(28)可进一步写为
(30)
式中，矩阵
表示与q(或zm)无关的常数。矩阵B第p行的向量二范数平方
可以写为
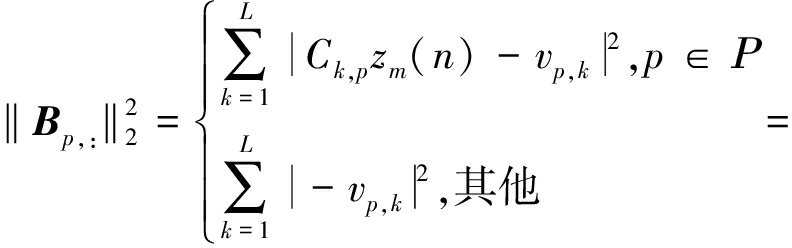
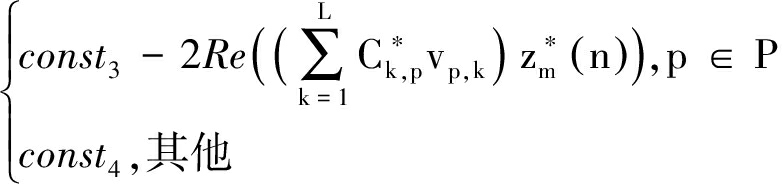
(31)
其中，const3和const4是和变量q(或zm)无关的常数项，vp,k为矩阵
中第p行第k列元素。当p∈Ρ时，m的取值为m= ⎣p/2N
+1，⎣·表示向下取整。n的取值为n=mod(p,N)，表示p对N取余，且当p被N整除时n=N。集合Ρ为
Ρ=[1,N]∪[2N+1,3N]∪…
∪[2(M-1)N+1,(2M-1)N]
(32)
将式(31)代入式(30)有
const5
(33)
式中，const5表示与q(或zm)无关的常数项。
式(22)目标函数的后一部分
可表示为
(34)
式中，const6表示与q(或zm)无关的常数，cm为
中前N个元素组成的列向量。
由式(33)和式(34)可得第二步的优化目标函数为
OCSF(q)=
(35)
式中，const7=const5+const6。
由式(35)可得到优化变量q中的第m个序列zm的闭式解为
(36)
循环迭代上述步骤，便可得到基于CIA的CSF序列集优化设计流程，如表1所示。
表1 CIA算法流程
输入参数:权重因子η,wf,γk。停止条件为优化变量q的迭代误差精度ε和算法最长运行时间T。Step 0: 初始化q(0)。Step 1: 固定q(k),分别利用式(24)、式(25)求b(k+1)m,V(k+1)。Step 2: 固定b(k+1)m和V(k+1),利用式(36)求z(k+1)m,进而求得q(k+1)。Step 3: 如果‖q(k+1)- q(k)‖≤ε或运行时间t≥T时,结束;否则,k=k+1, 跳转到Step 1。
3 实验仿真分析
为验证本文所提CIA算法的有效性、所设计CSF序列集良好的相关性和稀疏频率特性，定义两个关于序列集的性能评估指标，分别为WISL和平均通带阻带功率比(Average Passband Stopband Power Ratio, APSPR)。具体地，WISL和APSPR指标可由下式来计算：
(37)
(38)
式中，Pp为序列集的通带平均功率，Ps为序列集的阻带平均功率。WISL越小，序列集的相关性能越好；APSPR越大，序列集的频谱特性越好。以式(37)和式(38)为衡量指标，将本文所提算法CIA和文献[11]算法进行比较。为了保证比较的公平性，两种算法的初始序列保持相同，均采用随机相位的单模序列集。除了WISL和APSPR之外，亦评估了本文CSF序列集设计算法的运算速度。所有的仿真均在一台CPU为3.60 GHz，i7-4790，内存为8 GB的PC机上用Matlab软件运行计算的。
3.1 CSF序列集优化设计
假设所设计CSF序列集中序列个数和各序列长度分别为M=2，N=143，加权系数η=0.012 2,自相关函数加权系数为
(39)
算法终止条件为优化变量q的迭代误差精度ε=10-5或总迭代时间t=15 000 s。将频率进行归一化，设置5个频率阻带，分别为[0.04,0.21],[0.23,0.25],[0.28,0.37],[0.39,0.49],[0.52,0.56]；剩下的频率范围为频率通带。图1为本文算法和文献[11]算法优化得到的CSF序列集的自相关函数。图中，本文算法与文献[11]算法均可设计较低旁瓣的CSF序列集；且本文算法和文献[11]算法设计CSF序列集的WISL均是-3.91 dB。图2和图3分别为本文算法和文献[11]算法优化CSF序列集的两个序列的PSD。图2和图3中灰色阴影区域为所设定的5个阻带区域，由图可知，在设定的频率阻带区域，经两种算法优化后序列具备较低的幅度(能量)。具体地，本文算法设计的APSPR分别是24.40 dB，24.47 dB，文献[11]所设计两个序列的APSPR分别是24.06 dB，24.06 dB。将图1、图2和图3中两种算法所设计序列的WISL和APSPR相比较，可知，在WISL性能相同的情况下，本文所提算法的APSPR性能优于文献[11]中的算法。
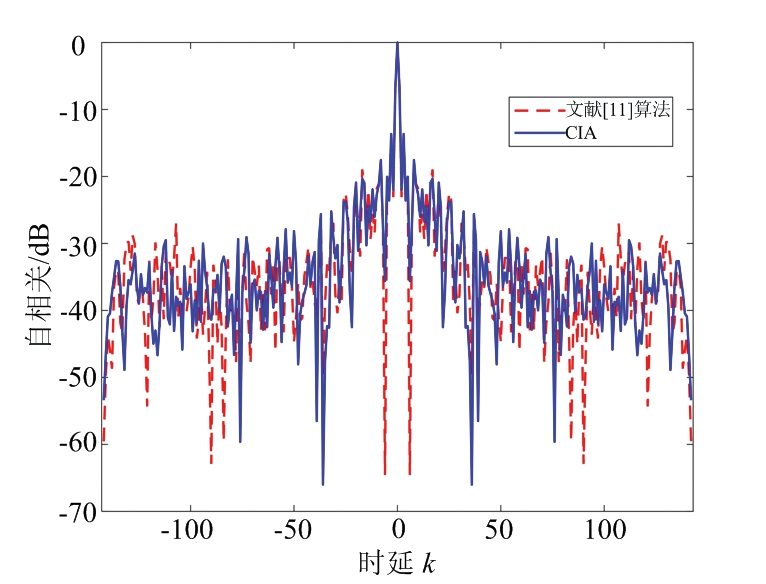
图1 互补稀疏频率序列集的自相关
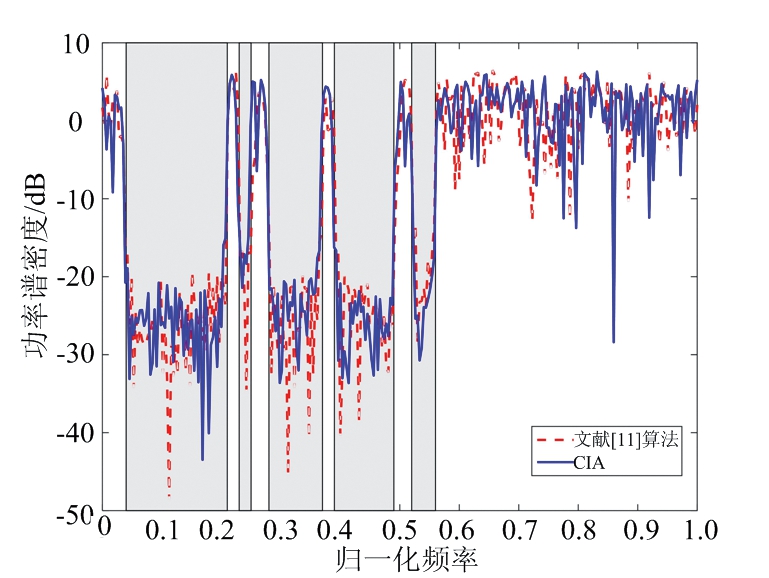
图2 CSF序列1的PSD
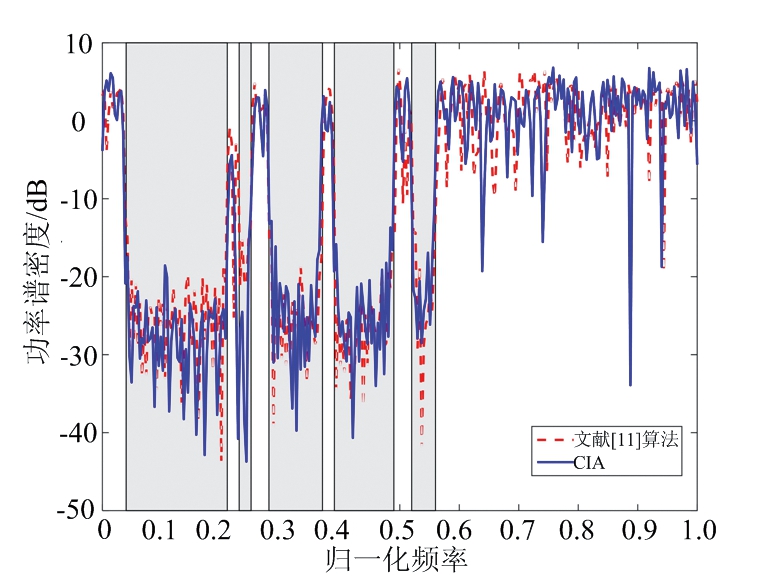
图3 CSF序列2的PSD
进一步地，考虑CSF序列集M=3，序列长度N=143的情况。此时，加权系数设为η=0.012 4，自相关函数加权系数为式(39)，算法的终止条件分别设置为ε=10-5或t=24 000 s。将该情况(M=3)和图1～3中情况(M=2)下，两种算法所设计CSF序列集的WISL和APSPR值总结在表2中。由表2可知，当序列个数为M=2和M=3时，两种算法在WISL基本相同(本文算法WISL甚至稍优于文献[11]算法的情况下，本文算法的阻带能量抑制能力优于文献[11]算法。由此可知，本文算法优化得到的CSF序列集具有更低自相关旁瓣特性以及更好的稀疏频率特性。
表2 CIA和文献[11]算法设计CSF序列集的数据对比dB
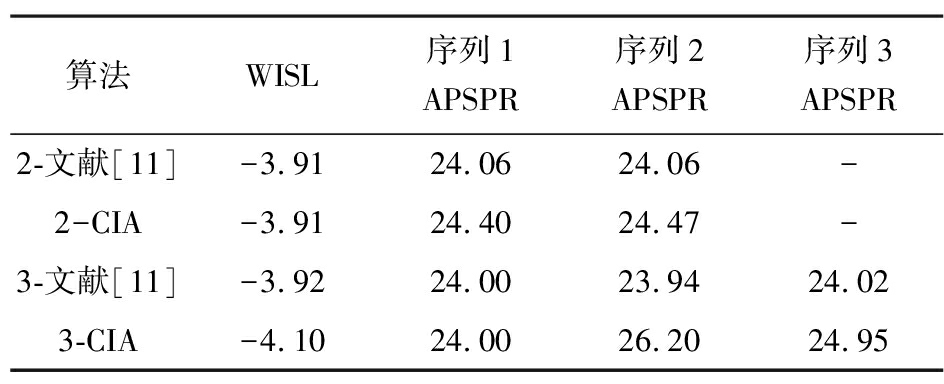
算法WISL序列1APSPR序列2 APSPR序列3APSPR2-文献[11]-3.9124.0624.06-2-CIA-3.9124.4024.47-3-文献[11]-3.9224.0023.9424.023-CIA-4.1024.0026.2024.95
3.2 算法收敛速度
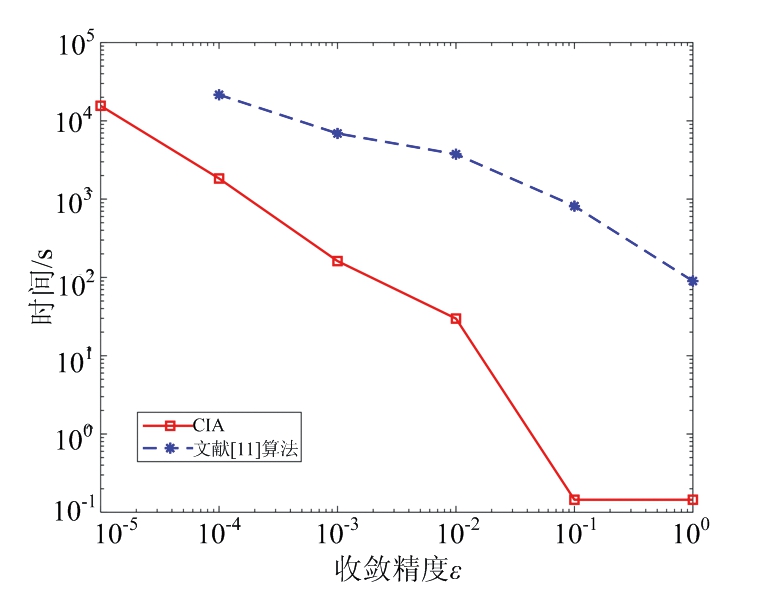
图4 不同收敛精度ε下的算法运行时间
为进一步对比两种算法优化设计CSF序列集的收敛速度，研究了两种算法在不同收敛精度ε下的运行时间。序列集的WISL和EFS间的加权系数设置为η=0.012 2，自相关函数加权系数和频率阻带通带设置与3.1节实验相同，两种算法设计的序列个数和长度为M=2，N=143。图4给出了两种算法在不同收敛精度下所需要的时间，横坐标表示不同的收敛精度ε。由于文献[11]算法在收敛精度ε=10-5条件下，运行时间过长，因此仅记录前5个收敛精度下算法的运行时间。由图可知，两种算法的运行时间都随着收敛精度的提高而增加。然而，在相同的收敛精度下，本文算法CIA设计CSF序列集所需的时间小于文献[11]算法。因此，本文算法优化设计CSF序列集的收敛速度快于文献[11]算法。
3.3 部分旁瓣抑制的CSF序列集设计
实际情况中的一些特殊场景需要在特定的延迟范围内抑制CSF序列集的自相关旁瓣，而非在全部延迟范围内抑制自相关旁瓣。此时，文献[11]的设计算法失效，而本文算法可以有效实现CSF序列集自相关旁瓣在指定区域内的优化和稀疏频谱优化。
假定优化设计一个CSF序列集，其序列个数和长度分别为M=2，N=143；且需要在k∈[40,60]∪[80,100]延迟范围内抑制CSF序列集旁瓣，k表示延迟点。则可将式(37)中自相关旁瓣加权系数修改为
(40)
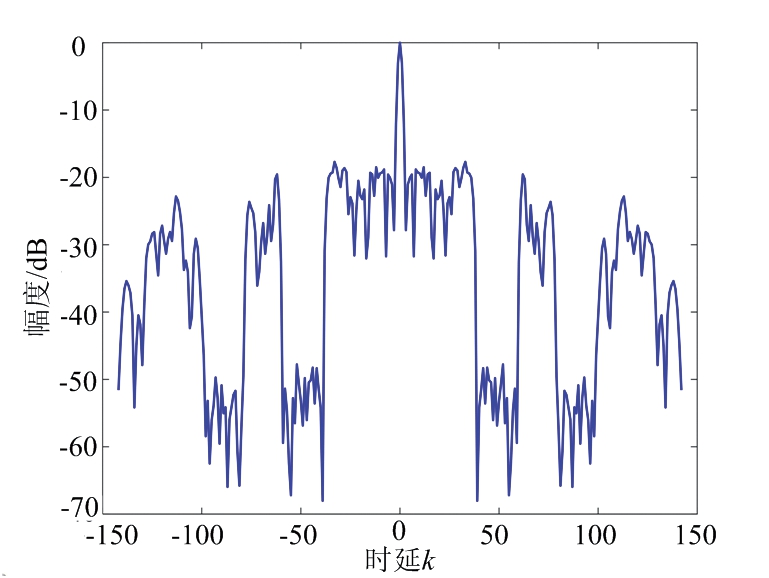
图5 部分旁瓣抑制的CSF序列集自相关
假设所要求的频率阻带范围和3.1节中的要求相同。设定算法的终止条件为ε=10-6或t=25 000 s，加权系数为η=0.001。图5为CIA算法优化设计得到的CSF序列集的自相关函数。由图可知，在所设定的旁瓣抑制范围k∈[40,60]∪[80,100]和对称范围k∈[-60,-40]∪[-100,-80]内，CSF的旁瓣得到了有效抑制。图中，在设定的旁瓣抑制范围内，自相关旁瓣可抑制至-50 dB，全部延迟范围内的WISL为-33.35 dB。图6和图7分别为所设计的序列1和序列2的PSD。由图可知，所设计序列满足所设定的阻带频谱要求，且两个序列的APSPR分别为26.52 dB和27.32 dB。由于文献[11]算法不可对部分自相关旁瓣进行抑制；因此，本文算法相比文献[11]算法更具广泛性。
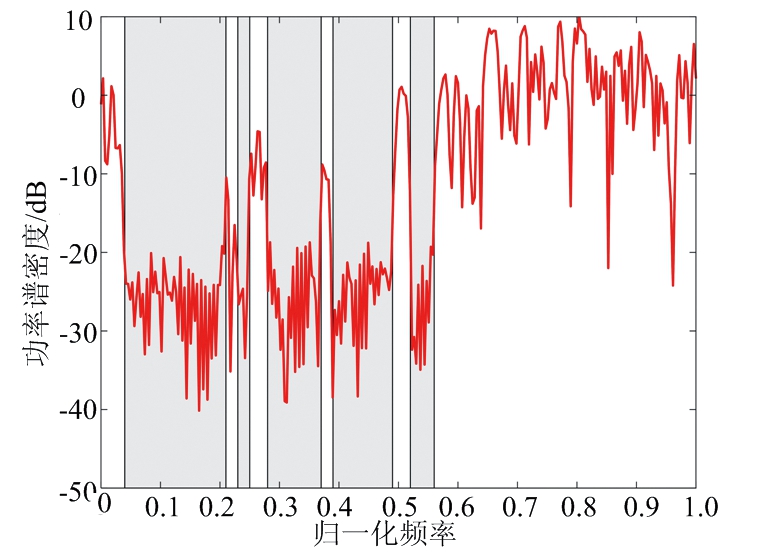
图6 CSF序列1的PSD
图7 CSF序列2的PSD
4 结束语
本文提出了一种基于CIA的雷达CSF序列集优化设计方法。该算法以最小化序列WISL和各序列EFS之间的加权为目标，引入辅助变量，将辅助变量和待优化的序列集变量进行迭代优化。由于在每次迭代中都可以求出恒模序列集的闭式解，方便快速地解决了恒模约束的困难。和已有算法相比较，本文算法优化性能高、收敛速度快，并且具备更广泛的应用性。
[1] 潘孟冠，胡金龙，陈伯孝，等. 基于CLEAN思想的互补码信号脉冲压缩算法[J]. 雷达科学与技术，2020，18(3):254-261.
[2] 李晓柏，杨瑞娟，程伟，等. 新的互补序列在雷达通信一体化中应用[J]. 系统工程与电子技术，2021，43(3):693-699.
[3] 赵航，祁琳琳，伍光新，等. 完全互补码在雷达通信一体化中应用[J]. 现代雷达，2021，43(10):41-46.
[4] 万显荣，吕敏，谢德强，等. 基于信号结构特点的外源雷达干扰方法研究[J]. 雷达学报，2020，9(6):987-997.
[5] FAN Wen，LIANG Junli，YU Guoyang，et al. Minimum Local Peak Sidelobe Level Waveform Design with Correlation and/or Spectral Constraints[J]. Signal Processing，2020，171:1-7.
[6] 庄珊娜，贺亚鹏，朱晓华. 低距离旁瓣稀疏频谱波形相位编码设计[J]. 电子与信息学报，2012，34(5):1088-1095.
[7] 李玉翔，任修坤，孙杨，等. 一种循环迭代的宽带MIMO雷达正交稀疏频谱波形设计方法[J]. 电子与信息学报，2017，39(4):953-959.
[8] 周宇，张林让，赵珊珊. 组网雷达低自相关旁瓣和互相关干扰的稀疏频谱波形设计方法[J]. 电子与信息学报，2014，36(6):1394-1399.
[9] WANG Guohua, LU Yilong. Designing Single/Multiple Spares Frequency Waveforms with Sidelobe Constraint [J]. IET Radar，Sonar & Navigation，2011，5(1):32-38.
[10] FAN Wen，LIANG Junli，CHEN Zihao，et al. Spectrally Compatible Aperiodic Sequence Set Design with Low Cross- and Auto-Correlation PSL [J]. Signal Processing，2021，183:1-7.
[11] 项俐，麦超云，甘俊英. 互补码设计稀疏频率雷达波形[J]. 信号处理，2019，35(8):1432-1438.
[12] STOICA P，HE H，LI J,et al. New Algorithms for Designing Unimodular Sequences with Good Correlation Properties [J]. IEEE Trans on Signal Processing，2009，57(4):1415-1425.
[13] HE H，STOICA P，LI J. Waveform Design with Stopband and Correlation Constraints for Cognitive Radar[C]∥ 2010 2nd International Workshop on Cognitive Information Processing (CIP)，Elba，Italy: IEEE，2010:344-349.
