0 引 言
雷达信号分选算法是在接收到的交错重叠的各类雷达信号基础上,通过对信号分析处理获得雷达特征参数信息,然后通过分类算法,利用相同雷达信号的参数相关性和不同雷达信号的参数差异性来实现雷达信号的区分和识别[1]。
传统的信号分选方法依据全脉冲信号的脉间特征以及脉冲到达时间提取出的脉冲重复周期信息来进行分选。但是随着调制方式的多样化发展,战场电磁环境日益复杂,仅使用脉间特征信息难以达到理想的分选识别准确率。而信号的脉内特征相比脉间特征具有更强的稳定性,且可以兼顾信号的脉内调制信息。文献[2-7]将信号的相像系数、三维熵、Holder系数等脉内特征引入分选领域,应用到雷达辐射源信号分选之中,在一定程度上提高了信号分选的准确率。文献[5]提取信号自相关函数的三维熵特征并作为分选参数,增强了特征的抗噪性和稳定性。文献[7]对相像系数的扩展—Holder系数法进行改进,提出具有更高寻优空间的高次频谱对称Holder系数。
当前雷达辐射源信号分类算法主要是基于机器学习算法,但是传统算法在精确度上难以满足现代战场对复杂辐射源信号的分选需求。目前已有一些学者将一维雷达信号经过处理后与神经网络算法相结合,比如与卷积神经网络[8]、VGG网络[9]、深度置信网络[10]、深度信念网络[11]、长短期记忆网络[12]相结合,取得了较好成果。还有一些学者将信号的时频图像作为特征结合神经网络进行分选[13-15]。但由于信号的时频图像只能反映出雷达信号的脉内调制信息,无法体现现代雷达信号复杂多变的脉间调制信息;且时频图像方法存在图像转换过程,运算复杂度较高。相比而言,直接对信号进行处理和特征学习可以更好地提取信号的脉间以及脉内特征信息,同时缩短训练所需时间。但是与时频图像方法相比,雷达信号特征参数有限,往往难以直接输入网络进行训练和学习。
针对以上问题,本文将脉间特征和脉内特征相结合作为雷达辐射源信号分选参数,并提出一种特征参数差值预处理方式,将低维特征数据扩充到足以输入网络训练的数据维度,选用DenseNet作为分选网络。实验结果表明,本文算法能有效实现复杂雷达辐射源信号的分选,在0 dB的信噪比下可以达到98%以上的分选准确率。
1 特征提取
1.1 脉间特征
1) 脉冲到达时间(Time of Arrival, TOA)
TOA为雷达发射脉冲时起到接收到反射脉冲时止所经历的时间,对于TOA进行分析可以推算出脉冲重复频率这一重要分选参数,由于不同雷达辐射源信号的脉冲重复周期各不相同,因此可以作为信号分选的依据。
2) 脉冲宽度(Pulse Width, PW)
PW即单一脉冲的持续时间,它的产生与雷达的固有特性相关联,对于同一辐射源一般不易发生变化,可以区分来自不同辐射源的雷达信号。
3) 载波频率(Radio Frequency, RF)
现代雷达为了提高自身的抗干扰能力以及目标检测能力,脉冲频率的变化形式愈发多样,它可以是固定不变的,也可以遵循一定规律发生跳变、捷变等,RF描述的就是所接收脉冲序列的频域特性,是电子对抗中最为重要的参数。
1.2 脉内特征
1) 高次频谱对称Holder系数
信号的频谱可以体现出信号的频率、幅值、相位以及能量分布信息,不同脉内调制的辐射源信号其频谱图存在差异,因此可以通过对信号频谱提取特征参与分选来区分不同调制的辐射源信号。
对称Holder系数法[16]由Holder不等式[17]发展而来,它包含了常用于衡量信号相似程度的相像系数法,但是相比而言大大降低了算法复杂度,且其参数可变,拥有更大的寻优空间。
信号的k次频谱是指对信号的频谱做k次方运算,可以放大频谱中的细微信息。通过计算辐射源信号的高次频谱和两个基准信号的对称Holder系数,可以得到二维的高次频谱对称Holder系数[7][Cr1,Cr2],加入特征体系作为分选依据可以更精确地反映调制信号在频谱上的细微特征。
2) 自相关函数三维熵特征
自相关函数能够体现时间序列内部的联系和相互关系,并且具有对噪声不敏感的特点,可用于区分不同雷达辐射源信号。但是其维数较高,不利于直接加入特征分选体系,需要进行降维处理。为了既能体现信号间差异,同时又能实现网络分选,需对自相关函数做进一步特征提取。
信号的香农熵(Hs)具有量化信号复杂度的作用,指数熵(HE)可以弥补香农熵中的不收敛现象,同时提升计算精度,范数熵(HR)可用于定量描述信号的能量分布情况[5]。因此选取自相关函数的香农熵、指数熵和范数熵组合成为三维熵特征来刻画信号特征,并参与分选。
2 特征参数预处理
文献[9]中提出一种基于单脉冲特性的参数预处理方法,选定r个脉冲信号,对于每个脉冲的TOA特征依次作差,得到到达时间差矩阵ΔTOA,如式(1)所示。对PW、RF特征进行相同预处理后,组合输入深度神经网络进行训练并实现分选。
ΔTOAi,i+1=|TOAi+1-TOAi|
(1)
式中,i=1,2,…,r。
上述预处理方式只利用了前后两个脉冲之间特征差的相关性差异进行分选,所能提供的信息有限,在高维度的数据支持下才能达到理想效果,同时带来的问题是更大的数据集输入和更耗时的运算过程。而在混杂信号中,当前信号与后续一系列脉冲之间均存在一定的潜在联系,有效提取这些信息即可在低维度条件下获得更优的分选效果。
针对这一问题,本文提出一种特征参数差值预处理方式。用X代表所使用的雷达特征参数,在得到一定数量的混合辐射源信号后,选定所需信号数量n,对于第i个脉冲信号,将接下来r个脉冲的X特征值与第i个脉冲的X特征值依次作差:
DXij=|Xi+j-Xi|
(2)
式中,i=1,2,…,n,j=1,2,…,r。
得到的矩阵DX便为X特征的差值矩阵,使用选取的TOA,PW,RF,Hs,HE,HR,Cr1,Cr2八个特征分别按式(2)方法计算,可以得到DTOA,DPW,DRF,DHs,DHE,DHR,DCr1,DCr2八个特征差值矩阵。矩阵中的每一行都包含当前脉冲与后续脉冲之间的相关性差异信息。在充分利用已有数据的同时能更有效地体现特征参数差值中包含的信息。
但是当r值扩大时,直接使用TOA参数进行差值处理会产生DTOA中元素量级过大的问题,如图1所示,这可能会导致内存不足的情况,也不利于神经网络的学习。
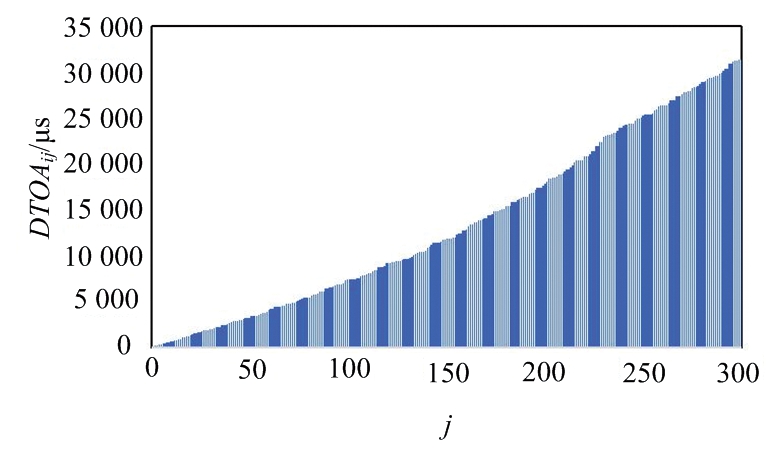
图1 DTOAij随j增大产生的量级变化
因此,对本文方法做出如下改进:针对TOA这一特征,预处理中不直接进行差值预处理,而是对TOA逐项作差后得到的到达时间差特征进行差值预处理操作,如式(3)、式(4)所示。
ΔTOAi=|TOAi+1-TOAi|
(3)
DΔTOAij=|ΔTOAi+j-ΔTOAi|
(4)
式中,i=1,2,…,n,j=1,2,…,r。
使用DΔTOA矩阵代替上文得到的DTOA矩阵参与分选流程,可以使得数据处于同一量级,避免了生成高维度差值矩阵数据时可能产生的内存分配不足问题。
考虑到实际战场中接收到的信号往往是多个雷达信号的叠加,来自不同雷达辐射源的信号可能在部分脉冲上发生重叠,导致某些特征参数相同,但其他参数仍然具有独立性,能起到分选的作用,因此,对多特征参数分别进行差值矩阵处理,拼接联合作为分选依据,可以大大提高分选结果的准确性。
将得到的8个n×r阶特征差值矩阵组合为[DΔTOA, DPW, DRF, DHs, DHE, DHR, DCr1, DCr2],可以得到一个n×8r阶的联合差值矩阵(M),其中包含更多关于脉冲间相关性差异的信息,能带来更好的分选结果。
3 密集连接卷积网络
早期提升卷积神经网络效果的方向,主要是增加网络层数或者宽度,但是网络深度增加又会带来新的问题,比如梯度消失、梯度爆炸等。2015年提出的残差网络(ResNet)[18],出现了将网络层前后连接的残差单元,有利于梯度的反向传播,解决了梯度消失问题。2017年提出的密集连接卷积神经网络——DenseNet[19]与ResNet的思想一致,但是它建立的是后层与前面所有层的密集连接结构。此外,DenseNet的一大优势是可以通过密集连接结构使特征在通道中拼接复用,达到特征重用的效果。这使得DenseNet网络使用更少的计算、更少的参数仍然能达到较好的效果。
3.1 密集连接
传统神经网络中,L层网络包含L次连接,而DenseNet的密集连接结构由于其所有层都被连接,即每一层都会与之前所有层相连接的特性,L层网络会产生L(L+1)/2次网络层连接。借助这种连接方式,DenseNet将不同层的特征图拼接在一起,可以实现特征重用,进一步提升效率。DenseNet网络的密集连接结构如图2所示。
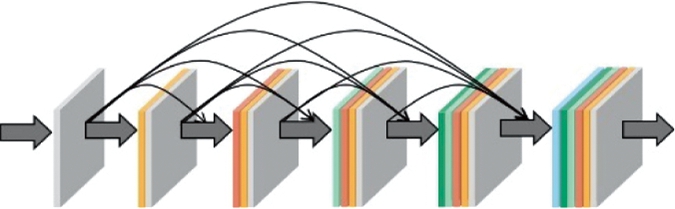
图2 密集连接结构
传统网络第L层网络的输出可以用公式表示为
xl=Gl(xl-1)
(5)
ResNet的第L层输出加入了L-1层的输出函数,用公式表示为
xl=Gl(xl-1)+xl-1
(6)
在DenseNet中,第L层将前面所有层连接作为输入,用公式表示为
xl=Gl([x0,x1,…,xl-1])
(7)
式中Gl(·)代表一种复合函数,是卷积神经网络中常用的一种组合操作,在此中会包含卷积 (Conv)、批标准化 (Batch Normalization, BN)、激活函数 (Relu) 及池化 (Pooling) 等步骤。
3.2 网络结构
DenseNet网络模型主要由若干个密集块(Dense Block)和用于连接两个密集块的过渡层(Transition Layer)组合而成。
常用的DenseNet网络结构如图3所示。输入图片,经过卷积操作,进入第一个Dense Block层,再经过过渡层卷积池化后,进入下一个Dense Block层,直到第n个Dense Block层,最后进入全连接层,通过softmax函数预测分类结果。

图3 DenseNet网络结构
DenseNet网络目前大多用于图像分类,输入数据为二维图像,其在卷积层中可以与二维卷积核进行完全的卷积运算。而对于本文预处理方式所生成的n×8r阶M矩阵,其不同行向量代表不同脉冲信号,行向量之间没有关联性,使用方阵作为输入没有意义,而一维的行向量输入网络无法与二维卷积核进行卷积运算。因此,本文对常用DenseNet网络中的卷积核维度进行调整,使用更适合处理序列模型的一维DenseNet网络进行辐射源信号分选。
一维DenseNet网络中每个Dense Block内部由若干连续的BN+Relu+1×3Conv结构组成。过渡层包含瓶颈层 (Bottleneck Layer,即1×1卷积层) 和1×2池化层。
其中BN层用于对卷积后的输出进行归一化处理,降低样本间差异,使每层的数据分布一致,同时也起到了控制梯度过大和防止梯度消失的作用。
由于DenseNet特征重用的特性,Dense Block中每一层输出的特征图都需要和前面所有层的输出在通道维度上进行合并,所以即使每层的输出通道数k并不大,但通道连接后每个Dense Block输出的通道数k+k(k-1)将会是较大的数字。因此,在过渡层引入1*1卷积层作为瓶颈层,利用瓶颈层和池化层压缩参数,降低特征图数量,提高计算效率。
以宽度为8 000维的一维输入数据为例,本文所使用的一维DenseNet网络结构如表1所示。
表1 一维DenseNet网络结构

网络层输出尺寸(h∗w∗c)网络结构输入1×8 000×1卷积1×4 000×241×7卷积池化1×2 000×241×3最大池化密集块11×2 000×961×1卷积1×3卷积[]×6过渡层11×2 000×481×1卷积1×1 000×481×2平均池化密集块21×1 000×1921×1卷积1×3卷积[]×12过渡层21×1 000×961×1卷积1×500×961×2平均池化密集块31×500×3841×1卷积1×3卷积[]×24过渡层31×500×1921×1卷积1×250×1921×2平均池化密集块41×250×3841×1卷积1×3卷积[]×16分类1×1×3841×250最大池化Softmax分类器
4 算法流程
1) 仿真生成雷达信号数据集:为了更真实地模拟现代新型雷达辐射源信号数据,本实验采用了脉间调制较为复杂的十类辐射源信号和二进制相移键控(BPSK)、线性调频(LFM)、频移键控(FSK)、非线性调频(NLFM)、正交相移键控(QPSK) 五种脉内调制方式,对数据集进行划分生成训练集、验证集、测试集。
2) 提取特征参数:由仿真数据可直接获取PW、RF参数。对仿真数据中的TOA参数进行作差运算得到ΔTOA参数。
三维熵特征参数(Hs,HE,HR) 的提取流程为:
Step 1: 计算辐射源信号的自相关函数;
Step 2: 根据自相关函数分别计算辐射源信号的Hs,HE和HR特征值。
高次频谱对称Holder系数(Cr1,Cr2) 的提取流程为:
Step 1: 对辐射源信号做快速傅里叶变换(Fast Fourier Transform, FFT),得到信号的一次频谱,将信号从时域转换到频域;
Step 2: 在频域中对信号做能量归一化处理;
Step 3: 计算信号的高次频谱,并提取高次频谱的对称Holder系数,得到特征值Cr1,Cr2。
3) 数据预处理:对于数据集中获取的八维特征参数矩阵进行特征参数差值预处理,组合生成八维的M矩阵。
4) 网络学习:将M矩阵作为一维DenseNet网络的输入,通过网络进行信号的特征学习,在深度网络输出层得到样本的分选结果。
5) 验证:使用测试集验证分选效果,以测试集的分选准确率γ作为最终的评估标准:
(8)
式中,n0为测试集数据经网络正确分选的各类辐射源信号总量,n为测试集各类辐射源信号总量。
为减少特征提取部分的算法时间复杂度,在计算三维熵特征的信号自相关函数时,先对信号做FFT,使用频域相乘法来代替自相关函数计算中的时域卷积,从而将O(N2)的复杂度降低到![]() 同时,信号的FFT结果可直接用于高次频谱对称Holder系数的提取流程,降低了特征参数提取过程中的运算量。
同时,信号的FFT结果可直接用于高次频谱对称Holder系数的提取流程,降低了特征参数提取过程中的运算量。
5 仿真实验分析
5.1 参数设置
十类辐射源信号的脉间调制参数设置如表2所示。使用Matlab仿真生成数据集,随机生成10部雷达的发射起始时间值,利用参数表中的数据来仿真真实情况下的混杂雷达辐射源信号 (信噪比设定为0 dB)。
表2 雷达辐射源信号脉间调制参数设置

编号载频/MHz脉宽/μs脉冲重复间隔/μs13 520531 00023 03023脉组:390(rep12) 427(rep18)550(rep24) 372(rep28)415(rep16) 505(rep24)402(rep28) 446(rep32)506(rep24)3脉间捷变:3 000~3 150(每15一个频点)1111 1604固定:3 025105滑变:1 505~1 5655脉间捷变:2 890~3 050(每10一个频点)104.5,24参差:1 339/1 695/1 866/2 040/2 053/2 140/2 250/1 996/(PW104.5)543/656/612/665(PW24)6固定:3 04095抖动:1 260 (5%)7脉间捷变:3 100~3 310(每5一个频点)94.5抖动:900 (5%)8跳变:3 290~3 470跳变点:[3 410 3 470 3 440 3 2903 380 3 350]10250093 15595.5,22.5参差:1 890/1 968/1 905/1 983/1 921/2 000/1 937/2 008/1 945/1 991/(PW95.5)543/601/521/655(PW22.5)10脉组捷变:2 900#2 960#2 940#3 000#2 980#3 020#3 060#3 040#3 080#3 10552脉组:1 295#1 315#1 300#1 335#1 355#1 375#1 350#1 330#1 360#1 375(rep16)
实验数据集规模大小均为60 000条,在保证数据集数据分布一致的情况下,对数据集进行10∶1∶1的划分,分别作为输入神经网络的训练集、验证集、测试集。
5.2 预处理方法对比实验
对文献[9]的预处理方法以及本文提出的特征参数差值预处理方法,通过对比实验验证本文方法有效性。
使用10部雷达的辐射源信号作为输入,信号的调制方式采用常规的LFM调制,差值矩阵维度均采用2 000维度。实验将特征参数差值矩阵M中的预处理方法作为变量,用两种预处理方法生成两种数据集。输入DenseNet网络进行训练。测试集准确率结果如表3所示。
表3 预处理方法对比实验结果

预处理方法准确率/%文献[9]方法47.72本文方法97.79
由表3可以看出,在复杂信号中,使用本文方法在2 000阶的低维度下即可达到97.79%的准确率,对比文献[9]方法,提升了50.07%。验证了相对文献[9]前后项作差的方法,使用本文方法将后2 000项特征值依次与当前特征值作差能更有效地提取脉冲间信息,且有利于神经网络的学习。
5.3 网络选取对比实验
采用10部雷达的辐射源信号作为输入,信号的调制方式采用常规的LFM调制,并使用本文预处理方式生成2 000维度的差值矩阵。
在网络选取方面,实验对比了文献[9]中使用的VGG-16神经网络,较新的ResNet神经网络以及DenseNet神经网络,均对网络卷积层以及池化层进行改动以适应一维的输入数据。实验结果如图4和表4所示。
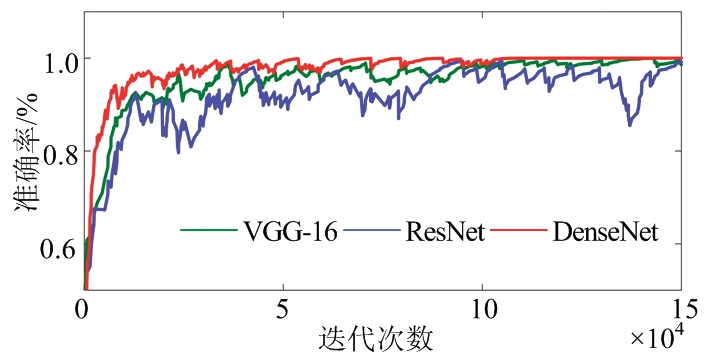
(a) 训练集准确率
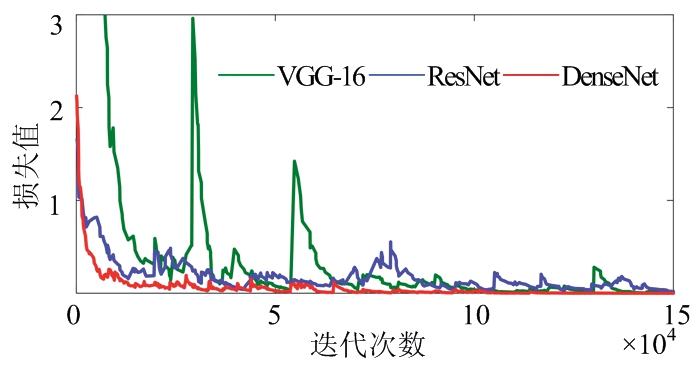
(b) 训练集损失值
图4 网络选取对比实验结果
表4 网络选取对比实验训练用时

所用网络训练用时/sVGG-1691 206ResNet53 877DenseNet14 561
可以看出,使用DenseNet网络可以达到最高的分选准确率和最优的损失收敛速度。且DenseNet网络由于其参数量少的特点,在训练所需的时间上优于其他两个网络,大幅提高了数据的训练效率。
5.4 特征参数差值矩阵维度对比实验
采用10部雷达的辐射源信号作为输入,信号的调制方式采用常规的LFM调制。实验采用八维特征参数,并将特征参数差值矩阵M矩阵的维度大小作为变量,即每个特征差值矩阵长度的取值区间,这决定了网络所能获取到信号间信息量的多少。
作为对比实验,采用相同的混杂信号输入,在特征选取上只选择TOA、PW和RF组成三维特征作为分选依据。对比实验结果如图5所示。
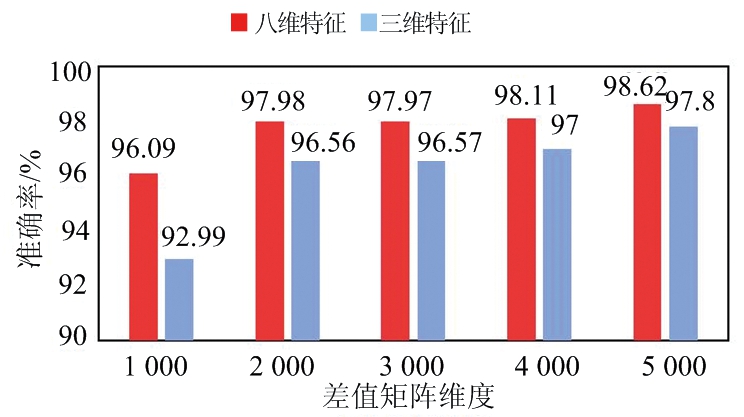
图5 差值矩阵维度对比实验结果
由图5可知,对于本文所仿真的信号,随着差值矩阵维度增大,分选准确率逐步上升,在差矩阵维度达到5 000时能达到98.62%;并且加入三维熵特征和高次频谱对称Holder系数特征后,分选效果均有提升。
为分析新增特征对分选效果的影响,对1 000维度差值矩阵下使用三维特征,三维特征加二维高次频谱对称Holder系数特征、三维特征加三维熵特征和八维特征共同作用的各类信号分选情况进行对比。实验结果如表5所示。
表5 1 000维度差值矩阵下各类信号分选情况
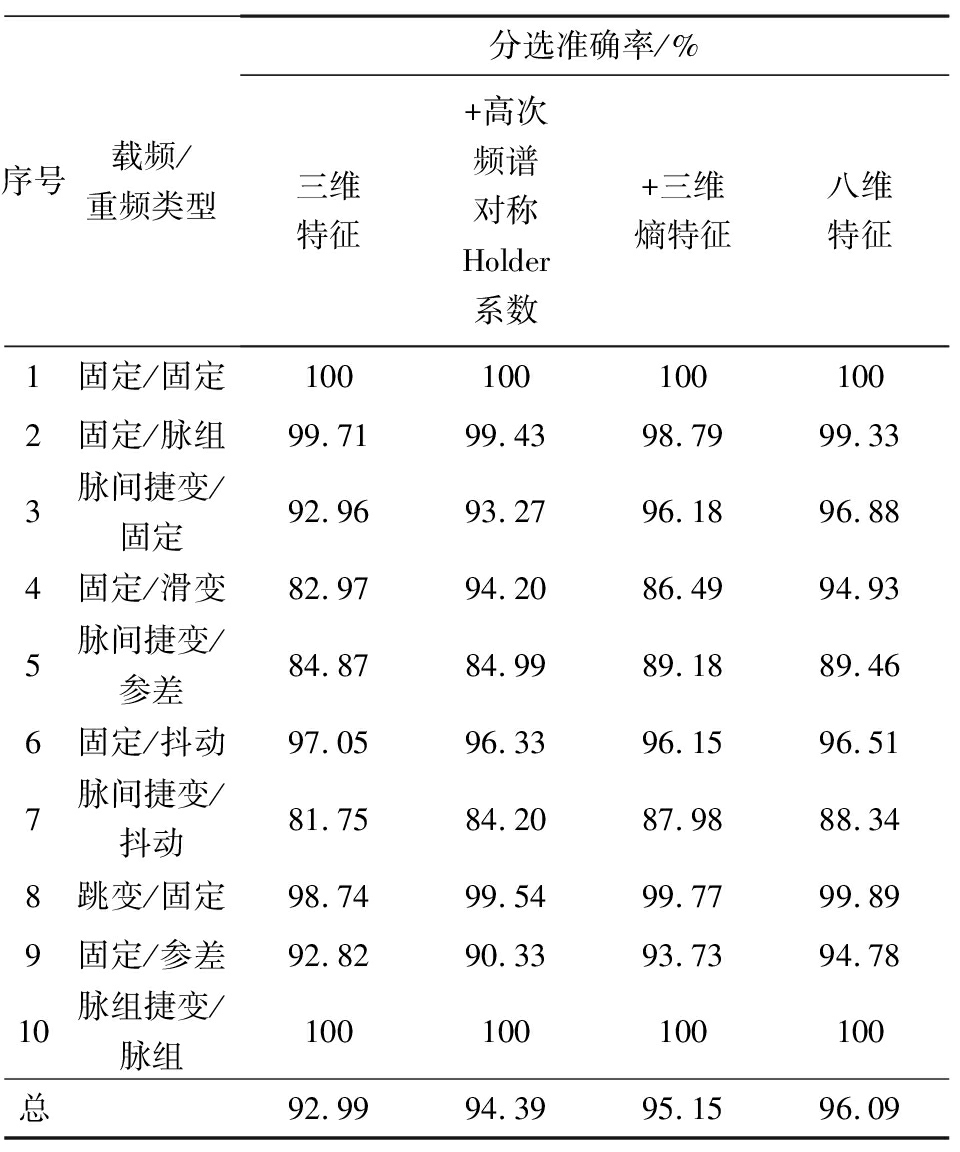
序号载频/重频类型分选准确率/%三维特征+高次频谱对称Holder系数+三维熵特征八维特征1固定/固定1001001001002固定/脉组99.7199.4398.7999.333脉间捷变/固定92.9693.2796.1896.884固定/滑变82.9794.2086.4994.935脉间捷变/参差84.8784.9989.1889.466固定/抖动97.0596.3396.1596.517脉间捷变/抖动81.7584.2087.9888.348跳变/固定98.7499.5499.7799.899固定/参差92.8290.3393.7394.7810脉组捷变/脉组100100100100总92.9994.3995.1596.09
由表5可以看出,使用三维特征为依据分选,能较好地分离固定类型的信号,而对3,4,5,7号捷变、滑变和参差变化的信号分选效果不理想;加入高次频谱对称Holder系数特征后,对于4号滑变的信号分选效果有11.23%的提升;加入三维熵特征后,对于3,5,6号捷变和参差变化的信号分选效果有5%左右的提升,对于4号滑变信号也有3.52%的提升。使用八维特征体系训练学习后,对于滑变、捷变和参差信号的分离准确率得到进一步提升。
5.5 对于复杂调制信号的分选效果
实验选取表2中1,3,8,9,10五类差距较大的脉间调制雷达信号,每一类又分别采用BPSK,LFM,FSK,NLFM,QPSK五种脉内调制方式生成5部雷达,仿真生成共计25部雷达的辐射源信号作为输入,差值矩阵维度采用2 000维度。
作为对比实验,采用相同的混杂信号输入,在特征选取上只选择三维特征作为分选依据。对比实验结果如图6所示。
对于本文仿真的25种辐射源信号,同类脉间调制信号之间的特征值差距极小,仅存在脉内调制方式的不同。由图6可以得出,使用八维特征联合分选可以将分选准确率提升41.02%,并且可以获得更快的损失收敛速度,极大提升了网络对于复杂调制信号的识别能力。
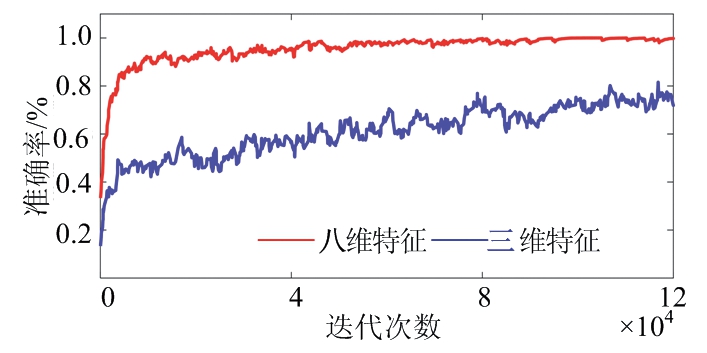
(a) 训练集准确率
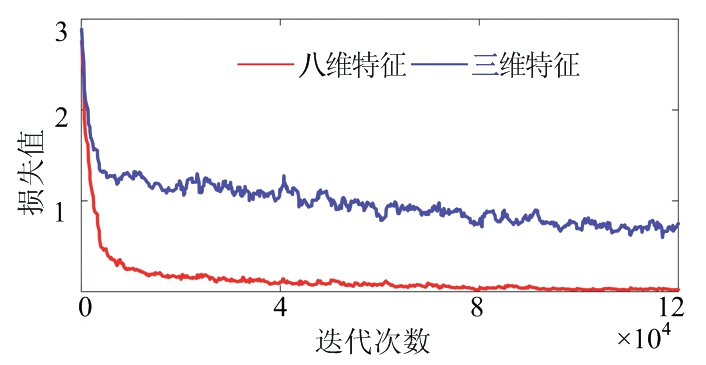
(b) 训练集损失值
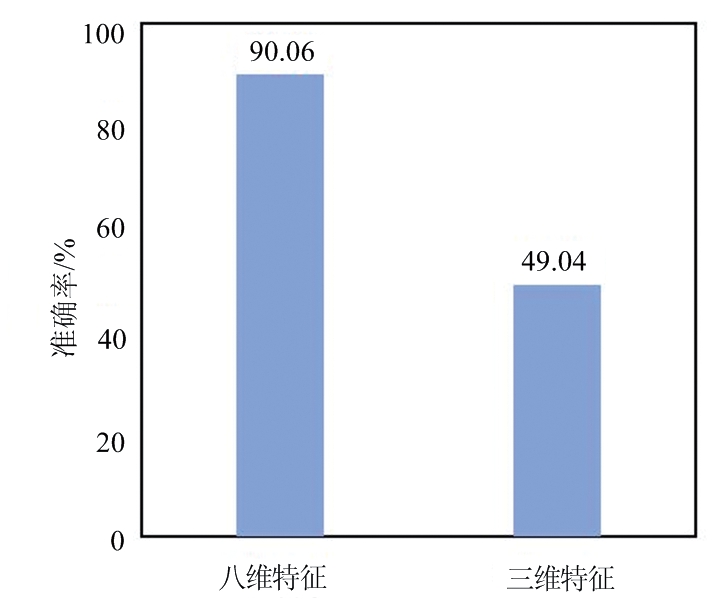
(c) 测试集准确率
图6 对复杂调制信号的分选实验结果
6 结束语
本文针对复杂调制方式下雷达辐射源信号分选准确率低这一问题,从雷达辐射源信号特征选取方面出发,在雷达脉间3参数的基础上加入三维熵特征和高次频谱对称Holder系数两种脉内特征,并采用特征参数差值矩阵的方式进行数据预处理,结合DenseNet深度学习网络对数据进行训练,达到雷达辐射源信号分选的最终目的。仿真实验结果表明,本文提出的方法可以对复杂调制辐射源信号进行有效区分。
[1] 邬诚, 史建涛, 任财. 雷达信号分选算法研究与展望[J]. 信息化研究, 2020, 46(1):1-7.
[2] 袁泽恒, 田润澜, 袁如月,等. 一种新的雷达信号脉内分选方法[J]. 航天电子对抗, 2018, 34(5):24-28.
[3] 刘凯, 韩嘉宾, 黄青华. 基于改进相像系数和奇异谱熵的雷达信号分选[J]. 现代雷达, 2015,37(9):80-85.
[4] 陈恒, 张友益, 王玉梅. 基于常规参数和脉内特征参数的雷达信号分选[J]. 舰船电子工程, 2018, 38(6):58-61.
[5] 韦旭, 潘谊春, 韩俊, 等. 基于自相关函数三维熵的雷达信号分选[J]. 雷达科学与技术, 2017, 15(6):593-599.
[6] 王功明, 陈世文, 黄洁, 等. 基于分数阶Fourier变换的雷达信号分选识别[J]. 计算机应用研究, 2020,37(S1):126-128.
[7] 苑军见, 陈世文, 刘智鑫, 等. 基于高次频谱对称Holder系数的雷达信号分选方法[J]. 信号处理, 2020, 36(10):1775-1783.
[8] 井博军. 基于深度学习的雷达辐射源识别技术研究[D]. 西安:西安电子科技大学, 2017.
[9] 史雨璇. 认知侦察中的信号分选算法研究[D]. 哈尔滨:哈尔滨工程大学, 2019.
[10] 付小利. 并行化深度学习算法及其应用研究[D]. 成都:西南交通大学, 2016.
[11] 陈春利, 金炜东. 一种改进的DNN算法在雷达信号分选中的应用[J]. 计算机应用研究, 2019, 36(4):1178-1180.
[12] 刘括然. 基于LSTM的雷达辐射源识别技术[J]. 舰船电子工程, 2019, 39(12):92-95.
[13] 王功明, 陈世文, 黄 洁,等. 基于迁移深度学习的雷达信号分选识别[J]. 计算机科学与应用, 2019, 9(9):1761-1778.
[14] 秦鑫. 雷达辐射源脉内特征分析与识别关键技术研究[D]. 郑州:战略支援部队信息工程大学, 2020.
[15] 曹晓航, 汪立新, 束学渊. 基于小波不变矩的雷达辐射源信号识别[J]. 计算机工程与应用, 2020, 56(19):269-272.
[16] 王海华, 沈晓峰. 基于对称Holder系数的雷达辐射源信号特征分析[J]. 空间电子技术, 2010, 7(3):55-59.
[17] 黄廷祝, 钟守铭, 李正良. 矩阵理论[M]. 北京:高等教育出版社, 2003:51-52.
[18] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep Residual Learning for Image Recognition[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR),Las Vegas, NV, USA: IEEE, 2016:770-778.
[19] HUANG G, LIU Z, DER MAATEN L V, et al. Densely Connected Convolutional Networks[C]∥2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA:IEEE,2017:2261-2269.




