0 引 言
机载气象雷达作为飞机实时感知航路气象的重要设备，可以帮助飞机即时探测雷雨、风切变、湍流等危险天气现象，机载气象雷达探测技术是大气科学研究和业务应用领域必不可少的技术基础[1]。随着科学技术的发展，航空安全对雷达目标探测性能提出了越来越高的要求，但由于雷达天线安装于天线罩内，其天线孔径受雷达罩约束，导致雷达空间分辨率难以提高。采用共形相控阵天线可以通过增大天线孔径提高方位向分辨率[2]，因此采用柱形共形阵天线有助于提高雷达的气象目标探测性能。除此之外，随着民航发展，航空电子设备逐渐增加，采用柱形共形阵可为机内其他设备提供更大空间，提高空间资源利用率。同时，“翼身融合”技术作为下一代民航飞机的主要设计理念[3]，具有流线感的外形设计，为柱形共形阵布阵创造了有利条件。因此，机载柱形共形阵气象雷达对于气象目标检测具有重要意义。
低空风切变是航空气象领域一种极具危险的气象目标，是指在高度600 m以下，风速和风向都发生急剧变化的一种天气现象[4]，具有变化时间短、强度大、不易检测等特点[5]。在飞机处于起飞或者降落阶段时，飞机飞行高度较低，气象条件较为复杂，若突然遭遇低空风切变，飞行员将无法及时调整，极易造成严重的飞行事故。由此可见，对低空风切变的检测和预警的研究具有较大现实意义，而低空风切变风速估计是整个检测流程的基础。
当机载气象雷达探测低空风切变时，地杂波分布范围广、强度大的特点掩盖了风场信号回波，因此杂波抑制是风切变检测的基础，其抑制效果严重影响着风速估计结果。机载共形阵阵列结构较为特殊，其杂波特性更为复杂，杂波抑制更加困难。目前针对共形阵杂波抑制技术解决方法有：降维空时自适应方法[6]、稀疏迭代自适应方法[7]、参数化方法[8]等，其都未利用共形阵特殊阵列流型进行数据补偿估计杂波协方差矩阵。对于低空风切变检测技术虽然也有相关文献[9-11]报道，但其方法均是针对面阵体制提出的，针对机载共形阵体制下低空风切变风速估计还未有相关文献研究分析。
基于此，本文提出了一种机载柱形共形阵低空风切变风速估计方法。由于共形阵的阵列流型多种多样，本文主要分析柱形共形阵这种典型阵列。本文方法首先分析柱形共形阵列与线性阵列相比杂波抑制困难的本质原因，求得柱形共形阵列的杂波补偿因子，对风场的回波信号进行补偿，然后将补偿后的信号利用空时最优处理器进行杂波抑制，提取每个距离单元的最大多普勒值并估计出风场速度。
1 信号模型
首先对柱形共形阵列进行分析，由于机载柱形共形阵气象雷达设备种类多、信号处理较为复杂，通常将N个阵元在微波段按列进行合成，等效为一个二维弧阵，然后再进行分析与处理。而在进行回波模型仿真时，柱形共形阵与线性阵列在空间角频率与天线方向图方面有较大区别。
1.1 地杂波
如图1所示为机载前视阵雷达模型，地面散射单元水平方位角与俯仰角为θ和φ，波束空间锥角为ψ。
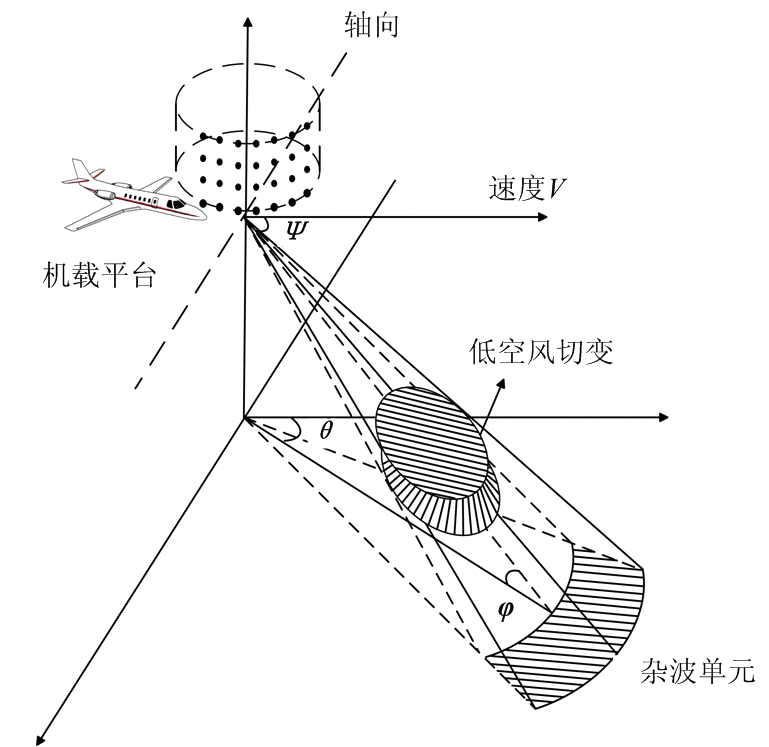
图1 机载柱形共形阵前视阵示意图
由此可以求得柱形共形阵杂波的空间角频率ωsc、时间角频率ωtc:
ωsc(n,θ,φ)=
sin-1(sinθcosφl))
(1)
(2)
式中：V为载机平台速度；ξ为柱形共形阵元对应圆弧角；ρ为柱形共形阵元圆弧对应的圆弧半径；n=1,2,…, N，N为合成后的阵元数；l=1,2,…,L,L为回波距离单元数；k=1,2,…, K，K为相干处理脉冲数；fr为雷达的脉冲重复频率；λ为波长；φl为第l距离单元的俯仰角。并求得柱形共形阵的天线方向图[12]：
F(θ,ψ)=
(3)
式中：ωek,ωak为列子阵、行子阵的阵元加权;ψ0,φ0分别为主波束的空间锥角和俯仰角;m=1,2,…, M，M为柱形共形阵阵元行数；βak为合成行子阵波束的相位修正因子，即
βak=
(4)
假设cl(n,k)为第n个阵元(列子阵合成后的等效阵元)的第k个脉冲对第l个距离环的接收数据，则有
(5)
式中，Rl为第l个距离单元相对应的雷达斜距。
1.2 低空风切变信号
利用流体力学的三维风场模型[13]得到风场速度信息和相关场密度信息，利用撒点法将波束范围内每个散射点的回波叠加[14]。对于风场中第q个散射点，由雷达方程[15]可推导其回波信号幅度为
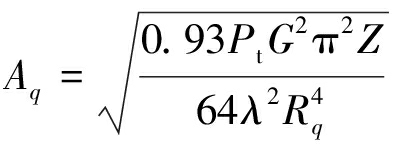
(6)
式中,Pt为雷达发射机功率，G为柱形共形阵天线增益，Rq为第q个散射点与载机平台的径向距离，Z为风场反射率因子。
假设sl(n,k)表示柱形共形阵第n个阵元的第k个脉冲对第l个距离单元内风场的接收数据，则有
(7)
式中，Q为散射点数，ωss(θq,φq)为柱形共形阵的空间角频率，ωts(θq,φq)为柱形共形阵的时间角频率，vq为径向速度，ψq为第q个散射点与载机平台的空间锥角，并且
(8)
1.3 回波信号
雷达回波信号由低空风切变信号、地杂波信号和高斯白噪声信号组成，即x=s+c+n，柱形共形阵进行列合成以后，柱形共形阵列等效接收阵元数为N，假设雷达一个相干处理时间内发射脉冲数为K，则每个距离单元的接收矩阵为
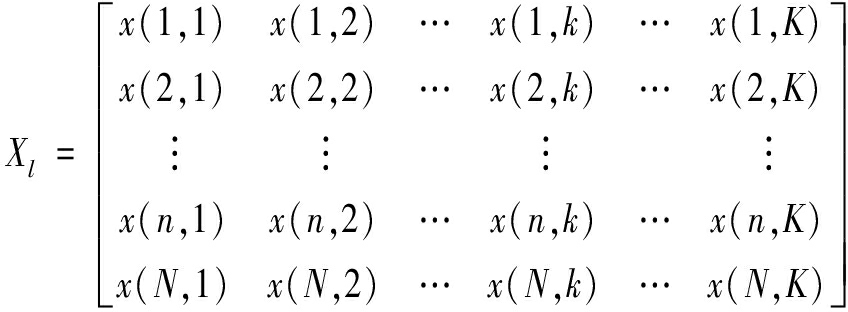
(9)
假设共有L个距离单元，所有距离单元回波数据可表示为X=[X1X2…XL]T。
2 基于空域角频率补偿+STAP的低空风切变风速估计方法
由于柱形共形阵列合成后阵元变化是在空间上是二维的，因此常规的多普勒频率补偿法将不再适用。与面阵相比，柱形共形阵的杂波非均匀性更强，杂波抑制更为困难，若直接估计杂波协方差矩阵会导致STAP杂波抑制性能严重下降。针对柱形共形阵列，本文先采取空域角频率补偿法对回波数据进行补偿，使得估计杂波协方差矩阵所需的样本满足独立同分布的条件，然后利用最优STAP抑制地杂波，提取各个距离单元内风切变信号的最大多普勒频率，完成风速估计。下面对空域角频率补偿法、基于STAP的低空风切变风速估计进行详细描述。
2.1 空域角频率补偿法
针对柱形共形阵引起杂波非均匀现象的本质原因，以机载线性阵列体制下一种非正侧面多普勒补偿方法为参考[16]，分析柱形共形阵特殊阵列流型导致杂波非均匀的根本，提出了一种机载柱形共形阵体制下空域角频率补偿法，算法流程图如图2所示。多普勒频移补偿等方法仅从多普勒频率的角度进行回波补偿，并未考虑共形阵由于特殊阵列结构引起的杂波非平稳性，而空域角频率补偿法从共形阵阵列流型出发解决共形阵杂波抑制困难的问题。
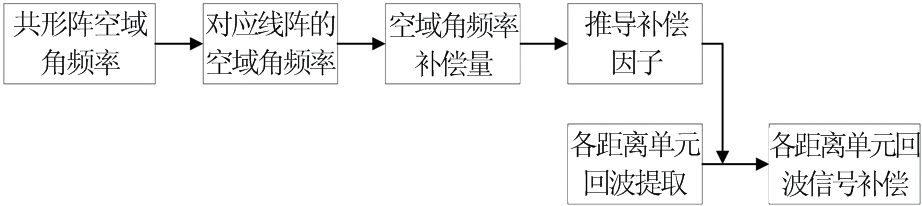
图2 空域角频率补偿法流程图
首先对柱形共形阵列造成非均匀现象的本质原因进行分析，若
为第i个距离单元的回波幅度值，Si为空时二维导向矢量，Nc为某距离环内所含有的距离单元数，则柱形共形阵列某距离环的回波信号可以表示为
(10)
式中Si=Sti⊗Ssi，⊗表示Kronecker积，
Sti= [1,ejwti,…,ej(k-1)wti]T
(11)
(12)
Ssi= [ejwsi1C,ejwsi2C,…,ejwsiNC]T
(13)
(14)
其中xn，yn为柱形共形阵元按列合成后的阵元位置坐标。
而对于均匀线阵来说，空域角频率为
由此可以得出，柱形共形阵杂波严重非均匀现象的本质原因在于其空域角频率与均匀线阵有极大区别。
针对此本质原因，以柱形共形阵对应线性阵列波束指向处的空域角频率值为基准，求得柱形共形阵空域角频率的补偿量并推导补偿因子，然后对柱形共形阵各个距离单元的回波数据进行补偿，对消掉由于柱形共形阵特殊阵列配置造成的空域角频率不同部分，进而精确估计待检测距离单元的杂波协方差矩阵，为后续空时自适应做预处理。具体如下：
首先，以柱形共形阵列的主波束方向角θ0为基准，求得柱形共形阵雷达回波某距离单元的补偿量[17]:
ws0n=ws0nC-ws0np
(15)
(16)
(17)
式中，ws0nC表示柱形共形阵列的空域角频率，ws0np表示对应线阵的空域角频率，求得当前距离单元的补偿因子为
T=diag(Sr)⊗IN
(18)
其中，Sr= [ejws01,ejws02，…,ejws0N]T,IN为N×N维的单位矩阵。当前距离单元补偿回波信号经补偿后为
(19)
此时，经过预处理以后的回波数据得到一定的改善，由于柱形共形阵阵列流型导致的杂波严重非均匀性得到一定程度的抑制，各个距离单元的回波数据基本满足独立同分布条件。
然后，选取第l个距离单元为待检测距离单元，根据先验信息补偿载机运动对回波的相位影响并估计待检测距离单元的杂波协方差矩阵为
(20)
2.2 基于STAP的风速估计方法
空时自适应处理器技术依据回波空时耦合性进行杂波抑制与信号匹配[18]，最优处理器可以描述为如下的数学优化问题：
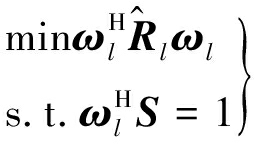
(21)
式中,ωl为最优处理器权矢量，
为柱形共形阵下第l个距离单元接收回波的协方差矩阵，S为柱形共形阵空时二维导向矢量:
S= SS⊗ St
(22)
其中,
SS= [ejws1,ejws2,…,ejwsN]T
(23)
St= [1,ejwt,…,ej(K-1)wt]T
(24)
其中，wsn为归一化空间角频率，wt为归一化时间角频率。此时可以求出柱形共形阵空时自适应滤波器的最优权矢量：
(25)
将估计的带入上式中，由此可以得到柱形共形阵匹配的结果为yl:
(26)
对不同多普勒频段目标信号进行匹配滤波，求解最优处理器的输出信号功率值，输出功率最大时，处理器可有效抑制地杂波并积累风切变信号，此时对待检测距离单元的多普勒频率做一维搜索，可求得待检测距离单元的多普勒频率估计值
由此得到该距离单元的风速估计值为
(27)
最后，对柱形共形阵各个距离单元的回波数据都进行最优空时自适应处理并估计风场速度，便可以得出不同距离单元低空风切变风速的变化情况。
2.3 算法流程
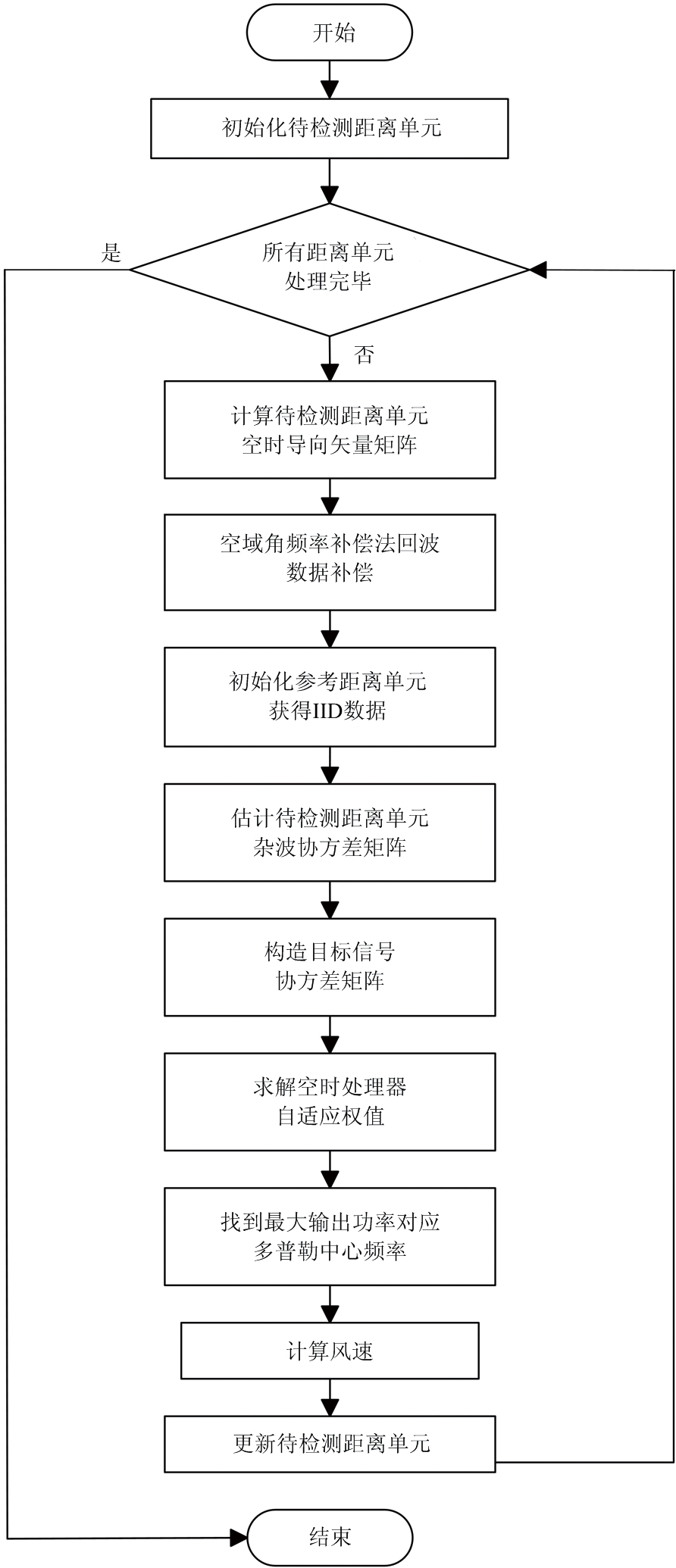
图3 机载柱形共形阵体制下低空风切变风速估计方法的基本流程
图3为机载柱形共形阵体制下低空风切变风速估计方法的基本流程图。针对柱形共形阵气象雷达体制，该方法采用空域角频率补偿法解决由于共形阵特殊阵列流型引起的杂波严重非均匀性，获得独立同分布样本后构造柱形共形阵最优空时处理器进行杂波抑制，提取各个距离单元的最大多普勒频率并估计低空风切变风速。
在高杂噪比下，本文方法也能够精确估计风场速度，对回波数据处理步骤如下：
步骤1： 利用空域角频率补偿法对回波数据进行补偿，补偿柱形共形阵体制下地杂波严重非均匀性，使得各个距离单元的回波数据满足独立同分布的条件;
步骤2： 对接收回波数据进行相位补偿，消除由于载机平台运动带来的雷达回波信号多普勒偏移;
步骤3： 通过参考距离单元的回波数据估计待检测距离单元的杂波协方差矩阵;
步骤4： 构造柱形共形阵空时自适应处理器，求得柱形共形阵处理器的最优权矢量，实现柱形共形阵地杂波抑制并进行信号匹配，估计当前距离单元内低空风切变信号的中心频率，得到低空风切变风速估计结果;
步骤5： 更新待检测距离单元，处理雷达工作范围内的各个距离单元的回波数据，得到风速估计曲线。
3 仿真结果及分析
3.1 仿真条件设置
表1所示为仿真时系统的主要参数值。
表1 载机及雷达仿真参数
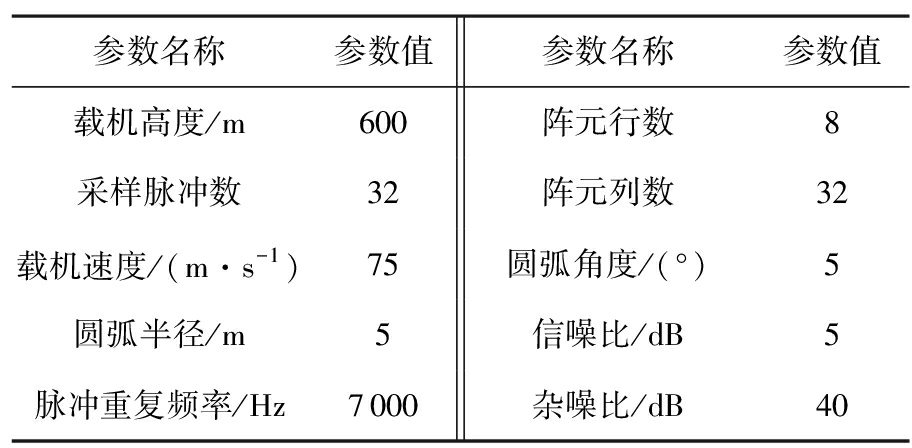
参数名称参数值参数名称参数值载机高度/m600阵元行数8采样脉冲数32阵元列数32载机速度/(m·s-1)75圆弧角度/(°)5圆弧半径/m5信噪比/dB5脉冲重复频率/Hz7000杂噪比/dB40
3.2 仿真结果分析
图4为柱形共形阵回波信号的距离-多普勒，由图中可知，地杂波信号主要集中在零频上，强杂波信号的中心频率在零多普勒频率附近，且其信号幅度明显高于风切变信号的幅度。由图还可知，波束照射到地面杂波散射单元，其产生的强杂波幅度明显高于风切变信号回波，甚至将有用的风切变信号淹没。并且不同距离单元的回波幅度不同，随探测距离的增加，对于同时包括风切变信号、地杂波信号和噪声的距离单元，其回波幅度分布整体呈下降趋势。
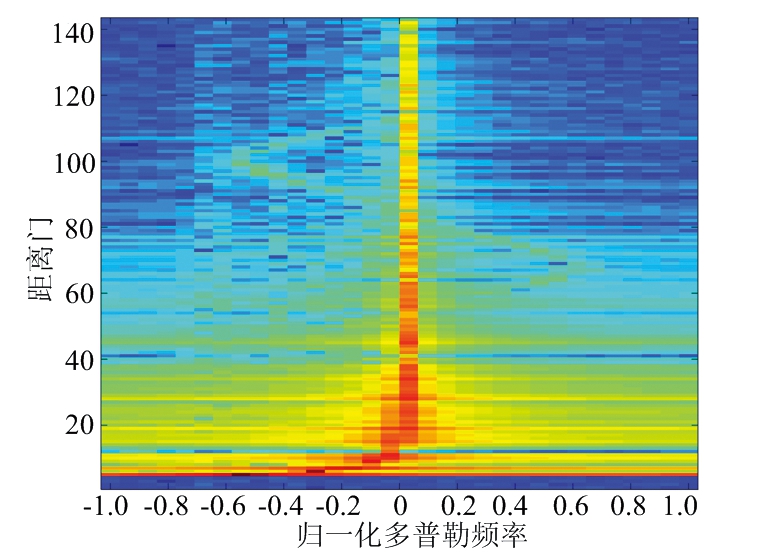
图4 机载柱形共形阵回波信号距离-多普勒
对天线阵列回波的杂波协方差矩阵进行特征分解，可以得到杂波特征值的分布情况。图5是面阵与柱形共形阵杂波特征值分布情况。柱形共形阵杂波协方差矩阵与面阵相比，柱形共形阵杂波大的特征值个数明显多于面阵杂波大的特征值，因此柱形共形阵的杂波抑制需要更多的系统自由度。
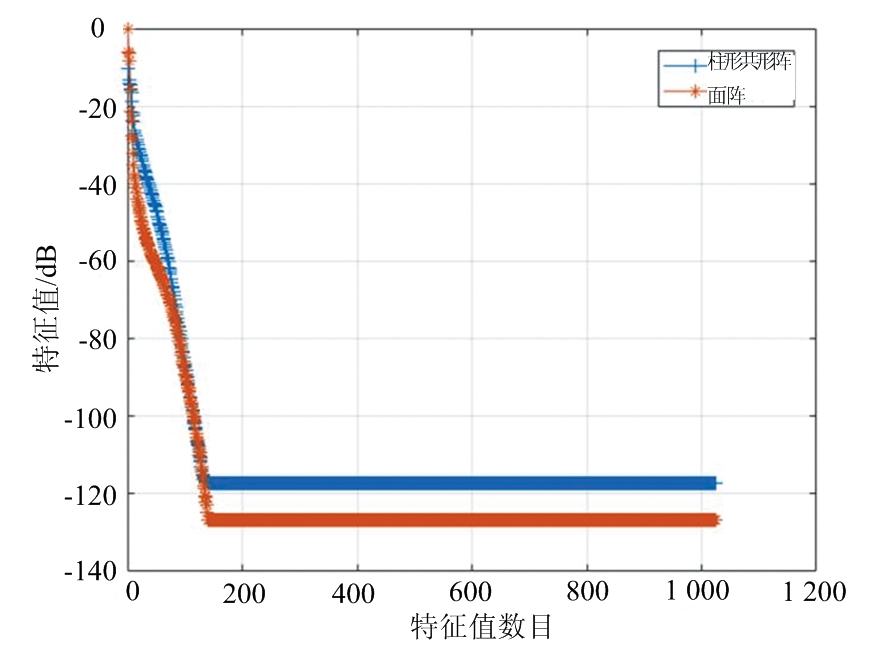
图5 杂波特征值分布情况
图6以第74～78号距离单元为例的柱形共形阵空时自适应处理器的频响特性，可以看出最优处理器在信号方向有最强的输出，处理器在强杂波信号零多普勒频率处形成凹口以滤除杂波，达到良好的滤波效果，以便后续实现低空风切变的检测。
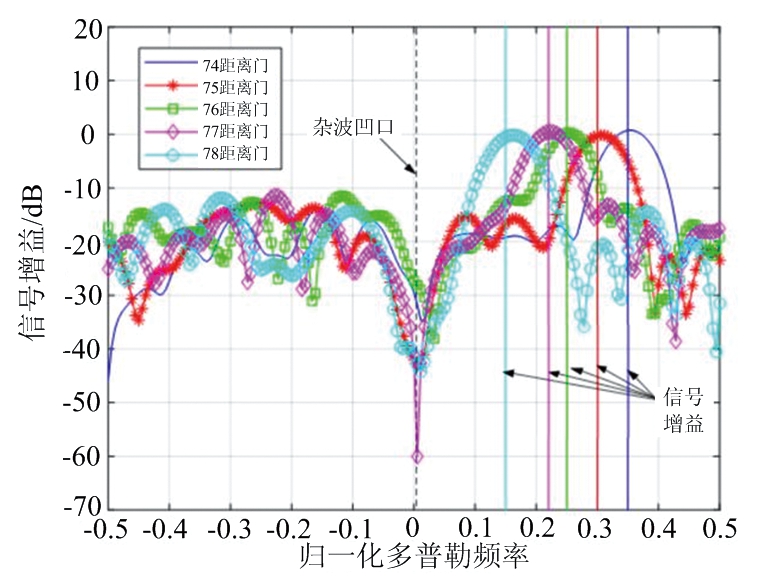
图6 第74～78距离单元滤波器频响
在同等杂噪比与信噪比条件下，本文方法处理效果明显优于多普勒频率补偿空时自适应法与多普勒补偿(DW)法、协方差矩阵加权法(SMI-CMT)法等传统方法。结果证明，本文提出的基于空域角频率补偿空时自适应的低空风切变风速估计方法可以在强杂波条件下有效地抑制地杂波，并精确估计风场速度。风场速度估计结果如图7所示。
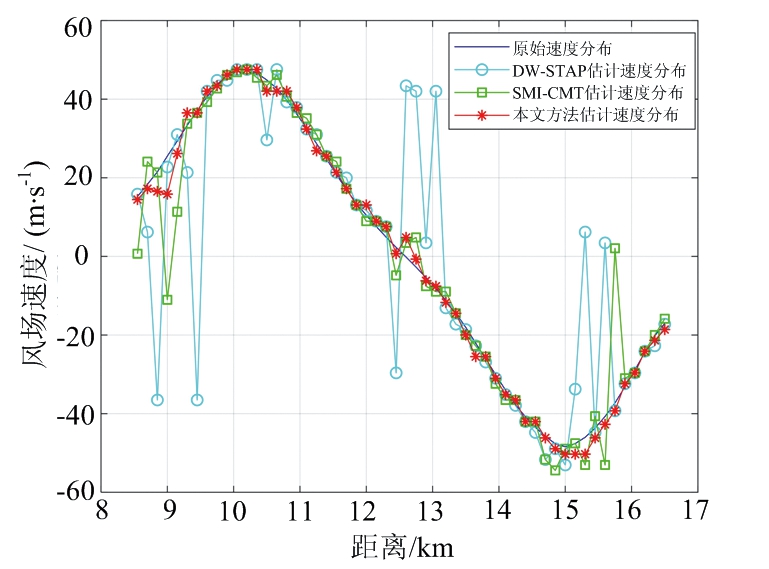
图7 风场速度估计结果
4 结束语
针对柱形共形阵体制下对低空风切变探测目标信号会严重受到地杂波的影响，导致低空风切变风速估计结果不准的问题，提出一种基于空域角频率补偿法的自适应低空风切变检测方法。该方法是将柱形共形阵列引入到机载气象雷达中，分析柱形共形阵其特殊阵列流型引起杂波抑制困难的本质原因，针对共形阵的特殊阵列流型并对比均匀线阵，采用空域角频率补偿法对柱形共形阵的回波数据进行预处理，利用处理后的数据估计柱形共形阵体制下的杂波协方差矩阵，代入求解最优处理器权矢量，自适应滤波后估计风切变信号的多普勒中心频率，从而实现精确的风速估计。仿真结果表明，在机载柱形共形阵体制下，本方法可以自适应地抑制地杂波并精确估计风场速度。
[1] 陈娟,周晔,高霞,等.机载气象雷达发展趋势分析[J].航空工程进展,2021,12(1):113-120.
[2] 吕坤,马晖,刘宏伟.基于涡旋电磁波体制的三维SAR成像方法[J].雷达学报,2021,10(5):691-698.
[3] 蒋瑾,钟伯文,符松.翼身融合布局飞机总体参数对气动性能的影响[J].航空学报,2016,37(1):278-289.
[4] 王冠华.延吉机场强对流天气过程中各气象要素分析[J].中国科技信息,2020(7):40-41.
[5] 段佳玲.基于多通道LFMCW雷达的低空风切变检测技术[D].天津：中国民航大学,2019.
[6] 刘映影.机载共形阵天线的信号处理技术研究[D]. 西安：西安电子科技大学,2019.
[7] 陶芙宇. 共形阵天线机载雷达杂波和干扰抑制方法研究[D]. 西安：西安电子科技大学,2020.
[8] 段克清,谢文冲,王永良,等. 一种稳健的共形阵机载雷达杂波抑制方法[J].电子学报,2011,39(6):1321-1326.
[9] 李海,刘志鑫,王杰,等.基于DDD-GMB的低空风切变风速估计方法[J].信号处理,2020,36(1):67-76.
[10] 李海,王杰.基于CMCAP的低空风切变风速估计方法[J].系统工程与电子技术,2019,41(3):529-533.
[11] 李海,李怡静,吴仁彪.载机偏航下基于广义相邻多波束自适应处理的低空风切变风速估计[J].电子与信息学报,2019,41(7):1728-1734.
[12] 汤子跃,王永良,蒋兴舟. 机载共形相控阵雷达二维杂波建模与分析[J]. 系统工程与电子技术,2001(2):42-47.
[13] 李静,何姣阳,李田家,等.基于FLUENT的下击暴流三维风场建模[J].成都信息工程大学学报,2021,36(5):508-511.
[14] 焦中生，沈超铃，张云. 气象雷达原理[M].北京：气象出版社，2005：302-329.
[15] CHEONG B L，PALMER R D，XUE M. A Time Series Weather Radar Simulator Based on High-Resolution Atmospheric Models[J]. Journal of Atmospheric and Oceanic Technology，2008，25(2)：230-243.
[16] BORSARI G K. Mitugating Effects on STAP Processing Caused by an Inclined Array[C]∥Proceedings of the 1998 IEEE Radar Conference, Dallas, TX, USA:IEEE，1998：135-140.
[17] 谢文冲,王永良. 圆柱型阵机载雷达杂波抑制新方法[J]. 电子与信息学报,2007,29(10):2371-2374.
[18] 刘锦辉,廖桂生,李明. 机载前视阵雷达杂波谱空时分离插值方法[J].电子与信息学报,2011,33(9): 2120-2124.
