0 引 言
航天器再入返回[1-3]地球过程中，为使其着陆于特定的位置或区域，再入飞行时需要不断调整飞行方向，使其按照事先设计好的制导方法向目标点或目标区域飞行。在一些机动能力较强的航天器再入飞行中，有时需要对其飞行过程的转弯方向进行实时辨识，以便更好地判断及预测其实际的飞行路径情况(有时飞行器因为离轨制动控制差异、大气环境变化影响等而未能按照事先设定的路径飞行)。
由于黑障[4-6]的影响，航天器再入飞行过程部分时段会出现遥测下传中断的现象，此时就无法从遥测数据中获取有效的飞行姿态及气动参数信息，故而辨识不出其转弯方向。这种情况下，来自于地面外测[1]设备的观测数据就成为黑障中或姿态不稳定过程中航天器飞行状态估计的主要可依赖数据。另外在一些非合作目标的再入观测中，目前也主要依赖雷达[7]等外测测量数据。
因缺乏姿态信息，航天器再入飞行过程中仅外测观测下的转弯方向辨识只能从外测数据中的测距、方位角、仰角、测速(测距变化率)等观测量上入手，而这几类数据运动特征不明显，不能直接转换出速度信息，从而给转弯方向的辨识带来一定困难。
关于再入飞行转弯方向的实时辨识问题，经查询很难找到类似的解决案例或文献作为参考。为此，针对部分航天器再入返回工程实施过程中遇到的这一实际问题，在对再入飞行过程受力分析的基础上给出了一种转弯方向的实时在线辨识方法。
1 转弯方向辨识方法
1.1 再入过程受力情况
航天器再入段飞行过程主要受到地球引力、大气阻力、气动升力的作用。而其他摄动力的量级较小，在再入飞行过程中可忽略不计[8]。这几个主要的作用力如图1所示。
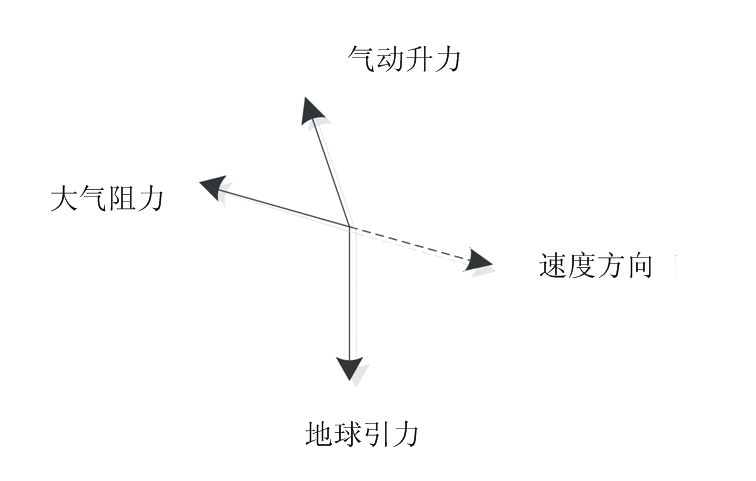
图1 再入过程主要受力示意图
定义航天器在J2000.0惯性系下位置矢量为r=(x,y,z)T，速度矢量为
仅考虑J2项时，地球引力加速度在地心矢径r和地球自转轴矢量we上的分量gr,gw分别为
(1)
式中：J2=1.082 63×10-3 为二阶带谐项系数；μ=3.986 005×1014 m3/s2为地球引力常数；Re为地球赤道半径。
设ρ为大气密度(kg/m3)，v是航天器相对大气的速度，其矢量模为v(m/s)，Sref为飞行器参考面积(m2)，m为飞行器质量(kg)， CL和CD为升力系数和阻力系数(无量纲)。
大气阻力在地球固连系(与J2000惯性系可相互转换)下的加速度为
(2)
气动升力在地球固连系下的加速度为
(3)
式中，C0为航天器所受总升力再入纵平面的侧向分量在地固系下的单位矢量，L0为航天器总升力再入纵平面内分量在地固系下的单位矢量, γ为倾侧角。
从这几个主要作用力的代数式可见，再入飞行过程中轨道面的法线方向主要受到气动阻力法向分量、气动升力法向分量、地球非球形摄动力法向分量的影响。而实际计算中发现，地球非球形摄动力的法线分量相对其他几个量明显较小[8]。
由此，航天器实际再入飞行过程中，通过对姿态角的控制，特别是在其发生滚转以后，升力在当地铅垂面和水平面上的分量会发生改变，从而使航天器具有了一定的纵向机动和侧向机动能力，进而可实现方向转弯。
也就是说，通过实时计算当前轨道平面法向的加速度或速度变化即可对滚转过程发生的转弯方向进行辨识。
基于以上分析，本文对滚转方向辨识的思路是：当只有外测测量数据时，先通过滤波算法使用外测观测量计算出飞行弹道的速度矢量，然后计算当前速度与前一点的速度差(速度增量)在前一点速度法线方向的分量；进而通过对一系列时间点处的法线方向速度分量的滑窗统计来获取对航天器转弯方向的判断。
1.2 再入飞行外弹道计算模型
再入飞行过程外弹道测量数据(主要为测距、测速、测角)无法直接计算出速度参数，除几何方法、差分方法外，可采用滤波算法来实现飞行弹道中速度参数的估计。考虑到再入飞行时受力情况较为复杂，无姿态及其他气动参数遥测信息时(仅外测观测下)，较难进行飞行状态的动力学建模[1]，故此处考虑采用非动力学建模算法进行滤波计算。
在非动力学建模方法中，“当前”统计模型[9-11]是机动目标建模的一种较常用算法。“当前”统计模型把机动目标加速度的一步预测看作是“当前”机动加速度，并采用该加速度作为修正瑞利分布的均值来实现目标自适应跟踪。由于采用非零均值的机动加速度和相应机动加速度方差的自适应调整，因此具有较好的机动目标跟踪能力。
无迹卡尔曼滤波[12-14](UKF)是由牛津大学机器人技术研究所Julier和Uhlman等人于1995年提出的，后来被推广到非线性动力学系统参数估计中。UKF算法的核心是UT变换，它选择2n+1个Sigma采样点来逼近样本非线性变换参量的矩，能达到真实值的三阶精度。同时UKF算法不需要求导计算Jacobian矩阵，不需要清楚地了解非线性函数的具体形式，便于进行模块化开发，因而在工程中有较大的应用价值。
基于以上考虑，本文将采用当前统计模型及UKF滤波算法来实现仅外测观测下飞行弹道中速度参数的估计。
在J2000惯性系下定义UKF滤波的系统状态矢量为
其中，各标量值分别代表位置、速度、加速度在x、y、z方向上的分量。
设α为“当前”统计模型中加速度时间常数的倒数，T为k时刻到k+1时刻的时间增量，
是加速度均值，其取值为
“当前”统计模型下的状态外推模型为
X(k+1|k)=Φ(k+1|k)X(k|k)+
(4)
式中，W(k)是均值为零、方差为
为加速度方差)的离散化的过程噪声，U为机动输入矩阵，Φ为状态转移矩阵。
因x、y、z各方向相互正交，则有Φ=diag{Φx,Φy,Φz},U=diag{Ux,Uy,Uz}。
状态噪声协方差阵
Q=E{W(k)·WT(k)}=diag{Qx,Qy,Qz}
(5)
对x、y、z各方向，有
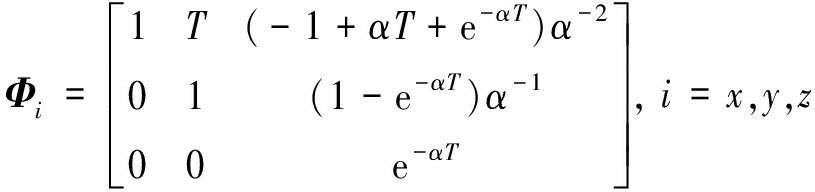
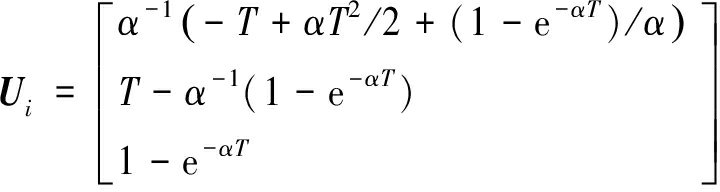
(6)
x、y、z三个方向上噪声协方差阵Qi(i=x,y,z)的计算公式为
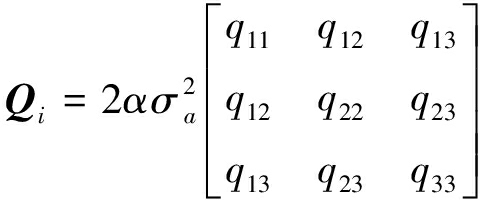
(7)
式中，
Qi中重要一项是加速度的目标方差，设i(i=x,y,z)方向加速度均值为
加速度正上限为aimax，负下限为aimin，其计算公式为:
当目标“当前加速度为正
时
(8)
当目标“当前加速度为负
时
(9)
这样就建立了一种外测观测下的基于当前统计模型的UKF滤波再入飞行弹道估计算法。
1.3 滤波观测模型建立
由于外弹道测量数据中各类观测数据的质量不一，一般情况下测距数据质量较高、而测角数据质量较差，为此，滤波时将观测模型建立在测站地平坐标系下，以便充分利用不同精度的观测量。则观测方程为
(10)
式中：
分别为测距、方位角、仰角、测距变化率(测速)观测量;ρx,ρy,ρz分别为测站到航天器观测视线在测站地平坐标系的分量;
为测站的位置及速度向量。
1.4 滤波初始化方法
滤波计算时的一个重要内容是起步初值的计算，考虑到再入过程中外测跟踪数据建立在测站地平坐标系下，无法直接转换为J2000.0坐标系的位置速度，但可以由测距和测角值计算出位置矢量，因此可通过多个点的曲线拟合完成起步计算。
取多个连续的观测点，设第j个点处测量值时间、测距、方位角、仰角分别为tj，ρj,Aj,Ej。由测站坐标可计算出测站东北天坐标系到J2000.0地心惯性系的转换矩阵为Mtj，则可计算出各点在测站东北天坐标系下的位置矢量为
Rdj=[ρjcosEjsinAj ρjcosEjcosAj ρjsinEj]
j=0,1,2,…
(11)
则各点在J2000.0坐标系下的位置矢量为
(12)
进而对该位置数列使用最小二乘曲线拟合后求导的方法可计算出速度初值。
状态方程中加速度等其他参数的起步初值可设置为0。这样就得到了滤波的起步初值。
1.5 单点转弯方向辨识
在上面计算出滤波状态参数后，对滤波计算出的某一时刻(设为k+1时刻)状态量X，可得到该时刻的位置、速度矢量分别为
设其前一时刻(设为k时刻)的位置、速度矢量分别为rk,vk。
则前一时刻轨道面的法线方向单位矢量为
Nk=rk×vk/‖rk‖/‖vk‖
(13)
当前时刻与前一时刻的速度差为
(14)
该速度差(速度增量)在前一时刻轨道面的法线方向上的分量值为
给定一个小值(定义为σ，σ≥0)，用于判断转弯方向是否为0。
则可定义转弯方向的辨别函数为
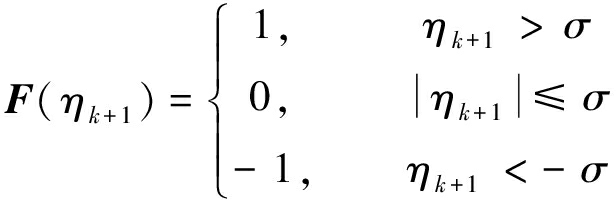
(15)
当F取值为1时，表示左转(顺着飞行速度方向观察时)；取值-1时，表示右转；取值为0时，表示未转弯(或值太小无法辨识)。
这样就得到了当前时刻的转弯方向的辨识值。
此方法是利用速度增量在轨道面法向上的分量进行转弯方向的辨识计算，考虑到转弯时轨道面法线方向上的速度增量将直接在下一时刻的速度矢量上体现出来，因而上述计算过程也可直接简化为计算k+1时刻的速度vk+1在k时刻轨道面法线方向Nk上的投影大小的判断。即用λk+1=vk+1·Nk代替ηk+1，并运用该判别函数进行转弯方向的判断。
1.6 多点滑窗统计
由于滤波计算时存在“震荡”收敛问题，以及某点数据质量较差[1]时可能影响单点判断结果的准确性。因而仅仅使用上面的单点转弯方向辨识方法可能会出现错判的情况。为此，实际工程使用中，还不能直接使用上面的单点判别结果，而需要进行多点数据的综合判断。
为此，在飞行过程的实时监视计算中，可采用多点滑窗统计的方法来进行转弯方向的辨识。
设固定使用当前时刻及其之前n-1个时间点上的单点辨别结果进行统计计算，这n个时间点上的辨识结果分别为f1,f2,…,fn，则可统计出值为1的点数为n1，值为-1的点数为n-1。设综合判断阈值为ε(0.5<ε≤1，值越大越可靠，但判断不出的可能性也将变大)，当n1/n>ε时可认为发生左向转弯，当n-1/n>ε时认为发生右向转弯，否则认为无法辨识出转弯方向(或未发生转弯)。
2 计算及分析
为了验证算法的正确性，采用某航天器再入返回过程的理论弹道数据进行仿真计算(该航天器再入飞行中的侧滑角为小量，可忽略)，按多站接力方式生成仿真数据，并对各站的测距、测角、测速分别设置50 m、0.02°、0.05 m/s的随机误差。
使用本文算法实时计算转弯方向，并与其在轨道系下的理论滚动姿态角给出的转弯方向进行对比。
对轨道系下的滚动姿态角(记为φ)，给定一个比较阈值σ2(σ2>0，此算例中取为0.01°)，结合滚动角的定义，当φ>σ2时，认为右转；当φ<-σ2时，认为左转。
为了对比明显，将两种方法表示的左转及右转值进行区分。
方法1为采用本文滤波及多点滑窗算法的判别结果，左转辨识结果取值为1，右转辨识结果取值为-1；方法2为滚动姿态角判别出的转弯方向，左转取值为0.9，右转取值为-0.9；无法判断时两种方法均取值为0。
使用这两种方法计算的转弯方向值对比如图2所示。
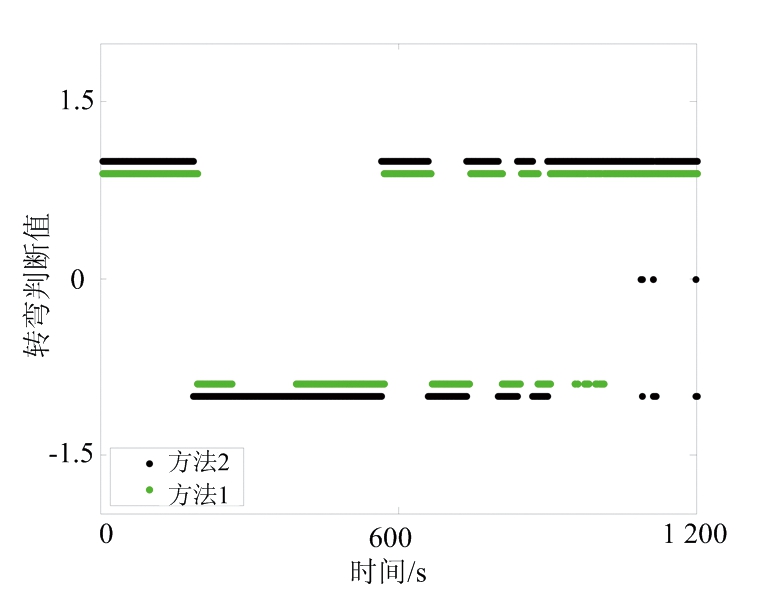
图2 两种方法转弯方向对比
需说明的是，因为所仿真的外测测量量有些弧段没有观测值(设备跟踪不上)，故图2中部分时段只有理论姿态角的计算值，而无外测滤波计算值的判别结果(方法1)。
从图中可见，两种方法判别的转弯方向基本上是一致的，这说明本文算法是可行的。由于滤波震荡问题使其部分点存在误判的情况，但大多数点均判别正确。另外，滤波输出的判断结果存在稍微滞后的现象(1～5 s，各处存在差异)。但总体上来看，本文算法是有效的，对转弯方向判别的正确率较高。
造成滤波判断稍滞后的原因在于：1)滤波计算结果相对于测量数据时标的滞后；2)多点滑窗统计造成的统计滞后。第一种因素改善稍显困难，需从提高数据的质量，以及寻找新的滤波算法模型上下功夫；第二种可从减少滑窗时长，或增加每秒时长内数据采样个数等方面入手，在采样频率不变的情况下，减少时长可能会使得误判的几率放大，所以需要权衡处理。因为本文的滑窗算法是时间上逐点滑动的，所以算法本身不会带来处理延迟。
需要说明的是，本文方法在转弯方向辨识时未考虑侧滑角的影响(当侧滑角很小时)，这样才可直接与滚动角判断出的转弯方向比较。否则，在实际计算和比较过程中还需要考虑侧滑角的影响。
3 结束语
针对仅外测观测下的再入飞行过程中转弯方向的实时辨识问题，提出了一种基于UKF滤波及速度增量(或速度)法向分解的解决方法。从仿真计算结果来看，本文算法是可行的。
在使用该方法时需要注意的是：对于飞行中转弯方向的实时辨识所用的判断阈值不应太小，否则可能将极小作用力的加速度考虑进去。也就是说，只有法线分量绝对值大于某一值后，才能认为转弯方向可判断(可通过事先对理论飞行弹道分析的方法给定阈值)。
考虑到一些航天器外形比较复杂，致使返回过程的受力飞行分析更加困难，下一步将在考虑侧滑角的转弯方向辨识方面进行研究。
[1] 淡鹏, 李志军, 李代伟. 较差质量数据下的返回弹道计算及对落点影响的分析[J]. 电讯技术, 2018,58(1):30-35.
[2] 何威, 刘国刚, 施臣钢,等. 滑翔飞行器再入段弹道特性分析[J]. 兵工自动化, 2019,38(7):82-85.
[3] 郭杰, 郑金库, 王浩凝, 等. 高超声速滑翔飞行器再入制导方法及热点问题研究综述[J].空天技术, 2022(1):54-63.
[4] 刘智惟, 夏国江, 邓永福, 等. 等离子鞘套热力学波动对电磁波传播的影响[J]. 宇航学报,2019,40(6):711-718.
[5] 杨鹰, 于哲峰, 董维中,等. 外加电磁窗减缓再入飞行器的通信中断[J]. 强激光与粒子束, 2018,30(12):62-66.
[6] 王家胜, 杨显强, 经姚翔, 等. 钝头型航天器再入通信黑障及对策研究[J]. 航天器工程, 2014,23(1):6-16.
[7] 张小涵, 刘润华, 汪枫. 一种改进的球载雷达气象杂波建模方法[J]. 雷达科学与技术, 2019, 17(3): 324-334.
[8] 淡鹏, 王超, 王丹. 航天器陨落落点计算偏差分析[J]. 无线电工程, 2020, 50(6):504-508.
[9] 刘明忠, 冯建锋, 孟军, 等. 一种无人飞行器监控数据预处理方法[J]. 雷达科学与技术, 2019, 17(3):285-288.
[10] 欧能杰, 于雪莲, 汪学刚. 修正的当前统计模型及自适应跟踪算法[J]. 现代雷达, 2018,40(9):50-54.
[11] 张彪, 薛俊杰, 杨自豪, 等. 基于“当前”统计模型的容积卡尔曼滤波算法[J]. 现代雷达,2022,44(2):9-15.
[12] JULIER S J，UHLMANN J K. A New Extension of the Kalman Filter to Nonlinear Systems[J]. Proceeding of the Society of Photo-Optical Instrumentation Engineers,1997(3):182-193.
[13] 潘泉, 杨峰, 叶亮,等. 一类非线性滤波器——UKF综述[J]. 控制与决策, 2005, 20(5):481-489.
[14] 曹后龙. 最佳自适应无迹卡尔曼滤波算法应用研究[J]. 城市勘测, 2022(1):80-83.
