0 引 言
X波段双偏振雷达由于其价格低、天线体积小、空间分辨率高等优点受到了气象雷达研究学者的广泛关注[1-2]。与传统的单极化雷达相比，双极化雷达不仅可以测量得到水平反射率因子Zhh，还可以通过发射和接收水平,竖直两种电磁波，从而得到差分反射率Zdr，总差分相位Ψdp和差分相移率Kdp[3-5]。其中差分相移率在传播路径上存在优异的性能：Kdp仅仅与介电常数、密度以及空气中降水粒子的形态有关，在传播路径上受到波束阻挡以及降水粒子衰减的影响较小，且对雨滴谱的变化不敏感[6]。因此对于气象参数的应用也主要依赖于差分相移率的值。
通常情况下，根据雷达回波直接得到的总差分相位Ψdp是由两部分组成：后向差分相位δdp和前向散射引起的差分相位Φdp。其中，差分传播相移率Kdp是前向散射引起的差分相位Φdp在径向距离上的斜率。后向差分相位δdp与降水粒子的散射特性相关。若雷达传播路径中降水粒子满足瑞利散射条件，则可以忽略δdp的值，但随着降水量的增加，降水粒子的直径不断增加，后向差分相位δdp也会随之增加。一般认为达到中雨时，降水区不再满足瑞利散射条件，此时δdp的值不可忽略。后向差分相位可以作为一个单独的气象雷达观测值，也具有很多的应用，可以用于降水微物理量的检测以及操作雷达的校准。
在探究测量得到差分相位的准确性中，很多国内外学者都提出不同的方法。常见的是采用滤波的方式对差分相位进行处理。Hubbert等提出了采用无线冲激响应和有限冲激响应[7]对实测差分相位值进行处理。何宇翔通过研究总差分相位Ψdp的特点，将卡尔曼滤波[8]的方法加入到数据的处理当中。HU等人提出运用小波分析[9]的方法来对测量得到的总差分相位进行处理。但上述的处理方法仅依赖于单一径向上差分相位的变化特点，在实际降雨区的测量过程中，相邻径向上差分相位的值存在一定的联系。本文将结合测量得到的总差分相位在PPI(Plan Position Indicator)图中呈现的特点进行滤波处理。去除电磁波传播路径上其他电磁波的干扰，并利用后向差分相位与差分反射率之间的关系，通过构建新的矩阵，充分利用径向差分相位变化的特点，从而得到差分相移率，重构前向散射引起的差分相位，实现对前向散射相位和后向差分相位的分离。
1 双极化雷达参数和数据
为验证本文提出方法的有效性，将选取代尔夫特理工大学的双偏振X波段国际通信和雷达研究中心(International Research Centre for Telecommunications and Radar,IRCTR)的数据说明差分相位质量控制的情况。这是一种X波段的小雨雷达(IRCTR Drizzle Radar,IDRA)[10-11]。该气象雷达的天线每一分钟转一圈，即每分钟扫描360°，天线的辐射角度约为0.05 rad，每个径向的辐射距离都为15 330 m， 将每一条射线的径向辐射范围分为512个距离库，则每个距离库的长度为30 m。雷达的主要参数值如表1所示。图1为2009年5月23日20时33分雷达实测得到的总差分相位Ψdp,等效反射率因子Zhh和差分反射率因子Zdr的PPI图。
表1 IDRA双极化雷达参数表
参数参数值参数参数值中心频率/GHz9.475径向辐射角度/rad0.05发射功率/W20辐射距离/m15330半功率带宽/rad0.03414天线俯仰角/(°)0.0087
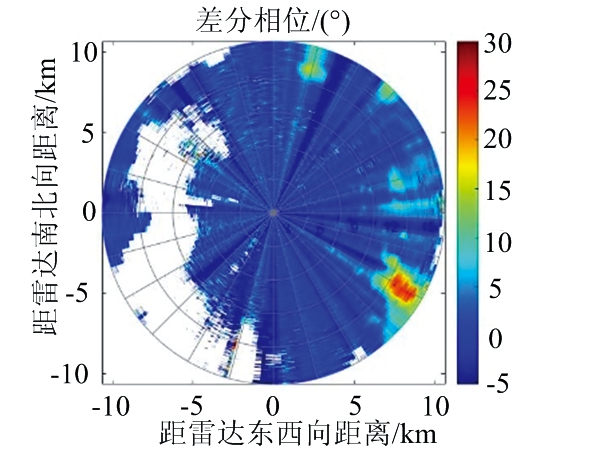
(a) 总差分相位Ψdp
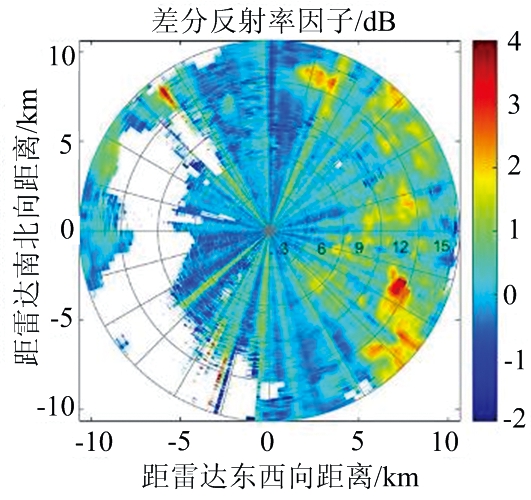
(b) 差分反射率因子Zdr
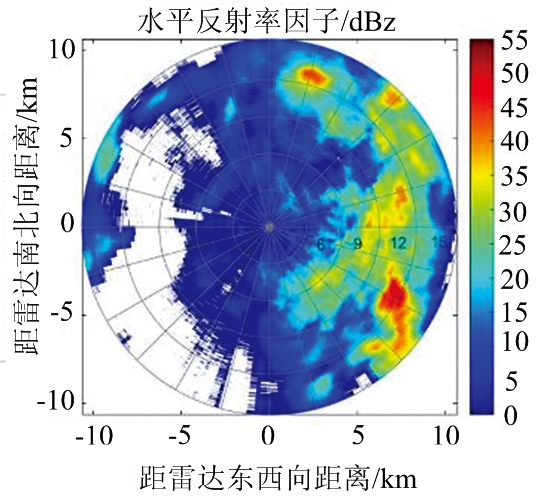
(c) 水平反射率因子Zhh
图1 2009-05-23T20：33：00雷达实测数据PPI图
此时天线的俯仰角为0.008 7°。雷达的发射信号在9.475 Hz的中心频率周围以5 MHz的带宽进行线性调制。雷达测得的数据以NetCDF格式存储。
2 差分相位的预处理
通过气象雷达接收所发射电磁波的回波，可以得到对气象类型和气象情况判别的基本物理量。但在实际情况中，大气环境多变复杂，外界电磁波对雷达系统的干扰会造成雷达回波异常，从而严重影响测量数据的质量并对后续的数据应用产生干扰。电磁波的干扰造成的数据异常在PPI的显示端主要有三种表现：麻点状杂波、数据的突出杂点和条幅状的异常区域。干扰的来源主要有两种：
1) 在接收回波时，会受到非降水回波的干扰，包括外界频率源的干扰和较远距离上一定带宽的干扰源。
2) 气象雷达探测的远端某个方向上存在固定的单频点噪声。
气象雷达的每个径向方位角之间有一定的间隔，构成了360°的PPI数据。如图2所示为沿双极化雷达某一射线方向的工作示意图。
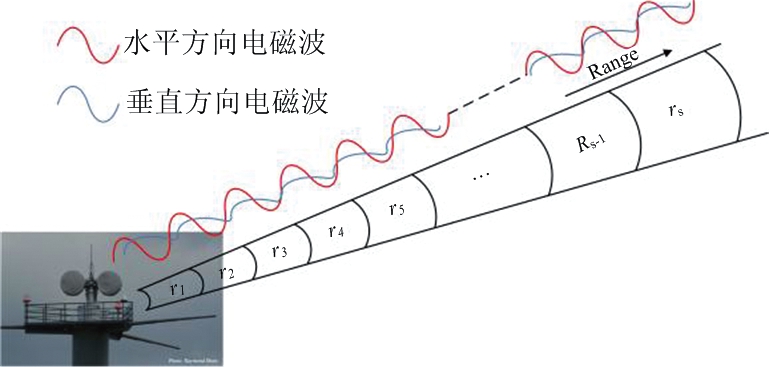
图2 双极化雷达工作示意图
2.1 消除非气象回波数据点
认为差分相位的PPI图中麻点状杂波和突出的杂点主要来源是非气象回波，以滑动数据窗口格来进行处理，以每个要处理的距离单元为中心点，建立一个(2m+1)×(2n+1)大小的滑动窗口，其中i表示为方位向距离库顺序，j表示为径向距离库顺序。
1) 对于某些区域内为非降水地区，即这些区域的距离单元内差分相位没有值，但由于回波的影响，使得该距离单元产生了数据，可能会导致降水区域的误判。计算滑动窗口内有效距离单元个数占总滑动窗口距离单元个数的百分比，当占比率小于设定阈值γ时，则认为该滑动窗口中心距离单元为无效数据点而进行去除，即
(1)
式中，Ψdp(i,j)为双极化雷达测量所得数据给定距离库点(i,j)的总差分相位值，Pi,j为选定滑动窗口内有效距离单元个数占总距离单元个数的百分比，NaN表示距离单元内的无效数据。为了保证处理之后回波数据的真实性，还需要注意当前距离单元内数据的移除不影响下一次窗口内的数据，且不受上一次剔除数据的影响。
2) 对有些区域可能本身存在降水粒子的值，但由于还受到其他非气象回波的影响，某些独立的距离单元内出现很大的数据波动，对于这些数据点，需要先找到波动数据点的位置，进行数据的剔除，并利用径向距离单元数据的变化特点进行填补。首先需要确定这些点的位置，计算滑动窗口内其他距离库上的差分相位值与中心距离库上差分相位值之间的差值。设定每次滑动后滑动窗口中心距离库上的差分相位值为
其他窗口上的差分相位值为
有
(2)
则每个窗口格中可以得到(2m+1)×(2n+1)-1个ΔΨdp的值。记录下滑动窗口格内ΔΨdp大于设定阈值β1的个数μ，并计算：
(3)
若α的值超过设定的阈值β2，则判定该数据点为突出杂点，需要对该数据点进行剔除。
由于该距离单元内本身就存在气象回波数据，因此需要对剔除后的距离单元进行插值处理，使得该距离单元内的数据满足径向上差分相位的变化规律。在该距离单元为中心的滑动窗口内，对窗口中其他距离单元数据进行均值处理，处理得到的数据作为该距离单元的插入值。图3显示了数据处理前后差分相位的PPI图。其中，红色框内显示的是无效数据点处理的情况，对比图3(a)和(b),可以看出无效数据可以有效的被去除。图3(b)中的黄色框内显示的是非气象回波造成的突出杂点，可以明显看到同一径向上相位值的突变情况，造成径向上差分相位值的波动。从图3(c)中可以看到，通过上述处理，同一径向上的差分相位数据的质量得到很好的控制。
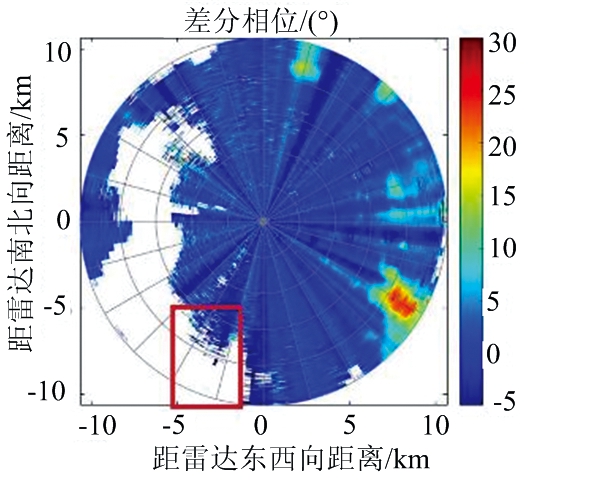
(a) 实测总差分相位Ψdp
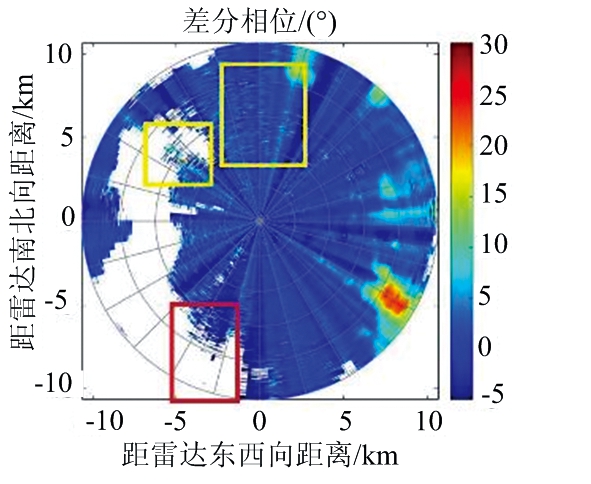
(b) 去除非降水数据后差分相位
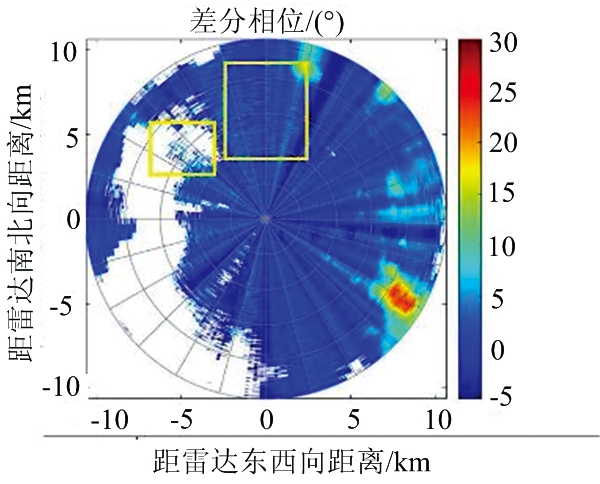
(c) 去除非气象回波后差分相位
图3 去除非气象回波数据前后差分相位PPI图
2.2 条幅状杂波的去除
由于雷达在某一方位向接收回波时，可能会受到该方位向上单频点的电磁干扰，造成测量得到的某些相邻径向上数据出现与周围环境不匹配的情况。这种大规模的数据误差，可以通过构造特征参量来检测方位向上和距离向上的连续性，定位误差数据所在的位置。
设定相邻径向上差分相位的差为ΔΨdp=|Ψdp(i)-Ψdp(i-1)|，其中，i表示方位上的位置，Ψdp为总差分相位的值。由于在每个方位向距离库上，存在多个距离单元个数，因此，记录下ΔΨdp中大于θ1的个数，记为Nth。记Nth1为第i行和第i-1行之间的差分相位值大于θ1的个数，Nth2为第i行和第i+1行之间的个数。设定参数ΔNth=|Nth1-Nth2|，若ΔNth大于某一设定参数θ2时，则判定该径向上的数据存在误差。
在确定条幅状干扰回波的具体位置之后，将该条幅状干扰回波全部去除，再采用插值法保证数据的准确性。条幅状杂波的出现往往会伴随着多条径向出现问题。在对条幅状杂波位置进行判断时，是对每个径向的数据进行遍历，因此利用相邻径向差分相位大于设定阈值的距离库个数差，可以有效地定位条幅状杂波开始和结束的位置。首先将条幅状杂波所在所有的径向数据进行去除，再从相邻径向同一距离库上正常的回波数据径向差值进行填补，恢复真实回波数据值。设定条幅状干扰回波共有n条径向，k为这一干扰回波中所有方位之间的某一个方位，则处理之后的差分相位值为
(4)
去除杂波条幅状杂波前后的差分相位PPI对比结果如图4所示。图4(a)为去除非气象回波后的差分相位结果，此时未进行条幅状杂波的去除，可以看出橙色框内的数据存在明显的误差，对整个径向上的数据都造成了影响。通过定位该径向的位置并进行数据处理之后，其结果如图4(b)所示，方位向差分相位的变化符合实际情况。
3 分离后向差分相位
(a) 去除非气象回波后差分相位
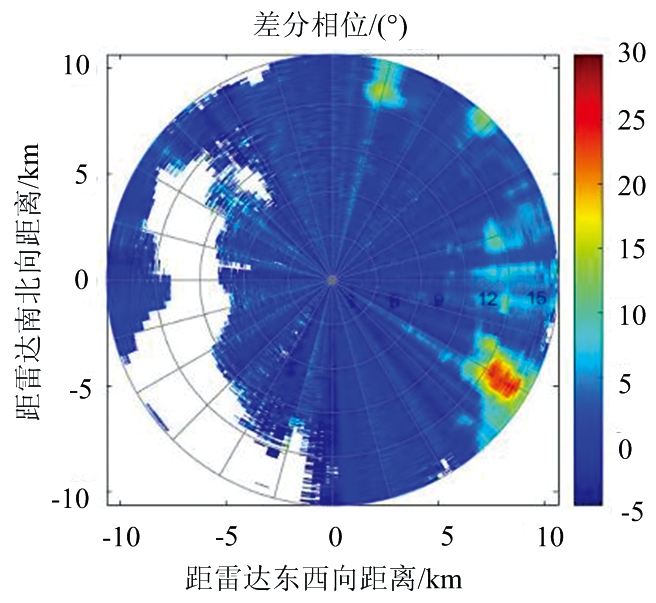
(b) 去除条幅状杂波后差分相位
图4 去除条幅状杂波前后差分相位PPI图
对于波长较长的雷达，在计算前向散射引起的差分相位时，常常忽略掉后向差分相位的值。随着雷达频率的增大，非瑞利散射效应无法忽略，因此需要对后向差分相位进行去除。本文主要通过计算差分相移率，重构前向差分相位，达到了对后向差分相位去除的目的。
3.1 理论分析
雷达直接测量得到的总差分相位，后向差分相位以及前向散射引起的差分相位之间存在简单的和式关系[12]：
Ψdp=Φdp+δdp
(5)
其中，后向差分相位δdp与差分反射率因子Zdr之间存在很好的相互关联，因此可以通过测量差分反射率的值来估计后向差分相位。δdp和Zdr这两个参数都不受到射线传播效应的影响。δdp和Zdr之间的关系可以表示为
(6)
参数a0,a1和a2都是多项式回归系数。假定某一径向距离上的两个距离库分别表示为ra和rb(rb>ra)，两距离库上的差分反射率因子分别为Zdr(ra)和Zdr(rb)。若存在Zdr(ra)=Zdr(rb)，则有ΔΨdp=Ψdp(rb)-Ψdp(ra)=ΔΦdp，即可以认为两距离库上差分反射率相同时，差分相位的插值可以认为等于前向差分相位的插值。但在实际的测量中，由于在差分反射率相等的两距离库范围内降水的微物理量以及雷达测量过程中的统计变化，差分相位之间可能选在扰动干扰，即ΔΨdp=ΔΦdp+ε，ε即为扰动的误差值。为了弥补这些测量中可能存在的缺陷，设定当一条雷达射线上测量得到的两个距离库上的每个差分反射率差组合|Zdr(rb)-Zdr(ra)|小于某一设定的值λ时，即认为此时的ΔΨdp=ΔΦdp。
设定某一条雷达射线上测量所得到的数据矢量差分反射率因子Zdr和差分相位Ψdp分别为
Zdr=[Zdr(r1),Zdr(r2)，…，Zdr(rN)]TΨdp=[Ψdp(r1),Ψdp(r2),…,Ψdp(rN)]T
(7)
式中T表示转置，N表示雷达射线上距离库上的总距离库数。对于本文所用的IDRA数据中N值为512。本文主要利用相同差分反射率的距离库上可以用总差分相位差估计前向差分相位来计算差分相移率的特点，需要知道同一径向上不同距离库之间的差值特点，因此构建了两个矩阵A和B。
(8)
式中
为数学排列组合概念中的组合数。根据矩阵A中的值，可以得到矩阵B的值。假定矩阵A中的某一点的值用A(i,j)表示，其中i表示为矩阵的行，j表示为矩阵的列，则有
(9)
矩阵B的第i行即为值b的二进制表示方式(左边为低位)。例如：
在第一行中，
所以B的第一行为
则矩阵B可以表示为
(10)
通过使用矩阵A，可以计算一条雷达射线上每两个不同距离库之间的差分反射率因子和差分相位之间的差值：
ΔZdr=A·ZdrΔΨdp=A·Ψdp
(11)
计算得到的ΔZdr和ΔΨdp都为一列长度为
的数组。在ΔZdr的数组列中只关心|ΔZdr(i)|<λ所在的行数，此时的i表示为行数。这些行数中的ΔΦdp=ΔΨdp。将这些行数单独列出来，分别得到矩阵A′和B′。接着，通过构建了一个加权系数w，来克服传统差分相位估计粗距离分辨率的问题。
w=B′diag[(ζhh)d]diag[10(-e·Zdr)]Zhh=10log10(ζhh)
(12)
式中，Zhh的单位为dBz，ζhh的单位为mm6m-3。参数d,e是根据降雨偏振分量测量的自适应性得到的。对加权系数w的每一行进行归一化，即
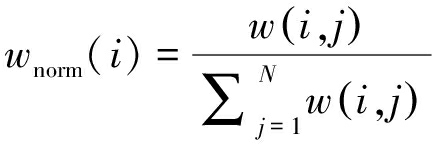
(13)
接着，将得到的差分相位差矩阵ΔΦdp中的元素沿着距离向进行分配。
(14)
式中Δr为同一径向上相邻距离单元之间的距离。因此可以得到单向差分相移的值为
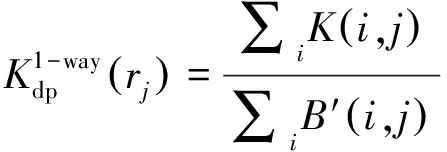
(15)
通过构建评估系数σKdp来检验计算所得到的Kdp[13]的准确性。
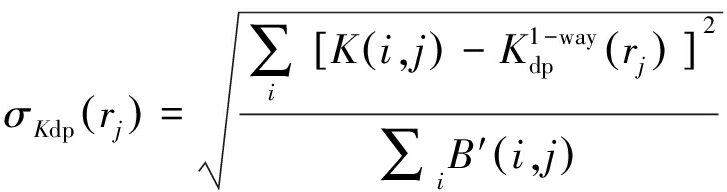
(16)
理论情况下，在雷达的径向范围内，若该区域存在降水区，则前向散射引起的差分相位值会增加，即该距离单元内存在差分相移率的值。若某区域内无降水现象，则前向散射引起的差分相位的值将保持不变，此时距离单元内不存在差分相移率。因此，在对前向散射引起的差分相位进行重构时，只需要关注存在降水区域的差分相位就可以。
3.2 个例分析
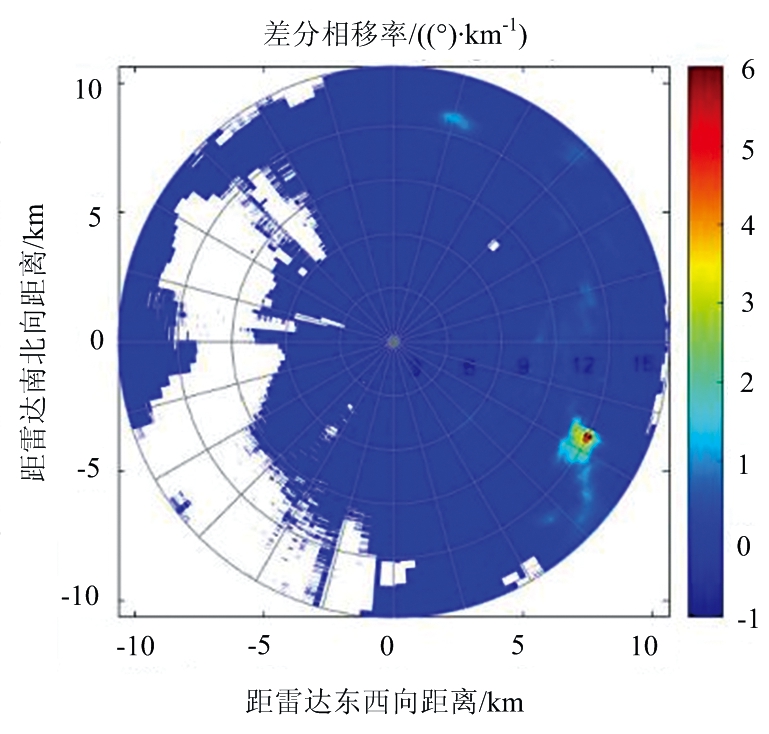
为了验证后向差分相位和前向散射引起的差分相位的值，我们将提出的方法应用于上文提出的位于荷兰213 m高的气象塔顶部的偏振X波段雷达IDRA的数据集。由于后向差分相位和差分反射率之间的关系(式(6))在Zdr大于0 dBz的情况下成立，因此，在实验过程中排除了反射率低于0 dBz且线性退极化比大于-15 dBz的距离库，这种处理方式也确保了气象散射体的存在。结合表1中X波段双极化雷达的数据情况以及雨滴谱的特点，对于去除后向散射相位数据处理过程中需要用到的参数选择为：λ=0.3 dBz,d=0.68,e=0.042。通过计算得到差分相移率，并通过差分相移率重构得到前向散射导致的差分相位[14]。利用实测数据得到的总差分相位值，计算得到了后向差分相位值。图5为计算所得气象数据的PPI图。
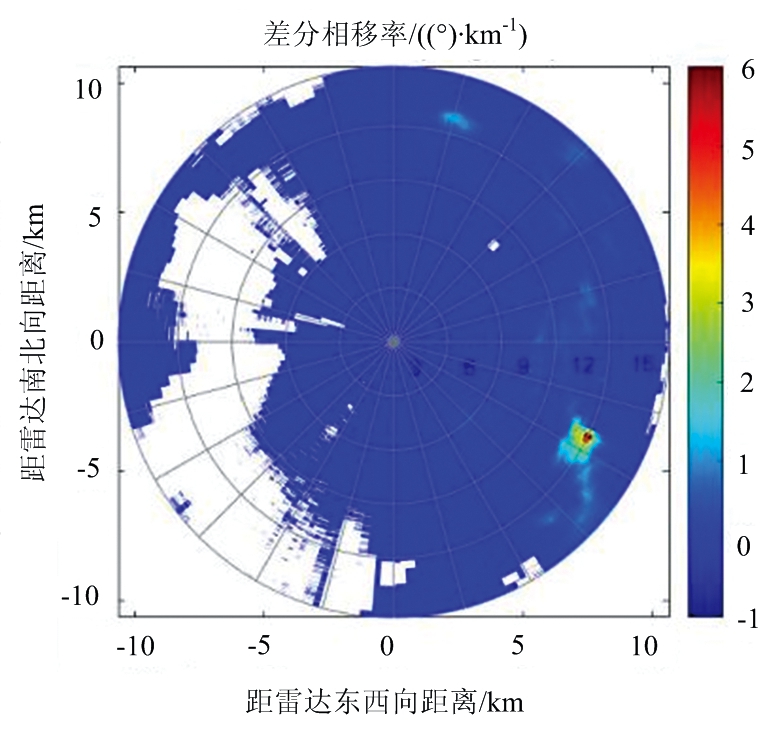
(a) 差分相移率Kdp
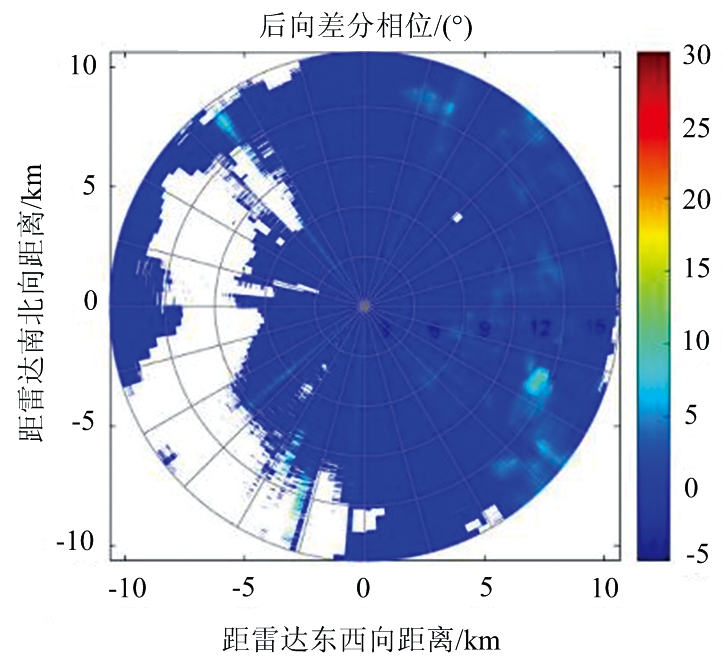
(b) 后向差分相位δdp
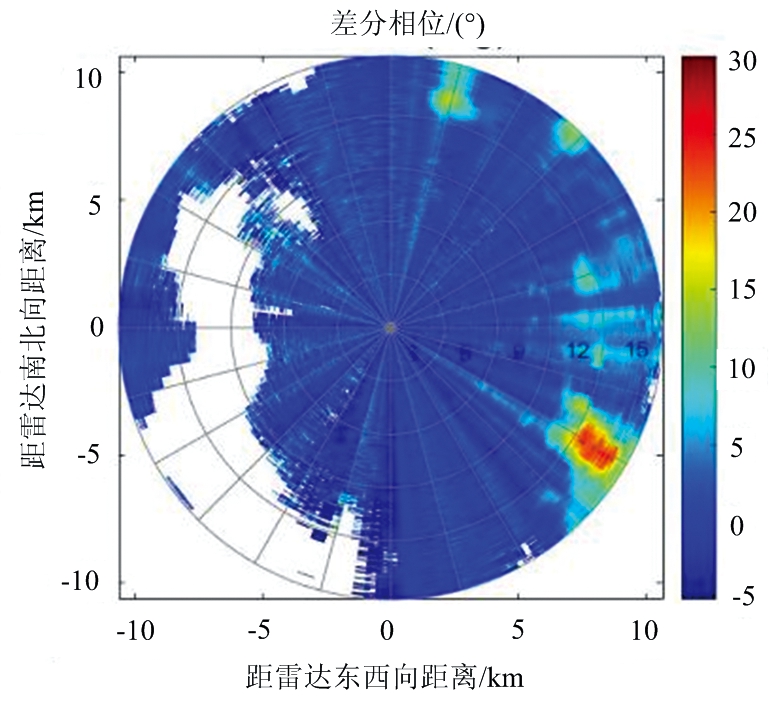
(c) 前向散射引起的差分相位Φdp
图5 差分相位分离所得参量PPI图
对于上文提出的后向差分相位估计方法的准确性，可以通过观察差分反射率因子Zdr，后向差分相位δdp显示图之间的匹配模式情况[15]。理论情况下，后向差分相位和差分反射率因子之间满足式(6)。本文得到的后向差分相位是由实际测量得到的总差分相位减去重构得到的前向散射引起的差分相位。若得到的后向差分相位和差分反射率因子之间的散射关系基本满足理论情况，则证明本文提出分离后向散射相位方法的可行性。
4 结束语
雷达实际测量得到的差分相位值可能会受到传播路径中其他单频点电磁波或者非气象杂波的影响，导致测量得到的后向差分相位的质量不高，利用雷达测量数据中同一径向差分相位的变化特点以及相邻径向差分相位的特点，针对差分相位PPI图中出现的无效数据点，突出杂点和条幅状杂波进行处理。由于差分相移率在雷达数据处理中优越的性能，提出估计差分相移率和后向差分相位的方法。并可以将估计得到的后向差分相位和差分反射率之间的散射关系来验证方法的准确性。
本文已经成功将上文提出的方法应用于代尔夫特理工大学X波段双偏振雷达一组差分相位的估计。最终得到的差分相位符合理论上径向变化的规律。
[1] SILVIA B M, CLAUDIA C, CARMINE M, et al. The Use of Weather Radar Data: Possibilities, Challenges and Advanced Applications[J]. Earth, 2022, 3:157-171.
[2] 李玮,唐辟如,李皓.移动式X波段双偏振雷达资料处理[J].中低纬山地气象,2021,45(3):111-116.
[3] SUNYue, XIAO Hui, YANG Huiling, et al.An Inverse Mapping Table Method for Raindrop Size Distribution Parameters Retrieval Using X-band Dual-Polarization Radar Observations[J]. IEEE Trans on Geoscience and Remote Sensing, 2020, 58(11):7611-7632.
[4] 高涌荇,王旭东,汪玲,等. 基于RCNN的双极化气象雷达天气信号检测[J/OL].系统工程与电子技术,2021:1-9[2022-10-10].http://kns.cnki.net/kcms/detail/11.2422.TN.20211227.1525.030.html.
[5] ZHAO Chuanhong, ZHANG Yiyun, ZHENG Dong, et al. An Improved Hydrometeor Identification Method for X-Band Dual-Polarization Radar and Its Application for One Summer Hailstorm Over Northern China[J]. Atmospheric Research, 2020, 245:1-12.
[6] 张林,李峰,冯婉悦,等.移动X波段双线偏振雷达数据质量分析及偏差订正[J].气象, 2021, 47(3):337-347.
[7] 刘磊. 低迟滞数字信号处理单元研究与设计[D].成都：电子科技大学,2019.
[8] CHANG Guobin, CHEN Chao, ZHANG Qiuzhao,et al. Variational Bayesian Adaptation of Process Noise Covariance Matrix in Kalman Filtering[J]. Journal of the Franklin Institute, 2021, 358(7):3980-3993.
[9] 巩腾飞. 基于小波分析的电机AGC质量控制方法设计[D]. 西安:西安电子科技大学,2020.
[10] YANG Z,HUANG W,CHEN X.Evaluation and Mi-tigation of Ran Effect on Wave Direction Estimation from X-Band Marine Radar Data[C]∥2021 IEEE International Geoscience and Remote Sensing Symposium, Brussels,Belgum:[s.n.],2021:7509-7512.
[11] FIGUERAS I, VENTURA J, RUSSCHENBERG H W J. Towards a Better Understanding of the Impact of Anthropogenic Aerosols in the Hydrological Cycle:IDRA, IRCTR Drizzle Radar[J]. Physics and Chemi-stry of the Earth, 2009, 34(1/2):88-92.
[12] 李海,罗原,冯兴寰,等.基于P-K滤波的X波段雷达雨衰补偿研究[J].雷达科学与技术, 2020, 18(5):487-493.
[13] 李宗飞,肖辉,冯亮,等.X波段双偏振天气雷达衰减订正方法及效果检验[J].气象科技,2019,47(5):731-739.
[14] 罗原. 基于MCMC方法的雨衰补偿算法研究[D].天津：中国民航大学, 2020.
[15] OTTO T, RUSSCHENBERG H W J. Estimation of Specific Differential Phase and Differential Backscatter Phase from Polarimetric Weather Radar Measurements of Rain[J]. IEEE Geoscience and Remote Sensing Letters, 2011，8(5)：988-992.
