0 引 言
随着自动驾驶技术的不断发展，自动驾驶安全问题日益突出。为了减少交通事故的发生，确保道路安全，可以使用雷达来检测周围环境并及时发现危险。汽车工业中最常用的是调频连续波(Frequency Modulated Continuous Wave,FMCW)雷达[1]，此类雷达从接收信号中可以估计附近目标(例如，车辆、行人或其他障碍物)的距离和速度。随着越来越多的汽车使用雷达，不同车辆的雷达之间产生相互干扰的可能性大大增加，导致检测性能下降。事实上，射频干扰(RFI)会大幅度提高本底噪声，潜在目标可能被噪声隐藏，从而降低目标检测方法的灵敏度[2]。
经典的抗干扰方法有很多[3-7]，干扰抑制可在极化、时域、频域、编码域或空间域中处理，关于这些方法的详细分析可在文献[8]中找到。当发射信号为线性调频信号(Chirp信号)时，目前最常见的消除干扰的方法是通过各种方法检测出接收信号中受干扰影响的部分[9]，并在时域内将其替换为零，然后对边界进行可选的平滑处理，这通常被称为归零法。虽然这种方法相当简单，但它会去除部分有用的信号，当干扰持续时间较长时会失效。文献[10]提出了一种卷积神经网络(Convolutional Neural Network, CNN)来解决射频干扰(Radio Frequency Interference，RFI)问题，旨在降低本底噪声的同时保留检测到的目标信号分量。文献[11]提出了一种带门控循环单元(Gated Recurrent Unit, GRU)的循环神经网络(RNN)模型，并将其应用在时域上抑制干扰。与之前的信号处理方法相比，性能更好，处理时间更短。文献[12]在文献[11]的基础上增加了新的注意力机制,该方法取得了比文献[11]更好的结果，实验证明注意力机制可以提升模型性能。文献[13]提出了两个用于汽车雷达干扰抑制新的全卷积网络(Fully Convolutional Network，FCN)模型，它们能够将受干扰影响的短时傅里叶变换(Short-Time Fourier Transform，STFT)频谱图转换为相应的干净距离像。这些模型虽然对真实数据有泛化能力，但它们并不能估计目标相位。在文献[14]中Ristea等人扩展了他们在文献[13]中的工作，引入了一种旨在提高神经网络权值信噪比的训练机制WeNoRT(Weight Noise Reduction Training)，它可以同时估计有多个干扰时汽车雷达信号的目标幅度和相位。语音分离方向的最新进展[15-17]引起了本文作者对时域方法的兴趣，与频域、时频域等方法相比，时域方法能更好地保留信号的幅度和相位信息。
本文使用的自注意双路径循环神经网络(DPRNN-SelfAttention)可以组织任意类型的RNN层对长序列输入进行建模。它将输入信号分成较短的块，并将两个RNN(块内RNN和块间RNN)分别用于局部和全局建模。在DPRNN-SelfAttention块中，块内RNN首先独立处理本地块信息，然后块间RNN聚合来自所有块的信息以执行整个序列的信息处理。该网络以带干扰的接收信号的实部、虚部作为输入，输出是抑制干扰后的实部、虚部，通过输出的实部和虚部可以简单计算出相位估计值。虽然以前的深度学习方法研究的是单个干扰的雷达干扰抑制[9-11]，但本文目标是解决存在多个干扰的抗干扰问题。为了实现这一目标，本文使用了文献[14]提出的大规模数据集，该数据集模拟了多个干扰源存在的现实汽车场景，在训练过程中考虑了多达3个干扰。本文还介绍了一种新的损失函数，相比于平均绝对误差(Mean Absolute Error, MAE)或均方误差(Mean Squared Error，MSE)，能更好地提升模型性能。
1 FMCW雷达及其干扰
1.1 FMCW雷达
在FMCW雷达[1]中，发射信号STX(t)是线性调频脉冲(Chirp信号)，如图1(a)所示。发射信号STX(t)定义如下：
(1)
式中，t为时域变量，f0为初始时刻t=0的频率，Tchirp为Chirp持续时间(扫频时间)，α为Chirp斜率(调频斜率)，α=BSW/Tchirp，其中BSW为扫频带宽。
接收天线接收目标反射的信号SRX(t)，对于单个目标，其定义如下：
(2)
式中,
为传播延迟时间，R为目标距离，c为光速，
为接收信号的复振幅。
接收信号进一步与发射信号混频后经过低通滤波器后得到差频信号(Beat Signal)，如图1(b)所示，其频率fb=α·τ。差频信号也可以表示为
(3)
式中，
表示SRX(t)的复共轭。
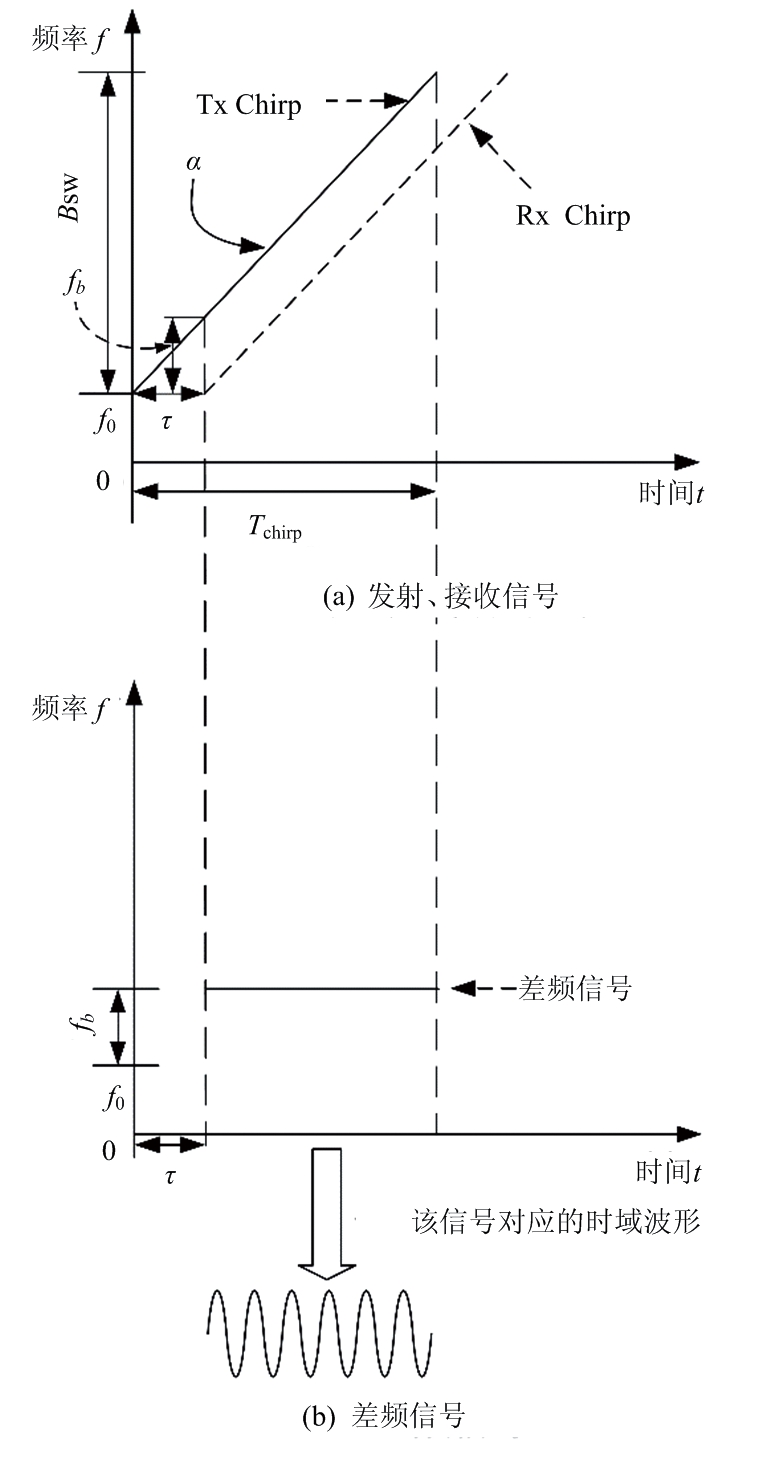
图1 FMCW信号时频图
1.2 FMCW干扰
如图2所示，来自FMCW雷达的单个干扰类似于式(2)描述为
(4)
式中，AI为干扰幅度，Δτ为干扰源相对于FMCW雷达发射开始时间的传播延迟时间，并且干扰源的调频斜率αI=BI/TI,其中BI为干扰源的带宽，TI为扫频时间。
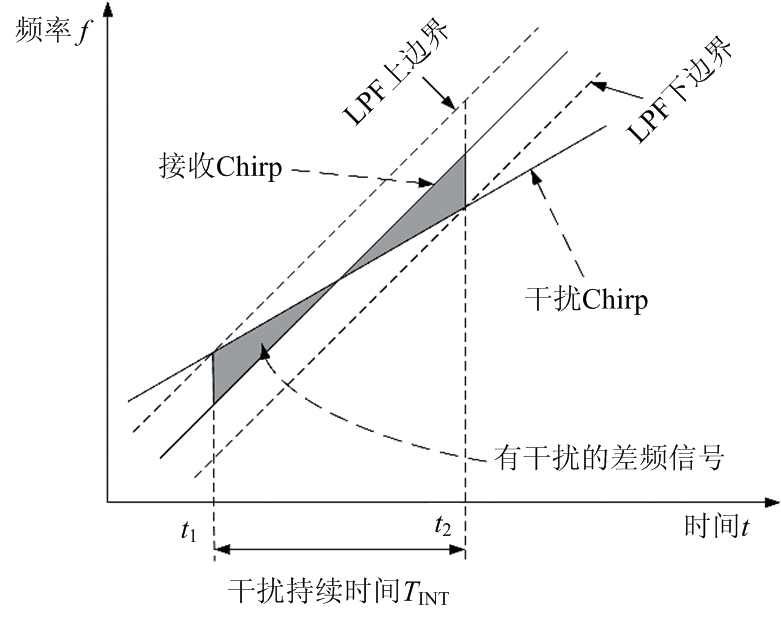
图2 有干扰的FMCW差频信号
在存在相互干扰的情况下，接收机接收到反射信号和干扰的混合信号，即
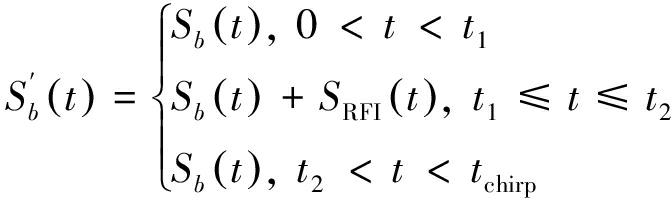
(5)
其中，根据文献[3]中的推导，干扰持续时间TINT=t2-t1。
在存在多个目标和干扰源的情况下，接收机的接收信号定义如下:
SRX(t)=
(6)
式中,Nt为目标数，Nint为干扰源数目。非相干干扰信号SRFI(t)(其线性调频速率与发射信号不同)与发射信号混合后的接收信号，其带宽受到抗混叠滤波器的限制[3]。
2 RNN-SelfAttention模型设计
本文目标是使用深度学习方法抑制雷达干扰，并能估计目标的幅度、相位。在文献[17]的启发下，本文在时域音频分离网络(Time-domain Audio Separation Network, TasNet)[16]的基础上使用DPRNN改进的DPRNN-SelfAttention代替一维CNN。图3是本文模型的系统流程图。在图3中可以看到DPRNN-SelfAttention由3个阶段组成：分割、块处理和重叠相加。分割阶段将输入序列拆分成互相重叠的块，并将所有块拼接成一个三维张量。然后将张量传递给堆叠起来的DPRNN-SelfAttention块，以交替方式迭代应用局部(块内)和全局(块间)建模。最后一层的输出通过重叠相加转换回序列输出。
2.1 DPRNN-SelfAttention模型
2.1.1 分割
对于序列输入W∈
N×L，其中N代表特征维度，L是时间步长，分割阶段将W拆分成大小为F的块，块每次移动大小为P。第一个和最后一个块用零填充，使得W中的每个样本都出现且只出现在F/P个块中，产生E个相等大小的块DE∈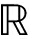N×F(e = 1,…,E)，接着将所有块拼接得到一个三维张量Y=[D1,…,DE]∈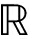N×H×E。
2.1.2 块处理
分割输出Y被传递到M个DPRNN-SelfAt-tention块的堆栈中。每个块将输入的三维张量转换成另一个具有相同形状的张量。本文将每个块Bm(m=1,…,M)的输入张量表示为Ym∈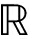N×F×E,其中Y1=Y。每个块包含两个子模块分别对应块内处理和块间处理，块内RNN始终是双向的，并且被应用于Ym的第二维度，即在E个块中的每个块内：
图3 DPRNN-SelfAttention系统流程图
Um=fm(Ym[:,:,i]),i=1,…,E
(7)
式中,Um=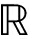H×F×E是RNN的输出，fm(·)是RNN定义的映射函数，Ym[:,:,i]∈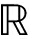N×F是由i定义的序列。
此外，由于干扰发生在整个序列中，因此模型需要捕捉每个块的块内全部时间步长之间的关系。在文献[12]的启发下，本文在块内RNN层后添加了注意力块。注意力块的关键是缩放点积注意力(scaled dot-product attention)：
(8)
式中，Q(Query)、K(Key)和V(Value)分别为查询、键和值向量，dk为键向量的维数。通过使用注意力块，模型可以更好地学习块内时间步长之间的关系。
然后应用线性全连接(Fully-Connected，FC)层将Um的特征维度转换回Ym的特征维度：
(9)
式中,
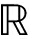N×F×E是转换后的特征,G∈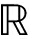N×H和v∈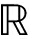N×1分别是FC层的权重和偏置，Um[:,:,i]∈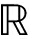H×F表示Um中的块i。然后对
使用层归一化(Layer Normalization，LN)，提升模型泛化能力：
(10)
式中,z,r∈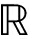N×1是缩放因子，ε是保证数值稳定性的一个小正数，⊙表示Hadamard乘积,μ(·)和σ(·)是
的均值和方差：
(11)
(12)
接着在LN输出及输入Ym之间添加一个残差连接：
(13)
之后
被用作块间RNN子模块的输入，其中RNN被应用于最后维度，即M个块中的每个块所对齐的时间步长F：
(14)
式中,Vm∈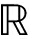H×F×E是RNN的输出，
是由RNN定义的映射函数，
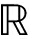N×E是由所有E个块的第i个时间步长定义的序列。由于块内RNN是双向的，
中的每个时间步长都包含其所属块的全部信息，这使得块间RNN可以执行全序列级别的建模。与分块内RNN一样，Vm上也应用了线性FC层和LN操作。DPRNN-SelfAttention块Bm输出和之间还添加了一个残差连接，当m<M时，输出将作为下一个块Ym+1的输入。
2.1.3 重叠相加
最后一个块的输出表示为YM+1∈N×F×E，最后把E个块重叠相加后转换回长序列，输出为Q∈N×L。
如图3所示，考虑单个块中的块内和块间RNN的输入序列长度之和F+E，其中重叠率设为50%(即P=F/2)。其中E=[2L/F]+1，[·]表示上限函数。为了实现最小总输入长度F+E=F+[2L/F]+1，应使
本文模型输入序列长度为
而不是原始序列输入长度O(L)，这大大降低了L极大时的优化难度。
2.2 损失函数
本文使用了Log-Cosh损失和多尺度STFT损失 (multi-resolution STFT loss)的线性组合，以便适当地训练模型并获得最优结果。
Log-Cosh损失函数是一种比MSE更为平滑的损失函数，利用双曲余弦计算预测误差：
(15)
式中，x为真实值，
为预测值，log表示以e为底数的自然对数。
它的优点在于对于较小的误差
其近似于MSE，收敛下降较快；而对于较大的误差其近似等于
损失函数的作用大部分类似于均方误差，但不会受到偶然误差预测的强烈影响。
单个STFT损失定义为
(16)
式中,表示生成样本，LSC以及Lmag分别表示谱收敛损失和对数STFT幅度损失[17]，它们各自的定义如下：
(17)
(18)
其中‖·‖F和‖·‖1分别代表F范数以及L1范数，STFT(·)表示STFT幅度，N表示元素个数。
多尺度STFT损失是不同分析参数(即FFT采样点、窗长和帧移)的STFT损失的总和。设Z为STFT损失的数量，多尺度STFT辅助损失(Laux)表示为
(19)
在基于STFT的信号时频表示中，存在时间分辨率和频率分辨率之间的权衡； 例如，增加窗口大小可提供更高的频率分辨率，同时降低时间分辨率。 通过将多个STFT损失与不同的分析参数结合起来，帮助神经网络学习信号的时频分布信息从而可以更好地去除信号中的干扰分量。此外，它还可以防止神经网络过拟合固定的STFT表示。
本文最终的损失函数被定义为多尺度STFT辅助损失和Log-Cosh损失的线性组合：
(20)
式中,λ表示平衡两个损失项的超参数。
3 实验设计与结果分析
3.1 数据集
汽车雷达干扰抑制(Automotive Radar Interference Mitigation Version 2，ARIM-v2)数据集[14]是一个公开用于汽车雷达抗干扰任务的大型数据库，由144 000个无线电信号样本组成，这些样本模拟了存在一个或多个干扰源的复杂现实汽车场景。数据集被分为120 000个样本的训练集和24 000个样本的测试集。每个样本由以下参数的随机选择值生成：信噪比(Signal to Noise Ratio，SNR)、信号干扰比 (Signal to Interference Ratio，SIR)、相对干扰斜率β=αI/α(干扰源线性调频速率αI和信号线性调频速率α的比值)、目标数量、每个目标的幅度、相位和距离，其参数设置如表1、表2所示。干扰源的数量和信噪比(SNR)值是使用最小值和最大值之间的固定步长来选择的。表2中的其他参数是在最小值和最大值之间均匀分布的随机变量。
表1 模拟真实汽车雷达参数设置
参数参数值扫频带宽BSW1.6 GHz扫频时间Tchirp25.6 μs采样率fs40 MHz雷达中心频率f078 GHz
3.2 模型配置
DPRNN-SelfAttention可应用于任何需要长序列建模的系统，本文研究了其在时域音频分离网络(TasNet)[15]中的应用，可在ARIM-v2数据集上完成雷达抗干扰任务。TasNet包含3个部分：1)线性一维卷积编码器；2)分离器；3)线性一维转置卷积解码器。本文使用与文献[16]相同的编码器和解码器设计，滤波器的数量设置为64。在分离器中叠加使用6个DPRNN-SelfAttention块，使用Bi-GRU[12]作为块内和块间RNN，每个方向有128个隐藏单元。输入信号是有干扰的带噪差频信号，其特征维度N为1，长度L为1 024，因此本文将DPRNN-SelfAttention的块大小F设为64，标签信号是对应的带噪的差频信号。
表2 ARIM-v2数据库样本参数设置
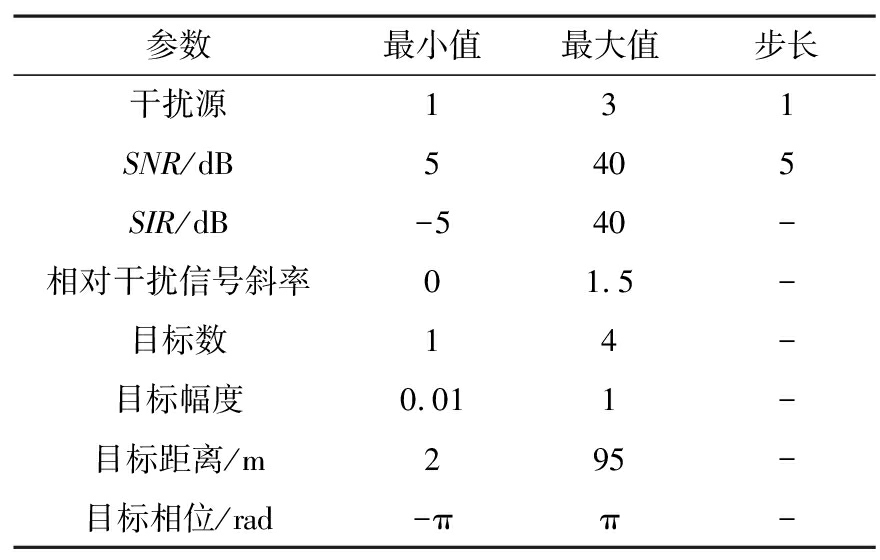
参数最小值最大值步长干扰源131SNR/dB5405SIR/dB-540-相对干扰信号斜率01.5-目标数14-目标幅度0.011-目标距离/m295-目标相位/rad-ππ-
所有模型均在Intel Core i7 CPU和NVIDIA RTX 3080Ti GPU上训练，多尺度STFT损失由表3中描述的三种不同尺度STFT损失的总和计算，根据多次实验的结果将超参数λ设为0.000 01。模型使用RAdam优化器来稳定训练，激活函数为relu,学习率设为0.000 01。
表3 多尺度STFT损失不同尺度参数设置
(窗口类型为汉宁窗)
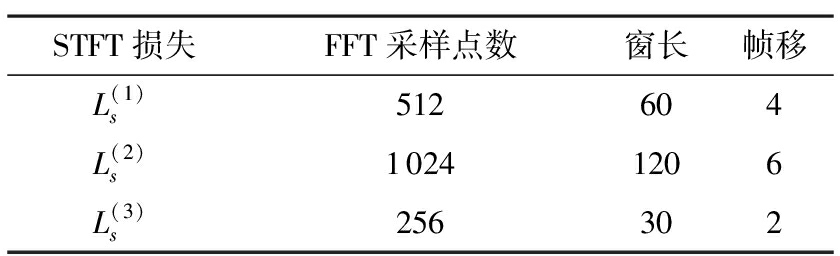
STFT损失FFT采样点数窗长帧移L(1)s512604L(2)s10241206L(3)s256302
3.3 测量指标
标签信号的目标幅度与预测信号的目标幅度之间的平均绝对误差(Mean Absolute Error，MAE)是评价雷达抗干扰性能的一个重要指标，单位为dB。在雷达信号处理中，不仅目标的幅度很重要，相位也很重要，因为后者是估计其他基本参数(如目标速度)或波束形成所必需的。因此，本文还计算了由标签信号实部、虚部计算的目标相位和由预测信号实部、虚部计算的目标相位之间的平均绝对误差，单位为度。在本文的评估中，还使用了平均信噪比改善(mean SNR 
是同一接收信号中幅值最大的目标在干扰抑制前后的信噪比差值。
3.4 实验结果与分析
本文将基于DPRNN-SelfAttention模型与最常见的归零法(Zeroing)[9]、文献[16]中的DPRNN模型以及根据标签(无干扰信号)计算的结果进行对比，相应结果在表4给出。从表4中可以看出本文方法在所有性能指标上与归零法相比都有很大优势。当将DPRNN模型与本文模型进行对比时，本文模型能获得更好的结果。这清楚地表明为了改进模型性能，有必要添加注意力块。注意力块的引入使DPRNN模型性能得到提升，在幅度MAE、相位MAE和
上均超过其他模型。
表4中的结果显示，本文方法输出与标签相当接近。ARIM-v2模拟了多个干扰存在的复杂场景，在该场景中，诸如归零法之类的传统方法似乎无法抑制多个干扰源造成的影响。就目标相位MAE而言，本文方法是归零法的近六分之一，本文模型对目标幅度MAE的估计比归零法要好近16倍。另外一个显著的不同之处在于平均信噪比的提高，本文的网络比归零法要好4.42 dB。
表4 本文模型与归零法、DPRNN模型在ARIM-v2测试集上的结果(符号↑表示值越大越好，符号↓表示值越小越好)
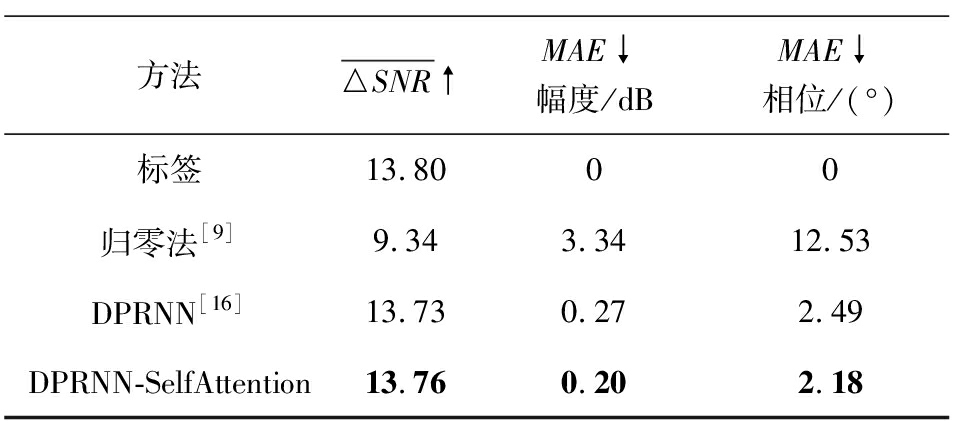
方法△SNRMAE幅度/dBMAE相位/(°)标签13.8000归零法[9]9.343.3412.53DPRNN[16]13.730.272.49DPRNN-SelfAttention13.760.202.18
图4(a)为无干扰的标签信号(蓝色)，图4(b)为有干扰的输入信号(绿色)，图4(c)为使用本文方法进行干扰抑制后的输出信号(红色)。图4(d)、(e)、(f)是它们分别经过快速傅里叶变换(Fast Fourier Transform, FFT)后的距离幅度图。图4(c)中可以看出输入信号经过本文方法抑制干扰后，干扰都被成功分离出去，恢复成与标签信号相似的信号，其距离幅度图如图4(f)所示，与标签信号的距离幅度图即图4(d)非常相似，预测的目标幅度和标签幅度值之间的差值很小。
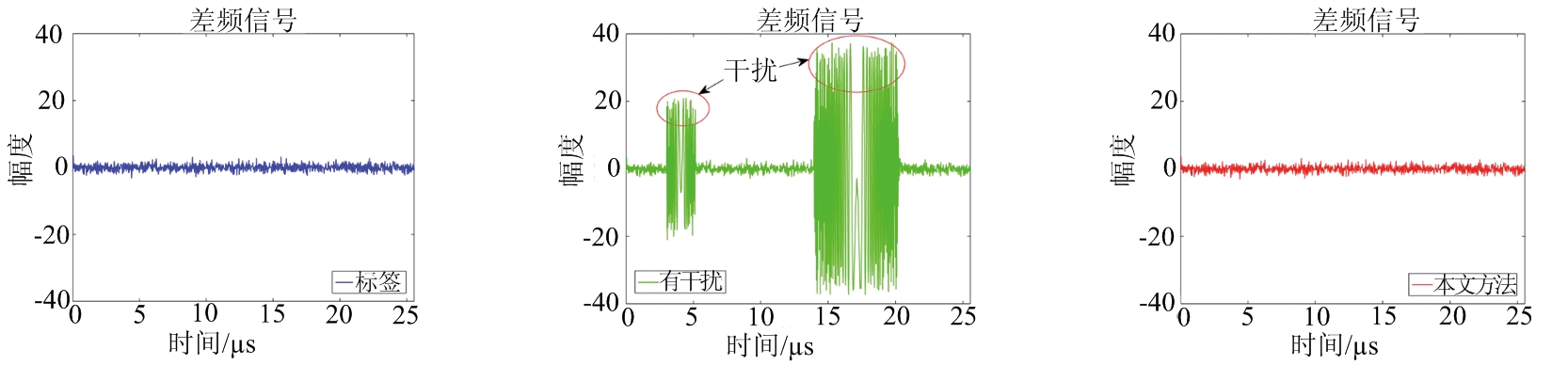
(a) 标签信号(无干扰) (b) 输入信号(有干扰) (c) 输出信号(抑制干扰后)
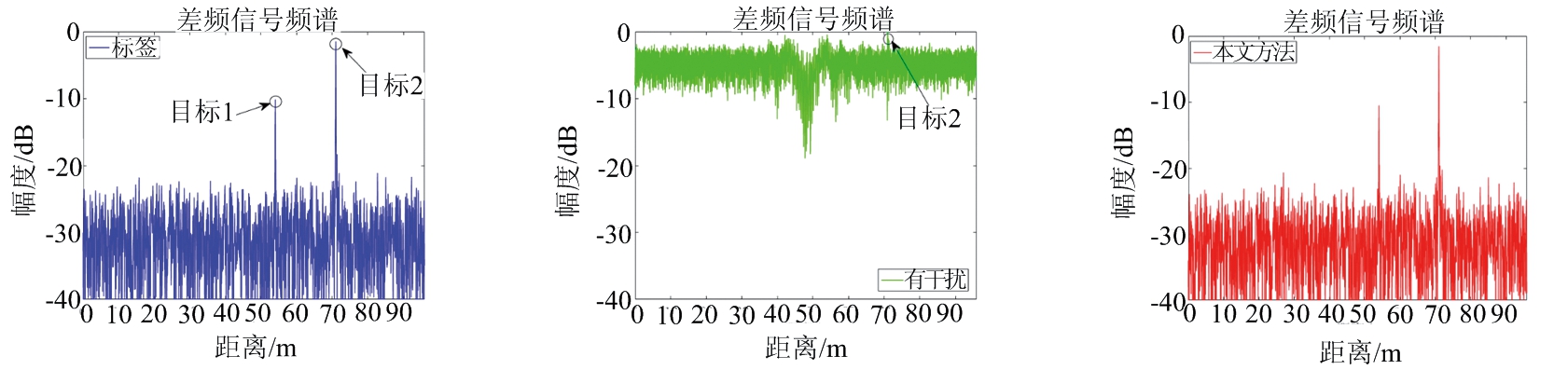
(d) 标签经过FFT后的距离幅度图 (e) 输入经过FFT后的距离幅度图 (f) 输出经过FFT后的距离幅度图
图4 干扰抑制前后的差频信号及其距离幅度图
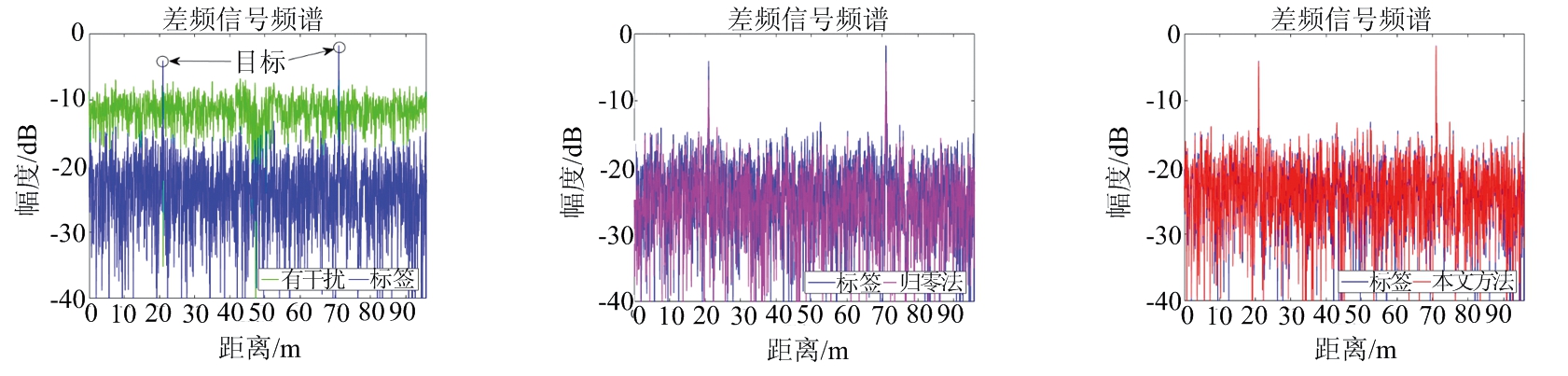
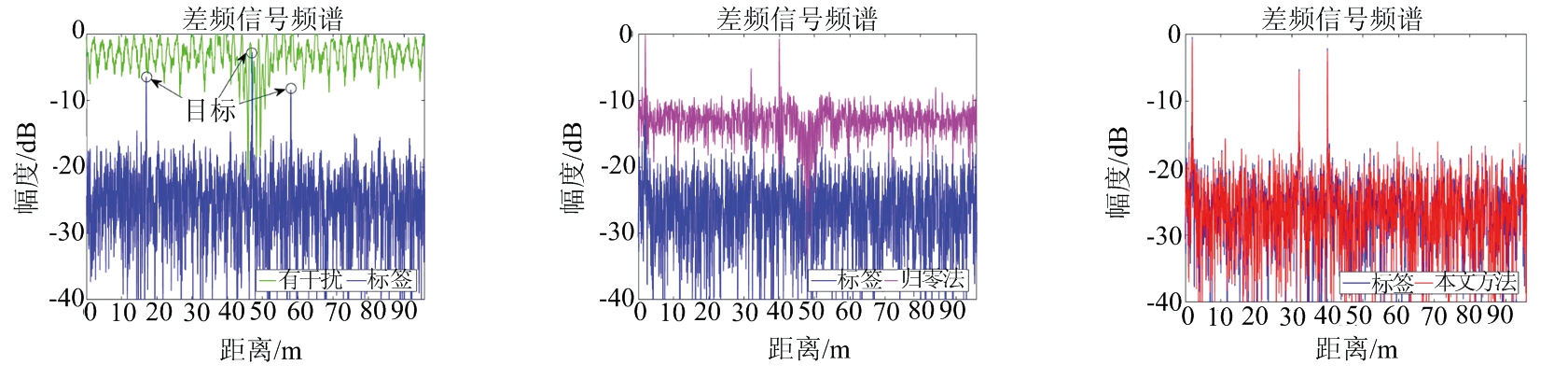
图5中将本文方法与归零法在只有一个干扰时的干扰抑制结果进行了对比，其中图5(a)、(d)、(g)是有干扰的输入信号(绿色)、标签信号(蓝色)；图5(b)、(e)、(h)是它们分别经过归零法(粉红色)抑制干扰后的输出结果；图5(c)、(f)、(i) 是它们分别使用本文方法(红色)进行干扰抑制后的结果。除了相对干扰斜率β不同，其他参数条件都相同。参数β量化了相对于标签信号的干扰时间长度，更准确地说，β越接近1， 干扰持续时间越长，β=1时表示相干干扰。在图5中，可以观察到本文方法成功产生了与标签相似的预测信号，而归零法随β增加效果逐渐变差。
图6中将本文方法与归零法在有多个干扰时的干扰抑制结果进行了对比，其中参数Nint代表干扰数目。在图6中观察到归零法随着干扰数目增加效果逐渐变差直至失效；而本文方法成功完成存在多个干扰时的干扰抑制任务。从图5、图6中可看出当干扰持续时间较短时，本文方法表现出与基线方法(归零法)相似的性能，但在有多个干扰源或干扰持续时间长的困难情况时，本文方法明显优于归零法。
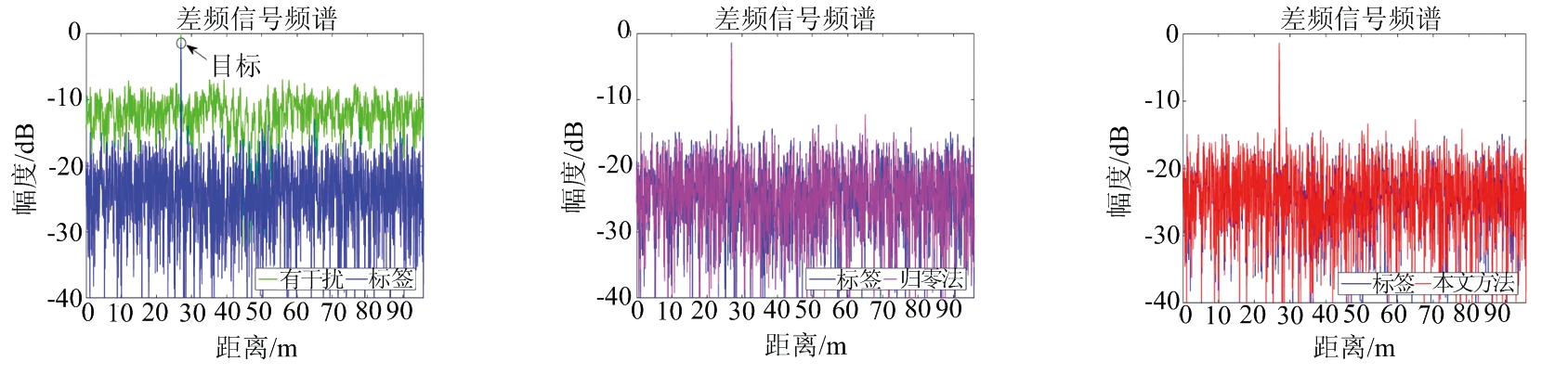
(a) SNR=20 dB,SIR=10 dB,β=0.5 (b) 归零法，参数设置与(a)相同 (c) 本文方法，参数设置与(a)相同
(d) SNR=20 dB,SIR=10 dB,β=0.7 (e) 归零法，参数设置与(d)相同 (f) 本文方法，参数设置与(d)相同
(g) SNR=20 dB,SIR=10 dB,β=0.9 (h) 归零法，参数设置与(g)相同 (i) 本文方法，参数设置与(g)相同
图5 归零法与本文方法的干扰抑制结果对比(一个干扰)
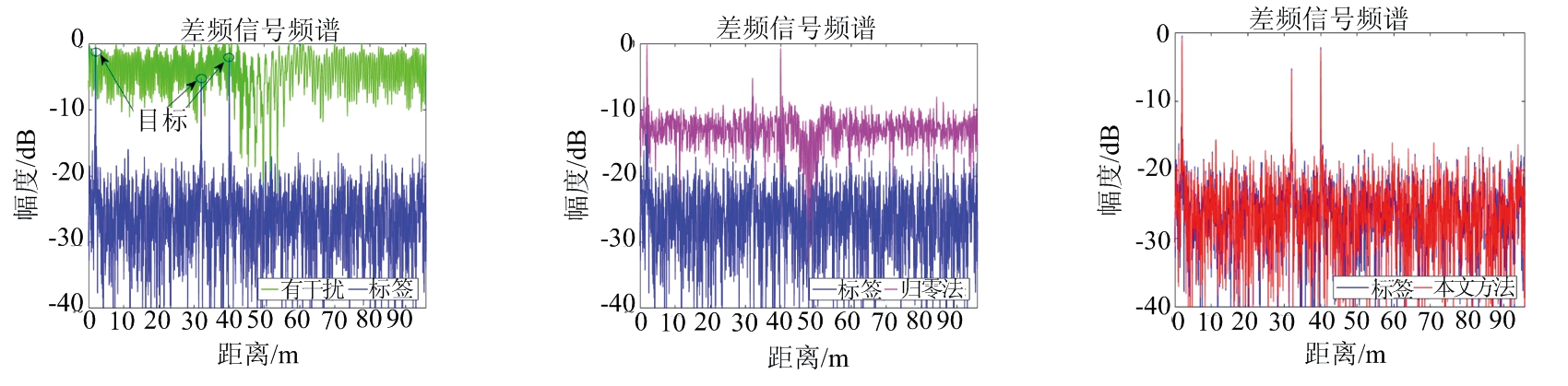
(a) 干扰数Nint=2 (b) 归零法，参数设置与(a)相同 (c) 本文方法，参数设置与(a)相同
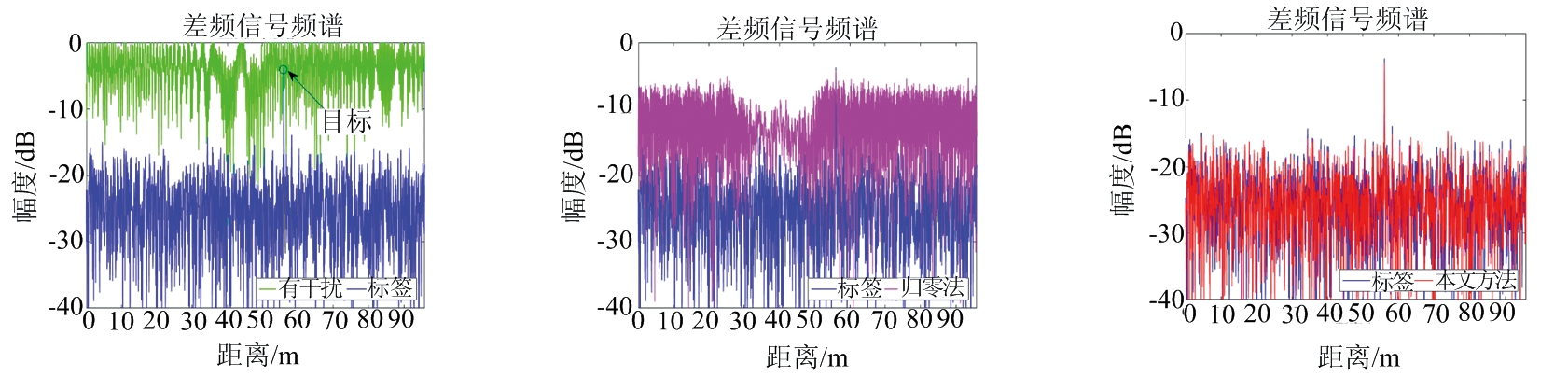
(d) 干扰数Nint=3 (e) 归零法，参数设置与(d)相同 (f) 本文方法，参数设置与(d)相同
图6 归零法与本文方法的干扰抑制结果对比(多个干扰)
为了更好地描述本文方法随着SNR和干扰数目变化导致的性能变化，在图7中分别说明了在考虑1个干扰(图7(a)、(b)、(c))、2个干扰(图7(d)、(e)、(f))和3个干扰(图7(g)、(h)、(i))的情况下，本文方法在3个性能指标
幅度MAE和相位MAE)上与归零法、DPRNN的对比结果。可以观察到，本文方法和归零法性能之间的差异随着干扰数目增加而增加，而且当信噪比(SNR)小于20 dB时，本文方法在幅度MAE和相位MAE上与归零法的差异更加明显。在图7中还可以观察到本文的DPRNN-SelfAttention模型与DPRNN模型相比表现出更好的性能。
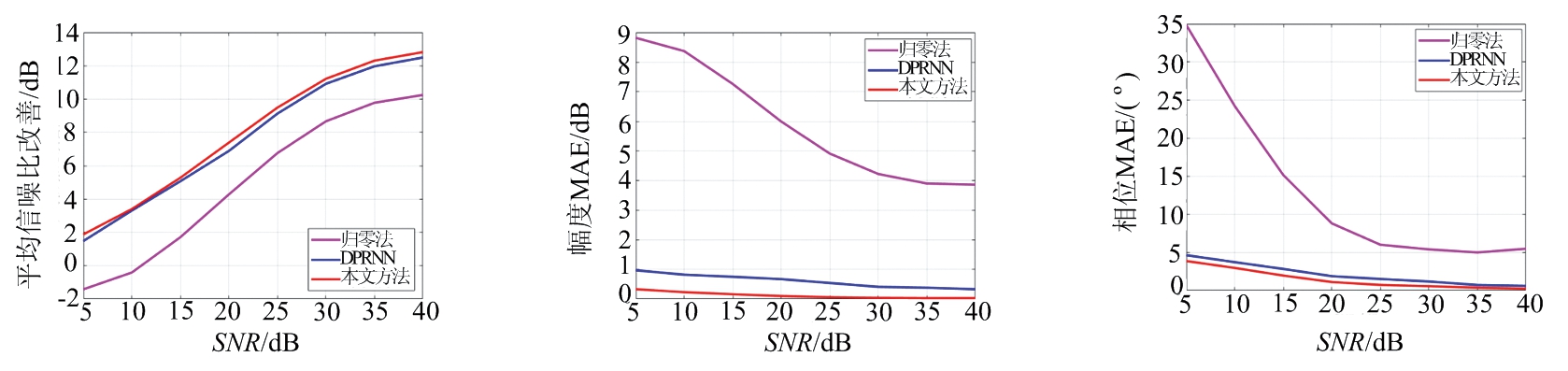
(a) 干扰数Nint=1 (b) 干扰数Nint=1 (c) 干扰数Nint=1
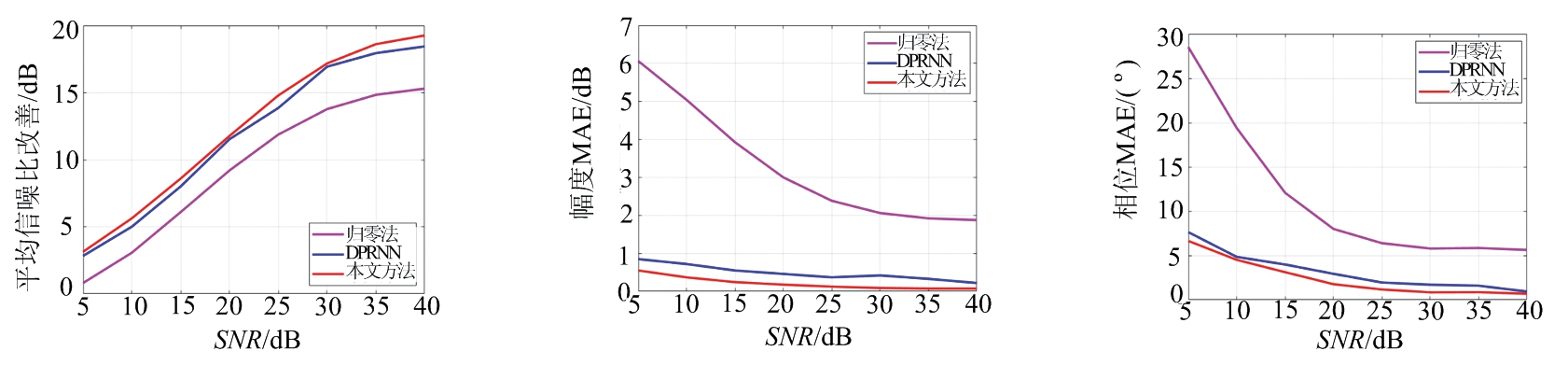
(d) 干扰数Nint=2 (e) 干扰数Nint=2 (f) 干扰数Nint=2
(g) 干扰数Nint=3 (h) 干扰数Nint=3 (i) 干扰数Nint=3
图7 归零法、DPRNN与本文方法的干扰抑制结果对比
4 结束语
本文将自注意双路径循环神经网络(DPRNN-SelfAttention)用于汽车雷达干扰抑制，仿真实验表明了该方法的有效性。引入的损失函数，即Log-Cosh损失和多尺度STFT损失的线性组合，能让模型更有效地学习FMCW雷达差频信号的时频分布信息从而提升性能。本文在一系列综合实验中将DPRNN-SelfAttention模型与基线方法(归零法)[9]、DPRNN[16]进行了对比，结果表明DPRNN-SelfAttention效果更为优越。目前由于实验室条件限制并未开展实际的车辆实验验证，未来工作将检验本文模型在真实汽车雷达场景中的泛化能力。
[1] KRONAUGE M, ROHLING H. New Chirp Sequence Radar Waveform[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50(4):2870-2877.
[2] UYSAL F, SANKA S. Mitigation of Automotive Radar Interference[C]∥ Proceedings of 2018 IEEE Radar Conference (RadarConf18), Oklahoma City:IEEE,2018:405-410.
[3] BECHTER J, WALDSCHMIDT C. Automotive Radar Interference Mitigation by Reconstruction and Cancellation of Interference Component[C]∥2015 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Heidelberg, Germany:IEEE, 2015:1-4.
[4] LIU Z Y, LU W, WU J Y, et al. A PELT-KCN Algorithm for FMCW Radar Interference Suppression Based on Signal Reconstruction[J]. IEEE Access, 2020, 8:45108-45118.
[5] KIM G, MUN J, LEE J. A Peer-to-Peer Interference Analysis for Automotive Chirp Sequence Radars[J]. IEEE Trans on Vehicular Technology, 2018, 67(9):8110-8117.
[6] BECHTER J, SIPPEL C, WALDSCHMIDT C. Bats-Inspired Frequency Hopping for Mitigation of Interfe-rence Between Automotive Radars[C]∥2016 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), San Diego, CA, USA:IEEE,2016:1-4.
[7] BECHTER J, RAMEEZ M, WALDSCHMIDT C. Analytical and Experimental Investigations on Mitigation of Interference in a DBF MIMO Radar[J]. IEEE Trans on Microwave Theory and Techniques, 2017, 65(5):1727-1734.
[8] ALLAND S, STARK W, ALI M, et al. Interference in Automotive Radar Systems: Characteristics,Mitigation Techniques, and Current and Future Research[J]. IEEE Signal Processing Magazine, 2019, 36(5):45-59.
[9] LAGHEZZA F, JANSEN F, OVERDEVEST J. Enhanced Interference Detection Method in Automotive FMCW Radar Systems[C]∥International Radar Symposium, Ulm, Germany:IEEE, 2019:1-7.
[10] ROCK J, TOTH M, MESSNER E, et al. Complex Signal Denoising and Interference Mitigation for Automotive Radar Using Convolutional Neural Networks[C]∥2019 22nd International Conference on Information Fusion(FUSION), Ottawa, Canada:IEEE, 2019:1-8.
[11] MUN J, KIM H, LEE J. A Deep Learning Approach for Automotive Radar Interference Mitigation[C]∥2018 IEEE 88th Vehicular Technology Conference, Chicago, IL:IEEE,2018:1-5.
[12] MUN J, HA S, LEE J. Automotive Radar Signal Interference Mitigation Using RNN with Self Attention[C]∥International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, SPAIN:IEEE,2020:3802-3806.
[13] RISTEA N C, ANGHEL A, IONESCU R T. Fully Convolutional Neural Networks for Automotive Radar Interference Mitigation[C]∥2020 IEEE 92nd Vehicular Technology Conference(VTC2020-Fall),Victoria, BC, Canada:IEEE, 2020:1-5.
[14] RISTEA N C, ANGHEL A, IONESCU R T. Estimating the Magnitude and Phase of Automotive Radar Signals Under Multiple Interference Sources with Fully Convolutional Networks[J].IEEE Access, 2021, 9:153491-153507.
[15] LUO Y, MESGARANI N.Conv-TasNet: Surpassing Ideal Time-Frequency Magnitude Masking for Speech Separation[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing (TASLP), 2019,27(8):1256-1266.
[16] LUO Y, CHEN Z, YOSHIOKA T. Dual-Path RNN: Efficient Long Sequence Modeling for Time-Domain Single-Channel Speech Separation[C]∥ International Conference on Acoustics, Speech and Signal Processing(ICASSP),Barcelona,Spain:IEEE,2020:46-50.
[17] YAMAMOTO R, SONG E, KIM J M. Parallel Wave-gan: A Fast Waveform Generation Model Based on Ge-nerative Adversarial Networks with Multi-Resolution Spectrogram[C]∥ International Conference on Acoustics, Speech and Signal Processing (ICASSP),Barcelona, Spain:IEEE, 2020:6199-6203.
