0 引 言
随着无人驾驶技术的发展,智能传感器成为自动驾驶中关键的一部分,如:相机、激光雷达、毫米波雷达等[1]。与其他传感器相比,毫米波雷达具有全天时、全天候的工作特性,具有更强的环境适应性。因此,毫米波雷达在汽车领域得到了广泛推广。但是如果两个或三个雷达共用同一个频带,雷达相互间就会发生干扰,而且随着越来越多的车辆装配毫米波雷达,每辆车上部署六个甚至更多的毫米波雷达。因此毫米波雷达间相互干扰成为了该行业必须解决的重大工程问题,并引发了许多学者的关注[2-3]。
2010年,欧洲启动的MOSARIM(More Safety for All by Radar Interference Mitigation)项目,从六个领域来抑制干扰:极化、时域、频域、空域、编码技术和策略方法[4]。文献[5]提出了一种基于Chirp序列调制干扰抑制方法,通过估计干扰信号的参数,来移除干扰并进行信号重构。文献[6]利用形态学分量分析方法将接收信号分解为干扰信号和目标中频信号,从而去除干扰信号达到干扰抑制的效果。文献[7]通过峰值检测来确定干扰发生的区域,然后利用卡尔曼滤波来重构干扰区域内的信号。文献[8]利用自适应噪声消除器来消除干扰。上述文献虽然在干扰抑制方面取得了很好的效果,但研究内容都集中于如何抑制干扰,而不是对干扰信号的识别和分类。目前已经有学者提出在进行干扰抑制之前,首先要对干扰信号进行分类[9],并且在信号干扰分类方面已经取得了一些成果[9-13]。文献[10]对干扰信号分别进行了快慢维度的傅里叶变换得到距离多普勒(Range-Doppler,RD)图,并用支持向量机(Support Vector Machines,SVM)对RD图进行分类,由于没有对RD图进行特征提取,因此可能需要大量的计算时间。在文献[11]中,提出了一种基于信号特征空间和SVM的干扰分类方法。文献[9]采用原始信号的均值、方差、偏度和峰度作为特征输入,利用SVM进行干扰分类。文献[9-11]都是采用SVM来进行干扰分类,虽然都能够实现分类,但是由于干扰信号类型有多种,而经典的SVM算法为二分类算法,要做多分类问题时,需要多个二分类器组合在一起来实现,算法复杂度较高。文献[12]使用功率谱密度和循环谱作为特征输入,使用深度神经网络来进行分类,但是功率谱密度和循环谱特征信息相比于RD图信息较少。文献[13]使用卷积神经网络对干扰信号生成的RD图进行干扰分类,但是在训练和验证过程中在反向传播的时候梯度可能消失,神经网络训练效果差,且收敛速度慢。
针对上述的问题,本文采用ResNet残差神经网络对干扰信号进行分类,不仅可以提高准确率,而且可以使网络尽快收敛,加快训练的速度。本文实验步骤:首先仿真出不同类型干扰数据,然后对干扰数据分别在快慢维度进行傅里叶变换得到RD图,最后采用残差神经网络对干扰信号进行分类。
1 信号模型
在这一小节中,对调频连续波(Frequency Modulated Continuous Wave,FMCW)基本原理、不同干扰信号数学模型进行详细描述。1.1节主要是对调频连续波的测距测速原理简要描述。1.2节主要是对不同干扰信号数学模型进行描述。
1.1 FMCW基本原理
图1为FMCW雷达基本结构,时序器和本地振荡器产生线性调频信号,调相器进行相位调制,功率放大器增强信号功率,最后由发射天线向外界传播。当信号在外界传输过程中遇到目标后会被反射,反射信号会被接收天线接收,通过低噪声放大器,与发射信号进行混频得到中频信号。中频信号包含目标的距离和速度信息。中频信号通过低通滤波器,经过模数转换后数据就可以用于提取目标信息。
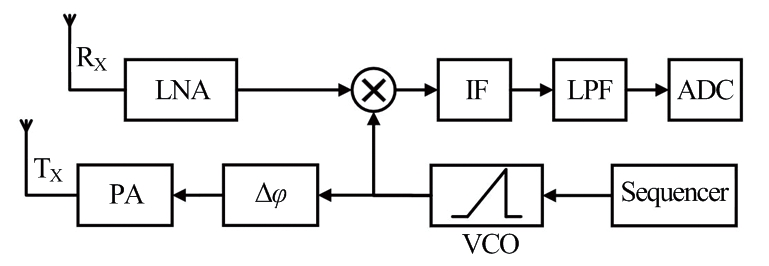
图1 FMCW雷达基本结构
线性调频信号又称为Chirp,其频率随着时间呈线性变化。则Chirp的瞬时频率为
f=fc+St
(1)
式中,fc表示信号载波频率,S=B/T表示信号扫频斜率,B表示信号带宽,T表示信号持续时间。
单个Chirp发射信号表达式为
(2)
式中,AT表示发射信号功率。
当发射信号遇到目标后,会被反射,形成回波信号,回波信号表达式为
(3)
式中,AR表示接收信号功率,td表示回波延迟,fd表示多普勒频移。图2为Chirp发射信号和接收信号序列。
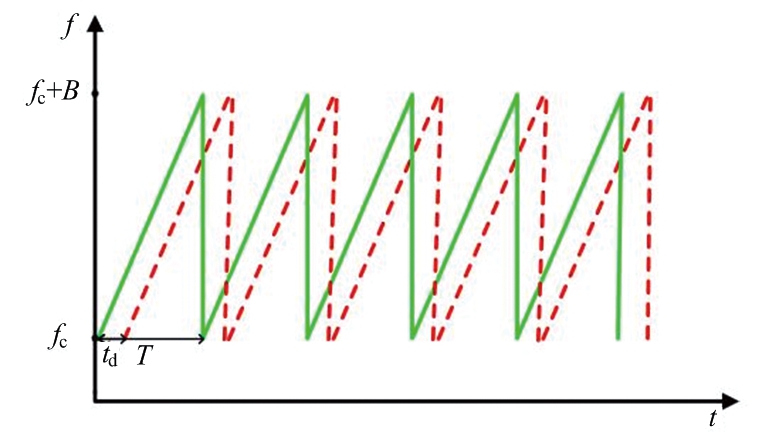
图2 Chirp发射信号和接收信号序列
接收到的目标的回波信号与发射信号进行混频得到中频信号,其表达式为
(4)
式中,AIF为中频信号功率。
当连续发送M个Chirp,在每个Chirp中采样N个点,就会形成一个M×N的二维矩阵,然后分别在两个维度上执行快速傅里叶变换以及CFAR检测算法,提取出目标所在的距离和速度单元,就可以实现对目标的距离和速度的测量。
1.2 不同类型的干扰信号
本小节主要对不同类型的干扰模型进行详细描述,干扰类型的信号有:长单频信号、慢调频信号、快调频信号、短单频信号、步进频率信号。
1.2.1 长单频信号
长单频信号:持续时间较长且频率恒定的信号,如图3所示。

图3 长单频信号
频率表达式为
(5)
时域信号表达式为
S=AIej2πft
(6)
式中,AI为干扰信号的功率。
1.2.2 慢调频信号
慢调频信号:频率随着时间缓慢变化的信号,如图4所示。
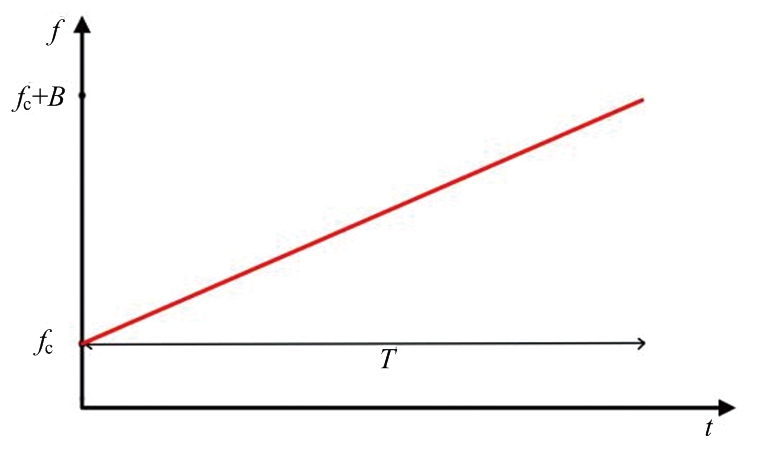
图4 慢调频信号
频率表达式为
f(t)=fc+St,0≤t<T
(7)
时域信号表达式和式(6)相同。
慢调频信号产生干扰是与回波信号发生交叉,则干扰持续时间为
(8)
式中,ST回波信号斜率,SI为干扰信号斜率,fL为低通滤波器带宽。
1.2.3 快调频信号
快调频信号:频率随时间快速变化的信号,如图5所示。
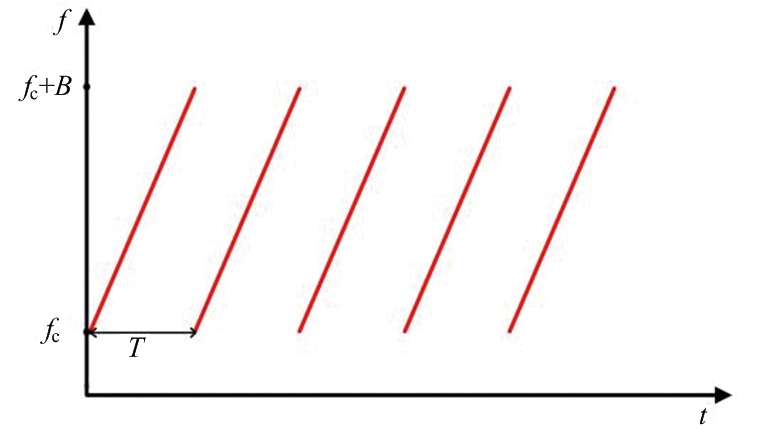
图5 快调频信号
其频率公式和时域公式与慢调频信号相同,只是频率随时间变化较快。
1.2.4 短单频信号
短单频信号:持续时间较短且频率恒定的信号,如图6所示。
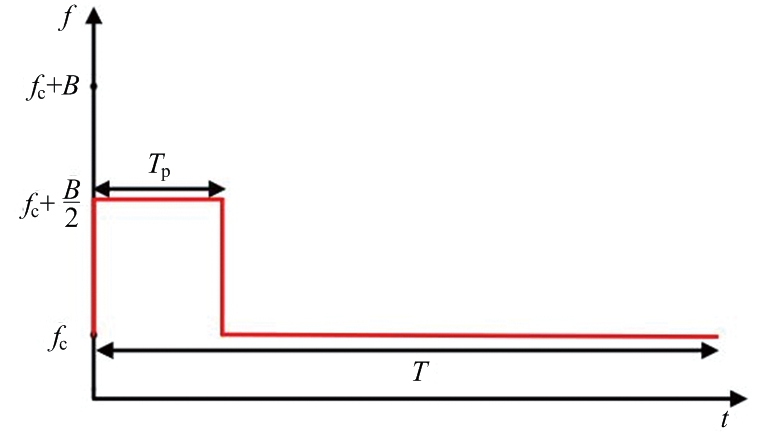
图6 短单频信号
频率表达式为
(9)
时域信号表达式和式(6)相同。
1.2.5 步进频率信号
步进频率信号就是频率每间隔Tp时间呈线性变化的信号,如图7所示。
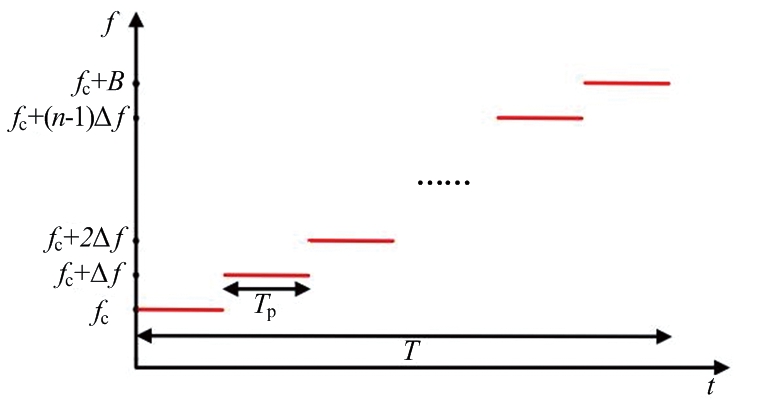
图7 步进频率信号
频率表达式为
i=floor(t/Tp),0≤t<T
(10)
式中,Tp表示一个脉冲要持续的时间,floor表示向下取整,i表示第几个脉冲。
f(t)=fc+iΔf
(11)
式中,Δf表示频率步进量。
时域信号表达式和式(6)相同。
2 干扰机理
在这一小节中,对雷达间互相干扰原理以及干扰功率与目标回波功率进行详细描述。2.1节主要是对雷达间互相干扰原理进行介绍。2.2节主要是对干扰功率与目标回波功率进行比较。
2.1 干扰原理
图8为道路上的干扰场景图。车辆1为受害车辆,装配有发射信号为快调频信号的雷达。车辆2为目标车辆,当车辆1发射信号时,车辆2会产生回波信号。车辆3为干扰车辆,装配有各种各样发射信号的雷达。
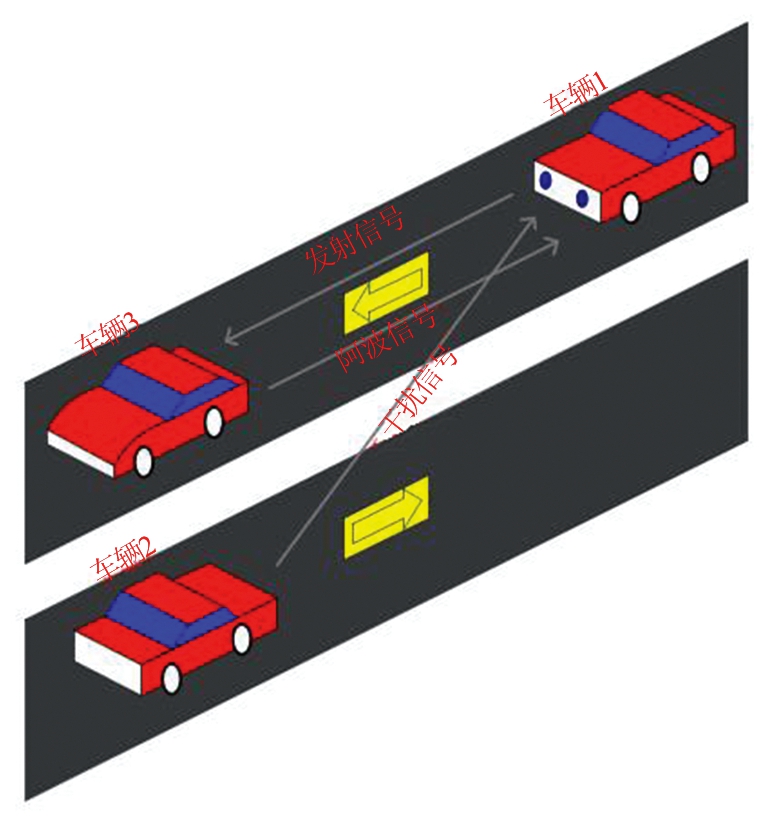
图8 道路干扰场景
当车辆3和车辆1的工作频率在相同频带内时,车辆3发射的干扰信号就会被车辆1装配的雷达所接收,则车辆1接收到的信号如下:
SR(t)=STarget(t)+SInterference(t)
(12)
式中,SR(t)为车辆1接收到总的信号,STarget(t)为车辆2的回波信号,SInterference(t)为车辆3发射的干扰信号。
2.2 功率比较
假定图8中的车辆1和车辆2的距离为R1,车辆1和车辆3的距离为R2,且车辆1和车辆3装配相同的雷达型号,则车辆1接收到车辆2的目标信号的功率为
(13)
式中,Pt为发射功率,Gt为发射天线增益,Gr为接收天线增益,λ为波长,σ为车辆2的散射截面积。
车辆1接收到车辆3的干扰信号的功率为
(14)
干扰信号功率与接收信号功率之比为
(15)
通过仿真实验,观察干扰信号功率与接收信号功率之比,假定R1为10 m,σ为5 m2,R2的范围为[5,30] m,间隔为5 m,仿真结果如图9所示,随着R2的增加,干扰信号功率与接收信号功率之比下降,但是比值仍然大于1,对目标检测仍然有很大的干扰,目标完全被淹没。
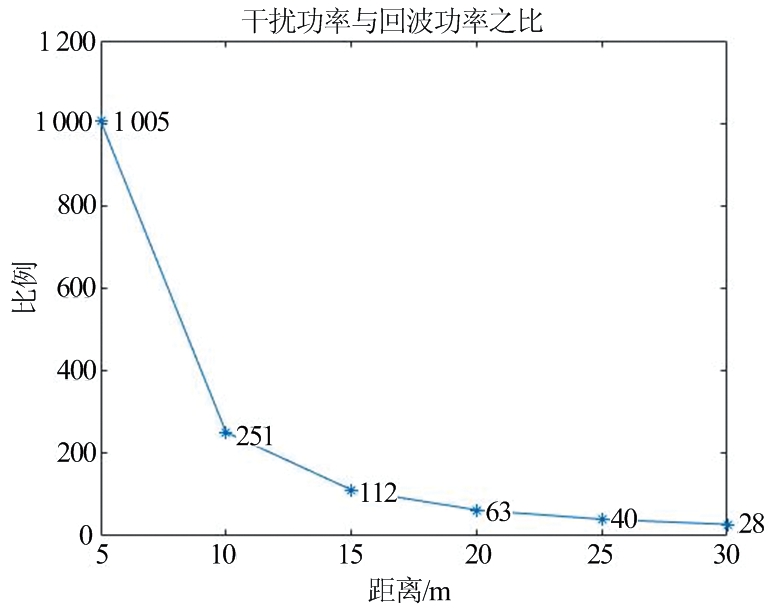
图9 干扰信号功率与接收信号功率之比
3 仿真实验
在这小节中,对仿真实验进行详细描述。3.1节中生成不同类型的干扰数据。3.2节中利用ResNet残差神经网络对干扰信号分类。3.3节中,在不同信号干扰噪声比的情况下来检测分类算法的性能。3.4节通过对比实验,验证ResNet残差神经网络对干扰分类的有效性。
3.1 干扰信号仿真
根据图8场景生成干扰数据。车辆1为受害车辆。车辆2为目标车辆,假定车辆2距车辆1的距离范围为5 m到50 m, 速度相对于车辆1为-30 km/h到30 km/h。车辆3为干扰车辆,假定车辆3距车辆1的距离范围为15 m到60 m,速度相对于车辆1为-40 km/h到40 km/h。
生成6种不同类型的数据,其中一种是没有干扰的数据,其余是1.2节提出的5种类型干扰数据。具体参数如下:表1为受害雷达所发射的参数,表2至表6为干扰雷达所发射的干扰信号。其中,表2为长单频干扰信号参数,表3为慢调频干扰信号参数,表4为快调频干扰信号参数,表5为短单频干扰信号参数,表6为发射步进频率干扰信号参数。在汽车雷达系统中,N表示接收信号的采样点数,M表示信号的数目,即Chirp数。
表1 受害雷达参数
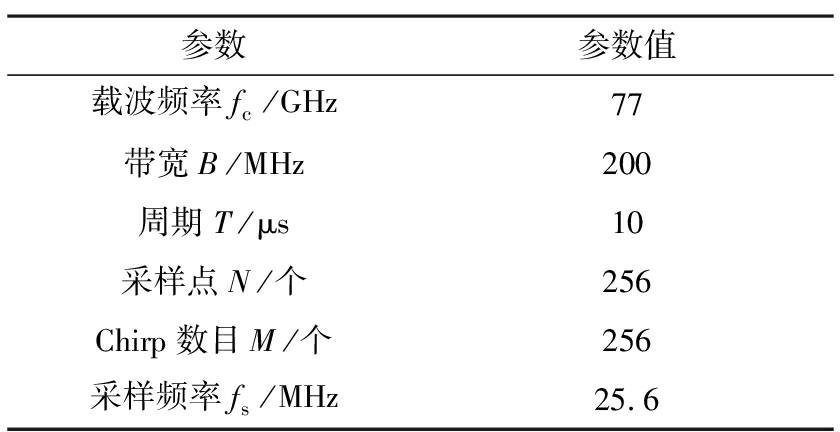
参数参数值载波频率fc/GHz77带宽B/MHz200周期T/μs10采样点N/个256Chirp数目M/个256采样频率fs/MHz25.6
表2 长单频信号参数
参数参数值载波频率fc/GHz77
表3 慢调频信号参数

参数参数值载波频率fc/GHz77带宽B/MHz600周期T/ms10
表4 快调频信号参数

参数参数值载波频率fc/GHz77带宽B/MHz600周期T/μs13
表5 短单频信号参数

参数参数值载波频率fc/GHz77持续周期TP/μs4周期T/μs12
表6 步进频率信号参数
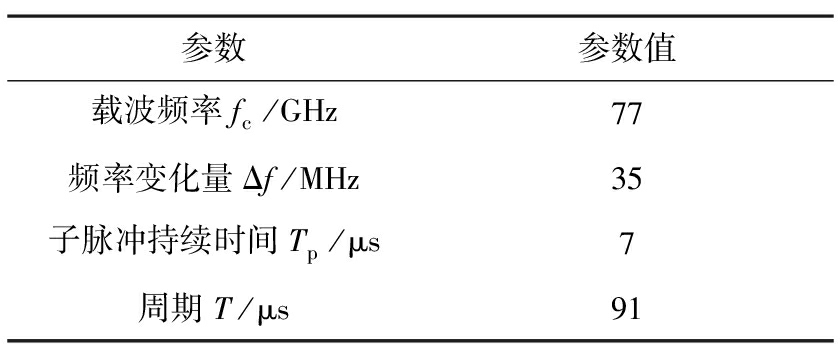
参数参数值载波频率fc/GHz77频率变化量Δf/MHz35子脉冲持续时间Tp/μs7周期T/μs91
根据上述不同干扰类型的参数对干扰数据进行仿真,其中SINR(信号干扰噪声比)的范围为-30 dB至30 dB,对生成的数据分别在快慢维度执行傅里叶变换,得到RD图,如图10所示。每种类型的数据为500张图片,总共为3 000张图片。 在图10(b)中,干扰信号为长单频信号,其频率在整个慢时间内都是恒定的,因此长单频信号仅与快时间频率有关,导致在RD图中沿距离维度为横线。图10(c)为慢调频干扰信号,其频率随着时间增加,因此,在沿多普勒轴具有偏移,导致在RD图中具有倾斜线条。
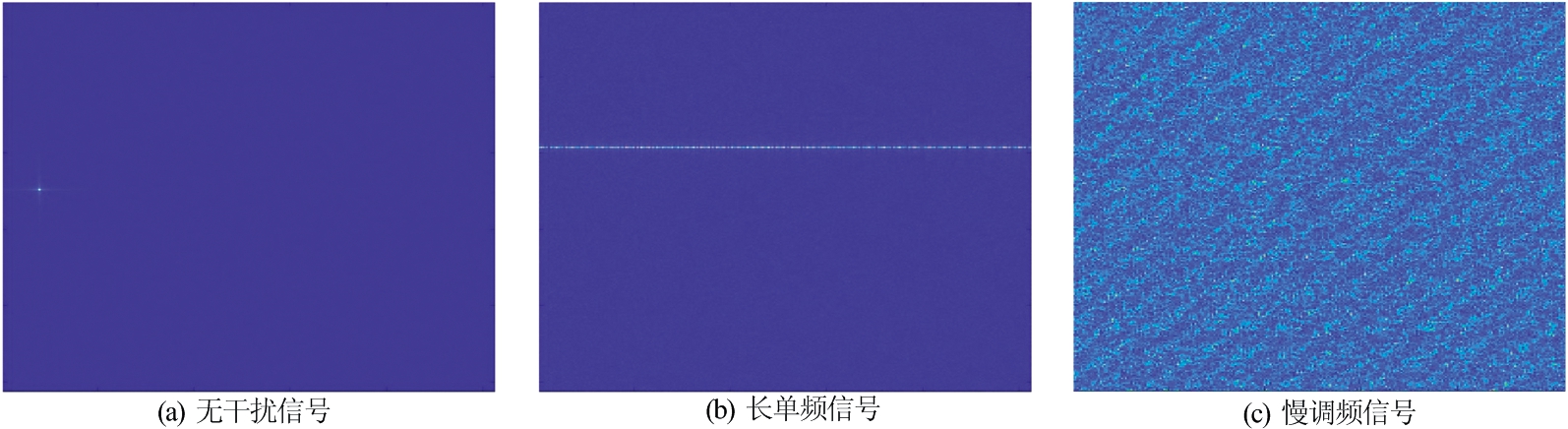
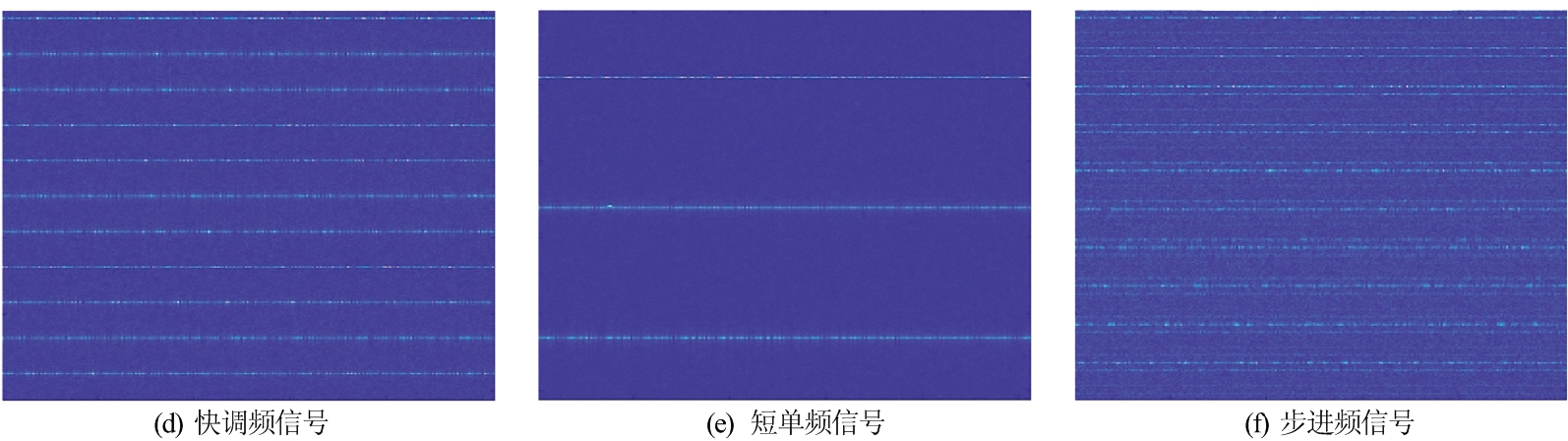
图10 6种干扰数据
3.2 分类实验
在分类过程中,采用的分类方法是何凯明提出的ResNet残差神经网络。ResNet block如图11所示。ResNet block在传统的CNN网络上增加了一个恒等映射,通过X的恒等映射来解决反向传播时梯度消失的问题,并且实验证明在训练集和验证集上loss值都非常小,可以保证得到很好的精度[14]。
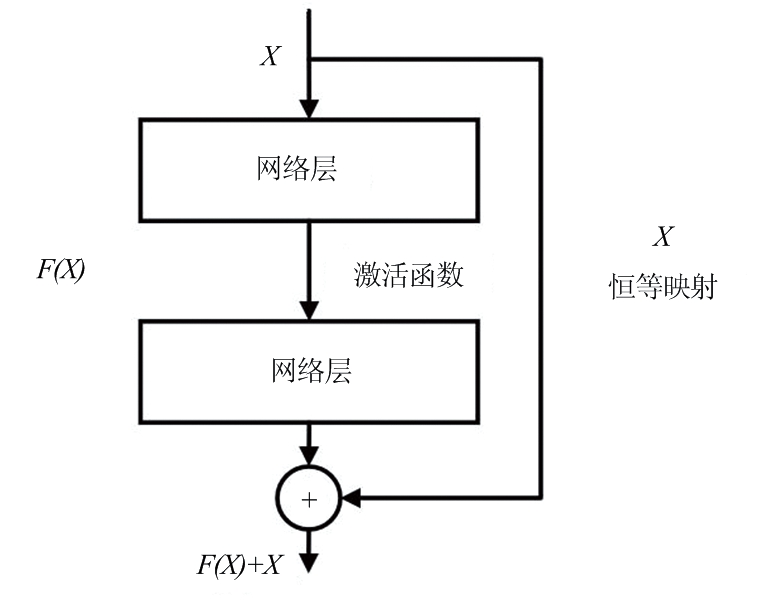
图11 残差网络块
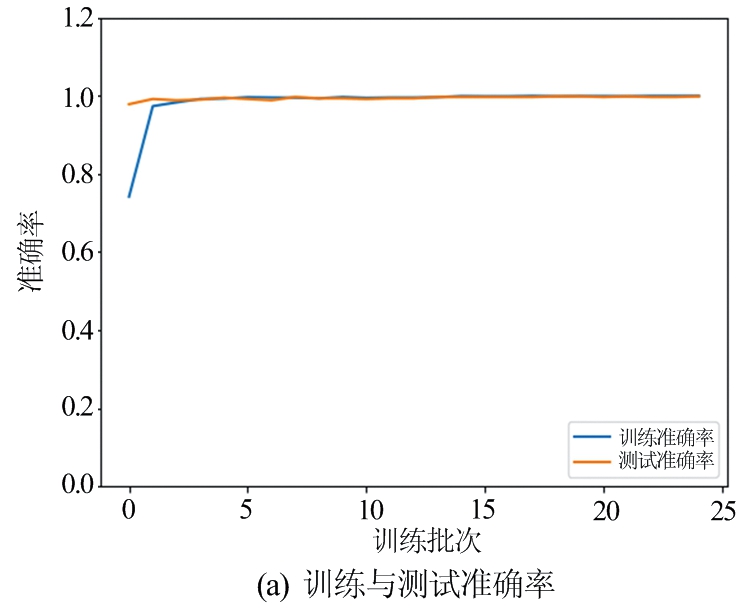
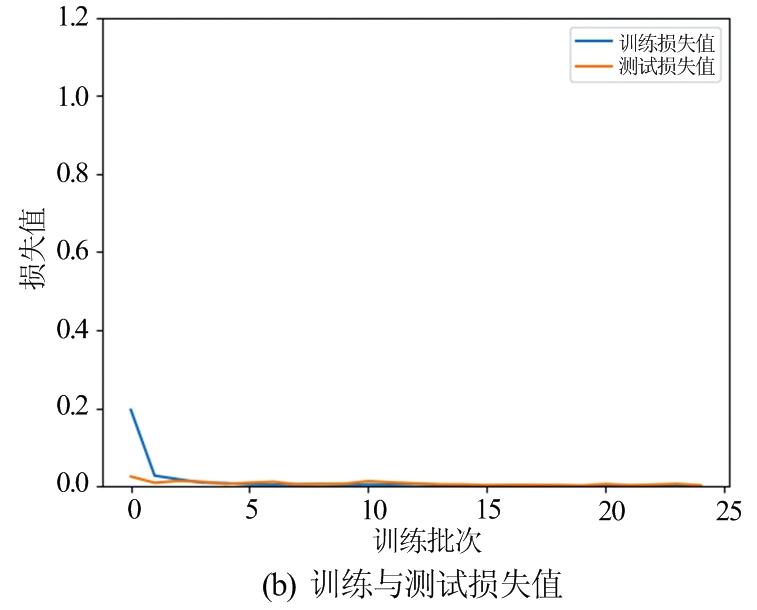
图12 ResNet网络训练的准确率和损失值
将生成的3 000张干扰数据作为ResNet残差网络的输入,其中80%作为训练集,20%作为验证集。损失函数采用交叉熵损失函数,学习率为0.01,优化函数为随机梯度下降。经过25批次迭代,训练准确率和损失值曲线如图12所示,从图中可以看到,训练准确率和验证准确率随着迭代次数增加,并且验证准确率甚至和训练准确率一样,与此同时,训练损失和验证损失随着迭代次数减小,从而验证了ResNet残差网络在干扰分类方面的有效性。
3.3 算法性能
为了进一步测试该分类算法的性能,在不同的SINR的情况下,检验该干扰信号分类算法的性能,分类的准确率与SINR的关系如图13所示。
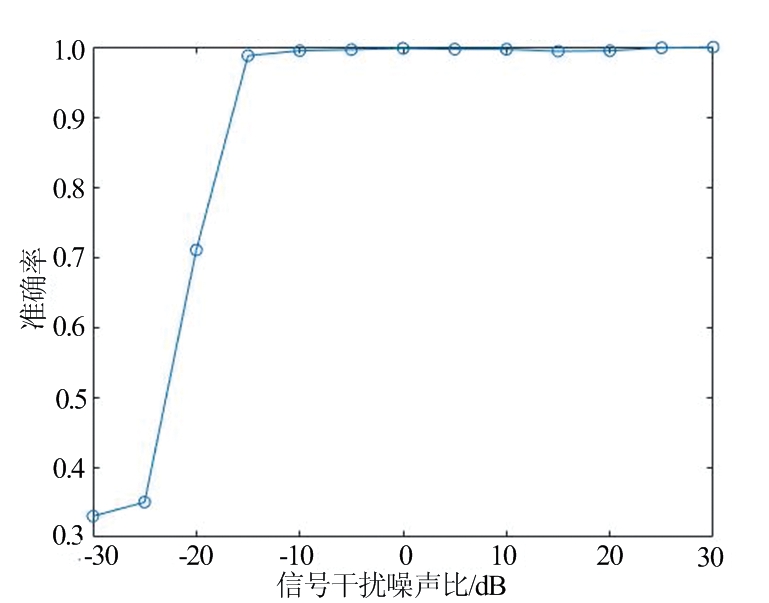
图13 准确率与信号干扰噪声比的关系
3.4 对比试验
为了验证ResNet残差网络在雷达干扰分类方面的有效性。在使用相同数据集的情况下,分别采用SVM和CNN作为对比实验。
3.4.1 SVM分类算法
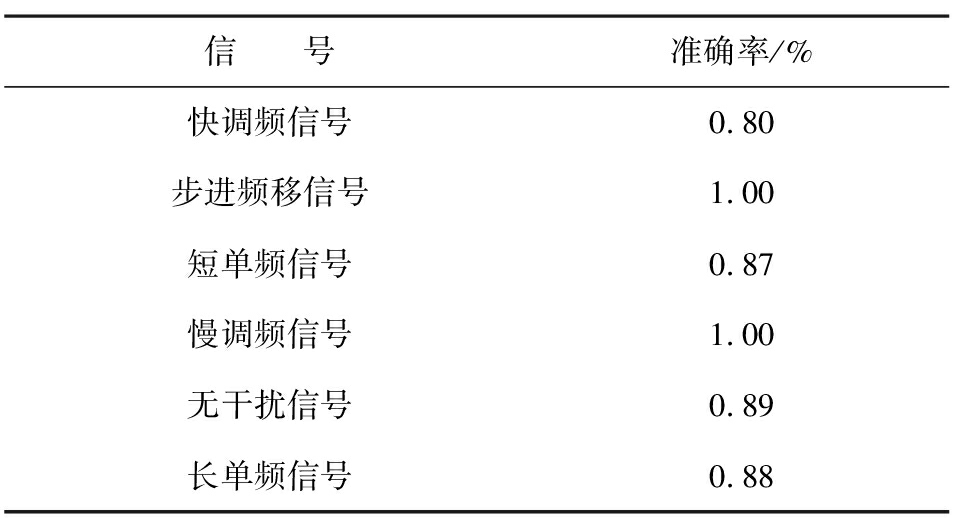
在使用SVM对数据分类之前,采用PCA特征提取技术,提取数据的主要特征,减少计算开销,实验结果如表7所示。从实验结果看出,步进频移信号和慢调频信号的识别准确率达到了100%,但是其他类的干扰信号准确率较低,导致总体识别率下降。
表7 PCA+SVM分类准确率
信 号准确率/%快调频信号0.80步进频移信号1.00短单频信号0.87慢调频信号1.00无干扰信号0.89长单频信号0.88
3.4.2 CNN分类算法
图14为 CNN网络训练的准确率和损失值,虽然在一定的程度上取得了不错的效果,但是在验证集的准确率仍然低于训练集的准确率。同时,损失值一直维持在0.5左右,而ResNet网络恰好解决了这个问题。
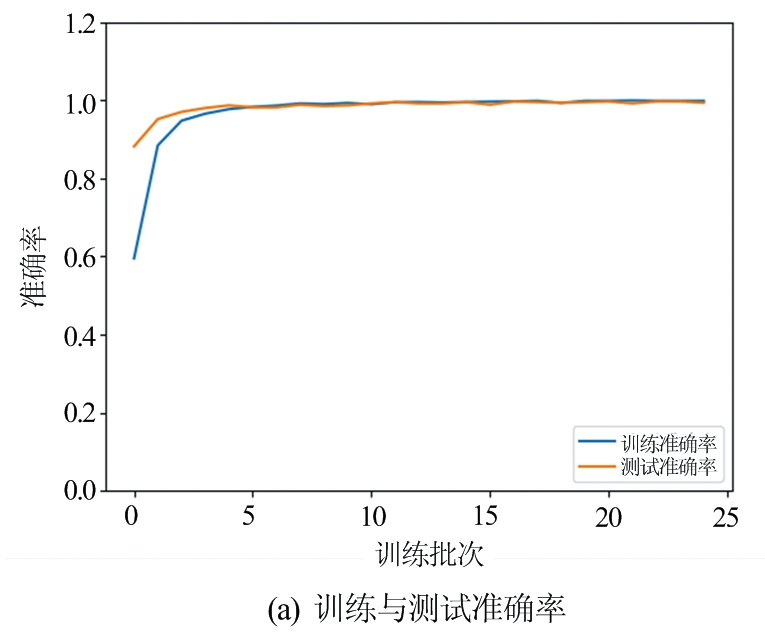
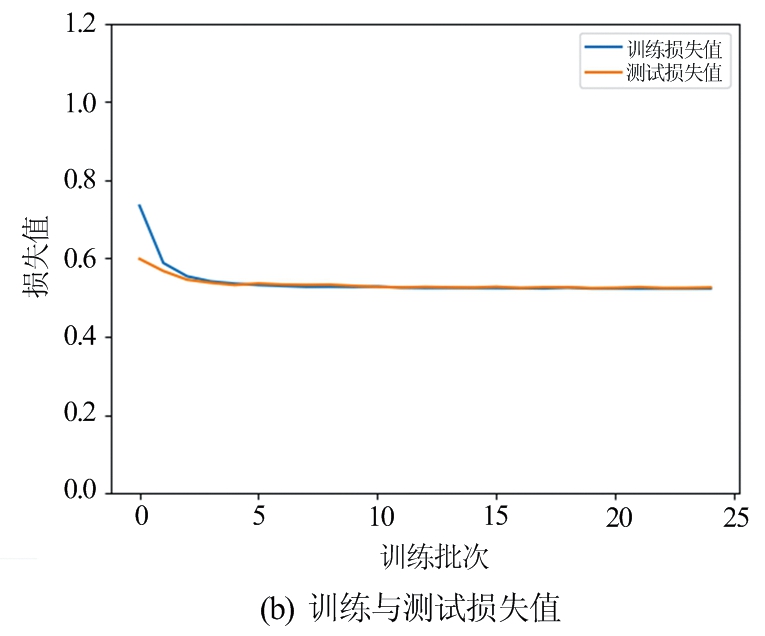
图14 CNN网络训练的准确率和损失值
通过对比实验可知,本文采用的ResNet网络对雷达干扰分类相比于SVM、CNN等已经采用的算法在准确率以及网络收敛速度上有很好的提升。
4 结束语
针对雷达间相互干扰信号分类的问题,提出了ResNet残差神经网络对雷达干扰信号进行分类。首先对雷达的不同干扰信号进行仿真,对其干扰信号分别在快慢维度做傅里叶变换,得到待分类的数据集,然后进行多种分类算法进行实验对比,分别采用了SVM、CNN分类算法作为对比,来验证本文采用的ResNet残差网络在雷达干扰分类方面有很好的效果。结果证明ResNet残差网络相比于其他分类算法准确率有很大提升,而且网络能够很好地收敛。
[1] RUDOLPH G,VOELZKE U. Three Sensor Types Drive Autonomous Vehicles[EB/OL]. Sensors Mag Nov 2017. https:∥www.sensorsmag.com/components/three-sensor-types-drive-autonomous-vehicles.
[2] ALLAND S, STARK W, ALI M, et al. Interference in Automotive Radar Systems: Characteristics, Mitigation Techniques, and Current and Future Research[J].IEEE Signal Processing Magazine,2019, 36(5):45-59.
[3] HEUEL S. Automotive Radar Interference Test[C]∥2017 18th International Radar Symposium (IRS), Prague, Czech Republic:IEEE, 2017:1-7.
[4] KUNERT M. The EU Project MOSARIM: A General Overview of Project Objectives and Conducted Work[C]∥ 2012 9th European Radar Conference, Nuremberg, Germany:VDE,2012:1-5.
[5] BECHTER J, WALDSCHMIDT C. Automotive Radar Interference Mitigation by Reconstruction and Cancellation of Interference Component[C]∥ 2015 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Heidelberg, Germany:IEEE, 2015:1-4.
[6] UYSAL F,SANKA S. Mitigation of Automotive Radar Interference[C]∥2018 IEEE Radar Conference, Oklahoma City, OK, USA:IEEE,2018:405-410.
[7] JUNG J,LIM S,KIM J, et al. Interference Suppression and Signal Restoration Using Kalman Filter in Automotive Radar Systems[C]∥2020 IEEE International Radar Conference,Washington,DC,USA:IEEE, 2020:726-731.
[8] JIN F, CAO S. Automotive Radar Interference Mitigation Using Adaptive Noise Canceller[J].IEEE Trans on Vehicular Technology, 2019, 68(4):3747-3754.
[9] KIM J, LEE S, KIM S. Modulation Type Classification of Interference Signals in Automotive Radar Systems[J]. IET Radar, Sonar & Navigation, 2019,13:944-952.
[10] ZHANG R, CAO S. Support Vector Machines for Classification of Automotive Radar Interference[C]∥2018 IEEE Radar Conference, Oklahoma City, OK, USA:IEEE,2018:366-371.
[11] WANG G S, REN Q H, SU Y Z. The Interference Classification and Recognition Based on SF-SVM Algorithm[C]∥2017 IEEE 9th International Conference on Communication Software and Networks (ICCSN), Guangzhou:IEEE,2017:835-841.
[12] YU J, ALHASSOUN M,BUEHRER R M. Interference Classification Using Deep Neural Networks[C]∥2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada :IEEE,2020:1-6.
[13] KIM J, LEE S, KIM Y H, et al. Classification of Interference Signal for Automotive Radar Systems with Convolutional Neural Network[J]. IEEE Access, 2020, 8:176717-176727.
[14] HE K, ZHANG X, REN S, et al. Deep Residual Learning for Image Recognition[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,Las Vegas,NV,USA:IEEE, 2016:770-778.

