0 引 言
机会阵雷达（Opportunistic Array Radar,OAR）是一种高度数字化和智能化的雷达系统，其“机会性”的资源管理模式能够有效完成“空-时-能”资源优化配置，使雷达“同时”实现一种或多种战术功能［1-3］。在现代电子战中，随着科学技术的发展，飞行器为躲避雷达的探测，其机动能力不断增强，及至低空突防技术的使用更是让目标难以被捕捉。因此，针对机动目标难以捕捉问题，如何快速预测机动目标运动状态，精确衡量机动目标跟踪性能成为亟待解决的技术难题。
传统研究方法中，对于强机动目标运动模型的建模主要分为多模型和单模型两类。多模型主要是将复杂的机动模型采用多个简单模型进行加权拟合。当采用交互多模型（Interacting Multiple Model,IMM）［4-5］来表示机动目标的运动状态时，其包含的简单模型仅有匀速运动、匀加速运动和协同转弯等。这不仅不能完全表示机动目标所有的运动形式，还将降低跟踪算法的实时性。对于单模型算法，主要有Singer 模型［6］，当前统计（Current Statistical,CS）模型［7］和Jerk 模型［8］。相比于其他两个模型，CS 模型能够更加全面地描述机动目标运动形式。文献［9］在CS模型基础上进行了改进，实现状态协方差、状态噪声协方差和机动频率的自适应调整，从而提高目标的滤波精度。
另一方面，在资源预分配时选择一个精确的目标跟踪性能衡量基准是实现雷达系统资源优化分配、提高目标跟踪性能的又一个重要原因。对于一般的匀速运动目标或机动性较弱的目标，标准的后验克拉美罗界（Posterior Cramér-Rao Lower Bound,PCRLB）能够为任何状态矢量无偏估计的均方误差（Mean Square Error,MSE）提供一个紧密的下界，从而实现雷达资源的预分配［10-11］。但是由于标准PCRLB 是基于从初始时间开始的状态矢量和测量矢量的联合概率密度所计算出来的平均值，因此标准PCRLB 是一个离线边界，不能准确衡量强机动目标的跟踪性能［12］。而预测的条件克拉美罗界（Predicted Conditional CRLB,PC-CRLB）是基于最新的测量信息推导所得，具有更高的时效性和准确性，能够提供一个更紧密的下界［13］。
基于以上分析，针对现有算法中机动目标的运动状态预测和跟踪性能衡量基准不准确的问题，本文提出了一种基于改进的CS（Modified CS,MCS）模型的组网机会阵雷达功率分配算法。且由于环境的复杂时变和目标信息的未知，在机会阵雷达体制下，将目标雷达散射截面（Radar Cross Section,RCS）用随机变量来进行表征［14］，建立基于机会约束规划（Chance-Constraint Programming,CCP）的功率分配模型，采用混合智能优化算法（Hybrid Intelligent Optimization Algorithm,HIOA）求解出功率优化分配结果。该算法不仅可以提高资源的利用效率，还可以平衡资源消耗和跟踪性能之间的关系，增强模型的稳健性。
1 系统模型
假定在xy 平面内，一个集中式组网机会阵雷达框架下包含M 个独立的机会阵雷达。每个雷达节点能且仅能生成一个雷达波束照射目标，且每个发射波束的最大发射功率为rPtotal（0≤r≤1），其中Ptotal为整个组网雷达系统的额定发射功率。第m个雷达的坐标为（xRm,yRm）。为了保证功率分配过程的顺利进行，这里作了一些合理假设：1）各雷达节点的发射信号载频频率各不相同，且该雷达接收机的滤波器可滤除目标反射的其他雷达的回波信号；2）该雷达系统的发射带宽、传输速率和计算能力能够支撑集中式雷达系统的正常运行。
1.1 信号模型
设在k 时刻，第m 个雷达向目标发射信号波形为
式中：Pm,k 表示发射功率；Sm,k（t）表示发射信号的归一化复包络；fm表示发射信号载波频率。
各雷达节点将接收到目标反射信号进行下变频之后的基带形式为
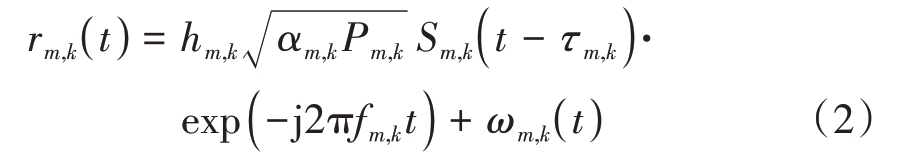
式中：hm,k表示目标RCS，是一个随机变量［14］；αm,k表示路径损耗导致的衰减系数，αm,k∝1/R4m,k［15］（表示第m 个雷达和目标之间的距离）；ωm,k 表示零均值、复高斯白噪声，其协方差为σ2ωδ（τ）。
1.2 运动模型
机动目标在xy 平面内离散状态方程的CS 模型为
式中：xk=
表示目标状态矢量，(xk,yk)、
和
分别表示目标位置、速度和加速度；Fk-1表示状态转移矩阵；Uk-1表示加速度输入矩阵；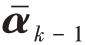
表示当前输入加速度的矩阵；wk-1表示零均值复高斯白噪声，其协方差为
其中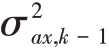
和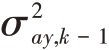
分别是目标加速度的方差，均服从瑞利分布；qcs,k-1由机动频率α 和采样间隔T0所决定［8］。为了能够采用标准滤波器跟踪机动目标，增补方程
与CS模型联立构成MCS模型：
式中
是平均Jerk矢量。那么方程（6）可简化为
其中F'k-1表达式为
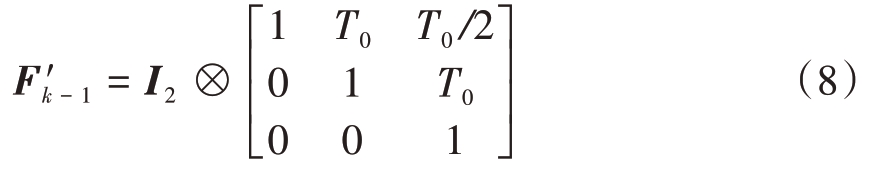
式中：⊗是克罗内克积运算符；I2 表示2 阶单位阵。U'k-1表达式为
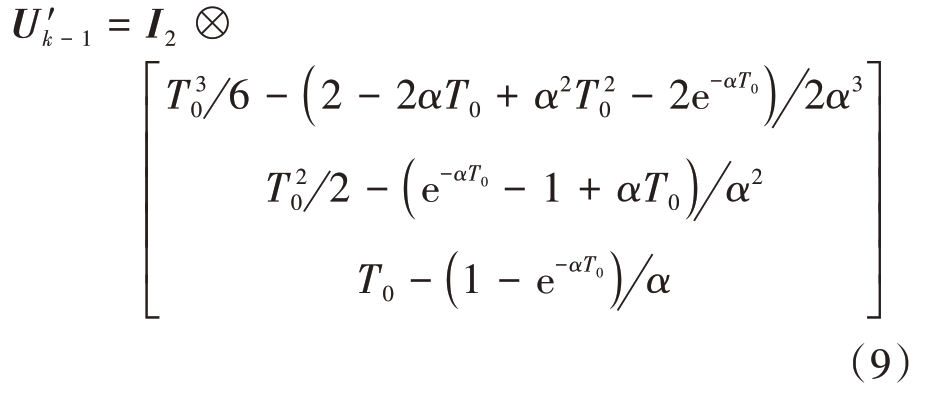
其中机动频率α受强机动检测函数控制［9］。
在MCS 模型中，过程噪声方差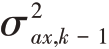
和
可通过输出的状态协方差矩阵Pk-1 中的对应元素进行更新，从而增强自适应跟踪能力。
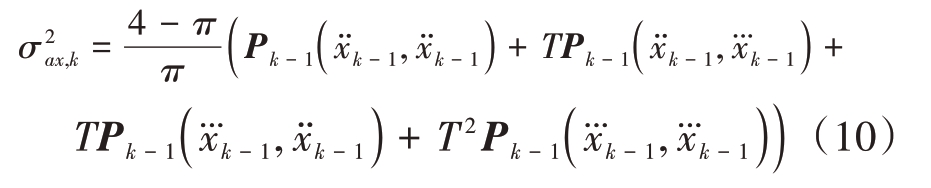
式中Pk-1（·，·）是对应位置上的元素，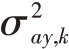
可通过类似的方法获得。
1.3 量测模型
可通过信息处理方法从雷达回波中提取目标距离、方位和多普勒频率等信息。在k 时刻，第m部雷达的量测方程为
其中非线性转移函数是
式中，Rm,k表示第m 部雷达与目标之间的距离，θm,k表示目标的方位角，fm,k表示目标和雷达之间的相对径向运动而产生的多普勒频移。这三个变量表达式为
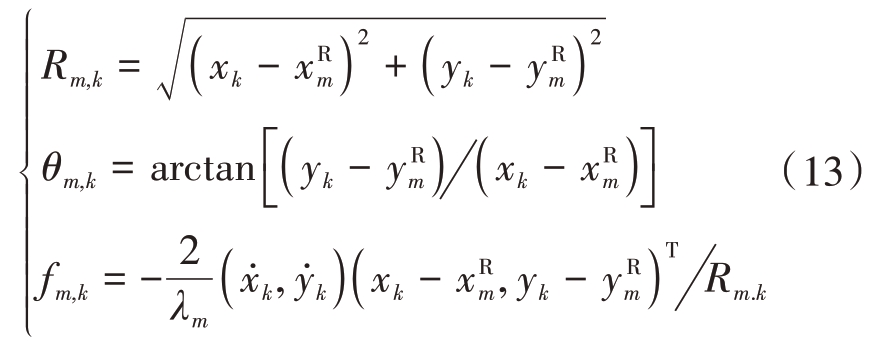
式中：λm表示载波波长；量测噪声vm,k是零均值高斯白噪声，其协方差为
式中：diag（•）表示对角矩阵运算符；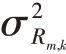
，
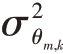和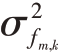
分别是在信噪比足够高情况下的距离、方位和多普勒频率的估计均方误差［15-16］，其表达式为
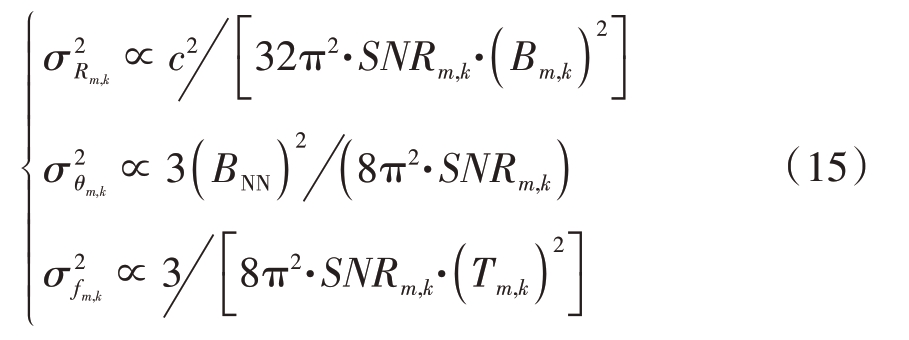
式中c 表示光速，BNN表示波束宽度，SNRm,k表示信噪比［17］。
2 集中式PC-CRLB
在贝叶斯框架下，PCRLB 为目标状态ξk的估计值的MSE提供了一个下界［18］
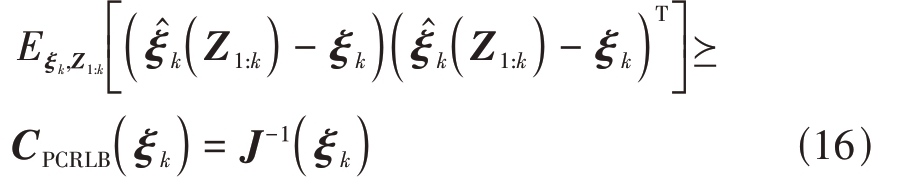
式中
表示ξk 的估计值，Eξk,Z1:k[]· 表示关于目标状态ξk和量测Zk从开始时刻至k 时刻的期望值，CPCRLB（•）表示PCRLB 矩阵，它是费舍尔信息矩阵（Fisher Information Matrix,FIM）的逆矩阵。完整的量测矢量Z1:k表达式为
此处采用集中式网络架构来融合各个雷达结点接收到的数据。
正如式（16）所示，在计算PCRLB 过程中量测值是作为随机矢量来进行考虑。然而，在正常情况下，当在k 时要对目标进行照射时，雷达系统已经获得了包括k-1 时刻在内的之前的所有量测数据。基于这些测量数据，可以为估计值的MSE 在线计算出一个更加精确的下界。在跟踪具有高动态属性的机动目标时，为了能够更精确地分配系统资源，我们采用PC-CRLB 衡量目标跟踪性能，其定义为
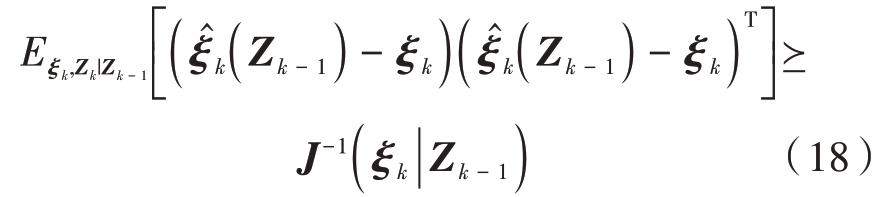
其中PC-FIM J-1（ξk|Zk-1）定义为
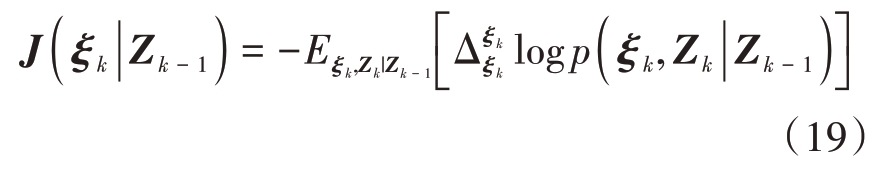
式中，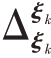
表示二阶偏导数，p（ξk,Zk|Zk-1）表示联合概率密度函数（Probability Density Function,PDF），PCCRLB是PC-FIM的逆矩阵。
和FIM 的递归计算方法类似，PC-FIM 也包含两个矩阵：
式中JP（ξk|Zk-1）和JD（ξk|Zk-1）分别是PC-FIM 的先验信息和数据信息。JP（ξk|Zk-1）表达式为
式中，p（ξk|Zk-1）表示预测的先验PDF。在许多情况下，很难求得JP（ξk|Zk-1）的解析解。在高斯分布情况下，可以通过粒子滤波器求得预测的协方差矩阵，近似算出先验信息［13］。所以先验信息矩阵也被称为预测的信息矩阵。
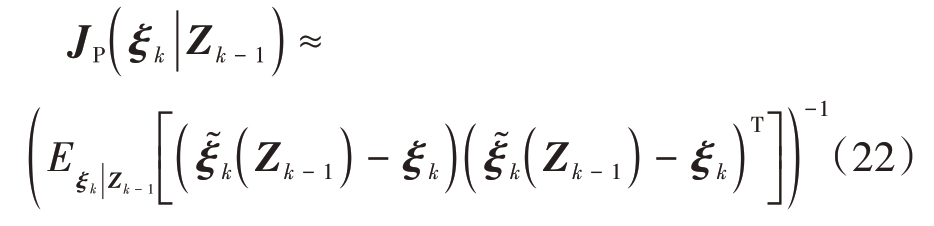
式中
根据量测模型给出数据信息矩阵JD（ξk|zm,k-1）的表达式为
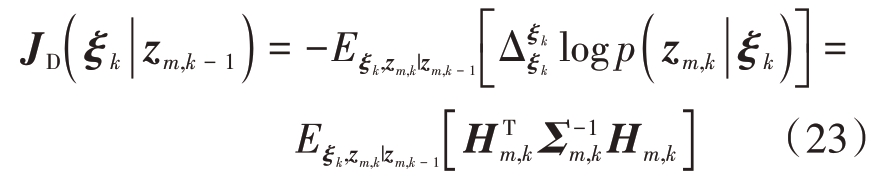
式中
由于不同雷达节点接收到的信号是相互独立的，完整的数据信息矩阵JD（ξk|Zk-1）表达式为
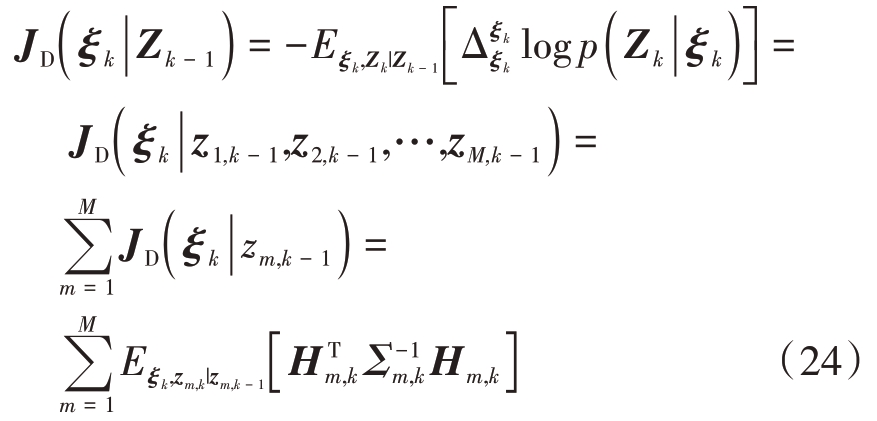
可以采用蒙特卡洛方法计算式（24），但是为了简化计算和降低计算时间，将JD（ξk|Zk-1）转化为［19］
式中ξk|k-1表示预测的目标信息。
将式（22）和式（25）代入式（20）中，最终的集中式PC-FIM J-1（ξk|Zk-1）表达式为
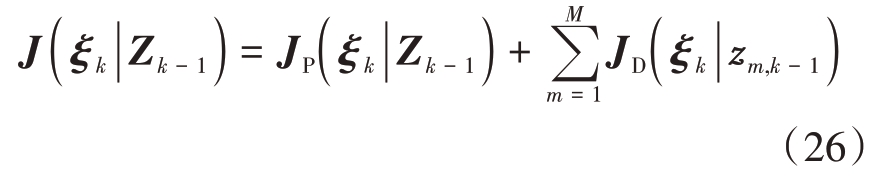
3 资源分配策略
将组网机会阵雷达功率分配问题转化为在满足期望跟踪性能条件下的功率优化分配。在量测数据的基础上，采用PC-CRLB 作为跟踪误差衡量基准。
3.1 优化模型
资源分配的关键在于预测目标的跟踪性能，从而使得雷达系统能够根据预测结果提前做出决策。CPCRLB（ξk）的对角元素是目标状态矢量ξk各个对应分量估计误差的下界，这就为目标跟踪误差提供了一个衡量基准，即为
式中Pk是各雷达发射功率的矢量，tr（•）是求迹符号，F（Pk）体现了k时刻组网雷达的整体跟踪性能。
从式（27）可以看出，Pk是决定目标跟踪性能的决策矢量，针对期望的跟踪误差，需要在各雷达之间优化分配功率，使得总发射功率最小。
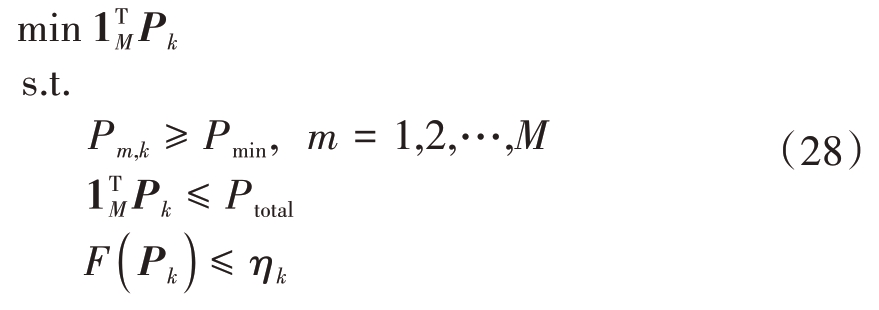
其中1TM=［1,1,…,1］1×M，ηk表示期望跟踪误差。
在实际跟踪过程中，由于环境的时变和目标信息的未知，目标RCS hm,k受到目标身份、姿态、位置、视角、波长、极化等多种因素的影响，是不确定的，这里用随机变量表示。而确定的资源管理模型不能处理不确定问题，也不能保证算法的稳健性。为了解决这个问题，这里采用随机CCP 模型把确定性资源管理模型进行封装：
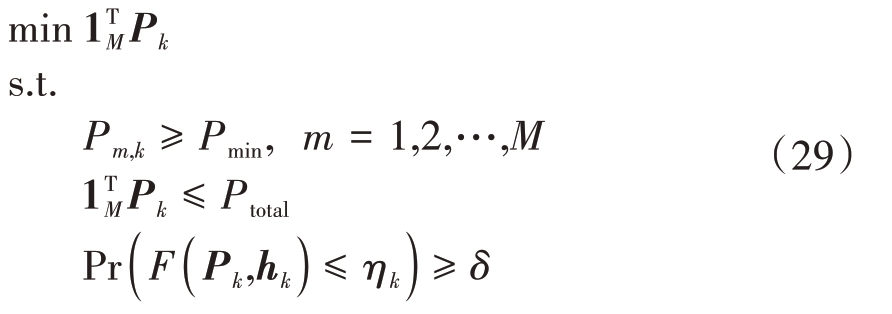
其中Pr（•）表示概率测度符号，δ 表示置信水平。模型的意思是在满足给定置信水平条件下，使得雷达的总发射功率越小越好。
3.2 求解算法
采用机会约束规划确保资源分配的随机约束至少在置信水平为δ时成立。为了求解机会约束，将随机模拟嵌入到遗传算法（Genetic Algorithm，GA）中构成HIOA 求解该模型。详细的流程如下所示。
3.2.1 随机模拟
根据专家经验和历史测量数据，假定针对所有雷达节点存在Nk个RCS 的历史测量数据hi,k（i=1,2,…,Nk），那么就可以生成Nk 个随机变量F(Pk,hi,k)。详细的求解步骤如下：
步骤1 令N'=0;
步骤2 根据hi,k生成F(Pk,hi,k)；
步骤3 若F(Pk,hi,k)≤ηk，则N'=N'+1；
步骤4 重复Nk次步骤2至步骤4；
步骤5 令Pr（F(Pk,hi,k)≤ηk）=N'/Nk，若N'/Nk≥δ，则Pk满足约束条件；否则不满足。
3.2.2 混合智能优化算法
将随机模拟算法嵌入到GA 中，构成混合智能优化算法［20］，从而可以预测出下一时刻满足约束条件的最优功率分配情况Popt,k+1。混合智能优化算法的求解流程如下：
1）初始化种群，采用随机模拟算法验证染色体的可行性；
2）采用交叉算子和变异算子更新染色体，并用随机模拟验证更新后的染色体的可行性；
3）计算所有染色体的目标函数值；
4）根据目标函数计算每个染色体适应度函数；
5）通过轮盘赌选择染色体；
6）重复2）至5），直至循环结束；
7）选出最好的染色体作为最优解Popt,k+1。
3.2.3 闭环状态处理框架
通过混合智能优化算法，能够预测下一时刻满足置信水平的波束最优功率分配Popt,k+1。在k+1时刻，就可以用该预测值指导雷达探测目标。
本文采用基于MCS 的强跟踪均方根容积卡尔曼滤波算法来处理非线性滤波问题，关于该滤波器的详细求解过程可参考文献［9］。则综合闭环反馈系统的完整流程如下：
1）令k=1，初始化最优功率为Popt,k=P0，其中P0均匀分配。
2）采用基于MCS的强跟踪平方根容积卡尔曼滤波算法进行滤波，其滤波过程采用顺序更新方式更新各雷达结点的测量数据。
3）根据刚更新的目标状态，计算集中式PCCRLB，然后利用HIOA 求基于CCP 的功率资源分配的最优解。
4）将最优解Popt,k+1发送给雷达以指导下一时刻的目标探测。
5）令k=k+1，转2）。
4 仿真结果与分析
为了验证本文功率分配算法的有效性，本节作了如下仿真，并对仿真结果进行了分析。
设组网机会阵雷达系统包含4个雷达结点和1个被跟踪的目标，每个节点能且只能生成一个波束来跟踪目标。各部雷达信号的有效带宽均为Bm,k=5 MHz，有效时宽均为Tm,k=1 ms。每个发射信号的载波波长为λm=0.03 m。相干脉冲数为64。各发射波束功率下界为Pmin=0.1 Ptotal。本次仿真共有40帧数据，每帧时间间隔为T0=1 s。机动目标初始机动频率为α=0.1，初始遗忘因子为ρf=0.95。不失一般性，假定各个雷达节点从不同角度观测的目标RCS 均服从Swerling I 分布，且取均值为0.27。雷达和目标相对位置如图1所示。
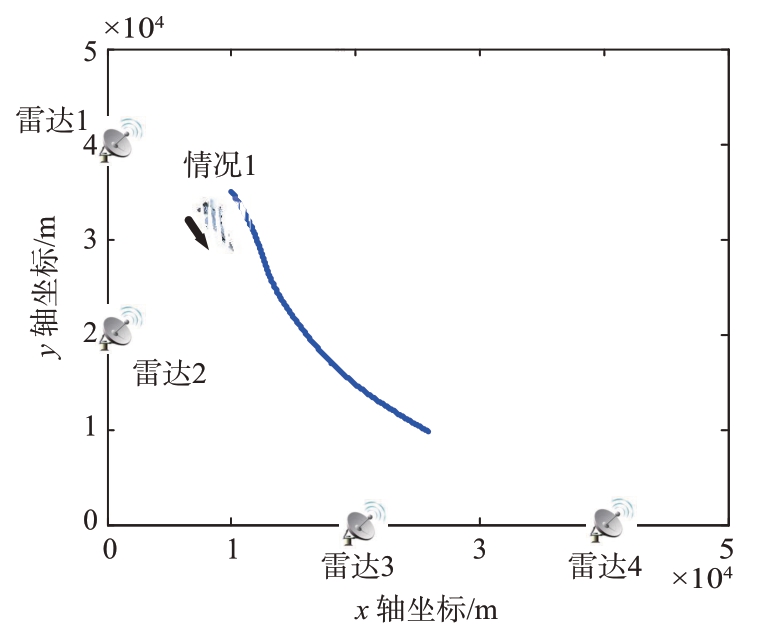
图1 雷达和目标分布图
各雷达坐标和飞机的起始坐标如表1所示。
表1 雷达坐标和目标的初始坐标
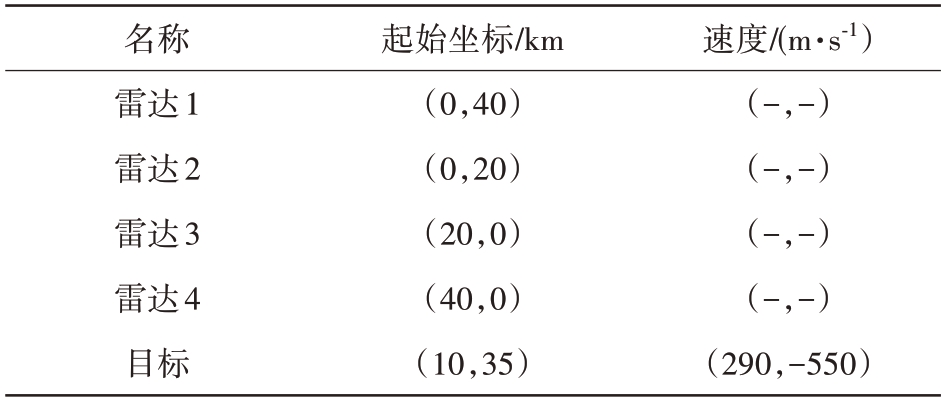
名称雷达1雷达2雷达3雷达4目标起始坐标/km（0，40）（0，20）（20，0）（40，0）（10，35）速度/(m·s-1）（-，-）（-，-）（-，-）（-，-）（290，-550）
机动目标的加速度模型如图2所示。
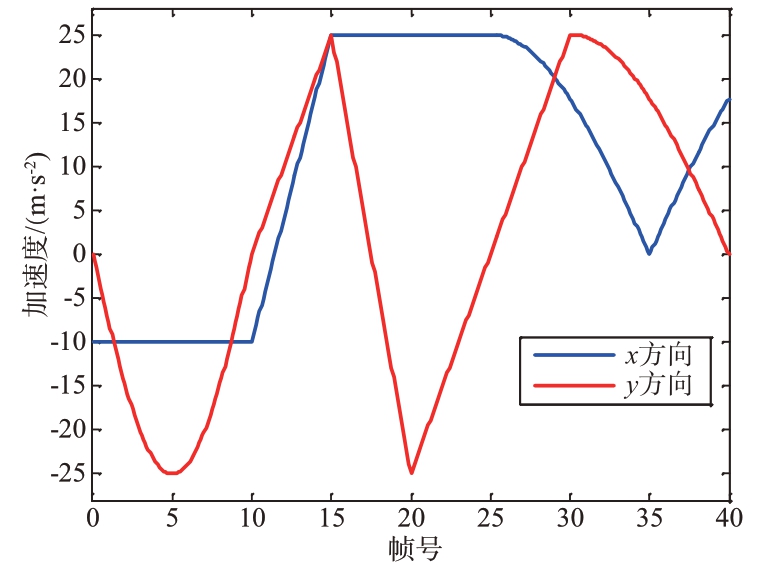
图2 目标的加速度模型
在以下仿真过程中，除了比较不同风险下总资源消耗时需要将δ 设置为不通过的置信水平外，其余仿真过程中均将置信水平设置为δ=0.9。在同一置信水平下采用不同的优化算法和跟踪性能衡量标准，不会影响资源分配算法的效果。
图3展示的是组网机会阵雷达系统目标跟踪时各雷达节点的功率资源分配情况。机动目标和雷达之间的距离，机动目标在不同方向上的速度和机动程度都是不同的，这严重影响功率资源分配结果。组网雷达系统会根据这些因素在各雷达之间优化分配功率，在满足约束条件下有效降低总消耗功率。
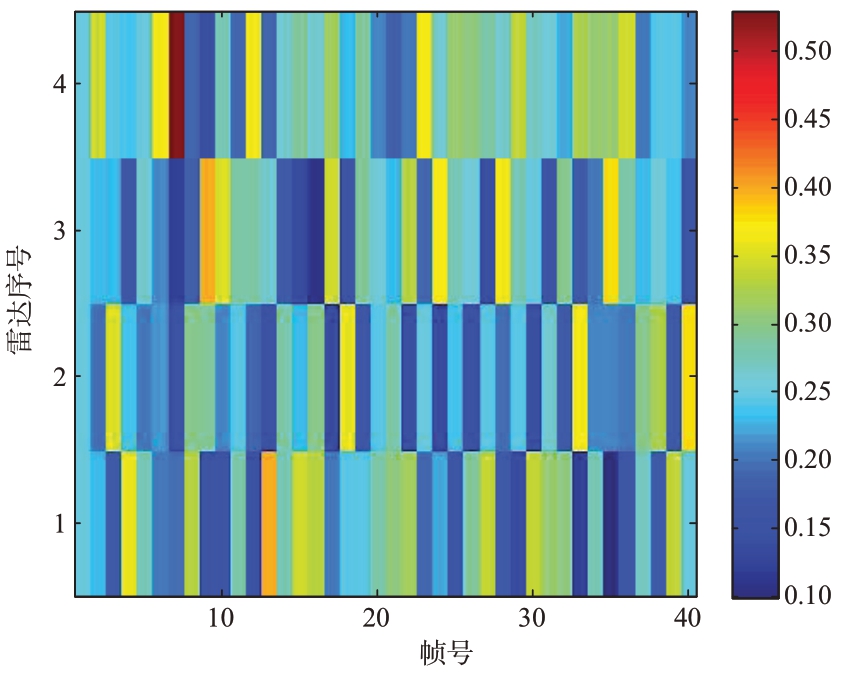
图3 各雷达功率分配
图4表示的是在不同条件下总功率消耗情况，其中Psum表示各雷达节点的总发射功率，Ptotal表示雷达系统的总功率。当都采用PC-CRLB 作为目标跟踪性能衡量标准时，在满足相等的期望跟踪误差条件下，本文的功率优化分配算法相比于均匀功率分配算法，总功率消耗节省了10%左右。另一种情况是当都采用功率优化分配算法时，采用PCRLB相比于采用PC-CRLB 作为跟踪性能衡量基准更节省功率。这里我们需要解释一下：在同样的条件下，PC-CRLB 能够为目标跟踪误差提供一个更加紧密的下界，而PCRLB 提供的下界更松散，值也更小。为了满足相同的期望跟踪误差，PCRLB 消耗功率更小。这一比较从反面证实了由于PC-CRLB 使用了最新的测量数据，其提供的下界更加紧密。
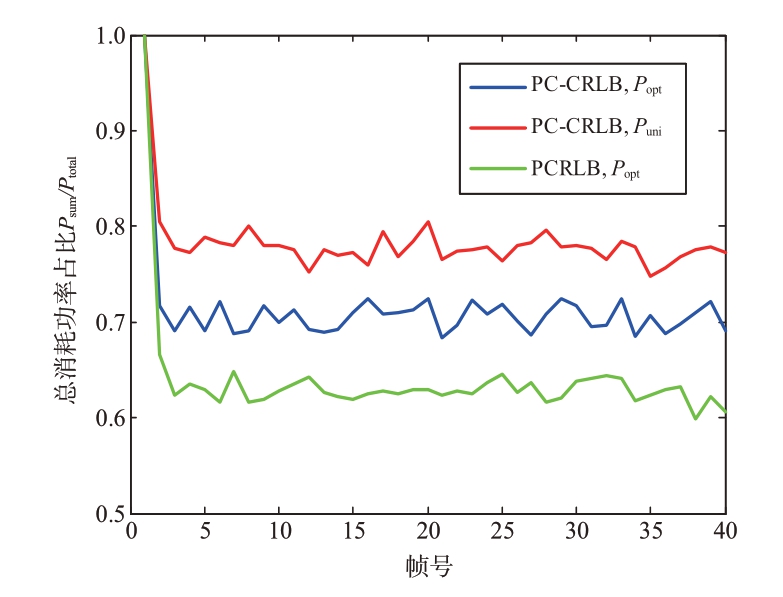
图4 不同条件下总功率消耗
置信水平体现了模型的稳健性程度，用来平衡跟踪性能和资源消耗之间的关系。从图5可以看出，置信水平越小，即为满足约束条件的可信性越小，则资源消耗越少，模型不成立的风险也就越大。在实际仿真中，根据雷达系统所处环境选择合适的置信水平，即当环境复杂时，可选择较高的置信水平值来保证约束成立，当环境简单时，可选择较低的置信水平来节省系统资源。
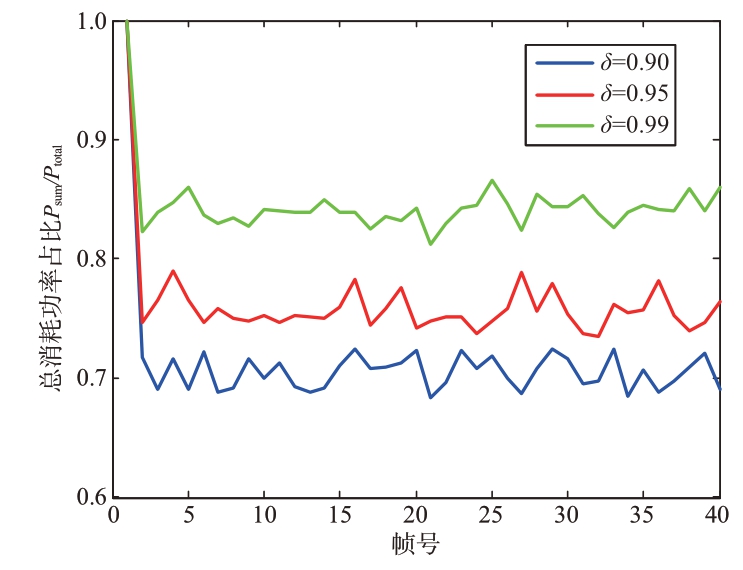
图5 不同置信水平下总功率资源消耗
图6给出了目标轨迹的跟踪情况。从图中看出，功率资源优化分配都是在保证目标跟踪性能条件下实现的，目标跟踪效果良好。
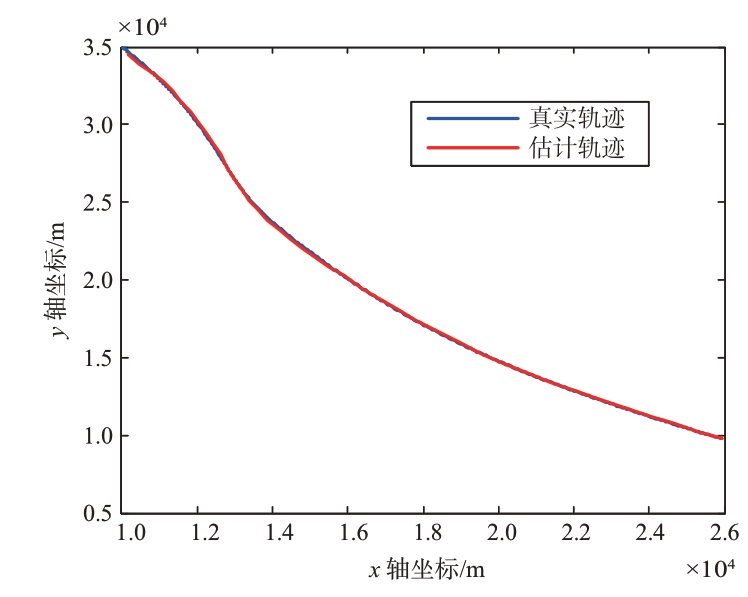
图6 目标轨迹对比图
5 结束语
本文针对组网OAR 跟踪机动目标情况，提出了一种基于CCP 的稳健功率分配算法，进而在满足给定置信水平的机会约束下，尽可能地节省功率资源。仿真实验表明：1）基于MCS 模型的机动目标运动方程能够更方便预测机动目标运动状态；2）PC-CRLB 能提供一个更紧密的下界衡量机动目标跟踪误差；3）基于CCP 的功率资源分配算法能够平衡功率和跟踪误差之间的关系，提供更加稳健的功率分配算法；4）相对于均匀功率分配算法，本文的功率分配算法能够大大节省功率资源。
［1］KOCAMAN I.Distributed Beamforming in a Swarm UAV Network［D］.Monterey,CA,USA: Naval Postgraduate School,2008.
［2］龙伟军,贲德,潘明海,等.机会数字阵雷达概念与应用技术分析［J］.南京航空航天大学学报,2009,41（6）:727-733.
［3］HAN Qinghua,ZHANG Yuanshi,YANG Zhen,et al.Antenna Array Aperture Resource Management of Opportunistic Array Radar for Multiple Target Tracking［J］.IEEE Access,2020,8:228357-228368.
［4］NADARAJAH N,THARMARASA R,MCDONALD M,et al.IMM Forward Filtering and Backward Smoothing for Maneuvering Target Tracking［J］.IEEE Trans on Signal Processing,2012,48（3）:2673-2678.
［5］MA Jian,GUO Xiaoting.Combination of IMM Algorithm and ASTRWCKF for Maneuvering Target Tracking［J］.IEEE Access,2020,8:143095-143103.
［6］SINGER R A.Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets［J］.IEEE Trans on Aerospace and Electronic Systems,1970,6（4）:473-483.
［7］KUMAR K S P,ZHOU H.A‘Current’Statistical Model and Adaptive Algorithm for Estimating Maneuvering Targets［J］.AIAA Journal of Guide,1984,7（5）:596-602.
［8］MEHROTRA K,MAHAPATRA P R.A Jerk Model for Tracking Highly Maneuvering Targets［J］.IEEE Trans on AerospaceandElectronicSystems,1997,33（4）:1094-1105.
［9］ZHANG Haowei,XIE Junwei,GE Jiaang,et al.Strong Tracking SCKF Based on Adaptive CS Model for Manoeuvring Aircraft Tracking［J］.IET Radar Sonar and Navigation,2018,12（7）:742-749.
［10］XIE Mingchi,YI Wei,KIRUBARAJAN T,et al,Joint Node Selection and Power Allocation Strategy for Multitarget Tracking in Decentralized Radar Networks［J］.IEEE Trans on Signal Processing,2018,66（3）:729-743.
［11］YAN Junkun,PU Wenqiang,ZHOU Shenghua,et al.Optimal Resource Allocation for Asynchronous Multiple Targets Tracking in Heterogeneous Radar Networks［J］.IEEE Trans on Signal Processing,2020,68:4055-4068.
［12］ZUO L,NIU R X,VARSHNEY P K.Conditional Posterior Cramér-Rao Lower Bounds for Nonlinear Sequential Bayesian Estimation［J］.IEEE Trans on Signal Processing,2011,59（1）:1-14.
［13］BELL K L,BAKER C J,SMITH G E,et al.Cognitive Radar Framework for Target Detection and Tracking［J］.IEEE Journal of Selected Topics in Signal Processing,2015,9（8）:1427-1439.
［14］SKOLNIK M I.Introduction to Radar System［M］.3rd ed.New Delhi: Tata McGraw-Hill Publishing Company Limited,2001:49-73.
［15］VAN TREES H L.Detection,Estimation,Modulation Theory Part III［M］.New York:Wiley,1971.
［16］VAN TREES H L.Optimum Array Processing: Detection,Estimation,Modulation Theory IV［M］.New York:Wiley,2001.
［17］GODRICH H,PETROPULU A P,POOR H V.Power Allocation Strategies for Target Localization in Distributed Multiple-Radar Architectures［J］.IEEE Trans on Signal Processing,2011,59（7）:3226-3240.
［18］VAN TREES H L,BELL K L.Bayesian Bounds for Parameter Estimation and Nonlinear Filtering/Tracking［M］.New York:Wiley,2007.
［19］GLASS J D,SMITH L D.MIMO Radar Resource Allocation Using Posterior Cramér-Rao Lower Bounds［C］//2011 IEEE Aerospace Conference,Big Sky,MT,USA:IEEE,2011:1-9.
［20］刘宝碇，赵瑞清，王纲.不确定规划及应用［M］.北京:清华大学出版社，2003.
