0 引 言
随着信息技术和控制理论的飞速发展[1],成本相对较低、可快速部署的集群无人机被选为分布式雷达阵列的新载体[2-3]。相较传统分布式雷达阵列,集群无人机载雷达阵列具有较多优势。首先,集群无人机载雷达阵列可以到达山地、海面、森林等复杂自然环境进行抵近式探测。其次,集群无人机载雷达阵列具有较高的机动性和空间自由度,在动目标检测、波达方向估计等方面具有更好的性能。此外,集群无人机载雷达阵列具有更强的战场生存能力,且避免了大型雷达阵列需要面对的成本、制造和部署等问题[3-5]。
波束合成是集群无人机载雷达阵列的重要功能之一。然而,由于受到由位置不确定性、时间同步不确定性、天线指向不确定性以及通道不确定性引起的幅度和相位误差影响,导致集群无人机载雷达阵列波束合成较难实现。下面从幅相误差估计与补偿、阵列构型优化两个方面回顾相关研究。
为了实现阵列波束合成,集群无人机载雷达阵列流型矩阵需要精确已知。然而,由于受到当前技术水平引发的幅相误差的影响,获得精确的阵列流型矩阵难度较大。阵列相位误差主要由位置不确定性、时间同步不确定性以及通道不确定性引起[6-7]。位置不确定性[8]与无人机定位系统精度有关。微小的位置偏差也会对集群无人机载雷达阵列波束合成造成较大影响。时间同步不确定性主要由时钟的偏移引起,在时钟不同步的情况下波束合成几乎无法实现[9]。通道不确定性主要与制造工艺、温度、湿度等因素有关[10]。阵列幅度误差主要由天线指向不确定性和通道不确定性引起。天线指向不确定性主要与无人机控制技术有关。
近年来,分布式雷达阵列幅相误差补偿技术研究已取得较大进展[7,11]。然而,这些方法大多需要已知阵列幅相误差的均值以及协方差等统计信息。当集群无人机载雷达阵列无法获得较为准确的统计信息或假设的误差模型与实际情况不符时,这些方法的性能将会严重下降。1 比特反馈算法[12]通过引入校准接收站,利用校准接收站的反馈结果进行误差估计与补偿,具有较好的误差估计与补偿性能。然而,为了保证较高的误差估计精度,校准接收站需要提供足够多的反馈信息,且阵列在每次误差估计后都需要等待校准接收站的下一次反馈,时间复杂度较高。此外,以上研究均基于构型固定的阵列。
除幅相误差估计与补偿之外,阵列构型对波束合成也具有重要影响。现有研究主要从峰值旁瓣电平和波束指向精度两方面进行构型优化提升波束合成效率。针对峰值旁瓣电平,由于集群无人机载雷达阵列的高度稀疏性(为防止碰撞),其峰值旁瓣电平通常较高。为降低峰值旁瓣电平,遗传算法[13]、粒子群算法[14]、模拟退火算法[15]、蚁群算法[16]等相继被应用于分布式雷达阵列构型优化。对于波束指向精度,克拉美罗界,即费舍信息矩阵的逆矩阵通常被选作阵列构型优化准则[17]。幅相误差影响下的分布式阵列波束合成信号模型克拉美罗界已得到较深入的研究与分析[11,18]。然而,以上研究几乎都是基于构型固定的阵列且忽略了阵列幅相误差。在误差存在的条件下,以上方法的性能下降严重。此外,以上研究均只考虑峰值旁瓣电平或只考虑波束指向精度,而没有综合考虑两方面因素,导致优化所得构型并非最优。集群无人机载雷达阵列构型优化研究亟待开展。
针对以上挑战,本文研究了幅相误差影响下的集群无人机载雷达阵列波束合成,并提出了一种实现集群无人机载雷达阵列波束合成方案。首先,构建了集群无人机载雷达阵列波束合成信号模型,并分析了幅相误差对模型的影响。其次,本文从克拉美罗界和峰值旁瓣电平两方面分析了集群无人机载雷达阵列波束合成性能,并提出了集群无人机载雷达阵列构型三维空间优化方法。最后,提出了一种快速高效的幅相误差处理策略。仿真结果和工程实验证实了所提出的集群无人机载雷达阵列波束合成方案的可行性。
1 波束合成信号模型与不确定性分析
如图1所示,假设集群无人机载雷达阵列由M架无人机组成,每架无人机搭载一个由L×L 个全向阵元组成的均匀方阵。第m(m=1,2,…,M)架无人机在tk时刻的坐标为ukm=[xkm,ykm,zkm]T,选取第一架无人机为参考无人机,即规定uk1=[0,0,0]T。
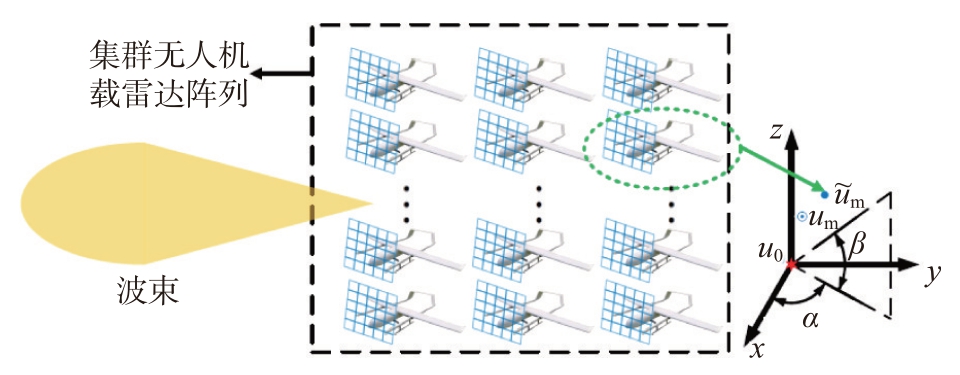
图1 集群无人机载雷达阵列波束合成信号模型
1.1 波束合成信号模型
假设集群无人机载雷达阵列在tk 时刻向远场发射信号s(tk),s(tk)为零均值高斯信号,方差为σ2s。
集群无人机载雷达阵列发射的信号可以表示为
式中:y(tk)=[y1(tk),y2(tk),…,yM(tk)]T 为阵列发射信号矢量;M 维零均值高斯白噪声矢量n(tk)=[n1(tk),n2(tk),…,nM(tk)]T,噪声方差为σ2n;α 与β 分别为发射波束方位角和俯仰角。a(α,β)为集群无人机阵列流型矩阵,其表达式为
φm 为第m 架无人机与参考无人机之间的相位差,其表达式为
r(α,β)=[cos α cos β,sin α cos β,sin β]T。Φ 为相位误差矩阵,G为幅度误差矩阵,其表达式分别为
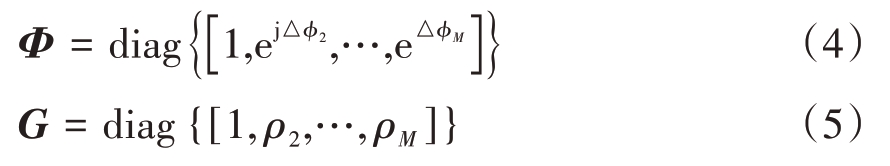
ρm和△ϕm分别为第m架无人机的相位误差和幅度误差。
相位误差主要由位置不确定性、时间同步不确定性以及通道不确定性引起。幅度误差主要由天线指向不确定性和通道不确定性引起。因此,第m 架无人机的相位误差和幅度误差可进一步表示为
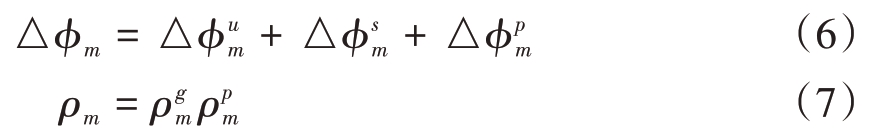
式中,△ϕum、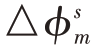 、△ϕpm分别为由位置不确定性、时间同步不确定性以及通道不确定性引起的相位误差,ρpm 与ρgm 分别为由天线指向不确定性和通道不确定性引起的幅度误差。为显示幅相误差的影响,假设集群无人机雷达阵列由10 架无人机组成且每架无人机携带一个由5×5 个间距为半波长的全向阵元组成的均匀方阵,以波束合成效率η评估相位误差和幅度误差的影响,其表达式为
、△ϕpm分别为由位置不确定性、时间同步不确定性以及通道不确定性引起的相位误差,ρpm 与ρgm 分别为由天线指向不确定性和通道不确定性引起的幅度误差。为显示幅相误差的影响,假设集群无人机雷达阵列由10 架无人机组成且每架无人机携带一个由5×5 个间距为半波长的全向阵元组成的均匀方阵,以波束合成效率η评估相位误差和幅度误差的影响,其表达式为
式中,He 为幅相误差影响下的主瓣高度,H 为无误差情况下的主瓣高度。当集群无人机向方位角和俯仰角均为0°的方向发射信号,图2(a)展示了不同幅度误差下,相位误差标准差在0°~40°范围内变化时波束合成效率的变化情况,图2(b)展示了不同相位误差下,幅度误差标准差在0~0.3 范围内变化时波束合成效率的变化情况。如图所示,较大的相位误差和幅度误差严重影响波束合成效率。
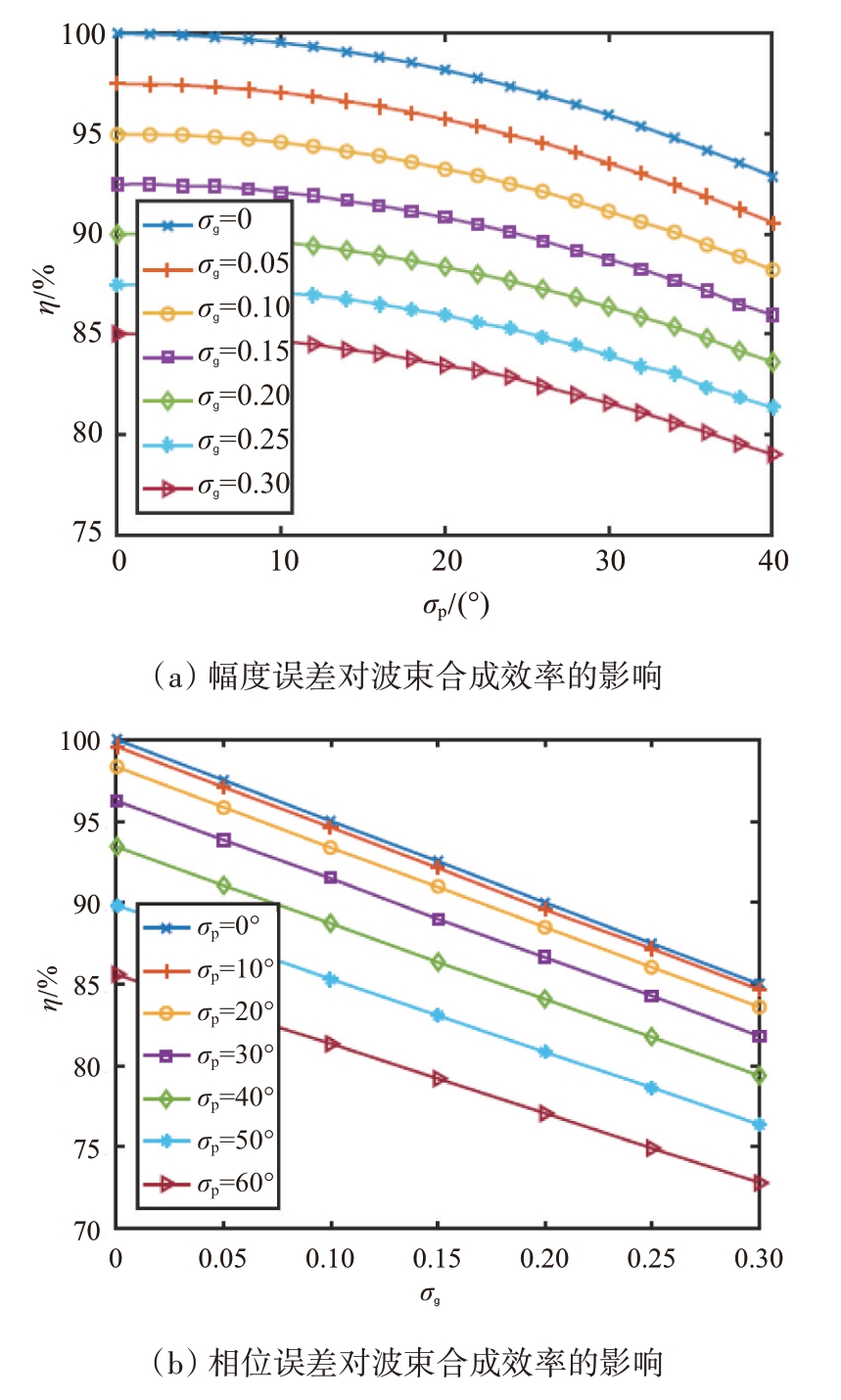
图2 幅相误差对波束合成效率的影响
1.2 不确定性分析
本节研究位置不确定性、时间同步不确定性、天线指向不确定性以及通道不确定性对幅度和相位误差的影响机理,并结合现有工程技术水平给出量化分析结果。
1.2.1 位置不确定性
位置不确定性通常由机载惯性导航系统、北斗导航系统或全球定位系统的精度引起。第m 架无人机的观测位置表示为
式中,△ukm=[△xkm,△ymk,△zkm]T 为位置误差,△xm,△ym以及△zm均被建模为方差为σ2u的零均值高斯变量。
由位置不确定性引起的相位误差可以表示为
结合机载惯性导航系统、北斗导航系统以及全球定位系统的工程技术水平,当位置不确定性为10 m,发射信号频率为1 GHz 时,引起的相位误差约为209°。
1.2.2 时间同步不确定性
时间同步不确定性通常由系统内部时钟、北斗导航系统或全球定位系统的授时精度引起。由时间同步不确定性引起的相位误差可以表示为
式中,f 表示发射信号频率,△tm 为第m 架无人机与参考无人机之间的时差。根据公式(11),由时间同步不确定性引起的相位误差与发射信号频率成正比,即发射信号频率越高,对时间同步精度要求就越高。结合系统内部时钟、北斗导航系统以及全球定位系统的工程技术水平,当时间同步不确定性为20 ns,发射信号频率为1 GHz 时,引起的相位误差约为126°。
1.2.3 通道不确定性
通道不确定性主要与制造工艺、温度、湿度等因素有关。通道不确定性同时影响相位误差与幅度误差。通道不确定性引起的相位误差通常被建模为方差为△ϕpm的零均值高斯随机变量。通道不确定性引起的幅度误差通常被建模为均匀分布的随机变量。结合现有工程技术水平,通道不确定性引起的相位误差和幅度误差一般小于10°和1 dB。
1.2.4 天线指向不确定性
天线指向不确定性主要引起幅度误差。结合现有工程技术水平,天线指向不确定性引起的幅度误差一般小于0.5 dB。
上述理论分析与仿真结果表明,与传统分布式阵列雷达波束合成不同,由于受到位置不确定性、时间同步不确定性、天线指向不确定性以及通道不确定性的影响,集群无人机载雷达阵列波束合成面临更多的挑战。因此,本文将从集群无人机构型优化和幅相误差处理两方面减小幅相误差的影响。
2 集群无人机载雷达阵列构型优化
克拉美罗界和峰值旁瓣电平常被用于评估阵列波束指向精度以及栅瓣抑制性能。本节将推导集群无人机载雷达阵列波束合成信号模型的克拉美罗界和峰值旁瓣电平,并以克拉美罗界和峰值旁瓣电平作为优化准则优化集群无人机构型以应对幅相误差引起的波束合成效率下降的问题。
2.1 克拉美罗界
费舍信息矩阵可用于表征测量值中所包含的信息[19]。费舍信息矩阵的行列式越大,包含的信息越多,采用这些信息所能获得的估计结果就越精确。费舍信息矩阵的逆,即克拉美罗界,为所有无偏估计提供了一个估计方差的下界,常被用于评估估计性能。
为方便推导克拉美罗界,根据文献[18],将公式(1)改写为
式中,c=![]() 是包含所有阵列幅相误差的列向量,其第p个元素表示为cp。[Qt]:,p=Γpa(α,β)s(t),Γp=∂(GΦ-IM)/∂cp。[•]:,p 表示矩阵第p 列。IM 表示M×M 维单位矩阵。Qt的一种更清晰的表述为
是包含所有阵列幅相误差的列向量,其第p个元素表示为cp。[Qt]:,p=Γpa(α,β)s(t),Γp=∂(GΦ-IM)/∂cp。[•]:,p 表示矩阵第p 列。IM 表示M×M 维单位矩阵。Qt的一种更清晰的表述为
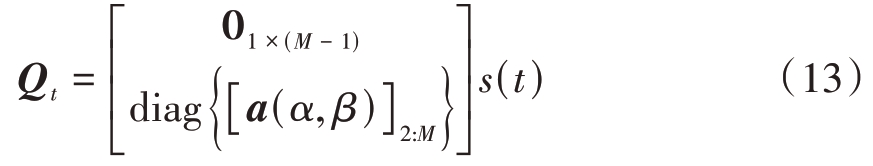
式中,[a(α,β)]2:M 表示a(α,β)的第2 行到第M 行。
集群无人机载雷达阵列波束合成信号模型的费舍信息矩阵可以以分块矩阵的形式表示:
式中,
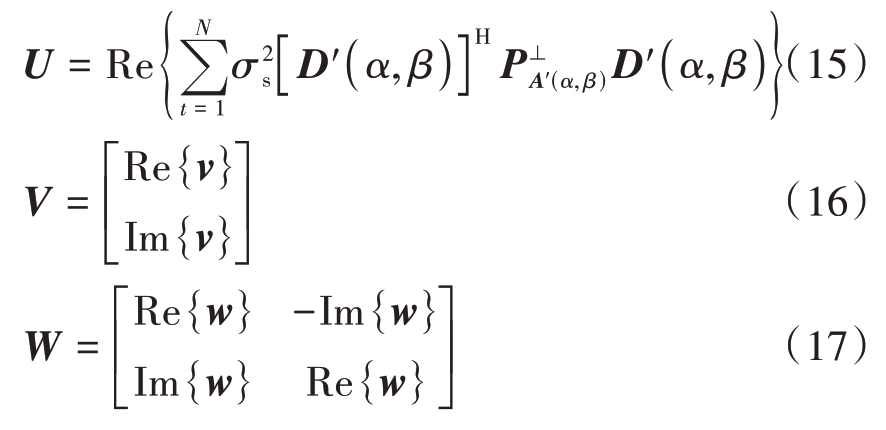
式中,a'(α,β)=GΦa(α,β),Re{•} 与Im{•} 分别表示取实部和虚部,d'(•)=∂a'(α,β)/∂(•),D'(α,β)=![]()
![]() [a'(α,β)]†={[a'(α,β)]Ha'(α,β)}-1[a'(α,β)]H。
[a'(α,β)]†={[a'(α,β)]Ha'(α,β)}-1[a'(α,β)]H。
计算公式(14)的舒尔补,并根据伍德伯里矩阵恒等式可以得到集群无人机载雷达阵列波束合成信号模型的克拉美罗界:
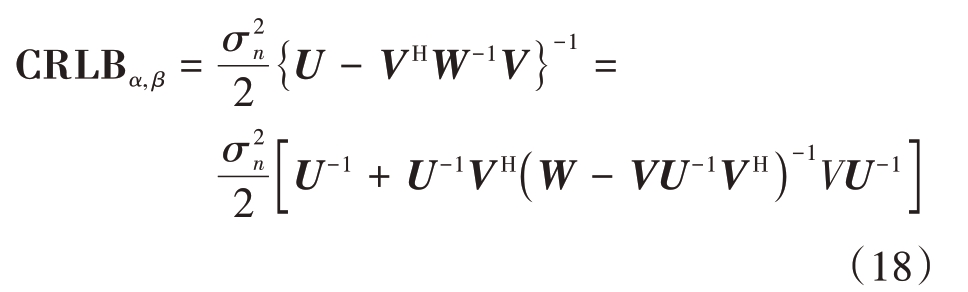
无误差情况下的集群无人机载雷达阵列波束合成信号模型的克拉美罗界[20]:
由于克拉美罗界为矩阵形式,不利于研究与分析。克拉美罗界的迹常被用作性能评价指标。克拉美罗界的迹越小意味着测量精度越高。根据文献[8],由于费舍信息矩阵是正定矩阵,矩阵U在费舍信息矩阵中的舒尔补σ2n/2(W-VU-1VH)-1是正定矩阵,进而得到(CRLBα,β-σ2n/2U-1)为正定矩阵。矩阵(CRLBα,β-σ2n/2U-1)正定表明![]() 其中,tr{•} 表示矩阵的迹。因此,我们可以得出结论,不确定性的存在影响了阵列波束合成性能。
其中,tr{•} 表示矩阵的迹。因此,我们可以得出结论,不确定性的存在影响了阵列波束合成性能。
2.2 峰值旁瓣电平
集群无人机载雷达阵列发射波束方向图函数可表示为
式中,|•|表示取绝对值,w为导向矢量。
由于无人机尺寸通常大于或等于无人机所携带的阵面尺寸,且为防止无人机间发生碰撞,集群无人机载雷达阵列通常为高度稀疏阵列,因此,集群无人机载雷达阵列波束合成具有较高的旁瓣甚至出现栅瓣。此外,幅相误差的存在也会导致方向图旁瓣电平升高。所有旁瓣电平的最大值即峰值旁瓣电平(PSL)通常被选作阵列设计的评价准则。
2.3 阵列构型优化
本小节以克拉美罗界和峰值旁瓣电平为优化准则进行集群无人机载雷达阵列构型优化以应对幅相误差问题。集群无人机载雷达阵列构型优化问题可以表示一个多目标决策问题,即在保证集群无人机满足距离与地理位置约束的前提下,最小化两目标函数,具体表示为
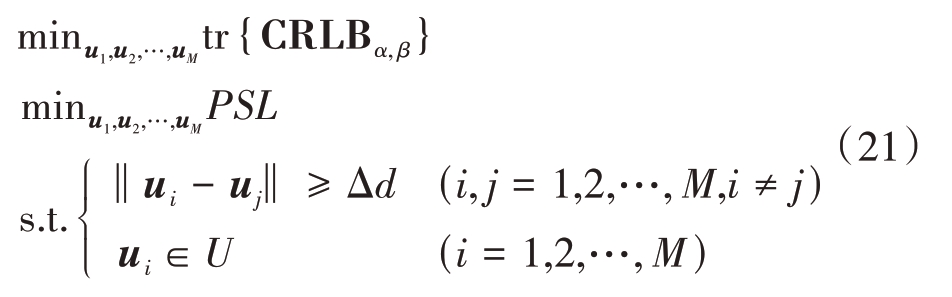
其中,△d 和U 分别表示无人机间不发生碰撞的最小距离和无人机飞行区域。
由于以上优化问题包含多个目标函数,直接求解结果为一帕累托面。对此,本文采用加权求和的方法,将这一多目标优化问题转化为单目标优化问题,如下式所示:
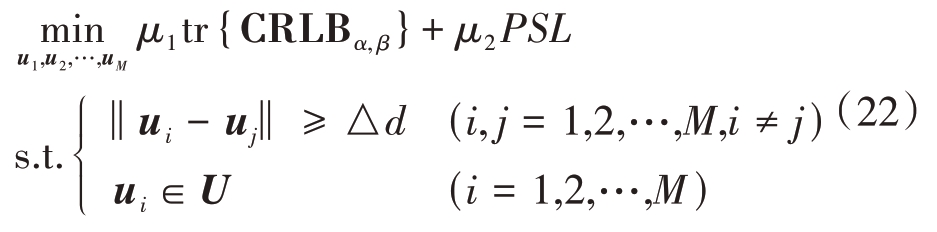
其中,μ1和μ2为加权系数。
对于由M 架无人机组成的集群无人机载雷达阵列,以上优化问题有3×M 个变量需要优化。对此,我们可以采用粒子群算法等提升构型优化速度。以粒子群算法为例,假设粒子群算法初始化K个粒子,Xt 为各个粒子在第t 次迭代过程中记录的无人机集群位置矩阵,Vt 为各个粒子在第t 次迭代过程中记录的无人机集群速度矩阵,则粒子群算法的位置更新公式与速度更新公式为
式中,Pt 为整个迭代过程中各个粒子的局部最优解矩阵,Gt 为整个迭代过程中所有粒子的全局最优解矩阵,c1 与c2 为胡克常量,η1 与η2 为随机数,用于引入不确定性,避免优化陷入局部最优。
3 幅相误差处理策略
正如1.2 节分析,各种不确定性引起的幅相误差通常较大,仅通过构型优化难以保证波束合成效率。本节从工程系统设计与幅相误差补偿两方面减小幅相误差的影响。
3.1 工程系统设计
由位置不确定性与时间同步不确定性引起的相位误差通常较大,且时变。本节提出一种减小位置不确定性与时间同步不确定性的工程系统设计方案。
DW1000[21]集成电路采用IEEE 802.15.4a 标准的超宽带物理层,其脉冲特性及大带宽使精确实时定位系统实现成为可能。基于DW1000 的实时定位系统精度可达ed=±10 cm。
为应对时间同步不确定性问题,本文设计基于高精度测距的时间同步系统,如图3所示。参考无人机同时向远场和集群中其他无人机发射信号,其他无人机接收到信号后首先补偿由距离造成的相位差,然而向远场发射信号。由于基于DW1000 的实时定位系统精度可达ed=±10 cm,时间同步不确定性可被减小至约Δt=ed/c=0.33 ns。

图3 工程系统设计示意图
3.2 幅相误差补偿
由位置不确定性、通道不确定性以及指向不确定性引起的幅相误差可以被分为固定部分和随机部分。本小节针对固定部分提出了一种有效的误差补偿方法。如图4所示,校准无人机从方位角α0,俯仰角β0 发射校准信号。集群无人机载雷达阵列接收到的信号可以表示为

图4 误差补偿示意图
式中,φm,0=![]()
根据文献[7],固定幅度误差可以根据下式估计:
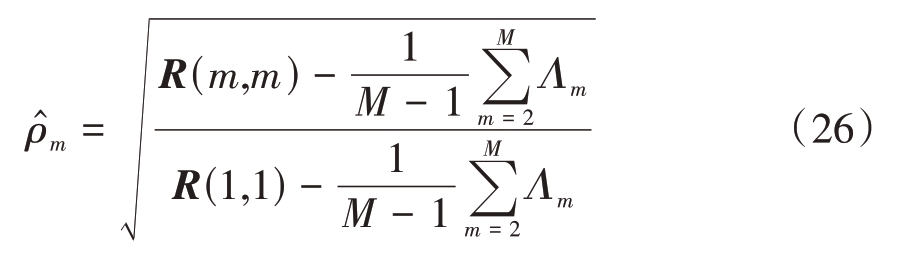
式中,R 为校准发射信号的协方差矩阵,Λm 为R 的第m个特征值。
获得固定幅度误差估计结果后,首先对幅度误差进行补偿,如下式所示:

式中,![]() 此后,通过下式估计相位误差:
此后,通过下式估计相位误差:
式中,![]() 考虑到以上优化问题可能面临较高的时间复杂度,我们同样可以采用粒子群算法等缩短优化时间。
考虑到以上优化问题可能面临较高的时间复杂度,我们同样可以采用粒子群算法等缩短优化时间。
需要指出的是,尽管本文为减小幅相误差的影响做了较多努力,但其结果依然受到定位系统精度以及误差补偿结果的影响,主要体现在:定位系统精度通常难以达到预期,且由于受到移相器技术水平的制约,雷达阵列在根据相位误差估计结果进行误差补偿时难以达到理想的效果。这些不足将会造成理论分析结果与实验结果之间存在一定的偏差。
4 仿真实验与结果分析
本节开展数值仿真验证所提出的集群无人机载阵列雷达波束合成方案的有效性。由于目前关于集群无人机载雷达阵列的研究较少,所以本节数值仿真主要致力于验证所提出的最优几何构型与幅相误差处理策略的有效性。为了分析算法收敛性能,本文将所提误差补偿方法与1比特反馈法进行对比。假设集群无人机载雷达阵列由20架工作在P波段的无人机组成,且每架无人机携带一个由5×5 个间隔半波长的全向阵元组成的均匀方阵,集群无人机载雷达阵列向方位角0°和俯仰角0°发射信号。
4.1 方案有效性
本小节验证所提集群无人机载雷达阵列波束合成方案的有效性。图5(a)展示了误差影响下未经任何处理的波束合成方向图,其主瓣明显偏离预期方向且方向图中最高峰值电平也只能达到无误差情况下主瓣电平的60%。图5(b)展示了经过幅相误差处理策略的波束合成方向图,虽然其主瓣指向了准确的方向,但是其波束合成效率只能达到78%,且峰值旁瓣电平高达-4.46 dB。图5(c)展示了经过幅相误差处理策略和构型优化的波束合成方向图,其主瓣指向准确方向,且波束合成效率达83%,峰值旁瓣电平下降到-6.41 dB。值得指出的是,经过幅相误差处理策略和构型优化,集群无人机载雷达阵列峰值旁瓣电平依然高于传统雷达阵列,其主要原因是集群无人机载雷达阵列的高度稀疏性,以及幅相误差依然存在。
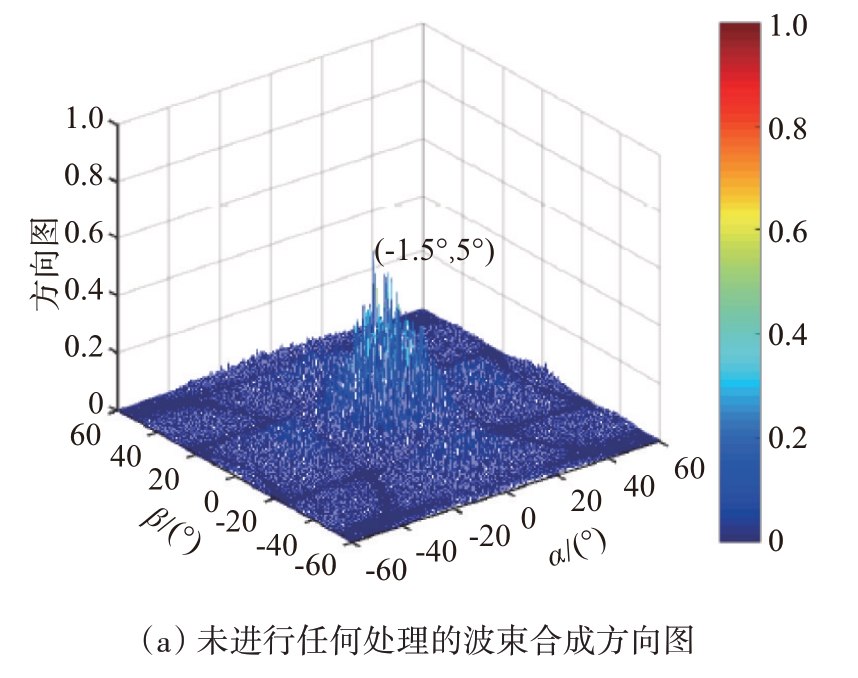
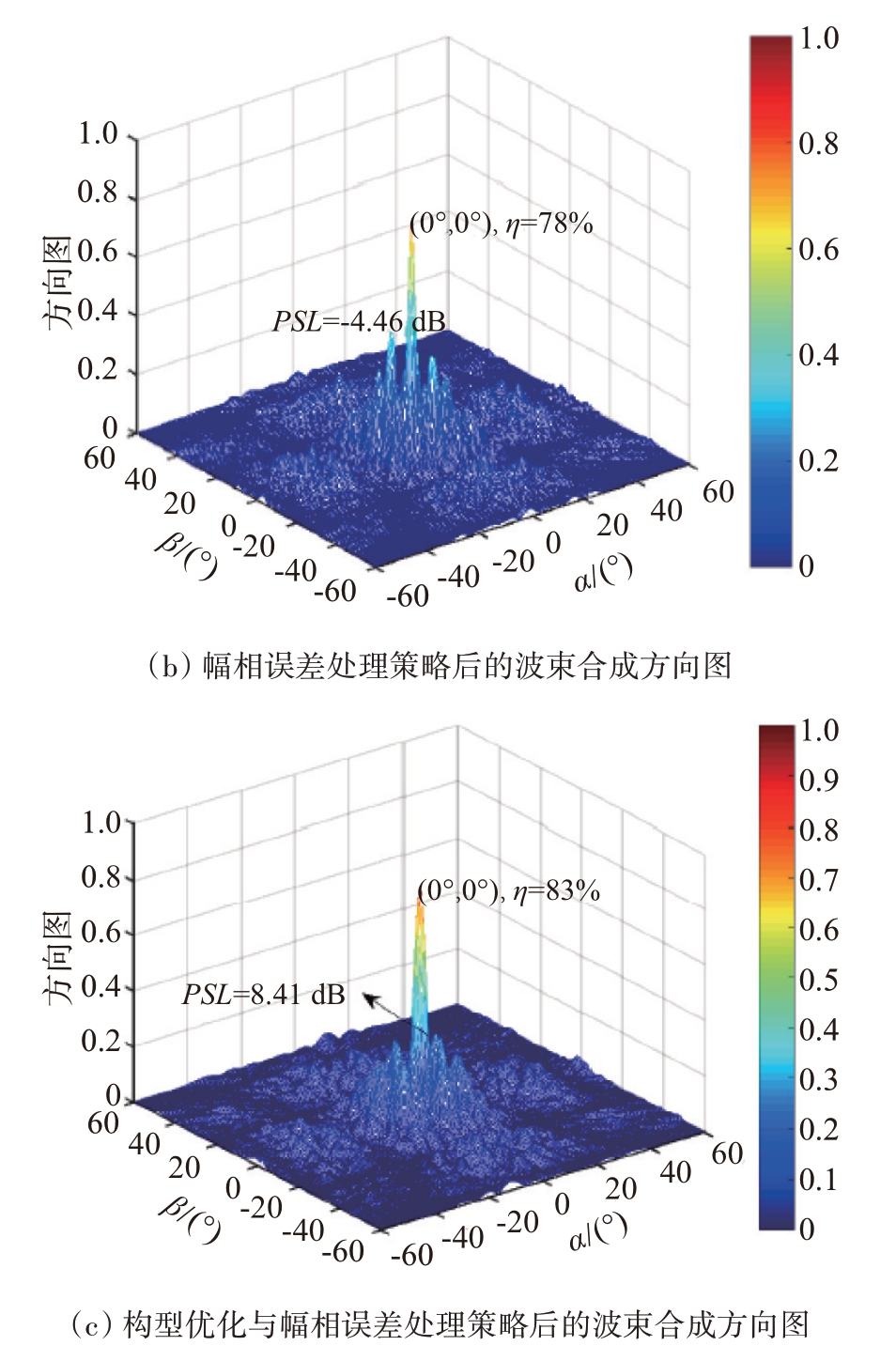
图5 集群无人机载雷达阵列波束合成方向图
通过这一数值仿真实验不难看出,本文所提的幅相误差处理策略和最优几何构型可以很大程度上提升集群无人机载雷达阵列的波束合成性能。
4.2 相位误差影响
由于幅度误差的影响相对较小且在现有技术水平下可以较好地补偿。对此,在相同幅度误差条件下,针对随机构型、经过误差处理的随机构型以及经过误差处理的最优构型三种情形,本小节研究相位误差对峰值旁瓣电平和波束合成效率的影响。图6(a)展示了当相位误差在0°~40°范围内变化时三种情形下的波束合成效率。如图所示,随着相位误差变化,经过幅相误差处理后的随机构型与最优构型均具有较为稳定的波束合成效率。图6(b)展示了当相位误差在0°~40°范围内变化时三种情形下的峰值旁瓣电平。显然,最优构型下的峰值旁瓣电平较低,且当相位误差增大时,其峰值旁瓣电平变化最缓慢。

图6 相位误差影响
本小节的仿真实验结果证明了本文所提出的幅相误差处理策略和最优几何构型可以较大程度上提升波束合成的稳定性。
4.3 无人机数量的影响
为分析无人机数量的影响,本小节仿真分析当相位误差为40°情况下随着集群中无人机数量由4 架增加至24 架时波束合成效率和峰值旁瓣电平的变化情况。图7(a)展示了随着无人机数量变化波束合成效率的变化情况。如图所示,当无人机数量增加时,波束合成效率出现了小幅度的下降,其原因是随着无人机数量增加,更多的幅相误差被引入阵列。图7(b)展示了随着无人机数量变化峰值旁瓣电平的变化情况。如图所示,随着无人机数量增加,峰值旁瓣电平下降,其原因是随着无人机数量增加,阵列稀疏性下降。
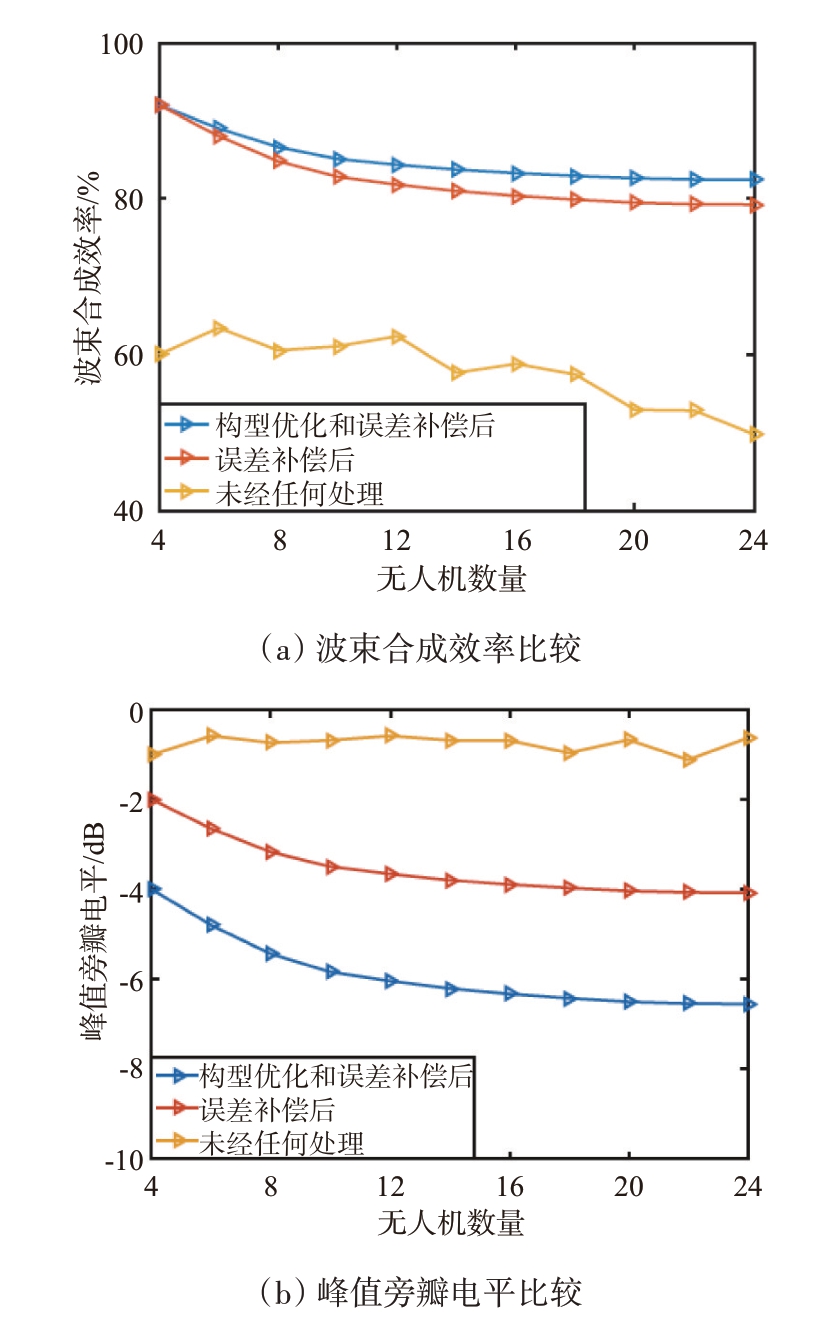
图7 无人机数量影响
值得指出的是,当无人机数量增加到一定程度时,波束合成效率与峰值旁瓣电平几乎都不再发生变化。在实际情况中,无人机数量应根据应用要求具体分析。
4.4 收敛速度
由于集群无人机最优构型可以提前求解并存储,本小节只需考虑误差补偿方法的收敛速度。为展示所提误差补偿方法的收敛性能,本文与1比特反馈法进行了对比。图8展示了当迭代次数从1增加至5 000 时,两种方法波束合成效率的变化情况。如图所示,为达到相同的波束合成效率,1 比特反馈法需要更多的迭代次数,而本文所提算法所需迭代次数较少。
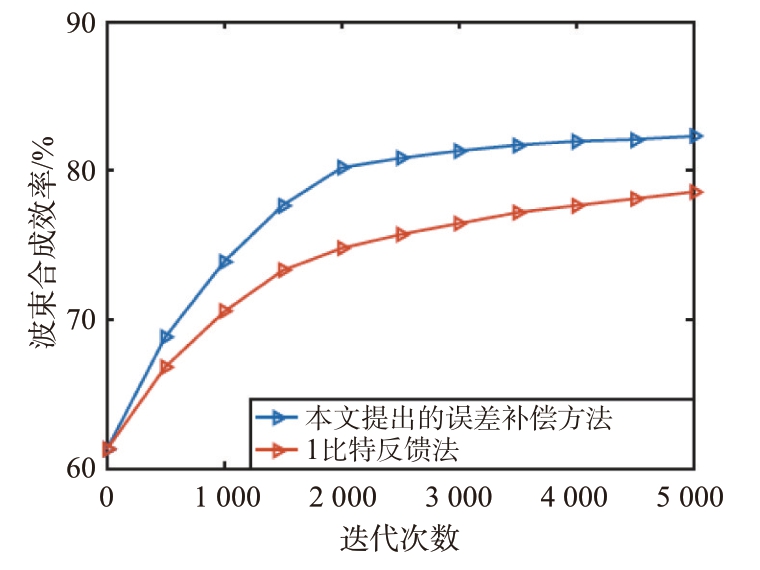
图8 误差补偿方法收敛速度
5 工程实验
本节通过动平台载分布式雷达阵列验证本文所提出的最优构型和幅相误差处理策略的有效性。如图9(a)所示,动平台载分布式雷达阵列由3 个动平台组成,且每个动平台携带一均匀方阵。接收装置被放置在距离发射阵列400 m 处,如图9(b)所示。

图9 工程实验场景
为降低位置不确定性和时间同步不确定性的影响,动平台载分布式雷达阵列应用了本文所提出的系统设计方案。首先动平台1 测量其与另外两动平台间的距离,并向远场以及另外两动平台发射信号,其余两动平台接收到信号后根据动平台1 距离测量结果对发射信号进行相位补偿后将信号发射至远场。本节通过两组实验展示本文所提方案的有效性。
5.1 幅相误差处理
为展示本文所提出的幅相误差处理方案的有效性,本文观测并比较了一段时间内来自两个动平台的信号。如图10所示,黄色线条和绿色线条分别表示来自两个动平台的信号,紫色线条为两信号之和,在未进行幅相误差处理的情况下,1~5 s内,幅相误差迅速发生不规则变化。图11展示了幅相误差处理后的信号观测结果,两信号基本保持稳定且相互同步。由此可知,幅相误差处理对动平台载分布式阵列波束合成具有重要作用。
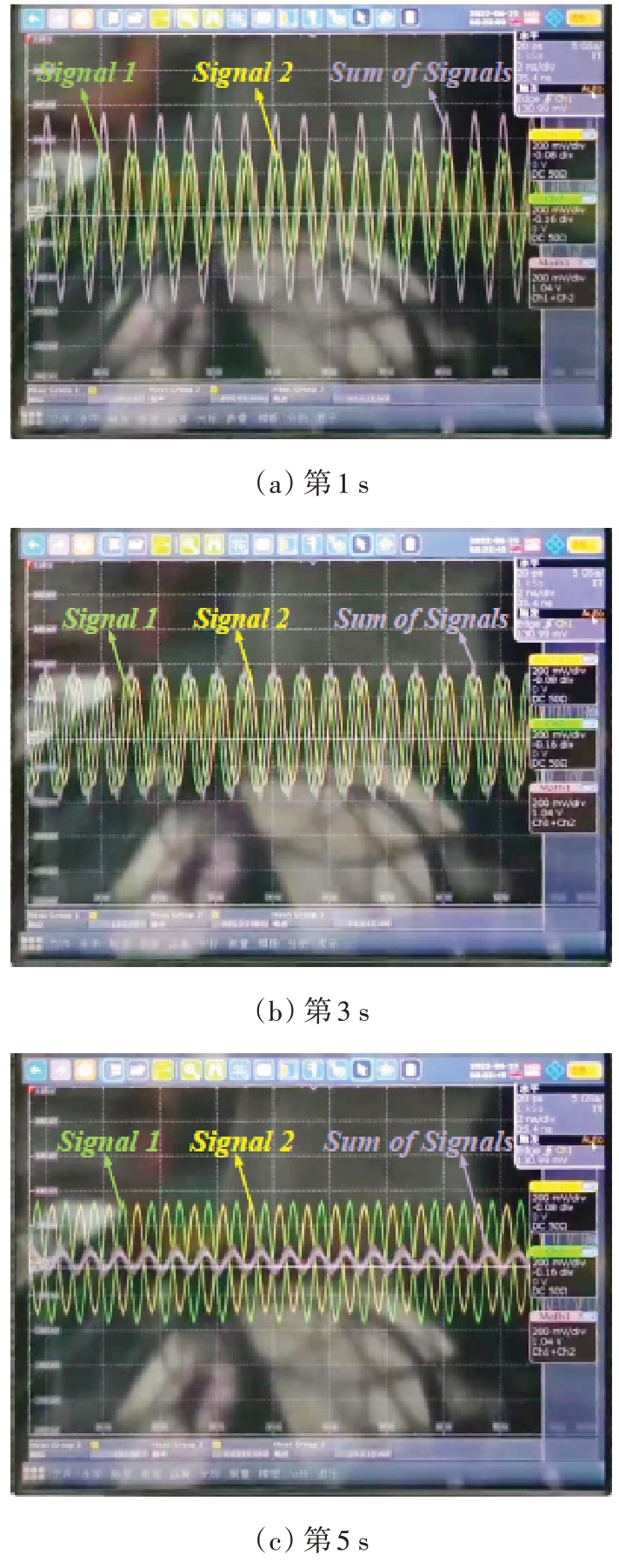
图10 误差变化情况
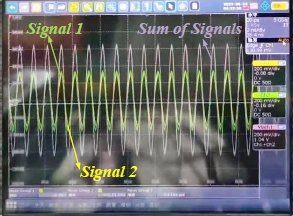
图11 幅相误差处理后信号
5.2 波束合成效率
本小节从波束合成效率的角度评估本文提出的误差补偿策略和最优构型的性能。为了便于比较,本文展示了功率计在不同情况下测得的信号功率。如图12(a)所示,单动平台工作时,功率计的测量值为1.66 dBm。如图12(b)所示,未经幅相误差处理和构型优化时,功率计测量值为3.67 dBm,其波束合成效率为
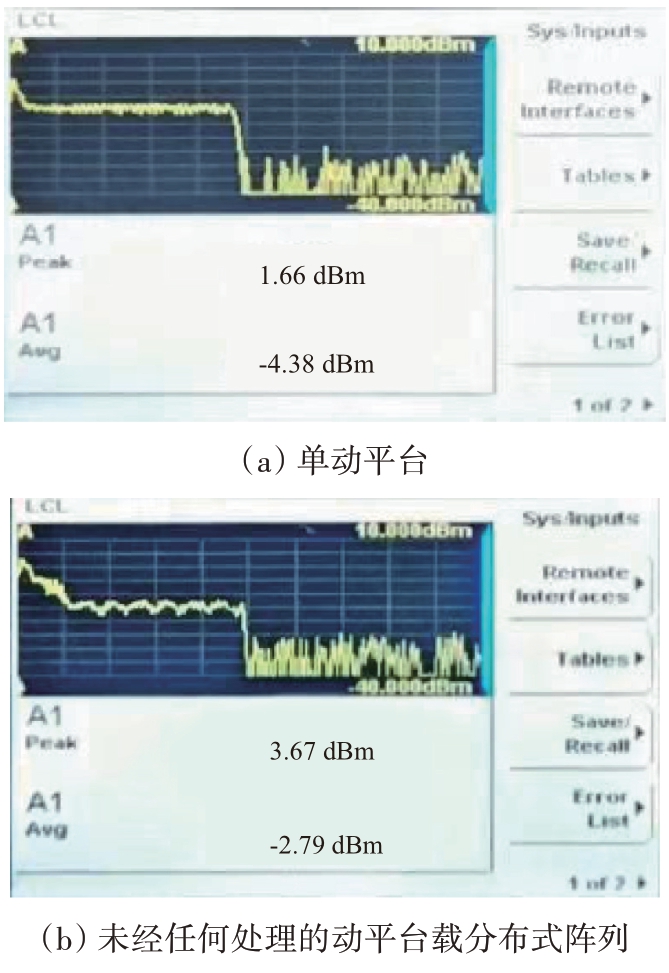
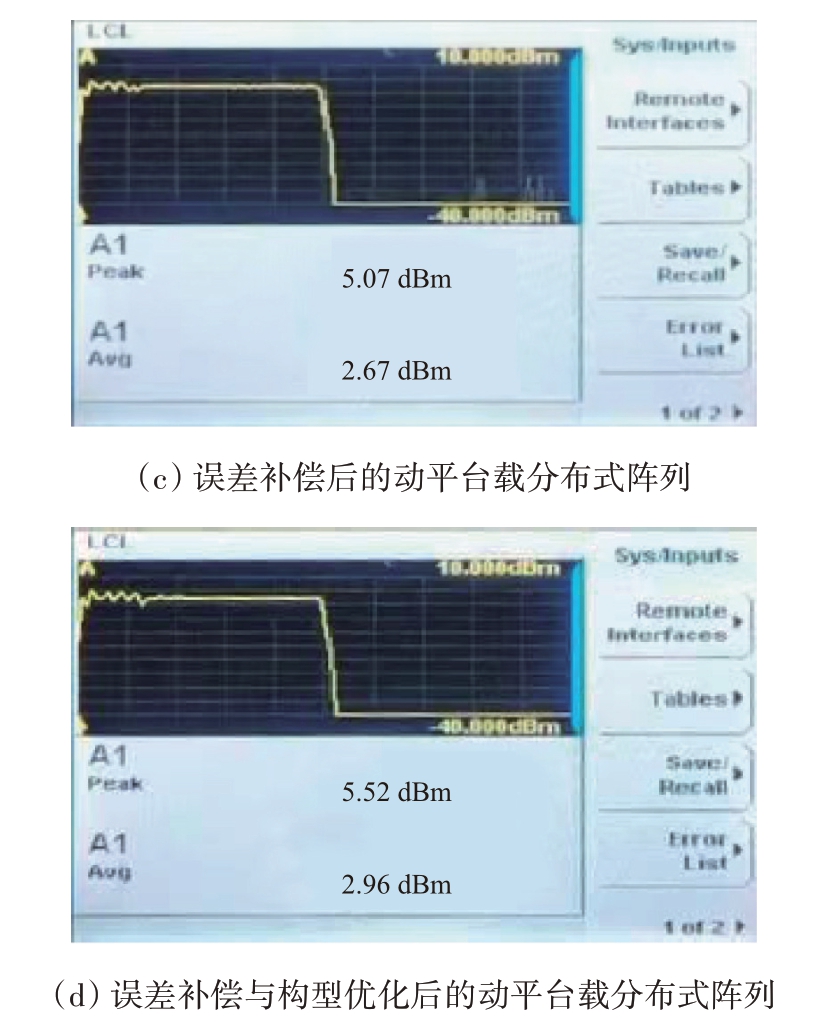
图12 功率计测量结果
如图12(c)所示,经过幅相误差处理,功率计测量值为5.07 dBm,其波束合成效率为
如图12(d)所示,经过幅相误差处理和构型优化,功率计测量值为5.52 dBm,其波束合成效率为
经过幅相误差处理和构型优化,波束合成效率上升了约28.12%。所提幅相误差处理和构型优化对动平台载分布式雷达阵列波束合成具有重要作用。经过幅相误差处理和构型优化后,波束合成效率只能达到81.07%的主要原因是定位系统精度通常难以达到预期,且误差补偿受到当前移相器工程技术水平的制约。此外,建筑物、植物的遮挡以及温度、湿度等环境因素也会对动平台载分布式雷达波束合成造成一定的影响。
6 结束语
本文研究了受到由位置不确定性、时间同步不确定性、天线指向不确定性以及通道不确定性引起的幅相误差影响的集群无人机载雷达阵列波束合成。首先,本文构建了集群无人机载雷达阵列波束合成信号模型并分析了幅相误差对波束合成的影响。其次,本文推导了集群无人机载雷达阵列波束合成信号模型的克拉美罗界和峰值旁瓣电平,并基于以上两个准则提出了集群无人机构型优化方法。最后,提出了快速高效的幅相误差补偿方法。数值仿真和工程实验验证了本文提出的幅相误差处理策略和最优构型的有效性。
[1]王祝,徐广通,龙腾.基于定制内点法的多无人机协同轨迹规划[J].自动化学报,2020,41:1-11.
[2]SHI Chengguang,WANG Yijie,SALOUS S,et al.Joint Transmit Resource Management and Waveform Selection Strategy for Target Tracking in Distributed Phased Array Radar Network[J].IEEE Trans on Aerospace and Electronic Systems,2022,58(4):2762-2778.
[3]XU Weidi,WANG Bingnan,XIANG Maosheng,et al.A Novel Autofocus Framework for UAV SAR Imagery: Motion Error Extraction from Symmetric Triangular FMCW Differential Signal[J].IEEE Trans on Geoscience and Remote Sensing,2022,60:1-15.
[4]WANG Yan,DING Zegang,LI Linghao,et al.First Demonstration of Single-Pass Distributed SAR Tomographic Imaging with a P-Band UAV SAR Prototype[J].IEEE Trans on Geoscience and Remote Sensing,2022,60:1-18.
[5]BEKAR A,ANTONIOU M,BAKER C J.Low-Cost,High-Resolution,Drone-Borne SAR Imaging[J].IEEE Trans on Geoscience and Remote Sensing,2022,60:1-11.
[6]ZHANG Xuejing,HE Zishu,ZHANG Xuepan,et al.DOA and Phase Error Estimation for a Partly Calibrated Array with Arbitrary Geometry[J].IEEE Trans on Aerospace and Electronic Systems,2020,56(1):497-511.
[7]WANG Wenyi,WU Renbiao,LIANG Junli,et al.Phase Retrieval Approach for DOA Estimation with Array Errors[J].IEEE Trans on Aerospace and Electronic Systems,2017,53(5):2610-2620.
[8]YANG Yang,ZHENG Jibin,LIU Hongwei,et al.Optimal Sensor Placement for Source Tracking Under Synchronization Offsets and Sensor Location Errors with Distance-Dependent Noises[J].Signal Processing,2021,193:108399.
[9]WANG Yiyin,MA Xiaoli,LEUS G.Robust Time-Based Localization for Asynchronous Networks[J].IEEE Trans on Signal Processing,2011,59(9):4397-4410.
[10]BOCHE H,SCHAEFER R F,POOR H V.Communication Under Channel Uncertainty:an Algorithmic Perspective and Effective Construction[J].IEEE transactions on Signal Processing,2020,68:6224-6239.
[11]TIAN Ye,WANG Yanru,RONG Xiaoliu,et al.Mixed Source Localization and Gain-Phase Perturbation Calibration in Partly Calibrated Symmetric Uniform Linear Arrays[J].Signal Processing,2020,166:107267.
[12]MUDUMBAI R,HESPANHA J,MADHOW U,et al.Distributed Transmit Beamforming Using Feedback Control[J].IEEE Trans on Information Theory,2010,56(1):411-426.
[13]BRAY M,WERNER D,BOERINGER D,et al.Optimization of Thinned Aperiodic Linear Phased Arrays Using Genetic Algorithms to Reduce Grating Lobes During Scanning[J].IEEE Trans on Antennas and Propagation,2002,50(12):1732-1742.
[14]BHATTACHARYA R,BHATTACHARYYA T K,GARG R.Position Mutated Hierarchical Particle Swarm Optimization and Its Application in Synthesis of Unequally Spaced Antenna Arrays[J].IEEE Trans on Antennas and Propagation,2012,60(7):3174-3181.
[15]TRUCCO A,MURINO V.Stochastic Optimization of Linear Sparse Arrays[J].IEEE Journal of Oceanic Engineering,1999,24(3):291-299.
[16]QUEVEDO-TERUEL O,RAJO-IGLESIAS E.Ant Colony Optimization in Thinned Array Synthesis with Minimum Sidelobe Level[J].IEEE Antennas and Wireless Propagation Letters,2006,5:349-352.
[17]HUANG Baoqi,XIE Lihua,YANG Zai.TDOA-Based Source Localization with Distance-Dependent Noises[J].IEEE Trans on Wireless Communications,2015,14(1):468-480.
[18]LIU Zhangmeng.Conditional Cramer-Rao Lower Bounds for DOA Estimation and Array Calibration[J]IEEE Signal Processing Letters,2014,21(3):361-364.
[19]BISHOP A N,FIDAN B,ANDERSON B D O,et al.Optimality Analysis of Sensor-Target Localization Geometries[J].Automatica,2010,46(3):479-492.
[20]STOICA P,NEHORAI A.Music,Maximum Likelihood,and Cramer-Rao Bound[J].IEEE Trans on Acoustics,Speech,and Signal Processing,1989,37(5):720-741.
[21]DOTLIC I,CONNELL A,MA Hang,et al.Angle of Arrival Estimation Using Decawave DW1000 Integrated Circuits[C]//Proceedings of 14th Workshop on Positioning,Navigation and Communications,Bremen,Germany:IEEE,2017:1-6.





