0 引 言
飞艇由气囊构成的艇体、起稳定作用的舵面、载重用的吊舱和动力推进设备组成。艇体内一般充有低密度的惰性气体氦气，以产生浮力。飞艇具有续航时间长、功耗低、噪音小、污染少等特点，是一种安全环保、经济可靠的飞行器，具有重要的研究意义和应用价值［1］。飞艇是一种优良的雷达载体平台，为了不影响飞行器的外形形状和严格的空气动力学性能及达到宽的波束扫描角范围，一般将雷达柔性阵面天线与飞艇两侧部分囊体共形。现有文献关于天线共形飞艇飞行姿态对雷达性能影响分析较少，文献［2］说明对于双基雷达，实际飞行状态不可避免的影响其检测性能，并从航线、俯仰、偏航三个方面进行研究。文献［3］论证了雷达的测距精度、测方位角精度和测俯仰角精度均与载体姿态角大小有关，且姿态角越大时探测误差越大；总的来说，飞艇的姿态变化对雷达探测有不良影响，在其进行盘旋侦察时，雷达要求飞艇姿态具有一定的稳定性。
由于飞艇自身的非线性环节、大惯性、数学模型未知、时变参数和外界干扰等因素，飞艇的控制较为困难。目前飞艇的控制研究主要包含如下方法：模糊PID 控制方法［4］、鲁棒控制方法［5］、H∞控制方法［6］和神经网络［7］等。本文对存在模型不确定性和风场等干扰的飞艇，设计鲁棒的飞艇盘旋控制算法,外环采用自适应PID 控制，姿态内环采用线性自抗扰控制。控制器参数整定简单、便于工程实现。经过仿真验证以及实际飞行试验，证明所提出的盘旋控制方法的有效性，并给出了飞艇实际盘旋飞行时的姿态变化范围，为搭载的雷达进行运动补偿等提供了设计参考。
1 飞艇建模
对飞艇盘旋飞行进行分析后，对飞艇全系统进行建模。主要包括建立含风场特性的飞艇通用六自由度非线性模型；完成空中飞艇本体、动力、伺服和传感器的全包线建模；对飞行全剖面下平衡状态点进行快速配平与小扰动线性化。
1.1 飞艇的运动学方程
描述姿态的参数有多种形式,本文采用欧拉角进行飞艇姿态描述，飞艇盘旋飞行时姿态运动学方程为
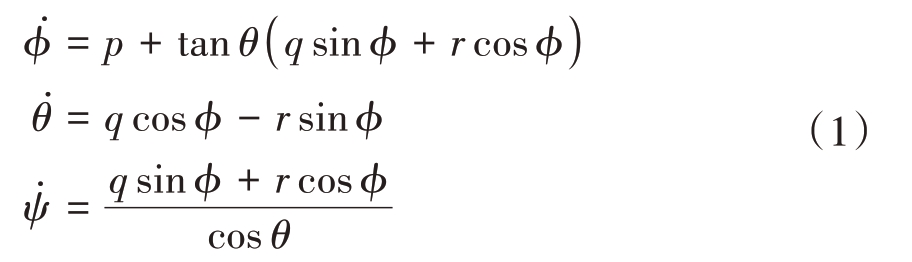
式中，ϕ,θ,ψ 分别为飞艇的滚转角、俯仰角和偏航角，p,q,r分别为飞艇的滚转角速度、俯仰角速度和偏航角速度在飞艇本体系下的分量。
1.2 飞艇的动力学方程
飞艇动力学建模时，其本体坐标系原点取在体心。考虑风场作用时，根据Lagrange 方程，可得出飞艇的如下动力学方程［8-9］：
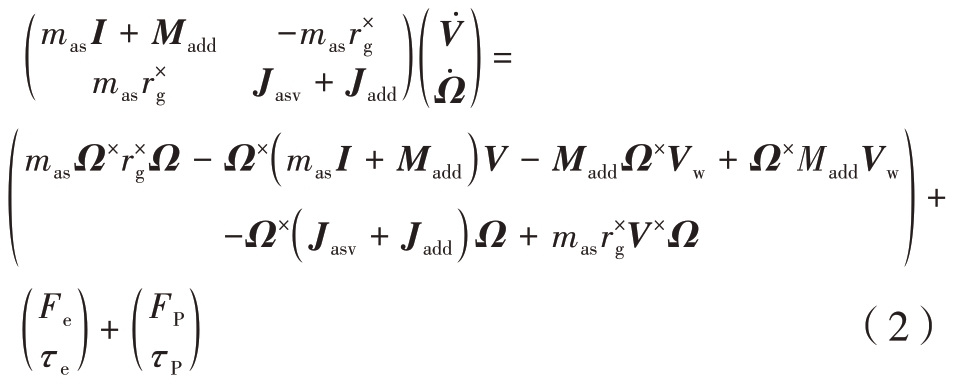
式中，V=(u v w)T 表示飞艇的飞行速度在本体系下的分量，Ω=(p q r)T 表示飞艇的角速度在本体系下的分量，mas 为飞艇的质量，rg 为飞艇的重心位置，Jasv 为飞艇的转动惯量，Madd 和Jadd 分别表示附加质量和附件转动惯量矩阵，Vw=(uwvwww)T 表示风速在本体系下的分量，I 表示三阶单位矩阵。FP和τP表示推力及其力矩在本体系下的分量，Fe 和τe 分别表示飞艇所受的其他力和力矩在本体系下的分量，包括重力及其力矩、浮力及其力矩和气动力及其力矩。
2 飞行盘旋控制器设计
2.1 控制目标
考虑上述飞艇的水平运动学与动力学模型，可以将飞艇的航线位置跟踪及姿态控制问题描述如下：
如图1所示，定义集合集:
={p1,p2,…,pn}，其中pi=(xi,yi)∈ℝ2,i=1,2,…,n 为飞艇位置。对于给定的pi,i=1,…,n-1，定义一个以Oc为圆心、Rc 为半径的圆形目标航线，即满足条件Bεi(pi)={p∈ℝ2:‖|Oc-pi| ‖=Rc}，则在存在风速风向及飞艇模型不确定性情况下，通过设计反馈控制律，最终控制飞艇位置能够始终满足上述的条件Bεi(pi),i=1,…,n-1 并最终稳定在Bεn(pn)范围内，同时满足飞艇俯仰角和滚转角姿态稳定。
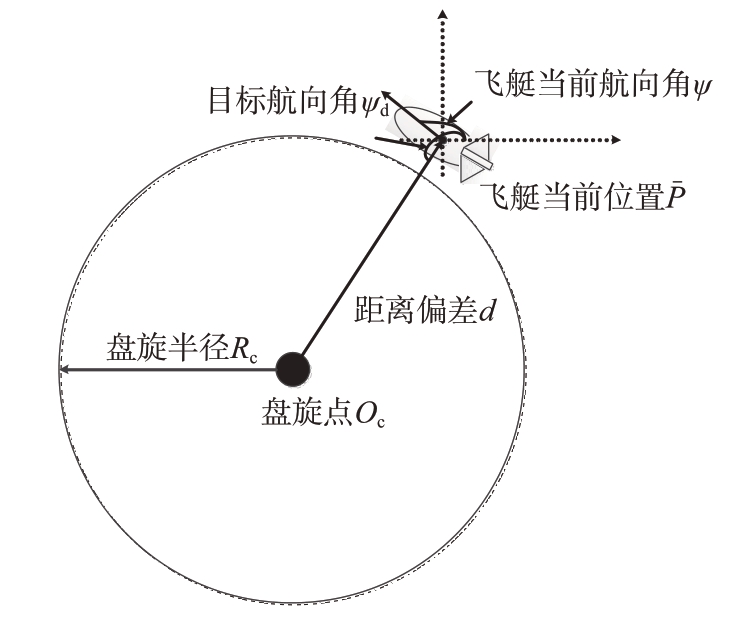
图1 飞艇盘旋飞行示意图
2.2 盘旋飞行控制器结构
飞艇盘旋飞行采用航线控制外回路（产生目标偏航角）和姿态控制内回路（跟踪目标偏航角）的双环控制结构：外回路是根据目标圆形航线、飞艇当前位置、水平速度产生目标偏航角；内回路设计姿态控制算法跟踪目标偏航角，同时对俯仰角和滚转角进行保持，进行控制分配后，操纵飞艇舵面。
控制功能的实现方式如图2所示。
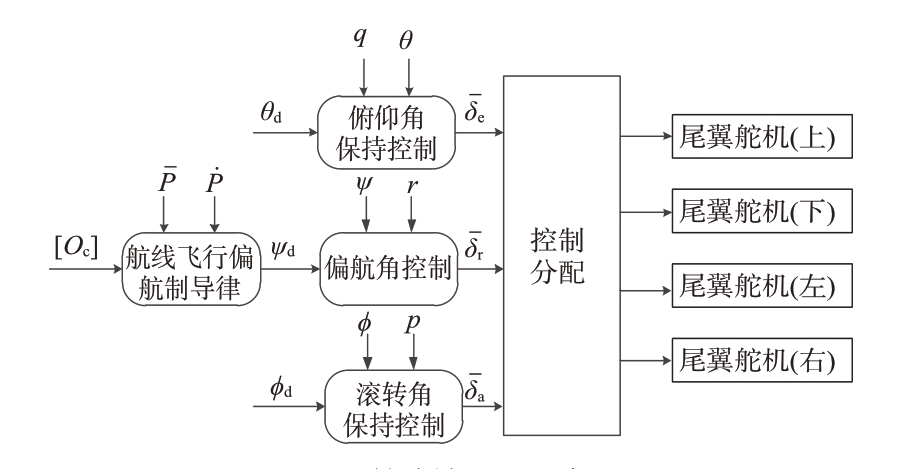
图2 控制框图示意图
2.3 盘旋航线外回路控制器设计
首先设计外环航线跟踪控制器。考虑平面内的运动，飞艇盘旋飞行时的位置记
飞艇盘旋飞行时的速度记作
=
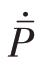飞艇盘旋飞行时的盘旋的点目标参数有[]RcOcλ；盘旋的目标航线是一条以Rc 为半径的圆，盘旋点Oc 坐标为
表示顺时针盘旋，λ=-1表示逆时针盘旋。
飞艇盘旋时的航线跟踪控制目标为
目标偏航角由如下表示：
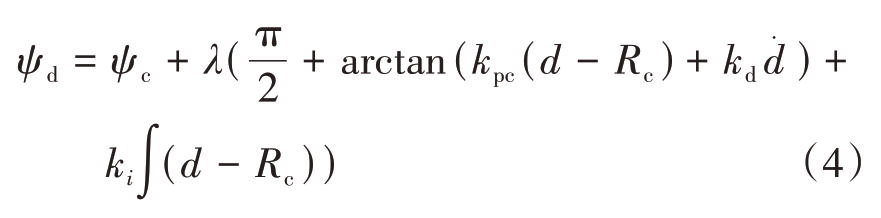
式中，
目标偏航角控制器式（4）中的比例系数kpc，为了避免可能存在的抖振现象，同时提升控制器误差消除的效果，将比例系数kpc改造成如式（6）。
飞艇当前位置与目标盘旋点间的距离d 和
满足:
sat 为饱和函数，上下标分别为函数值的上下限，arctan 为反正切函数，arctan 2 为四象限反正切函数，tanh为双曲正切函数：
2.4 姿态内回路控制器设计
姿态回路控制器主要是跟踪外回路计算的目标偏航角。考虑盘旋飞行时可视为平面内的运动，姿态和动力学方程分别退化为
式中J和d为
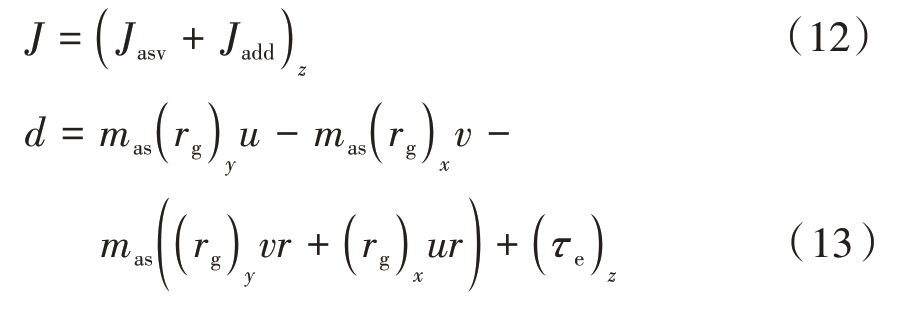
本文利用二阶线性自抗扰控制器完成目标偏航角的跟踪，主要由三部分组成：跟踪微分器、扩张状态观测器和线性状态误差反馈［10］。偏航内回路的姿态控制可以简化为二阶系统，其标准框如图3所示。
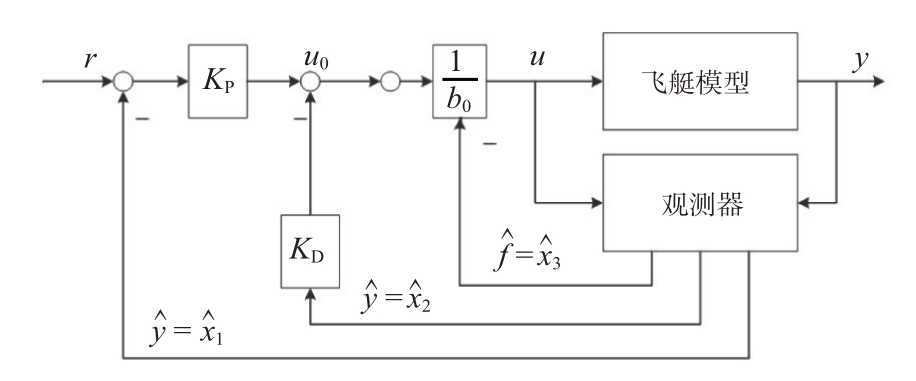
图3 二阶线性自抗扰控制框图
对于原系统，设计一个扩张状态观测器来实时估计系统状态以及包含系统内部不确定因素和外部扰动的总扰动。其最终形式如式（14）所示。
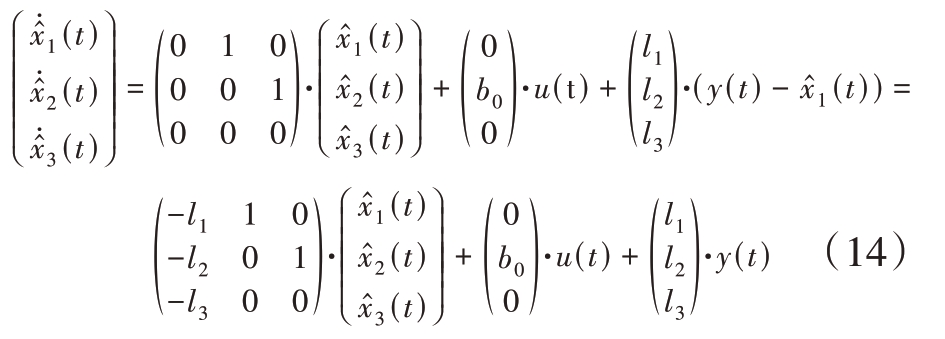
使用极点配置的方法设计增益，定义其观测器带宽为ω0，则其观测器增益为
设计如下其控制器来控制输出，同时可以将控制系统的极点配置在-ωc，根据文献［11］，一般选ω0 ≈（3～5）ωc；控制量设计如下：
对于飞艇控制内回路r(t)=ψd(t)，扩张状态观测器的x1(t)=ψ(t)。俯仰角和滚转角采用相同的控制算法进行设计。
2.5 仿真结果
本节对双回路盘旋飞行控制算法进行仿真,以验证其有效性。飞艇的目标航线为半径500 m 的圆形航线,飞艇的初始点坐标为（0,0），仿真固定时长。仿真结果如图4～6 所示，从仿真结果来看，所设计的控制器能够迅速跟踪目标偏航角，并稳定跟踪目标航线。
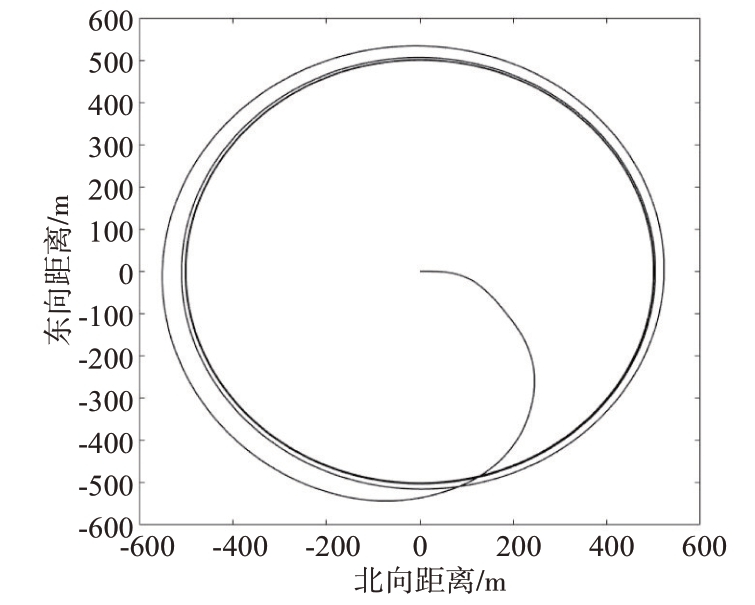
图4 飞行轨迹
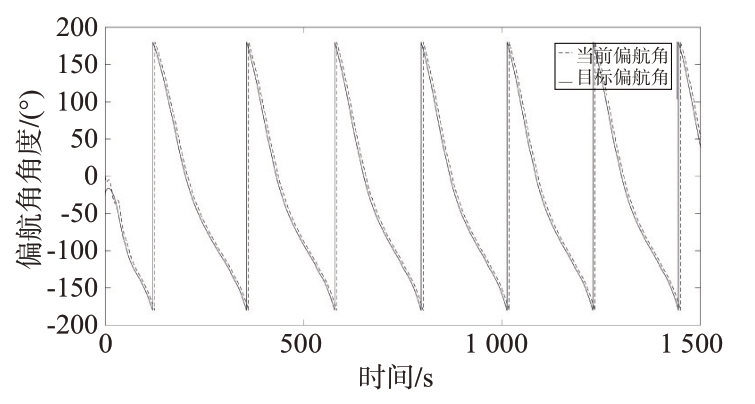
图5 偏航角跟踪情况
图6 航线跟踪侧偏距
2.6 飞行验证
使用该控制算法的飞艇在我国西北地区进行了长时间的飞行验证。某次航线飞行设计科目如下：飞艇首先地面遥控起飞到离地300 m 高度左右，调整姿态后切换为自主控制飞行模式，飞艇沿预定航线飞行1圈矩形航线，到达目标位置后执行定点盘旋飞行（盘旋半径500 m）。其试验飞行轨迹如图7所示。飞行过程中飞行盘旋轨迹变化如图8所示，盘旋半径误差小于2.1 m。俯仰角和横滚角连续变化，变换情况如图9所示，俯仰角变化范围［-1.5°，1.5°］，横滚角变化范围［-1°，2.5°］，经过评估实际飞行姿态变化情况满足所搭载雷达的要求。
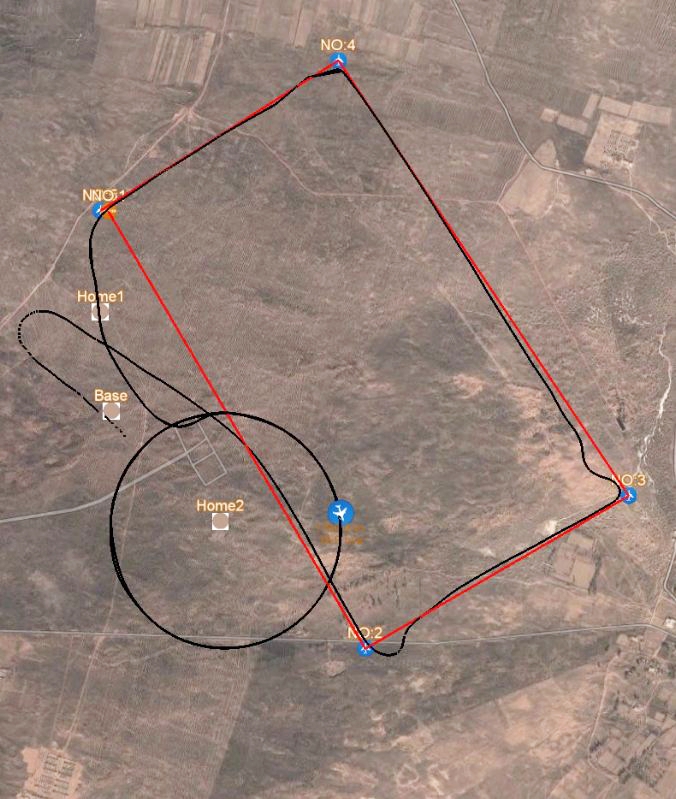
图7 飞行轨迹
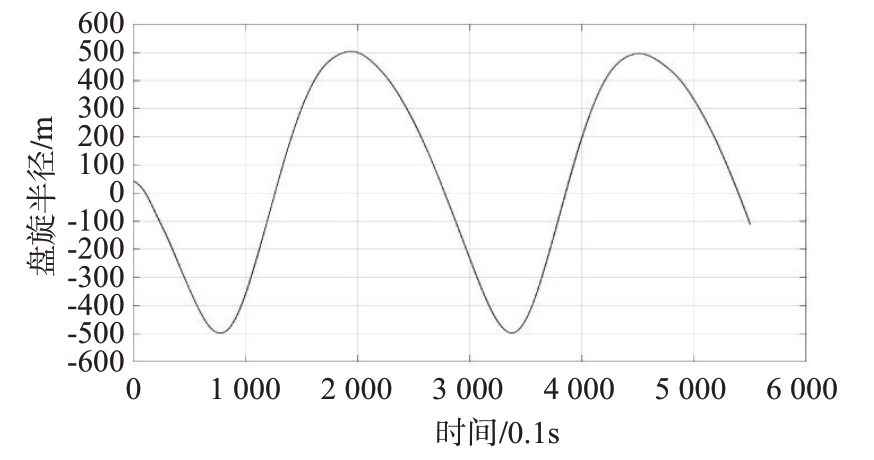
图8 盘旋半径
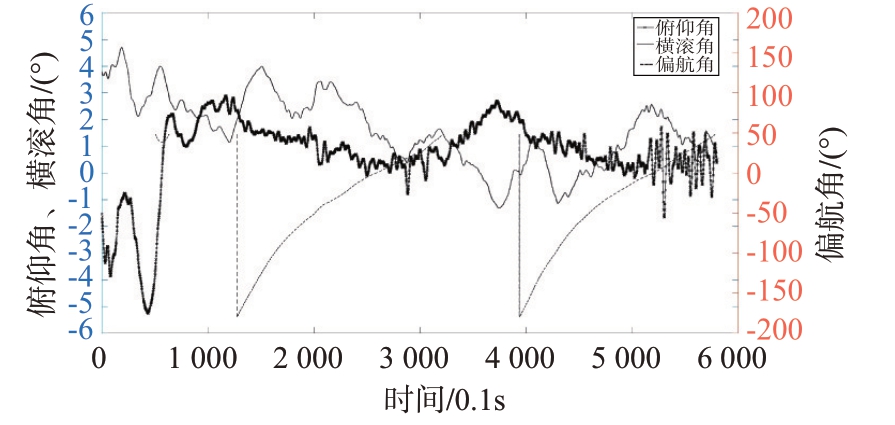
图9 盘旋姿态变化
3 结束语
本文针对天线共形飞艇搭载雷达载荷进行盘旋飞行的应用场景，使用自适应PID+线性自抗扰的双闭环控制算法，经过仿真验证和实际飞行试验，飞艇能够按照目标盘旋航线飞行，验证了控制算法的有效性，同时给出了实际盘旋飞行时的姿态变化情况，为后续雷达设计提供参考。
［1］初丽华.室内飞艇的建模与控制技术的研究［D］.沈阳：沈阳航空航天大学，2011．
［2］林兰瑾，何子述.平飞斜侧视双基雷达运动误差分析［J］.雷达科学与技术，2022，20（3）：347-354.
［3］季勤超，赵建军，贺林波，等.舰船姿态测量误差对雷达探测精度的影响分析［J］.计算机与数字工程，2019，47（2）：330-333.
［4］张经伦，杨希祥，邓小龙，等.基于模糊PID 的平流层飞艇姿态控制器设计［C］∥第五届中国航空科学技术大会论文集，青岛：中国航空学会，2021：29-35.
［5］SUVARNA S,CHUANG H,SINHA A,et al.Trajectory Planning Using Nonlinear Receding Horizon Optimization for an Autonomous Airship［C］//2021 Seventh Indian Control Conference（ICC）,Mumbai,India:［s.n.］,2021:99-104.
［6］WANG Y Y,WANG Q B,ZHOU P F,et al.Robust H_∞Directional Control for A Sampled-Data Autonomous Airship［J］.Journal of Central South University,2014,21（4）:1339-1346.
［7］KIM J H,YOO S J.Distributed Event-Triggered Adaptive Formation Tracking of Networked Uncertain Stratospheric Airships Using Neural Networks［J］.IEEE Access,2020,8:49977-49988.
［8］ADAMSKI W,PAZDERSKI D,HERMAN P.Robust 3D Tracking Control of an Underactuated Autonomous Airship［J］.IEEE Robotics and Automation Letters,2020,5（3）:4281-4288.
［9］PAIVA E C,AZINHEIRA J R,MOUTINHO A.Erratum on Influence of Wind Speed on Airship Dynamics［J］.Journal of Guidance,Control,and Dynamics,2008,31（2）:443-444.
［10］许锐，郭玉英.基于双闭环ADRC 的四旋翼飞行器轨迹跟踪控制［J］.飞行力学，2022，40（5）：59-65.
［11］HERBST G.A Simulative Study on Active Disturbance Rejection Control（ADRC）as A Control Tool for Practitioners［J］.Electronics,2013,2（3）:246-279.
