0 引 言
逆合成孔径雷达（ISAR）成像在军事和民用领域得到大量研究和应用，对ISAR 成像的精度与速度的要求也越来越高。压缩感知理论自提出以来，在可压缩信号处理方面体现出突出性能，得到了大量的关注和研究。在ISAR 成像中，雷达散射中心理论符合压缩感知对于未知参数稀疏分布的要求，使得压缩感知理论被成功应用于ISAR 成像，同时降低了对数据采样率的要求［1-3］。
压缩感知理论主要包括3个部分：信号的稀疏表示、测量矩阵以及重构算法。重构算法作为模型参数估计的重要步骤，一直是压缩感知理论的研究重点。根据重构模型直接寻求l0 范数最小化是一个NP 难问题，因此将l0 范数的最优化问题转化为l1 范数正则化最小二乘问题［4］。为解决此问题，已经被提出的算法有基追踪（BP）算法［5］、内点法［6］、稀疏重构（SpaRSA）算法［7］、阈值迭代（ISA）算法［8］、梯度投影稀疏重构（GPSR,Gradient Projection Sparse Reconstruction）算法［9］等。
为改进算法的性能，文献［10］对SpaRSA 算法进行了改进，使用一种非单调策略来确定迭代步长以加快收敛速度。文献［11］提出了迭代近似梯度投影（IAGP）算法，用近似的梯度来代替GPSR算法中的梯度模型，降低了计算量。文献［12］在常规GPSR 算法的基础上，通过Hessian 矩阵的近似得到迭代的二次近似模型，并结合延迟策略得出一种新的迭代步长，提高了算法的重构效率。
基于正则化参数在凸优化稀疏重构算法中的重要性［13-16］，本文提出一种自适应权重GPSR（AW GPSR）算法，并将其用于ISAR成像，此处的权重即为正则化参数。该快速算法中，在常规GPSR 算法的基础上，给ISAR 图像中每个散射点配以不同的正则化参数，并在迭代过程中自适应调整此正则化参数，以提升ISAR成像的迭代效率。
1 ISAR成像模型
在很短的相干累积时间内，ISAR 成像基本原理可等效为图1所示的二维转台模型。由于目标尺寸远远小于目标到雷达的距离，所以在对回波数据完成运动补偿及相位校正以后，目标上任一散射点p(a,b)到雷达的距离可近似为
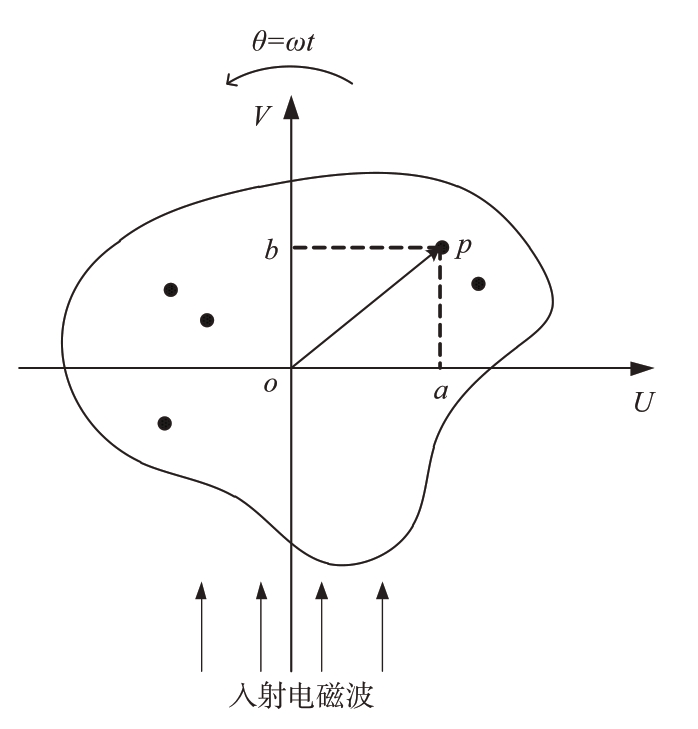
图1 ISAR成像二维转台模型
式中，a和b为散射点的坐标，R0为雷达到目标中心的距离，θ为目标转动的角度。
根据理想散射中心模型，目标的谱域后向散射场可表示为
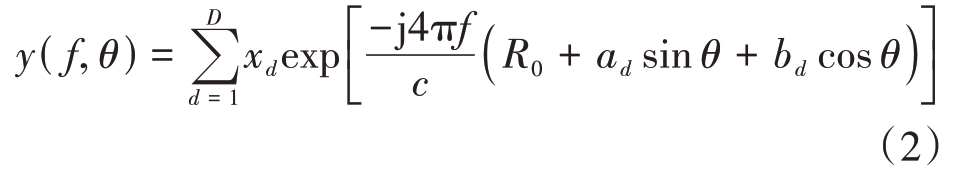
式中，f 为入射频率，xd 为第d 个散射点的散射幅度，d=1，2，…，D。其中exp(-j4πfR0/c)项不影响各个散射点之间的相位差，故在后续推导中将其忽略。
将雷达向目标发射信号的方位角离散为M 个角点，第m 个角点为θm，m=1,…,M。每个角点发射N 个频率步进的脉冲，第n 个频点为fn，n=1,…,N。由此，在第m个方位角的第n个频点的散射场经推导可得
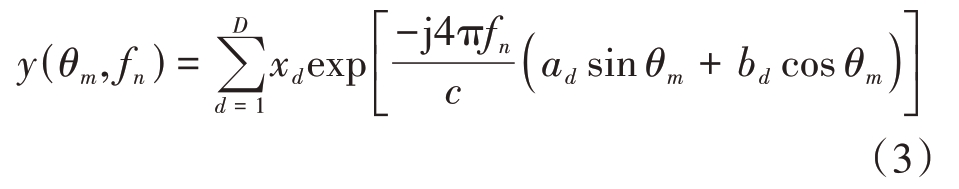
将二维成像场景离散采样P行Q列，在压缩感知里，P 通常取M 的倍数，Q 通常取N 的倍数。为使散射中心不发生越距离单元徙动，雷达的相对转动角度一般很小，因此可近似认为sin θm ≈θm，cos θm ≈1。由于在ISAR 成像中，雷达脉冲带宽相对于中心频率非常小，则可以认为在频率变化时，波长近似不变。基于以上条件，通过推导可得散射场表达式：
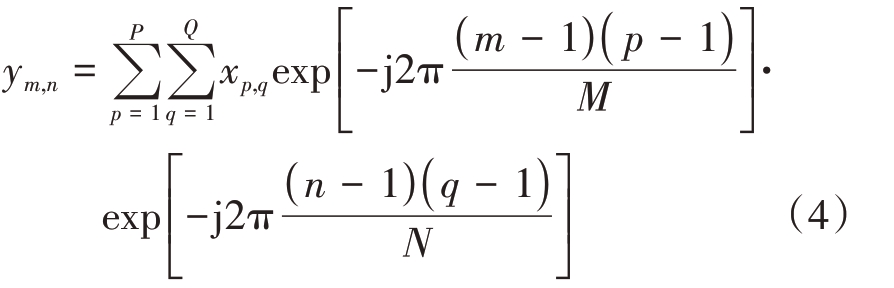
将上式改写为矩阵形式可得
式中Y∈CM×N 为散射回波信号的观测矩阵，X∈CP×Q为散射幅度矩阵，也是需要估计的未知参数。Φr∈CM×P 与Φa∈CN×Q 分别为距离向和方位向的信息矩阵，其具体表达式为
由于强散射点数量远小于散射幅度矩阵X 的尺寸，所以矩阵X 具有稀疏性，可以利用压缩感知理论的重构算法，基于观测信号Y予以重构。
为适应梯度投影稀疏重构（GPSR）算法的需要，将式（5）作矢量化处理，改为一维表达式：
式中y∈CMN×1、x∈CPQ×1 分别为观测矩阵Y、散射幅度矩阵X 矢量化后的一维数组，Θ=Θa⊗ΘTr∈CMN×PQ为矢量化后的感知矩阵，符号⊗为Kronecker积。
2 GPSR参数重构算法
2.1 常规GPSR算法
在压缩感知参数重构中，可基于l1范数最小化原则求解：
针对上式，可建立参数重构的目标函数为
τ 为正则化参数。为了将其转化成一个二次问题，将x分为正负两部分，引入置换式：
其中(x)+=max{0,x}，ui=(xi)+，vi=(-xi)+，i=1,2,3,…,I，I=PQ 是向量x 的长度。然后x 的l1 范数可表示为
1I=[1,1,…,1]T为长度为I的单位列向量。
然后可将式（10）改写为下边界受限的二次方程：
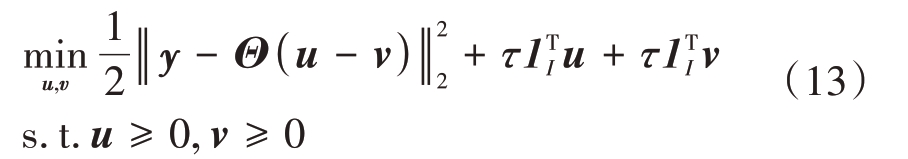
将上式再次改写为
式中，
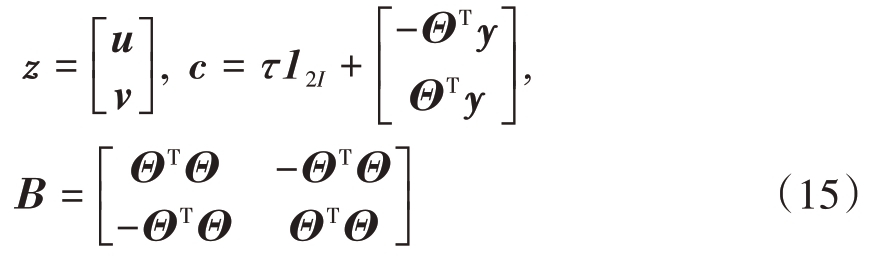
常规GPSR 算法利用梯度投影算法来求解式（14）［17］。在第k 次迭代中，将参数估计值zk 沿着负梯度-∇F(z(k)) 方向进行修正，修正公式如下：
式中，λ(k)∈[0,1]，α(k)需要确定。
然后定义函数g(jk)为
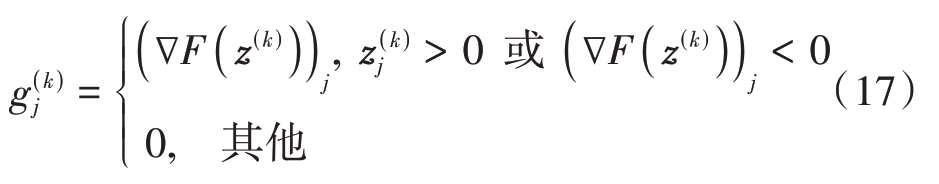
式中，j=1,2,…,J，J=2PQ 也是矢量z 的长度，且有g(k)={g(1k),g(2k),…,g(Jk)}。
确定第k次迭代中的初始迭代步长因子α(0k)：
常规GPSR算法步骤如下：
Step0：给定初始化的z(0)，选择常数β∈(0,1),μ∈(0,1/2)，令k=0。
Step1：通过式（18）计算初始步长因子α(0k)。
Step2：通过回溯线搜索，选择α(k)为序列α(0k),βα(0k),β2α(0k)…中第一个满足下式的数字：
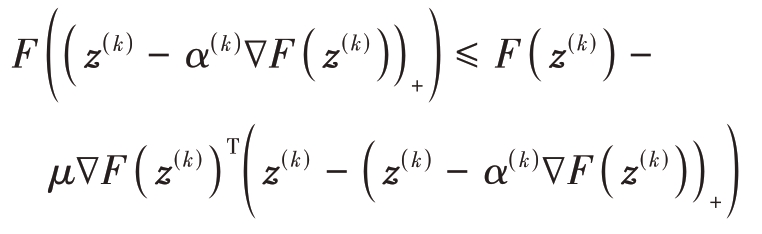
Step3：更新z值：z(k+1)=(z(k)-α(k)∇F(z(k)))+。
Step4：测试z(k+1) 是否满足终止条件。如满足条件则终止迭代；否则令k=k+1，并转回Step1。
2.2 自适应权重GPSR算法
自适应权重GPSR（AW GPSR）算法中，对于x中不同幅值的元素赋予不同的正则化参数，以加快参数重构的收敛速度。其参数优化的目标函数为
式中，wI∈RI为权重向量，表示为
式中，wi 是对应于参数x 中的第i 个元素的正则化参数。
得到参数优化的目标函数为
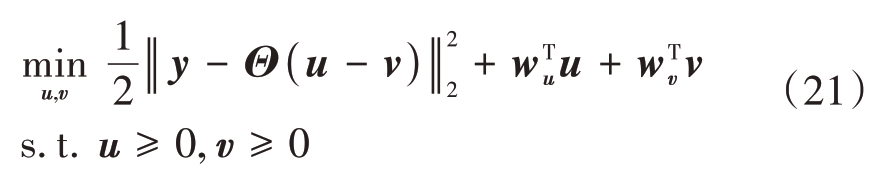
式中，wu 为对应于u 的权重矢量，wv 为对应于v 的权重矢量。将目标函数进一步写为
式中，
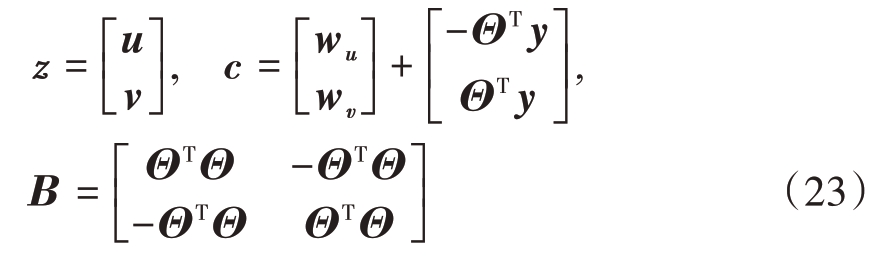
令w=
表示对应于z的权重矢量。
在AW GPSR算法里，也是利用梯度投影算法来求解未知参数z，其原理和常规GPSR算法相同。只是在迭代过程中，还存在一个加权系数w的更新问题。
为参数z 加权以提高迭代效率的思想是，在迭代过程中，对于一个值很小的zi，可以为其添加一个较大的正则化参数wi，从而使它在后面的迭代中快速地收敛至0；对于一个值较大的zi，可以为其添加一个较小的正则化参数wi，以使其在下次的迭代中保持不变。
在该算法中，通过前一次迭代的z(k)和w(k)对正则化参数w 进行更新，得到w(k+1)。设z(k)的支撑集为Γ(k)，也就是z(k)中非零元素的下标集合，则正则化参数w更新为
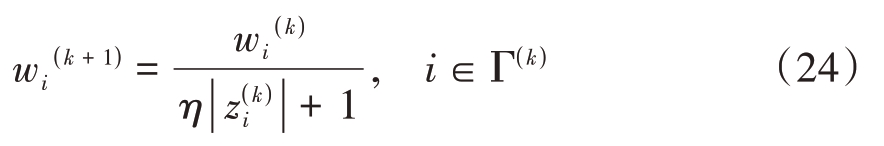
式中，η=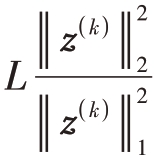
，L=2PQ是待重构参数z的长度。
AW GPSR算法步骤如下：
Step0：给定初始化的z(0)，w(0)，选择常数β∈(0,1),μ∈(0,1/2)，令k=0。
Step1：计算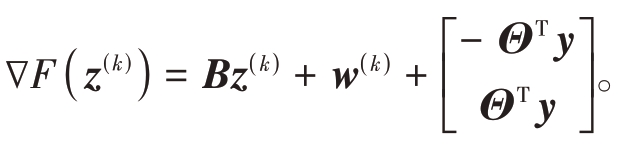
Step2：通过式（18）计算初始迭代步长因子α(0k)。
Step3：通过回溯线搜索，选择α(k)为序列α(0k),βα(0k),β2α(0k)…中第一个满足下式的数字：
Step4：更新z(k+1)=(z(k)-α(k)∇F(z(k)))+；根据式（24），更新wi(k+1)，得w(k+1)。
Step5：测试z(k+1) 是否满足终止条件。如满足条件则终止迭代；否则令k=k+1并转回Step1。
3 实验结果及分析
本文对AW GPSR 算法进行了Matlab 编程和ISAR 成像测试，使用仿真数据和实测数据进行ISAR 成像实验，并与常规GPSR 算法、距离-多普勒（R-D）算法、ESPRIT 算法在计算时间与成像效果方面进行了比较。
仿真实验使用的目标模型为Su27 战机，其CAD 模型如图2所示，电磁仿真的基本参数为：发射信号中心频率为10 GHz，带宽为0.5 GHz，步进频采样，采样频点为64；俯仰角固定为85°；方位角范围为［-1.432 4°，1.432 4°］，采样64 个角点；所以仿真得到的回波二维谱矩阵的尺寸为64×64。对应的径向和横向分辨率均为0.3 m。实验环境为CPU 主频3.20 Hz、64 位Windows10 操作系统、Matlab R2018a。
图2 Su27飞机CAD模型
为证明AW GPSR 算法在目标函数收敛速度方面的效果，本实验记录并给出了AW GPSR 算法与常规GPSR 算法的目标函数迭代曲线对比图，如图3所示，其横坐标为迭代次数，纵坐标代表目标函数值，从图中可以看出，AW GPSR 算法的目标函数收敛速度优于常规的GPSR算法。
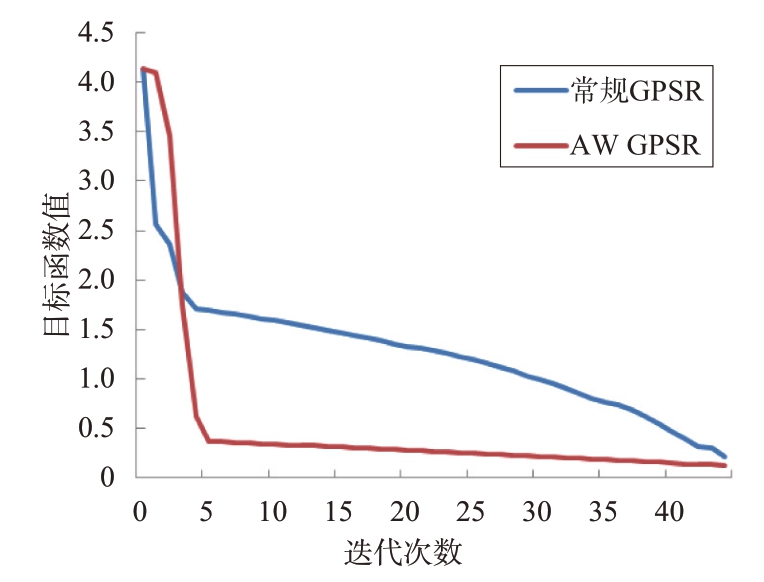
图3 目标函数收敛趋势比较
在对于仿真数据的成像效果方面，实验比较了4种算法在信噪比分别为0，5，10 dB条件下进行ISAR成像的结果，如图4所示。
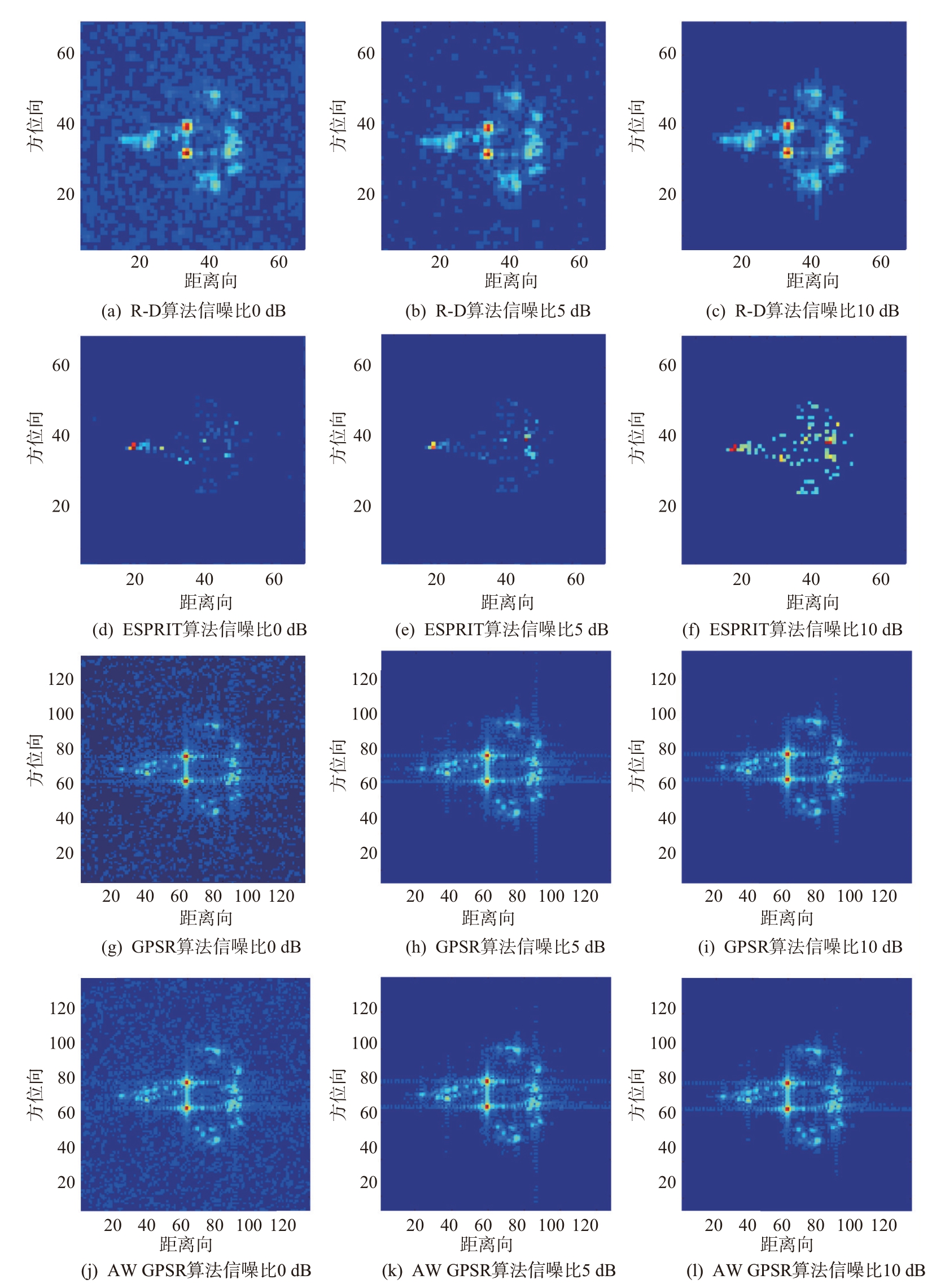
图4 基于仿真数据的ISAR成像结果
从图中可以看出，R-D 算法和ESPRIT 算法成像的尺寸与回波二维谱矩阵的尺寸相同，都为64×64。而常规GPSR 算法与AW GPSR 算法属于压缩感知类算法，散射幅度矩阵的尺寸可以大于回波二维谱矩阵，本实验设定的散射幅度矩阵X 的尺寸为128×128。从ISAR 成像效果来看，AW GPSR算法要好于R-D算法和ESPRIT算法，与常规GPSR算法相当。
为更准确地比较AW GPSR 算法与常规GPSR算法的ISAR成像效果，本文引入了ISAR图像的重构均方误差指标，即以常规GPSR 算法在无噪声条件下所成ISAR图像为参考图像，计算每幅ISAR图像相对于参考图像的均方误差。表1给出了两种算法在不同信噪比条件下的重构均方误差，从表中可以看出，两种算法在不同信噪比下的重构均方误差都十分接近，证明了AW GPSR 算法与常规GPSR成像效果相当。
表1 两种算法误差对比
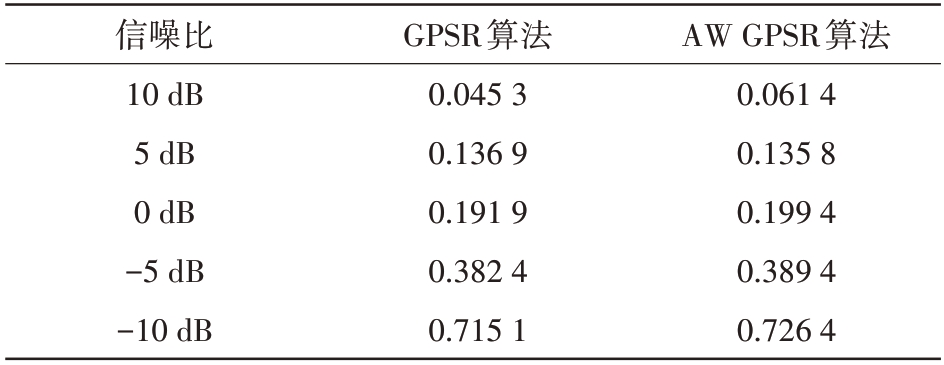
信噪比10 dB 5 dB 0 dB-5 dB-10 dB GPSR算法0.045 3 0.136 9 0.191 9 0.382 4 0.715 1 AW GPSR算法0.061 4 0.135 8 0.199 4 0.389 4 0.726 4
表2为4 种算法对于Su27 战机仿真数据的ISAR 成像时间对比，其中R-D 算法成像时间最短，ESPRIT 算法成像时间最长；AW GPSR 算法成像时间要短于常规的GPSR 算法，在本次实验中，AW GPSR 算法的成像时间相较于常规GPSR 算法大概减少了23%。
表2 4种算法成像时间对比
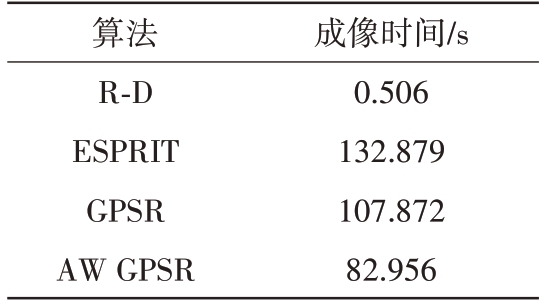
算法R-D ESPRIT GPSR AW GPSR成像时间/s 0.506 132.879 107.872 82.956
本实验采用实测数据进行了ISAR 成像，实测数据来自于Yak-42 飞机。发射信号的中心频率为5.52 GHz，带宽为0.4 GHz，脉冲重复频率为400 Hz，径向分辨率为0.375 m。上述4 种算法对于实测数据的ISAR成像结果如图5所示。
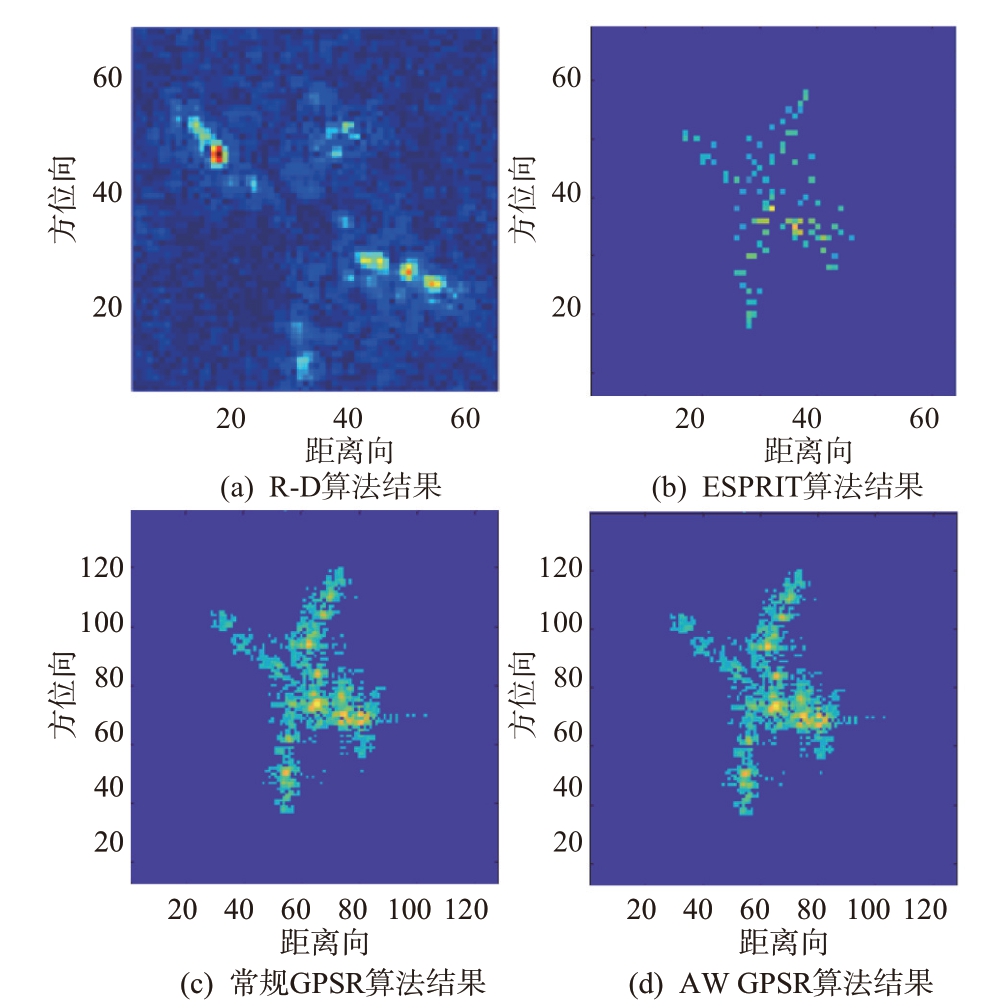
图5 ISAR成像实测数据
由图5可知，AW GPSR 算法的ISAR 成像效果与常规GPSR 算法相当，但明显好于传统的R-D 算法和ESPRIT算法。关于上述4种算法采用Yak-42飞机实测数据进行ISAR 成像的计算时间对比，其情况与仿真数据类似，此处不再列出。
4 结束语
本文在GPSR 算法的基础上，研究了正则化参数对算法迭代效率的影响，并提出一种AW GPSR算法，该算法针对ISAR 图像中的不同散射点使用不同正则化参数，以提高ISAR 成像迭代效率。本文采用仿真数据和实测数据，对比了AW GPSR 算法、常规GPSR 算法、传统的R-D 算法以及ESPRIT算法的计算时间和ISAR 成像效果。相较于常规GPSR算法，AW GPSR算法的参数重构迭代收敛更快，因此具有更短的ISAR 成像计算时间，其计算时间缩短了约23%。在ISAR 成像效果方面，AW GPSR 算法和常规GPSR 算法相当，但明显优于传统的R-D算法和ESPRIT算法。
［1］BI H,LI Y,ZHU D Y,et al.An Improved Iterative Thresholding Algorithm for L1-norm Regularization Based Sparse SAR Imaging［J］.Science China: Information Science,2020,63:219-301.
［2］SHAO S,ZHANG L,LIU H W.High-Resolution ISAR Imaging and Motion Compensation with 2-D Joint Sparse Reconstruction［J］.IEEE Trans on Geoscience and Remote Sensing,2020,58（10）:6791-6811.
［3］ZHANG Y,XING M D.Joint Method of ISAR Imaging and Scaling for Maneuvering Targets via Compressive Sensing［J］.IEEE Sensors Journal,2019,19（17）:7300-7307.
［4］CANDES E J,PLAN Y.A Probabilistic and RIPless Theory of Compressed Sensing［J］.IEEE Trans on Information Theory,2011,57（11）:7235-7254.
［5］LUO C,BA J,CARCIONE J M.Basis Pursuit Anisotropic Inversion Based on the L1-L2-Norm Regularization［J］.IEEE GeoscienceandRemoteSensingLetters,2021,19:1-5.
［6］JIANG H T,KATHURIA T,LEE Y T,et al.A Faster Interior Point Method for Semidefinite Programming［C］//2020 IEEE 61st Annual Symposium on Foundations of Computer Science（FOCS）,Durham,NC,USA: IEEE,2020:910-918.
［7］WRIGHT S J,NOWAK R D,FIGUEIREDO M A T.Sparse Reconstruction by Separable Approximation［J］.IEEE Trans on Signal Processing,2009,57（7）:2479-2493.
［8］QIAN Y,ZHU D Y.Suppression of Ghost Targets in Focusing Azimuth Periodically Gapped SAR Raw Data with Complex Iterative Thresholding Algorithm［J］.2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop（SAM）,Hangzhou,China:IEEE,2020:1-4.
［9］QIAN M,ZHANG X Y,LI R C.Gradient Projection for SAR Image Sparse Reconstruction Based on Shearlet［C］∥2019 3rd International Conference on Electronic Information Technology and Computer Engineering（EITCE）,Xiamen,China:IEEE,2019:551-556.
［10］HUANG Y,LIU H.A Barzilai-Borwein Type Method for Minimizing Composite Functions［J］.Numerical Algorithms,2015,69（4）:819-838.
［11］LIU Z Y,WEI Z H,SUN W Y.An Iteratively Approximated Gradient Projection Algorithm for Sparse Signal Reconstruction［J］.Applied Mathematics and Computation,2014,228:454-462.
［12］何川美，刘红卫，刘泽显.修正的迭代近似梯度投影算法在压缩感知中的应用［J］.吉林大学学报（理学版），2017,55（6）:1443-1448.
［13］ASIF M S,ROMBERG J.Fast and Accurate Algorithms for Re-Weighted ℓ1-Norm Minimization［J］.IEEE Trans on Signal Processing,2013,61（23）:5905-5916.
［14］GAO Y X,ZHANG X Y,XING M D,et al.ISAR Imaging Based on Homotopy Re-Weighted ℓ1-Norm Minimization［C］∥2019IEEEInternationalGeoscienceandRemoteSensing Symposium,Yokohama,Japan:IEEE,2019:1204-1207.
［15］HU X Y,MA C Z,LU X Y,et al.Compressive Sensing SAR Imaging Algorithm for LFMCW Systems［J］.IEEE Trans on Geoscience and Remote Sensing,2021,59（10）:8486-8500.
［16］李昕艺，刘三阳，张朝辉.自适应权重的GPSR 压缩感知重构算法［J］.浙江大学学报（理学版），2018，45（2）：156-161.
［17］梁瑞宇，邹采荣，王青云，等.基于自适应次梯度投影算法的压缩感知信号重构［J］.信号处理，2010，26（12）：1883-1889.
