0 引 言
高频地波雷达(High Frequency Surface Wave Radar,HFSWR)工作在短波段(3~30 MHz),极易接收到来自各种短波电台、通信设备的射频干扰信号(Radio Frequency Interference,RFI),导致雷达数据质量下降,严重影响高频地波雷达目标探测以及海态信息的提取。
避免RFI 的一种直接方法就是利用实时频谱监测结果,找到一个不被RFI污染的干净频段作为雷达的工作频段[1-2]。但是在实际应用中,几乎很难找到一段有足够带宽(>30 kHz)且无明显干扰的频段。RFI 抑制方法主要有基于压缩感知的方法[3]、经验模态分解方法[4-5]、分数阶傅里叶变换[6-8]等。近年来,正交子空间投影技术被应用于RFI的抑制并取得了较好的效果。正交子空间投影的关键在于如何准确估计出相互正交的信号子空间和干扰子空间。文献[9]讨论了RFI在“五域六图”的特性,子空间类算法利用RFI的强距离相关性和方向特性[10]对其进行抑制,可以在慢时域[11]、多普勒域[12]、空域[13-14]等单一域处理,也可以联合多个域的特征抑制RFI[15-16]。慢时域即雷达重复周期(Period),而快时域则指一个雷达重复周期内接收数据的采样点,快时间维做一次快速傅里叶变换(Fast Fourier Transform,FFT)解距离得到距离域,慢时间维做一次FFT 解速度得到多普勒域。文献[15]提出的基于高阶奇异值分解(Higher-Order Singular Value Decomposition,HOSVD)的多域联合子空间投影RFI 抑制算法,联合RFI 在多普勒域的强距离相关性和空域的方向特性,能够得到较单一域处理更好的干扰抑制效果。
现有的子空间类方法存在以下三个问题,难以应用到雷达数据的实时批处理中。首先,这类算法需要得到雷达数据的距离-周期(Range-Period,RP)谱或距离-多普勒(Range-Doppler,RD)谱,然后根据谱图特征划定干扰范围,再进行干扰抑制。应用到雷达数据实时批处理中时,一般通过滑窗的方法对每段数据进行无差别抗干扰处理,这样会大大降低数据处理效率,而且对于无污染的数据,强行估计干扰子空间作投影,也会影响回波数据质量。其次,这类算法估计干扰子空间没有一个判决标准,通常约定最大的一个或者两个特征值对应的特征矢量构成干扰子空间,数据批处理中往往会遇到不同的干扰情况,固定特征值的选取不利于干扰的准确消除,需要有一个选取标准,在数据批处理时能够根据不同数据特征自适应地估计干扰子空间。最后,这类算法都只关注左奇异矩阵列向量信息,忽略了右奇异矩阵行向量所包含的信息,限制了干扰子空间投影的方式,如文献[15]提出的HOSVD 方法在多普勒域消除RFI,由于RFI 在不同多普勒单元没有相关性,导致HOSVD 后的第一展开模式矩阵不能估计干扰子空间,利用右奇异矩阵信息,三种展开模式矩阵都可以估计干扰子空间,有利于提高干扰子空间估计准确性。本文主要针对以上三个问题,提出解决方案,形成可以在实测数据批量实时处理中使用的RFI抑制算法。
1 RFI检测
批处理雷达数据时,增加干扰检测的预处理流程,可以大大提高数据处理效率。常见的干扰检测算法有基于功率大小的门限检测[17]、恒虚警检测器[18]以及一些图像处理算法[19-20],以上方法都需要先得到雷达数据RD 谱,之后通过图像特征作进一步分析,不适合用在雷达数据实时批处理中。将雷达数据在慢时域分段后,利用频谱监测数据对每一段数据干扰情况进行判定,给出干扰有无的判定标志位,便于后续干扰抑制工作的进行,简化处理流程。
在2021年东山、龙海双站双频组网探测实验中,增加了频谱监测模块,采集了实时环境噪声数据,实时频谱监测数据在雷达工作频段的频谱特征能很好地反映雷达数据是否受RFI的影响,以该实验项目为背景介绍基于频谱监测数据的RFI 慢时域检测方法。频谱监测实现方式为在48 MS/s的采样率下,在接收脉冲末尾连续采集2 048 点环境噪声数据,采样时长约为43 μs。对该2 048点数据进行打包上传,在上位机实现FFT 得到实时的环境噪声频谱。频谱监测每隔2 s 实现一次,每次只实现单个天线的高低频环境的同时监测。每隔两秒切换下一个监测通道,实现完整的4根天线环境监测周期为8 s。
2 048 个采样点的频率分辨精度完全不够,为了提高精度,需要将4 根天线的环境监测采样数据按照时间先后顺序进行拼接,在雷达相干积累时间5 min 内有150 场采样数据,共有150×2 048=307 200个采样点,以25 600个采样点为一段进行拼接,共分为12段,此时频率分辨率为
扫频周期250 ms,5 min回波数据包含1 200个扫频周期,将100 个扫频周期划为一段,即每段时长为25 s,在慢时域上将数据分为12 段,每段数据按照时间先后依次对应到12 段频谱监测数据,通过对每段频谱监测数据的分析判断该段时间内是否存在RFI,对有RFI 影响的数据段进行定位,之后在慢时域上利用HOSVD 方法进行干扰的消除。图1展示了雷达高频范围(11.5~13.5 MHz)与低频范围(7~9 MHz)的频谱监测谱图,将距离这两个频段都较远的频段(20~24 MHz)作为背景噪声频段,定义为底噪窗,检测窗的频率范围设置取决于雷达工作频率、扫频带宽以及扫频模式,经过混频、低通滤波后,只有载频在雷达发射信号频带范围内的干扰信号方能影响回波数据。一般存在RFI时,检测窗内会有明显尖峰,通过检测窗峰值功率与底噪窗平均功率计算检测信噪比,大于设定阈值时即认为该时间段存在RFI。
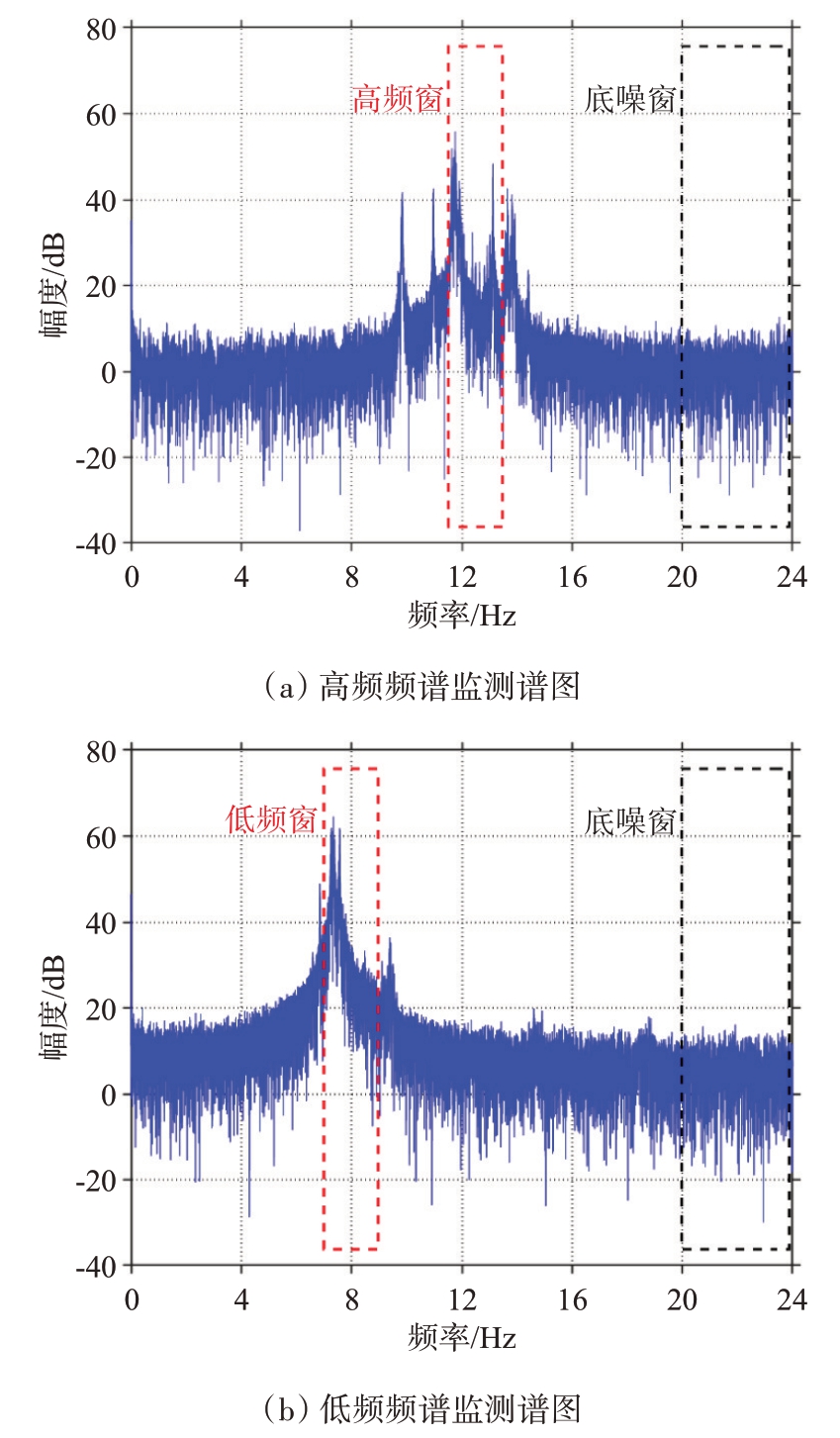
图1 频谱监测谱图
2 慢时域分段RFI抑制
雷达原始采样数据做第一次FFT 变换,解距离得到通道-距离-慢时间维数据,接着利用HOSVD 方法抑制RFI。干扰抑制前需要先将雷达数据在慢时域上分段,来降低HOSVD 算法的运算量,提高干扰抑制效率。与第1 节中频谱监测数据分段检测RFI相对应,将一个相干积累时间内雷达数据在慢时域分为12 段,即每段数据25 s。HOSVD通过矩阵展开的方式建立了张量和矩阵之间的联系,定义了一种张量分解方法[21],并已应用于图像处理[22]、人脸识别[23]、雷达信号处理[24]等多个领域。
2.1 训练张量构造
RFI分布于所有距离元,而海洋回波仅存在于近距离元,因此构造训练张量时尽量选取不包含海洋回波的远距离元或负距离元,有利于提高干扰子空间估计的准确性。假设在慢时间维上将每Q 个扫频周期分割为一段,每一段选取M 个通道、P 个远距离元或者负距离元数据构造一个大小为P×Q×M 的张量,称之为训练张量A,如图2所示。
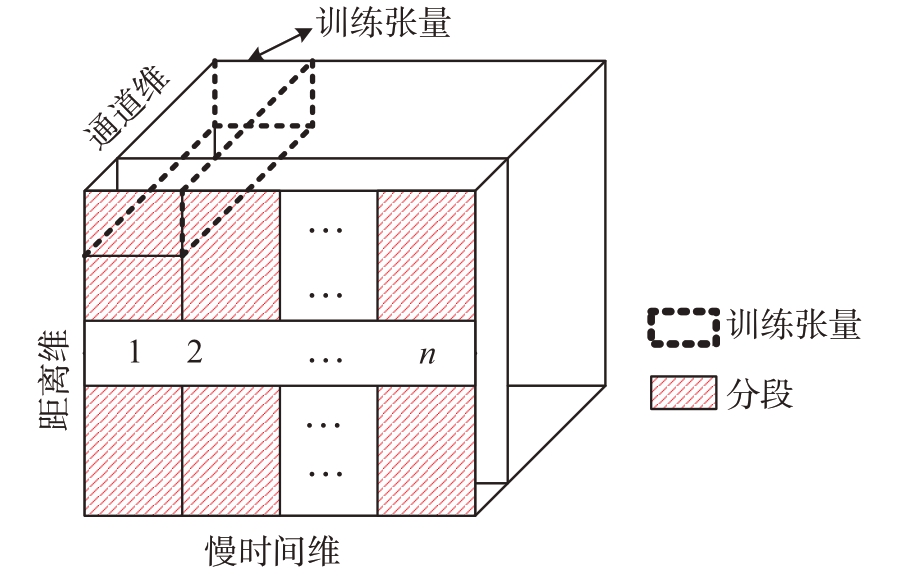
图2 训练张量构造示意图
2.2 RFI子空间估计
将训练张量A 展开,得到三种展开模式矩阵如图3所示,其中阴影部分代表RFI。分析三种模式展开矩阵的形式,利用其得到的左、右奇异矩阵包含的频率信息估计RFI 子空间,其中左奇异矩阵列向量表征模式矩阵中各分量列与列之间的相关性,而右奇异矩阵行向量表征模式矩阵中各分量行与行之间的相关性,左、右奇异向量对应的奇异值矩阵中奇异值的大小表征了模式矩阵各分量列与列或行与行之间相关性的强弱。数的判定确定d1,d2,d3 的取值,提高RFI 子空间估计的准确性,以免d 选取偏小导致RFI 不能被完全消除或者d 选取偏大将部分噪声分量划入RFI子空间,投影到其他距离元时影响有用信号分量。
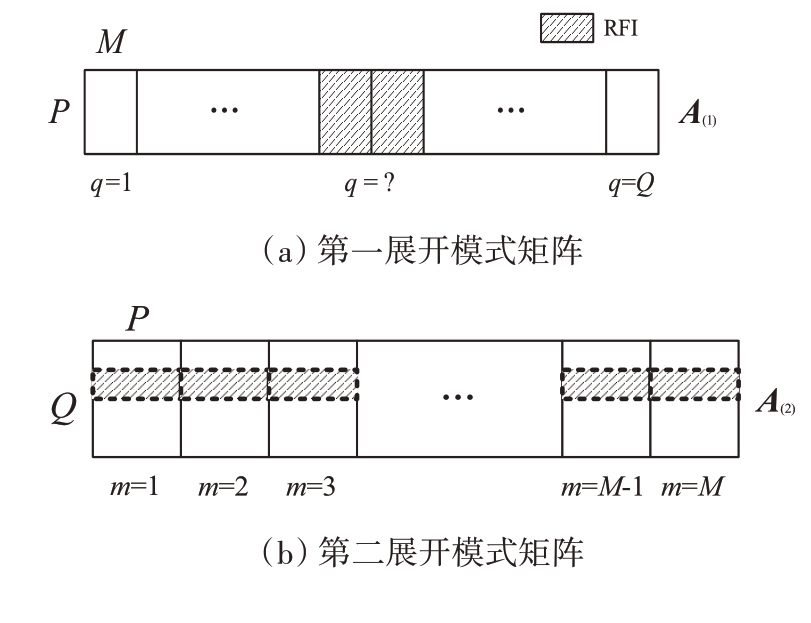

图3 训练张量矩阵展开示意图
对于第一展开模式矩阵A(1)∈CP×QM,每一列表示同一接收通道、同一扫频周期所有距离元数据,每一行表示一个距离元内所有数据的拼接。由于RFI在距离维的强相关性,可以利用右奇异矩阵行向量来估计RFI 子空间,得到的投影矩阵为P1=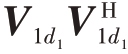 ,其中V1 表示A(1)奇异值分解得到的右奇异矩阵,d1表示RFI分量对应右奇异矩阵的行数。
,其中V1 表示A(1)奇异值分解得到的右奇异矩阵,d1表示RFI分量对应右奇异矩阵的行数。
对于第二展开模式矩阵A(2)∈CQ×MP,每一列代表同一距离元、同一接收通道所有扫频周期的数据,每一行表示一个扫频周期内所有数据的拼接。只能通过A(2)对应的左奇异矩阵列向量来估计RFI 子空间,得到的投影矩阵为P2=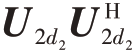 ,其中U2表示A(2)奇异值分解得到的左奇异矩阵,d2表示RFI分量对应左奇异矩阵的列数。
,其中U2表示A(2)奇异值分解得到的左奇异矩阵,d2表示RFI分量对应左奇异矩阵的列数。
对于第三展开模式矩阵A(3)∈CM×PQ,每一列表示同一扫频周期、同一距离元所有接收通道的数据,每一行表示一个接收通道内所有数据。左奇异矩阵列向量和右奇异矩阵行向量都可以用来估计RFI 子空间,虽然左、右奇异矩阵的自由度是相同的,都取决于奇异值矩阵的秩,但是左奇异矩阵的维度取决于接收通道的数目M,列向量点数过少,FFT 之后频率分辨率过低,无法反映真实的频率信息,相反右奇异矩阵的维度取决于训练集所选距离元与每段数据选取的扫频周期数的乘积,即P×Q,行向量FFT 之后可以准确反映相应分量的多普勒频率信息,于是选择右奇异矩阵行向量估计RFI 子空间,得到的投影矩阵为P3=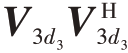 ,其中V3 表示A(3)奇异值分解得到的右奇异矩阵,d3表示RFI分量对应右奇异矩阵的行数。
,其中V3 表示A(3)奇异值分解得到的右奇异矩阵,d3表示RFI分量对应右奇异矩阵的行数。
定义各展开模式矩阵对应左奇异矩阵列向量做FFT 得到左奇异频域,对应右奇异矩阵行向量做FFT 得到右奇异频域,分析RFI和噪声在不同模式矩阵左奇异频域和右奇异频域的表现形式,利用该频率信息划定干扰子空间和噪声子空间。通过对谱峰频率、谱峰功率以及功率均值这三个参
2.3 处理张量子空间投影
估计出RFI子空间后,将每一段处理数据划分成与训练张量大小相等的若干处理张量D,将干扰子空间在处理张量上投影,得到处理张量中的RFI分量Dr:
这里的模n 乘积与传统的HOSVD 中的模n 乘积有所不同,由于P1 和P3 是利用右奇异矩阵构造的投影矩阵,张量与其进行模n乘积时应使得其对应模式展开矩阵左乘以投影矩阵,以P1为例,有如下关系:
而对于P2 而言,应使得对应模式展开矩阵右乘以投影矩阵。
将处理张量中的RFI 分量减去,就得到消除RFI后其余信号分量Ds:
2.4 算法步骤总结
基于HOSVD 的慢时域分段RFI抑制方法的具体步骤如下:
步骤1 分段:取第一次FFT 得到的数据,在慢时间维分段;
步骤2 构造训练张量:利用不包含海洋回波的远距离元或负距离元数据构造训练张量;
步骤3 估计RFI 子空间:分别利用各展开模式矩阵奇异值分解后左、右奇异矩阵包含的频率信息估计RFI子空间;
步骤4 处理张量子空间投影:将得到的干扰子空间投影到各处理张量D,得到只包含RFI的干扰张量Dr;
步骤5 消除RFI:利用处理张量D 减去干扰张量Dr,得到抑制干扰后的数据张量Ds;
步骤6 重复步骤2~6,直到每一段存在RFI的数据都处理完成。
RFI抑制算法流程图如图4所示。
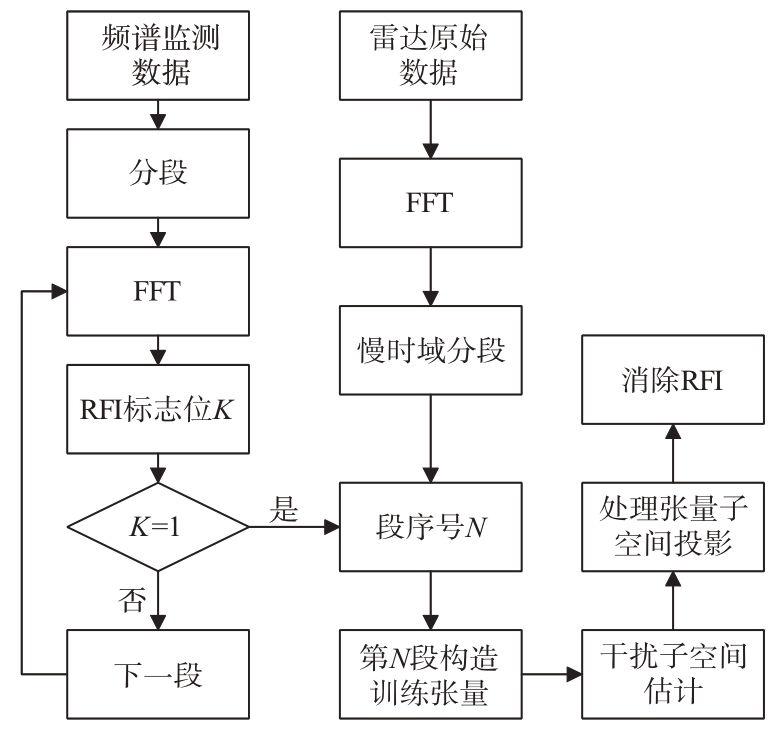
图4 算法流程图
3 实验结果分析
本节首先通过抑制仿真RFI检验算法有效性,随后利用2021年8月福建省东山、龙海高频地波雷达站实测数据验证算法实用性,最后统计分析该算法对一天双站双频数据的抑制效率与抑制效果。
3.1 仿真实验
选取一场不存在明显干扰的雷达接收数据,这里以2017年1月5日00:20赤湖高频地波雷达站接收数据为例,雷达参数如表1所示。
表1 仿真实验雷达系统参数

参数台站名称工作频率/MHz扫频周期/s扫频带宽/kHz相干积累时间/min单程距离分辨率/km参数值赤湖站13.15 0.5 30 55
实测数据距离-周期(Range-Period,RP)谱和距离-多普勒(Range-Doppler,RD)谱分别如图5(a)、(b)所示,在该实测数据301 到400 扫频周期内添加两个射频干扰,载波频率分别为13 158 023.52 Hz、13 167 512.36 Hz,到达角相同,均为130°。绘制出添加仿真RFI 后的RP 谱和RD 谱分别如图5(c)、(d)所示,由于载波频率的不同,两个射频干扰分别位于RD 谱-0.48 Hz 与0.35 Hz 处,其中位于0.35 Hz处的RFI遮盖了正一阶Bragg峰区域。
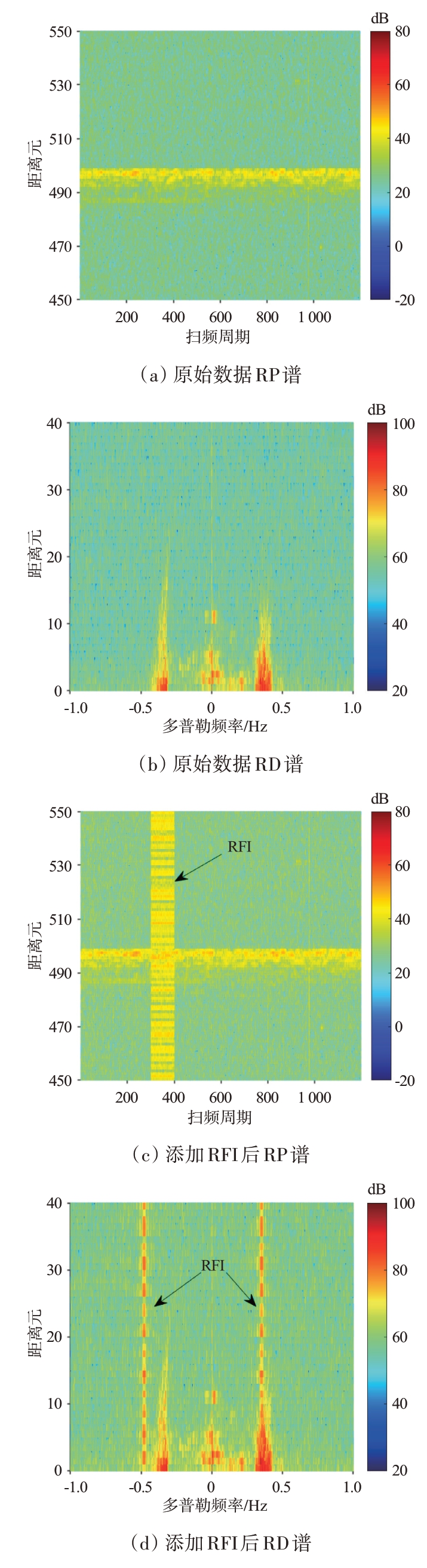
图5 原始数据与添加仿真RFI谱图
利用本文方法抑制RFI,首先将每100 个扫频周期分为一段,由于仿真RFI 仅存在于301 至400扫频周期内,所以只需要处理该段数据来验证算法有效性。该段数据为第301 到400 扫频周期内所有距离元和接收通道的数据,选取远距离元数据构造训练张量,这里497 对应0 距离元,距离元是反的,选457 到466,共10 个距离元的数据,将训练张量得到的三种展开模式矩阵依次进行SVD,归一化奇异值分布如图6所示,设置检测阈值为0.1,认为归一化奇异值大于0.1 则为大奇异值,从图6中可以看到三种展开模式矩阵分别有2,4,3个大奇异值,依次将第一展开模式矩阵对应右奇异矩阵前两行、第二展开模式矩阵对应左奇异矩阵前四列、第三展开模式矩阵对应右奇异矩阵前三行做FFT,如图7所示,可以看到第一展开模式矩阵对应右奇异矩阵第一行、第二展开模式矩阵对应左奇异矩阵第一列、第三展开模式矩阵对应右奇异矩阵第一行FFT 谱图中均有两个明显谱峰,谱峰频率分别为-0.48 Hz 和0.35 Hz,与仿真RFI多普勒频率相同。
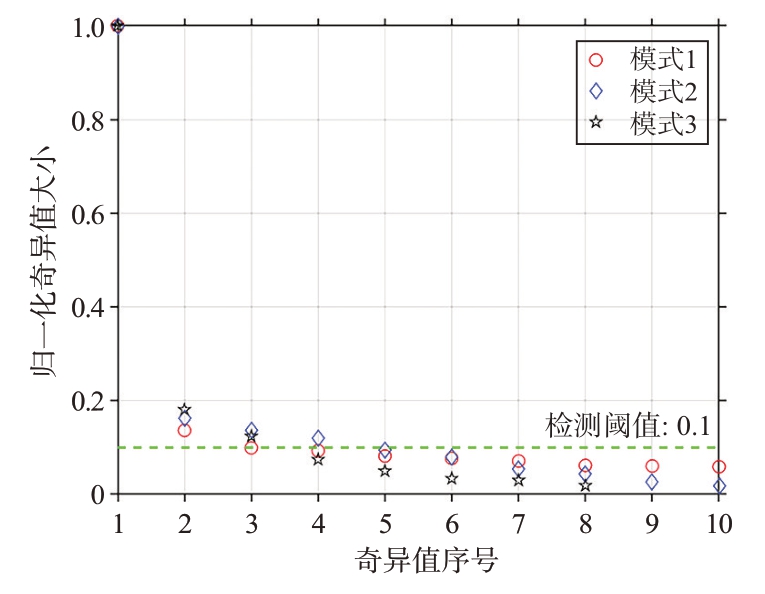
图6 归一化奇异值分布图
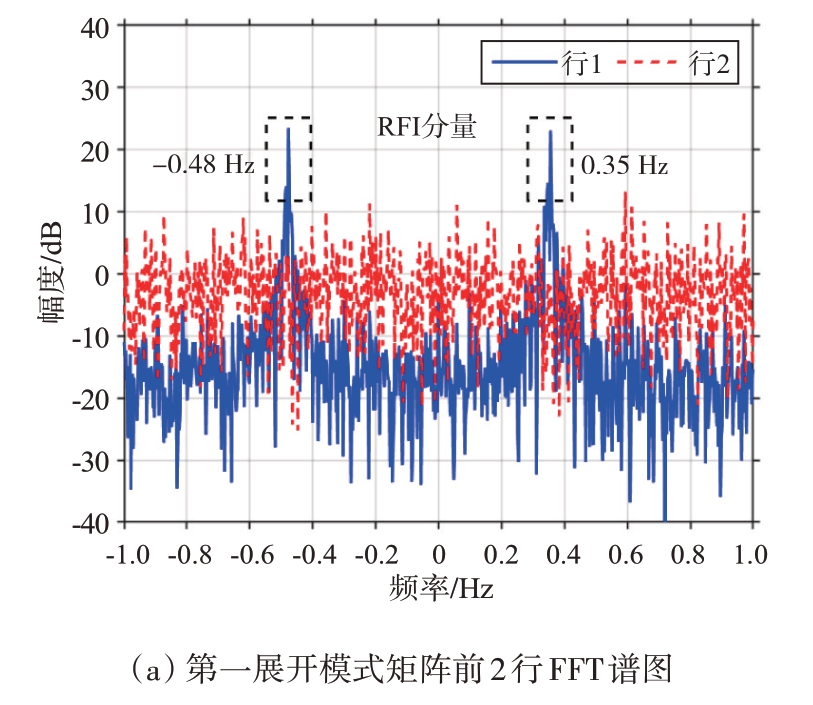
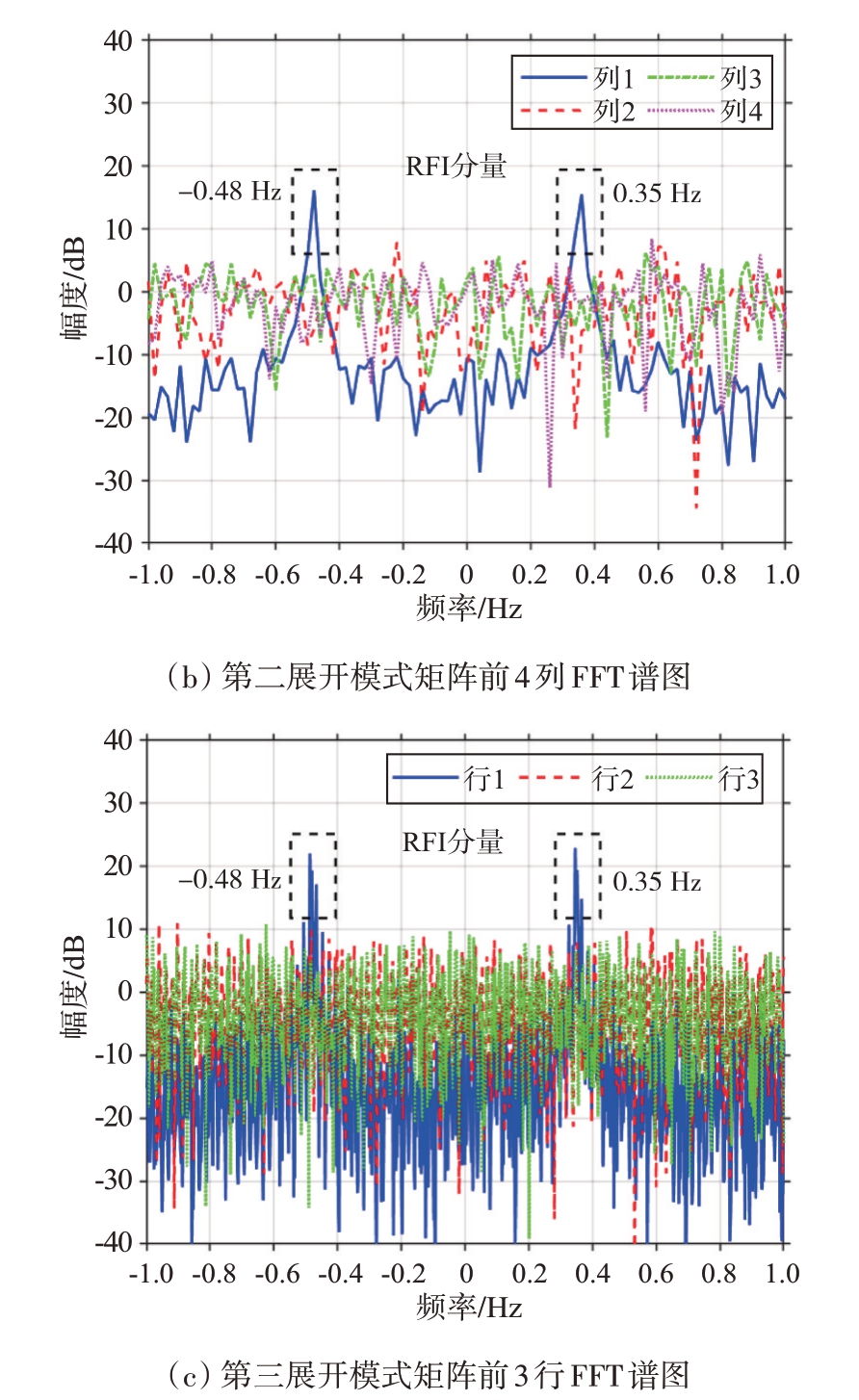
图7 三种展开模式矩阵各行、列FFT谱图
表2列出了各行各列FFT 谱图功率均值、谱峰功率,从表中可以读到各模式矩阵对应奇异矩阵第一行或第一列功率均值依次为-14.794 6,-12.629 9 和-16.002 4 dB,明显低于0 dB,通过对大量数据的验证分析,得到如下结论:若该行向量或列向量对应噪声子空间,做FFT 之后,频谱功率均值在0 dB 上下浮动,浮动范围一般不超过5 dB。因此可以用谱峰功率、功率均值两个指标来判断该行向量或列向量对应噪声子空间还是干扰子空间,而且可以通过谱峰对应频率确定RFI 在RD 谱上的多普勒频率位置。综上所述,第一展开模式矩阵对应右奇异矩阵第一行、第二展开模式矩阵对应左奇异矩阵第一列以及第三展开模式矩阵对应右奇异矩阵第一行对应到仿真的两个RFI 分量子空间,其余行、列向量对应噪声子空间,由此确定第一、第二、第三展开模式矩阵估计的RFI 子空间投影矩阵的参数分别为d1=1,d2=1,d3=1。
表2 功率均值、谱峰功率统计表

参数模式1模式2模式3行1行2列1列2列3列4行1行2行3功率均值/dB-14.794 6-3.423 5-12.629 9-3.005 0-2.378 1-2.637 4-16.002 4-4.974 8-4.835 7谱峰功率/dB 23.450 9 13.273 7 16.154 8 7.902 8 6.290 0 8.413 6 22.931 7 10.973 9 10.773 6
估计出RFI子空间后,投影到各处理张量并消除RFI,画出RP 谱和RD 谱分别如图8(a)、(b)所示,从RP 谱中可以看到,在301 到400 扫频周期添加的RFI 被完全消除,而且在RD 谱上也完全看不到RFI,正一阶Bragg峰凸显出来。
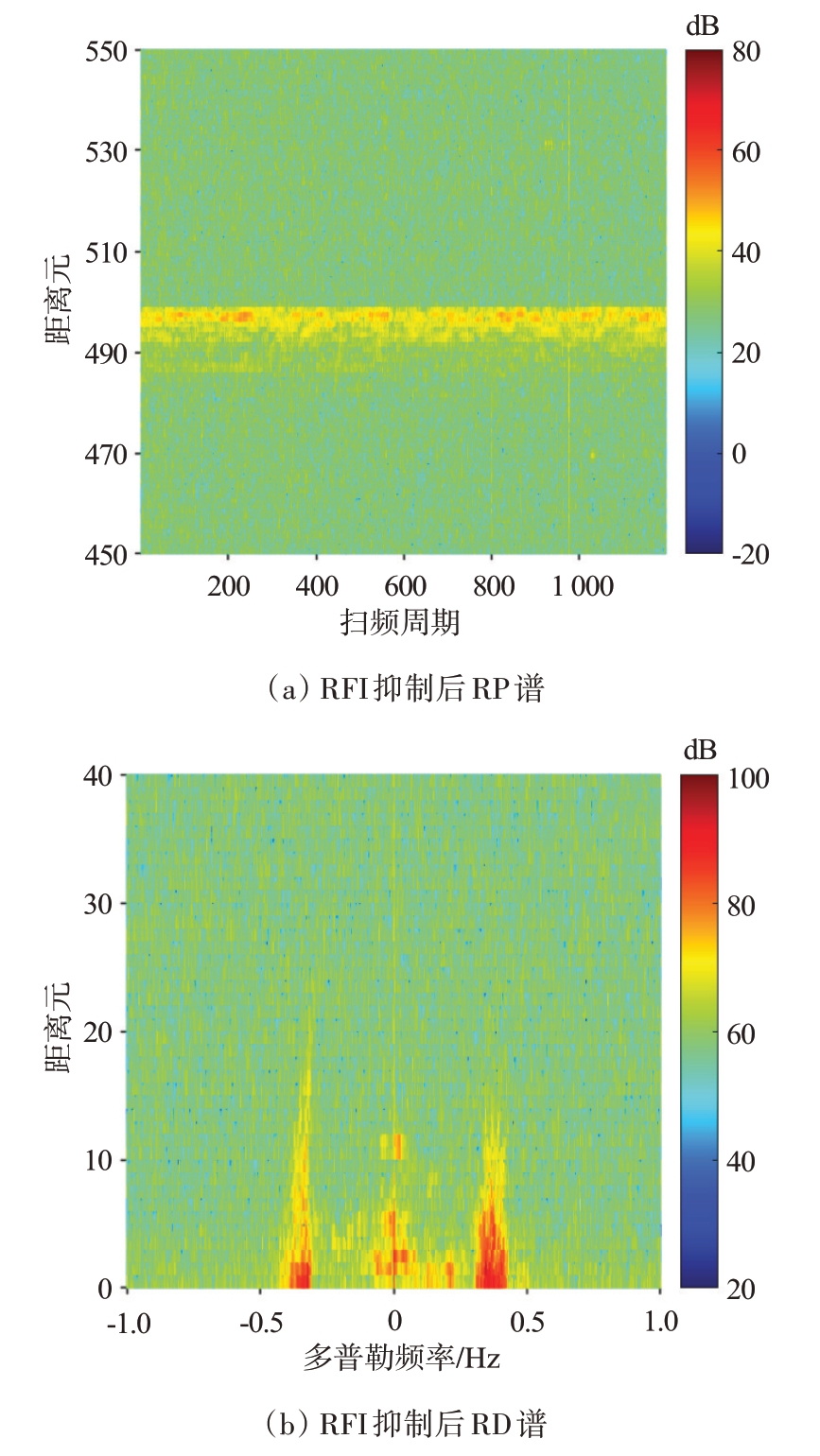
图8 干扰抑制后RP谱与RD谱
3.2 实测实验
利用2021年8月东山、龙海双站双频组网探测的实测数据验证本文RFI抑制算法的实用性,雷达系统参数如表3所示。
表3 实测实验雷达系统参数
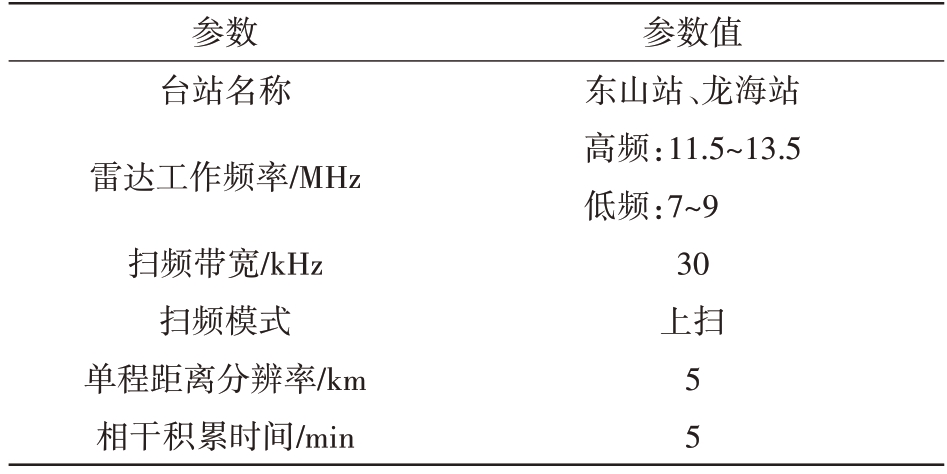
参数台站名称雷达工作频率/MHz扫频带宽/kHz扫频模式单程距离分辨率/km相干积累时间/min参数值东山站、龙海站高频:11.5~13.5低频:7~9 30上扫55
选取8月11日东山高频07:40 的数据,该时间段数据被RFI 污染。将该时段频谱监测数据拼接后均分为12 段,对每段数据做FFT 得到不同分段环境噪声频谱图。根据表3可知,雷达工作频率为12.500 MHz,扫频周期为30 kHz,扫频模式为上扫,因此检测窗范围设为12.500 MHz 至12.530 MHz,底噪窗范围为20~24 MHz。求出检测窗峰值功率与底噪窗功率均值做差,设定检测阈值为20 dB。得到12 段RFI 标志位,其中第1~3、8~12 段数据标志位为1,即1 至300、701 至1 200 扫频周期内的数据都被RFI 污染。画出第2、第4 段环境噪声频谱图如图9所示,红色虚线框表示检测窗范围,二者进行对比,可以看到第2段噪声频谱图在检测窗内有明显的尖峰,而第4段噪声频谱图在检测窗内并无明显尖峰。
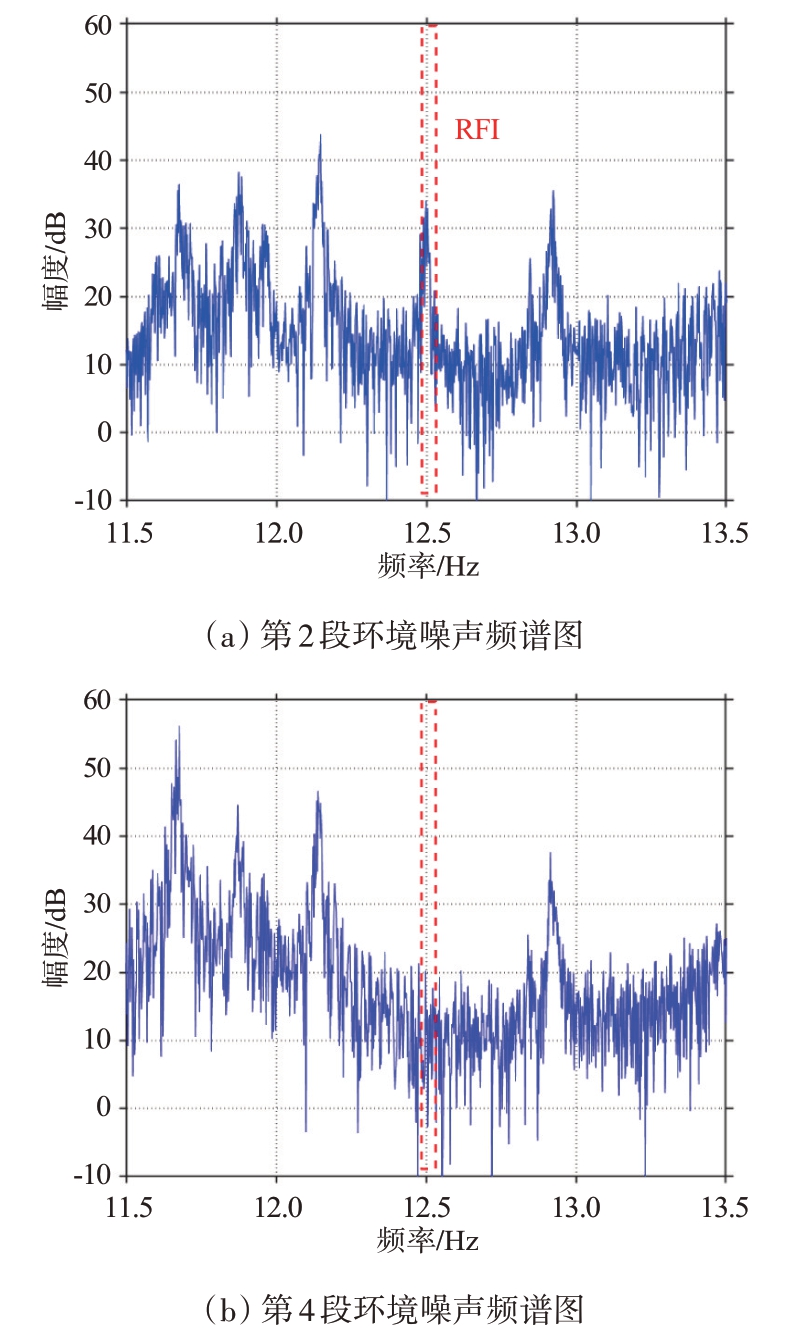
图9 环境噪声频谱图
实测数据RP 谱和RD 谱分别如图10(a)、(b)所示,可以看到,RP 谱中被RFI污染的扫频周期分段与频谱监测数据得到的检测结果一致,在RD 谱上,RFI 呈现为一带状竖条纹,多普勒频率大致为0.52 Hz,有一定程度的展宽,覆盖了龙海发东山收得到海洋回波谱的负一阶峰区域。本次实测雷达数据-80 至0 距离元是0 至80 距离元的搬移,即负距离元不再只包含RFI,而且由于是双站组网,一场数据中包含了东山、龙海双站的回波,图10(b)中0 至15 距离元的Bragg 峰是东山站自发自收的回波,40 至55 距离元是龙海发东山收得到的海洋回波,而且由于高低频发射都各有两路,因此通过加多普勒偏置来区分两路信号回波,导致两路信号产生的海洋回波在RD 谱对称分布。海洋回波占据了多数距离元,为保证RFI 抑制效果,需要自适应地选取不包含海洋回波的距离元进行训练。设定训练范围是10 个距离元,首先通过参数配置文件读取双站双频的距离偏置,根据距离偏置确定双站海洋回波所占据的距离元大致范围,在该范围外取10个距离元进行训练。
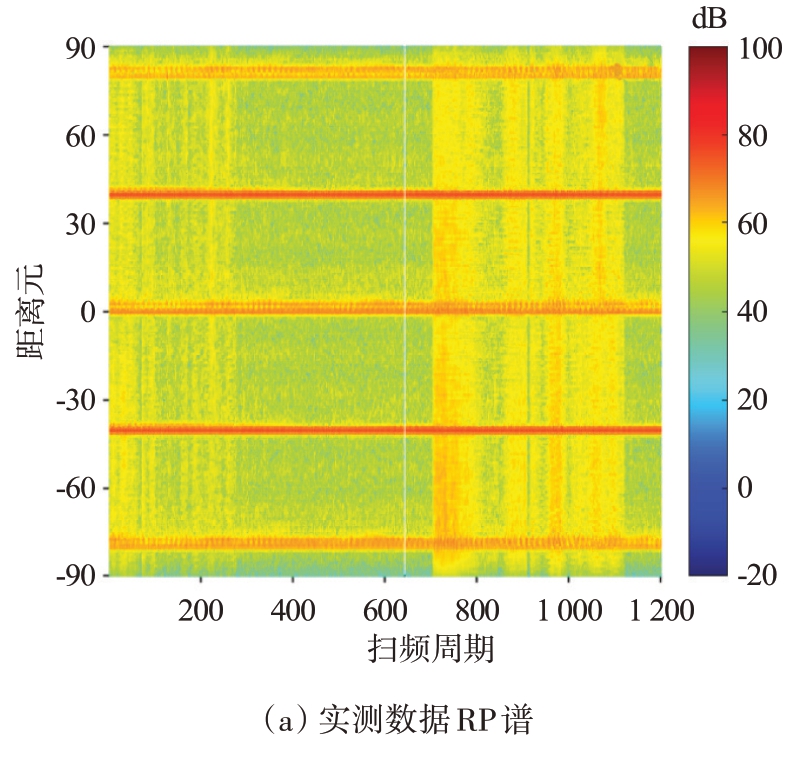
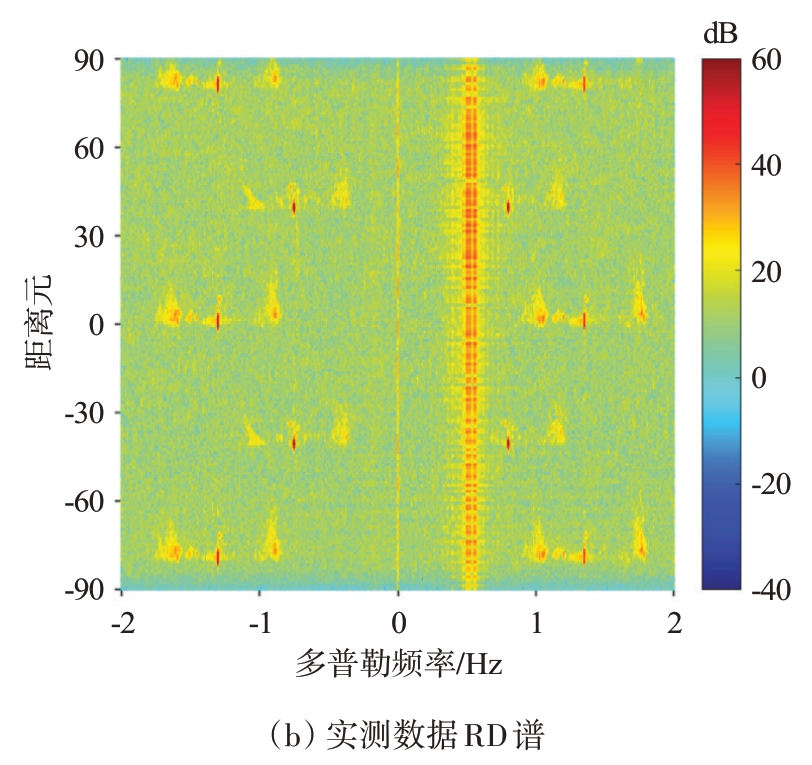
图10 实测数据RP谱与RD谱
以第二段数据,即101 至200 扫频周期的数据为例进行分析,训练距离元选取61 至70,得到训练张量各展开模式矩阵归一化奇异值分布如图11所示,可以得到三种展开模式矩阵对应大奇异值个数分别为3,3,2,得到各行、列FFT 谱图如图12所示,功率均值、谱峰功率如表4所示,分析得出第一展开模式矩阵对应右奇异矩阵第一行、第二展开模式矩阵对应左奇异矩阵第一列以及第三展开模式矩阵对应右奇异矩阵第一行对应RFI子空间,从第三展开模式矩阵前两行FFT 谱图中可以看到有两个明显谱峰,其中一个谱峰频率在0.52 Hz 左右,对应RD 谱中RFI 分量,而另一个谱峰频率在0 Hz 左右,对应RD 谱中的零频干扰(Zero Frequency Interference,ZFI)分量,可以将零频干扰一并消除。确定第一、第二、第三展开模式矩阵估计的RFI 子空间投影矩阵的参数分别为d1=1,d2=1,d3=2,将干扰子空间投影到待处理张量,完成该段数据RFI 的抑制。

图11 归一化奇异值分布
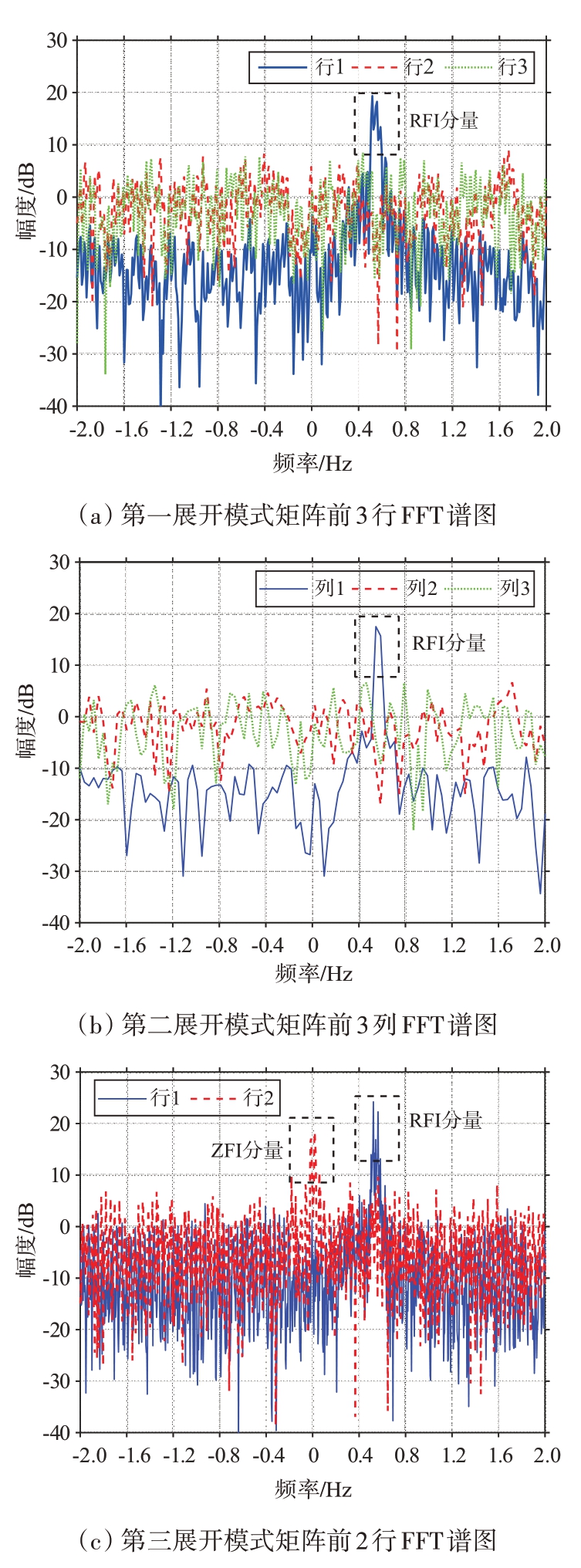
图12 三种展开模式矩阵各行、列FFT谱图
表4 功率均值、谱峰功率统计表
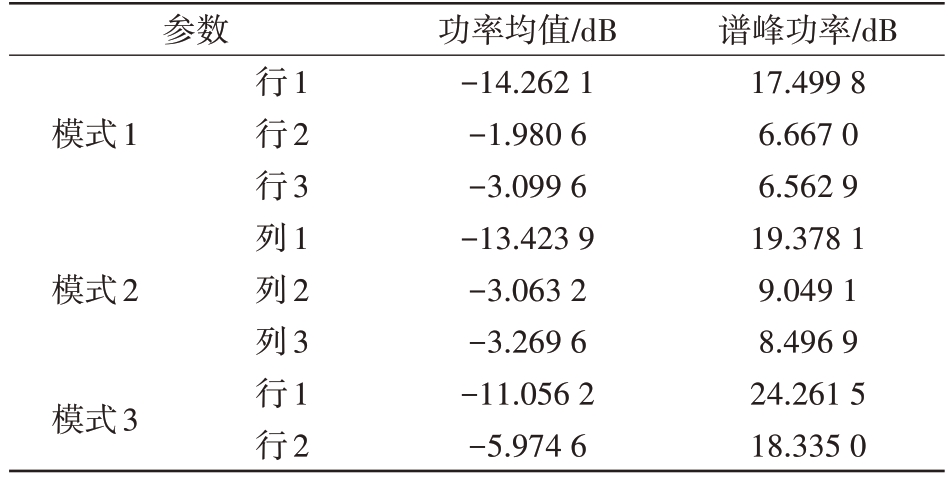
参数模式1模式2模式3行1行2行3列1列2列3行1行2功率均值/dB-14.262 1-1.980 6-3.099 6-13.423 9-3.063 2-3.269 6-11.056 2-5.974 6谱峰功率/dB 17.499 8 6.667 0 6.562 9 19.378 1 9.049 1 8.496 9 24.261 5 18.335 0
根据RFI标志位依次处理各段数据,得到干扰抑制后的RP 谱和RD 谱分别如图13(a)、(b)所示。从图中可以看到,RP 谱中每个扫频周期的RFI 都被抑制掉了,只有少量信噪比较低的残余量,从RD 谱中可以看到,在第二次FFT 之后,这些残余量基本降为底噪水平,RFI 被完全消除,被掩盖的一阶Bragg 峰凸显出来。图14(a)给出了RFI抑制前后第800 扫频周期的距离谱对比图,可以看到,RFI 被抑制,海洋回波并未受到影响,且信噪比抬升10 dB左右。图14(b)为RFI抑制前后第42距离元多普勒谱对比图,可以看到多普勒频率位于0.52 Hz左右的射频干扰以及0 Hz处的零频干扰都被完全消除,海洋回波完整保留,Bragg峰的信噪比得到提升。

图13 RFI抑制后RP谱与RD谱
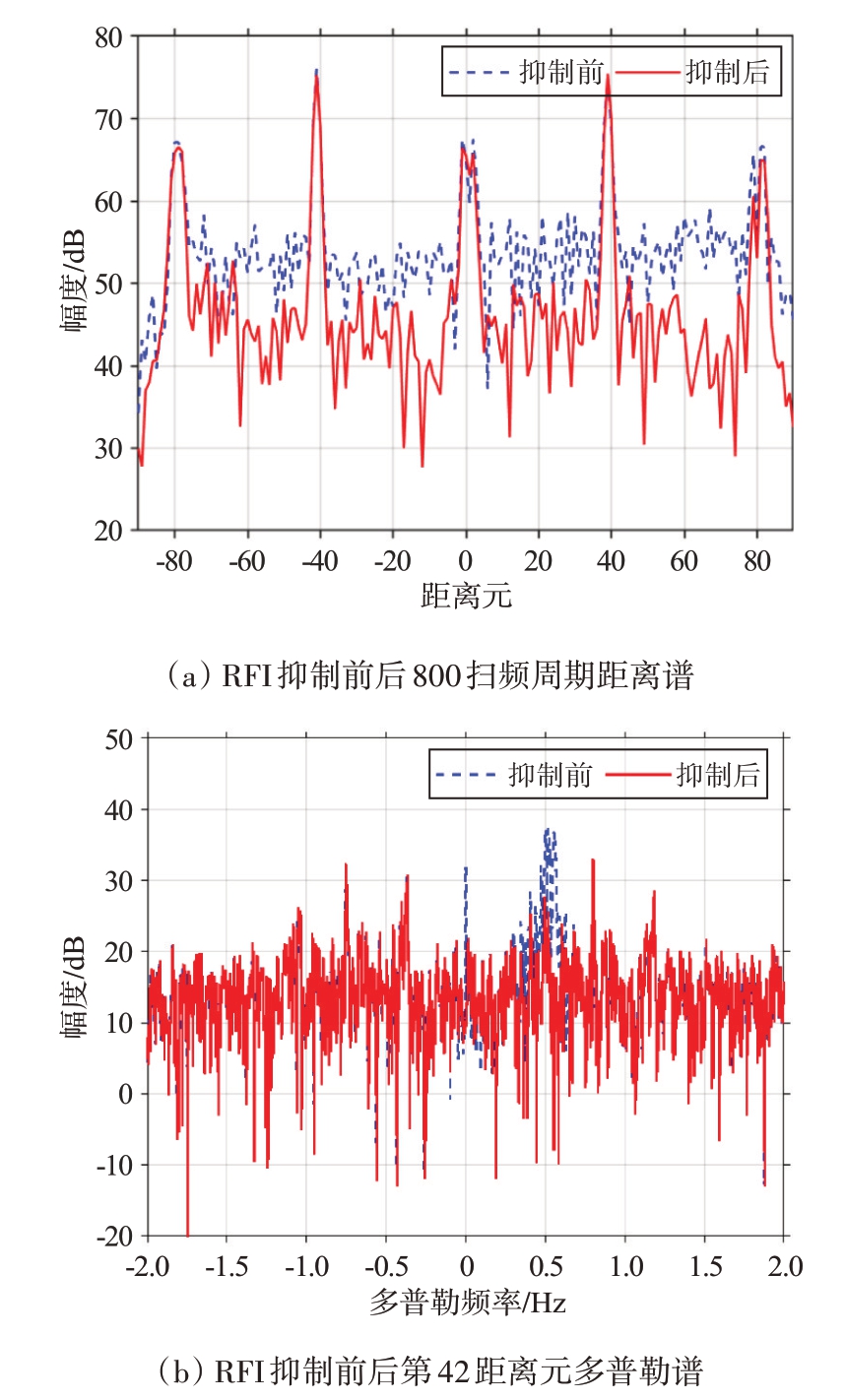
图14 RFI抑制前后距离谱与多普勒谱
3.3 统计分析
利用频谱监测数据得到的RFI 标志位画出2021年8月11日东山、龙海双站双频回波数据被RFI 污染情况时间分布,如图15所示,其中东山高频RFI 存在时间占比12.93%,东山低频RFI存在时间占比22.94%,龙海高频RFI 存在时间占比53.68%,龙海低频RFI 存在时间占比0.07%。总体来看,龙海低频数据质量较好,其他数据受RFI影响较大。利用本文算法对2021年8月11日一整天双站双频的数据进行无差别抑制,耗时3 494.531 373 s,加入RFI 检测算法后,耗时1 670.540 791 s。测试所用电脑GPU型号:Intel(R)Core(TM)i5-9400 CPU@2.90 GHz。在数据批处理中,加入RFI 检测算法可以有效降低干扰消除时间,提高数据批处理效率。

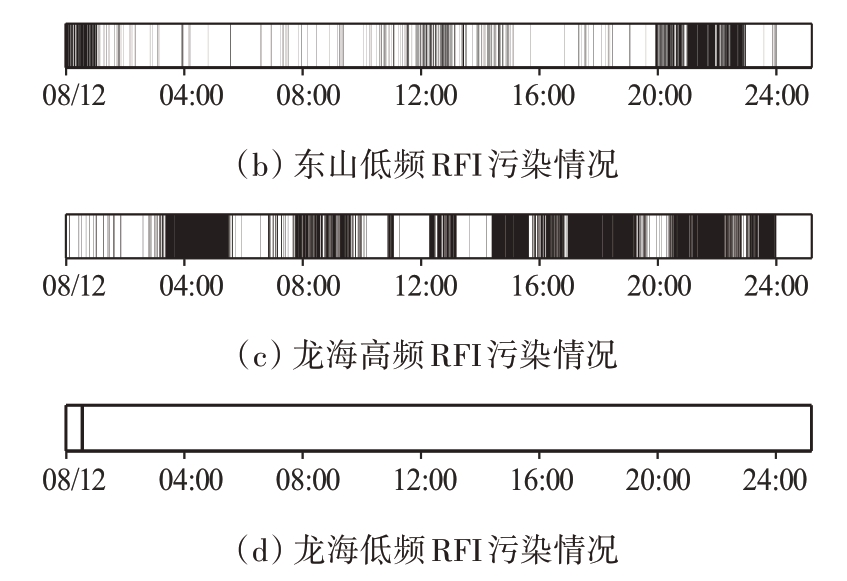
图15 双频双站RFI污染情况分布图
通过对干扰抑制后RP 谱的查看,得到干扰抑制后剩余RFI时间分布如图16所示,RFI存在时间占比依次为0.21%,2.66%,0.21%,0%。可以看到,干扰并未完全消除,而且在原本频谱监测数据未检测到RFI 的时间段也存在少量RFI,东山低频数据仍有较长一段时间被RFI影响,分析原因主要有以下两个:其一,由于RFI 检测信噪比阈值的设置略大导致漏警,使得部分时间段RFI 并未有效检测;其二,RFI并非总是由一系列单频信号构成,它们可能经过各种调制,导致距离相关性减弱,子空间投影的抑制方法未能奏效。不过总体来说,大部分RFI被检测并抑制,证明本文算法是有效的。
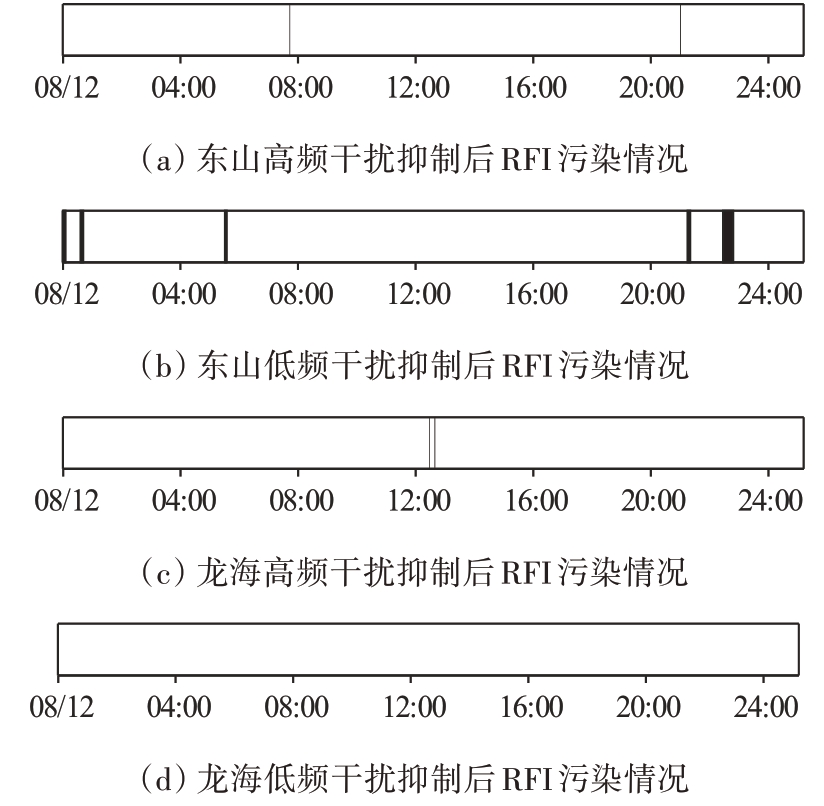
图16 干扰抑制后双频双站RFI污染情况分布图
4 结束语
本文针对高频地波雷达RFI抑制,提出了一种慢时域分段检测与抑制方法,该方法解决了传统子空间类方法无RFI检测、无干扰子空间严格判决标准、未关注右奇异矩阵行向量信息的问题。在预处理阶段,利用频谱监测数据对慢时域分段数据进行RFI 检测。在后处理阶段,利用HOSVD 方法对雷达接收数据进行第一次FFT后得到的通道-距离-慢时间维数据进行处理,首先将待处理数据在慢时间维上分段,对于存在RFI 的数据段,自适应地选择合适距离元数据构造训练张量,通过分析训练张量三种展开模式矩阵的形式,结合各展开模式矩阵奇异值分解后得到的左奇异矩阵列向量或右奇异矩阵行向量所包含的频率信息,给出了干扰子空间估计的参数确定方法,准确估计出干扰子空间,进而得到信号子空间,在慢时域上完成RFI的抑制。实验结果表明,该方法可以有效检测并抑制RFI,提高了数据批处理的效率。
[1]沈伟,文必洋,吴世才,等.带实时频谱监测的高频雷达系统设计[J].系统工程与电子技术,2007,29(10):1635-1637.
[2]赵权睿.高频地波雷达频率管理系统研究与实现[D].哈尔滨:哈尔滨工业大学,2020.
[3]李宇环,岳显昌,张兰.基于压缩感知的时域抗射频干扰方法[J].科学技术与工程,2020,20(7):2767-2772.
[4]陈泽宗,谢飞,赵晨,等.高频地波雷达射频干扰抑制研究[J].华中科技大学学报(自然科学版),2017,45(9):18-22.
[5]NAZARI M E,HUANG W M,ZHAO C.Radio Frequency Interference Suppression for HF Surface Wave Radar Using CEMD and Temporal Windowing Methods[J].IEEE Geoscience and Remote Sensing Letters,2020,17(2):212-216.
[6]CHEN Zezong,XIE Fei,ZHAO Chen,et al.Radio Frequency Interference Mitigation for High-Frequency Surface Wave Radar[J].IEEE Geoscience and Remote Sensing Letters,2018,15(7):986-990.
[7]ZHOU Qing,ZHENG Hong,WU Xiongbin,et al.Fractional Fourier Transform-Based Radio Frequency Interference Suppression for High-Frequency Surface Wave Radar[J].Remote Sensing,2019,12(1):75.
[8]WANG Qinxiong,CHEN Zhangyou,ZHOU Qing,et al.Mitigation of Radio Frequency Interference in HFSWR Using Fractional Fourier Transform Based Filtering Algorithms[J].IEEE Geoscience and Remote Sensing Letters,2021,18(2):261-265.
[9]罗忠涛,严美慧,卢琨,等.超视距雷达海杂波与干扰信号的多域特征与海杂波检测[J].电子与信息学报,2021,43(3):580-588.
[10]CHEN Zezong,XIE Fei,ZHAO Chen,et al.An Orthogonal Projection Algorithm to Suppress Interference in High-Frequency Surface Wave Radar[J].Remote Sensing,2018,10(3):403.
[11]ZHOU Hao,WEN Biyang.Radio Frequency Interference Suppression in Small-Aperture High-Frequency Radars[J].IEEE Geoscience and Remote Sensing Letters,2012,9(4):788-792.
[12]文必洋,韩金柱,周企豪,等.高频地波雷达射频干扰抑制新算法的研究[J].电波科学学报,2016,31(4):639-646.
[13]TIAN Zhen,WEN Biyan,JIN Lijie,et al.Radio Frequency Interference Suppression Algorithm in Spatial Domain for Compact High-Frequency Radar[J].IEEE Geoscience and Remote Sensing Letters,2018,15(1):102-106.
[14]朱永恒,黎明,牛炯,等.基于方向分解的高频地波雷达射频干扰抑制[J].中国海洋大学学报(自然科学版),2018,48(7):142-148.
[15]LI Yuhuan,YUE Xianchang,WU Xiongbin,et al.A Higher-Order Singular Value Decomposition-Based Radio Frequency Interference Mitigation Method on High-Frequency Surface Wave Radar[J].IEEE Trans on Geoscience and Remote Sensing,2019,58(4):2770-2781.
[16]李宇环.高频地波雷达射频干扰抑制方法[D].武汉:武汉大学,2020.
[17]胡进峰,李万阁,艾慧,等.基于频域干扰剔除的OTHR 射频干扰抑制算法[J].系统工程与电子技术,2016,38(5):1046-1051.
[18]WANG Xinyang,LI Yang,ZHANG Ning,et al.An Automatic Target Detection Method Based on Multidirection Dictionary Learning for HFSWR[J].IEEE Geoscience and Remote Sensing Letters,2021(19):1-5.
[19]罗忠涛,吴太锋,何子述,等.基于图像分割的高频雷达射频干扰提取算法[J].系统工程与电子技术,2018,40(4):776-781.
[20]吴太锋.结合图像分割的高频雷达干扰抑制方法研究[D].重庆:重庆邮电大学,2019.
[21]LATHAUWER L D,MOOR B D,VANDEWALLE J.A Multilinear Singular Value Decomposition[J].Siam Journal on Matrix Analysis and Applications,2000,21(4):1253-1278.
[22]林森,廖亮,李伦,等.基于广义高阶奇异值分解的图像重建[J].信息与电脑(理论版),2022,34(2):74-77.
[23]何颖,陈淑鑫,王丰.基于HOSVD分类的非特定人脸表情识别算法[J].计算机仿真,2021,38(10):193-198.
[24]徐保庆,剡熠琛,同非,等.基于波束域实值HOSVD 的双基地MIMO雷达测角算法[J].火控雷达技术,2021,50(4):6-12.




