0 引 言
海杂波是海洋表面对雷达信号的后向散射回波,而对于海面漂浮小目标[1]的检测技术,由于受到海面复杂情况影响,存在着较大的阻碍,一直是雷达探测领域研究的热点。不同于轮船、军舰等大型目标可以利用回波能量进行检测[2],小船、浮标、蛙人等尺寸小的海面目标回波弱,小目标的雷达截面积(Radar Cross Section,RCS)低,已不适用传统的检测方法进行检测。目前,对海面小目标的检测方法有时频分析、分形特性、机器学习等方法,而利用机器学习算法对海杂波与目标回波数据特征提取与评估分类一直是近年来的研究热点。
早在1993年,Haykin 等人对海杂波时间序列的分形特性进行研究,发现可以利用海杂波分形维数这一特征来进行目标检测。随后,Lo 等[3]利用海杂波与目标回波数据单尺度分形维数的差异性进行了目标检测。Hu 等[4]利用海杂波与目标回波的多尺度分形特性的差异性,提出了基于Hurst指数的检测方法。邵夫驰等[5]结合分数布朗运动理论,利用多重分形去势波动法确定多重分形参数。于晓涵等[6]从时频分析的角度提出了基于短时稀疏分数阶变换和短时稀疏分数阶模糊函数的雷达机动目标检测和估计方法。Shui 等[7]从多特征联合的角度,选取一个时域幅度特征与两个频域多普勒几何特征相结合,提出了基于三特征的检测方法。此后,Shui等[8]又提出一种时频三特征检测方法,很大程度上改善了检测方法性能。时艳玲等[9]利用经验模态分解的方法,分离出高能量低阶IMF 分量,计算分量在平均能量中的占比作为特征。以上检测方法所采用的特征,都取得了较好的检测效果。但上述算法所有的特征都需要单独计算,加大了计算复杂度,同时随着特征的维度的增加,分类器设计难度进一步加大。
本文将利用堆栈自编码器自适应地提取海杂波与目标回波的深层次特征,使用时频域特征结合的方法来提高特征的差异性,并对几种不同的输出特征维数进行实验,对比得出最优特征维数。引入遗传优化算法(Genetic Algorithm,GA)对XGBoost 中的超参数组进行寻优,利用选择、交叉、变异算子迭代更新得到子代基因,快速找到最优超参数组,训练并优化模型。提出一种堆栈自编码器(Stacked Autoencoder,SAE)与GA-XGBoost 算法结合(SAE-GA-XGBoost)的检测方法,并利用IPIX 数据集来验证所提检测方法的稳定检测性能。
1 SAE-GA-XGBoost基本理论
基于堆栈自编码器与遗传算法优化XGBoost算法(SAE-GA-XGBoost)的检测方法利用了堆栈自编码器(Stacked Autoencoder,SAE),XGBoost 算法以及遗传算法(Genetic Algorithm,GA),分别用于提取深层次特征、对所提取特征进行评估分类和对XGBoost 网络中超参数进行寻优更新。下面分别对3种算法进行介绍。
1.1 堆栈自编码器
自编码器是一种由编码器与解码器两部分构成的神经网络结构,包含输入层、隐含层、输出层三层结构。其网络结构函数及损失函数[10-12]为
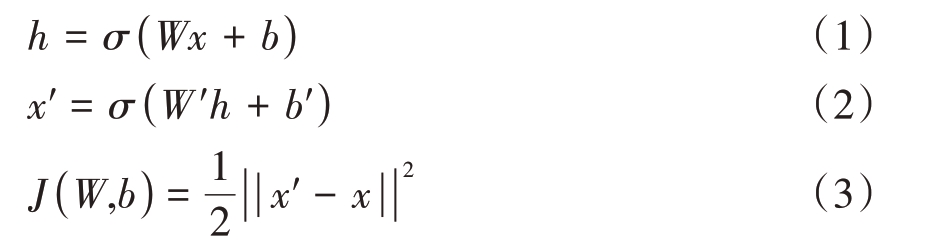
式中,x 为输入层,输入为数据时间序列,x'为输出层,h 为隐含层,W、W'、b、b'分别为编码与解码过程中的权重与偏置。σ为sigmoid函数,为
堆栈自编码器是将多个自编码器堆叠而成的神经网络结构,其优势在于能够对输入数据进行逐层编码、解码,将前一个编码器的隐含层作为下一个编码器的输入层,从而获得输入数据的高阶特征。在训练过程中,为解决模型退化、陷入局部最优等问题,网络往往采用逐层贪婪算法,即一次只训练一个自编码器。堆栈自编码器的损失函数为
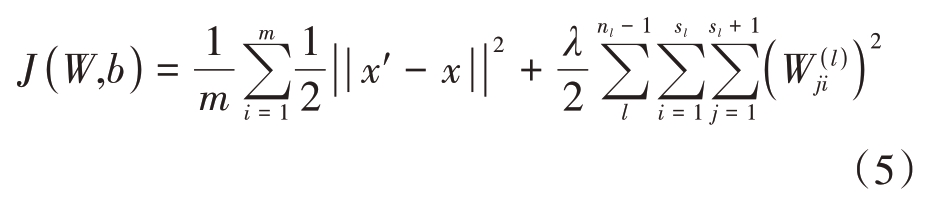
式中,m 为输入时间序列的单元个数,nl 为堆栈自编码器网络总共的层数,sl 为第一层的神经单元数,λ 为权重衰减参数。损失函数的第一项为实际值与网络输出的最小均方差之和,||·||为l2 范式。损失函数第二项为正则化项,作用在于减小权重幅值以防止过拟合,具体表示为编码、解码权重矩阵每一项系数的平方和。堆栈自编码器通过逐层反复迭代来更新参数,最终使整体网络的代价函数达到最小值。
1.2 XGBoost算法
XGBoost 算法是一种多分类回归树集成(Classification and Regression Trees,CART)的算法,属于Boosting 算法类别。其基本思路是把多棵性能各异的树模型组合成一个性能相对好的模型[13],模型可表示为
式中,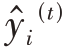 为t次迭代后模型对样本的预测值,t的树的总数目,fk为函数空间F中的一个函数,xi为输入的第i 个样本,
为t次迭代后模型对样本的预测值,t的树的总数目,fk为函数空间F中的一个函数,xi为输入的第i 个样本,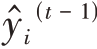 是前t-1 棵树的预测结果,ft(xi)为第t 棵树的模型。一般的集成学习算法很难具体列出所有回归树,而XGBoost算法使用的是梯度提升策略,在训练过程中不断添加新的树来拟合之前的学习误差。
是前t-1 棵树的预测结果,ft(xi)为第t 棵树的模型。一般的集成学习算法很难具体列出所有回归树,而XGBoost算法使用的是梯度提升策略,在训练过程中不断添加新的树来拟合之前的学习误差。
XGBoost算法的目标函数为
式中,l为损失函数,yi为真实样本值,Ω(ft)为全部决策树计算出的正则项,C为常数。模型目标函数由损失函数和正则项两部分组成。对目标函数进行二阶泰勒函数展开,得

式中,
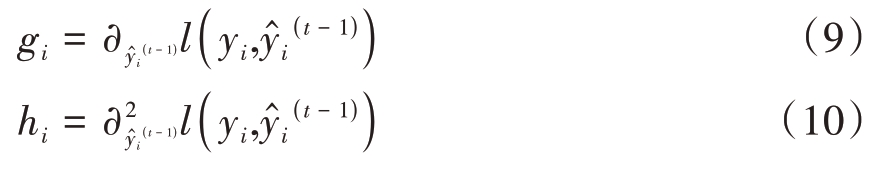
将第j个叶子结点的所有样本xi划入到一个叶子结点的样本集合中,定义为Ij={i|q(xi)=j},则式(6)可改写为
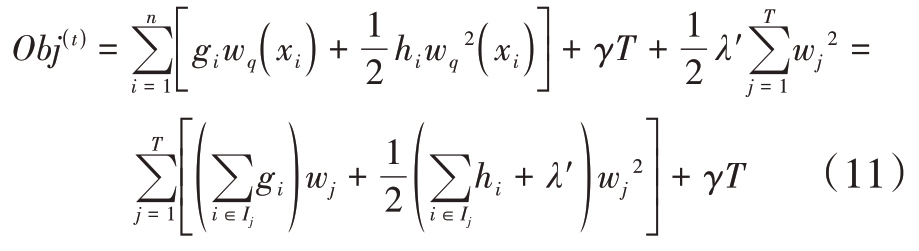
式中,γ 为节点切分难度系数,λ'为L2 正则化系数,T 为当前树的叶子节点个数,wj为叶子节点值。令![]() 同时令目标函数导数为0,得最优权重为
同时令目标函数导数为0,得最优权重为
得最终目标函数为
在训练过程中,模型的性能受超参数的影响较大。超参数详细信息如表1所示。可以看出,众多超参数的选取决定了XGBoost模型的训练效果,选取不当会严重影响分类结果,因此需要对XGBoost 网络的超参数组进行优化,以获取适应训练样本的模型,来提高最终检测概率。
表1 XGBoost的超参数

超参数名称learning_rate max_depth min_child_weight subsample超参数意义网络的学习速率树的最大深度子集中实例重量最小总和实例子样本比例默认值0.3 611
1.3 遗传算法
引用遗传算法[14]对XGBoost 模型中的超参数组进行寻优。遗传算法是一种随机自适应全局搜索算法,通过二进制编码,经过群体选择、交叉、变异和消除等过程后得到子代基因。遗传算法中3个算子如下:
1)选择算子。通过轮盘赌方法,计算每个个体的适应度值构成轮盘比例进行随机选择。
2)交叉算子。设立阈值k,在基因的第k 个位置进行交叉。
3)变异算子。根据突变概率选择基因突变位置,进行0-1转换,防止局部寻优。
通过遗传算法多次迭代寻优过后,设置算法迭代终止条件来决定遗传算法是否终止。将XGBoost 网络中的超参数组作为遗传算法的个体种群,种群总体个数设置为50组,将雷达回波数据的检测概率作为算法适应度函数,将最高适应度值与最低适应度值的差值是否小于10-5作为迭代终止条件,通过选择、交叉变异等过程搜索出最优参数,以提高检测方法性能。
2 基于SAE-GA-XGBoost算法的海面小目标检测
为提升海面小目标检测概率,基于SAE-GAXGBoost 算法的检测方法将分为训练与检测两部分来设计,通过将训练部分获得的堆栈自编码器模型,最优超参数组与判决门限输入检测部分模型中进行实时更新,提升最终检测效果。同时通过计算选取训练部分XGBoost 网络输出的预测值作为判决门限,实现检测方法恒虚警特性。
2.1 SAE-GA-XGBoost检测方法
SAE-GA-XGBoost 检测方法的流程图如图1所示,分为训练部分与检测部分。在训练部分过程中,为了更好地挖掘雷达回波数据的高维特征并适配堆栈自编码器模型,首先对海杂波与目标回波训练数据进行归一化预处理,构建两层堆栈自编码器进行特征提取。然后分别将海杂波与目标回波数据打上“0”与“1”的标签,输入到XGBoost网络中进行训练。接着利用遗传算法对XGBoost 训练模型进行寻优,得到最优超参数组并对检测部分XGBoost 网络进行超参数更新。同时结合虚警率Pfa计算,选取XGBoost网络输出的预测值ρ与判决门限ξ对比,更新判决门限。
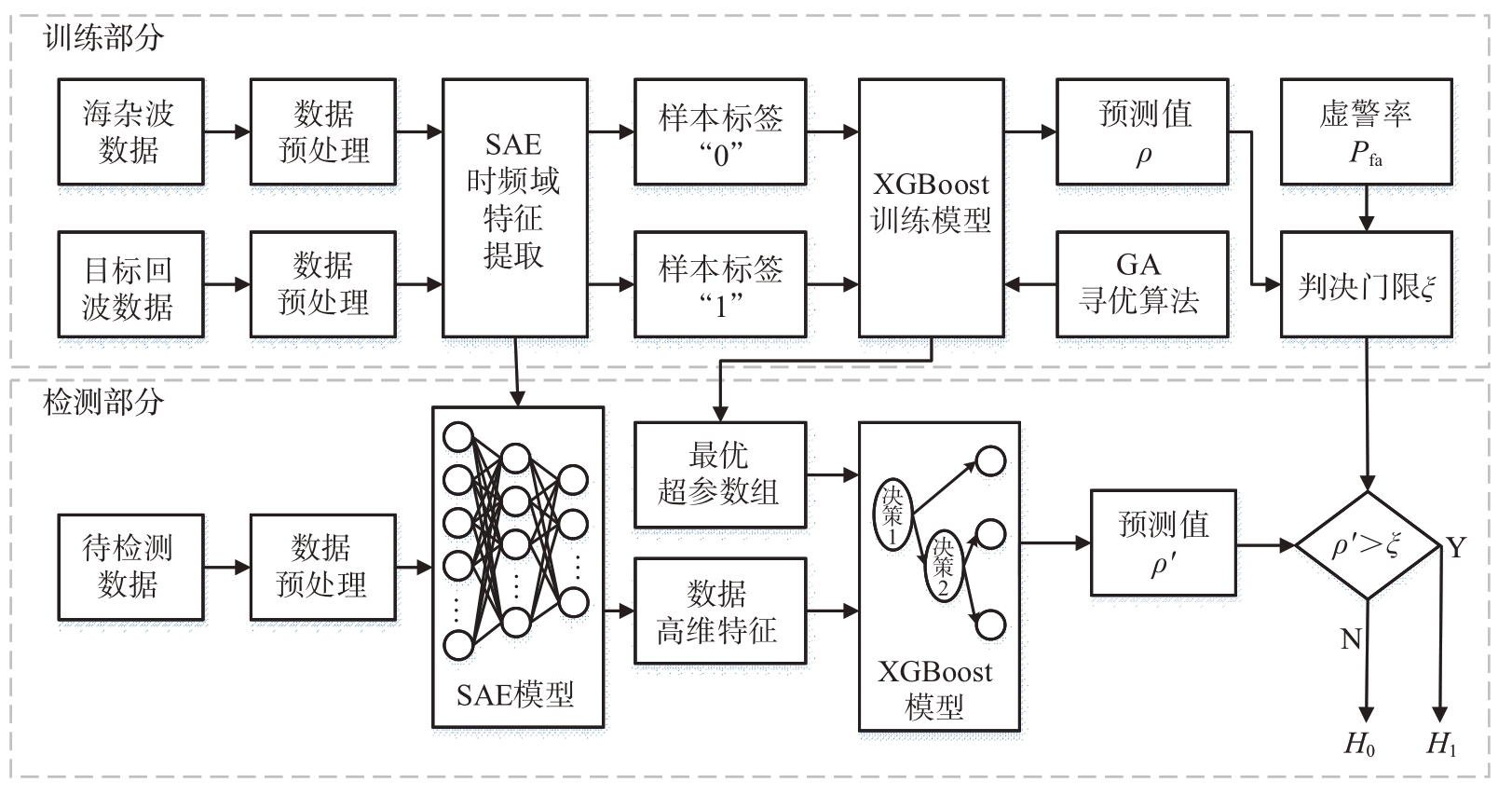
图1 SAE-GA-XGBoost检测方法流程图
在检测部分过程中,通过引入训练部分中训练好的堆栈自编码器网络模型、最优超参数组以及更新过的判决门限ξ,将待测数据训练得到的预测值ρ'与判决门限进行比较,得到最终的分类结果,当ρ' >ξ 时,判断为待测数据中有目标;当ρ' <ξ 时,判断待测数据为纯海杂波。当海况发生变化时,训练部分能够实时根据新的回波数据训练网络以及得到新的最优超参数与判决门限,从而实现虚警可控并提高在线检测概率。
在高维特征提取过程中,由于海杂波数据和目标回波数据均经过归一化处理,且利用一个堆栈自编码器提取特征时只能从单一域提取,提取的特征直观上没有较好的区分性。因此,提出一种时频域特征结合的方法,通过两个堆栈自编码器分别训练得到时域与频域的深层次特征,再将时频域提取的特征连接组合成新的高维特征,如图2所示。该方法可以增加海杂波与海面回波数据特征间的差异性,并稳定后续检测流程的检测性能。
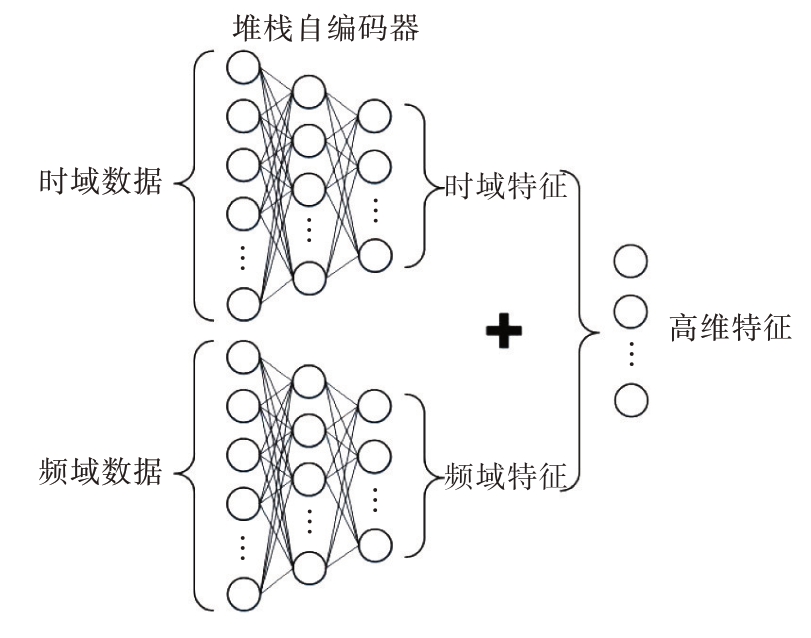
图2 时频域特征结合方法示意图
2.2 检测方法虚警可控实现
实现检测方法虚警可控先要取得GA-XGBoost检测方法评估分类的实际为海杂波的n组预测值,并按从大到小排列,记为ρ1,ρ2,…,ρn。在已知虚警率的情况下,可得判决门限
具体判决门限改动过程如图3所示。共有1 134个实际标签为“0”的总样本,如果将判决门限ξ=0.5,则有9 个虚警点,虚警率Pfa=0.79%。为了达到10-3虚警率,则需要将判决门限上调至如图所示位置。此时判决门限ξ=0.968 8,只有一个虚警点。因此通过改动判决门限,满足虚警率条件,从而达到分类器的虚警可控,使其具有恒虚警特性。同时,在改动过后的判决门限非常高的情况下,检测概率达到了94.30%,可见实际为有目标的预测值普遍高于0.968 8,有较好的聚敛性。
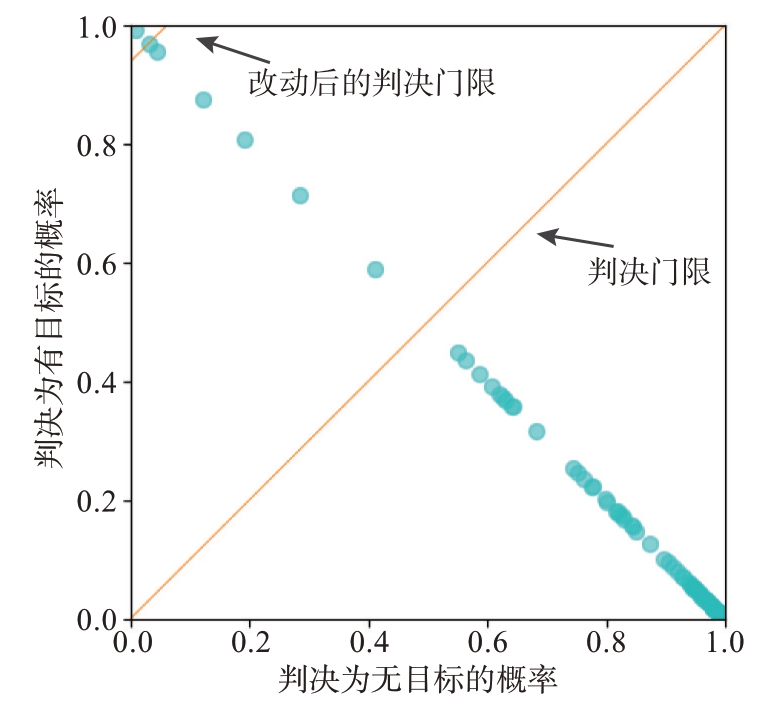
图3 判决门限改动具体过程
3 实验与性能分析
由于特征参数对检测结果的影响,本节将对高维特征进行实验验证。利用数据对SAE-GAXGBoost 检测方法进行性能检测,并通过与其他多组检测方法对比,验证所提检测方法的稳定高效性能。
本文所使用的数据来源于IPIX 雷达目标数据库,由加拿大McMaster 大学的Haykin 教授在1993年的加拿大东海岸采集获取。雷达工作在X波段,频率为9.39 GHz。实验采取了其中的10 组数据,每组数据由14 个相邻距离单元组成,每个距离单元包含131 072 个脉冲数,距离分辨率为30 m,目标为用金属丝网包裹的聚苯乙烯泡沫塑料球,直径长约1 m。根据数据发射和接收方式的不同得到4 种极化方式,分别为HH,HV,VH,VV。数据受海况影响,SCR 的起伏变化较大。表2为IPIX 雷达数据具体说明。数据中#17 和#280两组数据的浪高高于其他几组数据,属于高海况数据。
表2 IPIX雷达数据具体说明
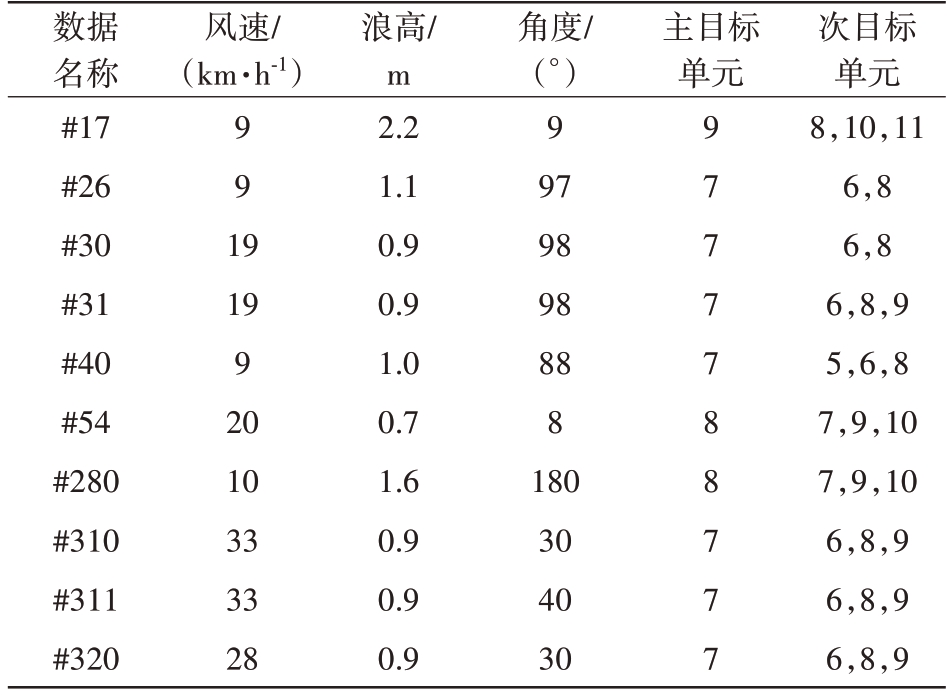
数据名称#17#26#30#31#40#54#280#310#311#320风速/(km·h-1)主目标单元991 9 19 9 20 10 33 33 28浪高/m 2.2 1.1 0.9 0.9 1.0 0.7 1.6 0.9 0.9 0.9角度/(°)9 97 98 98 88 8 180 30 40 30 9777788777次目标单元8,10,11 6,8 6,8 6,8,9 5,6,8 7,9,10 7,9,10 6,8,9 6,8,9 6,8,9
3.1 高维特征实验验证
不同域高维特征验证实验分别测试了使用时域、频域与时频域结合特征时SAE-GA-XGBoost 检测方法的检测性能,并将3种特征的检测效果进行了对比。实验选取了#54号数据HH极化下的时间序列,频域数据是将原数据通过FFT 预处理后,再归一化至[0,1]区间内。归一化函数使用的是sigmoid 函数。实验观测样本共有11 200 个,训练过程中,训练集与测试集的划分比例为8∶2。由于每个距离单元的数据都很长,且海杂波数据与目标数据数量不匹配,目标数据数量远少于海杂波数据数量。为了增加目标数据的样本量,实验中每段数据观测长度为N=1 024,且前后两组相邻数据的部分单元有所重叠,重叠单元数为P=924。数据选取如图4所示。
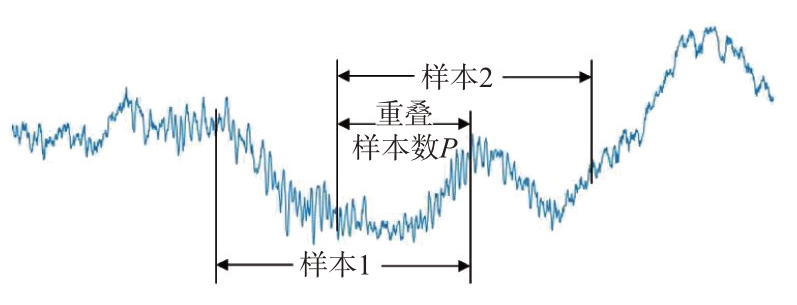
图4 数据选取示意图
堆栈自编码器构建两层,第一层隐含层的单元数设为256,时域、频域输出128 维特征,时频域结合分别输出64 维时域、频域特征,结合为128 维特征。图5为3 种不同特征在GA-XGBoost 检测方法下的分类器检测性能图。由图可知,在虚警率Pfa=10-3 时,时域特征的检测概率为56.60%,频域特征的检测概率为69.62%,时频域结合特征的检测概率为94.30%。可见时频域特征结合方法提取的高维特征的检测效果远高于单一域提取的高维特征的检测效果,这是因为不同训练模型训练过程也有所不同,同时结合不同域特征,能有效地提高特征的整体差异性。
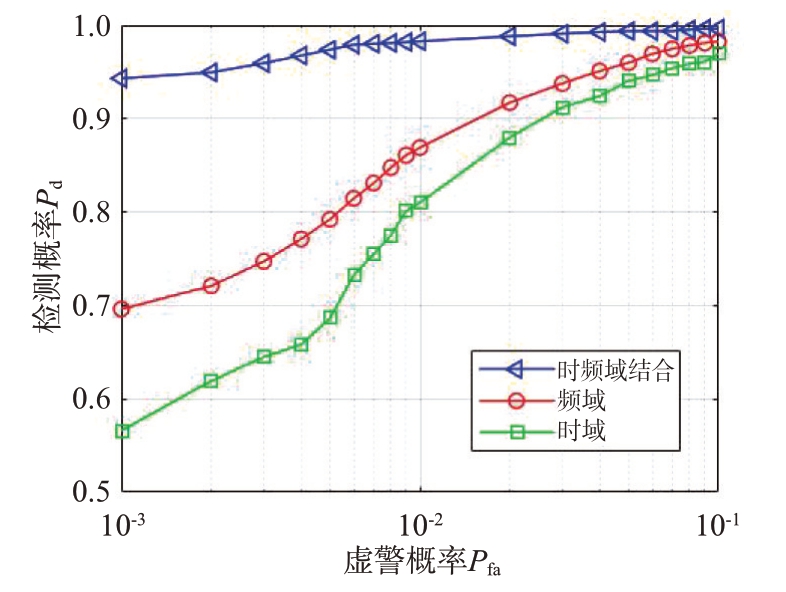
图5 3种不同域特征的检测性能图
此外,特征维数的不同,也会影响最终检测效果。为了探索特征在不同维数下对检测性能的影响,选取#54 数据,维数分别为32、64、128、192 及256 进行实验。图6为5 种不同维数特征的性能检测图。维数为32 的特征检测概率最差,只有35.71%,维数为64 与256 的特征检测概率分别为56.33%和60.13%,维数为192 的特征检测概率为91.67%,维数为128 的特征检测概率最高,达到了94.30%,因此确定高维特征的维数为128。
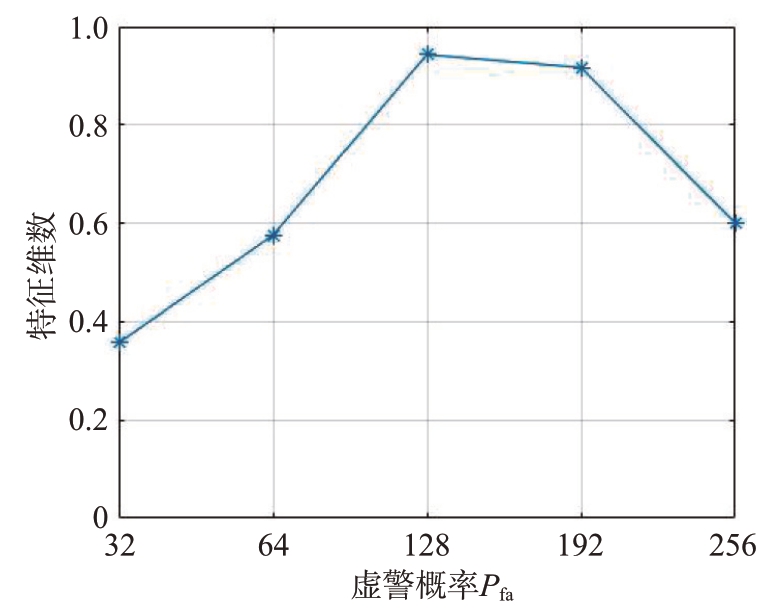
图6 不同维数特征的检测性能图
3.2 检测性能对比
对选取的10组数据进行不同极化下的性能检测。图7为10 组数据在4 种极化下的平均信杂比对比图。从图中可以看出,两种交叉极化方式下的平均信杂比普遍高于两种共极化方式下的平均信杂比。同时,由于VV 极化方式相比HH 极化方式产生了更大的布拉格散射,前者的平均信杂比会更低[13]。4 种极化下的平均信杂比不同,导致4种极化下的检测概率也有所差异。HV、VH极化方式要更优于HH、VV极化方式。
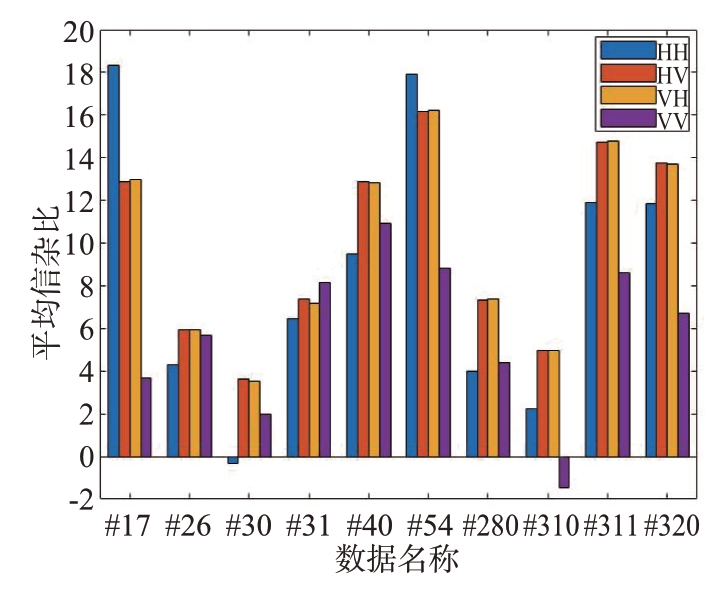
图7 4种极化下10组数据的平均信杂比
由于XGBoost 网络中超参数组对最终检测性能产生影响,对应的数据不同,检测效果就会不同。遗传优化算法会根据不同数据进行实时迭代更新。表3为HH 极化下部分数据迭代后选取的超参数组以及检测概率。
表3 GA-XGBoost选取的在HH极化下部分数据的最优超参数组
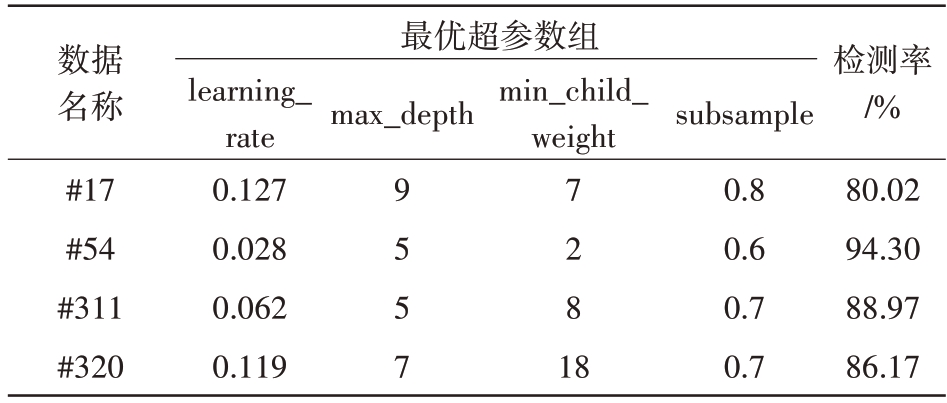
数据名称#17#54#311#320最优超参数组learning_rate 0.127 0.028 0.062 0.119 max_depth min_child_weight 9557 7281 8 subsample 0.8 0.6 0.7 0.7检测率/%80.02 94.30 88.97 86.17
图8为10 组数据在4 种极化下的检测性能对比图。图8中设虚警率Pfa=10-3,累计脉冲数N=1 024,重叠度P=924。从图中可以看出HH、HV、VH三种极化方式的检测效果远高于VV极化方式,且本实验提出的检测方法对HH极化方式的数据的检测效果较好,甚至部分略优于HV、VH极化方式。
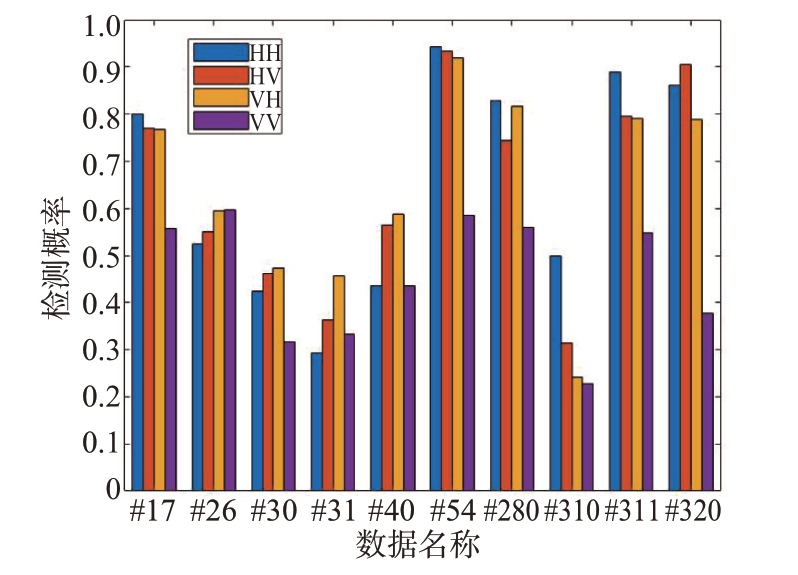
图8 10组数据在4种极化下的SAE-GA-XGBoost检测方法的检测性能对比(Pfa=10-3)
将SAE-GA-XGBoost 检测方法与其他检测方法对比,做进一步验证,如图9所示。在HH 和HV两种极化方式下将SAE-GA-XGBoost 检测方法与FFT、Hurst 指数[3]与三特征检测方法[6]进行对比。从图9(a)可以看出,基于FFT、Hurst指数和三特征的检测方法的平均检测率为19.17%、30.15%和51.33%,而SAE-GA-XGBoost 检测方法的平均检测概率最高,为64.27%,且10 组数据检测率均高于其他检测方法。图9(b)中,虽然在HV极化下SAEGA-XGBoost 检测方法对#54、#320 等几组数据的检测性能略低于三特征检测方法,但是其平均检测率为65.03%,而基于FFT、Hurst 指数和三特征检测方法的平均检测率分别为24.61%、46.88%和63.41%,可见SAE-GA-XGBoost 检测方法在HV 极化下的检测率较其他三种检测方法仍有优势。
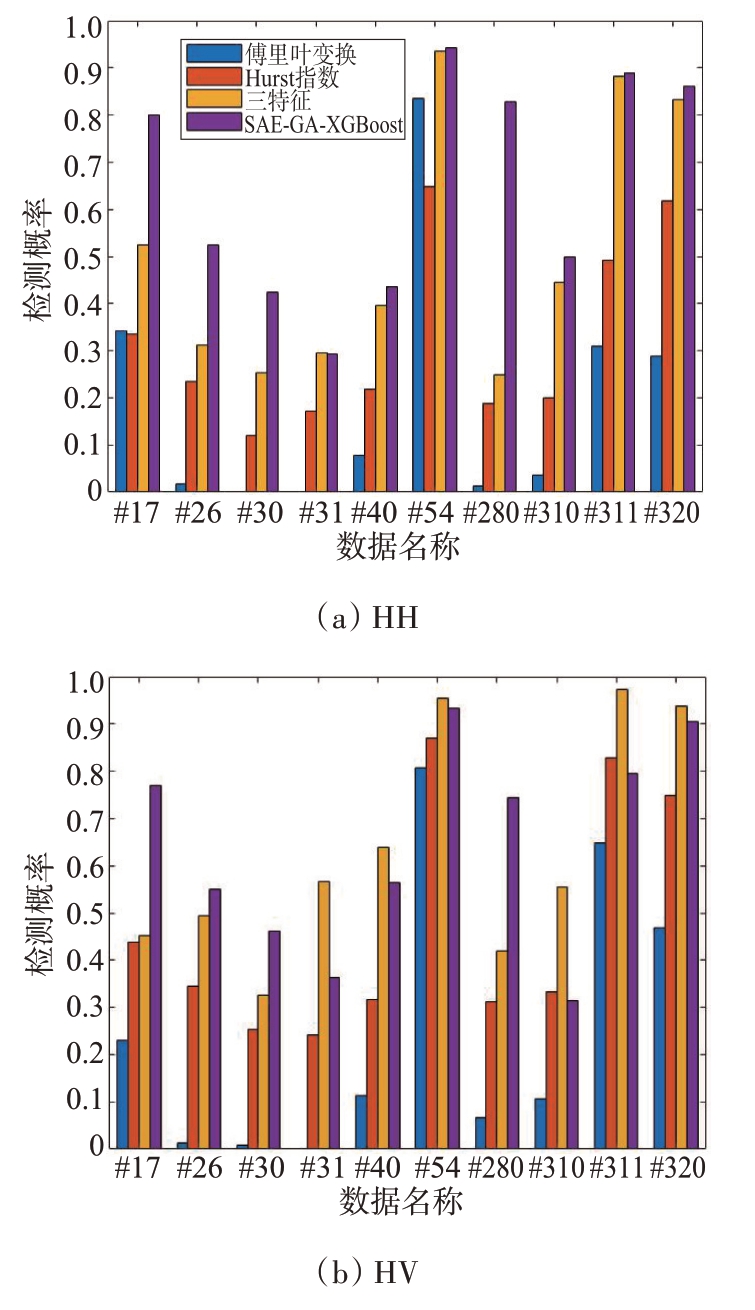
图9 HH和HV极化下4种检测方法的检测结果对比(Pfa=10-3)
进一步选取具体数据进行分析。表4例举了#17、#26、#30 和#280 数据的3 种检测方法的检测性能。由表4可知,SAE-GA-XGBoost 检测方法在4种极化方式下均有明显优势,并对#26 和#30 这些平均信杂比较低的数据仍有较好的检测效果。对#17 和#280 高海况数据的检测效果较其他检测方法有着显著的提高,可见SAE-GA-XGBoost 检测方法针对高海况下的海面回波数据有更加良好的检测效果。
表4 #17,#26,#30和#280在4种极化下的4种检测方法性能对比
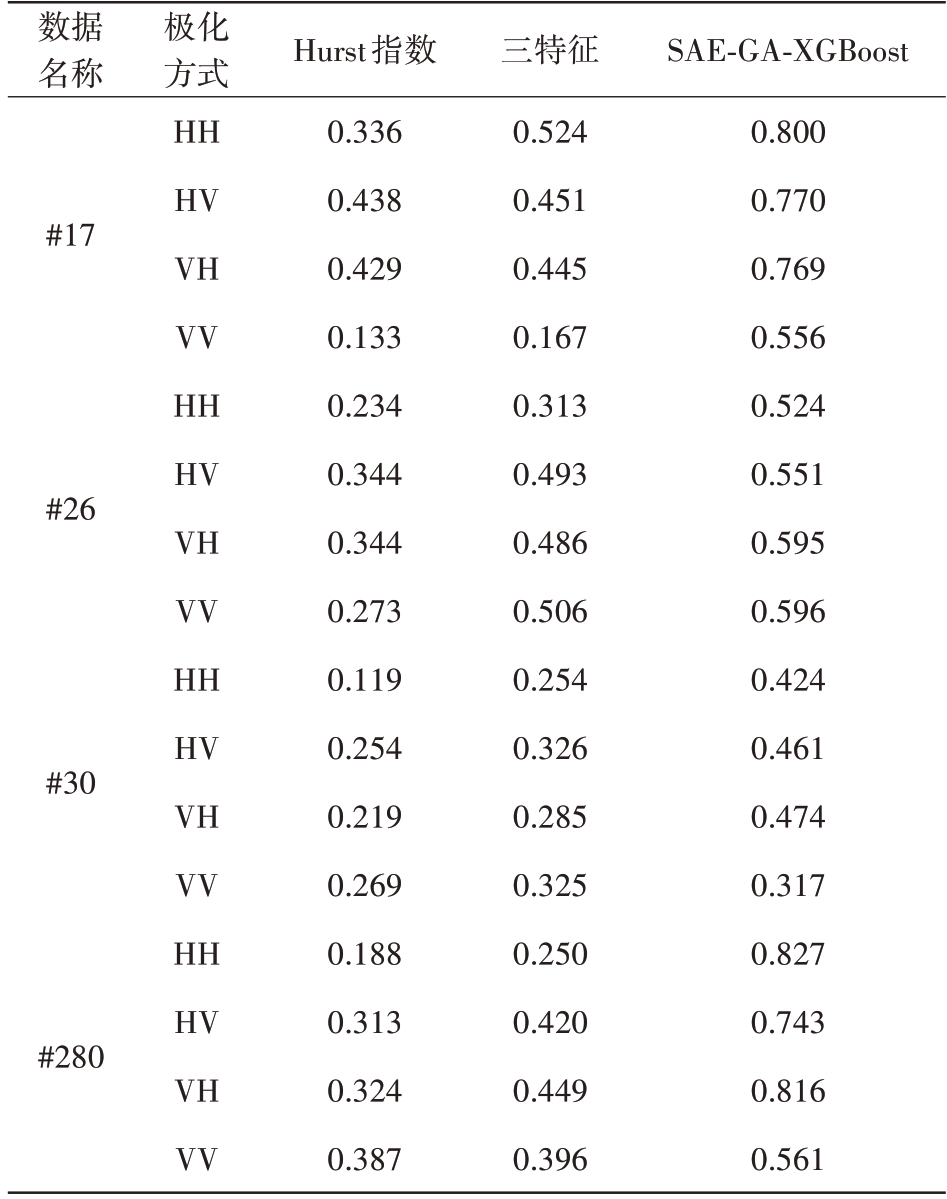
数据名称#17#26#30#280极化方式HH HV VH VV HH HV VH VV HH HV VH VV HH HV VH VV Hurst指数0.336 0.438 0.429 0.133 0.234 0.344 0.344 0.273 0.119 0.254 0.219 0.269 0.188 0.313 0.324 0.387三特征0.524 0.451 0.445 0.167 0.313 0.493 0.486 0.506 0.254 0.326 0.285 0.325 0.250 0.420 0.449 0.396 SAE-GA-XGBoost 0.800 0.770 0.769 0.556 0.524 0.551 0.595 0.596 0.424 0.461 0.474 0.317 0.827 0.743 0.816 0.561
4 结束语
本文使用了堆栈自编码器自适应地提取深层次特征,针对单一域中海杂波与目标回波数据特征区分度较低的问题,利用时频域特征结合的方法,将时域、频域分别提取的特征组合为高维特征,来提高特征的差异性,相较于单一域特征,时频域结合特征检测概率提高了24.68%。通过实验验证,选取特征维数为128时,达到最佳检测效果。同时对于XGBoost网络超参数组寻优问题,引入遗传优化算法,初始化随机生成50组染色体,设置迭代终止条件为最高适应度值与最低适应度值的差值小于10-5,利用选择、交叉、变异算子迭代更新得到子代基因,快速找到最优超参数组,训练并优化模型。提出了一种基于SAE-GA-XGBoost 算法的海面小目标检测方法并进行了实验验证。实验结果表明,SAE-GA-XGBoost 检测方法在HH 极化下检测结果最佳,检测概率提高了12.94%。#17和#280 高海况数据在HH 极化下的检测概率分别为80.02%和82.73%,提升效果显著,可见SAE-GAXGBoost 检测方法对高海况数据的检测效果更好。根据与其他三种检测方法的对比显示,SAE-GAXGBoost 检测方法总体上有更加良好的检测性能,可运用于高海况下的海面小目标检测中。
[1]丁昊,刘宁波,董云龙,等.雷达海杂波测量试验回顾与展望[J].雷达学报,2019,8(3):281-302.
[2]ZHOU W,XIE J H,LI G P,et al.Robust CFAR Detector with Weighted Amplitude Iteration in Nonhomogeneous Sea Clutter[J].IEEE Trans on Aerospace and Electronic Systems,2017,53(3):1520-1535.
[3]LO T,LEUNG H,LITVA J,et al.Fractal Characterization of Sea-Scattered Signals and Detection of Sea-Surface Targets[J].IEE Proceedings-F,1993,140(3):243-250.
[4]HU J,TUNG W W,GAO J B.Detection of Low Observable Targets Within Sea Clutter by Structure Function Based Multifractal Analysis[J].IEEE Trans on Antennas and Propagation,2006,54(1):136-143.
[5]邵夫驰,行鸿彦.基于FRFT 的多重分形海面小目标检测[J].探测与控制学报,2020,42(1):69-74.
[6]于晓涵,陈小龙,黄勇,等.雷达动目标短时稀疏分数阶表示域探测方法[J].系统工程与电子技术,2018,40(11):2426-2432.
[7]SHUI P L,LI D C,XU S W.Tri-Feature-Based Detection of Floating Small Targets in Sea Clutter[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(2):1416-1430.
[8]SHUI P L,GUO Z X,SHI S N.Feature-Compression-Based Detection of Sea-Surface Small Targets[J].IEEE Access,2019,8:8371-8385.
[9]时艳玲,刘子鹏,张学良,等.基于EMD 能量占比的海面漂浮小目标特征检测[J].系统工程与电子技术,2021,43(2):300-310.
[10]ASLAM M A,XUE C L,CHEN Y S,et al.Breath Analysis Based Early Gastric Cancer Classification From Deep Stacked Sparse Autoencoder Neural Network[J].Scientific Reports,2021(11):1-12.
[11]袁延鑫,孙莉,张群,等.基于堆栈稀疏自编码器和微动特征的身份认证技术[J].空军工程大学学报,2018,19(4):48-53.
[12]李浩,王卓健,李哲,等.基于堆栈自编码器和DeepAR的航空发动机剩余寿命预测[J].推进技术,2022,43(11):72-80.
[13]方继辉,李阳.基于IFA-XGBoost的燃气轮机故障诊断[J].上海电力大学学报,2021,37(4):367-384.
[14]WARD K,TOUGH R,WATTS S.Sea Clutter:Scattering.The K Distribution and Radar Performance[M].2nd ed.London,UK:IET,2013.
[15]JIANG Y,TONG G X,YIN H N,et al.A Pedestrian Detection Method Based on Genetic Algorithm for Optimize XGBoost Training Parameters[J].IEEE Access,2019(7):118310-118321.
[16]刘安邦,施赛楠,杨静,等.基于虚警可控梯度提升树的海面小目标检测[J].南京信息工程大学学报(自然科学版),2022,14(3):341-347.
[17]时艳玲,姚婷婷,郭亚星.基于图连通密度的海面小目标检测[J].电子与信息学报,2021,43(11):3185-3192.
[18]MA J Y,WANG S Y,ZHANG K N,et al.Fast and Robust Loop-Closure Detection via Convolutional Auto-Encoder and Motion Consensus[J].IEEE Trans on Industrial Informatics,2022,18(6):3681-3691.
[19]SHI S N,SHUI P L.Sea-Surface Floating Small Target Detection by One-Class Classifier in Time-Frequency Feature Space[J].IEEE Trans on Geoscience and Remote Sensing,2018,56(11):6395-6411.
[20]关键,伍僖杰,丁昊,等.基于对角积分双谱的海面慢速小目标检测方法[J].电子与信息学报,2022,44(7):2449-2460.
[21]CAO X W,CHENG Y Q,WU H,et al.Nonstationary Moving Target Detection in Spiky Sea Clutter via Time-Frequency Manifold[J].IEEE Geoscience and Remote Sensing Letters,2022,19:1-5.
[22]时艳玲,刘子鹏,贾邦玲.样本不平衡下的海杂波弱目标分类研究[J].信号处理,2021,37(9):1781-1789.
[23]孙江,行鸿彦,吴佳佳.基于IA-SVM 模型的混沌小信号检测方法[J].探测与控制学报,2020,42(3):119-125.



