0 引 言
利用雷达检测人体生理信息是人们当下研究的热门领域,呼吸和心跳是人体最重要的生命活动信息,能快速准确地对其检测至关重要。毫米波雷达通过非接触的方式检测人体生理信息,且不受温度、光照和尘埃等周围环境的影响,可以穿透衣物和被子等遮挡物进行检测,在医疗监测、睡眠监测和地震救援以及自动驾驶等领域具有广泛应用[1-3]。多普勒生物雷达通常被划分为连续波(CW)和超宽带(UWB)雷达,UWB 雷达可以探测距离,但其存在占用带宽宽和瞬时功率峰值过大[3],影响其他系统通信和雷达的测量精度的问题。FMCW 雷达具有波束窄、分辨率高、体积小等优点[1]。本文采用FMCW 毫米波雷达来采集和处理人体生命信号。
生命体征回波信号在传播回接收端时会受到周围环境的各种干扰,通常会变得很微弱,而且心跳和呼吸信号的频带范围非常接近。所以如何抑制干扰和从噪声中准确提取出呼吸和心跳信号是本文研究的重点。在国内外研究中,传统的信号提取方法主要有数字滤波器,设计一个性能优良的滤波器来提取和分离呼吸心跳信号是很困难的。文献[4]提出一种自适应信号分解方法—经验模态分解(EMD),但EMD 具有模态混叠和端点效应的缺点[5],使得IMF 分量不能真实说明信号本身的特点。文献[6]提出集合经验模式分解(EEMD)的方式,通过引入白噪声使信号自动分布到合适的参考尺度上来消除模态混叠问题,但IMF分量中会包含残余噪声。文献[7]提出互补集合经验模态分解(CEEMDAN)解决了白噪声从高频到低频的转移传递的问题,但分解得到的IMF 中仍包含残余噪声,而且在分解的前期,信号会出现一些“虚假”模式,导致在前几阶模态中仍包含了大量的噪声。
故针对CEEMDAN 模态分解存在以上不足以及在重构呼吸和心跳信号时的杂波干扰过大的问题,本文提出了改进的自适应集合经验模态分解[8-9](ICEEMDAN)和长数据序列截取的方法来分解信号,并利用相关性和能量阈值法分离提取心跳和呼吸信号,极大地解决了模态混叠现象和各本征模态函数(IMF)中的残余噪声和虚假分量的问题,提高了信号的真实性和准确性。
1 试验方法和试验方案
1.1 FMCW 雷达生命信号检测原理
FMCW 雷达能够连续发射调频信号,具有测量物体的距离、速度和角度信息的能力。图1为FMCW雷达的结构示意图。
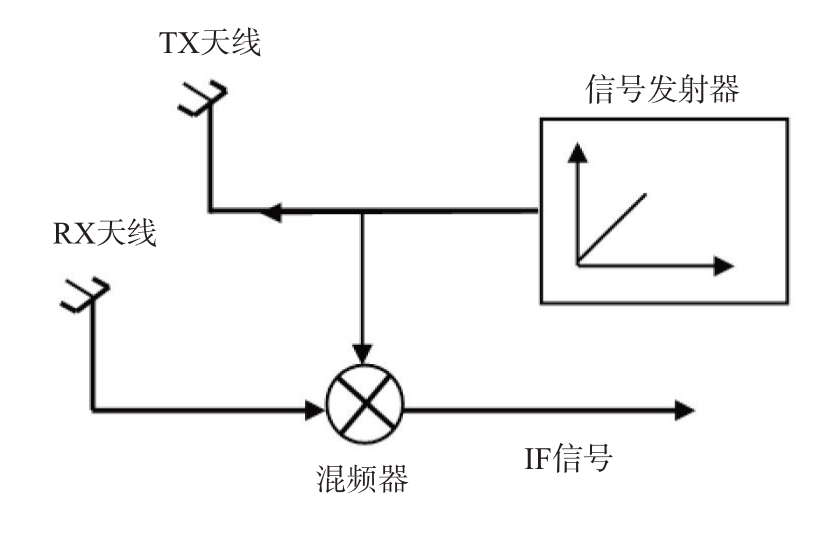
图1 FMCW雷达的结构示意图
FMCW雷达发射波形表示为
式中,fc为雷达中心频率,k为锯齿波斜率,θ为初始相位。
天线到人体胸腔表面的瞬时距离[10]:
式中,d0 为人体胸腔振动中心与天线的距离,x(t)为身体做生命运动造成的距离,
Ab 为呼吸的幅值,fb 为呼吸的频率,Bh 为心跳幅值,fh 为心跳的频率,r(t)为其他颤抖引起的距离变化。
雷达发射波遇到障碍物时,产生回波TX 信号,回波信号为
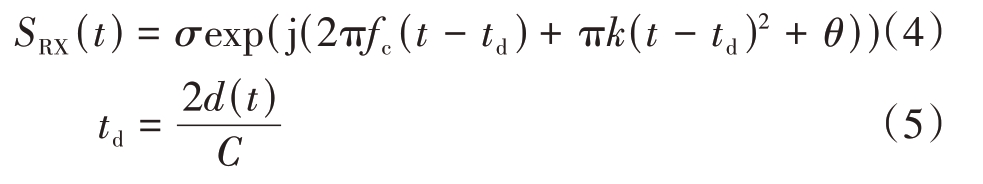
式中,C为光速,σ为幅度,td为回波时延。
两路信号经过混频器装置后得到IF 中频信号SIF(t),如图2所示。
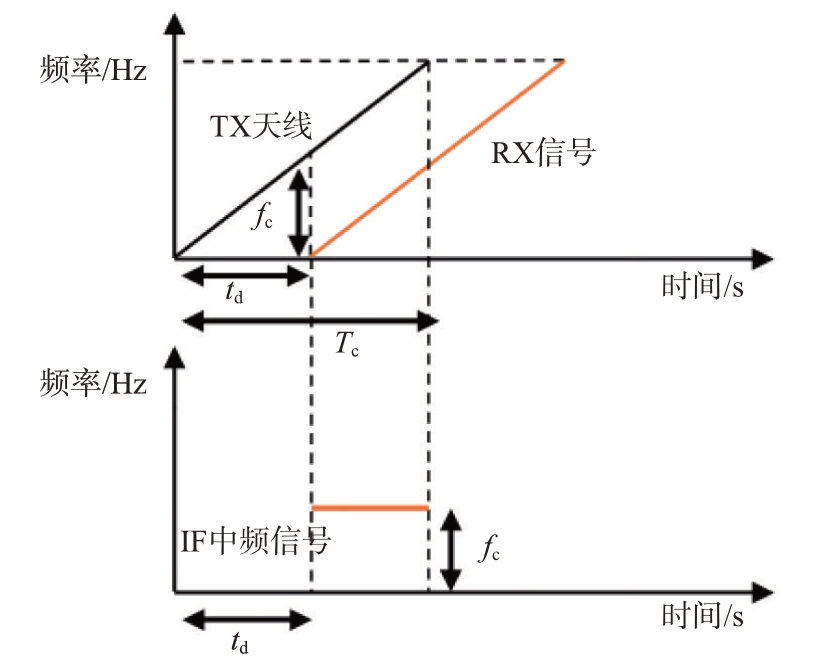
图2 RX、TX信号频域图和IF中频信号
式中,Tc 为锯齿波周期,fc=2kd/c 为中频信号频率,相位ϕ=4πd/λ。
由于呼吸和心跳使得胸腔的变化幅度很小,造成的频率变化也非常小,很难计算出胸腔的移动距离,但可根据中频信号的相位来计算得到胸腔的移动距离。
在进行实际实验时,雷达接收到的信号具有很大的不确定性,原始信号中包含很多杂波。因此需要对原始信号进行处理。首先将雷达信号通过距离门去除直达波,并进行移动平均的方法,去掉信号中的“毛刺”,减少误差,得到含有明显人体呼吸和心跳起伏的状态信号。雷达样本信号为图3,经过信号预处理之后为图4。
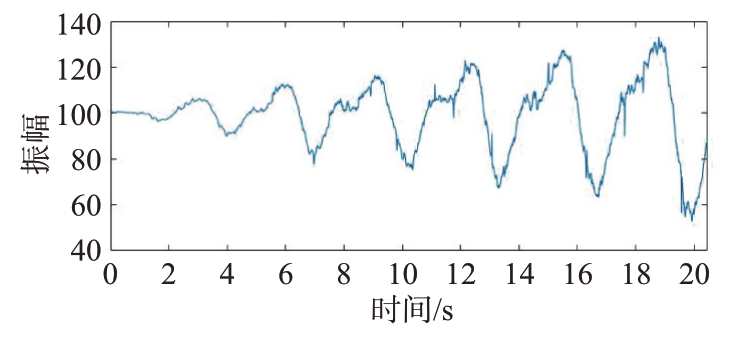
图3 生命信号
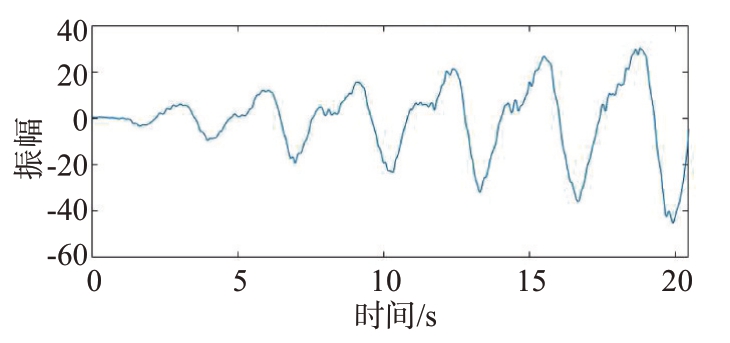
图4 预处理之后的信号
1.2 ICEEMDAN原理
CEEMD 是在EMD 和EEMD 的基础改进而来的,在待处理的信号中多次成对增加符号相反的白噪声信号,对每次EMD 后得到的结果进行总体平均计算,模态混叠问题得到较好的解决。ICEEMDAN 分解则进一步改进了CEEMDAN 在分解前期容易产生的虚假分量和模态混叠的缺点,大大减少了IMF 分量中的残余噪声,提高了计算效率和算法性能,明确了信号的物理意义。
设定x(n)为待分解的雷达信号,EMD 分解获得的第k 个IMF 表示为Ek(·),包络计算用M(·)表示,ICEEMDAN算法原理如下:
1)设定E1(x)=x-M(x),对于xi(n)=x(n)+β0E1(ω(i)),i=1,2,…,I,第一个残差信号的计算方法为r1(x)=<M(xi(n)) >,<·>表示均值计算。
2)设定IMF1=x-r1 是分解得到的第一个模态分量。
3)同理,再一次添加白噪声,利用均值计算得到第二个残差信号r2=<M(r1+β1E2(ω(i))>,得到第二个模态分量IMF2=r1-r2。
4)对于j=3,4…,计算第j个残差,rj=<M(rj-1+βj-1Ejω(i))>和第j个模态分量IMFj=rj-1-rj。
重复步骤4)获得所有残差数量和IMFs。
在EMD 分解过程中,信号的两端端点处不存在极大值点和极小值点共存的情况,因此分解时会产生端点效应,经过累积,严重时可能整个数据序列会丢失本来的实际意义。唯一的解决方法是在信号两端增加极小值点和极大值点,常用的处理方法有镜像法、神经网络预测法、多项式外延方法等。本文采用长数据序列截取的方法[11]。具体方法为:假定既定观测时间为t 的信号,选取数据信息时,在信号前后两端各增加Δt 的选取时间,即实际观测t+Δt 长的时间序列,然后对其进行模态分解,把去掉IMF分量两端各Δt时间的序列作为最终结果。截取的时间越长,解决端点效应的效果越好,左右两端各截取信号一半周期的数据长度,效果就会优于Rilling提出的改进算法。
1.3 模糊熵
在评判信号混乱程度时,通常采用熵值这一指标来衡量。有三种计算方法,分别为近似熵、样本熵和模糊熵。模糊熵不仅具有前二者的优点,还提高了在提取过程中熵值的连续性和原信号的独立程度,增加了信号的鲁棒性。本文的雷达信号特征分析采用模糊熵来提取。
1)定义N点采样序列为[u(1),u(2),…,u(N)]。
2)定义相似容限度r和相空间维数为m,重构相空间:X(i)=[u(i),u(i+1),…,u(i+m-1)-u0(i)],其中i=1,2,3,…,N-m+1,u0=![]()
3)通过引入模糊隶属函数计算两个矢量间的距离![]() 对于i=1,2,3,…,N-m+1。
对于i=1,2,3,…,N-m+1。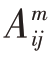 =exp[-ln(2) ·(
=exp[-ln(2) ·(![]() )2],j=1,2,3,…,N-m+1,并且j ≠i,其中
)2],j=1,2,3,…,N-m+1,并且j ≠i,其中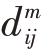 表示为
表示为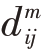 =max(|u(i+p-1)-u0(i)|-|u(j+p-1)-u0(j)|,p=1,2,…,m,dm ij表示X(i)和X(j)之间的最大距离。
=max(|u(i+p-1)-u0(i)|-|u(j+p-1)-u0(j)|,p=1,2,…,m,dm ij表示X(i)和X(j)之间的最大距离。
4)对于每个i,求其平均值,得到
5)定义![]()
6)故模糊熵为
当N为有限值时,得到模糊熵估计值:
上述函数中m取值为3,n取值为2,r取值为0.15。
1.4 相关系数计算
先将每个模态分量IMFX与原始雷达信号利用
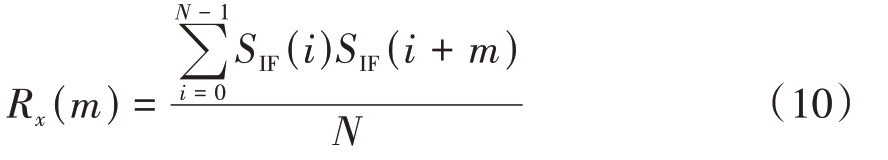
计算出(k+1)个自相关函数Rx,Rμ1,Rμ2,Rμ1…Rμk,然后将自相关函数归一化处理,分别求出Rx 与Rμ1,Rμ2,Rμ1…Rμk的相关系数,计算公式为
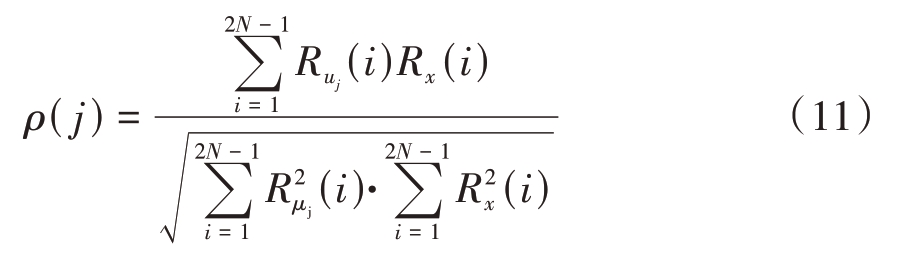
式中,N为信号的点数,μj为第j个模态。
相关系数筛选准则[12]:
如果相关系数的值大于ρ,则表明该模态分量与原始雷达信号的相似性大。
2 实验结果和分析
2.1 信号采集和预处理
本实验采用工作频率为57.1~63.9 GHz毫米波雷达芯片,在人体可接受的频率范围内。人体呼吸频率在[0.1~0.5 Hz]区间,心跳频率在[0.8~2 Hz]区间。本文设置的帧周期为10 ms,即慢时间采样率为100 Hz,满足奈奎斯特采样定理。一帧由多个锯齿波组成,本论文一帧设置为1个锯齿波。雷达的具体参数如表1所示。
表1 FMCW 雷达参数

数值6.8 GHz 57.1 GHz 55 μs 10 ms 2.5 MS/s 1参数带宽B起始频率fc锯齿波周期Tc帧周期Ts采样率一帧内发射锯齿波个数n
为了获得较好的实验效果,实验环境周围无异动,实验对象身体健康,无心脏和肺相关的疾病史,预先测量人体正常状态时的呼吸频率为0.294 Hz(17.6 次/分钟),心跳频率为1.61 Hz(96.6 次/分钟)。将实验对象的心脏位置与雷达放在相同高度处,人体保持正常状态,同时通过佩戴脉搏测量仪器来得到参考的心率值,形成对比试验。图5与图6为FMCW 雷达检测人体生命体征信息的实验环境与装置。

图5 实验测量

图6 实验设备
2.2 距离测量
对得到的每一个中频信号经过预处理后采样128 个点做距离维FFT 变换,并可以得到频率最大值,既定的慢时间观察窗口为20.48 s,如图7和图8所示。呼吸频率为0.293 Hz,周期约为3.41 s。半个周期约为1.7 s。故本论文实际观察窗口为24.48 s,如图9和图10所示。得到待测人员距离和慢时间轴的关系图如图11所示。黄颜色区域即为目标所处位置[13],处在22单元距离处,雷达距离分辨率为2.4 cm,即实验对象距离雷达为52.80 cm。
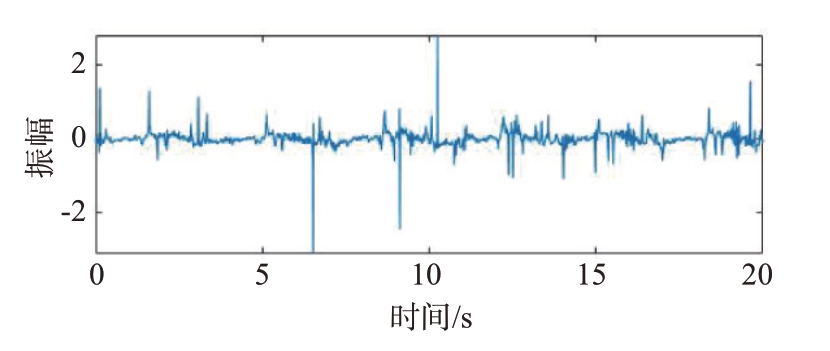
图7 20.48 s生命信号
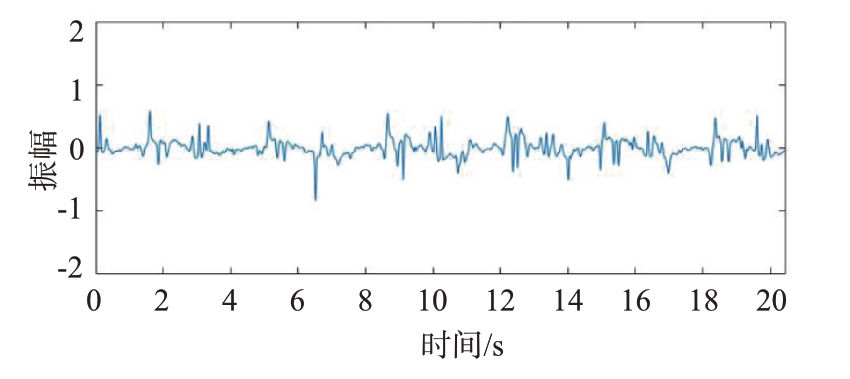
图8 预处理后的20.48 s生命信号
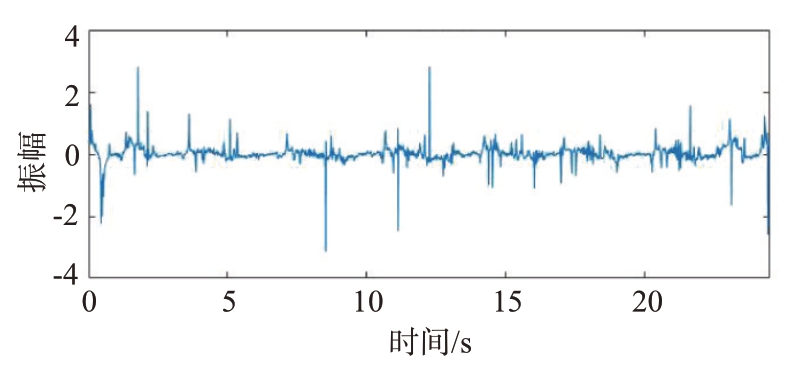
图9 24.48 s生命信号
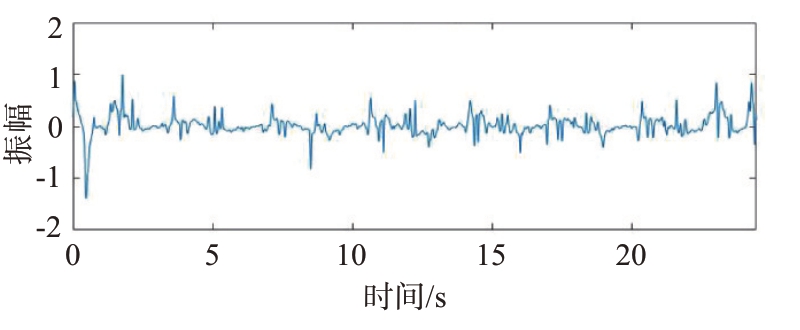
图10 预处理后的24.48 s生命信号
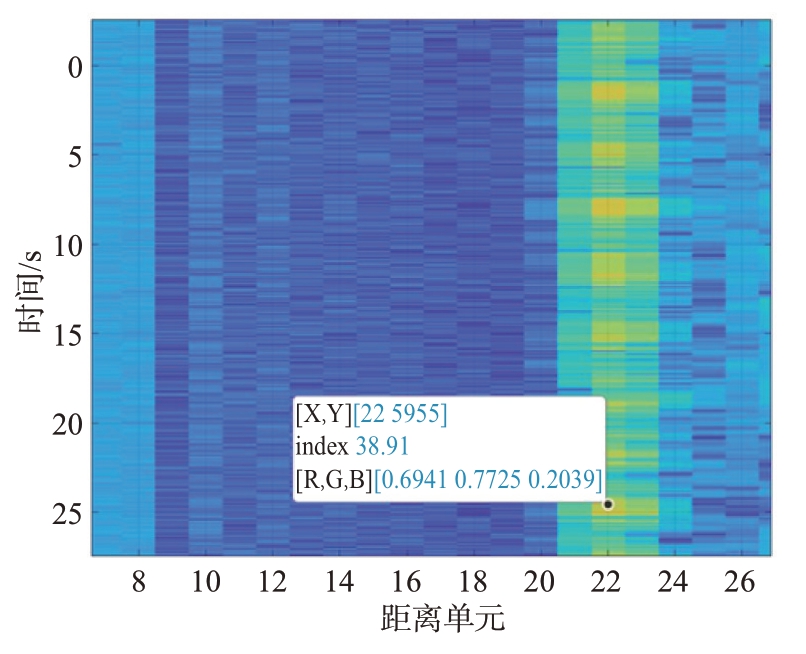
图11 距离和慢时间轴关系
2.3 方法验证
将得到的雷达信号,经过滤波处理后对其进行CEEMDAN、ICEEMDAN 分解,得到若干个IMF分量和一个残差信号。随着分解次数增多,IMF信号的频率在降低,即IMF所包含的特征时间尺度不同。把去掉IMF分量两端2 s的IMF作为最终结果。
为了验证算法ICEEMDAN 在降低模态分量噪声和减少虚假分量的效果,分别对信号进行24.48 s和20.48 s 的CEEMDAN 和ICEEMDAN 得到图12、图13、图14和图15的时域分解结果。
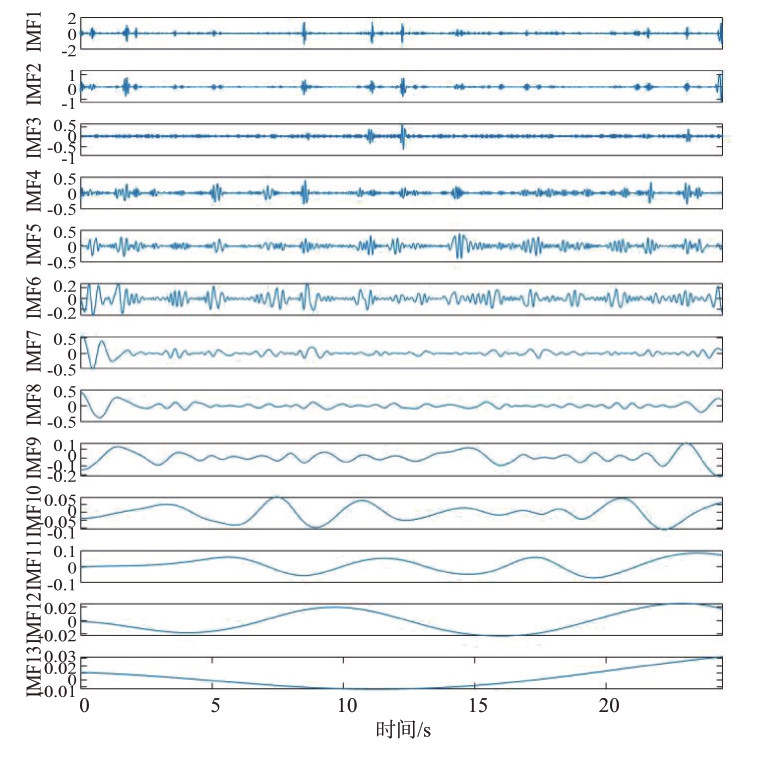
图12 24.48 s CEEMDAN分解
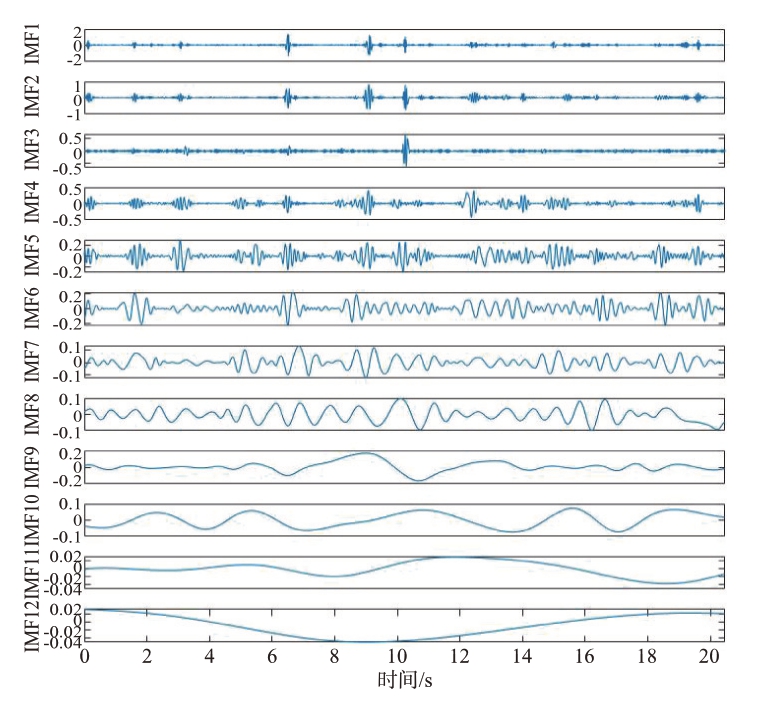
图13 20.48 s CEEMDAN分解
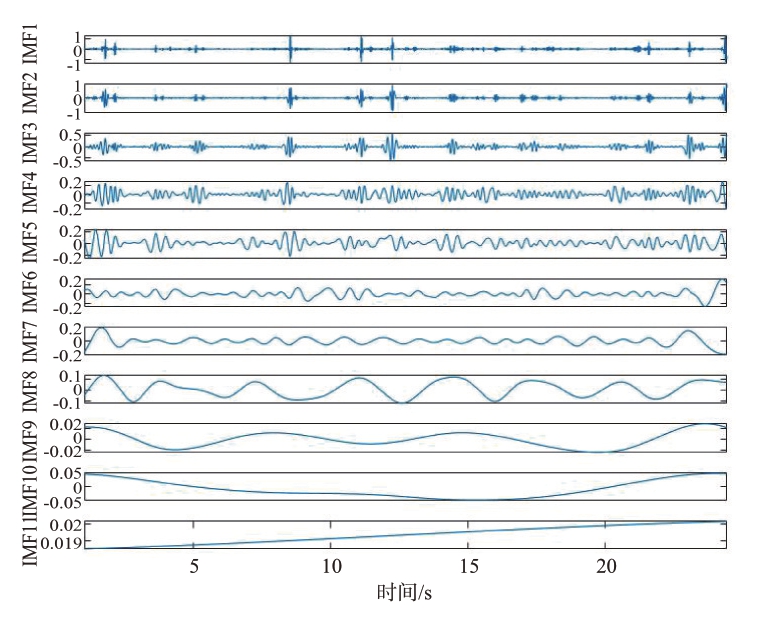
图14 24.48 s ICEEMDAN分解
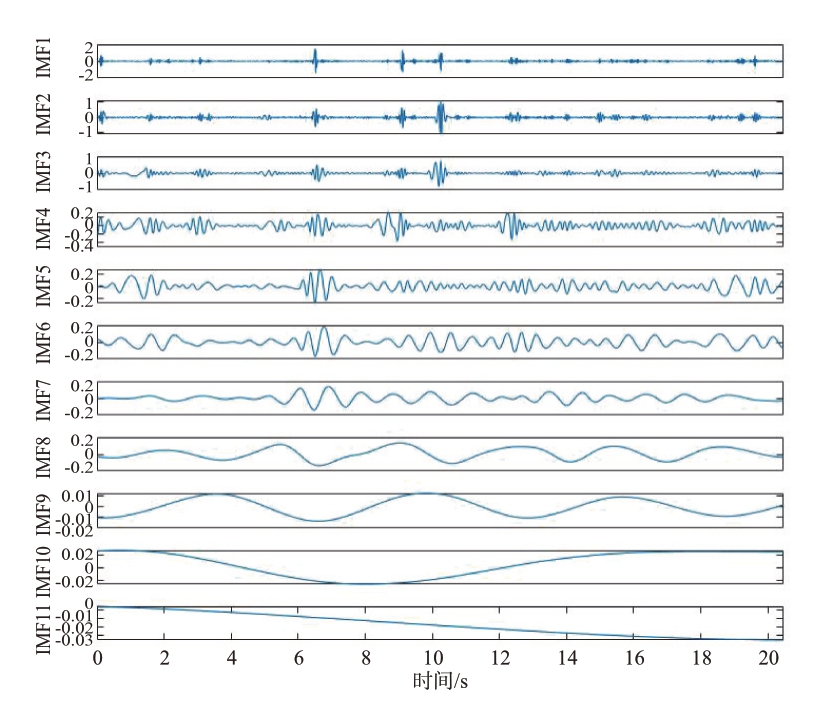
图15 20.48 s ICEEMDAN分解
分解时,会产生信号畸变,使分解前后的能量产生偏差。故可利用CEEMDAN、ICEEMDAN 分解前后的能量来评估模态分量中的残余噪声和虚假分量的现象。计算CEEMDAN、ICEEMDAN 分解得到的各IMF和原始信号的均方根的有效值:

式中,RMS 为信号有效值,n 为信号的采样点数,s(i)为信号序列。
评价指标β 为将原始信号有效值和各IMF 信号的有效值的总和作比较得出,见式(14)。

式中,RMS0 为原始信号的有效值,RMSi 为第i 个IMF模态分量的有效值,n为IMF的总数量。
表2为CEEMDAN、ICEEMDAN 分解原始雷达信号的参数和结果比较。
表2 CEEMDAN和ICEEMDAN分解参数
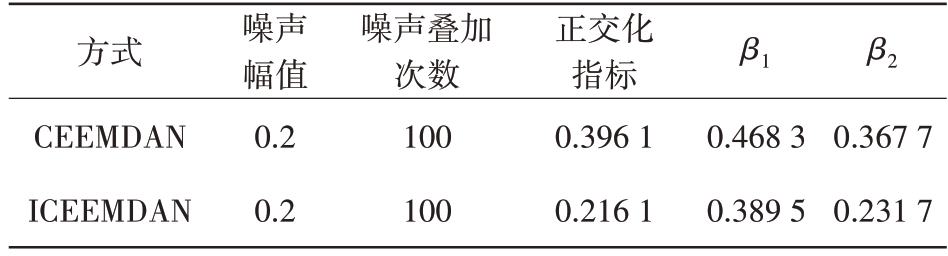
方式CEEMDAN ICEEMDAN噪声幅值0.2 0.2噪声叠加次数100 100正交化指标0.396 1 0.216 1 β1 β2 0.468 3 0.389 5 0.367 7 0.231 7
β1 为分别对20.48 s 的时间序列做CEEMDAN和ICEEMDAN 分解。β2为分别对24.48 s的时间序列分别做CEEMDAN+长数据序列截取和ICEEMDAN+长数据序列截取分解,由表2可知,ICEEMDAN比CEEMDAN算法降低了模态分量中的残余噪声和虚假分量。长数据序列截取的方法主要来解决端点效应,从而可以使得ICEEMDAN+长数据序列截取的方法能进一步提高模态分解的准确性和真实性。
2.4 计算模糊熵值
ICEEMDAN 分解雷达信号得到若干个从高频到低频分布的模态分量,频率越高的模态分量包含的噪声越多,为了进一步提高重构的呼吸和心跳信号的准确性,需要对分解之后的信号进行去噪处理。通过计算各个模态分量的模糊熵来量化含有噪音的模态分量信号,如表3所示。如果模态分量的模糊熵值大于1×10-3,就表明该IMF 含有较多噪声,需要进行去噪。
表3 模糊熵值
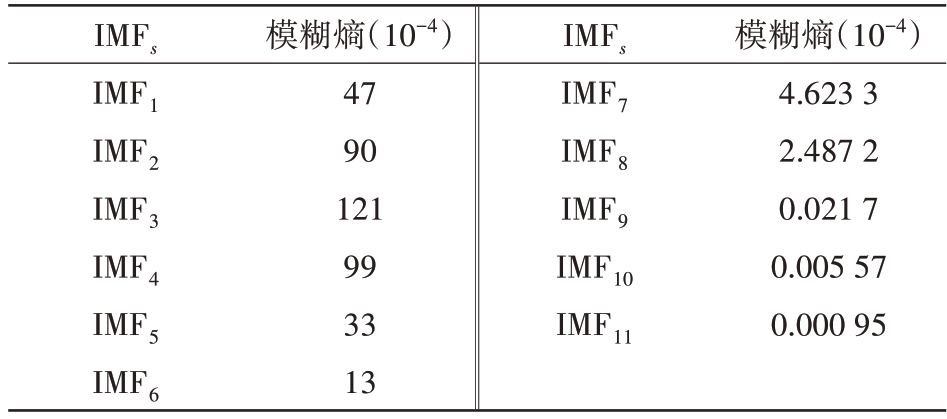
IMFs IMF1 IMF2 IMF3 IMF4 IMF5 IMF6模糊熵(10-4)47 90 121 99 33 13 IMFs IMF7 IMF8 IMF9 IMF10 IMF11模糊熵(10-4)4.623 3 2.487 2 0.021 7 0.005 57 0.000 95
将得到的前6个模态分量进行去噪处理,得到去噪后的信号及其频谱图,如图16和图17所示。符合心跳信号频率的IMF 分量是IMF6 和IMF7;符合呼吸信号频率的IMF 分量是IMF8、IMF9 和IMF10。
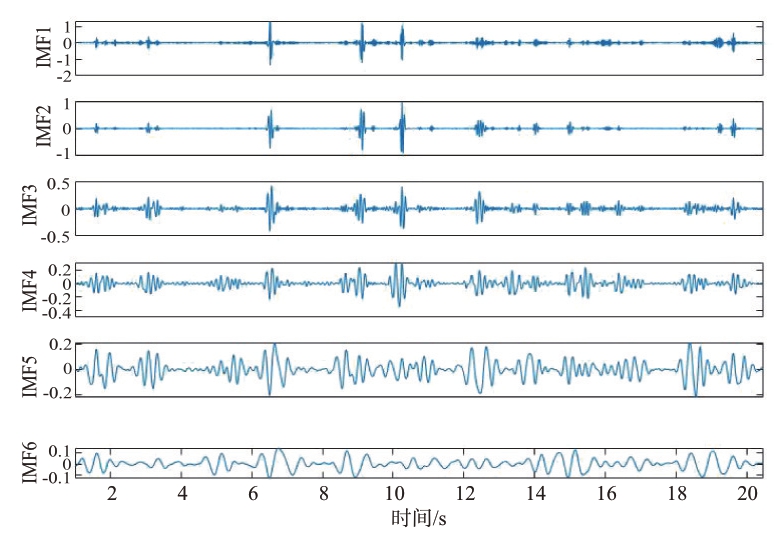
图16 去噪后的IMF信号
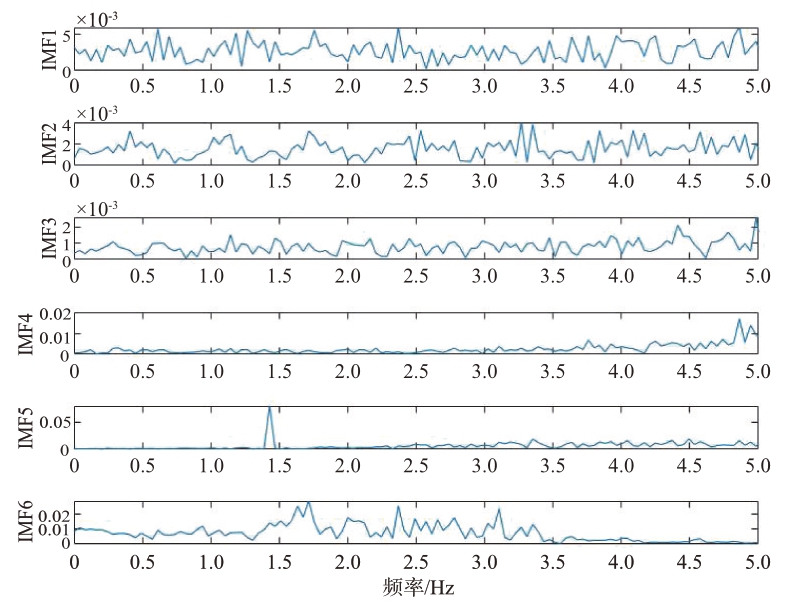
图17 去噪后的IMF频谱
2.5 生命信号提取
在心跳和呼吸频带范围内的信号能量记为Eh(j)和Eb(j),所有IMF 分量在频域的总能量,记为E(j)。心跳信号和呼吸信号在频域的能量相对总能量的比值记为ε,

实验发现,ε 取值太小,其他分量会被干扰提取效果,取值太大,反映生命信号的分量会被滤除。故ε 的取值关乎能否正确提取呼吸和心跳信号,并且计算IMF 分量与原始信号的相关性。得到相关性和能量阈值法如图18所示,相关性的阈值为0.25,能量阈值法的阈值为0.5。
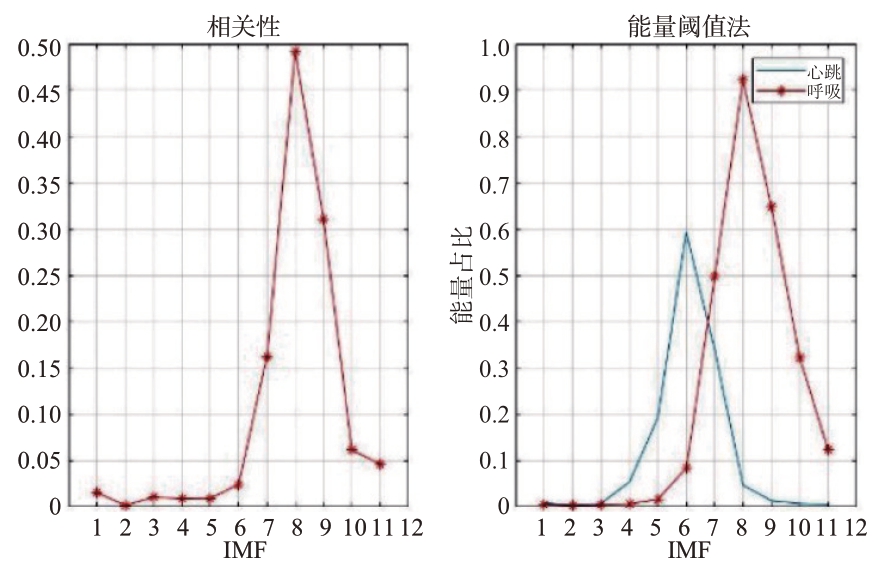
图18 相关性和能量阈值
相关性高的分量有IMF8 和IMF9,在呼吸频带范围内有IMF8、IMF9 分量的值大于阈值0.5,而在心跳频带范围内则是IMF6 分量。故经过综合分析,采用IMF6 和IMF7 重构心跳信号,IMF8 和IMF9 重构呼吸信号。提取重构的呼吸频率为0.293 Hz,心跳频率为1.66 Hz,与实际人体呼吸频率0.294 Hz(17.6 次/分钟),心跳频率为1.61 Hz(96.6 次/分钟)的结果在误差范围内。人体正常生命体征信号指标如表4所示。
表4 成人生命信号频率值

生命体征信号心跳呼吸频率0.8~2 Hz 0.1~0.5 Hz次数60~100次12~22次
图19和图21为采用CEEMDAN 的方法提取得到的心跳和呼吸信号及其频谱;图20和图22为采用ICEEMDAN+长数据序列截取的方法提取得到的心跳和呼吸信号及其频谱。分析可知虽然CEEMDAN 的方式能够提取出心跳和呼吸信号,但是本文提出的方法在此基础上能够明显抑制杂波信号的干扰,生命信号的谱峰更加集中,有效地解决了从含有噪声的雷达信号中,特别是不易从呼吸谐波和噪声中准确提取出心跳信号的问题。
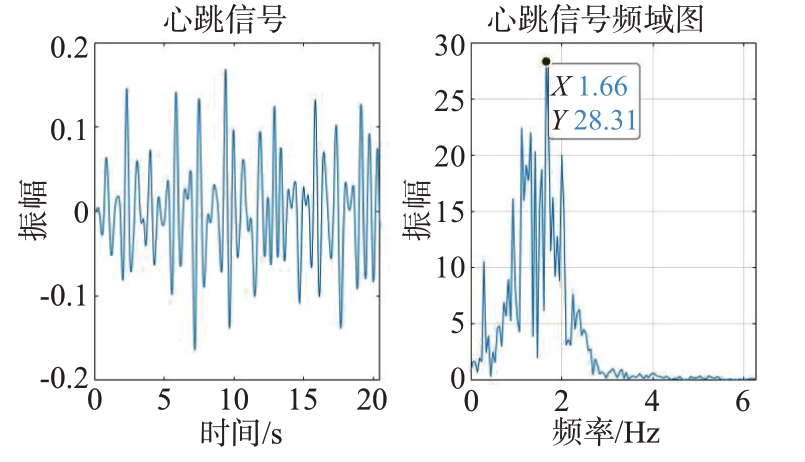
图19 CEEMDAN方法提取的心跳信号
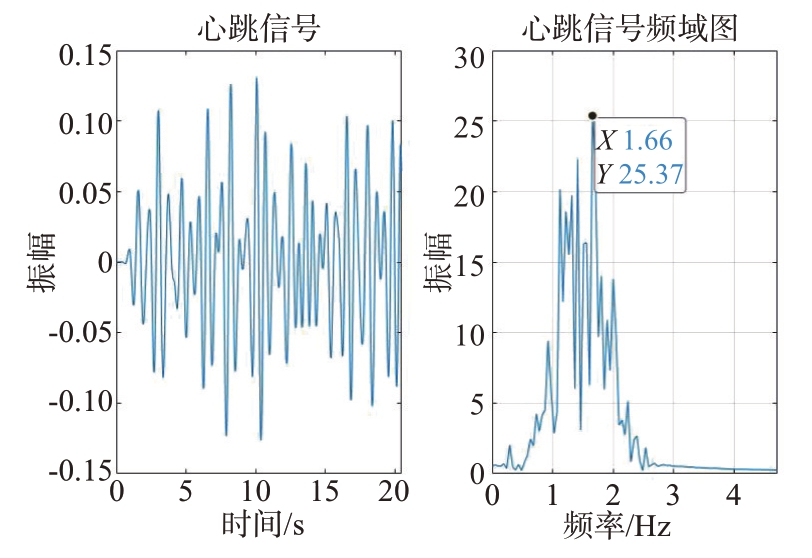
图20 ICEEMDAN方法提取的心跳信号
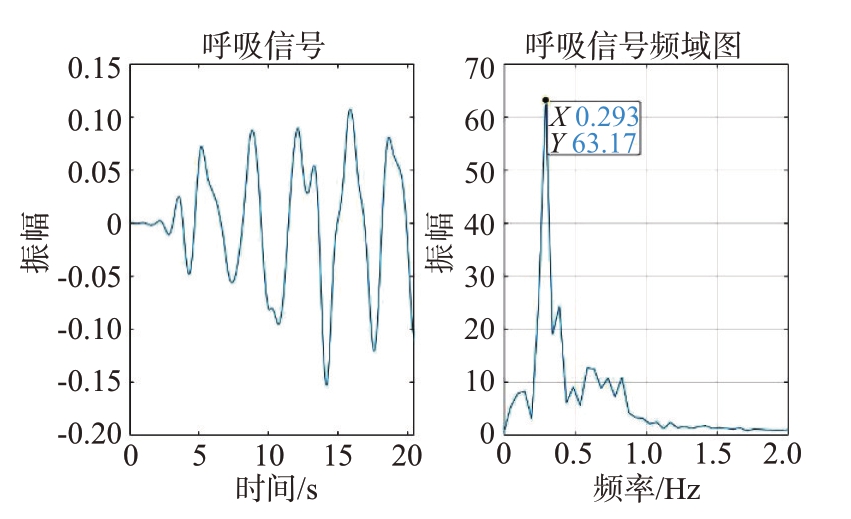
图21 CEEMDAN方法提取的呼吸信号
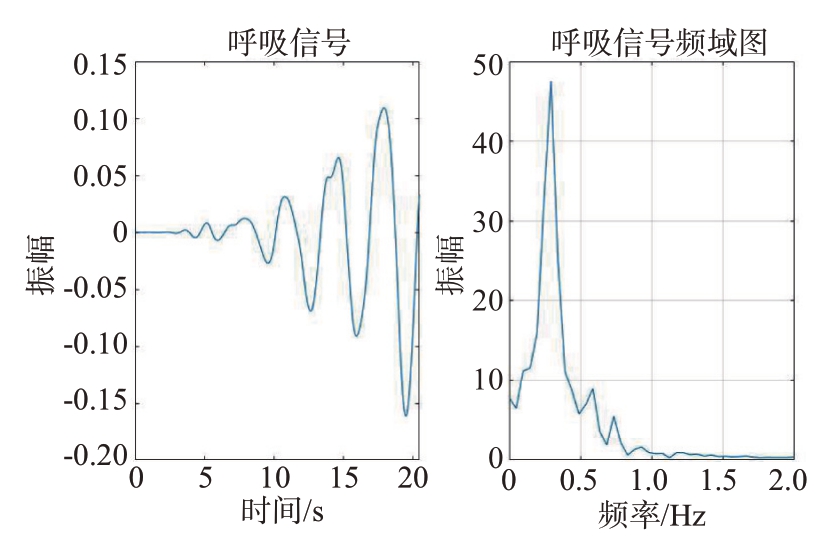
图22 ICEEMDAN方法提取的呼吸信号
对上述两种分解方式得到的信号,进行信噪比分析。信噪比定义如式(17):
式中,∑s2(f)为信号频谱的总能量,s2(l)为生命信号的频谱峰值。
如表5所示,方法1 为CEEMDAN 分解;方法2为ICEEMDAN+长数据序列截取方式。从表5可知,呼吸信号的信噪比提高1.53 dB,提升29%。心跳信号的信噪比平均提高1.33 dB,心跳信号提升11%。
表5 信噪比的结果

方法12呼吸频率0.293 0.293 SNR/dB-5.26-3.73心跳频率1.66 1.66 SNR/dB-11.98-10.65
3 结束语
为了能够更加准确地提取呼吸和心跳信号,本文提出了一种基于ICEEMDAN 和长数据序列截取的雷达生命信息提取算法,将经过预处理的雷达信号进行ICEEMDAN 分解,把去掉IMF 分量两端各2 s的时间序列作为最终分解结果。并将含噪的IMF信号进行去噪处理,根据各个IMF信号的相关性和能量阈值来重构呼吸和心跳信号,通过这种算法,提高了生命信号的鲁棒性,能从雷达信号中准确提取呼吸和心跳信号,有效解决了杂波干扰和噪音的问题,提高了提取信号的真实性和准确性。通过仿真设计验证了所提方案的有效性和可行性,具有较好的去噪性能,可应用于医疗和养老机构的健康检测。在未来工作中,在提高雷达提取生命信息的准确性的基础上能够实现对多人同时进行准确检测。
[1]吴志军,韦金宜,黄李波,等.基于调频连续波雷达的多目标生命体征实时检测[J].传感器与微系统,2021,40(3):112-115.
[2]段宗明,刘明,吴博文,等.应用于智能驾驶的77GHz毫米波汽车雷达收发机芯片[J].雷达科学与技术,2021,19(2):130-136.
[3]赖佳磊,阳召成,鲍润晗,等.一种基于超宽带雷达的日常活动分类方法[J].雷达科学与技术,2021,19(3):265-270.
[4]HUANG N E,SHEN Z ,LONG S R ,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J].Proceedings Mathematical Physical & Engineering Sciences,1998,454(1971):903-995.
[5]汤宝平,董绍江,马靖华.基于独立分量分析的EMD 模态混叠消除方法研究[J].仪器仪表学报,2012,33(7):1477-1482.
[6]WU Z,HUANG N E.Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[7]TORRES M E,COLOMINAS M A,SCHLOTTHAUER G,et al.A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise[C]// IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP),Prague,Czech Republic: IEEE,2011: 4144-4147.
[8]翟永杰,杨旭.基于ICEEMDAN-ICA 的焊缝信号去噪算法[J].热加工工艺,2022,51(1):96-102.
[9]金家伟,阮怀林,孙兵.基于改进CEEMDAN 的微多普勒特征提取[J].探测与控制学报,2021,43(5):86-91.
[10]张崇超,张长春,张群英.EEMD 在超宽带雷达生命信号提取中的应用[J].电子测量技术,2012,35(4):76-80.
[11]宁静,诸昌钤,高品贤,等.EMD 分解中端点数据的延长方法问题研究[J].计算机工程与应用,2011,47(3):125-128.
[12]李宏,李定文,朱海琦,等.一种优化的VMD 算法及其在语音信号去噪中的应用[J].吉林大学学报(理学版),2021,59(5):1219-1227.
[13]罗朗娟,张洽.非接触式人体生命信号检测方法研究[J].医疗卫生装备,2021,42(11):8-13.
